Enhanced Fluid Mixing in Microchannels Using Levitated Magnetic Microrobots: A Numerical Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microchannel Design
2.2. Magnetic Field
2.3. Fluid Flow
2.4. Transport of Diluted Species
3. Numerical Analysis
3.1. Magnetic Field and Propeller Velocity
3.2. Levitation Height and Propeller Orientation
4. Results and Discussion
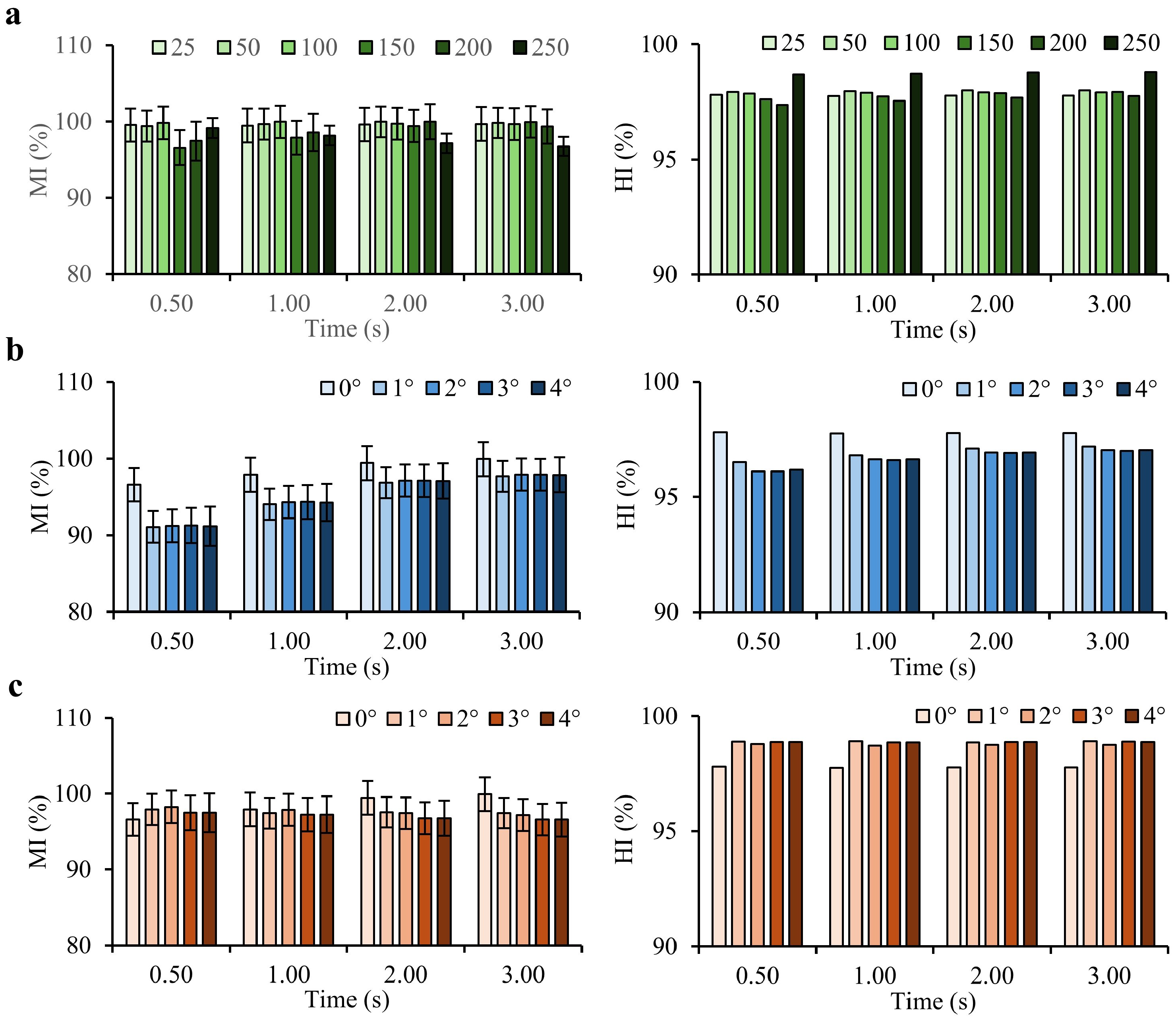
4.1. MI and HI Importance
4.2. Levitation Height Effect
4.3. Theta () and Phi () Effect
4.4. Propeller Speed and Inlet Flow Rate
4.5. Robot Length Effect
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Jeong, G.S.; Chung, S.; Kim, C.B.; Lee, S.H. Applications of micromixing technology. Analyst 2010, 135, 460–473. [Google Scholar] [CrossRef] [PubMed]
- Demircali, A.A.; Uvet, H. Stabilization of microrobot motion characteristics in liquid media. Micromachines 2018, 9, 363. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, Y.; Tang, H.; Zong, N.; Jiang, X. Microfluidics for biomedical analysis. Small Methods 2020, 4, 1900451. [Google Scholar] [CrossRef]
- Nette, J.; Howes, P.D.; deMello, A.J. Microfluidic synthesis of luminescent and plasmonic nanoparticles: Fast, efficient, and data-rich. Adv. Mater. Technol. 2020, 5, 2000060. [Google Scholar] [CrossRef]
- Srivastava, K.; Boyle, N.; Flaman, G.; Ramaswami, B.; van den Berg, A.; van der Stam, W.; Burgess, I.; Odijk, M. In situ spatiotemporal characterization and analysis of chemical reactions using an ATR-integrated microfluidic reactor. Lab Chip 2023, 23, 4690–4700. [Google Scholar] [CrossRef] [PubMed]
- Moghimi, M.; Jalali, N. Design and fabrication of an effective micromixer through passive method. J. Comput. Appl. Res. Mech. Eng. (JCARME) 2020, 9, 371–383. [Google Scholar]
- Zhang, S.; Chen, X.; Wu, Z.; Zheng, Y. Numerical study on stagger Koch fractal baffles micromixer. Int. J. Heat Mass Transf. 2019, 133, 1065–1073. [Google Scholar] [CrossRef]
- Mondal, B.; Mehta, S.K.; Patowari, P.K.; Pati, S. Numerical study of mixing in wavy micromixers: Comparison between raccoon and serpentine mixer. Chem. Eng. Process.-Process Intensif. 2019, 136, 44–61. [Google Scholar] [CrossRef]
- Clark, J.; Kaufman, M.; Fodor, P.S. Mixing enhancement in serpentine micromixers with a non-rectangular cross-section. Micromachines 2018, 9, 107. [Google Scholar] [CrossRef]
- Chen, X.; Li, T. A novel passive micromixer designed by applying an optimization algorithm to the zigzag microchannel. Chem. Eng. J. 2017, 313, 1406–1414. [Google Scholar] [CrossRef]
- Taheri, R.A.; Goodarzi, V.; Allahverdi, A. Mixing performance of a cost-effective split-and-recombine 3D micromixer fabricated by xurographic method. Micromachines 2019, 10, 786. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.T.; Huang, X. Mixing in microchannels based on hydrodynamic focusing and time-interleaved segmentation: Modelling and experiment. Lab Chip 2005, 5, 1320–1326. [Google Scholar] [CrossRef] [PubMed]
- Arockiam, S.; Cheng, Y.H.; Armenante, P.M.; Basuray, S. Experimental determination and computational prediction of the mixing efficiency of a simple, continuous, serpentine-channel microdevice. Chem. Eng. Res. Des. 2021, 167, 303–317. [Google Scholar] [CrossRef]
- Tokas, S.; Zunaid, M.; Ansari, M.A. Non–Newtonian fluid mixing in a Three-Dimensional spiral passive micromixer. Mater. Today Proc. 2021, 47, 3947–3952. [Google Scholar] [CrossRef]
- Rampalli, S.; Dundi, T.M.; Chandrasekhar, S.; Raju, V.; Chandramohan, V. Numerical evaluation of liquid mixing in a serpentine square convergent-divergent passive micromixer. Chem. Prod. Process Model. 2020, 15, 20190071. [Google Scholar] [CrossRef]
- Aubin, J.; Ferrando, M.; Jiricny, V. Current methods for characterising mixing and flow in microchannels. Chem. Eng. Sci. 2010, 65, 2065–2093. [Google Scholar] [CrossRef]
- Hessel, V.; Löwe, H.; Schönfeld, F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005, 60, 2479–2501. [Google Scholar] [CrossRef]
- Antognoli, M.; Stoecklein, D.; Galletti, C.; Brunazzi, E.; Di Carlo, D. Optimized design of obstacle sequences for microfluidic mixing in an inertial regime. Lab Chip 2021, 21, 3910–3923. [Google Scholar] [CrossRef]
- Cunegatto, E.H.T.; Zinani, F.S.F.; Biserni, C.; Rocha, L.A.O. Constructal design of passive micromixers with multiple obstacles via computational fluid dynamics. Int. J. Heat Mass Transf. 2023, 215, 124519. [Google Scholar] [CrossRef]
- Chen, L.; Wang, G.; Lim, C.; Seong, G.H.; Choo, J.; Lee, E.K.; Kang, S.H.; Song, J.M. Evaluation of passive mixing behaviors in a pillar obstruction poly (dimethylsiloxane) microfluidic mixer using fluorescence microscopy. Microfluid. Nanofluid. 2009, 7, 267–273. [Google Scholar] [CrossRef]
- Shi, X.; Huang, S.; Wang, L.; Li, F. Numerical analysis of passive micromixer with novel obstacle design. J. Dispers. Sci. Technol. 2021, 42, 440–456. [Google Scholar] [CrossRef]
- Mondal, B.; Mehta, S.K.; Pati, S.; Patowari, P.K. Numerical analysis of electroosmotic mixing in a heterogeneous charged micromixer with obstacles. Chem. Eng. Process.-Process Intensif. 2021, 168, 108585. [Google Scholar] [CrossRef]
- Husain, A.; Al-Rawahi, N.; Al-Azri, N.; Zunaid, M.; Ansari, M.Z. Mixing performance enhancement and parametric investigation of swirl-inlets split-and-recombine micromixer with pulsatile flow. Mater. Today Proc. 2021, 56, 609–616. [Google Scholar] [CrossRef]
- Ahmed, D.; Mao, X.; Shi, J.; Juluri, B.K.; Huang, T.J. A millisecond micromixer via single-bubble-based acoustic streaming. Lab Chip 2009, 9, 2738–2741. [Google Scholar] [CrossRef]
- Liu, R.H.; Yang, J.; Pindera, M.Z.; Athavale, M.; Grodzinski, P. Bubble-induced acoustic micromixing. Lab Chip 2002, 2, 151–157. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, H.; Zhao, X.; Ma, X.; Huang, L.; Qiu, Y.; Wei, J.; Hao, N. Acoustofluidic bubble-driven micromixers for the rational engineering of multifunctional ZnO nanoarray. Chem. Eng. J. 2022, 450, 138273. [Google Scholar] [CrossRef]
- Wiklund, M.; Green, R.; Ohlin, M. Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices. Lab Chip 2012, 12, 2438–2451. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, A.; Karavelioglu, Z.; Aydemir, G.; Demircali, A.A.; Varol, R.; Kosar, A.; Uvet, H. Microfluidic wound scratching platform based on an untethered microrobot with magnetic actuation. Sens. Actuators B Chem. 2022, 373, 132643. [Google Scholar] [CrossRef]
- Bayareh, M.; Usefian, A.; Ahmadi Nadooshan, A. Rapid mixing of Newtonian and non-Newtonian fluids in a three-dimensional micro-mixer using non-uniform magnetic field. J. Heat Mass Transf. Res. 2019, 6, 55–61. [Google Scholar]
- Chang, M.; Gabayno, J.L.F.; Ye, R.; Huang, K.W.; Chang, Y.J. Mixing efficiency enhancing in micromixer by controlled magnetic stirring of Fe3O4 nanomaterial. Microsyst. Technol. 2017, 23, 457–463. [Google Scholar] [CrossRef]
- Ballard, M.; Owen, D.; Mills, Z. Orbiting magnetic microbeads enable rapid microfluidic mixing. Microfluid. Nanofluid. 2016, 20, 88. [Google Scholar] [CrossRef]
- Nouri, D.; Hesari, A.; Passandideh-Fard, M. Rapid mixing in micromixers using magnetic field. Sens. Actuators A Phys. 2017, 255, 79–86. [Google Scholar] [CrossRef]
- Hejazian, M.; Nguyen, N. A rapid Magnetofluidic micromixer using diluted Ferrofluid. Micromachines 2017, 8, 37. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Alici, G. An inverted micro-mixer based on a magnetically-actuated cilium made of Fe doped PDMS. Smart Mater. Struct. 2016, 25, 095049. [Google Scholar] [CrossRef]
- Saroj, S.; Asfer, M.; Sunderka, A. Two-fluid mixing inside a sessile micro droplet using magnetic beads actuation. Sens. Actuators A Phys. 2016, 244, 112–120. [Google Scholar] [CrossRef]
- Boroun, S.; Larachi, F. Enhancing liquid micromixing using low-frequency rotating nanoparticles. AIChE J. 2017, 63, 337–346. [Google Scholar] [CrossRef]
- Shanko, E.S.; Ceelen, L.; Wang, Y.; van de Burgt, Y.; den Toonder, J. Enhanced microfluidic sample homogeneity and improved antibody-based assay kinetics due to magnetic mixing. ACS Sens. 2021, 6, 2553–2562. [Google Scholar] [CrossRef] [PubMed]
- Bahrami, D.; Nadooshan, A.A.; Bayareh, M. Effect of non-uniform magnetic field on mixing index of a sinusoidal micromixer. Korean J. Chem. Eng. 2022, 39, 316–327. [Google Scholar] [CrossRef]
- Saadat, M.; Ghassemi, M.; Shafii, M.B. Numerical investigation on the effect of external varying magnetic field on the mixing of ferrofluid with deionized water inside a microchannel for lab-on-chip systems. Energy Sources Part A Recover. Util. Environ. Eff. 2024, 46, 5000–5012. [Google Scholar] [CrossRef]
- Kumar, C.; Hejazian, M.; From, C.; Saha, S.C.; Sauret, E.; Gu, Y.; Nguyen, N.T. Modeling of mass transfer enhancement in a magnetofluidic micromixer. Phys. Fluids 2019, 31, 063603. [Google Scholar] [CrossRef]
- Usefian, A.; Bayareh, M.; Shateri, A.; Taheri, N. Numerical study of electro-osmotic micro-mixing of Newtonian and non-Newtonian fluids. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 238. [Google Scholar] [CrossRef]
- Zaher, A.; Ali, K.K.; Mekheimer, K.S. Electroosmosis forces EOF driven boundary layer flow for a non-Newtonian fluid with planktonic microorganism: Darcy Forchheimer model. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2534–2559. [Google Scholar] [CrossRef]
- Song, L.; Yu, L.; Li, D.; Jagdale, P.P.; Xuan, X. Elastic instabilities in the electroosmotic flow of non-Newtonian fluids through T-shaped microchannels. Electrophoresis 2020, 41, 588–597. [Google Scholar] [CrossRef] [PubMed]
- Usefian, A.; Bayareh, M. Numerical and experimental study on mixing performance of a novel electro-osmotic micro-mixer. Meccanica 2019, 54, 1149–1162. [Google Scholar] [CrossRef]
- Lu, L.H.; Ryu, K.S.; Liu, C. A magnetic microstirrer and array for microfluidic mixing. J. Microelectromech. Syst. 2002, 11, 462–469. [Google Scholar]
- Fu, L.; Tsai, C.; Leong, K.; Wen, C. Rapid micromixer via ferrofluids. Phys. Procedia 2010, 9, 270–273. [Google Scholar] [CrossRef]
- Yang, R.J.; Hou, H.H.; Wang, Y.N.; Fu, L.M. Micro-magnetofluidics in microfluidic systems: A review. Sens. Actuators B Chem. 2016, 224, 1–15. [Google Scholar] [CrossRef]
- Owen, D.; Ballard, M.; Alexeev, A.; Hesketh, P.J. Rapid microfluidic mixing via rotating magnetic microbeads. Sens. Actuators A Phys. 2016, 251, 84–91. [Google Scholar] [CrossRef]
- Buglie, W.; Tamrin, K. Enhanced mixing in dual-mode cylindrical magneto-hydrodynamic (MHD) micromixer. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 2491–2501. [Google Scholar] [CrossRef]
- Broeren, S.; Pereira, I.F.; Wang, T.; den Toonder, J.; Wang, Y. On-demand microfluidic mixing by actuating integrated magnetic microwalls. Lab Chip 2023, 23, 1524–1530. [Google Scholar] [CrossRef]
- Naghash, T.H.; Haghgoo, A.M.; Bijarchi, M.A.; Ghassemi, M.; Shafii, M.B. Performance of microball micromixers using a programmable magnetic system by applying novel movement patterns. Sens. Actuators B Chem. 2024, 406, 135403. [Google Scholar] [CrossRef]
- Demircali, A.; Varol, R.; Aydemir, G.; Saruhan, E.N.; Erkan, K.; Uvet, H. Longitudinal Motion Modeling and Experimental Verification of a Microrobot Subject to Liquid Laminar Flow. IEEE/ASME Trans. Mechatronics 2021, 26, 2956–2966. [Google Scholar] [CrossRef]
- Demircali, A.A.; Varol, R.; Erkan, K.; Uvet, H. Untethered Microrobot Motion Mechanism With Increased Longitudinal Force. J. Mech. Robot. 2021, 13, 061005. [Google Scholar] [CrossRef]
- Hama, B.; Mahajan, G.; Fodor, P.S.; Kaufman, M.; Kothapalli, C.R. Evolution of mixing in a microfluidic reverse-staggered herringbone micromixer. Microfluid. Nanofluid. 2018, 22, 54. [Google Scholar] [CrossRef]
- Tsai, R.T.; Wu, C.Y. An efficient micromixer based on multidirectional vortices due to baffles and channel curvature. Biomicrofluidics 2011, 5, 014103. [Google Scholar] [CrossRef]
- Demircali, A.; Erkan, K.; Uvet, H. A study on finding optimum parameters of a diamagnetically driven untethered microrobot. J. Magn. 2017, 22, 539–549. [Google Scholar] [CrossRef]
- COMSOL Multiphysics®, v. 6.0.; COMSOL AB: Stockholm, Sweden, 2020. Available online: www.comsol.com (accessed on 1 June 2024).
- Uvet, H.; Demircali, A.A.; Kahraman, Y.; Varol, R.; Kose, T.; Erkan, K. Micro-UFO (untethered floating object): A highly accurate microrobot manipulation technique. Micromachines 2018, 9, 126. [Google Scholar] [CrossRef]
- Fox, R.W.; McDonald, A.T.; Mitchell, J.W. Fox and McDonald’s Introduction to Fluid Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Wu, M.; Gao, Y.; Ghaznavi, A.; Zhao, W.; Xu, J. AC electroosmosis micromixing on a lab-on-a-foil electric microfluidic device. Sens. Actuators B Chem. 2022, 359, 131611. [Google Scholar] [CrossRef]
- Bahrami, D.; Bayareh, M. Experimental and numerical investigation of a novel spiral micromixer with sinusoidal channel walls. Chem. Eng. Technol. 2022, 45, 100–109. [Google Scholar] [CrossRef]
- Misra, I.; Kumaran, V. Microfluidic mixing by magnetic particles: Progress and prospects. Biomicrofluidics 2024, 18, 041501. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, P.; Dasgupta, D. Enhancing micromixing using external electric and magnetic fields. Phys. Fluids 2024, 36, 082013. [Google Scholar] [CrossRef]
- Bazaz, S.R.; Sayyah, A.; Hazeri, A.H.; Salomon, R.; Mehrizi, A.A.; Warkiani, M.E. Micromixer research trend of active and passive designs. Chem. Eng. Sci. 2024, 293, 120028. [Google Scholar] [CrossRef]
- Shiriny, A.; Bayareh, M. Inertial focusing of CTCs in a novel spiral microchannel. Chem. Eng. Sci. 2021, 229, 116102. [Google Scholar] [CrossRef]
- Rafeie, M.; Welleweerd, M.; Hassanzadeh-Barforoushi, A.; Asadnia, M.; Olthuis, W.; Ebrahimi Warkiani, M. An easily fabricated three-dimensional threaded lemniscate-shaped micromixer for a wide range of flow rates. Biomicrofluidics 2017, 11, 014108. [Google Scholar] [CrossRef] [PubMed]
- Cosentino, A.; Madadi, H.; Vergara, P.; Vecchione, R.; Causa, F.; Netti, P.A. An efficient planar accordion-shaped micromixer: From biochemical mixing to biological application. Sci. Rep. 2015, 5, 17876. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, E.; Patowari, P.K.; Pati, S. Comparative assessment of mixing characteristics and pressure drop in spiral and serpentine micromixers. Chem. Eng. Process.-Process Intensif. 2021, 162, 108335. [Google Scholar] [CrossRef]
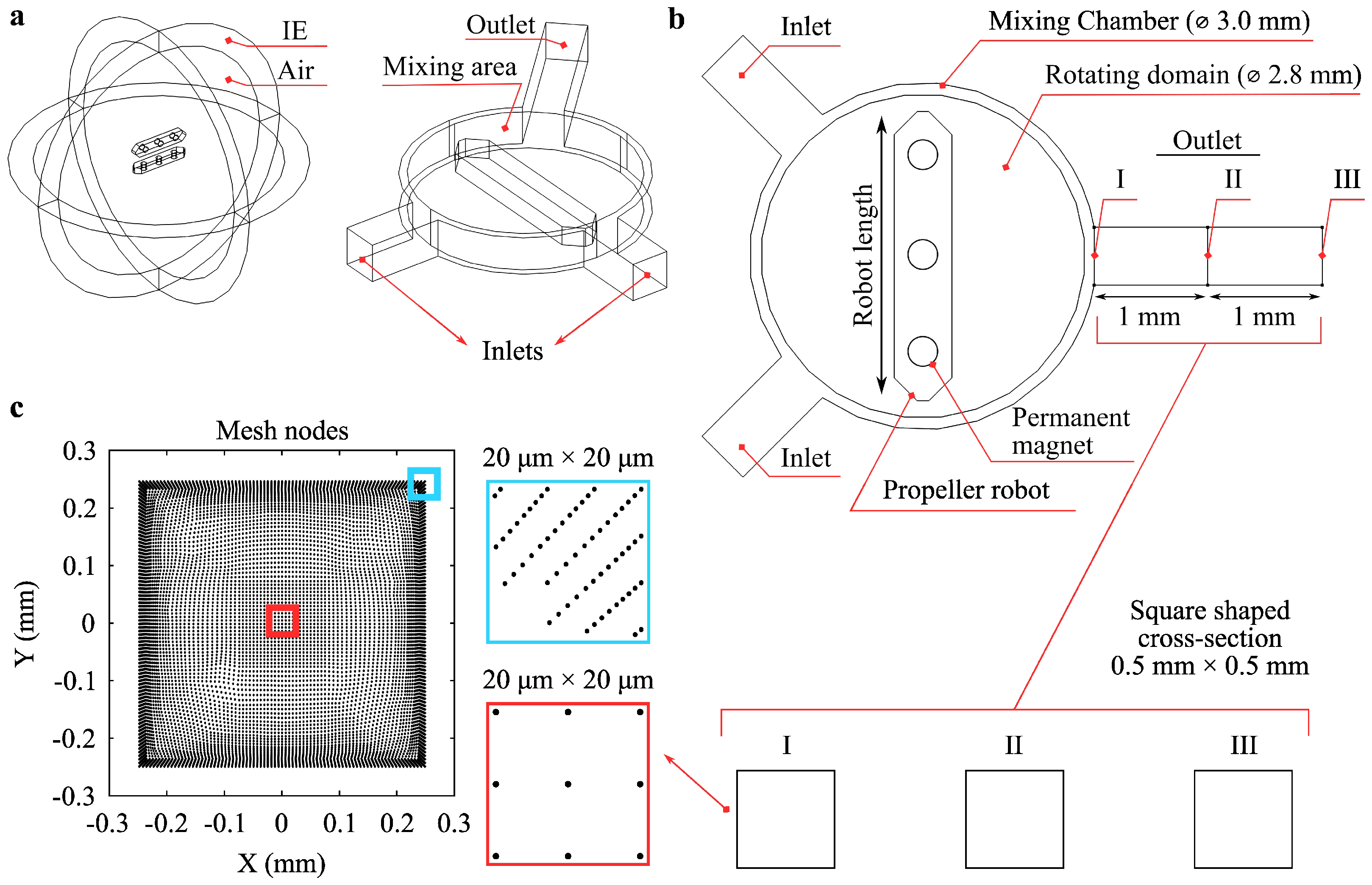
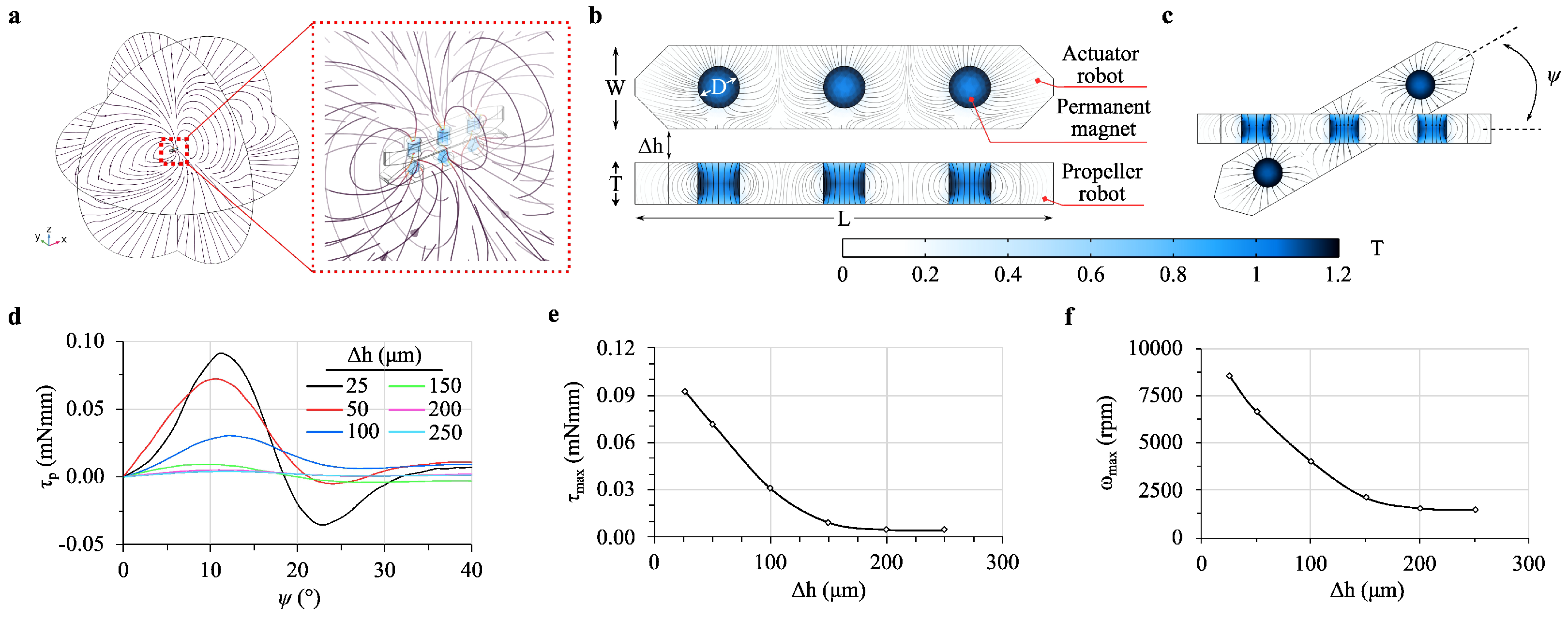

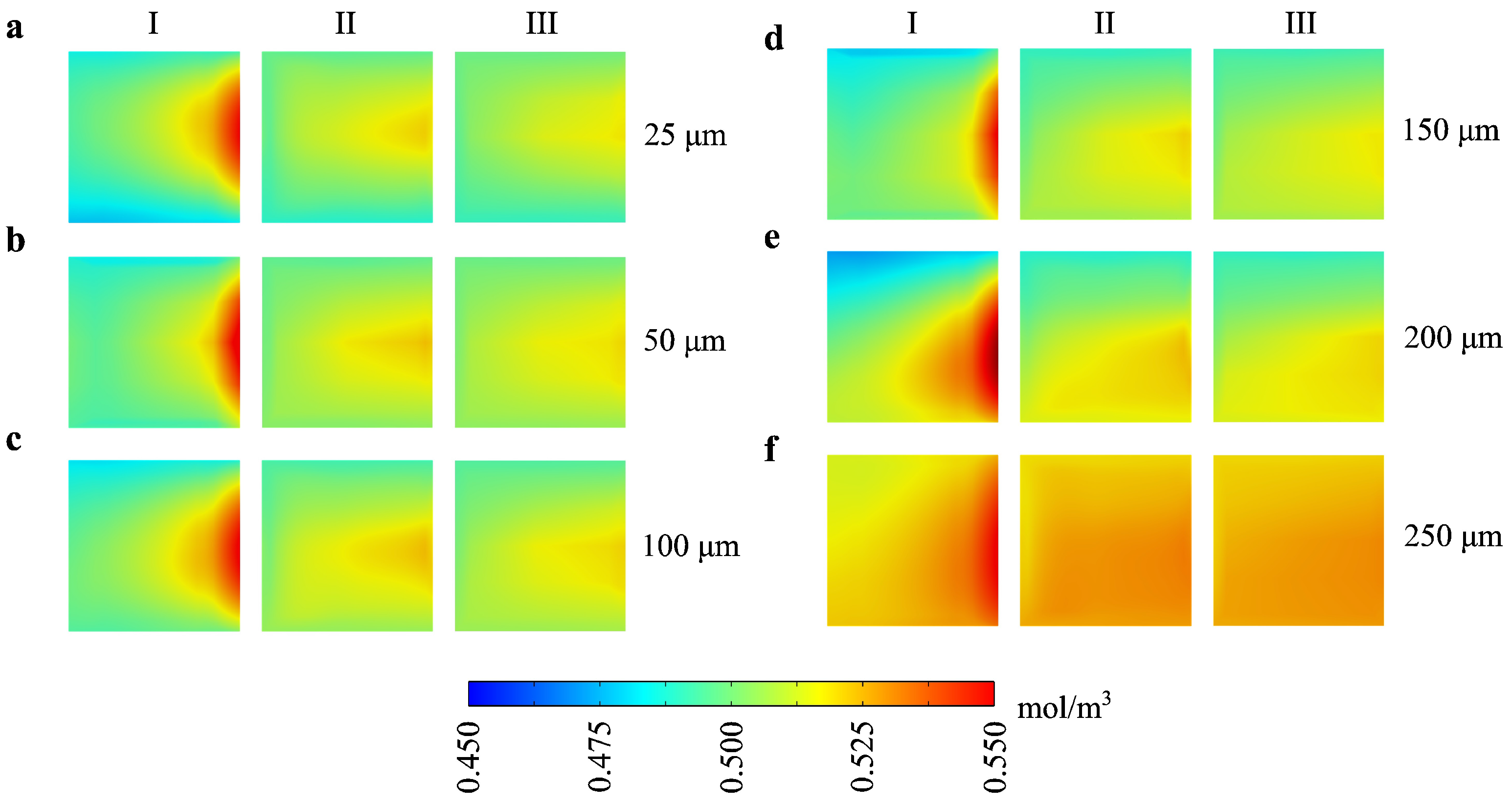
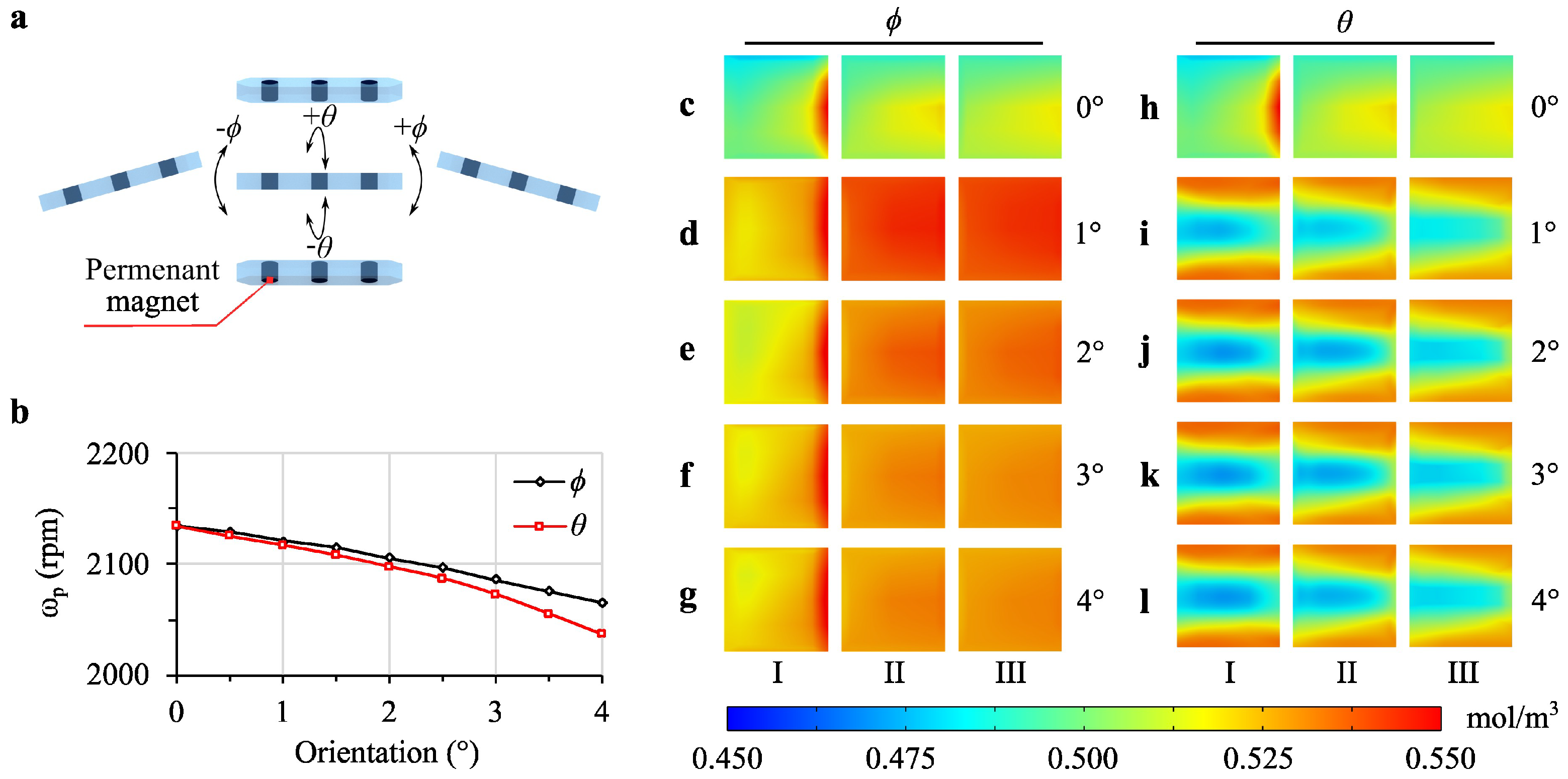

| Parameter | Value(s) | Unit |
|---|---|---|
| Inlet concentration | = 0, = 1 | mol/m3 |
| Wall effects | No slip; = 0 | mm/s |
| Outlet pressure | = 0 | Pa |
| Species flow rate ratio | = 1 | - |
| Remanent flux density | B = 1.4 | T |
| Reynolds numbers (Re) | 0.01, 0.1, 1, 10, 100, 1000 | - |
| Propeller speeds | 0, 60, 120, 180, 300, 600, 900, 1200, 1500, 3000, 6000 | rpm |
| Robot lengths | 0.75, 1, 1.25, 1.5, 1.75, 2, 2.25, 2.5 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demircali, A.A.; Yilmaz, A.; Uvet, H. Enhanced Fluid Mixing in Microchannels Using Levitated Magnetic Microrobots: A Numerical Study. Micromachines 2025, 16, 52. https://doi.org/10.3390/mi16010052
Demircali AA, Yilmaz A, Uvet H. Enhanced Fluid Mixing in Microchannels Using Levitated Magnetic Microrobots: A Numerical Study. Micromachines. 2025; 16(1):52. https://doi.org/10.3390/mi16010052
Chicago/Turabian StyleDemircali, Ali Anil, Abdurrahim Yilmaz, and Huseyin Uvet. 2025. "Enhanced Fluid Mixing in Microchannels Using Levitated Magnetic Microrobots: A Numerical Study" Micromachines 16, no. 1: 52. https://doi.org/10.3390/mi16010052
APA StyleDemircali, A. A., Yilmaz, A., & Uvet, H. (2025). Enhanced Fluid Mixing in Microchannels Using Levitated Magnetic Microrobots: A Numerical Study. Micromachines, 16(1), 52. https://doi.org/10.3390/mi16010052







