A Novel Active Polyphase Filter Employing Frequency-Dependent Image Rejection Enhancement Technique
Abstract
1. Introduction
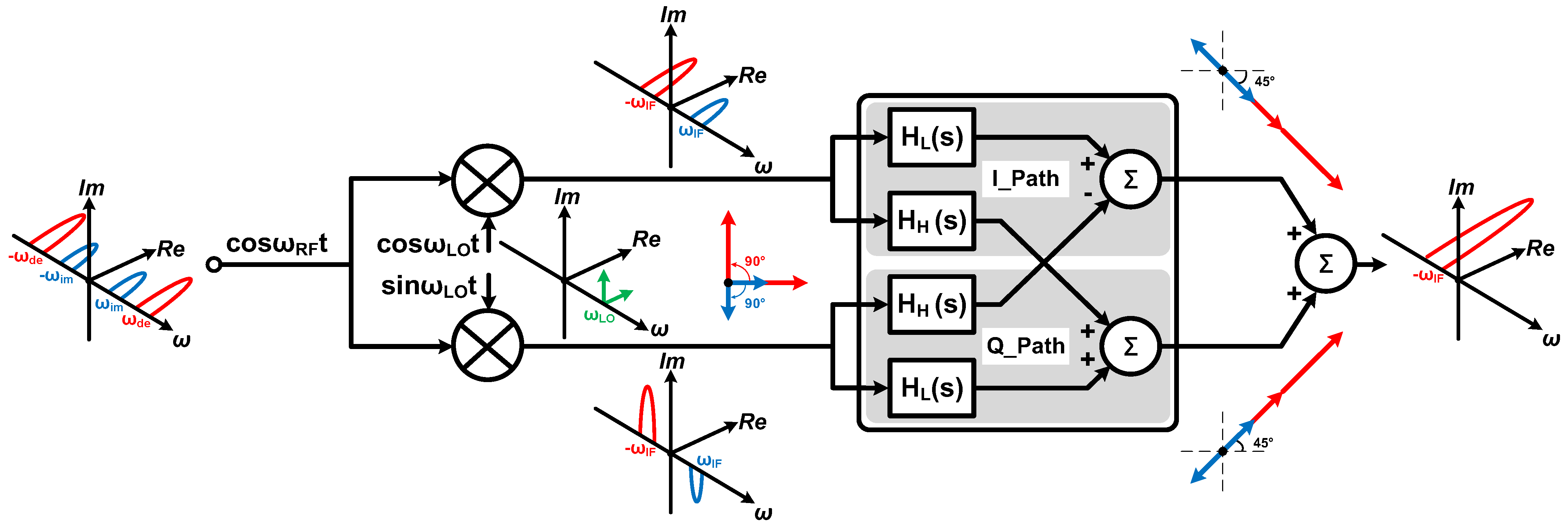
2. Circuit Analysis
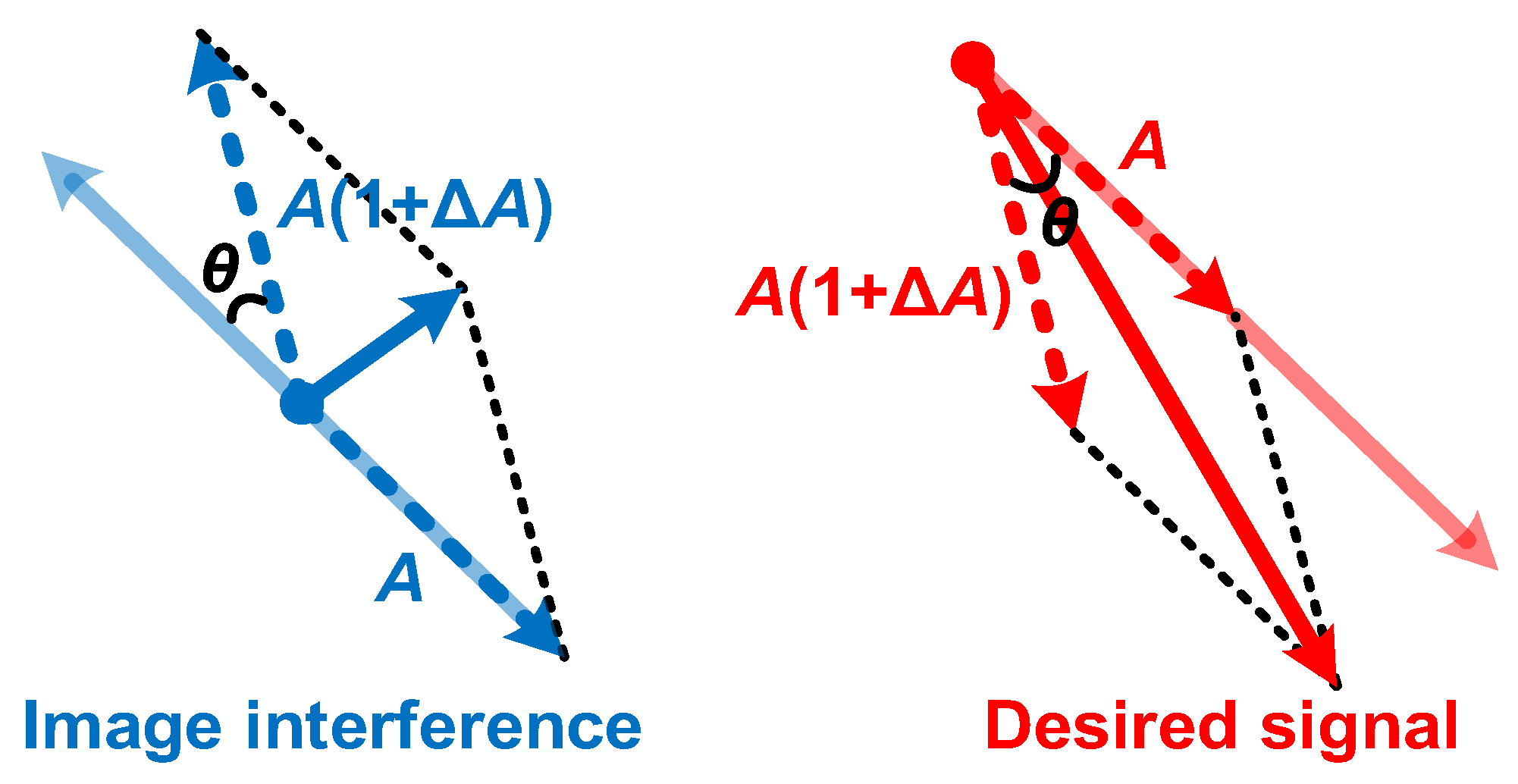
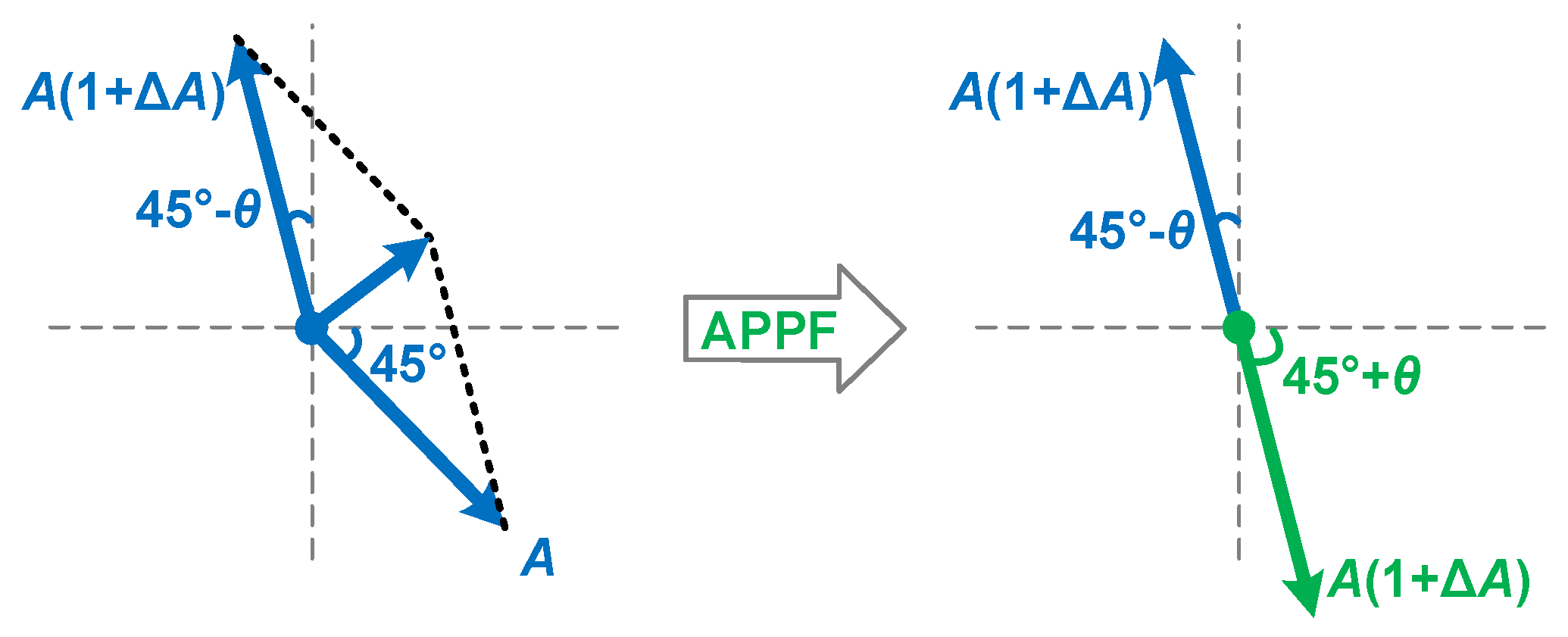
2.1. Theoretical Model of APPF
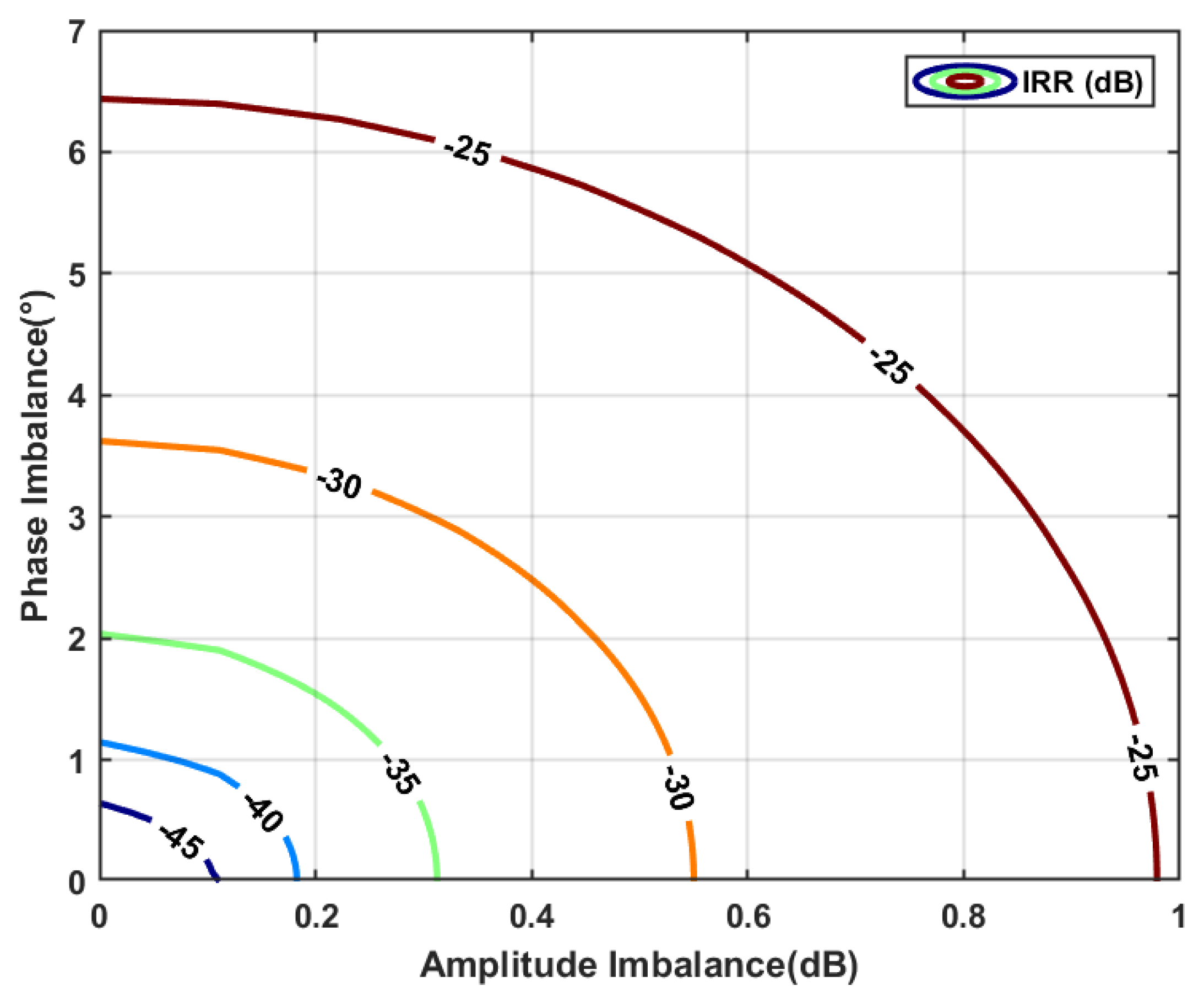
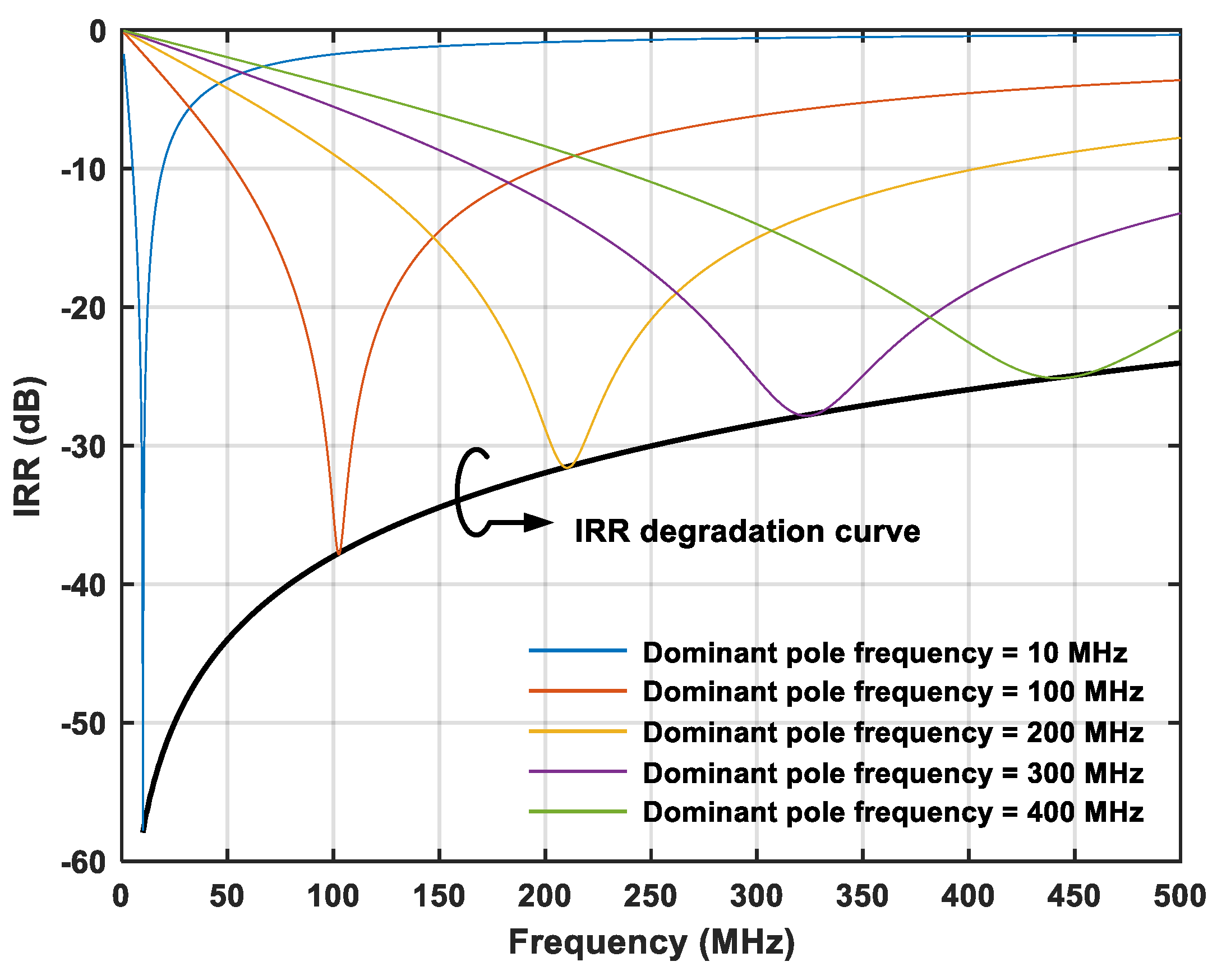
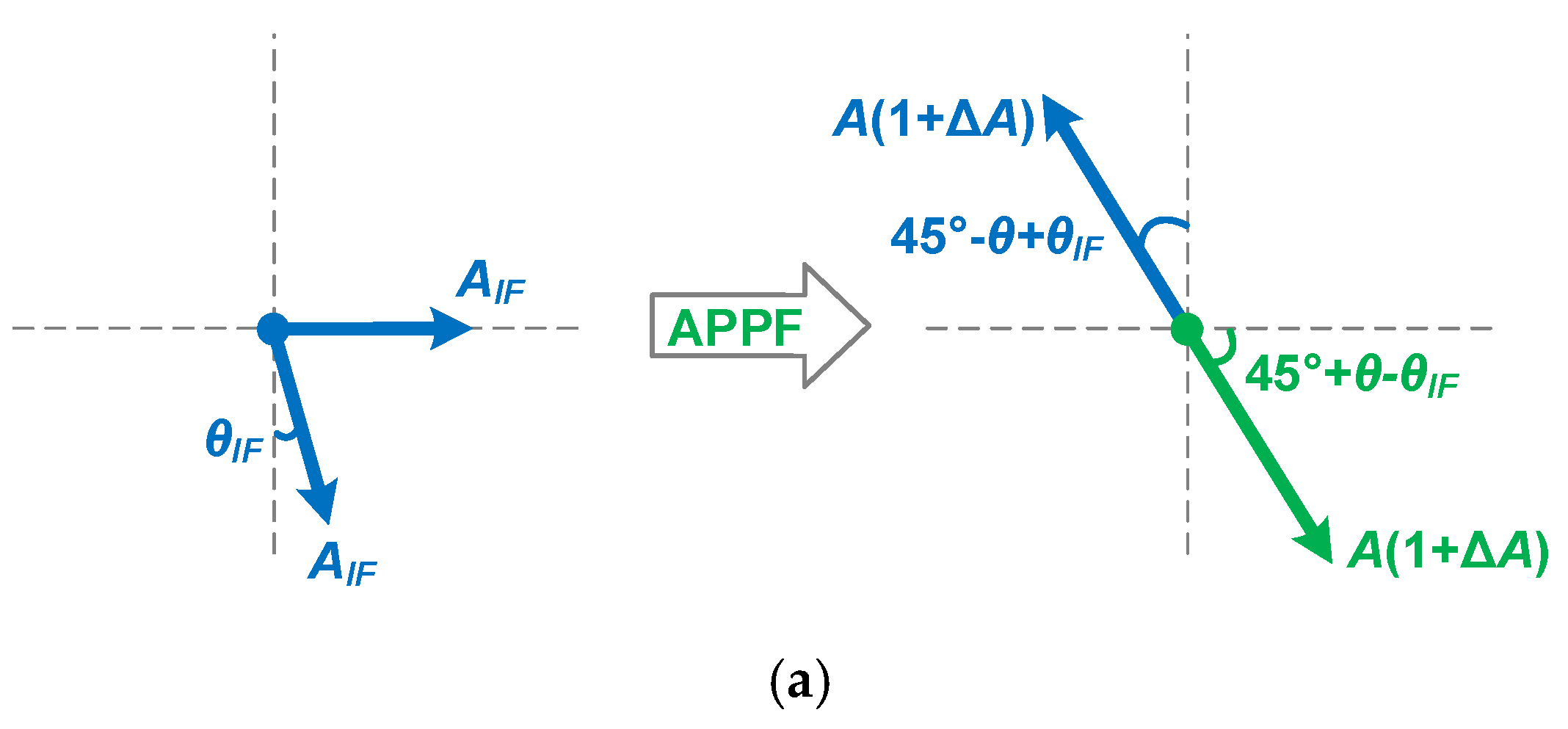
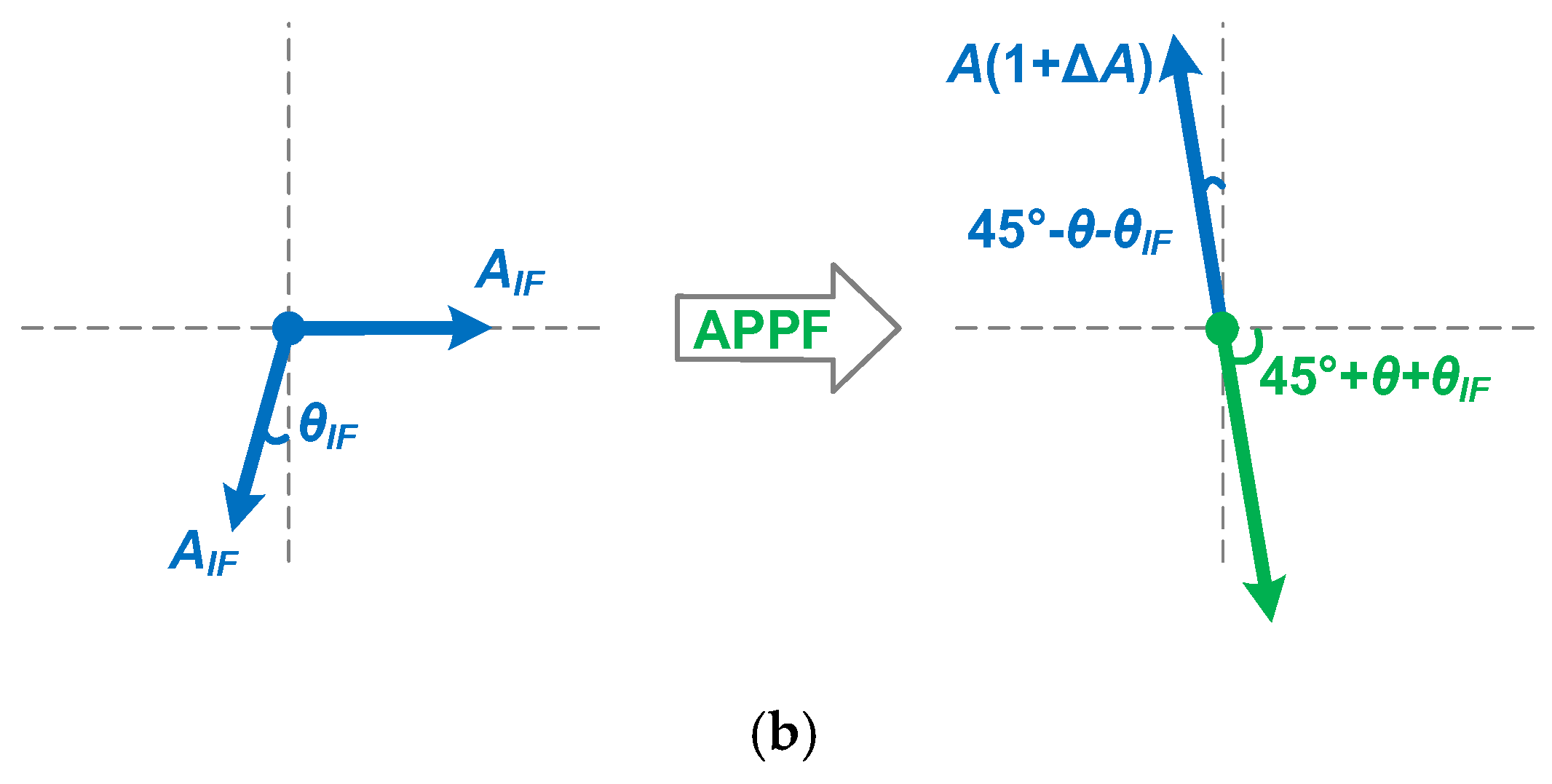
2.2. Frequency-Dependent Image Rejection Enhancement Technique Based on Secondary Pole Compensation
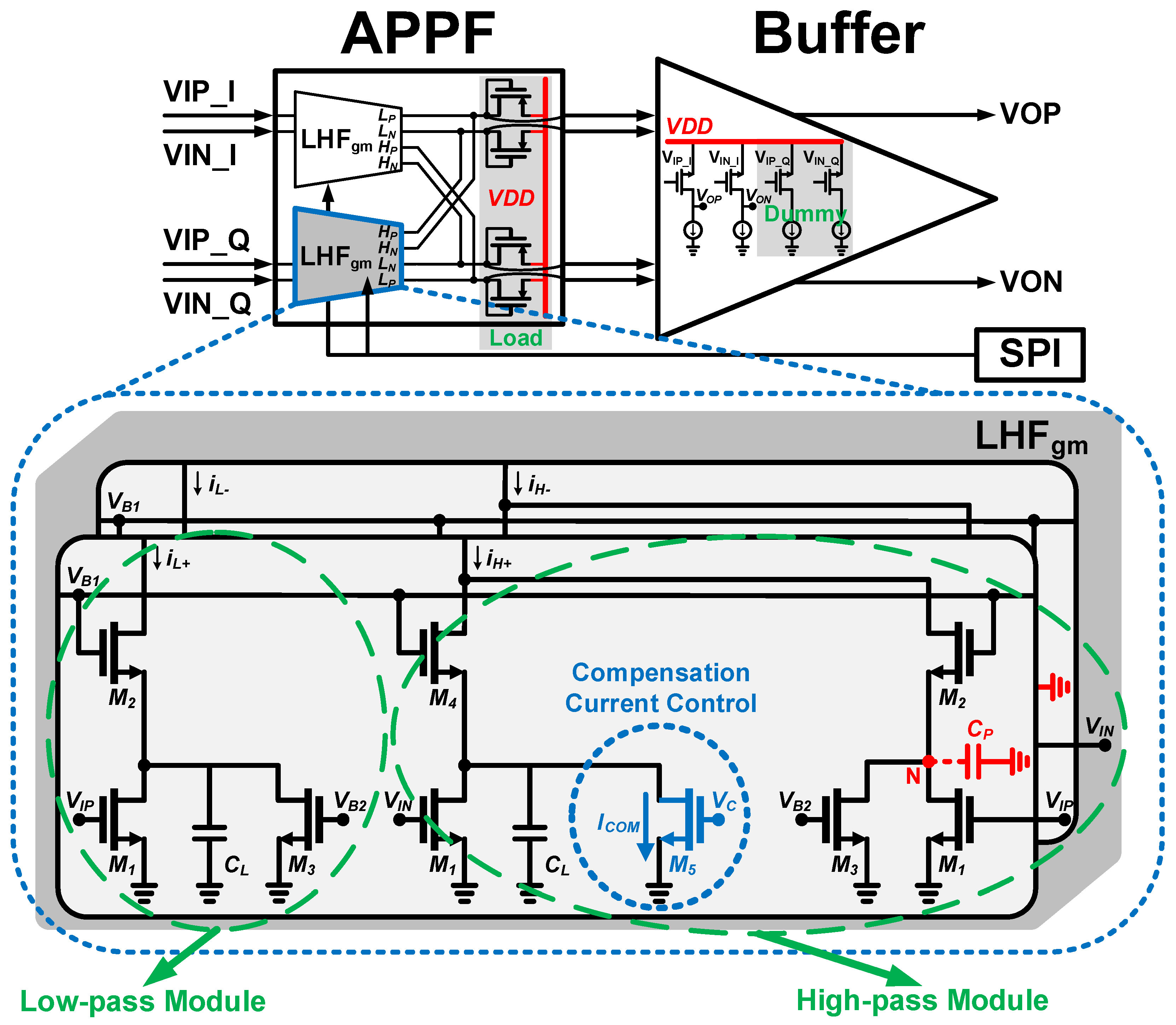
3. Circuit Implementation
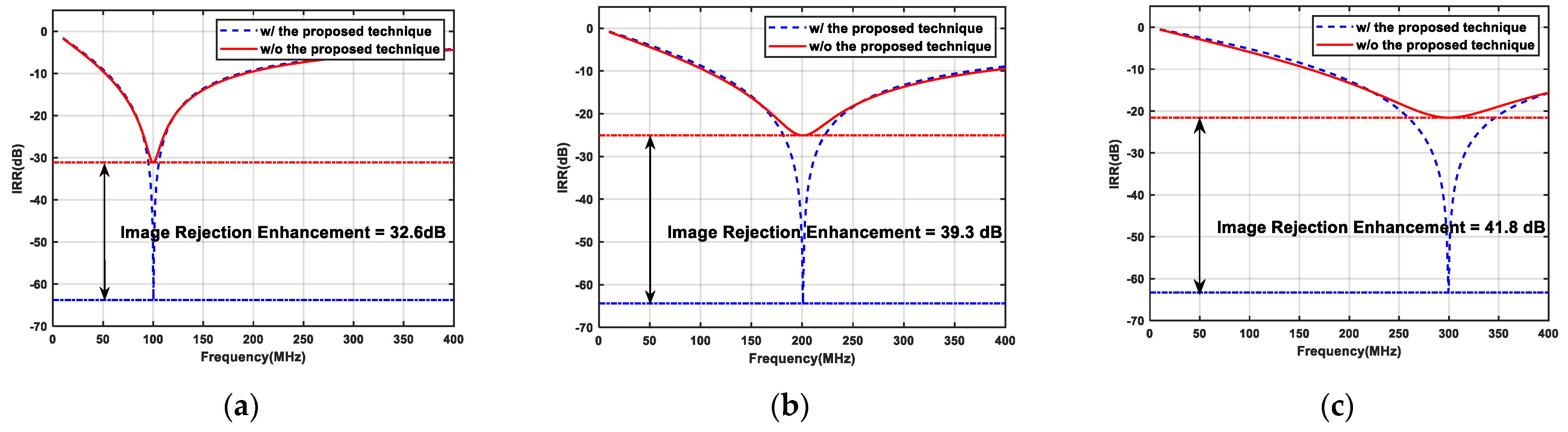
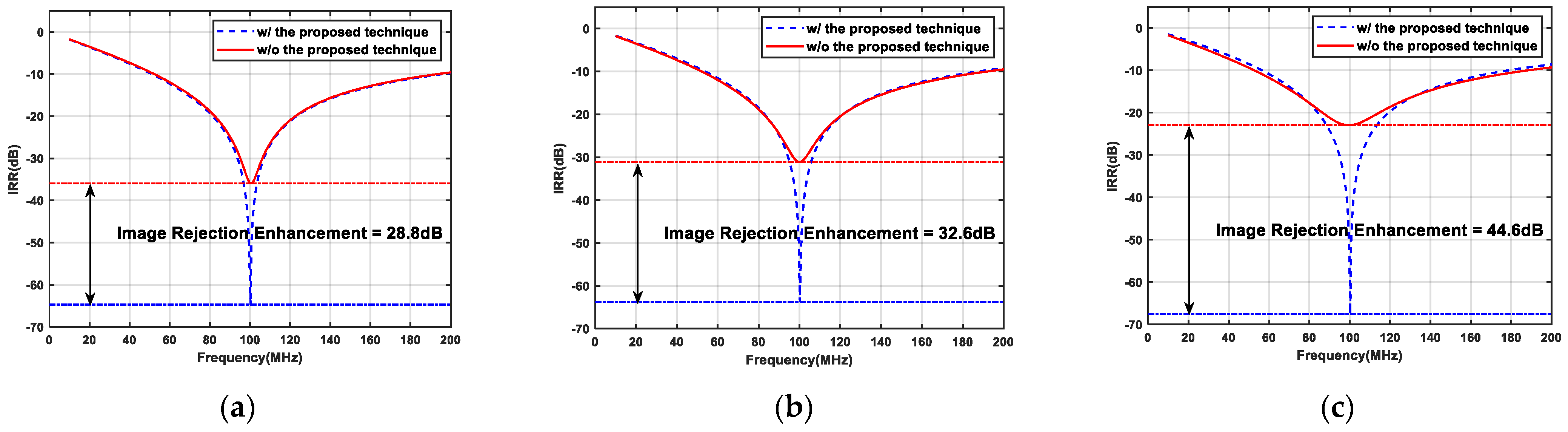
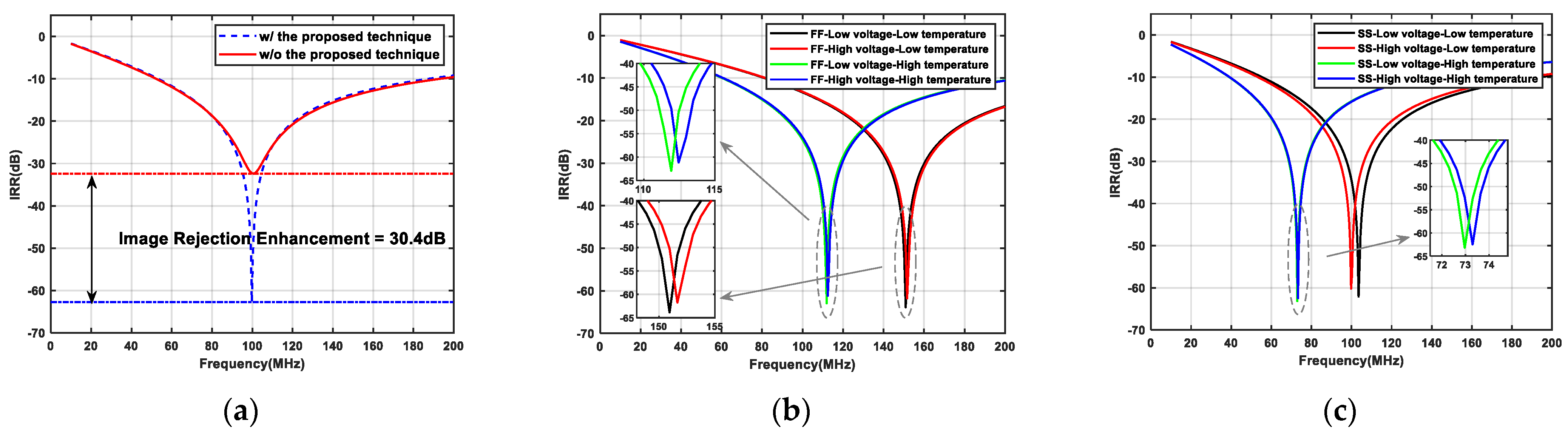
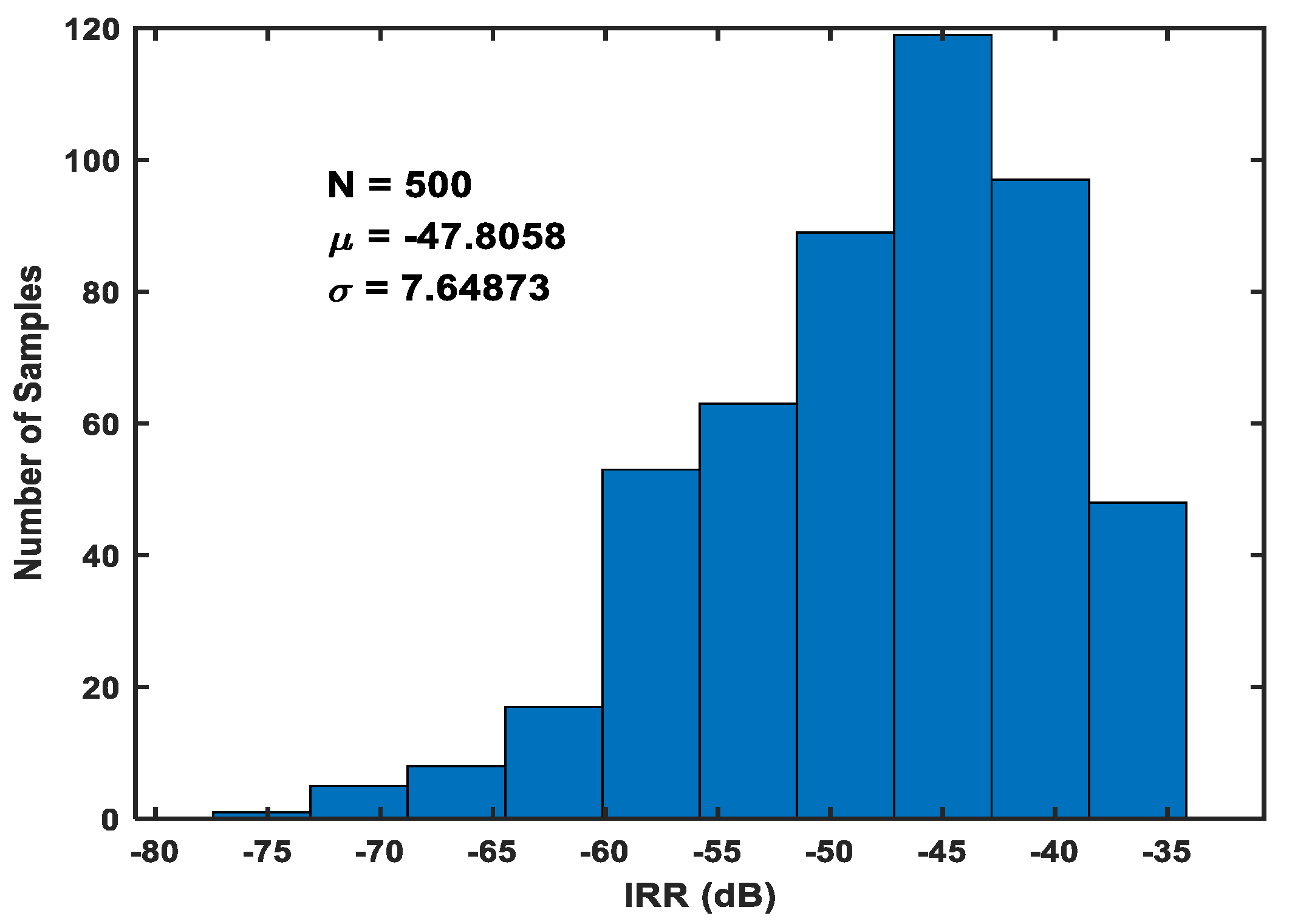
4. Simulation and Measurement Results
5. Comparative Analysis of Simulation and Measurement Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Y.; Ouyang, Z.; Huo, X.; Zhao, C.; Liu, H.; Wu, Y.; Kang, K. A 28-/60-GHz Dual-Band Receiver Front-End withSideband-Selection Technique in 65-nm CMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4550–4559. [Google Scholar] [CrossRef]
- Shin, D.; Lee, K.; Kwon, K. A Blocker-Tolerant Receiver Front End Employing Dual-Band N-Path Balun-LNA for 5G New Radio Cellular Applications. IEEE Trans. Microw. Theory Tech. 2022, 70, 1715–1724. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Li, H.; Yu, J.; Lu, Y.; Zhou, R.; Chen, Z.; Hong, W. A 220-GHz Sliding-IF Quadrature Transmitter and Receiver Chipset for High Data Rate Communication in 0.13-µm SiGe BiCMOS. IEEE J. Solid-State Circuits 2023, 58, 1913–1927. [Google Scholar] [CrossRef]
- Karakuzulu, A.; Ahmad, W.A.; Kissinger, D.; Malignaggi, A. A Four-Channel Bidirectional D-Band Phased-Array Transceiver for 200 Gb/s 6G Wireless Communications in a 130-nm BiCMOS Technology. IEEE J. Solid-State Circuits 2023, 58, 1310–1322. [Google Scholar] [CrossRef]
- Popescu, O. Power Budgets for CubeSat Radios to Support Ground Communications and Inter-Satellite Links. IEEE Access 2017, 5, 12618–12625. [Google Scholar] [CrossRef]
- Quadrelli, F.; Manente, D.; Seebacher, D.; Padovan, F.; Bassi, M.; Mazzanti, A.; Bevilacqua, A. A Broadband 22–31-GHz Bidirectional Image-Reject Up/Down Converter Module in 28-nm CMOS for 5G Communications. IEEE J. Solid-State Circuits 2022, 57, 1968–1981. [Google Scholar] [CrossRef]
- Barzgari, M.; Ghafari, A.; Meghdadi, M.; Medi, A. A Current Re-Use Quadrature RF Receiver Front-End for Low Power Applications: Blixator Circuit. IEEE J. Solid-State Circuits 2022, 57, 2672–2684. [Google Scholar] [CrossRef]
- Kim, S.; Kwon, K. A Low-Power RF-to-BB-Current-Reuse Receiver Employing Simultaneous Noise and Input Matching and 1/f Noise Reduction for IoT Applications. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 614–616. [Google Scholar] [CrossRef]
- Masnadi Shirazi, A.H.; Lavasani, H.M.; Sharifzadeh, M.; Rajavi, Y.; Mirabbasi, S.; Taghivand, M. An Ultralow-Power Current-Reused Direct-Conversion Bluetooth-Low-Energy Receiver Front-End in 40-nm CMOS. IEEE Trans. Microw. Theory Tech. 2021, 69, 2697–2711. [Google Scholar] [CrossRef]
- Park, B.; Kwon, K. 2.4-GHz Bluetooth Low Energy Receiver Employing New Quadrature Low-Noise Amplifier for Low-Power Low-Voltage IoT Applications. IEEE Trans. Microw. Theory Tech. 2021, 69, 1887–1895. [Google Scholar] [CrossRef]
- Madadi, I.; Tohidian, M.; Cornelissens, K.; Vandenameele, P.; Staszewski, R.B. A High IIP2 SAW-Less Superheterodyne Receiver withMultistage Harmonic Rejection. IEEE J. Solid-State Circuits 2016, 51, 332–347. [Google Scholar] [CrossRef]
- Silva-Pereira, M.; de Sousa, J.T.; Costa Freire, J.; Caldinhas Vaz, J. A 1.7-mW −92-dBm Sensitivity Low-IF Receiver in 0.13-μm CMOS for Bluetooth LE Applications. IEEE Trans. Microw. Theory Tech. 2019, 67, 332–346. [Google Scholar] [CrossRef]
- Xu, T.; Zhu, H.; Che, W.; Xue, Q. A 28-GHz Image-Reject Mixer withActive Polyphase Filter for 5G Wireless Applications. In Proceedings of the 2020 IEEE MTT-S International Wireless Symposium (IWS), Shanghai, China, 20–23 September 2020. [Google Scholar]
- Chung, H.; Ma, Q.; Yin, Y.; Gao, L.; Rebeiz, G.M. A 25–-29 GHz 64-Element Dual-Polarized/Dual-Beam Small-Cell with45 dBm 400 MHz 5GNR Operation and High Spectral Purity. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020. [Google Scholar]
- Dunworth, J.D.; Homayoun, A.; Ku, B.; Ou, Y.; Chakraborty, K.; Liu, G.; Segoria, T.; Lerdworatawee, J.; Park, J.W.; Park, H.; et al. A 28GHz Bulk-CMOS dual-polarization phased-array transceiver with24 channels for 5G user and basestation equipment. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 11–15 February 2018. [Google Scholar]
- Gao, L.; Ma, Q.; Rebeiz, G.M. A 20–44-GHz Image-Rejection Receiver with>75-dB Image-Rejection Ratio in 22-nm CMOS FD-SOI for 5G Applications. IEEE Trans. Microw. Theory Tech. 2020, 68, 2823–2832. [Google Scholar] [CrossRef]
- Pekcokguler, N.; Morche, D.; Burg, A.; Dehollain, C. An Ultra-Low-Power Widely-Tunable Complex Band-Pass Filter for RF Spectrum Sensing. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3879–3887. [Google Scholar] [CrossRef]
- Wu, M.-H.; Tsai, J.-H.; Huang, T.-W. Ka-Band Calibration-Free High Image-Rejection Up/Down Mixers With117% Fractional IF Bandwidth for SATCOM Applications. IEEE Access 2020, 8, 182133–182145. [Google Scholar] [CrossRef]
- Kaukovuori, J.; Stadius, K.; Ryynanen, J.; Halonen, K. Analysis and Design of Passive Polyphase Filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 3023–3037. [Google Scholar] [CrossRef]
- Zhang, Y.; Pang, J.; Li, Z.; Tang, M.; Liao, Y.; Fadila, A.A.; Shirane, A.; Okada, K. A Power-Efficient CMOS Multi-Band Phased-Array Receiver Covering 24–71-GHz Utilizing Harmonic-Selection Technique With36-dB Inter-Band Blocker Tolerance for 5G NR. IEEE J. Solid-State Circuits 2022, 57, 3617–3630. [Google Scholar] [CrossRef]
- Kim, T.; Lee, D.; Kwon, K. CMOS Channel-Selection Low-Noise Amplifier WithHigh-Q RF Band-Pass/Band-Rejection Filter for Highly Integrated RF Front-Ends. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 280–283. [Google Scholar] [CrossRef]
- Huang, M.-Y.; Chi, T.; Li, S.; Huang, T.-Y.; Wang, H. A 24.5–43.5-GHz Ultra-Compact CMOS Receiver Front End WithCalibration-Free Instantaneous Full-Band Image Rejection for Multiband 5G Massive MIMO. IEEE J. Solid-State Circuits 2020, 55, 1177–1186. [Google Scholar] [CrossRef]
- Zhang, T.; Najafi, A.; Taghivand, M.; Rudell, J.C. A Precision Wideband Quadrature Generation Technique withFeedback Control for Millimeter-Wave Communication Systems. IEEE Trans. Microw. Theory Tech. 2018, 66, 215–226. [Google Scholar] [CrossRef]
- Chung-Yun, C.; Chung-Yu, W. The design of wideband and low-power CMOS active polyphase filter and its application in RF double-quadrature receivers. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 825–833. [Google Scholar] [CrossRef]


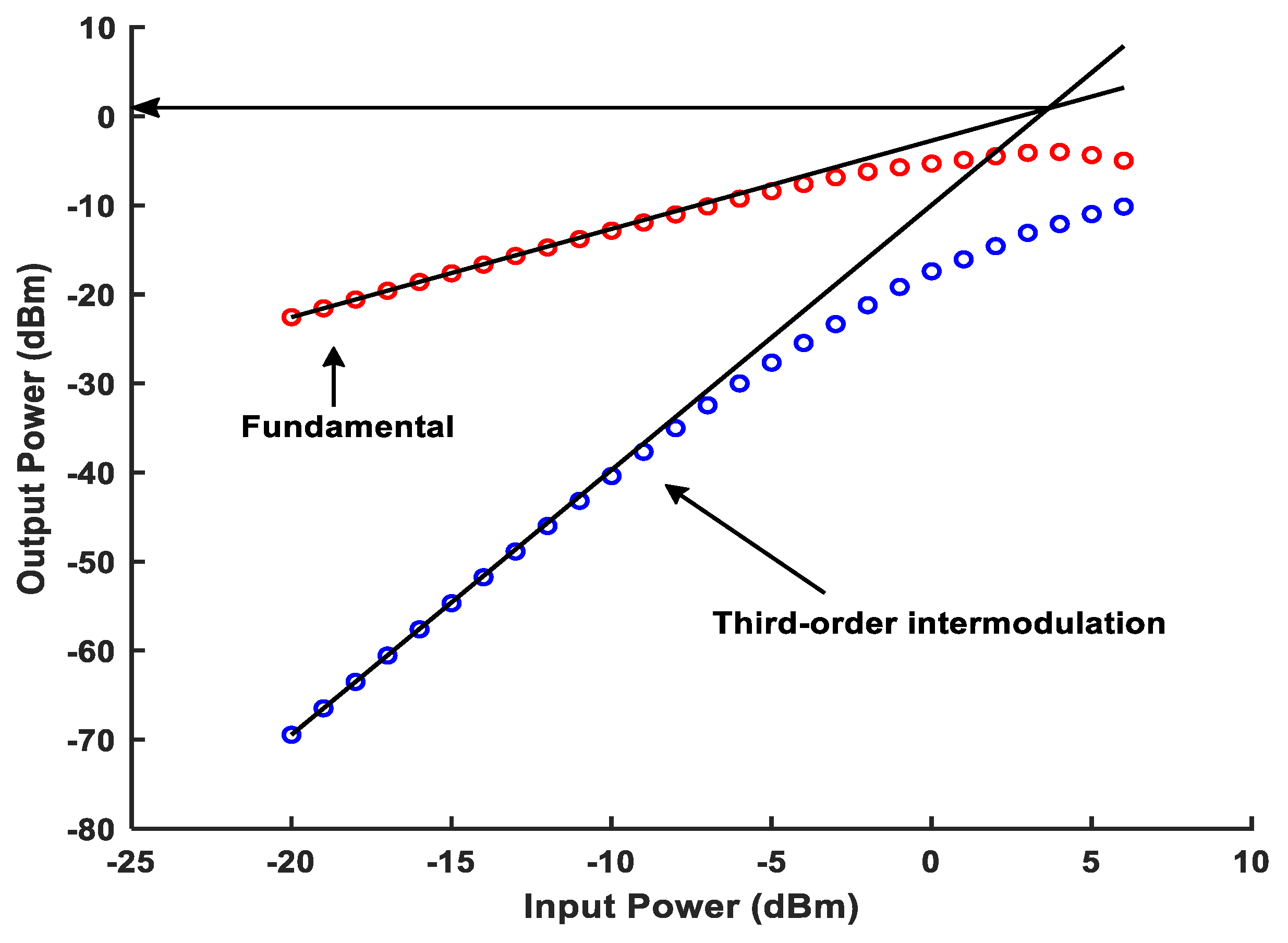
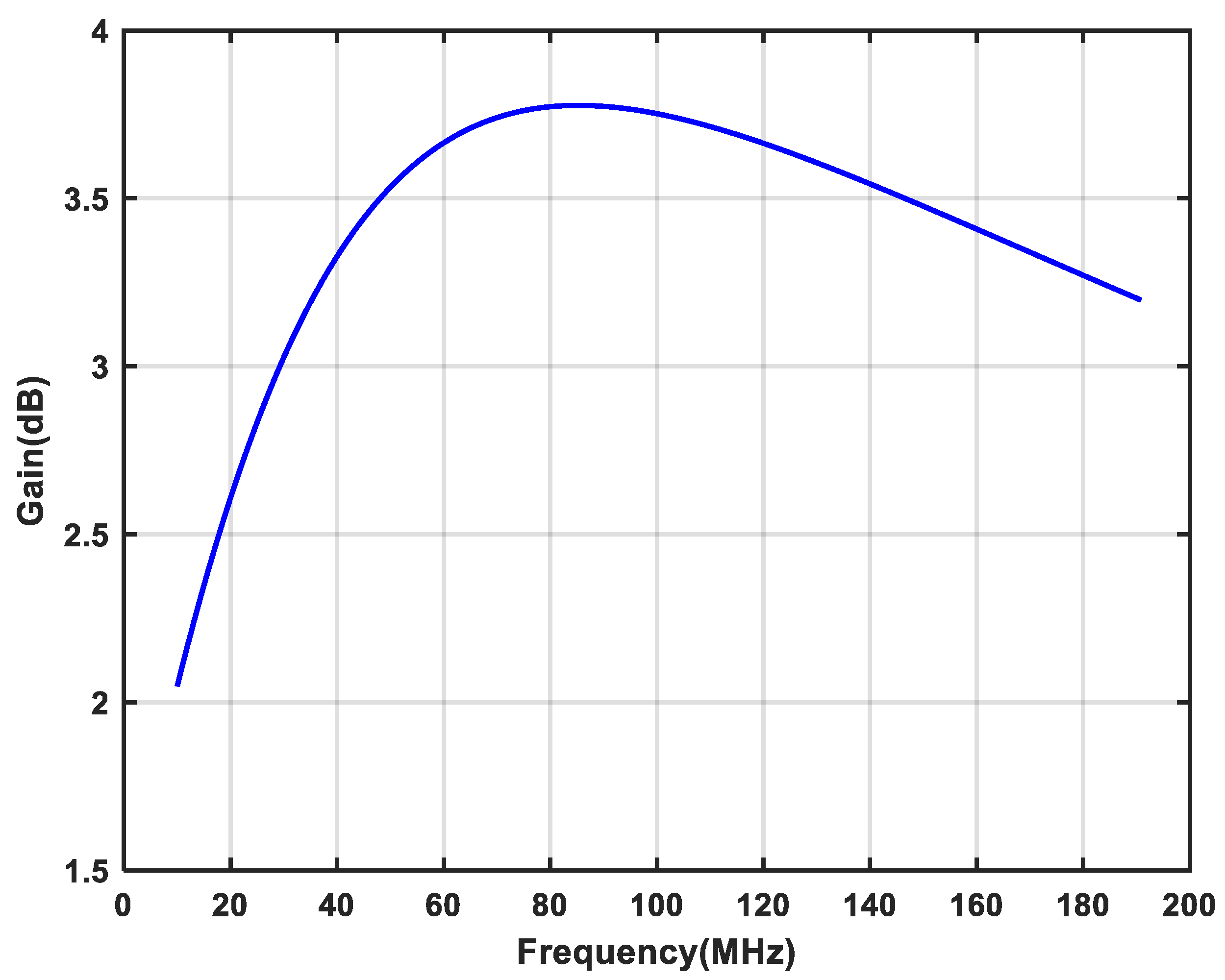
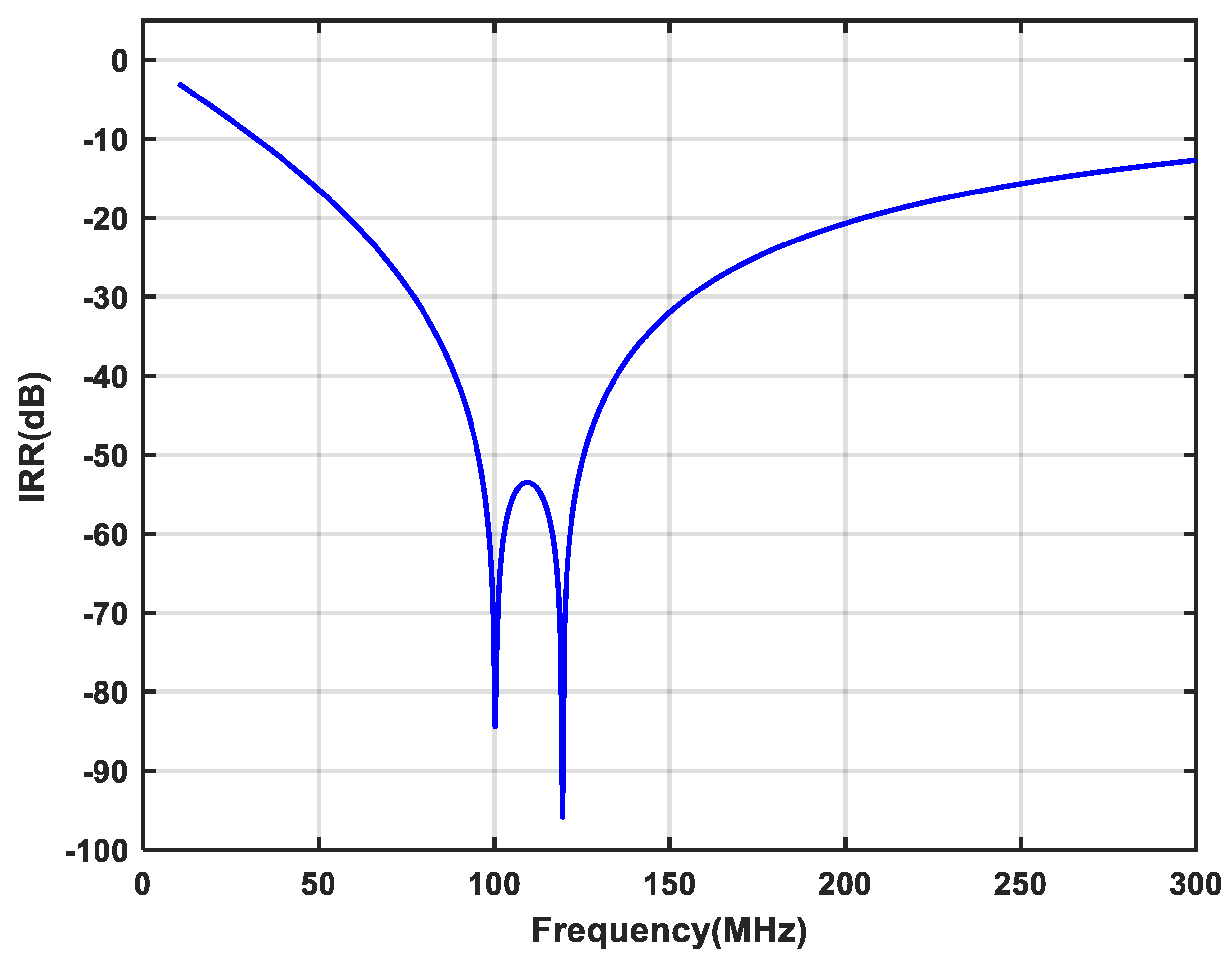
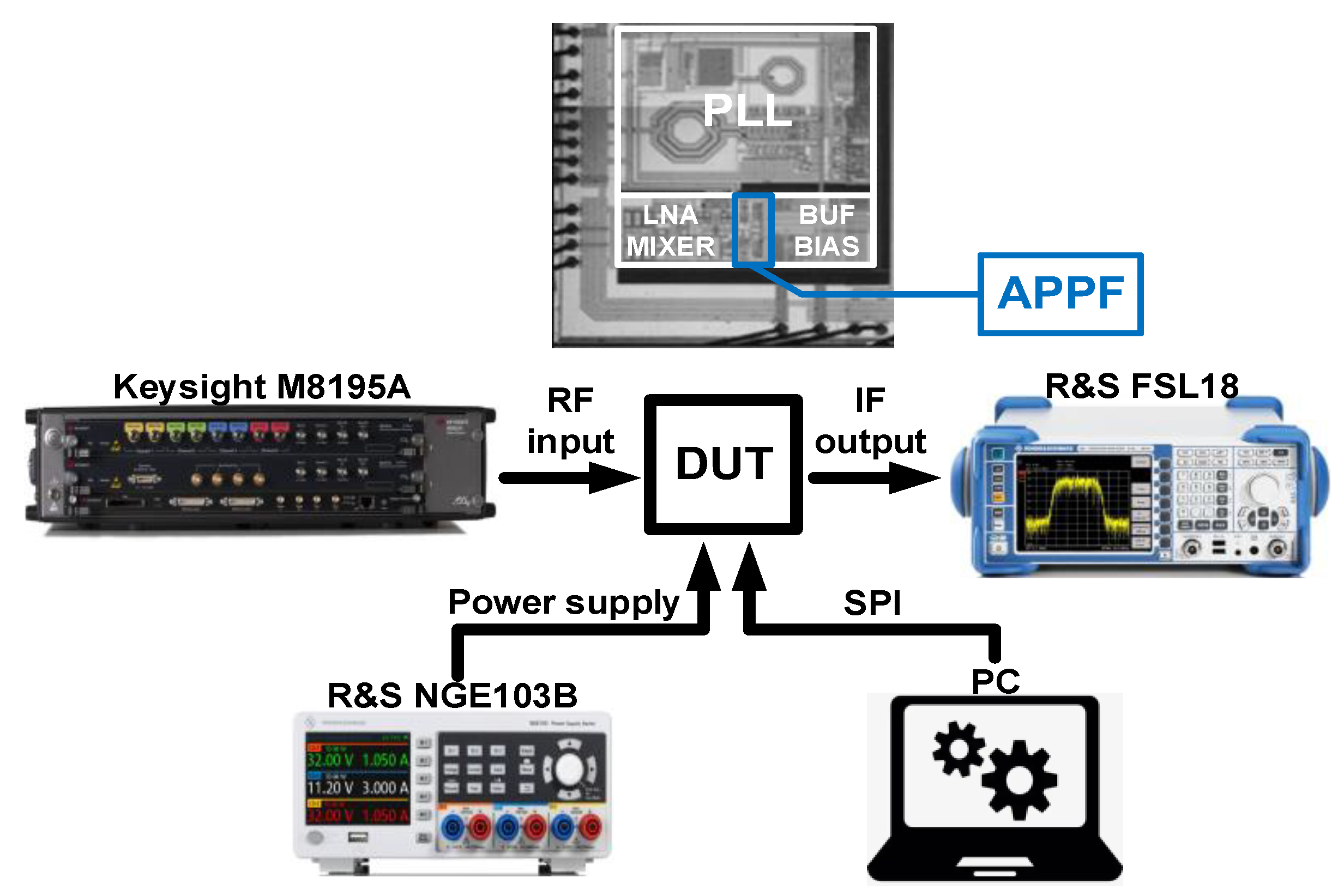
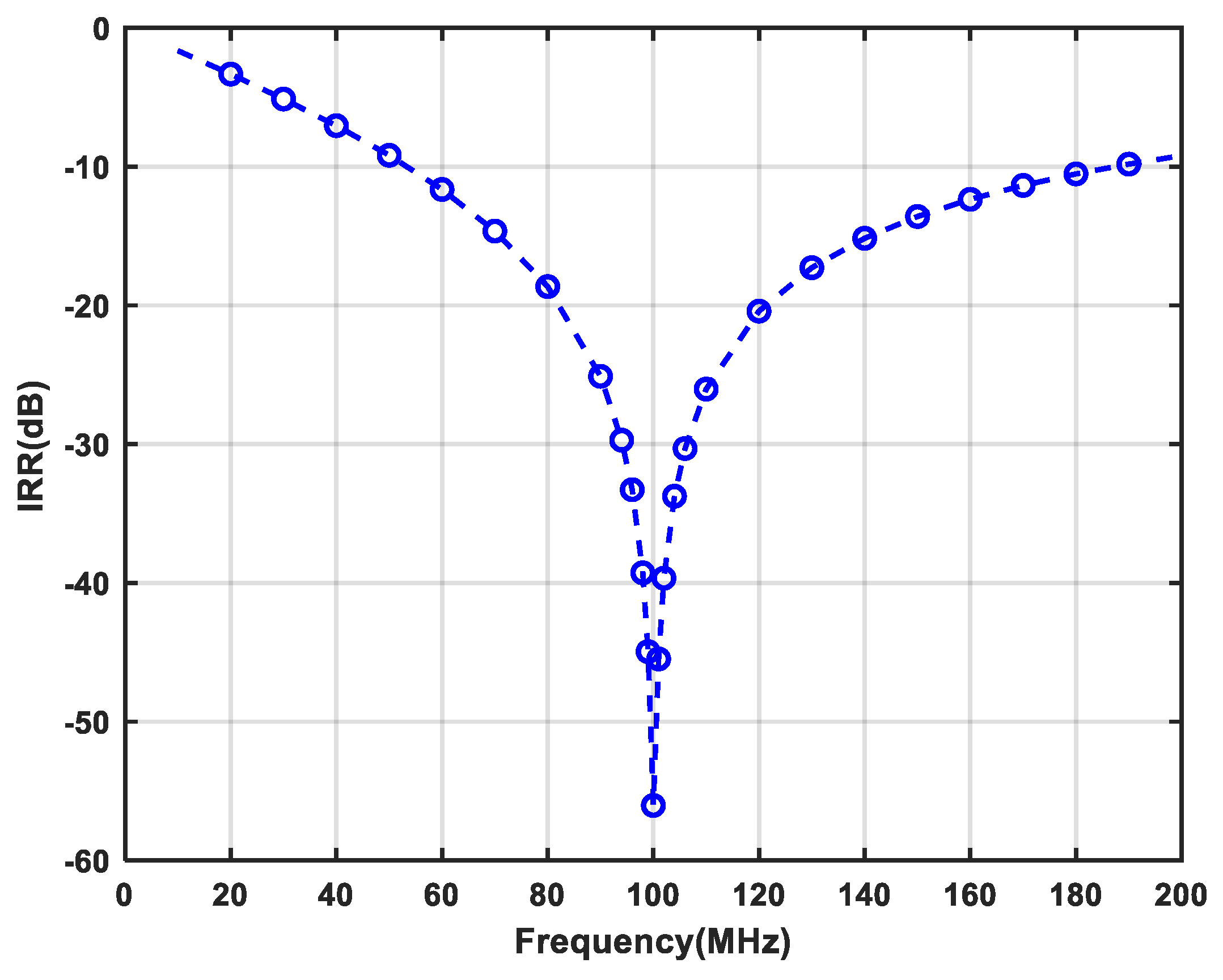
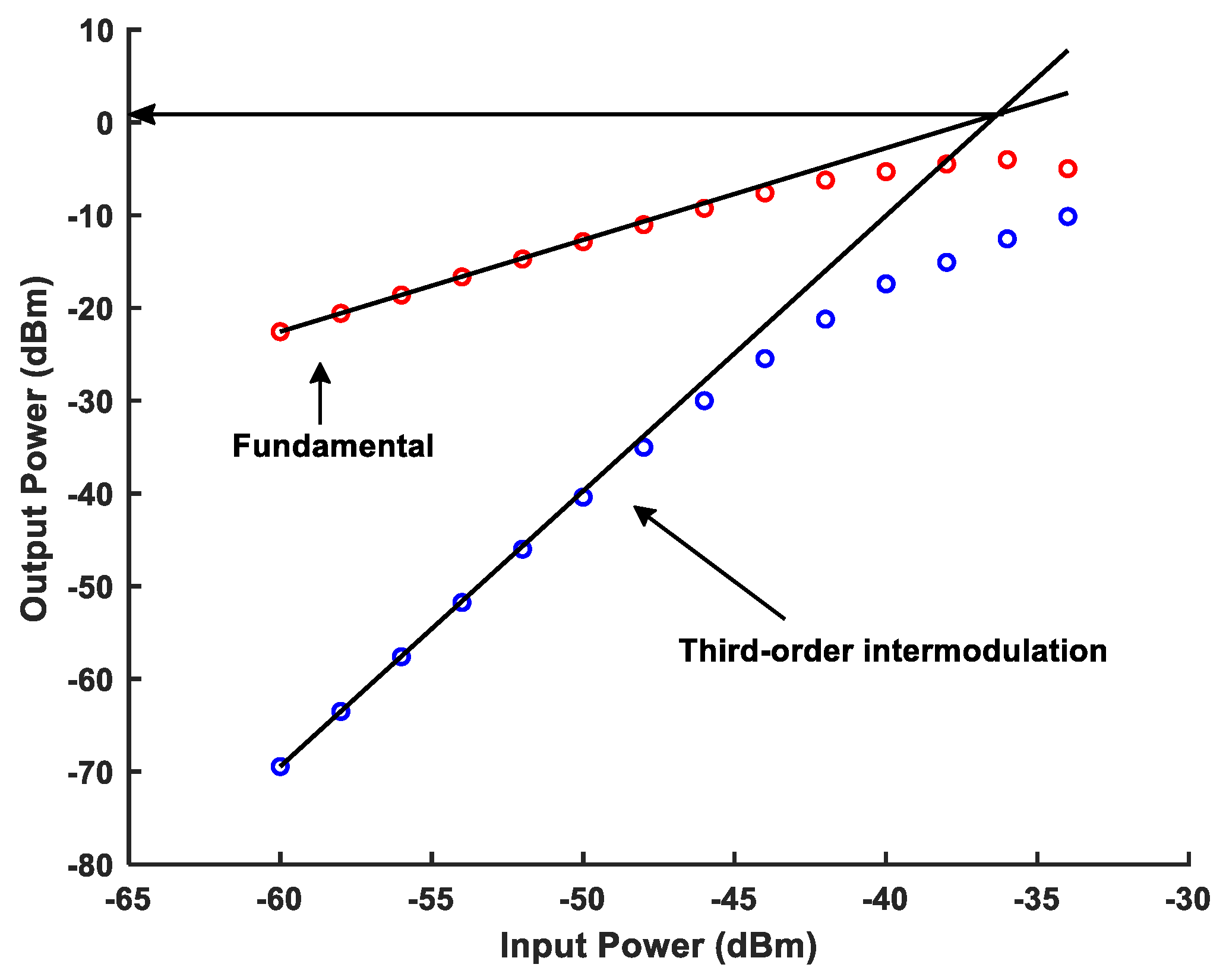
| Result | Optimum IRR (dB) | IRR (dB) @ Band-Width > 10 MHz | Power (mW) | Area (mm2) | OIP3 (dBm) | Gain (dB) | IRN (μV) |
|---|---|---|---|---|---|---|---|
| Simulation | 63.7 | 31.7 | 1.48 | 0.051 | 0.94 | 3.75 | 34.5 |
| Measurement | 57 | 31 | 1.5 | 0.051 | 0.9 | 3.53 | 37.4 |
| Parameter | 2020 [18] | 2020 [21] | 2020 [13] | 2023 [17] | 2005 [24] | This Work | |
|---|---|---|---|---|---|---|---|
| Process | 90 nm CMOS | 65 nm CMOS | 65 nm CMOS | 22 nm FD-SOI | 250 nm CMOS | 180 nm CMOS | |
| Type | RC-PPF | RC-PPF | Active-RC | CBPF | APPF | APPF | |
| Number of stages | 3 | 2 | 2 (2) | 1 | 4 | 1 | 2 (2) |
| Total IRR (dB) | −30 | −40 (1) | −40 (2) | −27 | −48 | −31 | −53.4 (2) |
| IRR per stage (dB) | −10 | −20 (1) | −20 (2) | −27 | −12 | −31 | −26.7 (2) |
| Bandwidth/Center frequency (MHz) | 1850/1580 | 20/200 | 2000/3000 (2) | 5/60 | 23.9/18.1 | 10/100 | 26/110 (2) |
| Power (mW) | N/A | N/A | 15 (2)(3) | 0.099 | 11 | 1.5 | 2.98 (2) |
| Core area (mm2) | 0.25 | 0.19 | 0.0091 (2) | 0.0049 | 0.95 | 0.051 | 0.081 (2) |
| OIP3 (dBm) | N/A | −6.0 (1) | 5.8 (2) | 3.4 (1) | 14.6 (1) | 0.9 | −1.55 (2) |
| Gain (dB) | −14.3 | N/A | 14 (2)(3) | 13.6 | 6.6 | 3.53 | 6.68 (2) |
| IRN (μV) | N/A | N/A | N/A | 107.7 | 78.1 | 37.4 | 58.6 (3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Qi, H.; Lu, H.; Feng, Z.; He, J.; Zhang, X.; Li, L.; Qi, X.; Feng, X. A Novel Active Polyphase Filter Employing Frequency-Dependent Image Rejection Enhancement Technique. Micromachines 2025, 16, 65. https://doi.org/10.3390/mi16010065
Yin Y, Qi H, Lu H, Feng Z, He J, Zhang X, Li L, Qi X, Feng X. A Novel Active Polyphase Filter Employing Frequency-Dependent Image Rejection Enhancement Technique. Micromachines. 2025; 16(1):65. https://doi.org/10.3390/mi16010065
Chicago/Turabian StyleYin, Yue, Haobo Qi, Haodong Lu, Ziting Feng, Jiayu He, Xinbing Zhang, Lei Li, Xiaofei Qi, and Xiyuan Feng. 2025. "A Novel Active Polyphase Filter Employing Frequency-Dependent Image Rejection Enhancement Technique" Micromachines 16, no. 1: 65. https://doi.org/10.3390/mi16010065
APA StyleYin, Y., Qi, H., Lu, H., Feng, Z., He, J., Zhang, X., Li, L., Qi, X., & Feng, X. (2025). A Novel Active Polyphase Filter Employing Frequency-Dependent Image Rejection Enhancement Technique. Micromachines, 16(1), 65. https://doi.org/10.3390/mi16010065







