Full-System Simulation and Analysis of a Four-Mass Vibratory MEMS Gyroscope
Abstract
:1. Introduction
2. Method
2.1. Device-Level Multiphysics Modeling
- (1)
- Modal order
- (2)
- Capacitance sensitivity and nonlinearity
- (3)
- Drive mode nonlinearity
- (4)
- Electrostatic tuning
- (5)
- Quality factor and mechanical thermal noise
- (6)
- Wiring and signal flow simulation
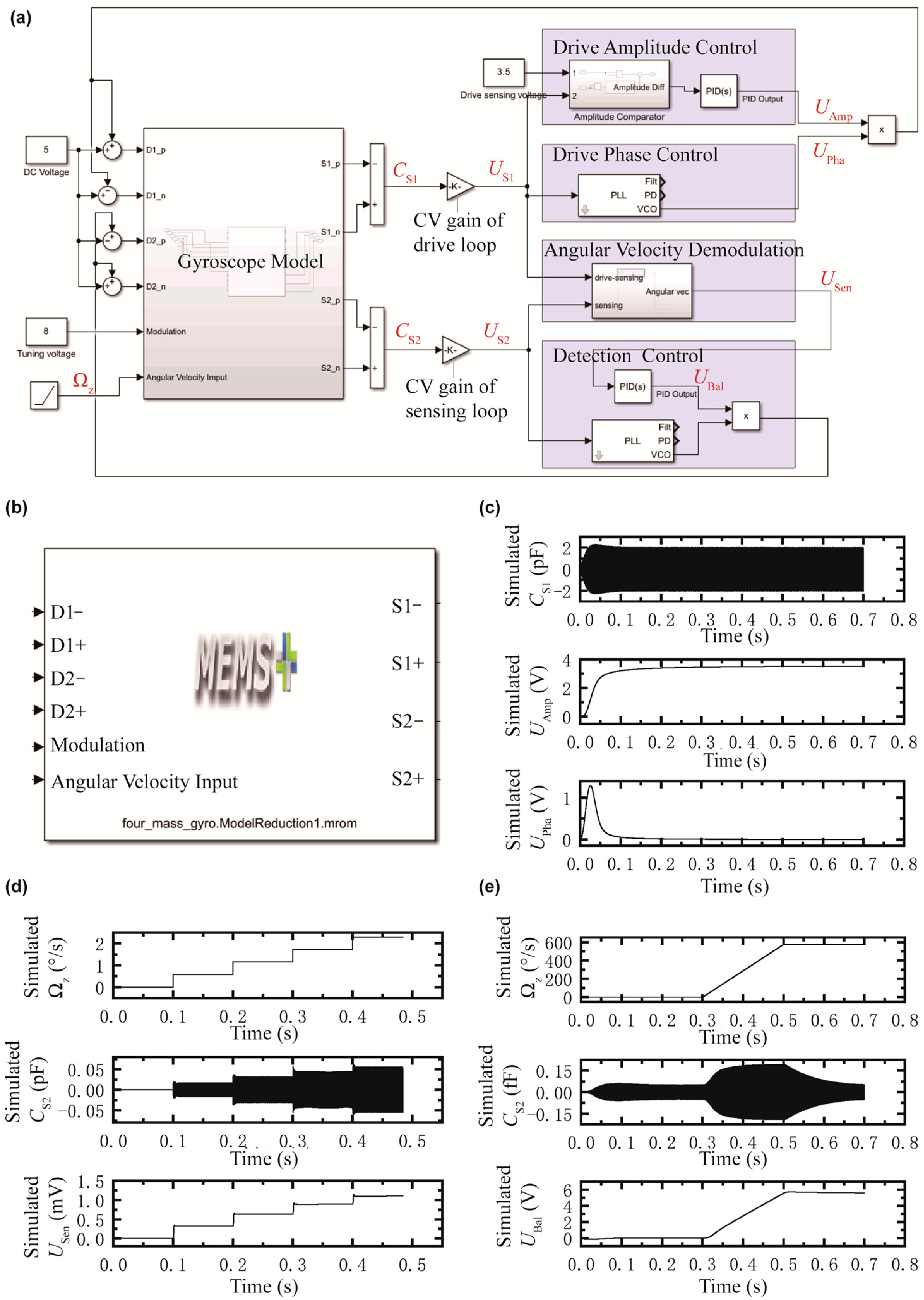
2.2. System-Level Behavioral Modeling
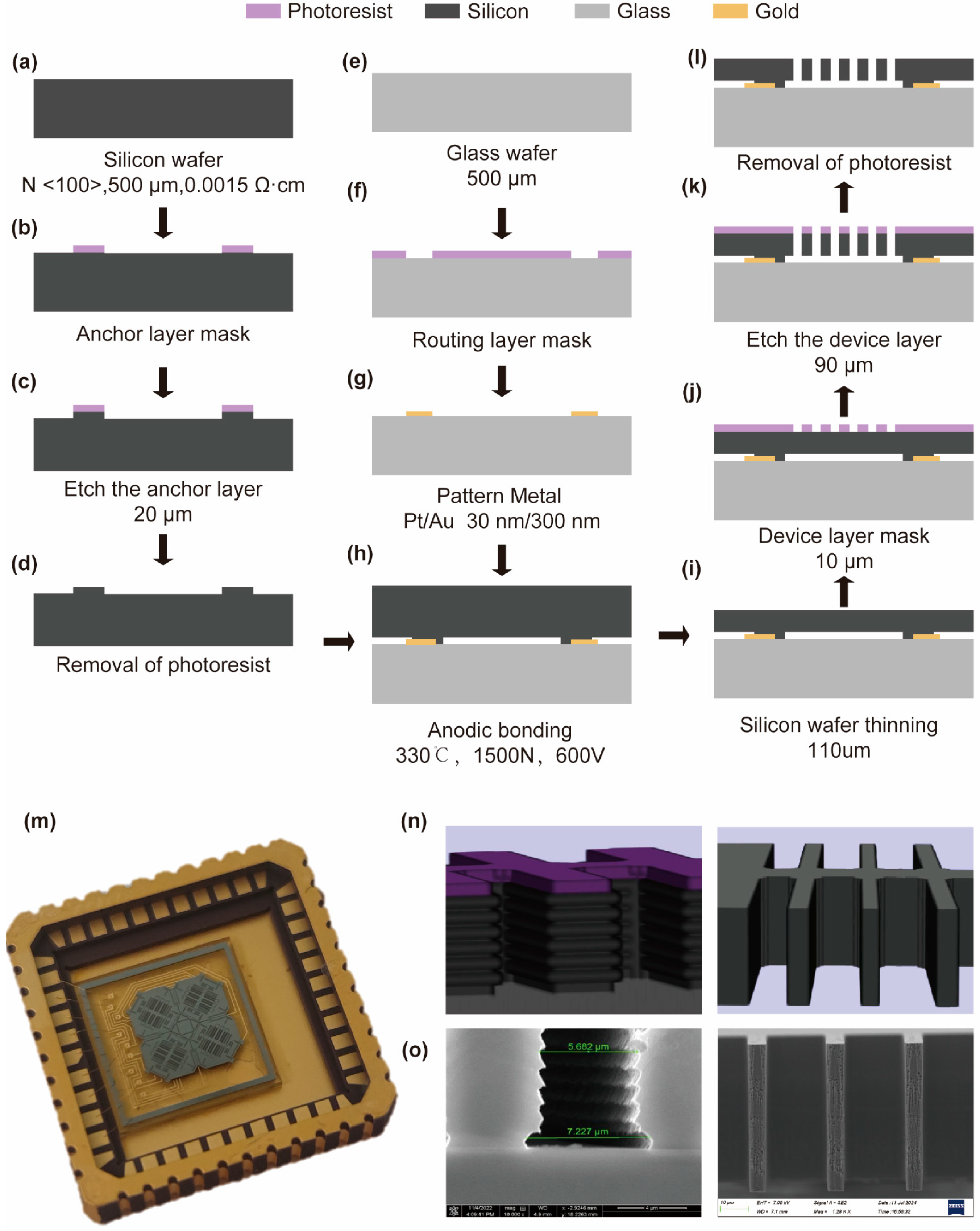
2.3. MEMS Process Simulation
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Torkashvand, Z.; Shayeganfar, F.; Ramazani, A. Nanomaterials based micro/nanoelectromechanical system (MEMS and NEMS) devices. Micromachines 2024, 15, 175. [Google Scholar] [CrossRef] [PubMed]
- Belwanshi, V.; Rane, K.; Kumar, V.; Pramanick, B. Design guidelines for thin diaphragm-based microsystems through comprehensive numerical and analytical studies. Micromachines 2023, 14, 1725. [Google Scholar] [CrossRef]
- Niranjan, A.; Gupta, P. Modeling and simulation software in mems design. Int. J. Eng. Adv. Technol. 2020, 9, 2501–2506. [Google Scholar]
- Ali, I.A. Modeling and simulation of MEMS components: Challenges and possible solutions. In Micromachining Techniques for Fabrication of MicroNano Structures; IntechOpen: London, UK, 2012; pp. 277–301. [Google Scholar]
- Qin, S.J.; Cherry, G.; Good, R.; Wang, J.; Harrison, C.A. Semiconductor manufacturing process control and monitoring: A fab-wide framework. J. Process Control 2006, 16, 179–191. [Google Scholar]
- Edgar, T.F.; Butler, S.W.; Campbell, W.J.; Pfeiffer, C.; Bode, C.; Hwang, S.B.; Balakrishnan, K.; Hahn, J.J.A. Automatic control in microelectronics manufacturing: Practices, challenges, and possibilities. Automatica 2000, 36, 1567–1603. [Google Scholar]
- Zhanshe, G.; Fucheng, C.; Boyu, L.; Le, C.; Chao, L.; Ke, S. Research development of silicon MEMS gyroscopes: A review. Microsyst. Technol. 2015, 21, 2053–2066. [Google Scholar]
- Patel, C.; McCluskey, P. Modeling and simulation of the MEMS vibratory gyroscope. In Proceedings of the 13th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, San Diego, CA, USA, 30 May–1 June 2012; pp. 928–933. [Google Scholar]
- Giannini, D.; Bonaccorsi, G.; Braghin, F. Rapid prototyping of inertial MEMS devices through structural optimization. Sensors 2021, 21, 5064. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, Y.; Xie, J.; Zhou, Z.; Yuan, W. Integrated behavior simulation and verification for a MEMS vibratory gyroscope using parametric model order reduction. J. Microelectromech. Syst. 2010, 19, 282–293. [Google Scholar]
- Kwon, H.J.; Seok, S.; Lim, G. System modeling of a MEMS vibratory gyroscope and integration to circuit simulation. Sensors 2017, 17, 2663. [Google Scholar] [CrossRef]
- Mohite, S.; Patil, N.; Pratap, R. Design, modelling and simulation of vibratory micromachined gyroscopes. J. Phys. Conf. Ser. 2006, 34, 757. [Google Scholar]
- Batur, C.; Sreeramreddy, T.; Khasawneh, Q. Sliding mode control of a simulated MEMS gyroscope. ISA Trans. 2006, 45, 99–108. [Google Scholar] [PubMed]
- Tatar, E.; Mukherjee, T.; Fedder, G.K. Simulation of stress effects on mode-matched MEMS gyroscope bias and scale factor. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium-PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 16–20. [Google Scholar]
- Roth, G. Simulation of the Effects of Acoustic Noise on Mems Gyroscopes. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2009. [Google Scholar]
- Putnik, M.; Cardanobile, S.; Nagel, C.; Degenfeld-Schonburg, P.; Mehner, J. Simulation and modelling of the drive mode nonlinearity in MEMS-gyroscopes. Procedia Eng. 2016, 168, 950–953. [Google Scholar]
- Tatar, E.; Alper, S.E.; Akin, T. Quadrature-error compensation and corresponding effects on the performance of fully decoupled MEMS gyroscopes. J. Microelectromech. Syst. 2012, 21, 656–667. [Google Scholar]
- Luo, Z.; Wang, X.; Jin, M.; Liu, S. MEMS gyroscope yield simulation based on Monte Carlo method. In Proceedings of the 2012 IEEE 62nd Electronic Components and Technology Conference, San Diego, CA, USA, 29 May–1 June 2012; pp. 1636–1639. [Google Scholar]
- Shah, M.A.; Iqbal, F.; Lee, B.-L. Design and analysis of a single-structure three-axis MEMS gyroscope with improved coupling spring. In Proceedings of the 2016 IEEE 11th Annual International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Sendai, Japan, 17–20 April 2016; pp. 188–191. [Google Scholar]
- Gujela, V.; Gujela, O.P. Simulation of cantilever beam using ANSYS for nano manipulator. In Proceedings of the 2016 International Conference on Microelectronics, Computing and Communications (MicroCom), Durgapur, India, 23–25 January 2016; pp. 1–5. [Google Scholar]
- Nazdrowicz, J.; Napieralski, A. Modelling, simulations and performance analysis of MEMS vibrating gyroscope in coventor MEMS+ environment. In Proceedings of the 2019 20th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Hannover, Germany, 24–27 March 2019; pp. 1–5. [Google Scholar]
- Yuvaraj, S.; Krushnasamy, V. Design and simulation of MEMS comb vibratory gyroscope. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2014, 3, 8185–8192. [Google Scholar]
- Li, P.; Wei, Q.; Zhou, B.; Luo, L. A 5.3 nv/rt Hz, 0.1 nA Input Bias Current Amplifier with both Low and High Voltage Output Capability, Range of 4–50V, Using a BJT Input Stage with a Novel Base Current Compensation Structure. In Proceedings of the 2022 IEEE 4th International Conference on Circuits and Systems (ICCS), Chengdu, China, 23–26 September 2022; pp. 118–123. [Google Scholar]
- Nazdrowicz, J. SIMULINK and COMSOL software application for MEMS accelerometer modeling and simulation. In Proceedings of the 2017 MIXDES-24th International Conference Mixed Design of Integrated Circuits and Systems, Bydgoszcz, Poland, 22–24 June 2017; pp. 429–434. [Google Scholar]
- CST Studio Suite. CST Microwave Studio; CST Studio Suite: Johnston, RI, USA, 2008. [Google Scholar]
- Zhang, H.; Zhang, C.; Chen, J.; Li, A. A review of symmetric silicon MEMS gyroscope mode-matching technologies. Micromachines 2022, 13, 1255. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Zhou, B.; Yin, P.; Chen, Z.; Zhang, R. Optimal design of a center support quadruple mass gyroscope (CSQMG). Sensors 2016, 16, 613. [Google Scholar] [CrossRef]
- Cao, H.; Cai, Q.; Zhang, Y.; Shen, C.; Shi, Y.; Liu, J. Design, fabrication, and experiment of a decoupled multi-frame vibration MEMS gyroscope. IEEE Sens. J. 2021, 21, 19815–19824. [Google Scholar]
- Alper, S.E.; Temiz, Y.; Akin, T. A compact angular rate sensor system using a fully decoupled silicon-on-glass MEMS gyroscope. J. Microelectromech. Syst. 2008, 17, 1418–1429. [Google Scholar]
- Hu, Z.; Gallacher, B.; Burdess, J.; Bowles, S.; Grigg, H. A systematic approach for precision electrostatic mode tuning of a MEMS gyroscope. J. Micromech. Microeng. 2014, 24, 125003. [Google Scholar]
- Tatar, E.; Mukherjee, T.; Fedder, G. Nonlinearity tuning and its effects on the performance of a MEMS gyroscope. In Proceedings of the 2015 Transducers-2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 1133–1136. [Google Scholar]
- Shao, L.; Niu, T.; Palaniapan, M. Nonlinearities in a high-Q SOI Lamé-mode bulk resonator. J. Micromech. Microeng. 2009, 19, 075002. [Google Scholar]
- Zener, C. Internal friction in solids II. General theory of thermoelastic internal friction. Phys. Rev. 1938, 53, 90. [Google Scholar]



| Symbol | Description | Unit |
|---|---|---|
| , | The displacements along the drive and sensing motion direction. | m |
| , | The resonant frequencies of the drive and sensing modes. | rad |
| , | The displacements of the anti-phase and in-phase motion. | m |
| , | The frequencies of the anti-phase and in-phase modes. | rad |
| , | The quality factors of the drive and sensing modes. | / |
| The external angular velocity and acceleration. | rad/s, m/s2 | |
| , | The amplitude and frequency of the drive force applied. | N, rad |
| The resonant mass. | kg | |
| K | The stiffness of resonant mode. | N/m |
| , | The change values of the drive-sensing and sensing capacitor. | F |
| , | The voltages of and after capacitance-to-voltage conversion. | V |
| , | The amplitude control and phase-locked control voltages in closed-loop drive. | V |
| , | The angular velocity demodulated signal voltage and force-balance voltage. | V |
| Parameter Name | Simulation Results | Experimental Results | Deviation |
|---|---|---|---|
| Drive mode frequency | 9931 Hz (9737 Hz after compensated) | 9733 Hz | −2.0% (−0.04%) |
| Sensing mode frequency | 9941 Hz (9763 Hz after compensated) | 9765 Hz | −1.8% (0.02%) |
| Thermoelastic quality factor of drive mode | / | ||
| Sensitivity (open-loop) | 0.50 mV/°/s | 0.55 mV/°/s | 10% |
| Tuning frequency | 12.7 Hz (8 V) | 11.8 Hz (8 V) | −7.1% |
| Drive frequency drift | 0.022 Hz (0.7 μm) 0.025 Hz for 1° etching verticality error | 0.040 Hz (0.7 μm) | 60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, C.; He, W.; Jia, L.; Wang, P.; Zhao, K.; Xing, F.; You, Z. Full-System Simulation and Analysis of a Four-Mass Vibratory MEMS Gyroscope. Micromachines 2025, 16, 414. https://doi.org/10.3390/mi16040414
Ouyang C, He W, Jia L, Wang P, Zhao K, Xing F, You Z. Full-System Simulation and Analysis of a Four-Mass Vibratory MEMS Gyroscope. Micromachines. 2025; 16(4):414. https://doi.org/10.3390/mi16040414
Chicago/Turabian StyleOuyang, Chenguang, Wenzheng He, Lu Jia, Peng Wang, Kaichun Zhao, Fei Xing, and Zheng You. 2025. "Full-System Simulation and Analysis of a Four-Mass Vibratory MEMS Gyroscope" Micromachines 16, no. 4: 414. https://doi.org/10.3390/mi16040414
APA StyleOuyang, C., He, W., Jia, L., Wang, P., Zhao, K., Xing, F., & You, Z. (2025). Full-System Simulation and Analysis of a Four-Mass Vibratory MEMS Gyroscope. Micromachines, 16(4), 414. https://doi.org/10.3390/mi16040414








