Precision Position Control of a Voice Coil Motor Using Self-Tuning Fractional Order Proportional-Integral-Derivative Control
Abstract
:1. Introduction
2. Linear Voice Coil Motor
3. Adaptive Differential Evolution Algorithm
- Population: In the initial population step, the DE algorithm generates the initial individual target vector randomly as follows:where i = 1, 2,…, NP, in which NP is the population size; and g represents the g-th generation of the population.
- Mutation: There are several techniques for the mutation of target vector . Commonly, three individual target vectors, , , and among the population are randomly selected to generate the mutant vector according to the following mutation mechanism:where r1 ≠ r2 ≠ r3 ≠ i, and F is a constant mutation factor. In general, the small constant mutation factor F may lead to premature convergence and even convergence at a local optimal solution, whereas a large one may result in poor efficiency with long convergence time. Therefore, an adaptive selection mechanism for the dynamic mutation factor F is adopted to address the mentioned problems as follows [31]:where is a uniformly distributed random variable between (0, 1), ζ is an momentum weight, and λ is an adaptive factor defined aswhere gmax is the maximum generation number, and gnow is the current generation number. Besides, the adaptive factor λ is designed to balance the global exploration and local search abilities as follows:where qd is the threshold of the acceptable improvement rate, λb and λs are the big and small step sizes, respectively, and q is the improvement rate of the fitness value in the specific generation. For the target vector , the improvement rate q can be obtained as follows:where Nq < g is a generation number used for evaluating the improvement rate of the fitness value. According to Equations (7) and (8), the adaptive factor λ is reduced to a small step size λs to strengthen the local search ability when the present fitness value has a favorable improvement. Conversely, the adaptive factor λ is enlarged to a big step size λb to strengthen the global exploration ability when the present fitness value has an unacceptable improvement. Figure 2 shows the mutation operation via a two-dimensional example.
- Crossover: The most common crossover strategy is uniform crossover in which the individual target vector is crossed over with its mutant vector for generating the new trial vector as follows:where , , and are the j-th elements of the vectors , , and , respectively; randj is a uniformly distributed random variable between (0,1); and CR is a predesigned constant crossover rate.
- Selection: The final step in DE algorithm is the selection of the better individual for maximizing the objective function f(D), as shown in Equation (2). The selection process uses a simple replacement of the original target vector with the obtained new trial vector if the latter has a better fitness value. The better individual vector is then selected as a new target vector for the next generation as follows:
4. Proposed Control Methods
4.1. Fractional Order Calculus
4.2. Fractional Order Proportional-Integral-Derivative Control
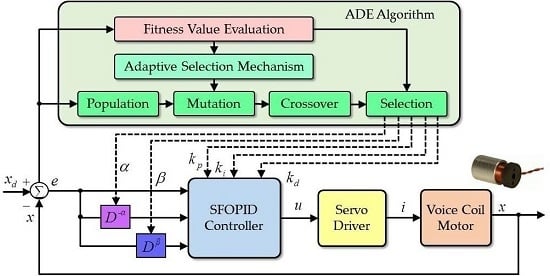
4.3. Self-Tuning Fractional Order Proportional-Integral-Derivative Control
4.4. Digital Implementation for Fractional Order Calculus
5. Experimentation
5.1. Experimental Setup
5.2. Performance Measures and Comparison
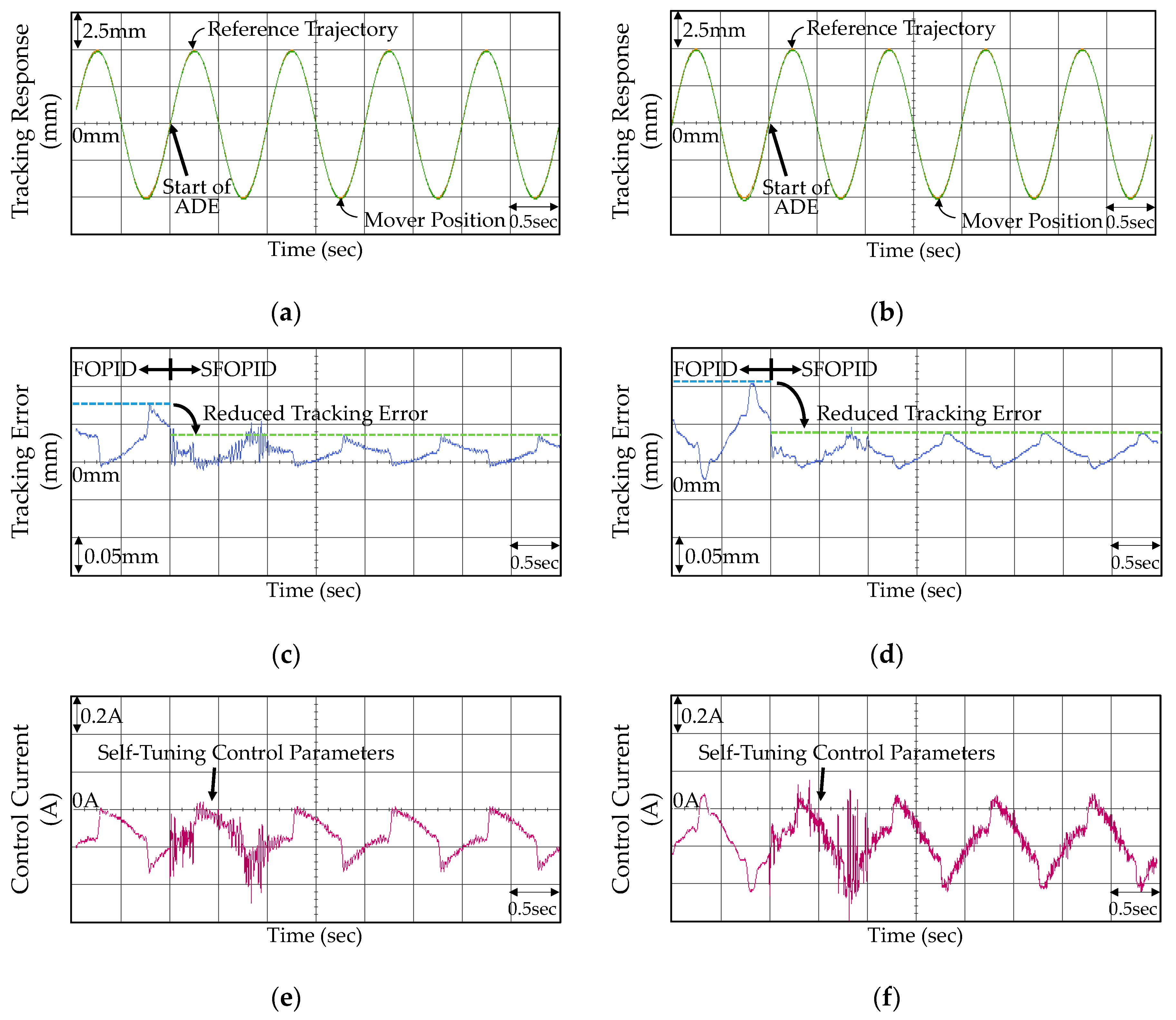
5.3. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Park, Y. Precision motion control of a three degrees of freedom hybrid stage with dual actuators. IET Control Theory Appl. 2008, 2, 392–401. [Google Scholar] [CrossRef]
- Landolsi, T.; Dhaouadi, R.; Aldabbas, O. Beam-stabilized optical switch using a voice-coil motor actuator. J. Frankl. Inst. 2011, 348, 1–11. [Google Scholar] [CrossRef]
- Wu, S.; Jiao, Z.; Yan, L.; Zhang, R.; Yu, J.; Chen, C.Y. Development of a direct-drive servo valve with high-frequency voice coil motor and advanced digital controller. IEEE ASME Trans. Mechatron. 2014, 19, 932–942. [Google Scholar] [CrossRef]
- Christiansen, B.; Maurer, H.; Zirn, O. Optimal control of servo actuators with flexible load and coulombic friction. Eur. J. Control 2011, 17, 19–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, P.; Zhang, Z. High precision tracking control of a servo gantry with dynamic friction compensation. ISA Trans. 2016, 62, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yang, B.T.; Zhu, Y. Modeling and analysis of a novel rectangular voice coil motor for the 6-DOF fine stage of lithographic equipment. Opt. Int. J. Light Electron Opt. 2016, 127, 2246–2250. [Google Scholar] [CrossRef]
- Atsumi, T.; Nakamura, S.; Furukawa, M.; Naniwa, I.; Xu, J. Triple-stage-actuator system of head-positioning control in hard disk drives. IEEE Trans. Magn. 2013, 49, 2738–2743. [Google Scholar] [CrossRef]
- Yu, H.C.; Chen, T.C.; Liu, C.S. Adaptive fuzzy logic proportional-integral-derivative control for a miniature autofocus voice coil motor actuator with retaining force. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Xu, Q. Design and development of a compact flexure-based XY precision positioning system with centimeter range. IEEE Trans. Ind. Electron. 2014, 61, 893–903. [Google Scholar] [CrossRef]
- Pan, J.; Or, S.W.; Zou, Y.; Cheung, N.C. Sliding-mode position control of medium-stroke voice coil motor based on system identification observer. IET Electr. Power Appl. 2015, 9, 620–627. [Google Scholar] [CrossRef]
- Hsu, C.F.; Chen, Y.C. Microcontroller-based B-spline neural position control for voice coil motors. IEEE Trans. Ind. Electron. 2015, 62, 5644–5654. [Google Scholar] [CrossRef]
- De Callafon, R.A.; Nagamune, R.; Horowitz, R. Robust dynamic modeling and control of dual-stage actuators. IEEE Trans. Magn. 2006, 42, 247–254. [Google Scholar] [CrossRef]
- Crowe, J. PID Control: New Identification and Design Methods; Springer: London, UK, 2005. [Google Scholar]
- Yamamoto, T.; Takao, K.; Yamada, T. Design of a data-driven PID controller. IEEE Trans. Control Syst. Technol. 2009, 17, 29–39. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, Y.Q.; Xue, D. Time-constant robust analysis of a fractional order [proportional derivative] controller. IET Control Theory Appl. 2011, 5, 164–172. [Google Scholar] [CrossRef]
- Rajasekhar, A.; Jatoth, R.K.; Abraham, A. Design of intelligent PID/PIλDμ speed controller for chopper fed DC motor drive using opposition based artificial bee colony algorithm. Eng. Appl. Artif. Intell. 2014, 29, 13–32. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Optimal tuning rules for proportional-integral-derivative and fractional-order proportional-integral-derivative controllers for integral and unstable processes. IET Control Theory Appl. 2012, 6, 776–786. [Google Scholar] [CrossRef]
- Zheng, S.; Tang, X.; Song, B. Tuning strategy of fractional-order proportional integral controllers for permanent magnet synchronous motor servo system based on enhanced stochastic multi-parameters divergence-based optimisation algorithm. IET Control Theory Appl. 2016, 10, 1240–1249. [Google Scholar] [CrossRef]
- Bingul, Z.; Karahan, O. Fractional PID controllers tuned by evolutionary algorithms for robot trajectory control. Turk. J. Electr. Eng. Comput. Sci. 2012, 20, 1123–1136. [Google Scholar]
- Tran, H.K.; Chiou, J.S. PSO-based algorithm applied to quadcopter micro air vehicle controller design. Micromachines 2016, 7, 168. [Google Scholar] [CrossRef]
- Panda, B.; Garg, A.; Jian, Z.; Heidarzadeh, A.; Gao, L. Characterization of the tensile properties of friction stir welded aluminum alloy joints based on axial force, traverse speed, and rotational speed. Front. Mech. Eng. 2016, 11, 289–298. [Google Scholar] [CrossRef]
- Wari, E.; Zhu, W. A survey on metaheuristics for optimization in food manufacturing industry. Appl. Soft Comput. 2016, 46, 328–343. [Google Scholar] [CrossRef]
- Mallol-Poyato, R.; Jiménez-Fernández, S.; Díaz-Villar, P.; Salcedo-Sanz, S. Joint optimization of a Microgrid’s structure design and its operation using a two-steps evolutionary algorithm. Energy 2016, 94, 775–785. [Google Scholar] [CrossRef]
- Fan, T.E.; Shao, G.F.; Ji, Q.S.; Zheng, J.W.; Liu, T.D.; Wen, Y.H. A multi-populations multi-strategies differential evolution algorithm for structural optimization of metal nanoclusters. Comput. Phys. Commun. 2016, 208, 64–72. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lu, X.; Tian, L.; Yu, Z.; Huang, K.; Wang, Y.; Li, T. Optimal layout design of obstacles for panic evacuation using differential evolution. Phys. A Stat. Mech. Appl. 2017, 465, 175–194. [Google Scholar] [CrossRef]
- Baraldi, P.; Cannarile, F.; Maio, F.D.; Zio, E. Hierarchical k-nearest neighbours classification and binary differential evolution for fault diagnostics of automotive bearings operating under variable conditions. Eng. Appl. Artif. Intell. 2016, 56, 1–13. [Google Scholar] [CrossRef]
- Chen, C.H.; Lin, C.J.; Lin, C.T. Nonlinear system control using adaptive neural fuzzy networks based on a modified differential evolution. IEEE Trans. Syst. Man Cybernet. Part C Appl. Rev. 2009, 39, 459–473. [Google Scholar] [CrossRef]
- Slowik, A. Application of an adaptive differential evolution algorithm with multiple trial vectors to artificial neural network training. IEEE Trans. Ind. Electron. 2011, 58, 3160–3167. [Google Scholar] [CrossRef]
- Meng, K.; Dong, Z.Y.; Wong, K.P. Self-adaptive radial basis function neural network for short-term electricity price forecasting. IET Gener. Transm. Distrib. 2009, 3, 325–335. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evolut. Comput. 2009, 13, 398–416. [Google Scholar] [CrossRef]
- Lee, W.P.; Chien, C.W.; Cai, W.T. Improving the performance of differential evolution algorithm with modified mutation factor. J. Adv. Eng. 2011, 10, 255–261. [Google Scholar]
- Islam, S.M.; Das, S.; Ghosh, S.; Roy, S.; Suganthan, P.N. An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization. IEEE Trans. Syst. Man Cybernet. Part B Cybernet. 2012, 42, 482–500. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Dong, Y.; Liu, J. Differential evolution with an individual-dependent mechanism. IEEE Trans. Evolut. Comput. 2015, 19, 560–573. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Petras, I.; Xue, D. Fractional order control—A tutorial. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411.
- Tang, Y.; Zhang, X.; Zhang, D.; Zhao, G.; Guan, X. Fractional order sliding mode controller design for antilock braking systems. Neurocomputing 2013, 111, 122–130. [Google Scholar] [CrossRef]
- Pashaei, S.; Badamchizadeh, M. A new fractional-order sliding mode controller via a nonlinear disturbance observer for a class of dynamical systems with mismatched disturbances. ISA Trans. 2016, 63, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Vinagre, B.M.; Chen, Y.Q.; Petras, I. Two direct Tustin discretization methods for fractional-order differentiator/integrator. J. Frankl. Inst. 2003, 340, 349–362. [Google Scholar] [CrossRef]











| Controllers | Performance Measures (μm) | Improvement Rates (%) | ||||
|---|---|---|---|---|---|---|
| PM | PA | PS | PM | PA | PS | |
| PID | 105 | 42 | 33 | Baseline | Baseline | Baseline |
| FOPID | 78 | 31 | 20 | 25.71 | 26.19 | 39.39 |
| SFOPID | 35 | 13 | 9 | 66.67 | 69.05 | 72.73 |
| Controllers | Performance Measures (μm) | Improvement Rates (%) | ||||
|---|---|---|---|---|---|---|
| PM | PA | PS | PM | PA | PS | |
| PID | 142 | 55 | 37 | Baseline | Baseline | Baseline |
| FOPID | 106 | 42 | 29 | 25.35 | 23.64 | 21.62 |
| SFOPID | 39 | 16 | 11 | 72.54 | 70.91 | 70.27 |
| Controllers | Performance Measures | Improvement Rates (%) | ||||
|---|---|---|---|---|---|---|
| Mo (mm) | PA (mm) | Ts (sec) | Mo | PA | Ts | |
| PID | 2.69 | 0.42 | 0.227 | Baseline | Baseline | Baseline |
| FOPID | 1.65 | 0.22 | 0.085 | 38.66 | 47.62 | 62.56 |
| SFOPID | 1.03 | 0.19 | 0.046 | 61.71 | 54.76 | 79.74 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-Y.; Chia, C.-S. Precision Position Control of a Voice Coil Motor Using Self-Tuning Fractional Order Proportional-Integral-Derivative Control. Micromachines 2016, 7, 207. https://doi.org/10.3390/mi7110207
Chen S-Y, Chia C-S. Precision Position Control of a Voice Coil Motor Using Self-Tuning Fractional Order Proportional-Integral-Derivative Control. Micromachines. 2016; 7(11):207. https://doi.org/10.3390/mi7110207
Chicago/Turabian StyleChen, Syuan-Yi, and Chen-Shuo Chia. 2016. "Precision Position Control of a Voice Coil Motor Using Self-Tuning Fractional Order Proportional-Integral-Derivative Control" Micromachines 7, no. 11: 207. https://doi.org/10.3390/mi7110207
APA StyleChen, S.-Y., & Chia, C.-S. (2016). Precision Position Control of a Voice Coil Motor Using Self-Tuning Fractional Order Proportional-Integral-Derivative Control. Micromachines, 7(11), 207. https://doi.org/10.3390/mi7110207