Size-Adjustable Microdroplets Generation Based on Microinjection
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Critical Injection Model
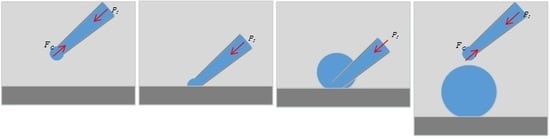
2.2. Substrate-Contacting Method of Microdroplet Generation
- (1)
- The micropipette is immersed in the oil-phase liquid medium and adjusted to a preset injection pressure.
- (2)
- The micropipette is moved down to contact the substrate, then, the interface at the micropipette opening collapses as a result of the intermolecular forces between the liquid molecules and the substrate molecules.
- (3)
- Maintaining the substrate-contacting situation of the micropipette, the liquid in the micropipette flows out under injection pressure; therefore, the microdroplet radius increases gradually.
- (4)
- The micropipette is lifted to end the substrate-contacting situation when the microdroplet radius reaches the desired size; thus, the microdroplet dispenses from the micropipette. The Laplace pressure of the interface balances the injection pressure, which ceases the liquid injection.
3. Results
3.1. System Setup and Materials
3.1.1. System Setup
3.1.2. Materials
3.1.3. The Hybrid Substrate
3.2. Critical Injection Experiments
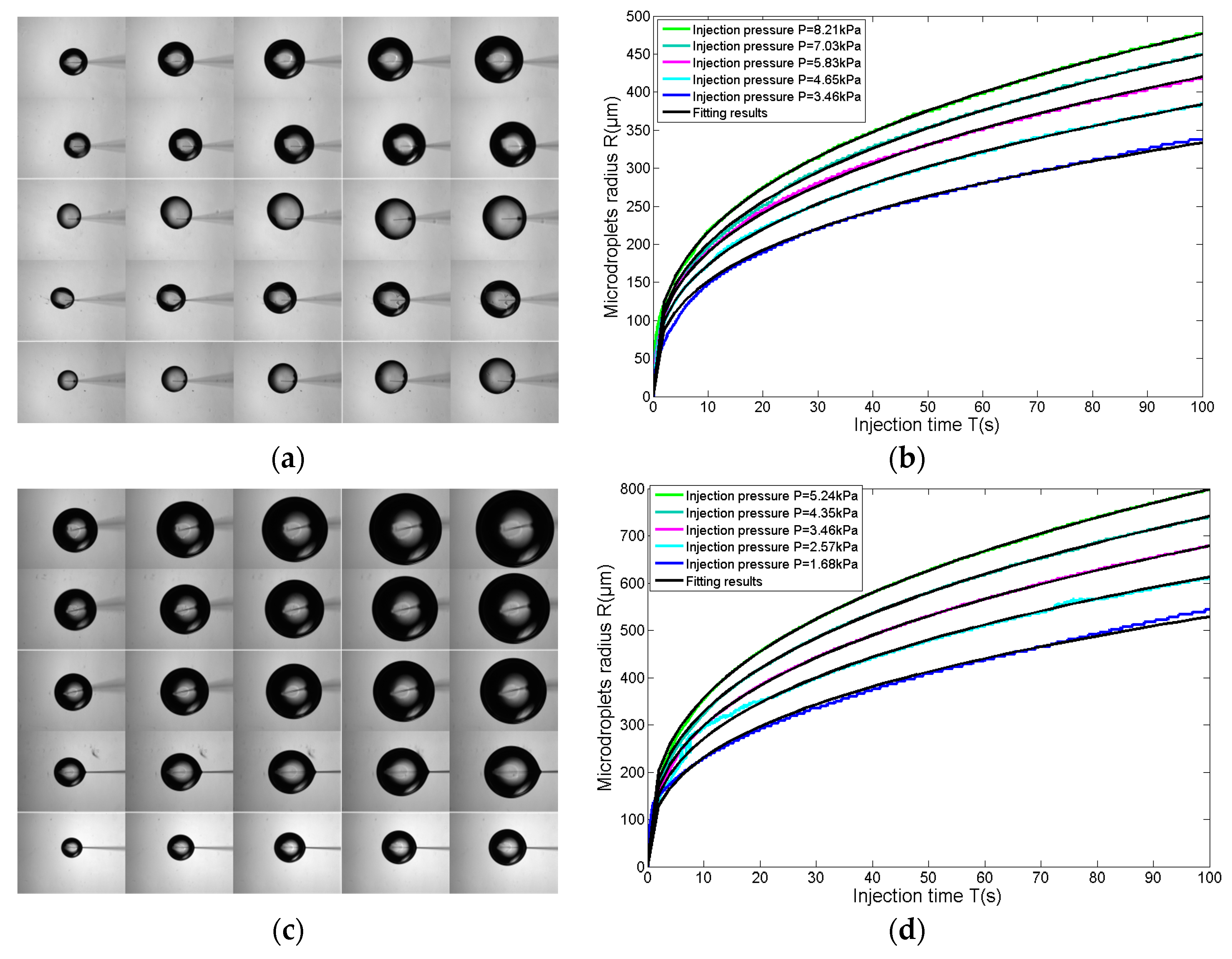
3.3. Size Adjustable Microdroplets Generation Based on the Substrate-Contacting Method
3.3.1. Microdroplet Generation Based on the Substrate-Contacting Method
3.3.2. Size-Adjustable Microdroplet Generation Based on the Substrate-Contacting Method
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Theberge, A.B.; Courtois, F.; Schaerli, Y.; Fischlechner, M.; Abell, C.; Hollfelder, F.; Huck, W.T. Microdroplets in microfluidics: An evolving platform for discoveries in chemistry and biology. Angew. Chem. Int. Ed. 2010, 49, 5846–5868. [Google Scholar] [CrossRef] [PubMed]
- Maeda, K.; Onoe, H.; Takinoue, M.; Takeuchi, S. Controlled synthesis of 3D multi-compartmental particles with centrifuge-based microdroplet formation from a multi-barrelled capillary. Adv. Mater. 2012, 24, 1340–1346. [Google Scholar] [CrossRef] [PubMed]
- Ng, K.C.; Whitten, W.B.; Arnold, S.; Ramsey, J.M. Digital chemical analysis of dilute microdroplets. Anal. Chem. 1992, 64, 2914–2919. [Google Scholar] [CrossRef]
- Maeki, M.; Yamaguchi, H.; Yamashita, K.; Nakamura, H.; Miyazaki, M.; Maeda, H. Analysis of kinetic behavior of protein crystallization in nanodroplets. Chem. Lett. 2011, 40, 825–827. [Google Scholar] [CrossRef]
- Um, E.; Lee, S.G.; Park, J.K. Random breakup of microdroplets for single-cell encapsulation. Appl. Phys. Lett. 2010, 97, 153703. [Google Scholar] [CrossRef]
- Weitz, M.; Mückl, A.; Kapsner, K.; Berg, R.; Meyer, A.; Simmel, F.C. Communication and computation by bacteria compartmentalized within microemulsion droplets. J. Am. Chem. Soc. 2014, 136, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Garstecki, P.; Fuerstman, M.J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction-scaling and mechanism of break-up. Lab Chip 2006, 6, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.H.; Li, S.W.; Tan, J.; Wang, Y.J.; Luo, G.S. Preparation of highly monodisperse droplet in a T-Junction microfluidic device. AIChE J. 2006, 52, 3005–3010. [Google Scholar] [CrossRef]
- Wang, K.; Lu, Y.C.; Xu, J.H.; Tan, J.; Luo, G.S. Generation of micromonodispersed droplets and bubbles in the capillary embedded T-junction microfluidic devices. AIChE J. 2010, 57, 299–306. [Google Scholar] [CrossRef]
- Hsiung, S.K.; Chen, C.T.; Lee, G.B. Micro-droplet formation utilizing microfluidic flow focusing and controllable moving-wall chopping techniques. J. Micromech. Microeng. 2006, 16, 2403–2410. [Google Scholar] [CrossRef]
- Wu, N.; Zhu, Y.; Leech, P.W.; Sexton, B.A.; Brown, S.; Easton, C. Effects of surfactants on the formation of microdroplets in the flow focusing microfluidic device. Proc. SPIE Int. Soc. Opt. Eng. 2007, 6799, U84–U91. [Google Scholar]
- Jiang, C.Y.; Dong, L.; Zhao, J.K.; Hu, X.; Shen, C.; Qiao, Y.; Zhang, X.; Wang, Y.; Ismagilov, R.F.; Liu, S.J.; et al. High-throughput single-cell cultivation on microfluidic streak plates. Appl. Environ. Microbiol. 2016, 82, 2210. [Google Scholar] [CrossRef] [PubMed]
- Barbulovic-Nad, I.; Lucente, M.; Sun, Y.; Zhang, M.; Wheeler, A.R.; Bussmann, M. Bio-microarray fabrication techniques—A review. Crit. Rev. Biotechnol. 2006, 26, 237–259. [Google Scholar] [CrossRef] [PubMed]











| r (μm) | Measured CI Pressure (kPa) | Theory CI Pressure (kPa) |
|---|---|---|
| 2.08 | 15.63 | 13.52 |
| 2.42 | 10.50 | 11.62 |
| 2.77 | 12.63 | 11.15 |
| 3.11 | 8.21 | 9.04 |
| 3.46 | 7.72 | 8.13 |
| 4.50 | 5.60 | 6.25 |
| 5.19 | 5.30 | 5.42 |
| 5.53 | 5.17 | 5.09 |
| 7.27 | 3.66 | 3.87 |
| 11.76 | 2.41 | 2.39 |
| 16.26 | 1.62 | 1.73 |
| P (kPa) | Fitting Formula | Goodness of Fit | Fitting Formula | Goodness of Fit |
|---|---|---|---|---|
| 6.73 | 0.9958 | 0.991 | ||
| 8.21 | 0.9905 | 0.989 | ||
| 9.7 | 0.9896 | 0.9807 | ||
| 11.18 | 0.9883 | 0.9805 | ||
| 12.67 | 0.9946 | 0.9921 |
| P (kPa) | Fitting Formula | Goodness of Fit |
|---|---|---|
| 3.46 | 0.99 | |
| 4.65 | 0.99 | |
| 5.83 | 0.99 | |
| 7.03 | 0.99 | |
| 8.21 | 0.99 |
| P (kPa) | Fitting Formula | Goodness of Fit |
|---|---|---|
| 1.68 | 0.99 | |
| 2.57 | 0.99 | |
| 3.46 | 0.99 | |
| 4.35 | 0.99 | |
| 5.24 | 0.99 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zheng, D.; Li, N.; Wang, X.; Liu, Y.; Sun, M.; Zhao, X. Size-Adjustable Microdroplets Generation Based on Microinjection. Micromachines 2017, 8, 88. https://doi.org/10.3390/mi8030088
Li S, Zheng D, Li N, Wang X, Liu Y, Sun M, Zhao X. Size-Adjustable Microdroplets Generation Based on Microinjection. Micromachines. 2017; 8(3):88. https://doi.org/10.3390/mi8030088
Chicago/Turabian StyleLi, Shibao, Deyin Zheng, Na Li, Xuefeng Wang, Yaowei Liu, Mingzhu Sun, and Xin Zhao. 2017. "Size-Adjustable Microdroplets Generation Based on Microinjection" Micromachines 8, no. 3: 88. https://doi.org/10.3390/mi8030088
APA StyleLi, S., Zheng, D., Li, N., Wang, X., Liu, Y., Sun, M., & Zhao, X. (2017). Size-Adjustable Microdroplets Generation Based on Microinjection. Micromachines, 8(3), 88. https://doi.org/10.3390/mi8030088