Method of Calculating the Inductance Value of MEMS Suspended Inductors with Silicon Substrates
Abstract
:1. Introduction
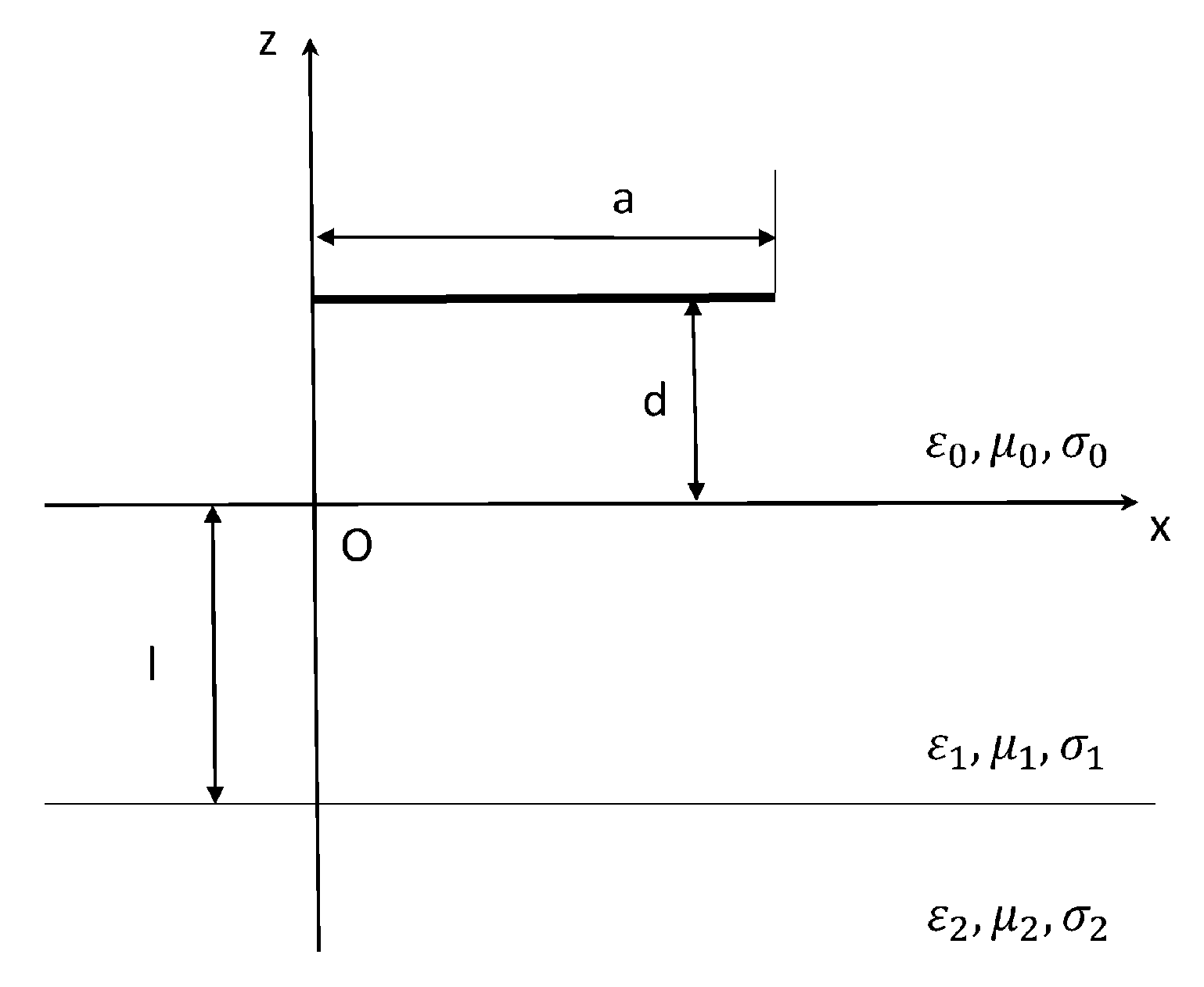
2. Inductance of the Suspended Inductors on a Silicon Substrate
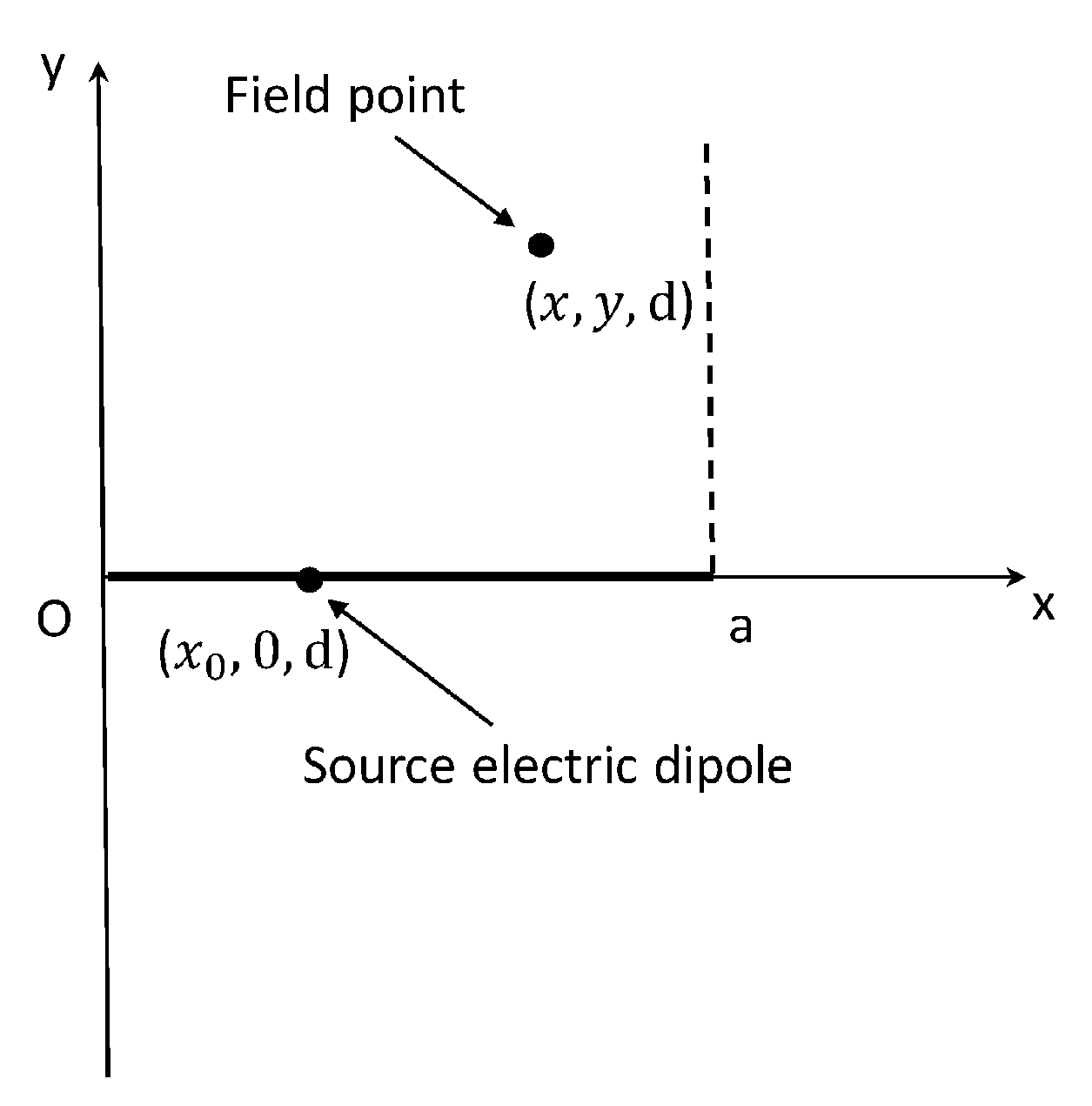
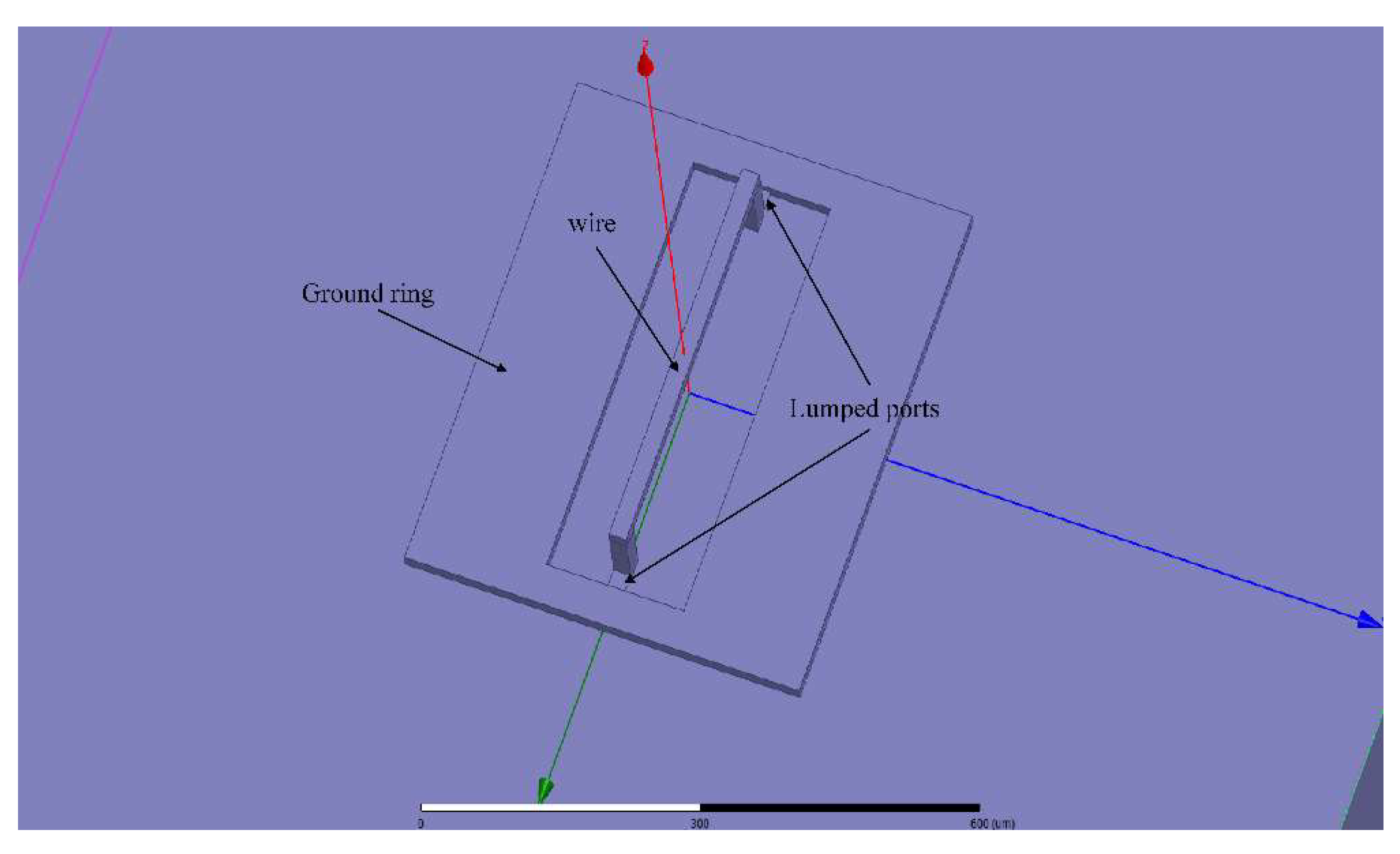
2.1. Calculation of the Inductance Value of the Suspended Inductor Consisting of a Single Wire
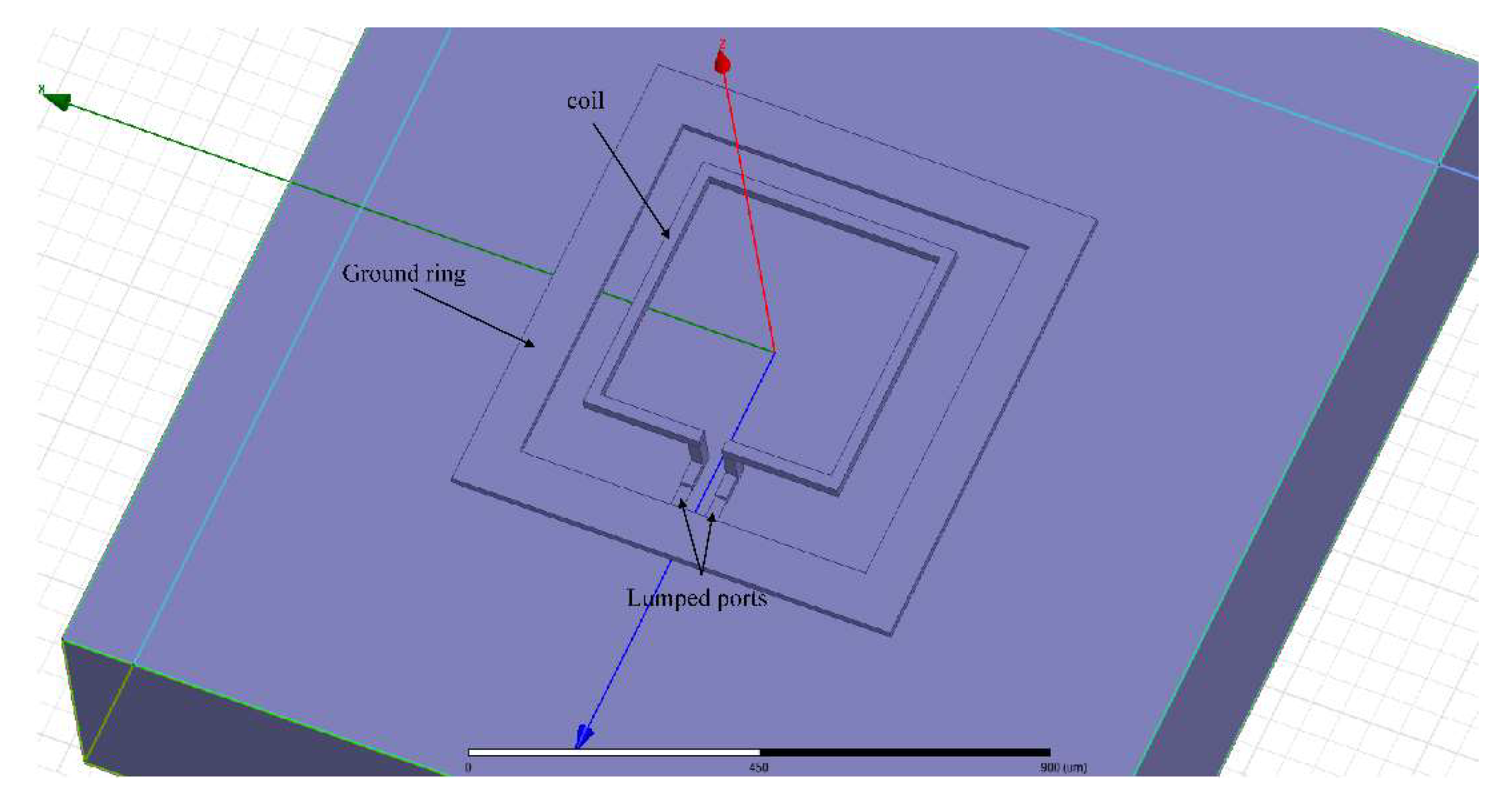
2.2. Calculation of the Inductance Value of the Suspended Inductor Consisting of a Single Rectangular Coil
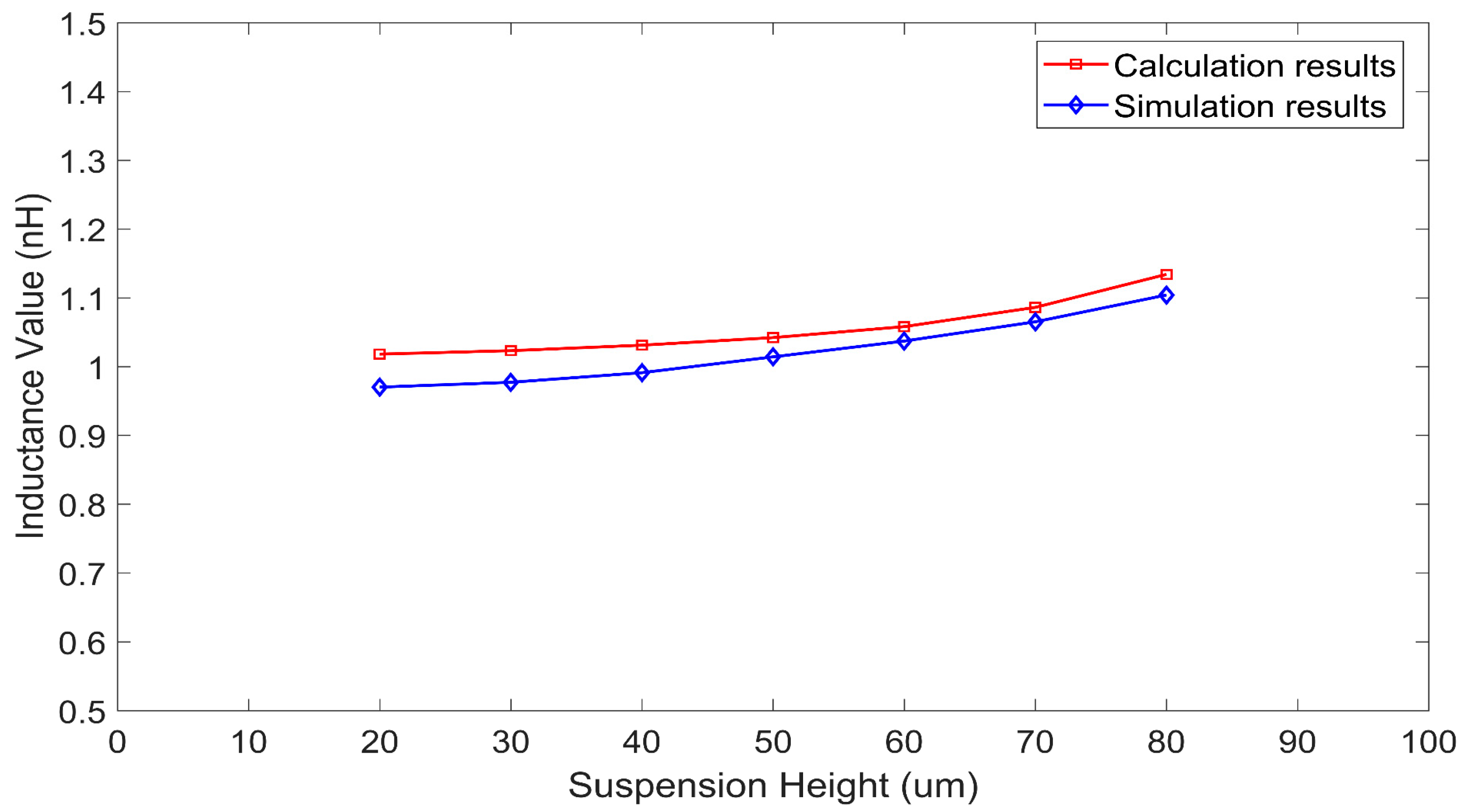
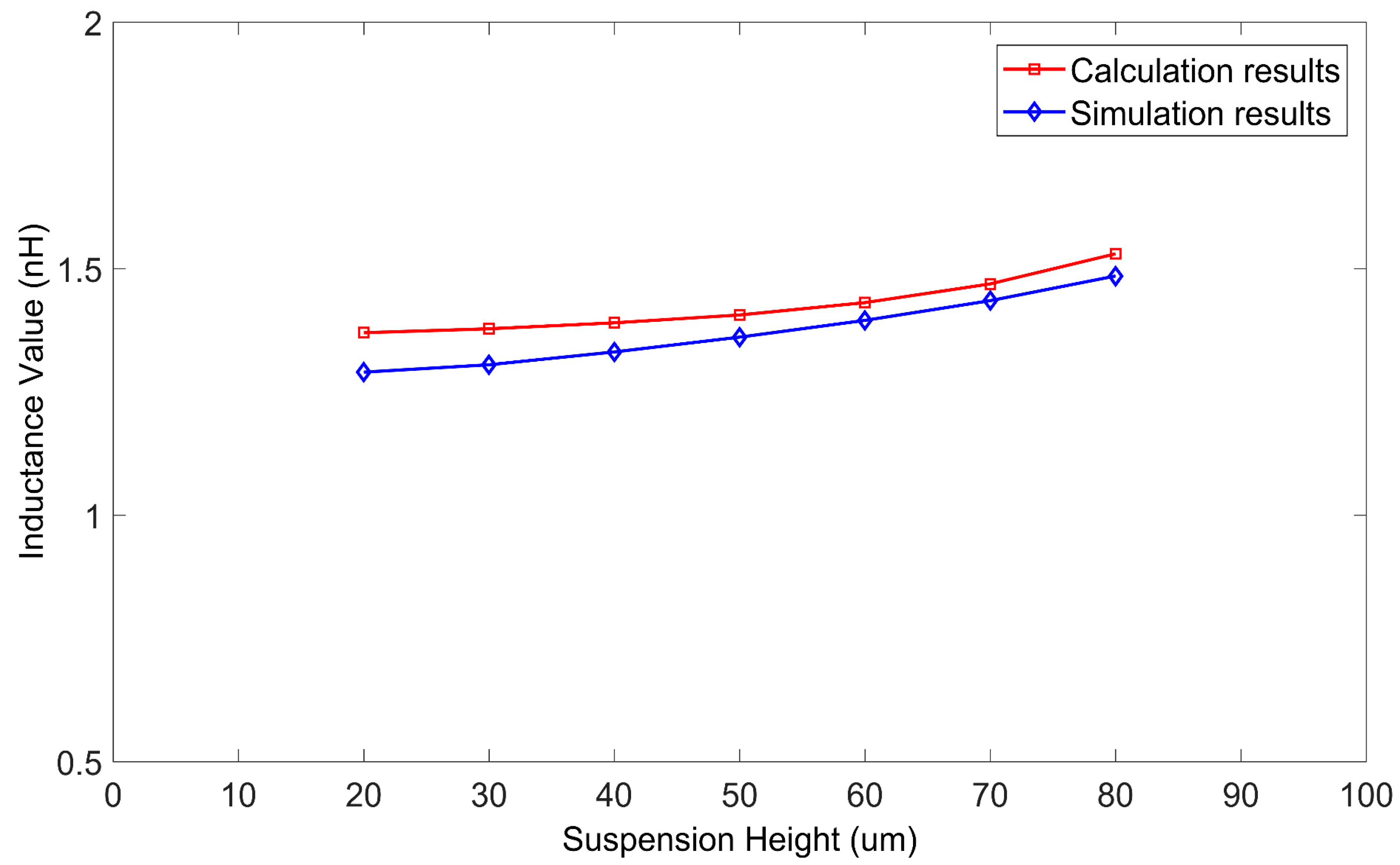
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hsieh, M.C.; Fang, Y.K.; Chen, C.H. Design and fabrication of deep submicron CMOS technology compatible suspended high-Q inductors. IEEE Trans. Electron Devices 2004, 51, 324–331. [Google Scholar] [CrossRef]
- Tai, C.M.; Liao, C.N. Multilevel suspended thin-film inductors on silicon wafers. IEEE Trans. Electron Devices 2007, 54, 1510–1514. [Google Scholar] [CrossRef]
- Yishay, R.B.; Stolyarova, S.; Shapira, S.; Musiya, M.; Kryger, D.; Shiloh, Y.; Nemirovsky, Y. A CMOS low noise amplifier with integrated front-side micromachined inductor. Microelectr. J. 2011, 42, 754–757. [Google Scholar] [CrossRef]
- Hikmat, O.F.; Ali, M.S.M. RF MEMS inductors and their applications—A Review. J. Microelectromech. Syst. 2017, 26, 17–44. [Google Scholar] [CrossRef]
- Yoon, J.B.; Han, C.H.; Yoon, E.; Kim, C.K. Monolithic high-Q overhang inductors fabricated on silicon and glass substrates. In Proceedings of the IEEE International Electron Devices Meeting, Washington, DC, USA, 5–8 December 1999; pp. 753–756. [Google Scholar]
- Yoon, J.B.; Han, C.H.; Yoon, E.; Kim, C.K. High-performance three-dimensional on-chip inductors fabricated by novel micromachining technology for RF MMIC. In Proceedings of the IEEE International Microwave Symposium Digest, Anaheim, CA, USA, 13–19 June 1999; pp. 1523–1526. [Google Scholar]
- Greenhouse, H.M. Design of planar rectangular microelectronic inductors. IEEE Trans. Parts Hybrids Packag. 1974, 10, 101–109. [Google Scholar] [CrossRef]
- Mohan, S.S.; del Mar Hershenson, M.; Boyd, S.P.; Lee, T.H. Simple accurate expressions for planar spiral inductors. IEEE J. Solid-State Circuits 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
- Yue, C.P.; Wong, S.S. Physical modeling of spiral inductors on silicon. IEEE Trans. Electron Devices 2000, 47, 560–568. [Google Scholar] [CrossRef] [Green Version]
- Palan, B.; Torki, K.; Courtois, B.; Husak, M. Design and characterization of levitated suspended RF inductors. Proc. SPIE Int. Soc. Opt. Eng. 2002, 4755, 97–104. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, C.; Sangster, A.J. Theoretical and experimental studies of flip-chip assembled high-Q suspended MEMS inductors. IEEE Trans. Microw. Theory Tech. 2007, 55, 1171–1181. [Google Scholar] [CrossRef]
- Lee, J.; Park, S.; Kim, H.C.; Chun, K. Substrates and dimension dependence of MEMS inductors. J. Micromech. Microeng. 2009, 19. [Google Scholar] [CrossRef]
- King, R.W.P. The electromagnetic field of a horizontal electric dipole in the presence of a three-layered region. J. Appl. Phys. 1991, 69, 7987–7995. [Google Scholar] [CrossRef]
- King, R.W.P. The electromagnetic field of a horizontal electric dipole in the presence of a three-layered region: Supplement. J. Appl. Phys. 1993, 74, 4845–4848. [Google Scholar] [CrossRef]
- King, R.W.P.; Sandler, S.S. The electromagnetic field of a vertical electric dipole in the presence of a three-layered region. Radio Sci. 1994, 29, 97–113. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Pan, W.Y. Electromagnetic field of a horizontal electric dipole over a perfect conductor coated with a dielectric layer. Chin. J. Radio Sci. 2001, 16, 367–374. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Pan, W.Y. Electromagnetic field of a vertical electric dipole on a perfect conductor coated with a dielectric layer. Radio Sci. 2002, 37, 1–7. [Google Scholar] [CrossRef]
- Li, K. Electromagnetic Fields in Stratified Media; Springer: New York, NY, USA, 2009. [Google Scholar]
- Zhi, Y.J.; Li, K.; Fang, Y.T. Electromagnetic field of a horizontal infinitely long wire over the dielectric-coated earth. IEEE Trans. Antennas Propag. 2012, 60, 360–366. [Google Scholar] [CrossRef]
- Abamowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Kalantarov, P.L.; Tseytlin, L.A. Handbook of Inductance Calculation; China Machine Press: Beijing, China, 1992. [Google Scholar]
- Yoon, J.B.; Choi, Y.S.; Kim, B.L.; Eo, Y.; Yoon, E. CMOS-compatible surface-micromachined suspended-spiral inductors for multi-GHz silicon RF ICs. IEEE Electron Device Lett. 2002, 23, 591–593. [Google Scholar] [CrossRef]







| Length of the Wire/μm | Computation Time of the Method in this Paper/s | Computation Time of HFSS/s |
|---|---|---|
| 100 | 10.82 | 43.81 |
| 150 | 11.72 | 46.39 |
| 200 | 19.55 | 46.67 |
| 250 | 22.58 | 46.14 |
| 300 | 24.98 | 46.66 |
| 350 | 26.05 | 45.82 |
| 400 | 28.66 | 49.68 |
| 450 | 30.09 | 50.10 |
| 500 | 31.45 | 56.04 |
| Side Length of the Wire/μm | Computation Time of the Method in this Paper/s | Computation Time of HFSS/s |
|---|---|---|
| 400 | 44.26 | 72.24 |
| 500 | 44.95 | 80.86 |
| Frequency/GHz | Skin Depth/μm |
|---|---|
| 0.1 | 6.61 |
| 0.5 | 2.96 |
| 1 | 2.09 |
| 3 | 1.21 |
| 5 | 0.94 |
| 7 | 0.79 |
| 9 | 0.69 |
| 10 | 0.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, J.; Xu, L. Method of Calculating the Inductance Value of MEMS Suspended Inductors with Silicon Substrates. Micromachines 2018, 9, 604. https://doi.org/10.3390/mi9110604
Li Y, Li J, Xu L. Method of Calculating the Inductance Value of MEMS Suspended Inductors with Silicon Substrates. Micromachines. 2018; 9(11):604. https://doi.org/10.3390/mi9110604
Chicago/Turabian StyleLi, Yiyuan, Jianhua Li, and Lixin Xu. 2018. "Method of Calculating the Inductance Value of MEMS Suspended Inductors with Silicon Substrates" Micromachines 9, no. 11: 604. https://doi.org/10.3390/mi9110604
APA StyleLi, Y., Li, J., & Xu, L. (2018). Method of Calculating the Inductance Value of MEMS Suspended Inductors with Silicon Substrates. Micromachines, 9(11), 604. https://doi.org/10.3390/mi9110604





