Design and Fabrication of a Microfluidic Viscometer Based on Electrofluidic Circuits
Abstract
:1. Introduction
2. Materials and Methods
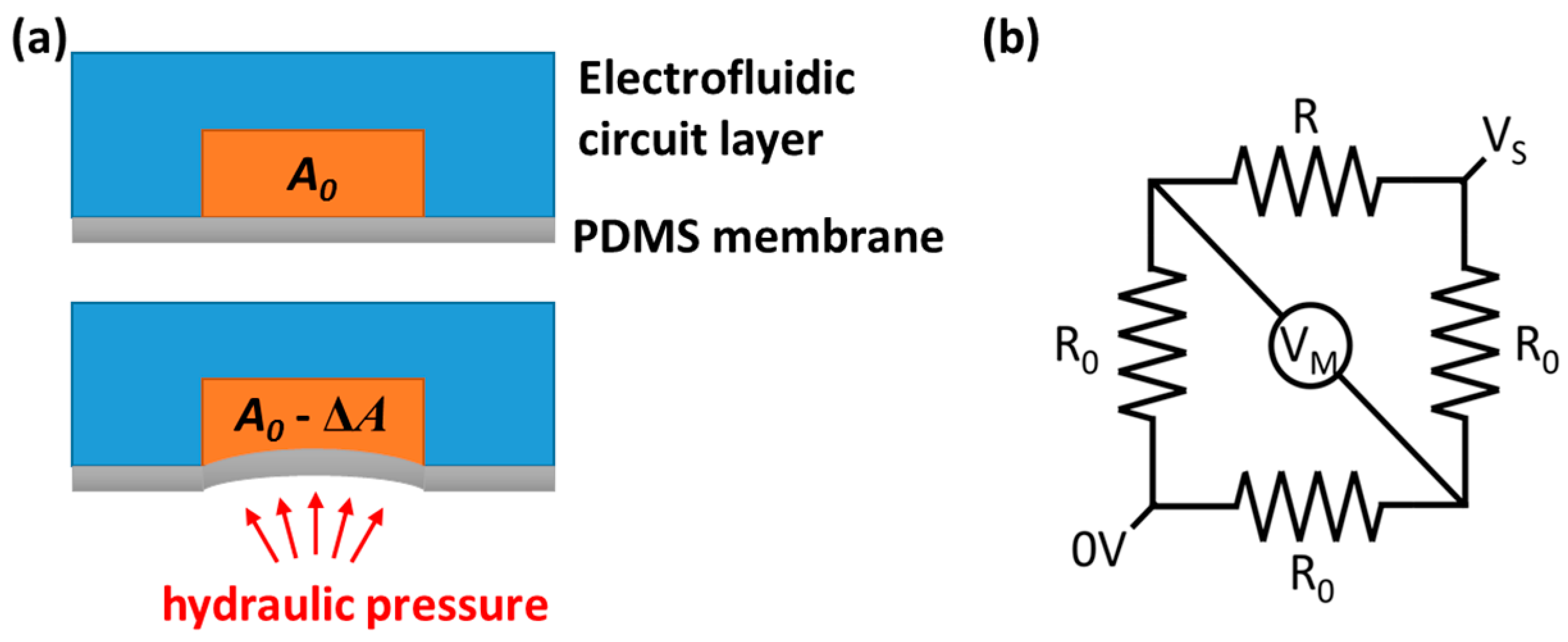
2.1. Design and Fabrication of the Microfluidic Chip
2.2. Theoretical Derivation and Simulation
2.3. Experimental Setup and Procedure
3. Results
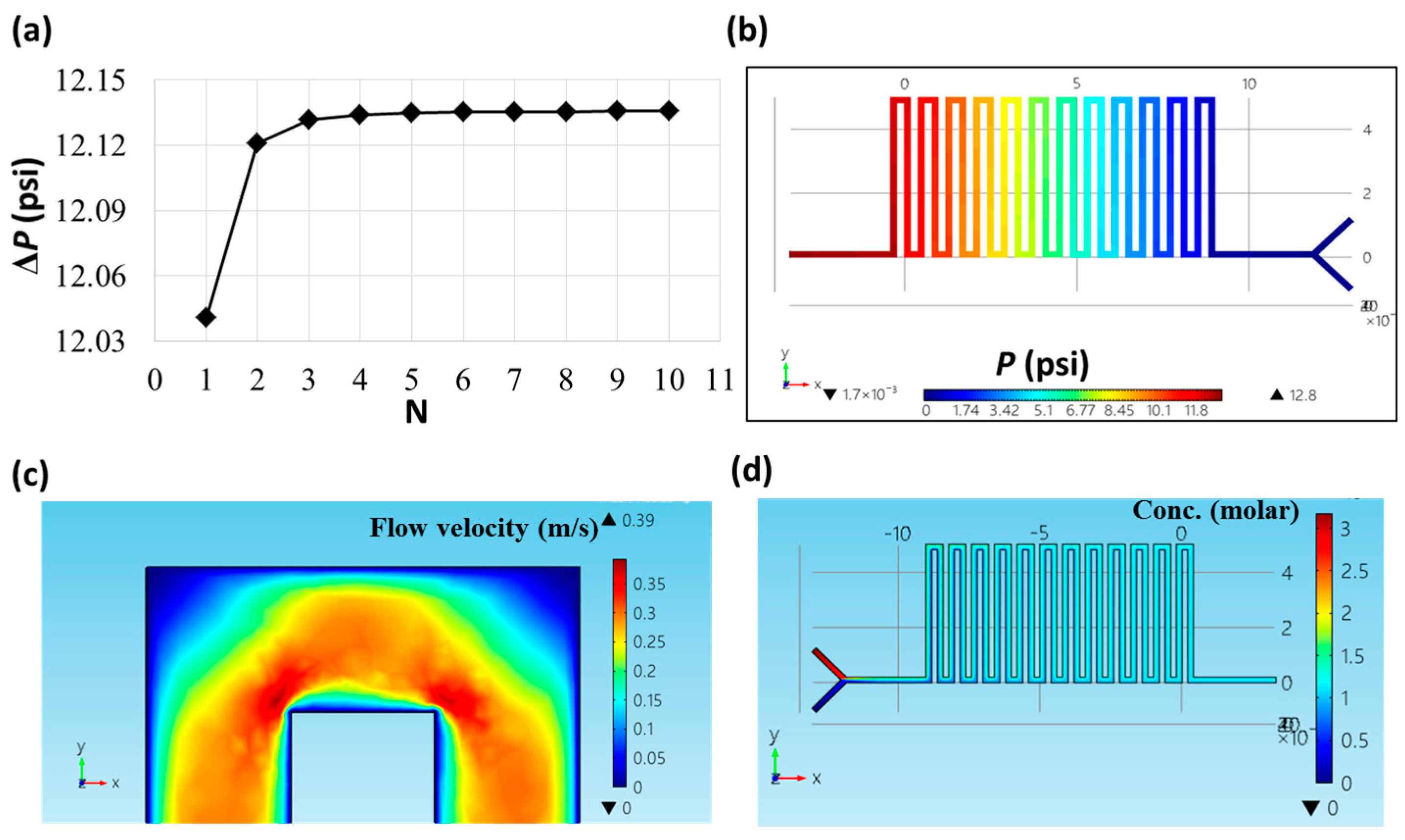
3.1. Calculation and Simulation
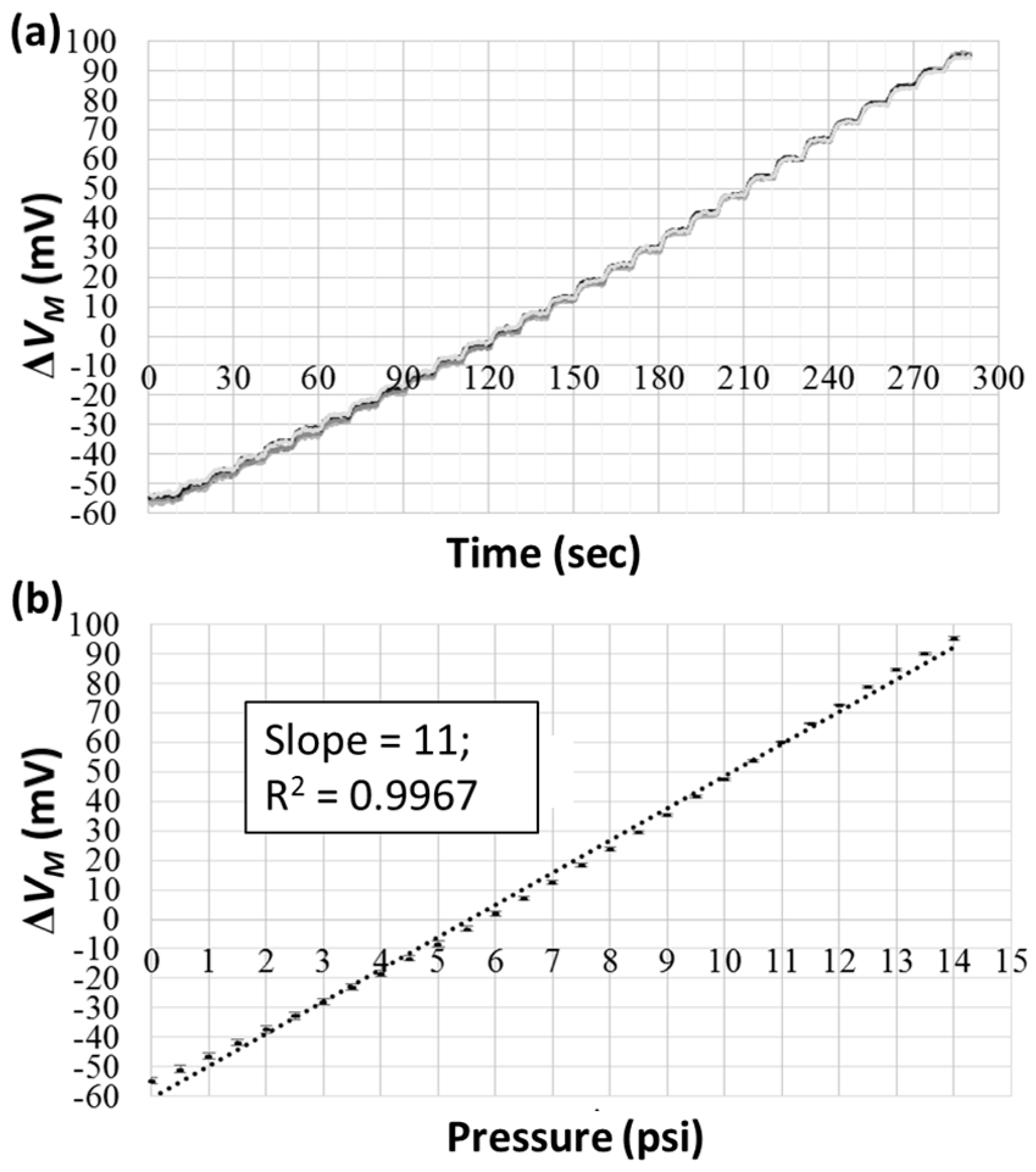
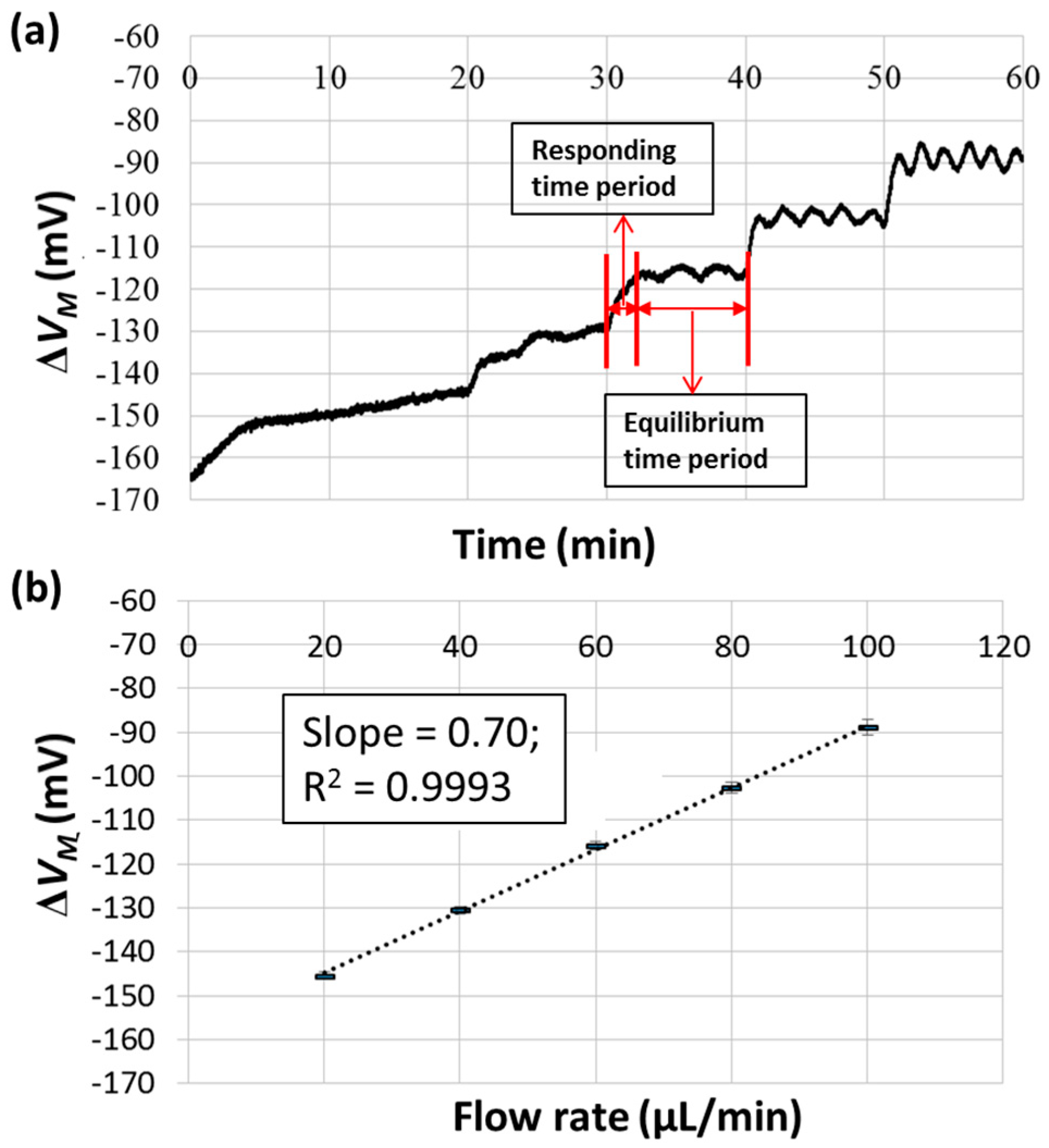
3.2. Gas and Pure Water Test
3.3. Samples with Different Viscosities
3.4. Comparison with Other Devices
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Inman, B.A.; Etienne, W.; Rubin, R.; Owusu, R.A.; Oliveira, T.R.; Rodriques, D.B.; Maccarini, P.F.; Stauffer, P.R.; Mashal, A.; Dewhirst, M.W. The impact of temperature and urinary constituents on urine viscosity and its relevance to bladder hyperthermia treatment. Int. J. Hyperth. 2013, 29, 206–210. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Blanco, J.C.; Martinez-Reina, F.J.; Cruz, D.; Pagador, J.B.; Sanchez-Margallo, F.M.; Soria, F. Fluid Structural Analysis of Urine Flow in a Stented Ureter. Comput. Math. Method. Med. 2016, 2016, 5710798. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.W.; Choi, Y.H.; Lee, S.B.; Baba, Y.; Kim, H.H.; Suh, S.H. Analysis of Urine Flow in Three Different Ureter Models. Comput. Math. Method. Med. 2017, 2017, 5172641. [Google Scholar] [CrossRef] [PubMed]
- Maple Syrup Urine Disease (MSUD). Available online: http://ashlandscience.shoutwiki.com/wiki/Maple_Syrup_Urine_Disease_(MSUD) (accessed on 17 July 2018).
- Roitman, E.V.; Dement’eva, I.I.; Kolpakov, P.E. [Urine viscosity in the evaluation of homeostasis in heart surgery patients in the early postoperative period]. Klin. Lab. Diagn. 1995, Jul–Aug, 29–31. [Google Scholar]
- Yabuno, H.; Higashino, K.; Kuroda, M.; Yamamoto, Y. Self-excited vibrational viscometer for high-viscosity sensing. J. Appl. Phys. 2014, 116, 124305. [Google Scholar] [CrossRef] [Green Version]
- Fukunaga, K.; Onuki, M.; Ohtsuka, Y.; Hirano, T.; Sakai, K.; Ohgoe, Y.; Katoh, A.; Yaguchi, T.; Funakubo, A.; Fukui, Y. Blood viscometer applying electromagnetically spinning method. J. Artif. Organs 2013, 16, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Sakai, K.; Hirano, T.; Hosoda, M. Electromagnetically Spinning Sphere Viscometer. Appl. Phys. Express 2010, 3, 016602. [Google Scholar] [CrossRef]
- Almasi, M. Temperature dependence and chain length effect on density and viscosity of binary mixtures of nitrobenzene and 2-alcohols. J. Mol. Liq. 2015, 209, 346–351. [Google Scholar] [CrossRef]
- Torin-Ollarves, G.A.; Martin, M.C.; Chamorro, C.R.; Segovia, J.J. Densities, viscosities, and isobaric heat capacities of the system (1-butanol + cyclohexane) at high pressures. J. Chem. Thermodyn. 2014, 74, 153–160. [Google Scholar] [CrossRef]
- Regueira, T.; Lugo, L.; Fandino, O.; Lopez, E.R.; Fernandez, J. Compressibilities and viscosities of reference and vegetable oils for their use as hydraulic fluids and lubricants. Green Chem. 2011, 13, 1293–1302. [Google Scholar] [CrossRef]
- Srivastava, N.; Davenport, R.D.; Burns, M.A. Nanoliter viscometer for analyzing blood plasma and other liquid samples. Anal. Chem. 2005, 77, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Burns, M.A. Analysis of non-Newtonian liquids using a microfluidic capillary viscometer. Anal. Chem. 2006, 78, 1690–1696. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Tang, X.; Zheng, B. A PDMS viscometer for microliter Newtonian fluid. J. Micromech. Microeng. 2007, 17, 1828–1834. [Google Scholar] [CrossRef]
- Kang, Y.J.; Yang, S. Integrated microfluidic viscometer equipped with fluid temperature controller for measurement of viscosity in complex fluids. Microfluid. Nanofluid. 2013, 14, 657–668. [Google Scholar] [CrossRef]
- Solomon, D.E.; Vanapalli, S.A. Multiplexed microfluidic viscometer for high-throughput complex fluid rheology. Microfluid. Nanofluid. 2014, 16, 677–690. [Google Scholar] [CrossRef]
- Gupta, S.; Wang, W.S.; Vanapalli, S.A. Microfluidic viscometers for shear rheology of complex fluids and biofluids. Biomicrofluidics 2016, 10, 043402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, T.A.; Liao, W.H.; Wu, Y.F.; Chen, Y.L.; Tung, Y.C. Electrofluidic Circuit-Based Microfluidic Viscometer for Analysis of Newtonian and Non-Newtonian Liquids under Different Temperatures. Anal. Chem. 2018, 90, 2317–2325. [Google Scholar] [CrossRef] [PubMed]
- Arosio, P.; Hu, K.; Aprile, F.A.; Muller, T.; Knowles, T.P. Microfluidic Diffusion Viscometer for Rapid Analysis of Complex Solutions. Anal. Chem. 2016, 88, 3488–3493. [Google Scholar] [CrossRef] [PubMed]
- Zou, M.; Cai, S.; Zhao, Z.; Chen, L.; Zhao, Y.; Fan, X.; Chen, S. A novel polydimethylsiloxane microfluidic viscometer fabricated using microwire-molding. Rev. Sci. Instrum. 2015, 86, 104302. [Google Scholar] [CrossRef] [PubMed]
- DeLaMarre, M.F.; Keyzer, A.; Shippy, S.A. Development of a simple droplet-based microfluidic capillary viscometer for low-viscosity Newtonian fluids. Anal. Chem. 2015, 87, 4649–4657. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Tan, L.; Pan, X.; Liu, G.; He, Y.; Jin, W.; Li, M.; Hu, Y.; Gu, H. Self-Powered Viscosity and Pressure Sensing in Microfluidic Systems Based on the Piezoelectric Energy Harvesting of Flowing Droplets. ACS Appl. Mater. Interfaces 2017, 9, 28586–28595. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ward, K.R.; Burns, M.A. Viscosity Measurements Using Microfluidic Droplet Length. Anal. Chem. 2017, 89, 3996–4006. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.C.; Shih, H.C.; Wu, J.G.; Weng, T.W.; Wu, C.Y.; Lu, J.C.; Tung, Y.C. Electrofluidic pressure sensor embedded microfluidic device: A study of endothelial cells under hydrostatic pressure and shear stress combinations. Lab Chip 2013, 13, 1743–1753. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.Y.; Liao, W.H.; Tung, Y.C. Integrated ionic liquid-based electrofluidic circuits for pressure sensing within polydimethylsiloxane microfluidic systems. Lab Chip 2011, 11, 1740–1746. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.Y.; Lu, J.C.; Liu, M.C.; Tung, Y.C. Integrated electrofluidic circuits: pressure sensing with analog and digital operation functionalities for microfluidics. Lab Chip 2012, 12, 3943–3951. [Google Scholar] [CrossRef] [PubMed]
- Lo, K.Y.; Wu, S.Y.; Sun, Y.S. A microfluidic device for studying the production of reactive oxygen species and the migration in lung cancer cells under single or coexisting chemical/electrical stimulation. Microfluid. Nanofluid. 2016, 20, 15. [Google Scholar] [CrossRef]
- Lo, K.Y.; Zhu, Y.; Tsai, H.F.; Sun, Y.S. Effects of shear stresses and antioxidant concentrations on the production of reactive oxygen species in lung cancer cells. Biomicrofluidics 2013, 7, 64108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, C.H.; Hou, H.S.; Lo, K.Y.; Cheng, J.Y.; Sun, Y.S. Use microfluidic chips to study the effects of ultraviolet lights on human fibroblasts. Microfluid. Nanofluid. 2017, 21, 79. [Google Scholar] [CrossRef]
- Mengeaud, V.; Josserand, J.; Girault, H.H. Mixing processes in a zigzag microchannel: Finite element simulations and optical study. Anal. Chem. 2002, 74, 4279–4286. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.K.; Yang, R.J. Electroosmotic flow mixing in zigzag microchannels. Electrophoresis 2007, 28, 975–983. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kim, H.J.; Jeon, N.L. Biological applications of microfluidic gradient devices. Integr. Biol. 2010, 2, 584–603. [Google Scholar] [CrossRef] [PubMed]
- Hosokawa, K.; Hanada, K.; Maeda, R. A polydimethylsiloxane (PDMS) deformable diffraction grating for monitoring of local pressure in microfluidic devices. J. Micromech. Microeng. 2002, 12, 1–6. [Google Scholar] [CrossRef]
- Cheng, N.S. Formula for the viscosity of a glycerol-water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Gervais, T.; El-Ali, J.; Gunther, A.; Jensen, K.F. Flow-induced deformation of shallow microfluidic channels. Lab Chip 2006, 6, 500–507. [Google Scholar] [CrossRef] [PubMed]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzeng, B.-B.; Sun, Y.-S. Design and Fabrication of a Microfluidic Viscometer Based on Electrofluidic Circuits. Micromachines 2018, 9, 375. https://doi.org/10.3390/mi9080375
Tzeng B-B, Sun Y-S. Design and Fabrication of a Microfluidic Viscometer Based on Electrofluidic Circuits. Micromachines. 2018; 9(8):375. https://doi.org/10.3390/mi9080375
Chicago/Turabian StyleTzeng, Bo-Bi, and Yung-Shin Sun. 2018. "Design and Fabrication of a Microfluidic Viscometer Based on Electrofluidic Circuits" Micromachines 9, no. 8: 375. https://doi.org/10.3390/mi9080375
APA StyleTzeng, B.-B., & Sun, Y.-S. (2018). Design and Fabrication of a Microfluidic Viscometer Based on Electrofluidic Circuits. Micromachines, 9(8), 375. https://doi.org/10.3390/mi9080375





