2. In Situ Crystallization: A Retrospective View
The first examples of in situ crystallization were published in the thirties of the past century. The first compounds that underwent in situ crystallization were benzene [
10] and cyclohexane [
11]. Their melting points are slightly below room temperature, which was crucial at that time, as programmable cooling devices were not available.
Cox E.G. grew a single crystal of benzene in a sealed capsule by cooling with frozen carbon dioxide [
12]. The equipment used in this work could not maintain temperatures lower than −40 °C; however, it was sufficient for benzene that started to crystallize at −22 °C in the orthorhombic cell (space group
Pbca). The attempt to study the crystal structure of cyclohexane initially failed. In 1930, Hassel and Kringstad [
13] used a Debye camera (FeKα-radiation) and solid CO
2-acetone mixture to crystallize cyclohexane but they could only reveal the cubic symmetry of the unit cell (a ≈ 8.41 Å). Later, Lonsdale and Smith successfully obtained a single crystal of cyclohexane in a preliminarily dried cellophane tube [
14] using advanced equipment that allowed them to reach −108 °C. Cellophane tubes are transparent to copper X-ray radiation and are not as fragile as glass capillaries. It was shown that cyclohexane crystallizes in a cubic cell (space group
Fm3m) and has a chair conformation.
In situ crystallization was applied to verify the idea of the 3c–2e bond in diborane developed by Price [
15,
16]. At that time, a number of compounds were known that could not be described by Lewis-based valence schemes, whereas MO-LCAO methods were not widely applicable. The explanation of the diborane structure was the cornerstone for the progress in the chemical bond theory, so it was necessary to solve the problem of the diborane structure as soon as possible. Streib and Libscomb developed an original cooling device that used liquid nitrogen and helium to achieve temperatures not far from absolute zero (2–5 K) [
17]. The cell used for in situ crystallization had beryllium windows that are transparent to X-rays. The crystals could be obtained from the gas phase upon condensation on the metal rod that, in turn, was connected to a Dewar’s vessel. The described device could control the temperature of the rod via a heating coil; however, it was not easy to control the process of crystallization. Fortunately, in 1965, W. Smith and W. Lipscomb successfully grew crystals of the two most thermodynamically stable α and β-phases of diborane [
18]. The B–B length in the crystals of these phases was in perfect agreement with the idea of a 3c–2e bond predicted in one of the early MO-LCAO calculations. The same apparatus was used to grow α- and β-phases of nitrogen, β-phase of fluorine, and γ-phase of oxygen [
19,
20]. These results had great importance because they allowed deriving the first van der Waals radii for fluorine and oxygen, which are still in use for analysis of crystal packing. In 1959, J. Trotter was the first who used a thin-walled capillary to grow single crystals of nitrobenzene [
21] using a low-temperature device initially developed by Burbank and Bensey in 1953 [
22]. The capillary was filled by liquid nitrobenzene and cooled down to −30 °C, and spontaneous crystallization was observed. This method is not applicable for the majority of liquid samples; however, thin walled glass is still widely used in common practice to grow crystals because it is simple to use and because the length and diameter of the capillary can be varied. Almost perfect single crystals can be grown by combining local cooling and heating, which was first introduced by W. Smith and W. Lipscomb. Unfortunately, it is very difficult to use in the case of samples that are gases at room temperature.
The progress in the in situ crystallization methods in the period from the mid-70 s to mid-90 s was related to the development of new crystallization techniques and hardware. At that point in time, flash freezing with subsequent recrystallization from a melting liquid was adapted for widespread use. Step-by-step local heating of a selected zone used for recrystallization provided an order in crystallites, and as a result, almost perfect single crystals were achieved. In order to control the crystal growth more precisely, the temperature of the heating coil could be controlled by changing the electric current intensity. Movement of the heating coil along the capillary and in the perpendicular direction allowed one to control the temperature gradient and the size of the local heating zone. In the same period of time, power light sources became used as heater elements for local heating instead of heating coils. In 1979, Zimmermann et al. published the scheme of equipment for in situ crystallization in a glass capillary where local heating was achieved using a power LED and elliptic mirrors to focus light on the selected zone. This equipment is suitable for achieving very high temperatures (up to 3000 K) and it can be used even in the absence of gravity, in a space laboratory [
23]. Similar equipment for in situ crystallization inside the cabinet of an X-ray diffractometer was applied by Boese and Bläser [
24] in the period of 1980–1985 to grow crystals of more than thirty phases and determine their structures. The main difference from the scheme proposed by Zimmerman was the usage of a movable elliptic mirror to shift the focus point.
Further development of heating elements was related to the application of laser light sources. In 1992, scientific groups headed by Boese and Antipin [
25,
26] used an infrared laser in their devices for in situ crystal growth. This scheme was then commercialized and equipment for in situ crystallization began to be sold as the Optical Heating and Crystallization Device (OHCD) [
27]. Presently, it is the only commercially available equipment for crystallization in thin-walled glass capillaries. Using this equipment, most of the structures published so far were crystallized from liquid samples and studied by X-ray diffraction. The experimental works related to in situ crystallization and subsequent X-ray diffraction studies allowed a big dataset to be collected. The quality of these data is increased, along with the progress in hardware and software used for X-ray diffraction. Early experiments in many cases resulted in very inaccurate structural data. There are several papers where information about the details of least-squares refinement (namely R-values, the values of s.u. for atomic coordinates) is missing. On the other hand, in some recent studies, the collected X-ray intensities were sufficient to carry out high-resolution experiments and multipolar refinement to simulate the charge density distribution. Thus, it is very hard to compare reliably, the bond lengths and angles from earlier and recent publications. For this reason, the main attention is paid to the analysis of crystal packing, especially short intermolecular contacts and packing motifs.
3. Organophosphorus, Organosilicon, and Organogermanium Compounds
In 1997, Karl Krueger’s team published an article with the structures of several chelating organophosphines
1–
5 (
Scheme 1) [
28]. In their article, they described the dependence of the P–C bond lengths on the organic substituent, showing a noticeable elongation of these bonds in cases where the steric hindrance of the substituent increased. In fact, for tris(tert-butyl)phosphine, the length of P–C bonds is 1.911(2) Å, and for tri(butyl)phosphine it is 1.844(2) Å [
29]. Also, the sum of the C–P–C angles for all compounds is 303(3)°, with the exception of tris(tert-butyl)phosphine whose C–P–C angle is 322.3(3)°. To determine the crystal structure, the authors grew crystals of the compounds in situ in a diffractometer. A focused IR laser was used for zone melting. This was necessary because compounds
1 and
4 melt near 0 °C and the crystals that are formed are unstable, so it is difficult to transfer them to the diffractometer. Other compounds (
2 and
3) melt at temperatures from −50 to −20 °C. Compound
5 melts above the room temperature, but the in situ methodology was used to obtain better single crystals too. A series of compounds studied in the article are organophosphines that contain two or four CH
2 groups between the phosphorus atoms. The authors explain that compounds with an odd number of methylene groups do not form crystalline phases upon cooling. In the crystal packing of all the compounds studied, the lone pairs of electrons of the phosphorus atoms look exactly in opposite directions, while in the case of three links in the linker they will probably look either in the same direction or orthogonally.
There are no strong intermolecular interactions in the crystal packing of compounds
1–
5. The molecules of these compounds are bonded by the H···H and C···H interactions. A dependency analysis between the calculated values of the molecular volume/surface area and the lattice energies indicates that the bonding between the molecules in the crystal of compound
5 is stronger than in the other ones. Conversely, in compounds
3 and
4, the molecules are bonded weaker than it is predicted based on the hypothesis of a linear relationship of these quantities (
Figure 1). It should be noted that the lone electron pair is not involved in any noticeable intermolecular interaction in crystals of
3 and
4. On the contrary, in a crystal of compound
5, the authors of [
28], based on the analysis of the distribution of deformation electron density, established the interaction between the lone pair of electrons of phosphorus atoms and the phenyl group of the neighboring molecule. The authors of [
28] believe that the above-mentioned interaction, along with the mutual steric influence of phenyl groups, is the result of the sp
3 hybridization of the phosphorus atoms. In turn, we can assume that it leads to a shrinkage of the crystal packing.
In 2015 the phosphorous and silicon-containing compound (C
2F
5)
3SiCH
2P(
t-Bu)
2 (compound
6) containing a frustrated Lewis pair [
30] was synthesized and its crystal structure was determined. The molecule is not involved in any noticeable intermolecular interaction, but the phosphorus atom is tetrahedral. After the addition of CO
2 or SO
2 to
6, a heteroatomic ring is formed. The silicon atom acquires a distorted trigonal-bipyramidal environment because one of the oxygen atoms of the added molecule is bonded to this silicon. The phosphorus atom becomes bonded to a sulfur or carbon atom. Since compound
6 becomes a zwitterion after a gas is added, the intermolecular interaction energy grows and the temperature of melting goes above the room temperature.
In the crystals of CO2 and SO2 adducts, the C–Si–O angles between the opposite sides of bipyramids are 179.2° and 173.0°, respectively. The lengths of the Si–O bonds are 1.853 and 1.822 Å in the CO2 and SO2 adducts, respectively. The Si–C–P angles are 113.1° (CO2 adduct), 117.1° (SO2 adduct), and 120.4° (compound 6). In all cases, these angles are bigger than the tetrahedral one (109.28°). Probably, the wide Si–C–P angle appears because of the high steric hindrance of silicon and phosphorus atoms, but this angle becomes smaller in adduct crystals because the five-membered ring “pulls together” the silicon and phosphorus atoms.
In the same year, a series of tris(pentafluoroethyl)silicon (TPFES) compounds was studied by Norbert W. Mitzel’s team [
31]. The purpose of that work was to search for intermolecular donor–acceptor interactions between the silicon atom and the electron pair of the β-atom in an α-TPFES-substituted compound (oxygen or nitrogen). The authors determined the structure of compounds with –CH
2CH
3 (
7), –CH
2OCH
3 (
8), –CH
2N(CH
3)
2 (
9), and –ON(CH
3)
2 (
10) groups. Based on interatomic distances, no interaction of the silicon atom with the β-atom was observed in the first three compounds. However, quantum chemistry calculations and X-ray structure analysis showed that this interaction appeared in the structure of compound
10 (
Table 1).
In order to establish whether the Si–N (Si–O) interaction was present, the X-ray diffraction experiment results were compared with the results of quantum chemistry calculations (B3LYP/6-31G(d,p), PBE0/cc–pVTZ, and MP2/cc–pVTZ). According to the authors, only the MP2/cc–pVTZ theory level allows one to approximate the experimental values cc-pVTZ of the Si···N distance for (C2F5)3SiONMe2. The experimentally obtained Si···N distance is smaller by 0.03 Å than that calculated using the MP2 method, and are 0.42 Å and 0.35 Å smaller, respectively, than those calculated by the B3LYP and PBE0 methods. If a methylene group between the silicon and nitrogen atoms existed, no Si-N interaction was found; therefore, the difference between the experiment and calculation was insignificant.
To explain the nature of the Si–N interaction, compound 10 was studied by gas electron diffraction. These molecules are conformationally flexible and the rotation barrier around every single bond is small. To evaluate the conformational flexibility of compound 10 in the gas phase, the experimental radial distribution function of interatomic distances was compared with the distribution of interatomic distances obtained from the calculation by the molecular dynamics method. The R-factors for the radial distribution found by molecular dynamics do not exceed 5.2%. The conformation whose radial distribution function is reproduced most accurately (4.0%) does not contain a short Si···N contact. Thus, this contact is found only in a crystal environment and is probably caused by steric hindrance.
The crystal packing of compounds
7–
10 is stabilized mainly due to weak H···F hydrogen bonds and F···F interactions. The F···F interatomic distances of intermolecular interactions are only slightly (by no more than 0.15 Å) shorter than the sum of the corresponding van der Waals radii. The only exception is the structure of compound
10, where the F···F interactions are stronger: some F···F distances are shorter than the sum of the van der Waals radii by more than 0.2 Å. However, the F···F interactions become stronger because of the disordering of one of the pentafluoroethyl groups. This is consistent with the fact that the crystal lattice energy (
Table S1 in
Supplementary Materials) of compounds
7–
9 varies in a very narrow range and is almost independent of the composition.
In 1955, the structure of the low-temperature phase of octamethylcyclotetrasiloxane (compound
11) was established [
32]. This compound crystallizes at 17.5 °C and has a phase transition at −16.3 °C [
33,
34]. The unit cell of the low-temperature phase is tetragonal, belongs to the
P4
2/n space group, and its parameters are
a =
b = 16.10 ± 0.02 Å,
c = 6.47 ± 0.01 Å [
32]. The molecules are in the pseudo-chair conformation in the low-temperature phase. For the high-temperature phase, only the space group (
I4
1/n) and the cell parameters were determined. The authors report that the unit cell parameters
a and
b change insignificantly (± 0.02 Å) during the phase transition, while the parameter
c changes from 6.47 Å to 6.83 Å.
In 2018, we published an article about the synthesis of siloxanols [
35]. We determined the structure of 1,1,1,3,5,5,5-heptamethyltrisiloxan-2-ol (compound
12) that is viscous at room temperature. It forms a strongly bonded (with O–H···O hydrogen bond) tetramer around the
axes in the crystal (
Figure 2). The O···O distance in the hydrogen bond is as short as 2.711(4) Å, which means that O–H···O is a strong hydrogen bond.
In 2017, Harald Stueger’s team obtained and studied 2,2,3,3,4,4-hexasilylpentasilane (compound
13) [
36]. This compound is a liquid, and the in situ crystallization method was used to determine its crystal structure. The synthetic method is also applicable for the subsequent synthesis of oligomers and polymers with similar structures.
In 2016, Berthold Hoge’s team published a series of works devoted to the synthesis and properties of perfluoroethyl-substituted organogermanium compounds [
37,
38,
39]. In these works, some physicochemical properties of compounds were examined, such as vibrations in the IR spectrum and crystal packing. Four of the eight compounds, namely, (C
2F
5)
2GeBr
2 (
14), (C
2F
5)
2GeH
2 (
15), (C
2F
5)
3GeBr (
16), and (C
2F
5)
2GePMe
3 (
17), are liquids at room temperature. In order to determine the structures of their crystalline phases by X-ray diffraction experiment, these samples were crystallized in situ.
A further study of the crystal structures of all four compounds showed that compounds
14 and
16 have similar intermolecular contacts but different packing motives. In the crystal, molecules
14 form stacks in a square packing (
Figure 3). The crystals of
15 and
16 form layered structures. The propensity of perfluorinated groups to form layered structures is also shown in [
40]. The layers in the crystal of compound
15 are identical and are composed of molecules in an all-
trans conformation. The interactions between the layers in the crystal of
16 alternate: half pairs of layers are connected only by F···F contacts, while the other pairs of layers are mainly connected by Br···F interactions (
Figure 3, right).
The germanium atom in compound 17 is formally divalent and has a lone electron pair. As a result, the lone electron pair of the germanium atom is involved in the C–H···Ge intermolecular interaction with the methyl group at the phosphorus atom. The C···Ge distance is 3.1793(6) Å, which is shorter than the sum of the van der Waals radii (3.31 Å). The Ge–P bond length is only 2.3989 (16) Å, which is only 0.14 Å longer than the sum of the covalent radii (2.27 Å). Otherwise, the crystal of this compound is not very different from the structure of compound 15: H···F and F···F contacts are also present.
Another interesting result of Hoge’s team was published in the European Journal of Inorganic Chemistry [
41]. This work was devoted to the study of various trisubstituted phosphines, di and tri-fluorophosphates. Compounds with acceptor substituents such as pentafluoroethyl, pentafluorophenyl, and tetrafluoropyridyl were prepared.
The most interesting example is a crystal of the compound (C2F5)3PF2 (18), in which the molecules are bonded only via F···F contacts. In this case, the fluorine atoms of the PF2-group are not involved in noticeable intermolecular interactions. The shortest distances F···F involving PF2 groups are 2.995(7) Å (the sum of van der Waals radii equals 3.31 Å).
5. Organohalogen Compounds
The team of Roland Boese, Ashwini Nangia, and Gautam R. Desiraju described the intermolecular interactions in the crystals of partially fluorinated benzenes
28–
34 (
Scheme 3) [
46]. The subject of the study included mono,
ortho, and
para-bi-, tri-, tetra-, and penta-fluorobenzenes, and
para-halo-substituted fluorobenzenes. Since all these compounds have low-melting points from 225 to 277 K, the in situ crystallization method was used for the crystal growth. An IR laser was used for zone melting.
In a monofluorobenzene
28 crystal, the main type of interatomic interaction is the weak C–H···F hydrogen bond. At the same time, the presence of the C–H···π and F···F interactions was also observed. According to the authors, the presence of these interactions makes the crystal packing of fluorobenzene similar to that in Py·HF, C
5H
5NO, and PhCN [
46]. It is interesting to note that the crystal packings of fluorobenzene and chlorobenzene are significantly different, while the crystals of fluorobenzene and benzonitrile are isostructural (if the fluoro and cyano groups are not taken into account). In the structures of difluorobenzenes, the molecules are packed in layers. The molecules in the layers of
ortho-difluorobenzene
29 interact with each other due to weak C–H···F hydrogen bonds and stacking interactions. At the same time, the interaction between the layers is due to the interaction of the lone pairs of fluorine atoms with the π-system of benzene rings (F···π). On the contrary, in a
para-difluorobenzene
30 crystal, layers are formed only due to weak hydrogen bonds. No interactions involving the π-system of the benzene ring were observed. In turn, the layers bind to each other through stacking and dipole-dipole interactions of the phenyl rings. The authors note explicit relations between the crystal packing of 1,4-benzoquinone and
para-difluorobenzene, which indicates that these molecules have similar electronic structures [
46]. Moreover, the crystals of these compounds are isostructural (the cell parameters and space groups coincide).
Similarly, the structures of dihalobenzene crystals are also similar to each other. In all these compounds (except the previously described
para-difluorobenzene), pronounced halogen bonds are present (Cl···Cl, Br···Br, F···I, all belonging to the second type [
47]) and the orientations of molecules in the layers alternate (
Figure 4).
The crystal packing of trifluorobenzene
31 is pseudohexagonal. The authors of [
46] draw a clear analogy with the packaging of 1,3,5-triazine [
48,
49]. In both cases, there is an electrophilic hydrogen atom interacting with two electron pairs of neighboring molecules, which allows one to predict the “hexagonal cell” structure.
The crystal packing of tetra-fluorobenzenes varies greatly. The crystal structure of 1,2,4,5-tetra-fluorobenzene
32 [
46] is similar to that of tetrazine [
50]. In these structures, molecules in one layer are bonded through dipole-dipole interactions between hydrogen atoms and lone pairs of a neighboring molecule. 1,2,3,4-Tetra-fluorobenzene
33 crystallizes in two polymorphic modifications. The first polymorph was grown at a temperature of 123 K close to the melting point, while the second polymorph was crystallized at a temperature of 195 K from the toluene:pentane system (1:3). Interactions of C–H···F type contribute a lot to the stabilization energy of both polymorphs. In the first polymorph, the molecules form stacking interactions between the layers. In the second one, another motive exists due to the bonding of this type: pairs of molecules are rotated relative to each other by an angle of almost 90° and alternate in a checkerboard pattern. A similar packing is also observed in a pentafluorobenzene crystal. However, dipole–dipole interactions are weaker due to a decrease in the number of hydrogen atoms.
Based on the studies, the authors of [
46] concluded that crystalline packing is determined by the presence of acceptor fluorine atoms. The type of packaging depends on the number of these atoms.
Para-dichlorobenzene
33 exists in the form of three polymorphs: α (
34a), β (
34b), and γ (
34c). According to Wheeler and Colson, the number of shortened Cl···Cl contacts (<3.9 Å) increases from three in the β polymorph to four in the α polymorph and five in the γ polymorph, which corresponds to the sequence of phase transition with decreasing temperature [
51,
52]. A CE–HF/3-21G calculation of the packing energy performed by us predicts that the γ-polymorph is the most stable. In this case, the energies of α and β-polymorphs differ insignificantly (by 1.7 kJ/mol), while the latter is more stable. In 2001, Roland Boese et al. grew crystals of dichlorobenzenes
35 and
36 by the in situ method [
53]. To predict the stability of the crystalline structures studied, calculations that included a computer search for the most thermodynamically stable modifications (UNI force field [
54]) were performed. The structures generated in the computer search were compared with the results of X-ray diffraction experiments carried out at temperatures of 100 and 220 K for
ortho (
36) and
meta-dichlorobenzenes (
35). The parameters of the most thermodynamically stable crystal cells obtained from the calculation are generally consistent with the experimental ones for all the phases. The only exception is the β-polymorph of
para-dichlorobenzene (
34b), for which the predicted cell parameters differ noticeably from the experimental ones.
In 2011, Desiraju et al. compared the crystal structures of phenylacetylene and its monofluorinated derivatives [
55]. For each of the 2- and 3-fluoro-substituted phenylacetylene derivatives (
37 and
38, respectively), the existence of two crystalline phases was determined. The orthorhombic phase
37a (Form 1) crystallizes in the orthorhombic cell (space group
Pna2
1). The molecules in this phase are disordered in such a way that the ratio of the population of fluorine atoms on one or the other side of the acetylene fragment is approximately 1:4. In this phase, there is an interaction of the terminal hydrogen atom of the acetylene fragment with the π-system of the acetylene fragment of the neighboring molecule, and non-classical hydrogen bonds of the C–H···F type. Due to these interactions, a zigzag motif (
Figure 5) of molecules along the
c axis is present in the crystalline packing. Two types of weak C–H···F hydrogen bonds were found in polymorph
37a: in the first case, the hydrogen atom of the acetylene fragment participates in the bonding, and in the second one, the phenyl ring hydrogen atom interacts with the fluorine atom. Polymorph
37b, which was obtained by slow cooling of a liquid in a capillary, crystallizes in space group
P2
1. In the crystal packing of this polymorph, the interaction of the terminal hydrogen atom of the acetylene fragment with the π-system of the acetylene fragment of the neighboring molecule also exists, but unlike
37a, only the hydrogen atoms of the phenyl fragment participate in the C–H···F weak hydrogen bond.
Both polymorphs of (3-fluorophenyl)acetylene
38 (forms 1 (
38a) and 2 (
38b)) are monoclinic, but they are characterized by noticeably different cell volumes and different space groups. In fact,
38a crystallizes in the centrosymmetric group
P2
1/n and contains three molecules in the unique part of the cell. The molecules are notable for a hydrogen atom in the phenyl ring which forms the strongest hydrogen bond. It should be noted that the hydrogen atom of the acetylene fragment forms a C–H···F hydrogen bond only in one molecule. In the other two molecules, the same terminal hydrogen atom interacts with the π-system of the acetylene fragment of another molecule. In the
38b crystal, like the
37b crystal, a zigzag-like interaction is present (
Figure 6).
(Para-fluorophenyl)acetylene 39 consists of layers in which the molecules are bonded by hydrogen bonds between the terminal acetylene fragment and the fluorine atom of the neighboring molecule in one direction and by stacking in the other direction. The layers are interconnected by weak H···H contacts. As a result, for ortho and meta-substituted monofluorophenylacetylenes, the main motive of crystal packing is the zigzag-like interaction of acetylene fragments, and for para-substituted ones, it is stacking.
It is known that interactions between halogens are usually formed due to the presence of a σ-hole of one atom, which interacts with the electron-saturated “belt” of another atom [
56]. Desiraju shows the interactions of cis-trans geometry and L-geometry [
47]. The most remarkable examples of compounds that can have crystals with halogen bonds include 4-fluorobenzoyl chloride
40 and 2,3-difluorobenzoyl chloride
41 [
57]. The Cl···F interactions in these crystals belong to the second type of geometry (L-geometry). It should be noted that different atoms act as donors and acceptors of a halogen bond. In a crystal of
40a, the fluorine atom is the halogen bond donor and the chlorine atom is the acceptor, while in a crystal of
41, the chlorine atom is the donor and the
ortho-fluorine atom is the acceptor. In both crystals, oxygen is involved in the formation of two hydrogen bonds with
ortho and
meta, or
meta and
para hydrogens. The second fluorine atom (
meta-fluorine) in compound
41 forms a hydrogen bond with the
meta hydrogen atom of a neighboring molecule, and in compound
40a a hydrogen bond is formed by an
ortho-atom with the single fluorine atom. Thus, the authors concluded that the chlorine atom of the acyl chloride group can act both as a donor and as an acceptor.
Two years later, the same authors published an article in which they described the intermediate phase
40b formed during the crystallization of
40 [
58]. The latter crystallized in the same space group and was characterized by a similar layered type of packing. In that work, the authors compared the molecular conformations in crystal phases with the ones calculated for the gas phase. The locations of the molecules within the layers are almost the same for both polymorphs. However, in the intermediate phase, the rings of the molecules form a parquet type packing, while in the previously studied phase
40a, the phenyl rings of the molecules are parallel to the planes of the layers. In addition, the layers are shifted relative to each other. In the layers of both phases, there are significant differences in the length of the Cl···F halogen bond (3.153 Å for the form
40a and 3.283 Å for the form
40b). This is due to the presence of a staircase structure. According to the authors, the crystals of the phase
40b are gradually transformed to phase
40a. Moreover, a crystal can be represented as a combination of domains of both phases during the experiment. Our calculations (
Table S1) are in agreement with the conclusion about the instability of
40b (
40a is about 5 kJ/mol more favorable than
40b).
Hirshfeld surface analysis (carried out using CrystalExplorer, Version 3.1, [
9,
59]) was performed by the authors for both crystal structures, and the diagrams of fingerprints of intermolecular interaction were calculated. The main contribution to the Hirschfeld surface corresponds to the C–H···O, C–H···F, and C–H···Cl hydrogen bonds. Nevertheless, the aromatic cycle stacking also makes a significant contribution to the
40b phase surface, while in the stable phase
40a, π–π interactions between the phenyl substituent and the anhydride group are observed instead. The C–C–C–Cl torsion angle between these fragments of the molecule in the
40b phase is as small as 0.4(8)°, while in the crystal of phase
40a it is 11.6(2)°. The deviation from the plane conformation in a crystal of
40a is probably caused by the formation of a stronger F···Cl halogen bond.
Dikundwar et al. published an article comparing the chloro, bromo, and iodo-derivatives of fluorobenzene [
60]. The main goal of that work was to determine the influence of the type of halogen and its position on the formation and geometry of the halogen bond. To determine the crystal structure of the compounds, nine crystals were grown by the in situ method. Two phases were found for
meta-chlorofluorobenzene, but only one for each of the remaining compounds.
Ortho-chlorofluorobenzene
42 molecules do not form halogen bonds; instead, they participate in the formation of hydrogen bonds and C–H···π interactions. In the first phase of
meta-chlorofluorobenzene
43a, the Cl···Cl halogen bonds exist in the L geometry, due to which the molecules form zigzag-like motifs in the crystal packing. In the other phase
43b, halogen bonds are not formed and all intermolecular interactions are related to hydrogen bonds. In a crystal of
para-chlorofluorobenzene
44, which was first described by Boese and Desiraju [
46] and later studied by Sarah Masters’ team [
61], zigzag-like halogen bonds are observed, like in the first phase of
meta-chlorofluorobenzene
43a, but they already correspond to the trans-type.
Ortho-bromofluorobenzene
45 forms zigzag-like chains in which molecules are bonded by Br···π interactions. In addition, in a
45 crystal, halogen bonds with both fluorine and bromine exist. A
meta-bromofluorobenzene
46 crystal contains two independent molecules that form the only trans-type halogen bond (Br···Br). The structure of
para-bromofluorobenzene
47 was previously determined by Boese and Desiraju [
46]. In a crystal of this compound, it was found that the bromine atoms interact with each other through first-type halogen contacts, while the fluorine atoms participate only in the formation of hydrogen bonds. A similar situation is observed in a crystal of
ortho-iodofluorobenzene
48, but, unlike compound
47, the I···I halogen bonds form a zigzag-like motif and belong to the second type. The structure of
meta-iodofluorobenzene
49 differs significantly from that described previously. This compound crystallizes in space group
P2
1, with five molecules in the unique part. Three of them are arranged in spirals along the screw pseudo-axis 3
1 (
Figure 7). The molecules around the pseudo-axis form second-type halogen bonds with each other (θ
1 ≈ 180°, θ
2 ≈ 90°). The remaining two molecules form zigzag-like structures based on halogen contacts, but closer to the first type (θ
1 ≈ 155°, θ
2 ≈ 124°,
Figure 7). The structure of
para-iodofluorobenzene
50, also previously studied by the Boese and Desiraju teams [
46], contains a zigzag-like structure of the I···I halogen bond, but F···I halogen bonds also exist.
Based on the above, fluorine atoms are more likely to form hydrogen bonds than halogen bonds, while heavier halogens behave in the opposite manner. According to the authors, this is due to the principle of “like likes like”, since the sizes of the fluorine and hydrogen atoms are similar.
In 2015, Nath and Naumov published the structure of a crystal of chlorobenzene
51 [
62]. To analyze the intermolecular interactions, the analysis of Hirschfeld partitioning was carried out for chlorobenzene. The calculation showed that a significant fraction of the surface (32.2%) corresponds to the π(C)···H contacts. The H···H and H···Cl contacts contribute 35.1% and 25.9% to the Hirschfeld surface, respectively. Also, in a crystal of chlorobenzene, the zigzag-like motif consisting of molecules bound by a halogen bond exists.
The Pierangelo Metrangolo and Giuseppe Resnati teams determined the crystal structure of a number of co-crystals of amines with halo-pentafluorobenzenes in which a halogen bond is present [
63]. This type of intermolecular bond is formed between bromine or iodine atoms in C
6F
5I or C
6F
5Br, respectively, and a lone pair of electrons of the nitrogen atom of substituted pyridine or TMEDA. The I···N distances in the compounds studied are 2.784 Å on average, which is shorter than the Br···N distance found (2.882 Å). Nevertheless, all these distances are much shorter than the corresponding sums of the van der Waals radii (3.53 Å for I···N and 3.40 Å for Br···N), which definitely indicates that a halogen bond exists in each of the crystals studied.
In 2014, Klapötke et al. published an article in which they compared the structures of halo-trinitromethanes
52–
55 obtained from gas electron diffraction, X-ray diffraction analysis, and quantum chemical calculations [
64]. Fluoro and bromo-trinitromethane crystals were grown in situ in a capillary using copper wire as the heating element. According to the authors, contrary to the literature, iodotrinitromethane did not decompose under MoKα radiation, as was stated in [
65]. The X-ray diffraction data for chlorotrinitromethane was taken from an earlier article [
66]. The results of X-ray diffraction experiments were compared with those from gas electron diffraction. The relative arrangement of nitro groups in the crystal and in the gas phase can be described as a “propeller”. The lengths of C–Hal bonds in a crystal are shorter than in the gas phase, while the opposite pattern is observed for C–N bonds. From the analysis of structural data, it was concluded that a difference in the type of halogen atoms has almost no effect on the C–N bond lengths and N–C–Hal angles in these compounds. On the other hand, the torsion angle of the nitro group has a tendency to increase with an increase in the atomic number of the halogen. As the van der Waals radius of the halogen atoms grows, the intra- and intermolecular interactions between them and the oxygen atoms of the nitro groups increase. According to the authors, intramolecular O···Hal interactions are forced, while intermolecular interactions are advantageous and can be considered as analogs of the L-type halogen bond. Using the NBO, AIM, and IQA methods, the atomic charges, atomic volumes, and interatomic interaction energies were calculated. IQA was performed using the RHF/cc–pVTZ wavefunctions for fluoro and chloro-derivatives and RHF/6-311G(d) for bromo and iodo-derivatives. Both NBO and AIM agree that a negative charge is present on fluorine atom, while it is positive on the other halogens. At the same time, the positive charge on carbon atoms decreases as the halogen atom increases. The charges on nitrogen and oxygen atoms do not depend on the type of halogen at all.
In 2016, Norbert W. Mitzel and Carlos O. Della Védova’s teams published a joint work in which perfluoropropanoic acid fluoride
56 (CF
3CF
2C(O)F) was described [
67]. The structure of this compound was studied by gas electron diffraction, IR, Raman, and ultraviolet spectroscopy, and by quantum chemical calculations (MP2/cc–pVTZ and B3LYP/cc–pVTZ). Compound
56 is a volatile liquid at room temperature, with a melting point of about 146 K. In order to determine the crystal structure, X-ray diffraction analysis and in situ crystallization were used. The crystal was grown at 144 K, after which the sample was slowly cooled to 100 K for the X-ray diffraction experiment. The results showed that all molecules in the crystal are in gauche-conformation, while in the gas phase, according to the results of gas electron diffraction, an equilibrium exists. It was shown that only 85(10)% of molecules are in the gauche-conformation, while the remaining 15(10)% are in the anti-conformation.
6. Intermolecular Interactions in the In Situ Crystallized Compounds
Analysis of crystal packing allowed us to conclude that organoelement compounds described in the present review can be divided into two groups. The first group consists of Si, Ge, P, and S-containing compounds. The heteroatoms in compounds of the first group are surrounded with a shell of hydrocarbon substituents (including perfluorinated ones) and do not participate in any intermolecular interactions. As a consequence, all structure-forming intermolecular interactions are weak classic and non-classic hydrogen bonds (X···H, H···H, C···H; X = Hal, O, N, C). The second group includes organofluorine aromatic compounds where intermolecular interactions between fluorine atoms play a significant role in the stabilization of crystal packing. Moreover, fluorine atoms’ interactions can be of many types—weak hydrogen bonds, halogen bonds, F···F interactions, and F···π interactions [
68]. Besides, a noticeable contribution to the stabilization of crystal packing is played by other intermolecular interactions with the participation of the π-systems of phenyl rings [
69,
70].
According to the calculation of the energy frameworks, compounds
1–
17 can be described as loosely packed ones. The ratio between the molecular volume (Å
3) and the lattice energy (kJ/mol) in the majority of these compounds is about 3.5-5 Å
3·mol/kJ (
Table S1). This fact can be explained by the dominance of H···H and C–H···π interactions over others (except for the strong hydrogen bond present in a crystal of
12 compound). The situation is quite different in the case of organosulfur compounds
21–
26 where the ratio varies within 2–3. The reason lies in the large contribution of weak C–H···O or C–H···N hydrogen bonds that exceed the contribution from the C···H, H···H, and H···π bonds. Possibly, the correlation between molecular volume and lattice energy can be explained by strong F···F interactions. Organofluorine aromatic compounds have the ratio value close to three due to a contribution from interactions of fluorine and other halogens.
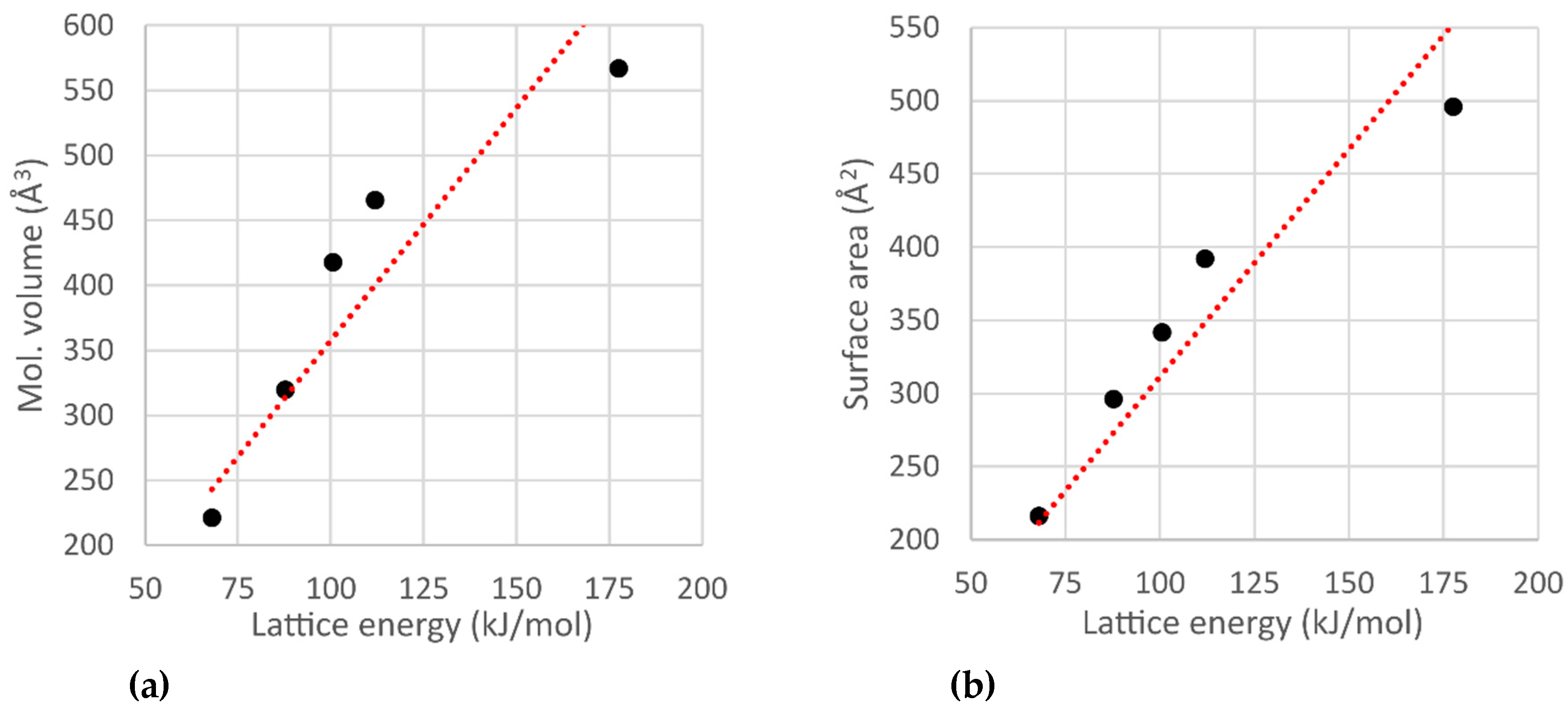
The correlations of the molecular volume/surface area with the lattice energy for all the compounds discussed above are shown in
Figure 8. Most of the compounds are liquids at room temperature and have molecular volumes in a range of 120–160 Å
3. The Hirshfeld surface areas of the majority of compounds do not exceed 170 Å
2. The maximum lattice energy of compounds that are liquid at room temperature is 112 kJ/mol (compound
4). However, most of the compounds have lattice energies between 45 and 65 kJ/mol.
The trend line was calculated on the assumption of a linear relationship between the molecular surface area, volume, and lattice energy values. The R
2 values for these trend lines are 0.7451 for plot (
a) and 0.7579 for plot (
b), respectively (
Figure 8). The compounds that are solid at room temperature and the phases that contain strongly disordered molecules were excluded from these relationships.
Several points in
Figure 8 lie far from the trend line (the points encircled in red lines). These are compounds
4,
6,
13 (compound
4 is encircled only in part (
b)). These compounds stand out because most of the intermolecular interactions in their crystals are weak, but the molecules are still big (the molar volumes are above 400 Å
3).
Relatively low R
2 values for the trend lines in
Figure 8 indicate a poor approximation of the entire data set. In this case, we separated the compounds into three groups. The separation is based on the largest Hirshfeld surface area occupied by the intermolecular interaction of a certain type (
Figure 9,
Tables S2 and S3). Compounds were separated into “H···H”, “H···Hal” (Hal = F, Cl, Br, I), and “Other” groups.
The first “H···H” group is well approximated linearly (
Figure 9a,b). One point (red triangle) was excluded. It corresponds to compound
13. In this crystal, Si–H···H–Si intermolecular contacts are observed instead of C–H···H–C contacts. The Si–H···H–Si interaction is much weaker, and the lattice energy is at least 30 kJ/mol smaller than that predicted by the trend line. The second group “H···Hal” is approximated much worse (
Figure 9c,d). Most of the compounds are small molecules. Their Hirshfeld surface area and molecular volume do not exceed 200 Å
2/Å
3. Three rounded dots correspond to organophosphorus compounds
6,
9, and
17. The last group, “Others”, is well approximated linearly, like the first one (
Figure 9e,f).
The dependence of the melting point on the lattice energy is shown in
Figure 10. We separated all data into black, blue, and red groups. Black dots correspond to compounds with a molecular surface area below 170 Å
2. Blue triangles correspond to compounds whose molecular surface areas are above 170 Å
2. The red square corresponds to compound
1. The tangent value (m.p./lattice energy) for the “black” group is between 3.13 and 6.10, and 4.75 on average. The same value for the “blue” group is between 1.63 and 3.12, and 2.41 on average. The molecules of compounds of the “black” group are small and most of them do not form strong intermolecular contacts. On the other hand, in the crystals of the “blue” group compounds, molecular interactions such as halogen bonds or C–H···P hydrogen bonds are present. Compound
1 was assigned to a separate group because the C–H···P bond existing in its crystal is not strong enough, but the Hirshfeld surface area is too large for the “black” group. It means that this compound should be in the “black” group because of its tangent (m.p./lattice energy) value, but it has potentially strong C–H···P interactions.