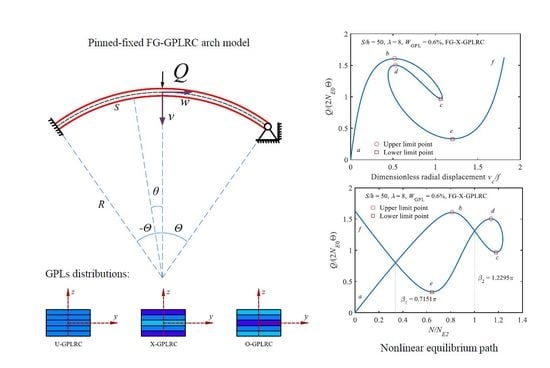
Multiple Equilibria and Buckling of Functionally Graded Graphene Nanoplatelet-Reinforced Composite Arches with Pinned-Fixed End
Abstract
1. Introduction
2. Effective Elastic Modulus
3. Non-Linear Analysis
3.1. Equilibrium Equations
3.2. Limit Point Buckling
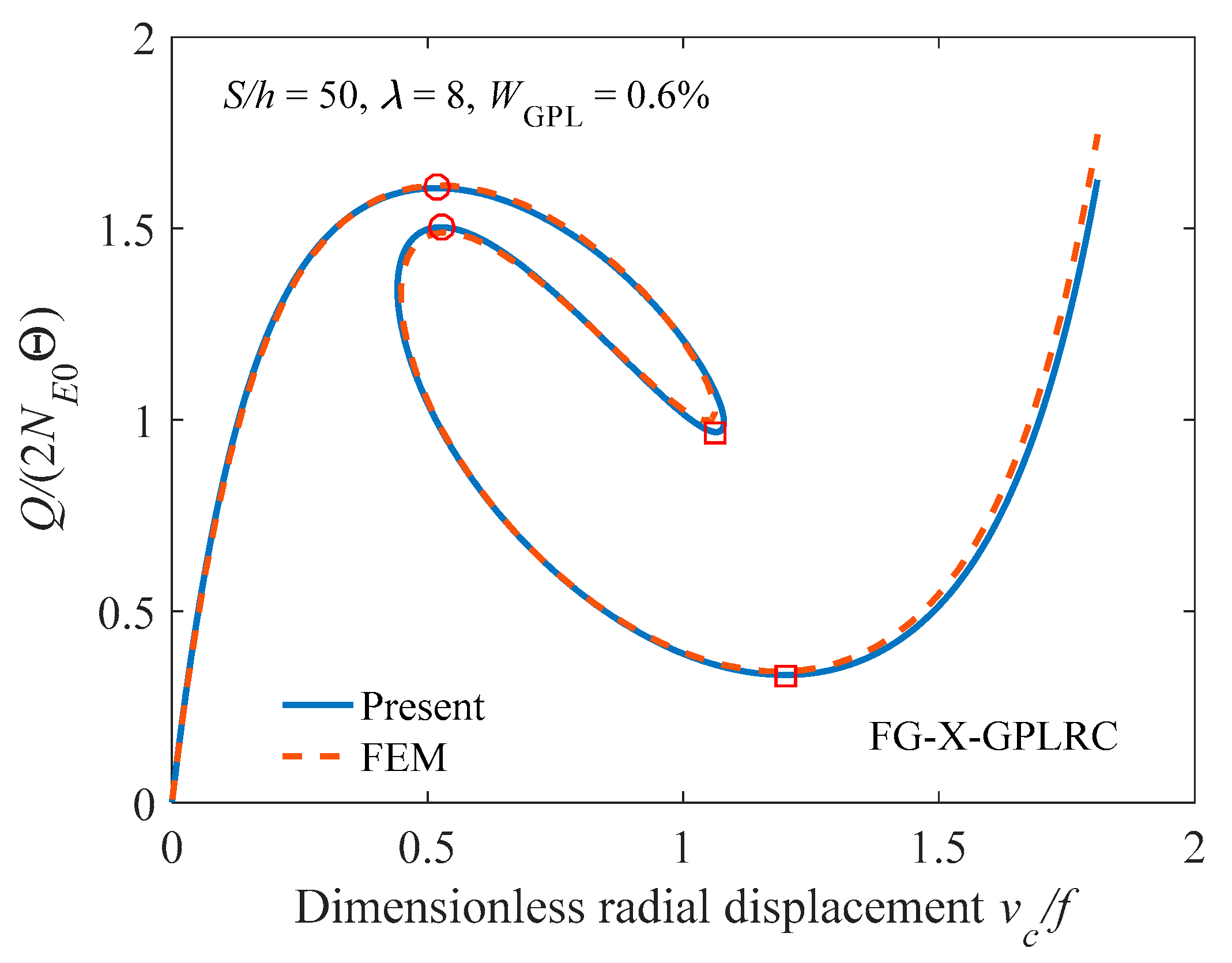
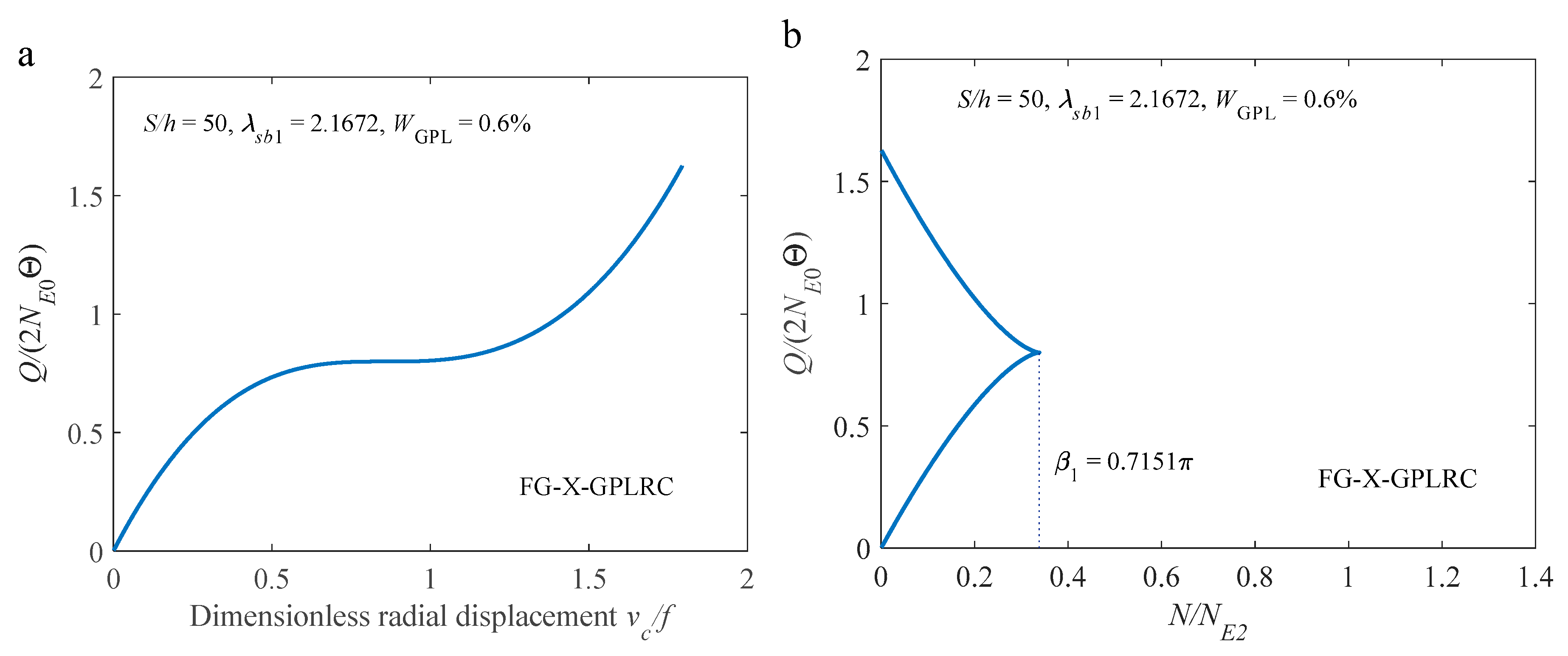
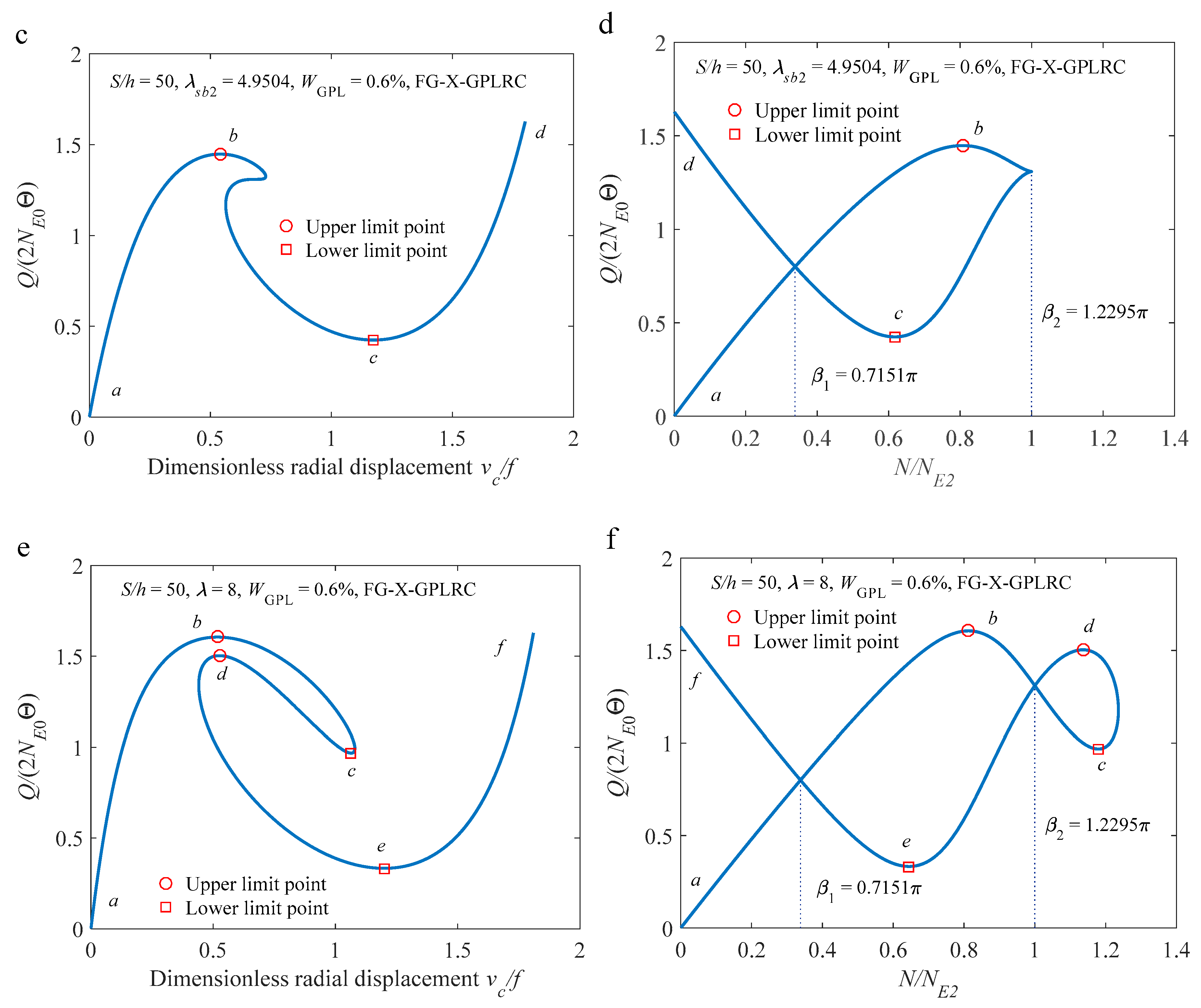
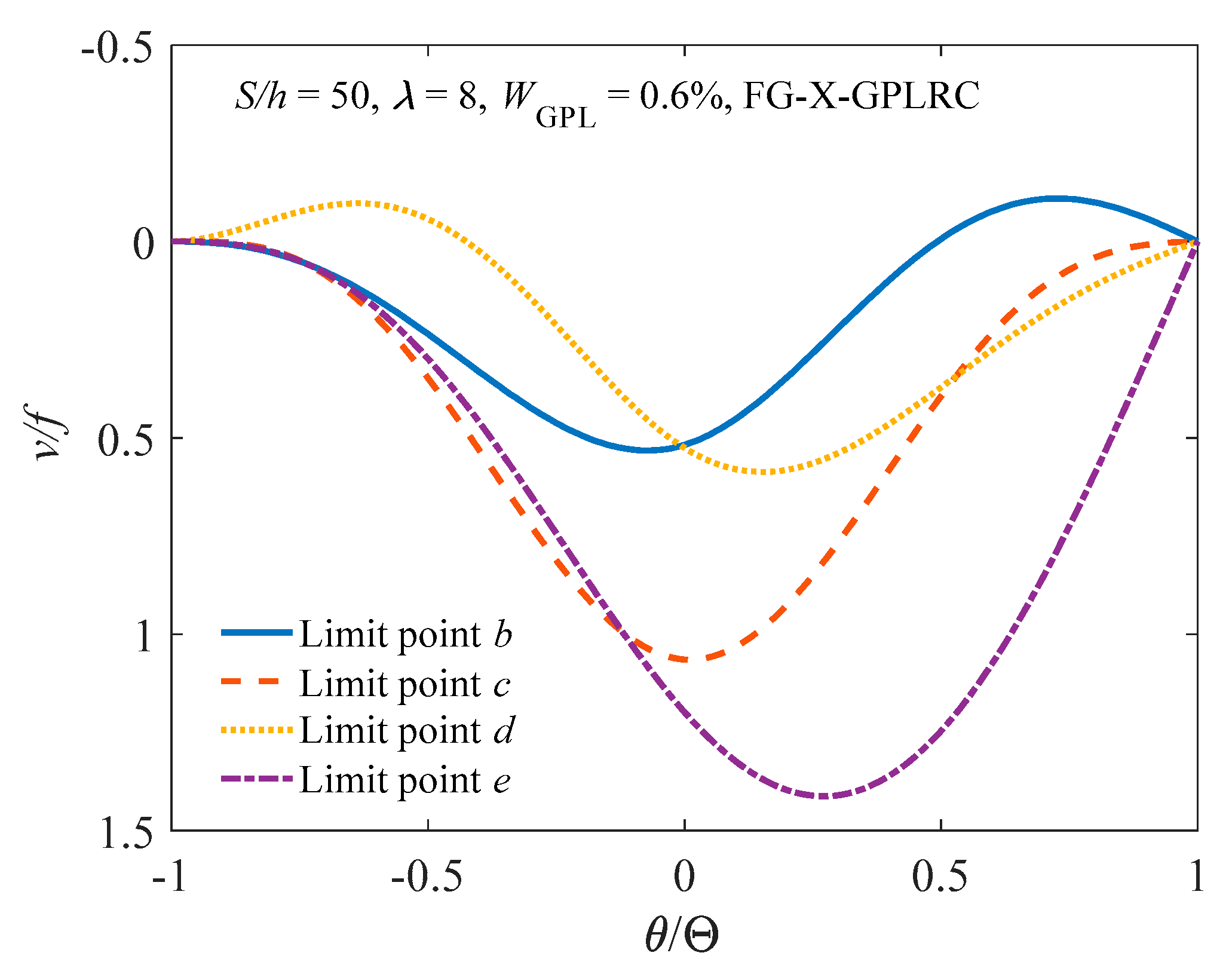
3.3. Multiple Equilibria and Inflection Point
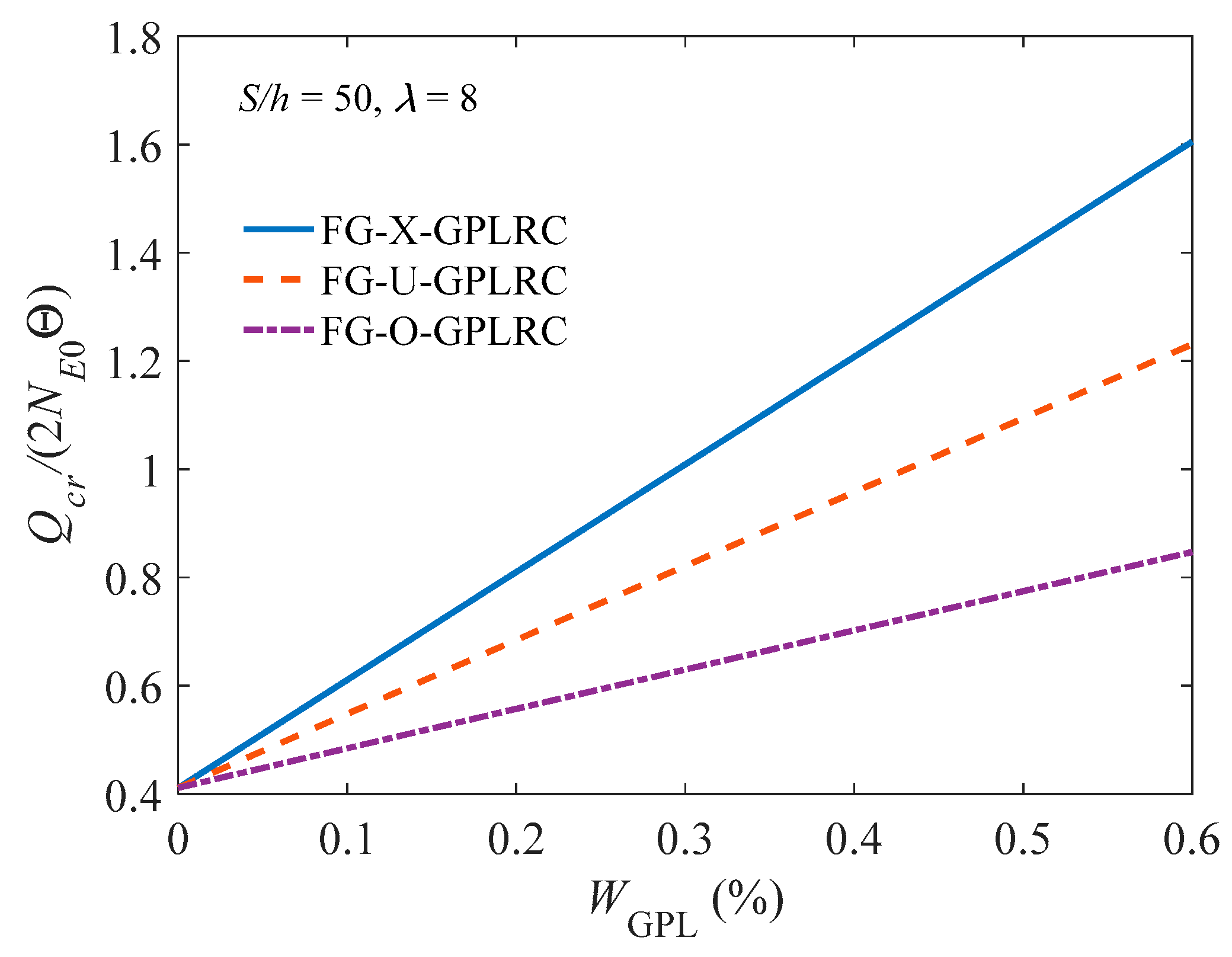
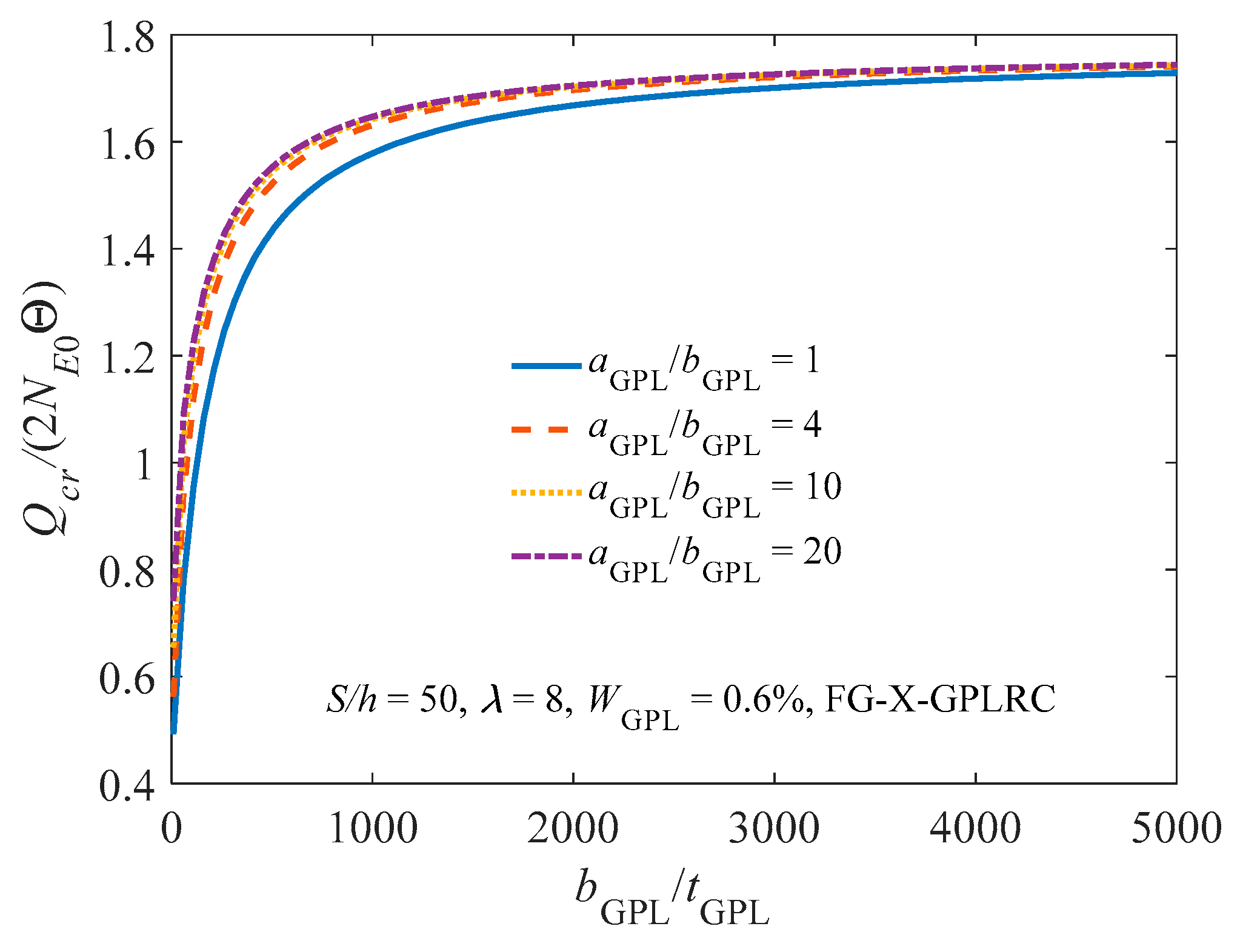
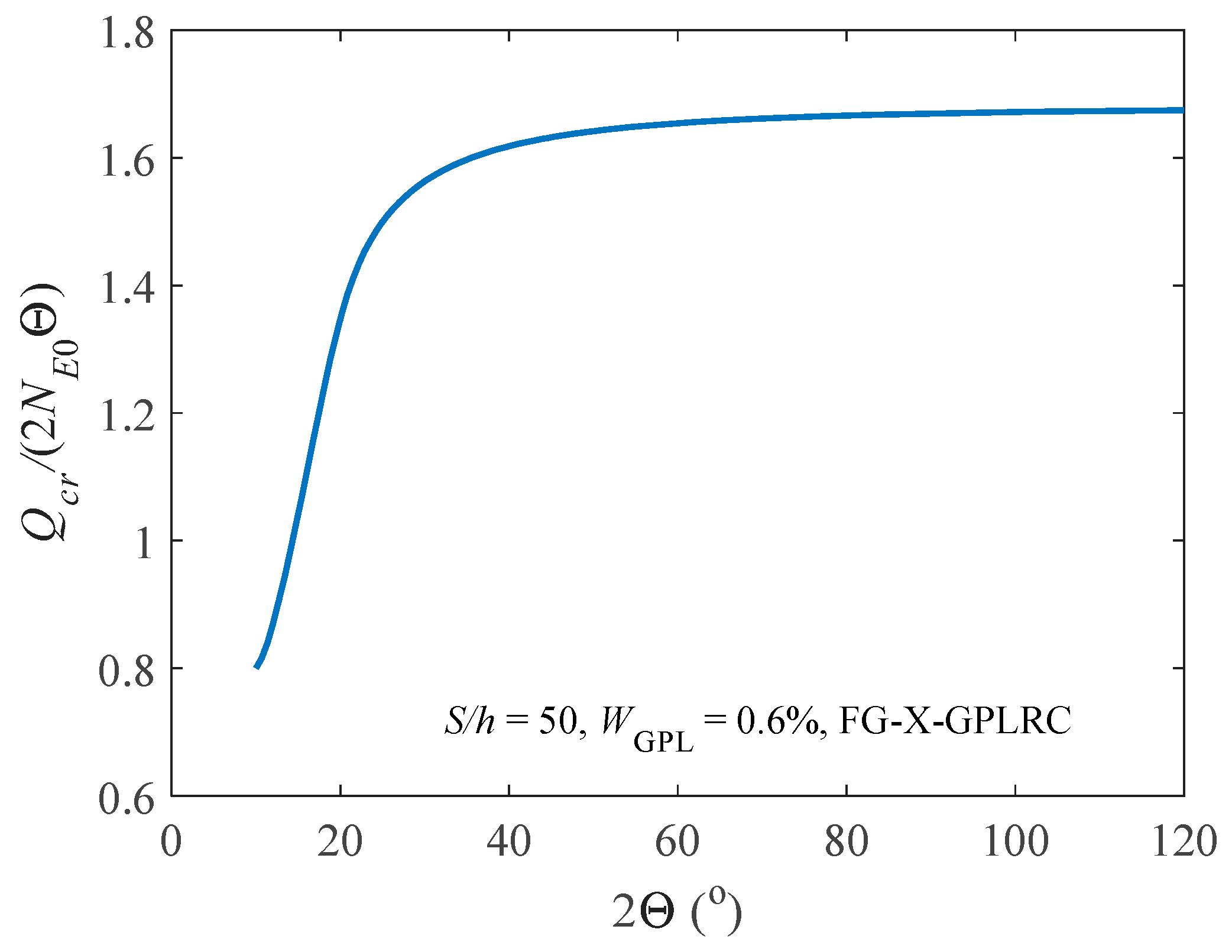
4. Parameters Studies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Kleinschmidt, A.C.; Almeida, J.H.S.; Donato, R.K.; Schrekker, H.S.; Marques, V.C.; Corat, E.J.; Amico, S.C. Functionalized-carbon nanotubes with physisorbed ionic liquid as filler for epoxy nanocomposites. J. Nanosci. Nanotechnol. 2016, 16, 9132–9140. [Google Scholar] [CrossRef]
- Moghimian, N.; Nazarpour, S. The Future of Carbon: An Update on Graphene’s Dermal, Inhalation, and Gene Toxicity. Crystals 2020, 10, 718. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Rafiee, M.A.; Rafiee, J.; Srivastava, I.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Fracture and fatigue in graphene nanocomposites. Small 2010, 6, 179–183. [Google Scholar] [CrossRef]
- Liu, J.; Yan, H.; Jiang, K. Mechanical properties of graphene platelet-reinforced alumina ceramic composites. Ceram. Int. 2013, 39, 6215–6221. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z.; Yan, H.; Jiang, K. Spark plasma sintering of alumina composites with graphene platelets and silicon carbide nanoparticles. Adv. Eng. Mater. 2014, 16, 1111–1118. [Google Scholar] [CrossRef]
- Tang, L.C.; Wan, Y.J.; Yan, D.; Pei, Y.B.; Zhao, L.; Li, Y.B.; Lai, G.Q. The effect of graphene dispersion on the mechanical properties of graphene/epoxy composites. Carbon 2013, 60, 16–27. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Q.; Chen, D.; Lu, P. Enhanced mechanical properties of graphene-based poly (vinyl alcohol) composites. Macromolecules 2010, 43, 2357–2363. [Google Scholar] [CrossRef]
- Yang, J.; Wu, H.; Kitipornchai, S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos. Struct. 2017, 161, 111–118. [Google Scholar] [CrossRef]
- Yang, Z.; Tam, M.; Zhang, Y.; Kitipornchai, S.; Lv, J.; Yang, J. Nonlinear dynamic response of fg graphene platelets reinforced composite beam with edge cracks in thermal environment. Int. J. Struct. Stab. Dy. 2020, 2043005. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. Part. B Eng. 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Wu, H.; Yang, J.; Kitipornchai, S. Dynamic instability of functionally graded multilayer graphene nanocomposite beams in thermal environment. Compos. Struct. 2017, 162, 244–254. [Google Scholar] [CrossRef]
- Dong, Y.; Li, X.; Gao, K.; Li, Y.; Yang, J. Harmonic resonances of graphene-reinforced nonlinear cylindrical shells: Effects of spinning motion and thermal environment. Nonlinear Dynam. 2020, 99, 981–1000. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Y.; Li, X.; Yang, J. Active control of dynamic behaviors of graded graphene reinforced cylindrical shells with piezoelectric actuator/sensor layers. Appl. Math. Model. 2020, 82, 252–270. [Google Scholar] [CrossRef]
- Dong, Y.H.; Zhu, B.; Wang, Y.; He, L.W.; Li, Y.H.; Yang, J. Analytical prediction of the impact response of graphene reinforced spinning cylindrical shells under axial and thermal loads. Appl. Math. Model. 2019, 71, 331–348. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y.; Fan, Y. A novel technique for nonlinear dynamic instability analysis of FG-GRC laminated plates. Thin. Walled Struct. 2019, 139, 389–397. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y.; Fan, Y. Vibration of thermally postbuckled FG-GRC laminated plates resting on elastic foundations. J. Vib. Control 2019, 25, 1507–1520. [Google Scholar] [CrossRef]
- Fan, Y.; Xiang, Y.; Shen, H.S. Nonlinear forced vibration of FG-GRC laminated plates resting on visco-Pasternak foundations. Compos. Struct. 2019, 209, 443–452. [Google Scholar] [CrossRef]
- Gao, K.; Do, D.M.; Li, R.; Kitipornchai, S.; Yang, J. Probabilistic stability analysis of functionally graded graphene reinforced porous beams. Aerosp. Sci. Technol. 2020, 98, 105738. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Wang, X.; Zhao, Z.; Romero, C.S.; Dong, Y.; Yang, J. Nonlinear static and dynamic responses of graphene platelets reinforced composite beam with dielectric permittivity. Appl. Math. Model. 2019, 71, 298–315. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Santiuste, C.; Zhao, Z.; Yang, J. Buckling and postbuckling of dielectric composite beam reinforced with Graphene Platelets (GPLs). Aerosp. Sci. Technol. 2019, 91, 208–218. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Wang, X.; Zhao, Z.; Romero, C.S.; Yang, J. Nonlinear free vibration of graphene platelets (GPLs)/polymer dielectric beam. Smart Mater. Struct. 2019, 28, 055013. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, J.; Liu, A.; Fu, J. Nonlinear in-plane instability of functionally graded multilayer graphene reinforced composite shallow arches. Compos. Struct. 2018, 204, 301–312. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, S.; Yang, J.; Lv, J.; Liu, A.; Fu, J. In-plane and out-of-plane free vibrations of functionally graded composite arches with graphene reinforcements. Mech. Adv. Mater. Struct. 2020, 1–11. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, Y.; Liu, A.; Fu, J.; Wu, D. Nonlinear in-plane buckling of fixed shallow functionally graded graphene reinforced composite arches subjected to mechanical and thermal loading. Appl. Math. Model. 2019, 70, 315–327. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, A.; Yang, J.; Fu, J.; Yang, B. Dynamic buckling of functionally graded graphene nanoplatelets reinforced composite shallow arches under a step central point load. J. Sound. Vib. 2020, 465, 115019. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, Z.; Kitipornchai, S.; Yang, J. Dynamic instability of functionally graded porous arches reinforced by graphene platelets. Thin Walled Struct. 2020, 147, 106491. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Z.; Liu, A.; Fu, J. Nonlinear buckling analysis of functionally graded graphene reinforced composite shallow arches with elastic rotational constraints under uniform radial load. Materials 2018, 11, 910. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yang, C.; Gao, W.; Wu, D.; Li, G. Nonlinear behaviour and stability of functionally graded porous arches with graphene platelets reinforcements. Int. J. Eng. Sci. 2019, 137, 37–56. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Chen, Y.; Sun, Q.; Zhang, Z. Effect of temperature variations on the stability mechanism of the confined functionally graded porous arch with nanocomposites reinforcement under mechanical loading. Compos. Part. B Eng. 2019, 176, 107330. [Google Scholar] [CrossRef]
- Affdl, J.H.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Lu, H.; Liu, L.; Liu, A.; Pi, Y.L.; Bradford, M.A.; Huang, Y. Effects of movement and rotation of supports on nonlinear instability of fixed shallow arches. Thin Walled Struct. 2020, 155, 106909. [Google Scholar] [CrossRef]
- Pi, Y.L.; Bradford, M.A. Non-linear in-plane analysis and buckling of pinned-fixed shallow arches subjected to a central concentrated load. Int. J. Nonlin. Mech. 2012, 47, 118–131. [Google Scholar] [CrossRef]

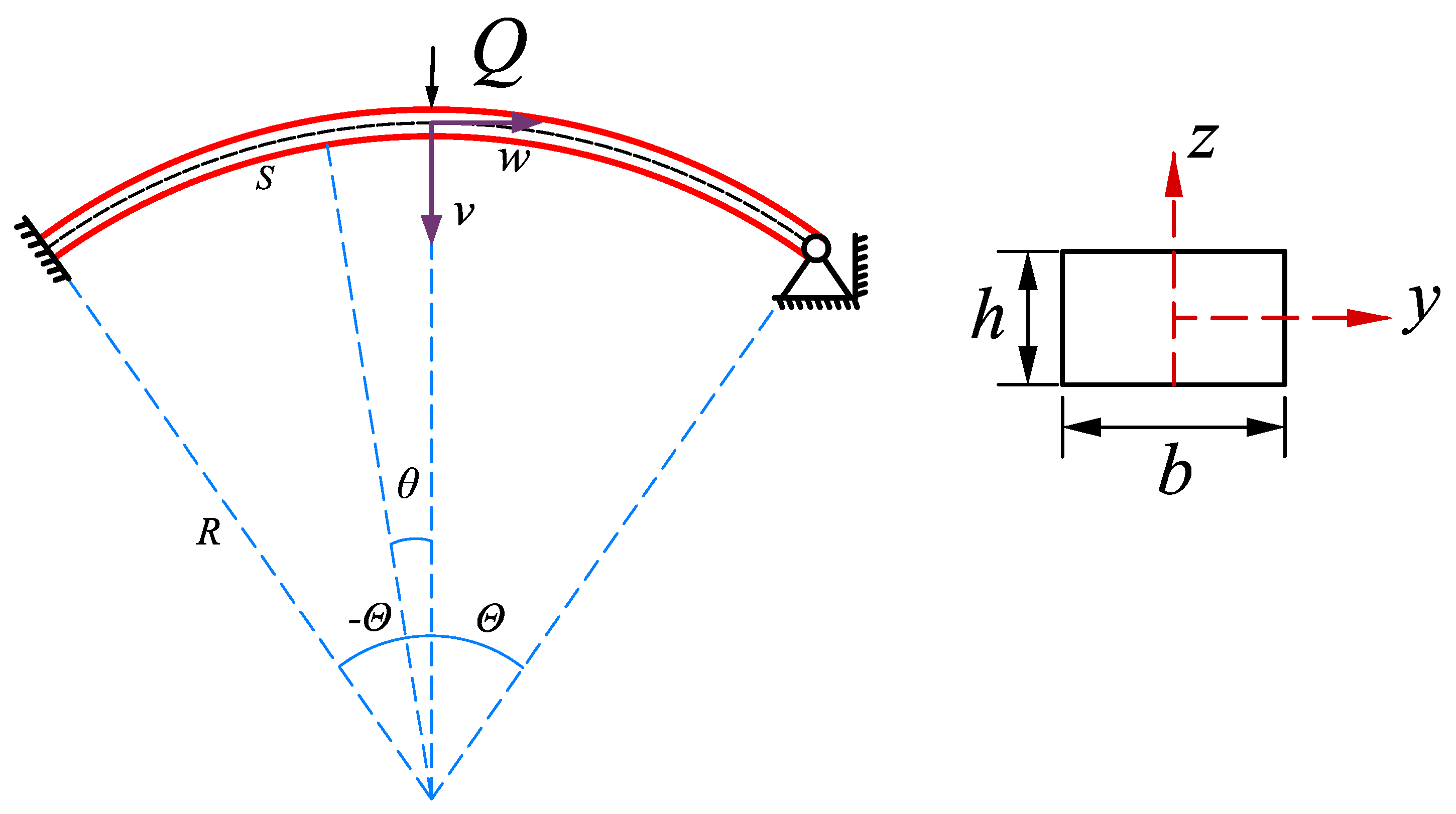
| Parameters | Values |
|---|---|
| Cross section (width × height) | 0.03 m × 0.025 m |
| Total number of GPLRC layers | 10 |
| GPL length | 2.5 µm |
| GPL width | 1.5 µm |
| GPL thickness | 1.5 nm |
| Young’s modulus (epoxy) | 3 GPa |
| Young’s modulus (GPL) | 1010 GPa |
| Patterns | WGPL (%) | |||
|---|---|---|---|---|
| U-GPLRC | 0.1 | 0.4251 | 0.5237 | 0.5451 |
| 0.2 | 0.5311 | 0.6543 | 0.6809 | |
| 0.3 | 0.6371 | 0.7848 | 0.8168 | |
| X-GPLRC | 0.1 | 0.4521 | 0.5796 | 0.6072 |
| 0.2 | 0.5839 | 0.7650 | 0.8047 | |
| 0.3 | 0.7152 | 0.9499 | 1.0021 | |
| O-GPLRC | 0.1 | 0.3946 | 0.4662 | 0.4823 |
| 0.2 | 0.4668 | 0.5382 | 0.5549 | |
| 0.3 | 0.5369 | 0.6098 | 0.6274 | |
| Pure epoxy | 0.0 | 0.3192 | 0.3932 | 0.4092 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Xu, J.; Lu, H.; Lv, J.; Liu, A.; Fu, J. Multiple Equilibria and Buckling of Functionally Graded Graphene Nanoplatelet-Reinforced Composite Arches with Pinned-Fixed End. Crystals 2020, 10, 1003. https://doi.org/10.3390/cryst10111003
Yang Z, Xu J, Lu H, Lv J, Liu A, Fu J. Multiple Equilibria and Buckling of Functionally Graded Graphene Nanoplatelet-Reinforced Composite Arches with Pinned-Fixed End. Crystals. 2020; 10(11):1003. https://doi.org/10.3390/cryst10111003
Chicago/Turabian StyleYang, Zhicheng, Jiamian Xu, Hanwen Lu, Jiangen Lv, Airong Liu, and Jiyang Fu. 2020. "Multiple Equilibria and Buckling of Functionally Graded Graphene Nanoplatelet-Reinforced Composite Arches with Pinned-Fixed End" Crystals 10, no. 11: 1003. https://doi.org/10.3390/cryst10111003
APA StyleYang, Z., Xu, J., Lu, H., Lv, J., Liu, A., & Fu, J. (2020). Multiple Equilibria and Buckling of Functionally Graded Graphene Nanoplatelet-Reinforced Composite Arches with Pinned-Fixed End. Crystals, 10(11), 1003. https://doi.org/10.3390/cryst10111003