Single Crystal Heat Capacity Measurement of Charge Glass Compound θ-(BEDT-TTF)2CsZn(SCN)4 Performed under Current and Voltage Application
Abstract
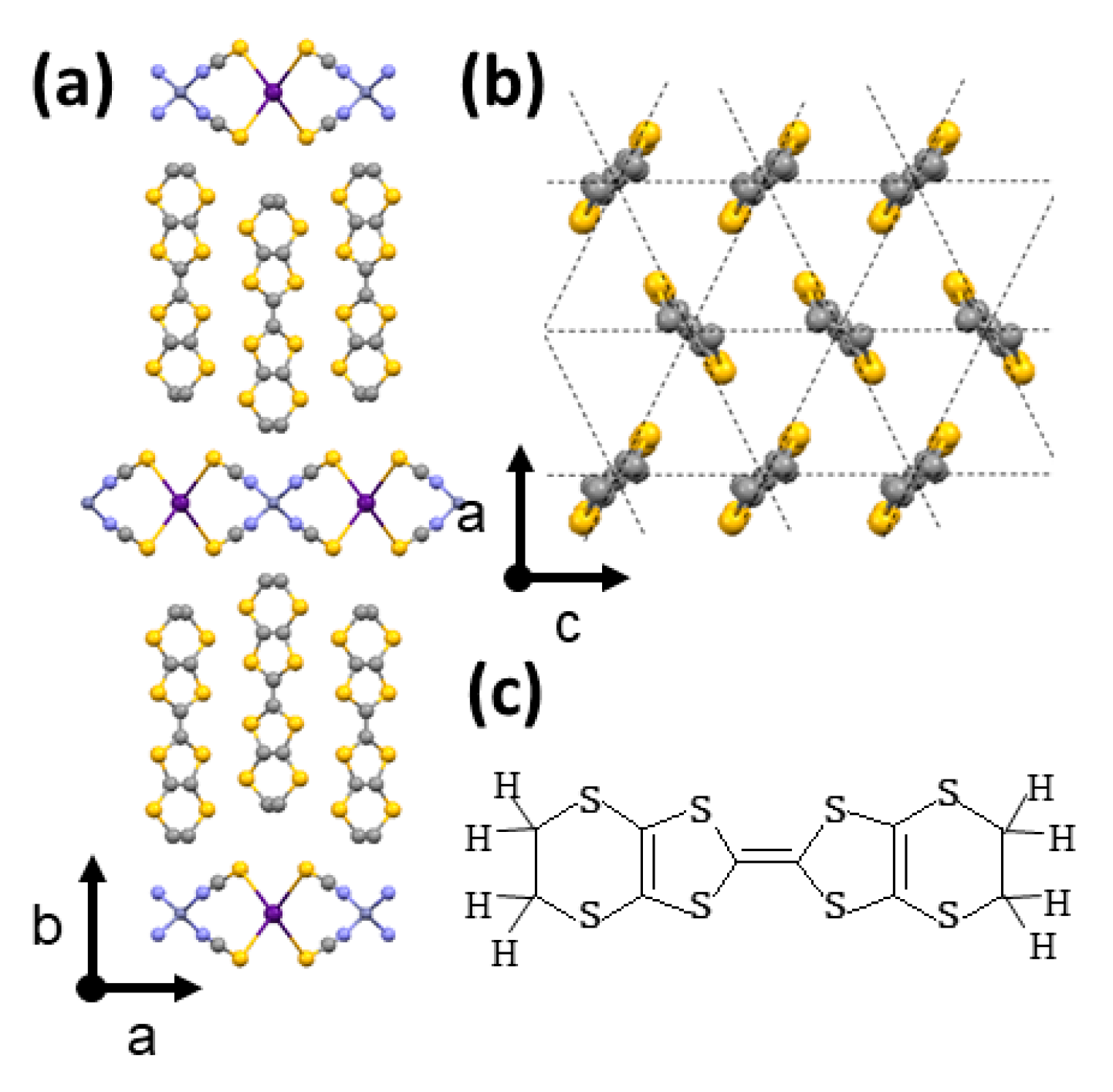
:1. Introduction
2. Experimental
2.1. Sample Preparation
2.2. Experimental Set Up of the Calorimetry Cell
2.3. Analytic Method
3. Results and Discussion
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mori, H. Materials Viewpoint of Organic Superconductors. J. Phys. Soc. Jpn. 2006, 75, 1–15. [Google Scholar] [CrossRef]
- Mori, T.; Kawamoto, T. Organic conductors—From fundamentals to nonlinear conductivity. Annu. Rep. Prog. Chem. Sect. C Phys. Chem. 2007, 103, 134–172. [Google Scholar] [CrossRef]
- Takahide, Y.; Konoike, T.; Enomoto, K.; Nishimura, M.; Terashima, T.; Uji, S.; Yamamoto, H.M. Large positive magnetoresistance of insulating organic crystals in the non-ohmic region. Phys. Rev. Lett. 2007, 98, 1–4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inagaki, K.; Terasaki, I.; Mori, H.; Mori, T. Large Dielectric Constant and Giant Nonlinear Conduction in the Organic Conductor θ-(BEDT-TTF)2CsZn(SCN)4. J. Phys. Soc. Jpn. 2004, 73, 3364–3369. [Google Scholar] [CrossRef] [Green Version]
- Sawano, F.; Terasaki, I.; Mori, H.; Mori, T.; Watanabe, M.; Ikeda, N.; Nogami, Y.; Noda, Y. An organic thyristor. Nature 2005, 437, 522–524. [Google Scholar] [CrossRef]
- Kagawa, F.; Sato, T.; Miyagawa, K.; Kanoda, K.; Tokura, Y.; Kobayashi, K.; Kumai, R.; Murakami, Y. Charge-cluster glass in an organic conductor. Nat. Phys. 2013, 9, 419–422. [Google Scholar] [CrossRef]
- Sasaki, S.; Hashimoto, K.; Kobayashi, R.; Itoh, K.; Iguchi, S.; Nishio, Y.; Ikemoto, Y.; Moriwaki, T.; Yoneyama, N.; Watanabe, M.; et al. Crystallization and vitrification of electrons in a glass-forming charge liquid. Science 2017, 357, 1381–1385. [Google Scholar] [CrossRef] [Green Version]
- Sato, T.; Miyagawa, K.; Kanoda, K. Electronic crystal growth. Science 2017, 357, 1378–1381. [Google Scholar] [CrossRef] [Green Version]
- Mori, H.; Tanaka, S.; Mori, T. Systematic study of the electronic state in θ-type BEDT-TTF organic conductors by changing the electronic correlation. Phys. Rev. B 1998, 57, 12023–12029. [Google Scholar] [CrossRef]
- Williams, J.M.; Ferraro, J.R.; Thorn, R.J.; Carlson, K.D.; Geiser, U.; Wang, H.H.; Kini, A.M.; Whangbo, N.-H. Organic Superconductors (Including Fullerenes): Synthesis, Structure, Properties, and Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1992; pp. 92–93. [Google Scholar]
- Mori, T. Non-Stripe Charge Order in the θ-Phase Organic Conductors. J. Phys. Soc. Jpn. 2003, 72, 1469–1475. [Google Scholar] [CrossRef]
- Seo, H. Charge Ordering in Organic ET Compounds. J. Phys. Soc. Jpn. 2000, 69, 805–820. [Google Scholar] [CrossRef] [Green Version]
- Clay, R.T.; Mazumdar, S.K.; Campbell, D. Charge Ordering in θ-(BEDT-TTF)2X Materials. J. Phys. Soc. Jpn. 2002, 71, 1816–1819. [Google Scholar] [CrossRef] [Green Version]
- McKenzie, R.H.; Merino, J.; Marston, J.B.; Sushkov, O.P. Charge ordering and antiferromagnetic exchange in layered molecular crystals of the type. Phys. Rev. B 2005, 64, 085109. [Google Scholar] [CrossRef] [Green Version]
- Mori, H.; Tanaka, S.; Mori, T. Magnetic Properties of Coexistent System of Itinerant and Localized Electrons, (BEDT-TTF)2MCo(SCN)4 (M = K, Rb, Cs). J. Phys. I 1996, 6, 1987–1996. [Google Scholar]
- Nogami, Y.; Pouget, J.P.; Watanabe, M.; Oshima, K.; Mori, H.; Tanaka, S.; Mori, T. Structural modulation in θ-(BEDT-TTF)2CsM′(SCN)4[M′=Co, Zn]. Synth. Met. 1999, 103, 1911. [Google Scholar] [CrossRef]
- Nogami, Y.; Hanasaki, N.; Watanabe, M.; Yamamoto, K.; Ito, T.; Ikeda, N.; Ohsumi, H.; Toyokawa, H.; Noda, Y.; Terasaki, I.; et al. Charge Order Competition Leading to Nonlinearity in Organic Thyristor Family. J. Phys. Soc. Jpn. 2010, 79, 1–5. [Google Scholar] [CrossRef]
- Sato, T.; Kagawa, F.; Kobayashi, K.; Ueda, A.; Mori, H.; Miyagawa, K.; Kanoda, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Systematic Variations in the Charge-Glass-Forming Ability of Geometrically Frustrated θ-(BEDT-TTF)2X Organic Conductors. J. Phys. Soc. Jpn. 2014, 83, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Yamamoto, K.; Yakushi, K.; Kawamoto, A. Infrared and Raman Studies of θ-(BEDT-TTF)2CsZn(SCN)4: Comparison with the Frozen State of θ-(BEDT-TTF)2RbZn(SCN)4. J. Phys. Soc. Jpn. 2005, 74, 2631–2639. [Google Scholar] [CrossRef]
- Yoshimoto, R.; Takane, Y.; Hino, K.; Yamashita, S.; Nakazawa, Y. Coupling of charge and lattice degrees of freedoms in θ-type BEDT-TTF compound probed by low-temperature heat capacity measurements. Physica B 2014, 449, 19–24. [Google Scholar] [CrossRef]
- Camnasio, J.A.; Gonzalo, A.J. Comparative Study of the Ferroelectric Specific Heat in TGS and DTGS. J. Phys. Soc. Jpn. 1975, 39, 451–459. [Google Scholar] [CrossRef]
- Ramos, S.; del Cerro, J.; Zamora, M. Specific heat of triglycine sulfate at several applied electric fields near the critical temperature. Phys. Status Solidi (a) 1980, 61, 307–313. [Google Scholar] [CrossRef]
- Del Cerro, J.; Martin, J.M.; Ramos, S. Specific heat measurements under non-equilibrium conditions. J. Therm. Anal. 1996, 47, 1691–1700. [Google Scholar] [CrossRef]
- Lashley, J.C.; Hundley, M.F.; Mihaila, B.; Smith, J.L.; Opeil, C.P.; Finlayson, T.R.; Fisher, R.A.; Hur, N. Heat capacity in magnetic and electric fields near the ferroelectric transition in triglycine sulfate. Appl. Phys. Lett. 2007, 90, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Imajo, S.; Fukuoka, S.; Yamashita, S.; Nakazawa, Y. Construction of relaxation calorimetry for 101–2 μg samples and heat capacity measurements of organic complexes. J. Therm. Anal. Calorim. 2015, 123, 1871–1876. [Google Scholar] [CrossRef]
- Fukuoka, S.; Horie, Y.; Yamashita, S.; Nakazawa, Y. Development of heat capacity measurement system for single crystals of molecule-based compounds. J. Therm. Anal. Calorim. 2013, 113, 1303–1308. [Google Scholar] [CrossRef]
- Duthil, P. Material Properties at Low Temperature. arXiv 2015, arXiv:1501.07100. [Google Scholar]
- Nishio, Y.; Nihei, Y.; Tamura, M.; Kajita, K.; Nakamura, T.; Takahashi, T. Specific heat and metal-insulator transition of (BEDT-TTF)2MZn(SCN)4(M = Cs, Rb). Synth. Met. 1999, 103, 1907–1908. [Google Scholar] [CrossRef]
- Nomoto, T.; Yesil, E.; Yamashita, S.; Akutsu, H.; Nakazawa, Y. Thermodynamic properties of glassy phonon states induced by strong electron correlations in θ-type organic charge transfer salts. Mod. Phys. Lett. B 2020, 34, 1–7. [Google Scholar] [CrossRef]
- Nomoto, T.; Yamashita, S.; Akutsu, H.; Nakazawa, Y.; Krivchikov, A.I. Phonon Glass Induced by Electron Correlation. J. Phys. Soc. Jpn. 2019, 88, 1–4. [Google Scholar] [CrossRef]
- Pouget, J.-P.; Alemany, P.; Canadell, E. Donor-anion interactions in quarter-filled low-dimensional organic conductors. Mat. Hori. 2018, 5, 590–640. [Google Scholar] [CrossRef] [Green Version]
- Alemany, P.; Pouget, J.-P.; Canadell, E. Structural and electronic control of the metal to insulator transition and local orderings in the θ-(BEDT-TTF)2X organic conductors. J. Phys. Condens. Mat. 2015, 27, 1–16. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hino, K.; Nomoto, T.; Yamashita, S.; Nakazawa, Y. Single Crystal Heat Capacity Measurement of Charge Glass Compound θ-(BEDT-TTF)2CsZn(SCN)4 Performed under Current and Voltage Application. Crystals 2020, 10, 1060. https://doi.org/10.3390/cryst10111060
Hino K, Nomoto T, Yamashita S, Nakazawa Y. Single Crystal Heat Capacity Measurement of Charge Glass Compound θ-(BEDT-TTF)2CsZn(SCN)4 Performed under Current and Voltage Application. Crystals. 2020; 10(11):1060. https://doi.org/10.3390/cryst10111060
Chicago/Turabian StyleHino, Kosei, Tetsuya Nomoto, Satoshi Yamashita, and Yasuhiro Nakazawa. 2020. "Single Crystal Heat Capacity Measurement of Charge Glass Compound θ-(BEDT-TTF)2CsZn(SCN)4 Performed under Current and Voltage Application" Crystals 10, no. 11: 1060. https://doi.org/10.3390/cryst10111060
APA StyleHino, K., Nomoto, T., Yamashita, S., & Nakazawa, Y. (2020). Single Crystal Heat Capacity Measurement of Charge Glass Compound θ-(BEDT-TTF)2CsZn(SCN)4 Performed under Current and Voltage Application. Crystals, 10(11), 1060. https://doi.org/10.3390/cryst10111060




