Hydrodynamics and Mass Transfer during the Solution Growth of the K₂(Co,Ni)(SO₄)₂•6H₂O Mixed Crystals in the Shapers

Abstract

Mathematical models of the hydrodynamics and mass transfer processes during the mixed crystal growth from low-temperature aqueous solutions have been analyzed. The features of these processes are caused by complex design of the crystallizer with a shaper. Two models of the solution flowing into the shaper have been considered. In the first model, the solution is fed to the central part of the crystal. The second model presents a peripheral solution supply along the shaper perimeter, which allows us to create a swirling flow. The calculation models correspond to laminar and turbulent regimes of solution flow during the growth of K₂(Co,Ni)(SO₄)₂•6H₂O mixed crystal from an aqueous solution.

1. Introduction

The control of the processes of hydrodynamics and mass transfer for the complex crystallizers is the fundamental problem of crystal growth from solution. This is complicated by the fact that a turbulent solution flow is realized by various stirring devices, a crystal rotation, high-speed solution feeding into the crystallizer, etc.

For acceleration of the mass transfer, the forced convection of the solution is used. The method of reversible growing crystal rotation is often used. Convection can both increase the growth rate and enhance the morphological instability of the crystal surface, which can degrade its quality.

The influence of hydrodynamics on the morphology of the growing crystal surface is determined by both the effect of the solution flow rate on supersaturation at the crystal surface and the dependence of the tangential step velocity on supersaturation. In the presence of the dead zone on the kinetic curve, there is a region of supersaturation where the dependence is a nonlinear step function. This supersaturation region is undesirable due to the formation of macrosteps and solution inclusions.

The inhomogeneous supersaturation distribution along the crystal surface leads to step velocity fluctuations and morphological surface instability. A number of experimental [1,2,3,4] and theoretical [5,6] studies had been carried out to determine the effect of convection on the surface instability and the inclusions formation. It was shown that the solution flow direction near the interface significantly influences the occurrence of the morphological instability. The morphological surface remains stable if the flow is directed against the growth step movement. Otherwise, the solution flow along the step movement direction leads to surface instability.

Due to the difference in the transport and physicochemical properties of isomorphic components, additional problems arise during the mixed crystal growth from aqueous solutions. The difference in the diffusion coefficients of the salt components of the growth solution and their distribution coefficients can lead to their nonregular distribution along the interface, followed by the heterogeneity of the growing mixed crystal.

Experimental determination of the surface supersaturation distribution is difficult, and therefore, for the crystal growth from solution, the numerical simulation of the flow and mass transfer is very important.

In the case of K₂(Co,Ni)(SO₄)₂•6H₂O (KCNSH) mixed crystals, a numerical simulation of the effect of a laminar hydrodynamics in a flow-through crystallizer at subcritical Reynolds numbers Re on the distribution of cobalt and nickel components of solution (K₂Co(SO₄)₂•6H₂O (KCSH) and K₂Ni(SO₄)₂•6H₂O (KNSH)) along the growing crystal face have been carried out [7]. The crystallizer setup for “from top to bottom” crystal growth by temperature difference technique was considered. In this case, the solution flows straight up from the tube in the lower part of the cylindrical shaper at a given speed and then around the growing crystal surface. It was found that difference in the diffusion coefficients of the Co and Ni components causes the inhomogeneity of the solution composition along the crystal surface to be within 0.1 at.%. The roughness of growing surface leads to the formation of many small vortices next to the surface that affects the mass transfer at the interface. It leads to the difference in the radial distributions of components concentrations and to supersaturation changing along the crystal surface. If the surface is smooth the variation in supersaturation decreases smoothly with a distance from the surface center, but in the case a rough surface, the supersaturation oscillations are corresponding to surface irregularities.

The features of the influence of turbulent flow on the solution crystallization process have been considered [8]. For this purpose, data for an intensive turbulent regime realized in a particular case of a flow in a smooth tube at large Re numbers were used. As a result, some general conclusions have been made for crystal growth from a solution with turbulent flow around the crystal surface, which became the basis for applying the results of the turbulent hydrodynamics modeling for growing a crystal from various crystallizers [9,10].

The mathematical model of hydrodynamics and mass transfer processes during the crystal growth based on the Navier–Stokes and convective diffusion equations for different solution components is considered in this work. The calculated parameters correspond to the mixed KCNSH crystal growth in a shaper from an aqueous solution containing KCSH and KNSH salts. Two ways of the solution flowing into the shaper have been considered: in the first one, the solution is fed to the central part of the crystal; in the second one, there is a peripheral solution supply along the shaper perimeter, which allows us to create a swirling flow. At the first stage, both of them have been considered at laminar regimes, with Re numbers significantly lower than critical. At the second stage, the second flow method’s shaper dimensions have been proportionally increased by five times, so the Re number reaches a large value of ~3 × 10⁴, which corresponds to a turbulent flow. Therefore, averaged Navier–Stokes equations in the form of a “standard” (k–ε) turbulence model for numerical simulation have been used. Details of the turbulence model for diffusion layers have been discussed in [11].

2. Methods of the Numerical Simulation

The numerical simulation was applied to the real KCNSH crystal growth by a temperature difference technique described in [12]. The main part of the experimental setup is a flow-through crystallizer (Figure 1a). The crystal was mounted in the upper part of the crystallizer into the shaper, and the growth ran from top to bottom. This made it possible to avoid the spontaneous crystallization on the shaper elements and to provide a solution supply to the surface of the growing crystal. The scheme of the experimental crystallizer is shown in Figure 1b.

2.1. Mathematical Problem Setting for Laminar Hydrodynamics

The scheme of the shaper with a central solution supply is shown in Figure 2a: the solution (3) flows straight up from a tube (1) to a shaper (2) with the growing crystal at a given velocity V_jet and around the growing crystal surface (4). Shaper dimensions are height H = 4 cm and diameter D = 3 cm. Tube (1) diameter is d = 0.3 cm. Then, the solution flows out through the lower part (5) of the shaper. Crystal grows from top to bottom along the whole shaper diameter.

The model with peripheral (tangential) solution supply was considered as a model providing a more uniform distribution of components along the crystal surface (Figure 2b).

To determine the components V_i of the flow velocity and pressure P in the solution, the Navier–Stokes and continuity equations are solved, being written in component-wise form as follows [13]:

$${\rho }_o\left(\frac{\partial V_i}{\partial t}+V_j\frac{\partial V_i}{\partial x_j}\right)=\frac{\partial {\sigma }_{ij}}{\partial x_j}, \frac{\partial V_i}{\partial x_i}=0,$$

(1)

where ${\sigma }_{ij}$ are stresses in liquid, which determined by the formula

$${\sigma }_{ij}=-P{\delta }_{ij}+\mu \left(\frac{\partial V_i}{\partial x_j}+\frac{\partial V_j}{\partial x_i}\right),$$

(2)

where t is time, ${\rho }_o$ is density, μ is dynamic, and ν = μ/${\rho }_o$ is thekinematic viscosity of the solution.

For the calculated velocity vector $V$= (V_r, V_y) the equations of the convective transfer in the solution for each component are solved:

$$\frac{\partial M_i}{\partial t}+V\mathsf{\nabla }{M}_i=D_i\mathsf{\Delta }{M}_i$$

(3)

where $M_i$ = ${\rho }_o$C_i is the component concentration in the solution [g/cm³], C_i is the component mass fraction by 1000 g of a solution, and i corresponds to component: 1—KCSH, 2—KNSH.

To calculate the normal crystal growth rate, the formula for a simple dislocation source is used [14].

$$R=\frac{\beta C_{e}hkT{\sigma }_o{}^2}{19\omega \alpha },$$

(4)

Overall supersaturation is ${\sigma }_0=\frac{(C_1+C_2)-(C_{e1}+C_{e2})}{C_{e1}+C_{e2}}\approx \ln \left(\frac{C_1+C_2}{C_{e1}+C_{e2}}\right)$ [14], where C_i—current and C_ei—equilibrium component concentration. Used data are given from [15] and are presented in

Table 1. Hydrodynamic model parameters.

Parameter	Value
Kinematic viscosity of the solution ν [cm2/s] [16]	5.06 × 10−3
Diffusion coefficient of the component Di [cm2/s]	D1 = 1.217 × 10−5 D2 = 1.075 × 10−5
Solution density ${\rho }_0$ [g/cm3]	1.115
equilibrium component concentration Cei at the T=317 K [g/1000 g H2O]	Ce1 = 4.93 Ce1 = 100.7

and

Table 2. Parameters for the crystal growth rate calculation.

Parameter	Value
T temperature [K]	317
${\sigma }_0$ overall supersaturation at supercooling ΔT = 0.5 K	0.09
$\omega$ molecule volume [cm3]	3.24 × 10−22
k Boltzmann constant [erg/K]	1.38 × 10−16
β kinetic coefficient of the step on the crystal face (110) [cm/s]	5 × 10−2
α free specific surface energy [erg/sm2]	19.5
h step height on (110) crystal face [sm]	5.3 × 10−8

.

Since the free specific surface energy α is unknown for KCNSH crystals, the value for the (100) KDP crystal face have been used [17]. Also, in the literature, there is no data on the diffusion coefficients of KCSH and KNSH salts in aqueous solutions; therefore, the values for CoCl₂ [18] and NiCl₂ [19] have been used, respectively. The difference in the distribution of the nickel and cobalt component concentrations along the crystal surface largely depends on the ratio of their diffusion coefficients. Since in CoCl₂ and NiCl₂ salts, as in KCSH and KNSH salts, the difference in the diffusion coefficients is determined by the difference in the Co²⁺ and Ni²⁺ ions mobility, it can be assumed that the ratio of the diffusion coefficients in both cases will be close. Thus, the calculations are estimates.

According to the data in Table 2, the crystal growth rate is R = 5.66 × 10⁻⁷ cm/s (0.489 mm/day). Supersaturation for each component is calculated as ${\sigma }_i=$ $\ln \left(\raisebox{1ex}{$C_i$}\!\left/ \!\raisebox{-1ex}{$C_{ei}$}\right.\right)\approx \frac{C_i-C_{ei}}{C_{ei}}$. Equilibrium concentrations at T = 39 °C are C₀₁ = 49.25 and C₀₂ = 101.77 g/1000 g H₂O. Initial supersaturation is ${\sigma }_0= {\sigma }_{01}= {\sigma }_{02}=0.09$.

To calculate the rate and component concentration distributions by Equations (1) and (3), the boundary conditions are set:

-

in the area of solution inflow the jet velocity and component concentration are V_y = V_jet, C_i = C_oi, where C_oi = ${\rho }_o$ × exp(σ_o) × C_ei;

-

at the outflow boundary the velocity gradient and component flows are zero;

-

on the shaper side wall the speed and component flows are zero;

-

at the interface the mass balance ratio (Equation (6)) for each component is set taking into account the value of the crystal growth rate calculated by the Equation (4).

The mixed crystal KCNSH density is ρ_s = 2.24 g/cm³. The values C_si are set subject to distribution coefficient K which connects the component concentrations in the crystal and solution [20]:

$$K=\frac{C_{s2}{C}_1}{C_{s1}{C}_2}=3.7$$

where C_s1 + C_s2 = 1. Therefore, the C_si are

$$C_{s1}=\frac{C_1}{C_1+K{C}_2}, C_{s2}=\frac{K{C}_2}{C_1+K{C}_2} ,$$

(5)

where C_i is the component concentration at the phase boundary in solution that are determined in the iterative counting. Assuming the supersaturation is small it is fair to say that C_i ≈ C_ei and the material balance equation at the crystallization front are written as

$${\rho }_{oi}{D}_i\frac{\partial C_i}{\partial n}=R\left(C_{si}{\rho }_s-C_{ei}{\rho }_o\right) ,$$

(6)

The left side of Equation (6) describes the matter flow to the crystallization front by diffusion. The right side describes its absorption by the growing crystal. By this means, Equation (6) combines the hydrodynamics model and thermodynamic one.

The software implementations of the models are developed on the basis of the AnsysFluent software package [21] supplemented with custom UDF subroutines in the C language.

2.2. Mathematical Problem Setting for Turbulent Hydrodynamics

Compared to the model shown in Figure 2a, the dimensions of the model in Figure 2b were proportionally increased by five times. At the same inflow rate into the shaper the Reynolds number increased to the critical value Re = 2.25 × 10⁴ which correspond to a turbulent flow regime.

The standard (k–ε)-model of turbulence [22] extensively studied in [23,24] was used for calculation. In this model the Navier-Stokes equations are solved in averaged form. The flow variables are written as the sum of the average and fluctuating components (i. e. $V=\overline{V}+V^{\prime }, P=\overline{P}+P^{\prime }$, etc.).

Time averaging of the Navier–Stokes equations (Equation (1)) causes additional terms characterizing the turbulent (Reynolds) stresses. Besides, an additional “turbulent” viscosity μ_t is introduced into the (k–ε)-model. It differs from the molecular viscosity μ and characterizes the development of a flow changing in time and space.

For each component equations for average values are written as [13]

$${\rho }_o\left(\frac{\partial {\overline{V}}_i}{\partial t}+{\overline{V}}_j\frac{\partial {\overline{V}}_i}{\partial x_j}\right)=\frac{\partial }{\partial x_j}\left(\overline{{\sigma }_{ij}}-\rho \overline{V_i^{’}{V}_j^{’}}\right) ,$$

(7)

Equation (7) is known as Reynolds equation, and the $\rho \overline{V_i^{’}{V}_j^{’}}$ component is called Reynolds stress. The turbulent flow is described by four equations with 10 unknowns: three rate components, pressure, and six Reynolds stresses.

In hydrodynamics, different approaches are used to determine the relationship between the Reynolds stresses and the parameters of the averaged flow in order to close Equation (7). One of them is introduction of the turbulent viscosity μ_t by analogy with the molecular dynamic viscosity:

$$-\rho \overline{V_i^{’}{V}_j^{’}}={\mu }_t\left(\frac{\partial V_i}{\partial x_j}+\frac{\partial V_j}{\partial x_i}\right) ,$$

(8)

The development of turbulence is analyzed using the turbulent kinetic energy k and the velocity of turbulent dissipation ε. To calculate them, two additional semi-empirical equations are used:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho k{V}_i\right)}{\partial x_i}= \frac{\partial }{\partial x_j}\left[\frac{{\mu }_t}{{\sigma }_k}\frac{\partial k}{\partial x_j}\right]+2{\mu }_t{E}_{ij}{E}_{ij}-\rho \epsilon ,$$

(9)

$$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+\frac{\partial \left(\rho \epsilon V_i\right)}{\partial x_i}= \frac{\partial }{\partial x_j}\left[\frac{{\mu }_t}{{\sigma }_{\epsilon }}\frac{\partial \epsilon }{\partial x_j}\right]+C_{1\epsilon }\frac{\epsilon }{k}2{\mu }_t{E}_{ij}{E}_{ij}-2C_{2\epsilon }\rho \frac{{\epsilon }^2}{k},$$

(10)

where V_i is speed components for respective directions and E_ij are strain rate components. Several constants are used in these equations: C_p = 0.09, σ_k = 1.00, σ_ε = 1.30, C_1ε = 1.44, C_2ε = 1.92 [16]. The turbulent viscosity μ_t is determined using calculated variables k and ε: ${\mu }_t=\rho C_p\frac{k^2}{\epsilon }$.

The turbulent boundary layer at solid surfaces is modeled using the wall function [16,22] which relates the velocity to the shear stress at the calculated grid point closest to the surface. The formula is written as

$$\overline{V}\left(y^{+}\right)=u^{+}\left[\frac{1}{a}ln(y^{+})+b\right], y^{+}>30,$$

(11)

where V(y⁺) is the calculated velocity at the nearest to the surface grid point, y⁺ is the normalized distance from the surface to this grid point, and u⁺ is the friction velocity related to the shear stress on the surface. Here, a = 0.41 and b = 5.0.

Equation (11) gives an implicit expression for the surface shear stress in terms of the calculated velocity at the nearest to the surface grid point. It is valid for the logarithmic part of the profile of the turbulent boundary layer at y⁺ > 30. That limits the minimum grid step near the surface as y > 0.3 cm and corresponds to the step y = 0.35 cm used in these calculations. Despite the fact that the algorithm for calculation of the turbulent logarithmic profile corresponds to a turbulent flow over a flat plate, it is used to analyze the turbulent flows in other geometries [8].

3. Results and Discussion

3.1. Laminar Hydrodynamics and Distribution of Components Concentration during the Central Solution Supply to the Crystal Surface

The flow direction during the central supply to the crystal surface is schematically shown in Figure 2a. The calculations were performed for four values of the inflow velocity: V_jet = 10, 55, 90, and 200 cm/s, which correspond to the values used in experiments on K₂(Co,Ni)(SO₄)₂•6H₂O crystals growth. The solution circulation in the shaper at the inflow velocity V_jet = 90 cm/s is shown in Figure 3a. In the case of inflow velocity range of 10–200 cm/s the corresponding Reynolds number is in the range of 300–6000.

The inflow jet changes the axial direction of the flow to radial one when it reaches the crystal surface. Because of the high speed of the inflow jet, an intense vortex circulation arises near the crystal surface when the inflow jet collides with the shaper wall. The solution flows down intensively in the central part of the shaper (outside the inflow area). A weak closed (blocking flow) circulation arises in the peripheral area.

Due to the turn of the inflow jet, at first, its radial velocity V_r sharply increases from 0 cm/s to 60 cm/s at the interface then sharply decreases to 20 cm/s and remains the same over most of the crystal surface. The above considered hydrodynamics features affect the distribution of the component concentrations in solution.

In general, the appearances of isolines of the KCSH and KNSH concentrations are similar. Therefore, it is sufficient to analyze the distribution of one of them—KCSH (Figure 3b). A component concentration is maximal in the axial area and remains the same at the crystal surface due to the radial turn of the inward flow. In the rest area of the shaper the component concentration decreases due to the crystal growth.

According to the data in Figure 3b, the cobalt component supersaturation in the inward jet center is ~9% and monotonically decreases with distance from the axis to 7–8% because of the difference in the distribution coefficients of Co and Ni the components supersaturation significantly differ from each other along the radial direction (Figure 4).

Since the Ni distribution coefficient is greater than unity and Co one is less than unity, the solution is more impoverished by nickel than by cobalt during the solution movement along the growing surface. It leads to a changing in the Co/Ni concentration ratio in the solution along the crystal surface. The increasing of the flow rate leads to decreasing of the compositional variations.

With decreasing supersaturation of the solution, the growth rate decreases in proportion to the square of supersaturation (Equation (4)). That means that the solution flow is less depleted during the movement along the growing surface and the inhomogeneity of the component distribution decreases.

3.2. Laminar Hydrodynamics and Components Concentration Distribution during Peripheral Solution Supply

The jet swirling is realized by feeding the solution from a tube (0.3 cm in diameter) into the lower shaper part at an angle of 60° to the vertical axis (the deviation from the horizontal axis is 30°). Outward flow is run out tangential to the shaper wall. The crystal grows from top to bottom throughout the shaper. 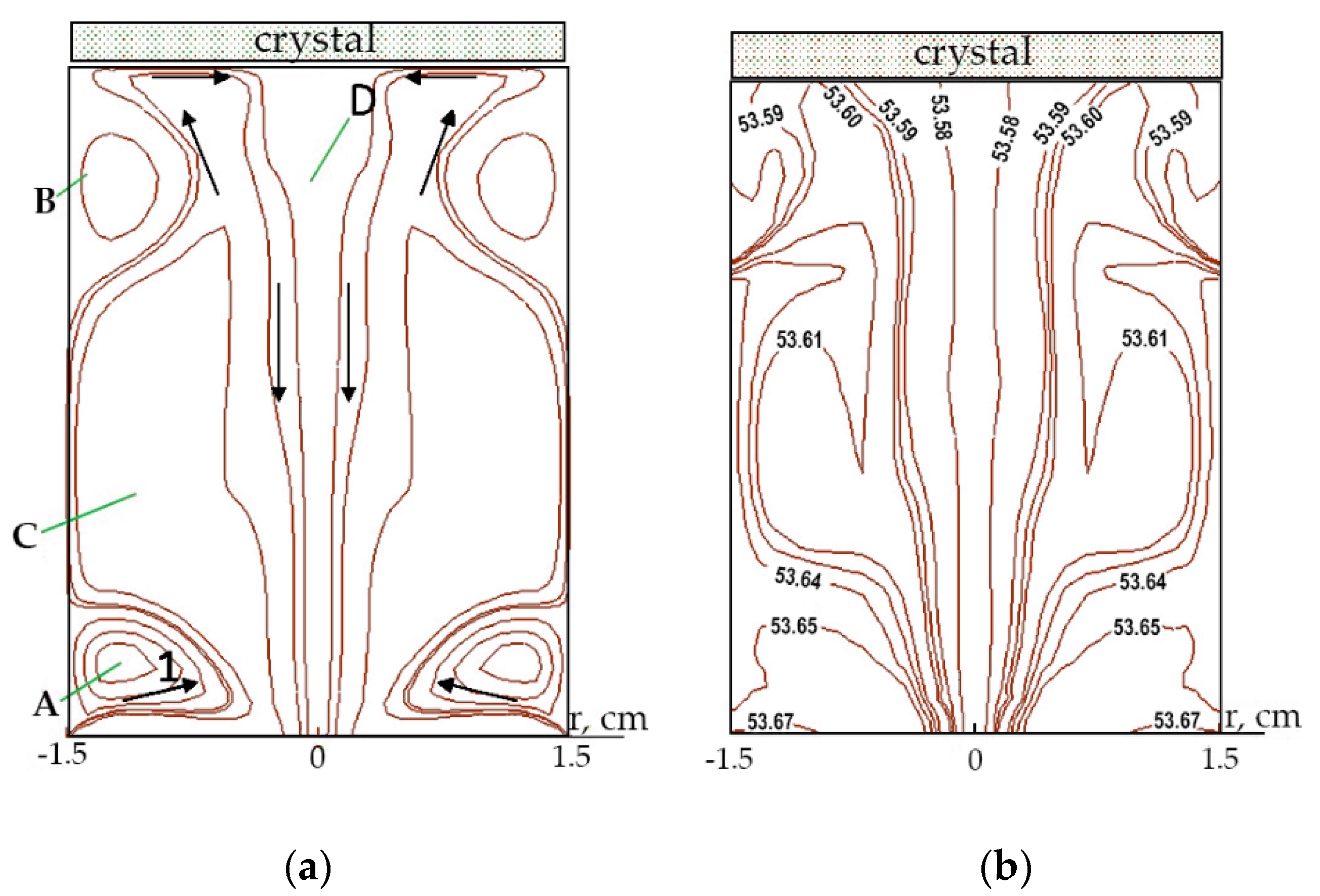In contrast to the experimental set-up the mathematical model is assumed to be axisymmetric (Figure 2b), i.e., the inward jet flows through the ring (0.3 cm wide) with the given velocity components V_r = −V × cos (60°), V_z = V × sin (60°), and V_Ω = V × cos (30°)/π. The solution flows into a cylindrical shaper with a given swirl and inclination to the axes and causes a rather complex meridional vortex flow. The diagram of the solution flow in the meridional plane is shown in Figure 5a, and the inflow velocity is V = 55 cm/s.

The inward flow (1) streams up forming vortex meridional swirls (A) and (B). Then after flowing the crystal it flows down through the vortex swirl (C) and the central outflow (D). As the velocity increases from 10 cm/s to 55 cm/sm the enhancement of the vortex swirl (A) weakens an effect of the swirl (B) near the crystal surface. At the same time, the swirl size (C) increases, and the area of the central outflow (D) expands.

The isolines of KCSH concentration in the meridional plane are shown in Figure 5b. The highest concentration is observed near the ring tube with the inflowing solution (the isoline with a value of 53.67 g/1000 g H₂O). Due to convective diffusion in the bulk of the solution the concentration isolines are elongated in the flow direction for specific vortex structures. It becomes more visible at a higher speed of 55 cm/s. The values of concentration isoline near the crystal surface decrease with a distance from its edge to the center area, and the decrease is more significant at a lower rate of solution supply into the shaper.

The solution supersaturation for each component are shown in Figure 6 at a different inflow velocity V.

It can be noted that at the higher inflow velocity, the higher supersaturation and homogeneity of the solution composition along the crystal surface can be achieved. This is due to the intense and homogeneous flow around crystal surface. At a lower flow velocity, the supersaturation on the surface decreases. This causes a noticeable radial composition inhomogeneity observed at the surface center which is explained by the presence of a more intense central vortex flow around the crystal.

3.3. Turbulent Hydrodynamics and Components Concentration Distribution during Peripheral Solution Supply into an Increased Shaper

The streamlines of the averaged turbulent flow are shown in Figure 7a: the main vortex (A) is caused by the peripheral solution supply in the direction (1). The slope of the inward jet causes the formation of a secondary vortex (B). After flowing around the crystal, the solution flows down in the central shaper area (D). In this case the Reynolds number is 13,500–30,000 at inflow rates of 90–200 cm/s.

Analyzing the distribution k(y) (y axis is normal to the crystal surface) for longitudinal sections of the whole shaper volume, it may be deduced that the greatest part of kinetic energy of the turbulent flow is concentrated in lower shaper area. Insignificant differences in k distributions are noted in the bulk of solution. However, in the upper shaper area the significant differences in the k(y) profiles for the longitudinal sections in the boundary layer can be observed (Figure 7b). Also, near the center (r = 1.825 cm), the kinetic energy is significantly lower than near the wall of the shaper (r = 5.625 cm). The graphs of the dissipation of flux energy ε(y) for the same longitudinal sections in the boundary layer differ accordingly.

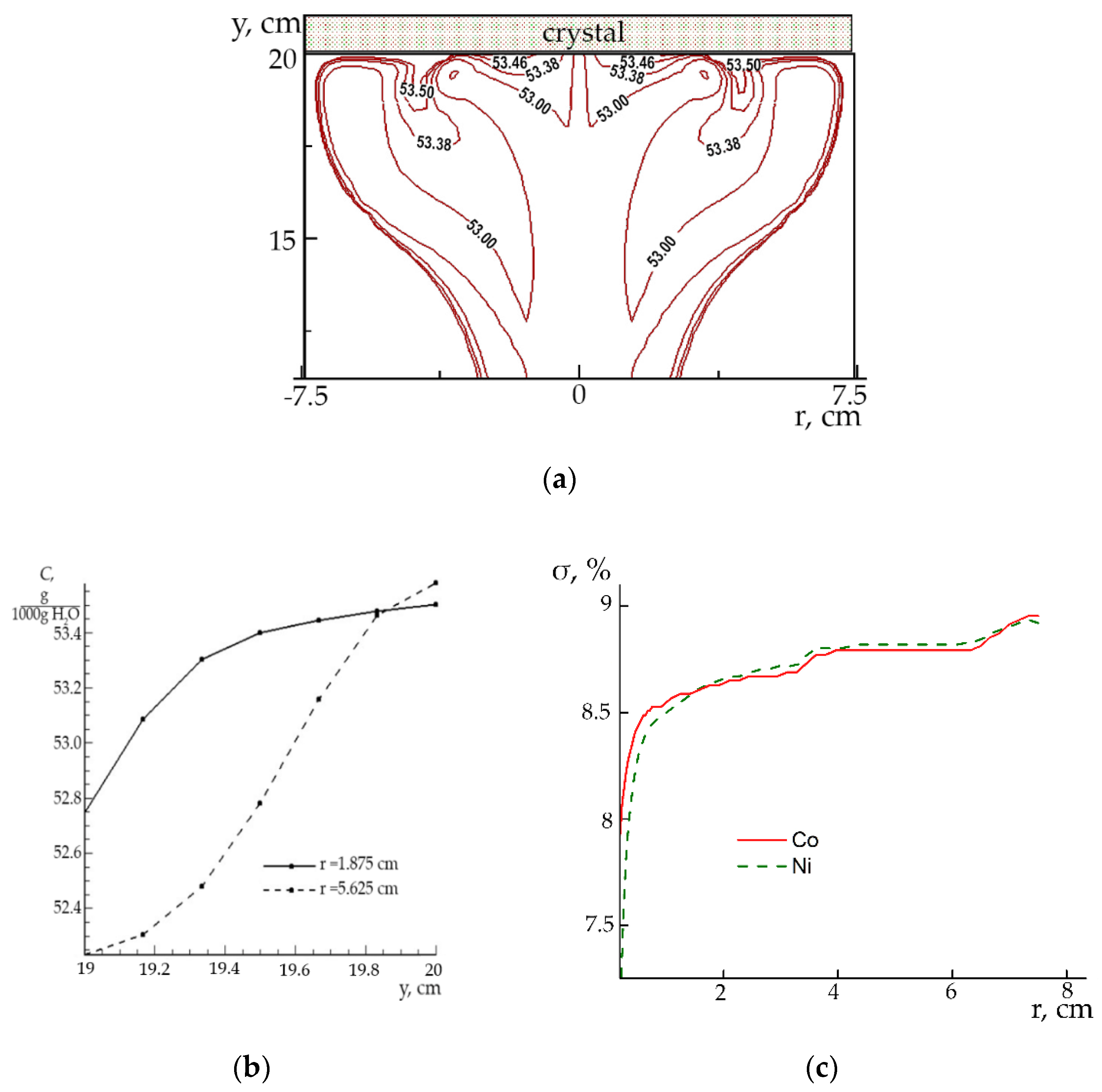
The character of the influence of turbulent flow on the distribution of Co concentration in the upper area of the shaper can be estimated from the isoline distribution in Figure 8a. The limited volume of the shaper causes the radial inhomogeneity of the distribution of the component concentration. The characteristic curvatures of isolines near the crystal surface are caused by the flow inhomogeneity around the crystal. Comparing the graph of Co concentration for two longitudinal sections near the crystal (r = 1.875 and 5.625 cm) (Figure 8b), one can observed the significant differences in Co distributions over the thickness of the boundary layer and rather close Co concentration at the interface. Thus, the peripheral jet inflow leading to the flow swirling causes the peculiarities of the flow along the crystal surface. It affects the radial inhomogeneity of the distribution of both the kinetic energy of the turbulent flow (Figure 7b) and the salt concentration (Figure 8a) near the crystal surface.

The solution supersaturation for Co and Ni components near the crystal surface is shown in Figure 8c. It can be noted that the difference in the supersaturations of Co and Ni components over the whole surface is significantly less than in the cases considered above. The exception is the central area with a radius of about 1 mm, where the supersaturations differ by more than 1%. It can result in significant composition inhomogeneity in the central part of the crystal and very high homogeneity of composition in most part of the crystal.

The calculated values of the concentrations of Co and Ni components in solution near the surface make it possible to calculate the crystal composition using Equation (5). The calculation results for all studied hydrodynamic modes are presented in Figure 9. It can be seen that the most inhomogeneous crystals are formed during solution supply to the center of the surface and the composition variations are ~2.5 mass %. With peripheral solution supply at velocity V_jet = 10 cm/s the inhomogeneity is greatly less (about 0.8 mass %). With increase of the velocity to V_jet = 55 cm/s the inhomogeneity decreases to 0.2 mass. %. That is the best result from the considered cases. In a turbulent flow, the composition variations also do not exceed 0.2 mass % in the most part of crystal surface. Nevertheless, in the central crystal area with a radius ~0.5 mm, the composition variations reach 0.8%. It can be related with the fact that the flow rate significantly changes in this surface area: its vertical component sharply increases, and the horizontal component drops to zero. As a consequence, the thickness of the diffusion layer greatly increases, and the components concentrations change at the crystallization front.

The radial distribution of the horizontal flow velocity V_surf near the crystal surface (projection on the crystal surface) for the three studied cases is shown in Figure 10. The fundamental difference between the central and peripheral jet supplies is that, in the first case, the jet hitting the center of the crystal surface spreads uniformly in all directions. As a result, the horizontal flow velocity rapidly decreases in proportion to the square of the distance (~1/r²). With the peripheral supply of the solution, a rotating flow is formed in the bulk of the shaper, where the flow rate changes slightly. A sharp decrease in the horizontal component V_surf is observed only in a center narrow region near the downstream flow. This explains the differences of a mass transport in the considered examples.

4. Conclusions

The developed laminar mathematical model allowed us to calculate the hydrodynamics and mass transfer with dependence on the inflow velocity and the mode of solution feeding into the shaper with a growing crystal. Based on this model, the components distribution has been calculated for the solution feeding both to the center of the crystal surface and to the peripheral area.

The peripheral solution supply with flow swirling ensures a more uniform distribution of supersaturation along the crystal surface. It contributes to a more stable surface morphology and, therefore, to decrease a number of crystal defects. In this case, the inhomogeneity of the crystal composition also decreases: a peripheral solution supply with a velocity V_jet = 55 cm/s provides the most uniform components distribution over the bulk of the crystal. It should also be noted that a reduction of supersaturation (i.e., reduction of the crystal growth rate) increases the uniformity of the solution components distribution along the surface, which leads to increase of the uniformity of the crystal composition too.

The shaper dimensions were proportionally increased by five times to study the peripheral solution supply process. At that, the Reynolds number reached a large value of ~ 3×10⁴, which corresponded to the onset of a turbulent flow. In this case, the homogeneity of the crystal increased in the most part of its volume with the exception of the central part. The averaged Navier–Stokes equations in the form of the standard (k–ε)-model of turbulence have been used for numerically simulation of this flow. According to the results of the calculations, the tube shape was changed to make a swirl solution supply to the crystal.