Thermal Behavior of Pyromorphite (Pb10(PO4)6Cl2): In Situ High Temperature Powder X-ray Diffraction Study
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. XRD Patterns
3.2. Unit-Cell Parameters and Thermal Expansibility
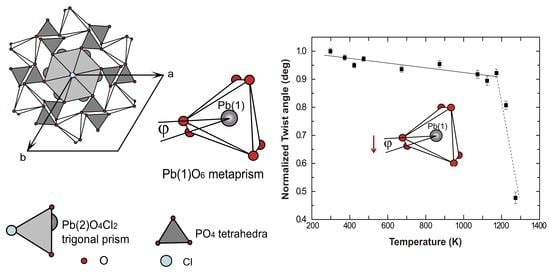
3.3. Thermal Effects on Crystal Structure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McConnell, D. Apatite: Its Crystal Chemistry, Mineralogy, Utilization, and Geologic and Biologic Occurrences; Applied Mineralogy; Springer: Wien, Austria, 1973; pp. 22–32. [Google Scholar]
- White, T.J.; Dong, Z.L. Structural derivation and crystal chemistry of apatites. Acta Crystallogr. B Struct. Sci. 2003, 59, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Schriewer, M.S.; Jeitschko, W. Preparation and crystal structure of the isotypic orthorhombic strontium perrhenate halides Sr5(ReO5)3X (X = Cl, Br, I) and structure refinement of the related hexagonal apatite-like compound Ba5(ReO5)3Cl. J. Solid State Chem. 1993, 107, 1–11. [Google Scholar] [CrossRef]
- Shearer, C.K.; Burger, P.V.; Papike, J.J.; McCubbin, F.M.; Bell, A.S. Crystal chemistry of merrillite from Martian meteorites: Mineralogical recorders of magmatic processes and planetary differentiation. Meteorit. Planet. Sci. 2015, 50, 649–673. [Google Scholar] [CrossRef]
- Yaroshevsky, A.A. Abundances of chemical elements in the Earth’s crust. Geochem. Int. 2006, 44, 48–55. [Google Scholar] [CrossRef]
- Boyce, J.W.; Liu, Y.; Rossman, G.R.; Guan, Y.; Eiler, J.M.; Stolper, E.M.; Taylor, L.A. Lunar apatite with terrestrial volatile abundances. Nature 2010, 466, 466–469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, X.; Wright, J.V.; Conca, J.L.; Peurrung, L.M. Evaluation of heavy metal remediation using mineral apatite. Water Air Soil Pollut. 1997, 98, 57–78. [Google Scholar] [CrossRef]
- Kim, J.Y.; Dong, Z.; White, T. Model apatite systems for the stabilization of toxic metals: II, cation and metalloid substitutions in chlorapatites. J. Am. Ceramic Soc. 2005, 88, 1253–1260. [Google Scholar] [CrossRef]
- Ibrahim, M.; Labaki, M.; Giraudon, J.-M.; Lamonier, J.-F. Hydroxyapatite, a multifunctional material for air, water and soil pollution control—A review. J. Hazard. Mater. 2019, 383, 121139. [Google Scholar] [CrossRef] [PubMed]
- Hovis, G.L.; Scott, B.T.; Altomare, C.M.; Leaman, A.R.; Morris, M.D.; Tomaino, G.P.; McCubbin, F.M. Thermal expansion of fluorapatite-hydroxylapatite crystalline solutions. Am. Mineral. 2014, 99, 2171–2175. [Google Scholar] [CrossRef] [Green Version]
- Hovis, G.; Abraham, T.; Hudacek, W.; Wildermuth, S.; Scott, B.; Altomare, C.; Medford, A.; Conlon, M.; Morris, M.; Leaman, A.; et al. Thermal expansion of F-Cl apatite crystalline solutions. Am. Mineral. 2015, 100, 1040–1046. [Google Scholar] [CrossRef]
- Chernorukov, N.G.; Knyazev, A.V.; Bulanov, E.N. Phase transitions and thermal expansion of apatite-structured compounds. Inorg. Mater. 2011, 47, 172–177. [Google Scholar] [CrossRef]
- Knyazev, A.V.; Chernorukov, N.G.; Bulanov, E.N. Phase diagram of apatite system Ca10(PO4)6Cl2-Pb10(PO4)6Cl2. Thermochim. Acta 2011, 526, 72–77. [Google Scholar] [CrossRef]
- Tzvetanova, Y. Lead phosphate minerals from Brussevtzi deposit (Eastern Rhodopes, Bulgaria)-SEM, JR and DTA studies. Comptes Rendus Acad. Bulg. Sci. 2003, 56, 5–55. [Google Scholar]
- McCusker, L.B.; von Dreele, R.B.; Cox, D.E.; Louër, D.; Scardi, P. Rietveld refinement guidelines. J. Appl Crystallogr. 1999, 32, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Dai, Y.; Hughes, J. Crystal structure refinements of vanadinite and pyromorphite. Can. Mineral. 1989, 27, 189–192. [Google Scholar]
- Lytle, D.A.; Schock, M.R. The formation of Pb(IV) oxides in chlorinated water. J. Am. Water Works Assoc. 2005, 97, 102–114. [Google Scholar] [CrossRef]
- Bauer, M.; Klee, W.E. The monoclinic-hexagonal phase transition in chlorapatite. Eur. J. Mineral. 1993, 5, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A Cryst. Phys. Diffr. Theor. Gen. Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]





| T/K | a/Å | c/Å | V/Å3 | a/c | ϕ/° | wRp/% |
|---|---|---|---|---|---|---|
| 298 | 9.9896 (1) | 7.3457 (2) | 634.83 (1) | 1.356 | 21.8 (2) | 12.57 |
| 373 | 9.9973 (2) | 7.3540 (2) | 636.53 (2) | 1.359 | 21.3 (2) | 10.37 |
| 423 | 10.0036 (1) | 7.3610 (1) | 637.94 (1) | 1.359 | 20.7 (2) | 10.53 |
| 473 | 10.0050 (2) | 7.3646 (2) | 638.44 (2) | 1.359 | 21.2 (2) | 13.51 |
| 673 | 10.0365 (2) | 7.3978 (2) | 645.36 (2) | 1.357 | 20.4 (2) | 12.57 |
| 873 | 10.0606 (2) | 7.4262 (3) | 650.94 (3) | 1.355 | 20.8 (3) | 24.95 |
| 1073 | 10.0846 (3) | 7.4612 (4) | 657.14 (4) | 1.352 | 20.0 (3) | 30.50 |
| 1123 | 10.0886 (3) | 7.4715 (3) | 658.57 (4) | 1.350 | 19.5 (4) | 29.72 |
| 1173 | 10.0920 (3) | 7.4793 (3) | 659.68 (3) | 1.349 | 20.1 (3) | 28.85 |
| 1223 | 10.0878 (4) | 7.4977 (4) | 660.78 (5) | 1.345 | 17.6 (3) | 25.02 |
| 1273 | 10.0830 (3) | 7.5062 (3) | 660.90 (4) | 1.343 | 10.4 (5) | 19.93 |
| αV (×10−5 K−1) | αa (×10−5 K−1) | αc (×10−5 K−1) | Reference | |
|---|---|---|---|---|
| Pb10(PO4)6Cl2 | 4.5 (±0.02) | 1.1 (±0.06) | 2.2 (±0.06) | This Study |
| Ca10(PO4)6Cl2 | 4.19 | 0.96 | 2.22 | [10,11] |
| Ca10(PO4)6F2 | 4.15 | 1.38 | 1.32 | [10,11] |
| Ca10(PO4)6(OH)2 | 4.24 | − | − | [10,11] |
| Cd5(PO4)3Cl | 2.7 | 0.17 | 2.35 | [12] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, T.; Qin, S.; Wu, X. Thermal Behavior of Pyromorphite (Pb10(PO4)6Cl2): In Situ High Temperature Powder X-ray Diffraction Study. Crystals 2020, 10, 1070. https://doi.org/10.3390/cryst10121070
Gu T, Qin S, Wu X. Thermal Behavior of Pyromorphite (Pb10(PO4)6Cl2): In Situ High Temperature Powder X-ray Diffraction Study. Crystals. 2020; 10(12):1070. https://doi.org/10.3390/cryst10121070
Chicago/Turabian StyleGu, Tingting, Shan Qin, and Xiang Wu. 2020. "Thermal Behavior of Pyromorphite (Pb10(PO4)6Cl2): In Situ High Temperature Powder X-ray Diffraction Study" Crystals 10, no. 12: 1070. https://doi.org/10.3390/cryst10121070