Mathematical Modeling of Plastic Deformation of a Tube from Dispersion-Hardened Aluminum Alloy in an Inhomogeneous Temperature Field
Abstract
:1. Introduction
2. Methods
2.1. Mathematical Model of Plastic Deformations
2.2. Elastoplastic Material Properties
2.3. Verification of the Results
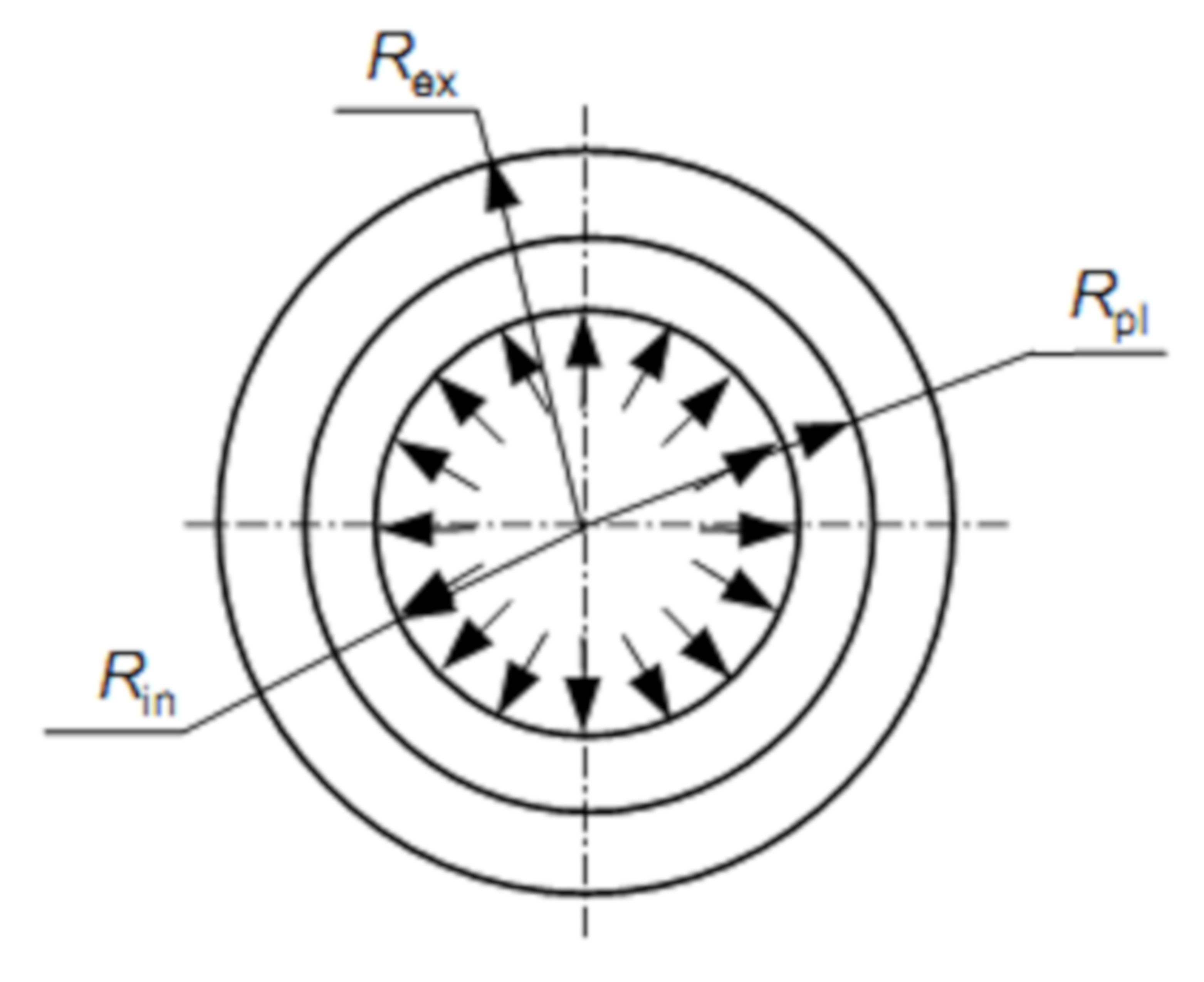
2.4. Temperature Distribution in the Tube Wall
2.5. Stresses in Tube Walls
2.6. Displacements and Strains in Tube Walls
2.7. Numerical Method
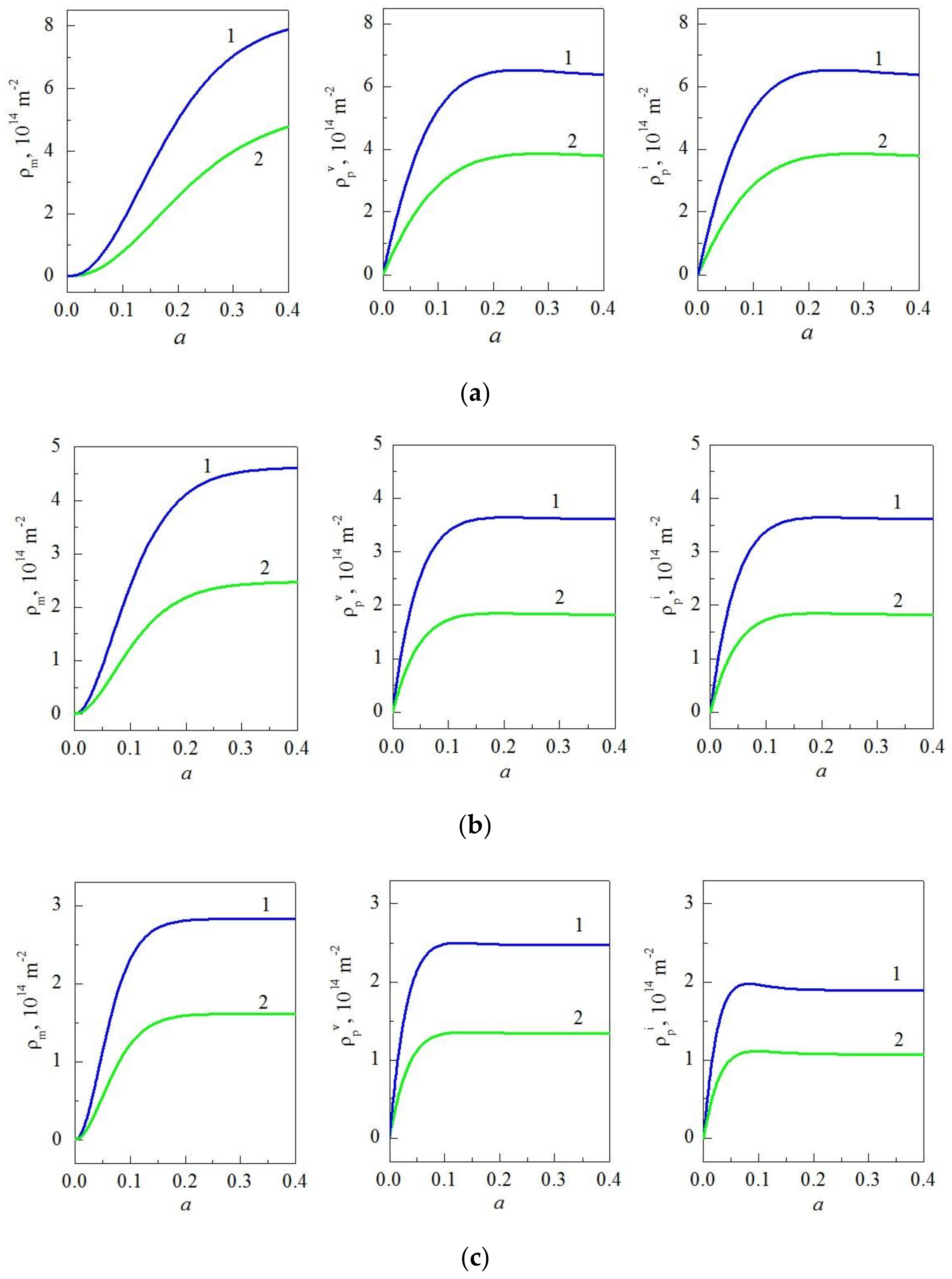
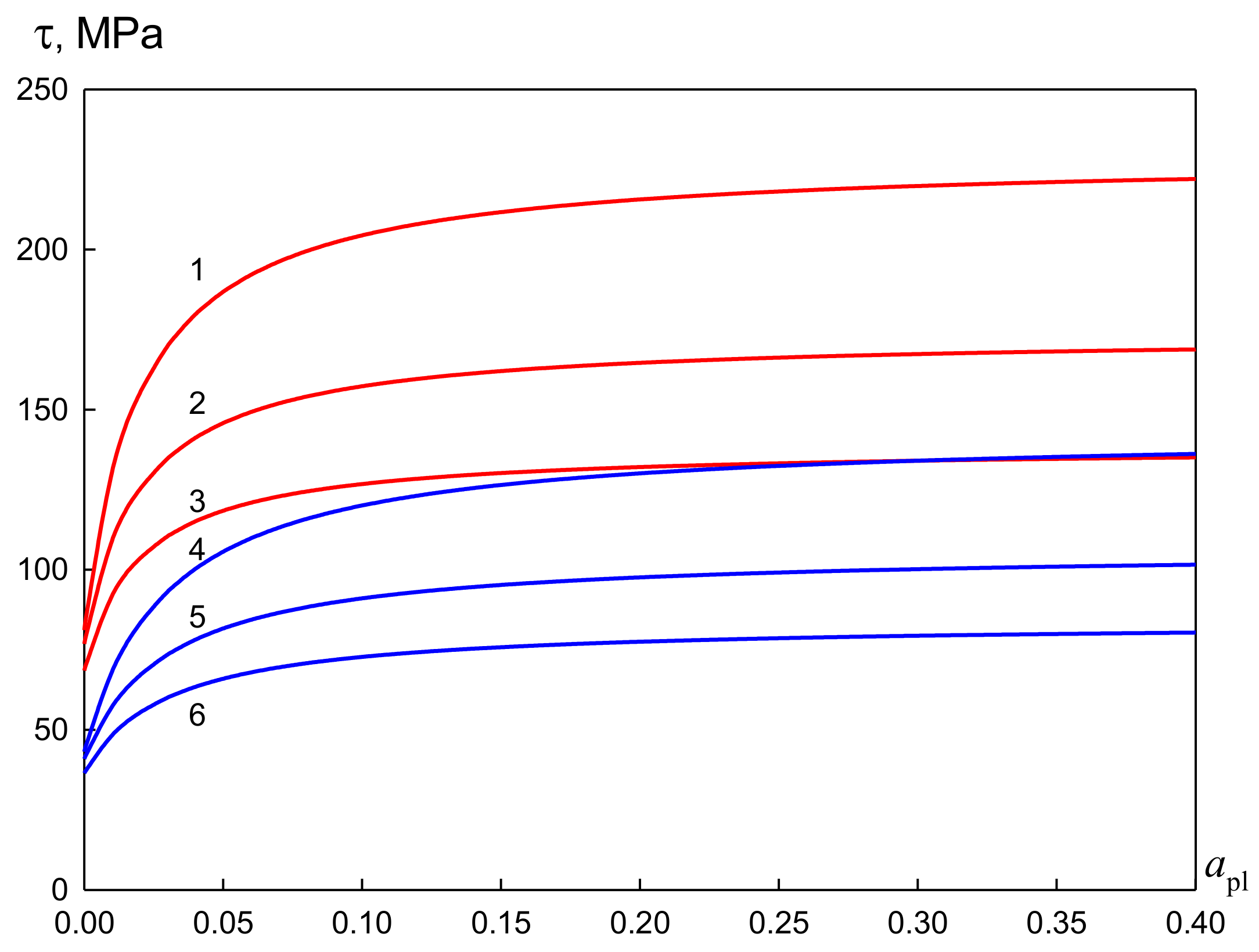
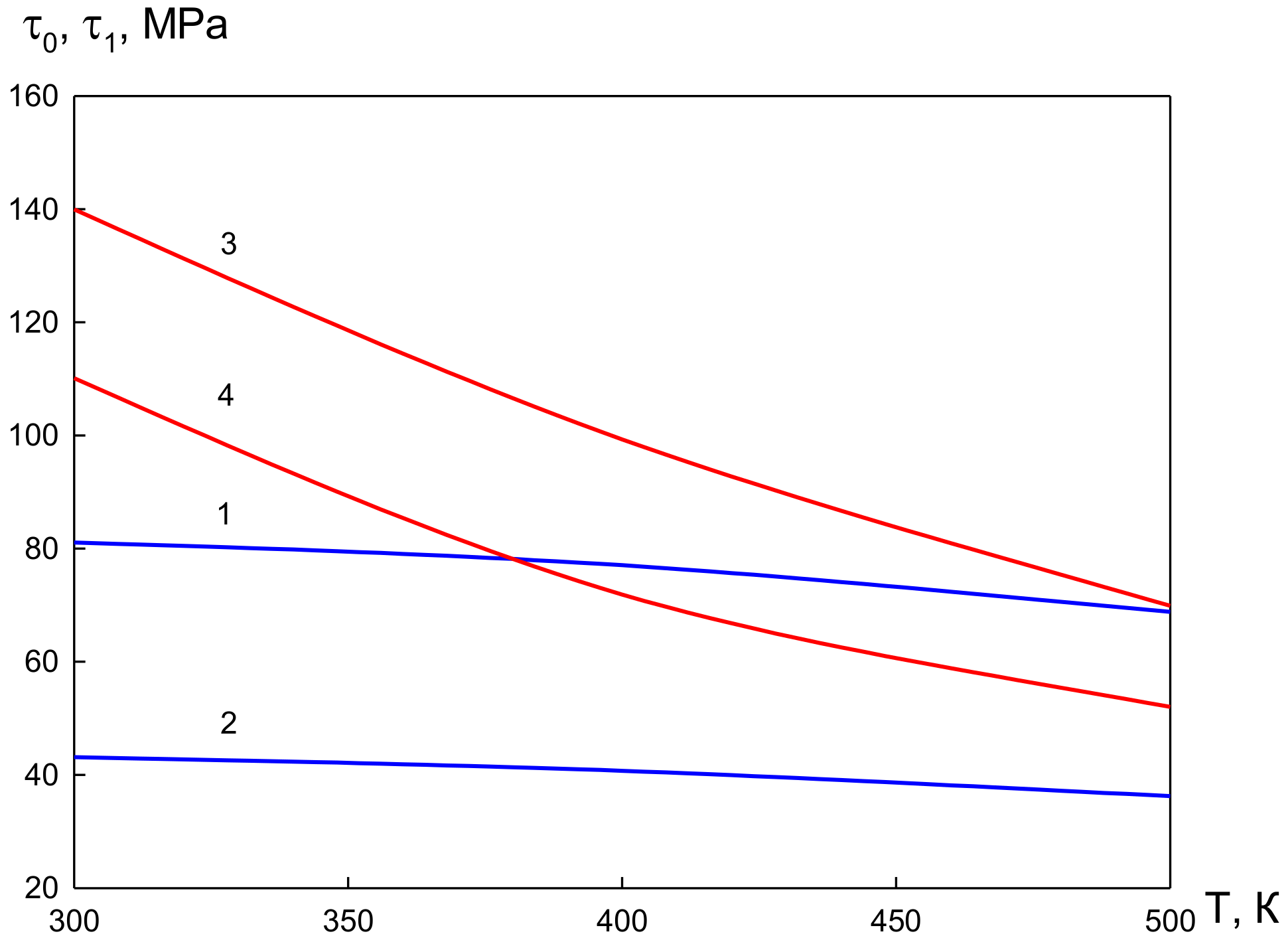
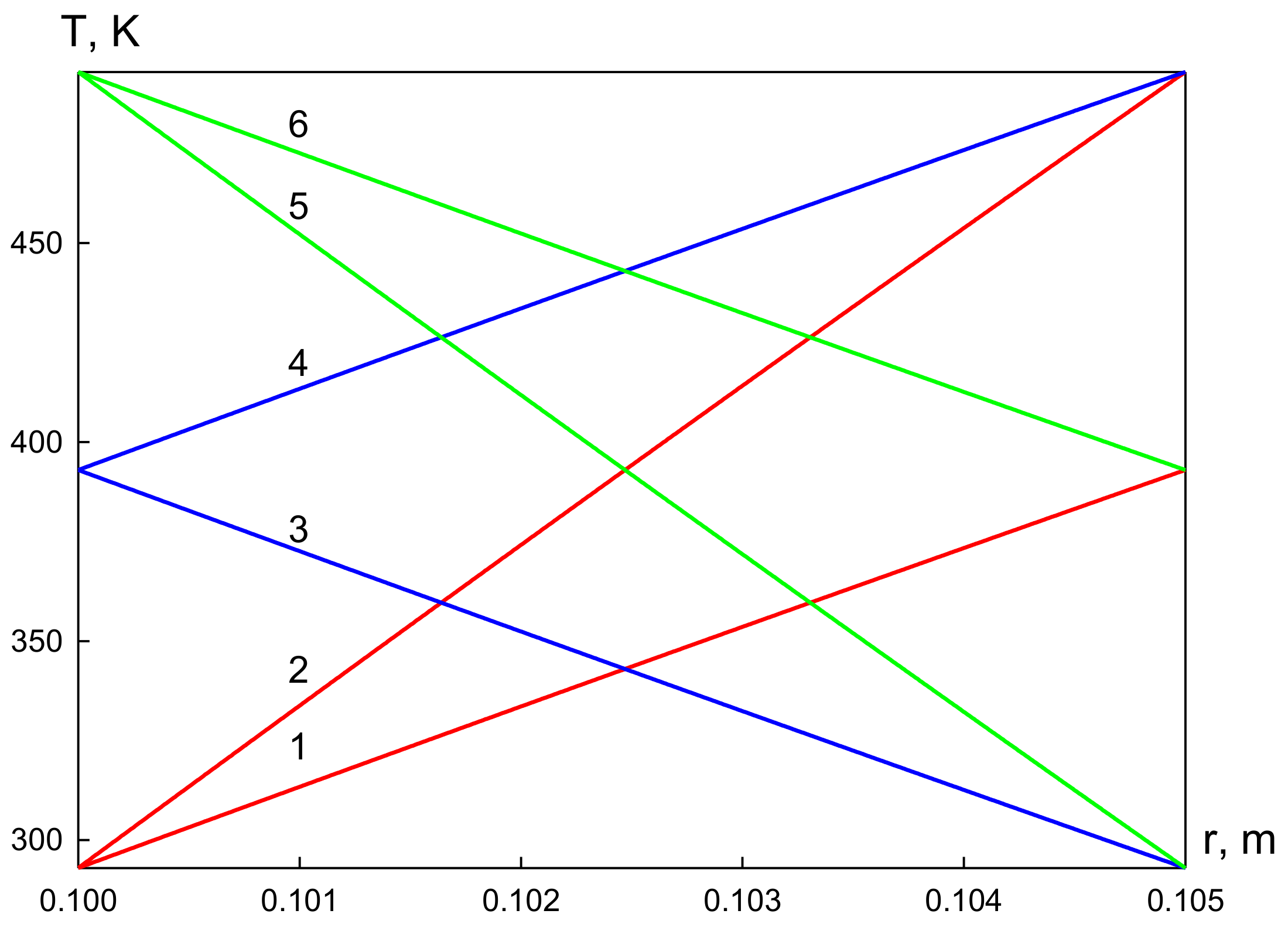
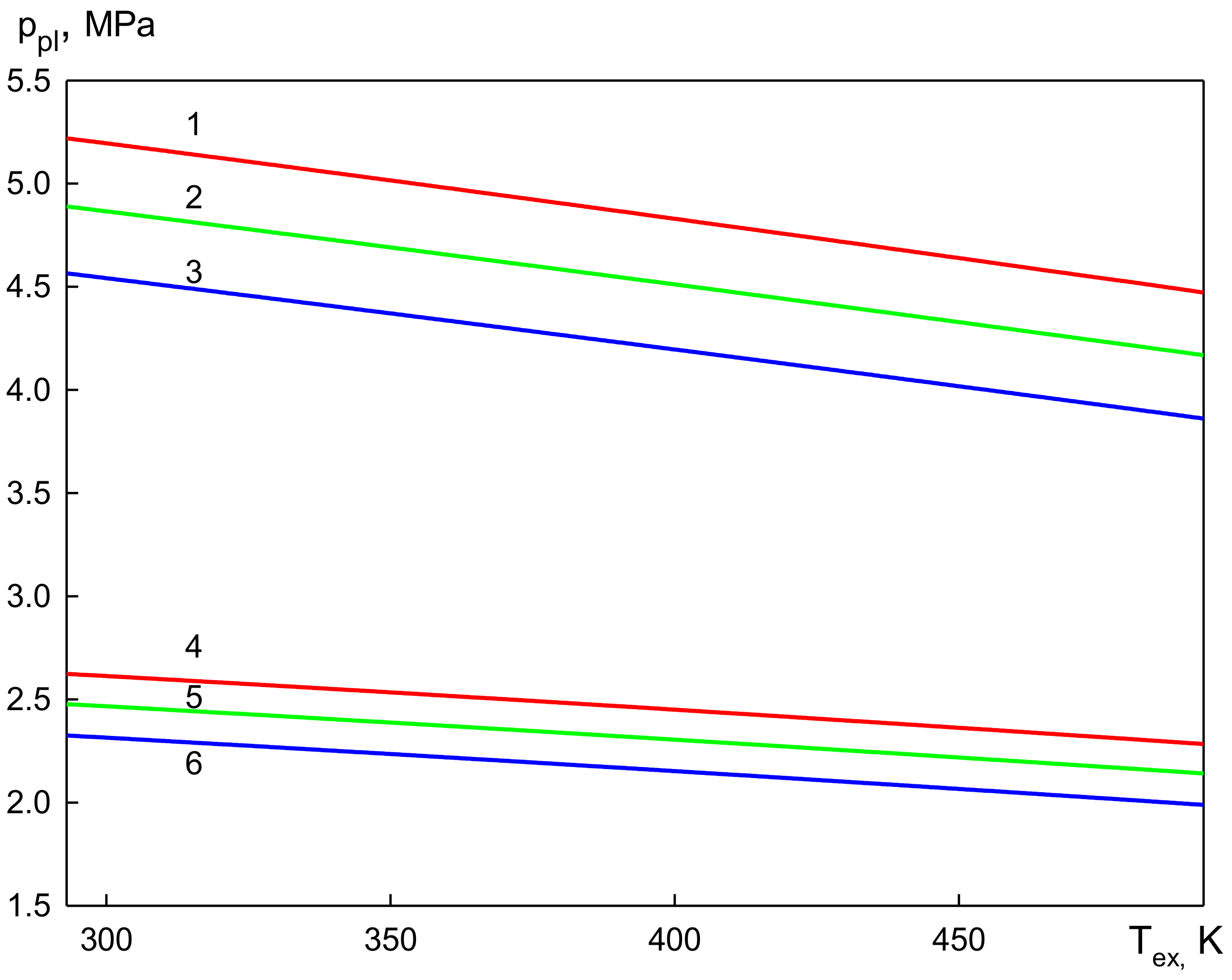
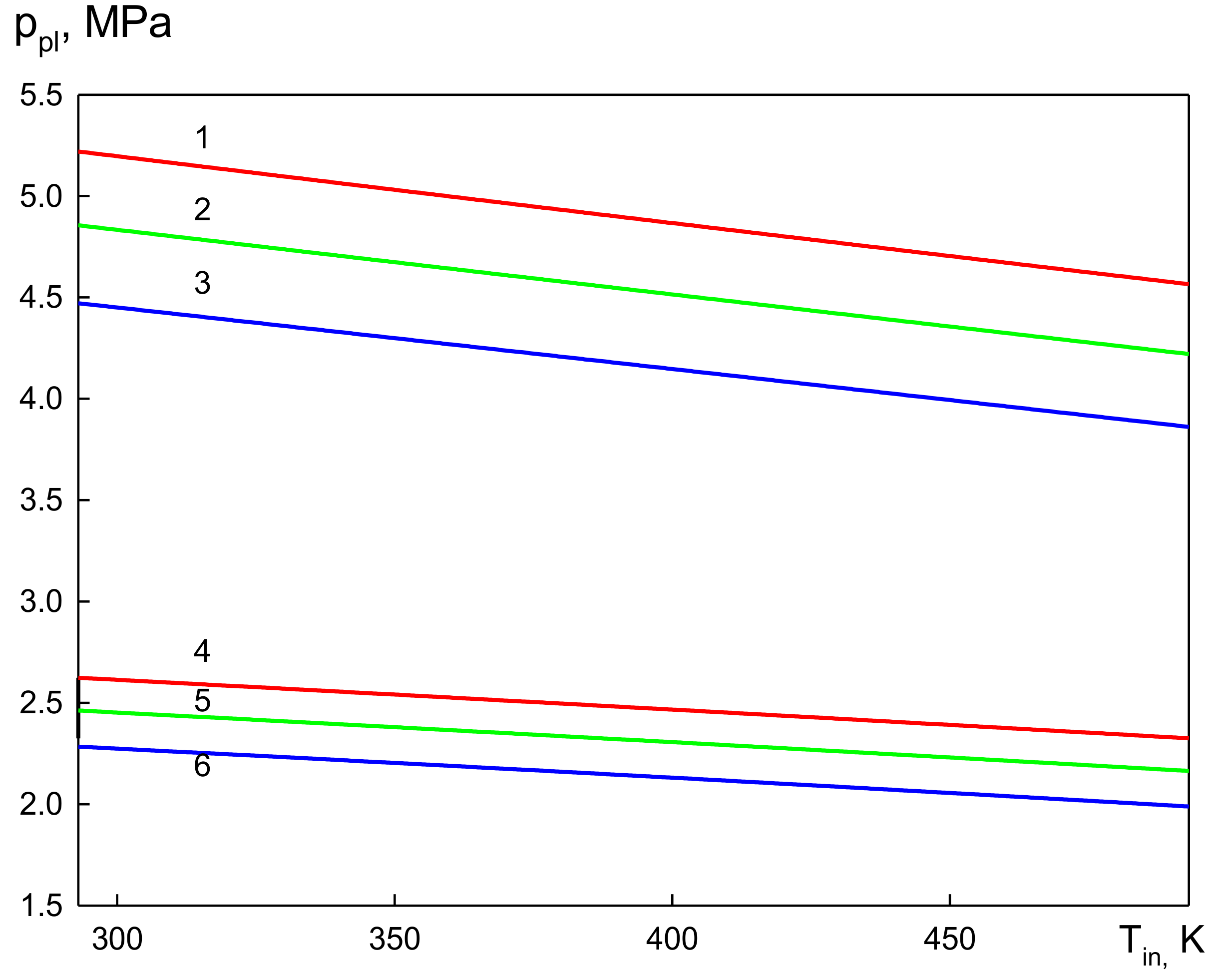
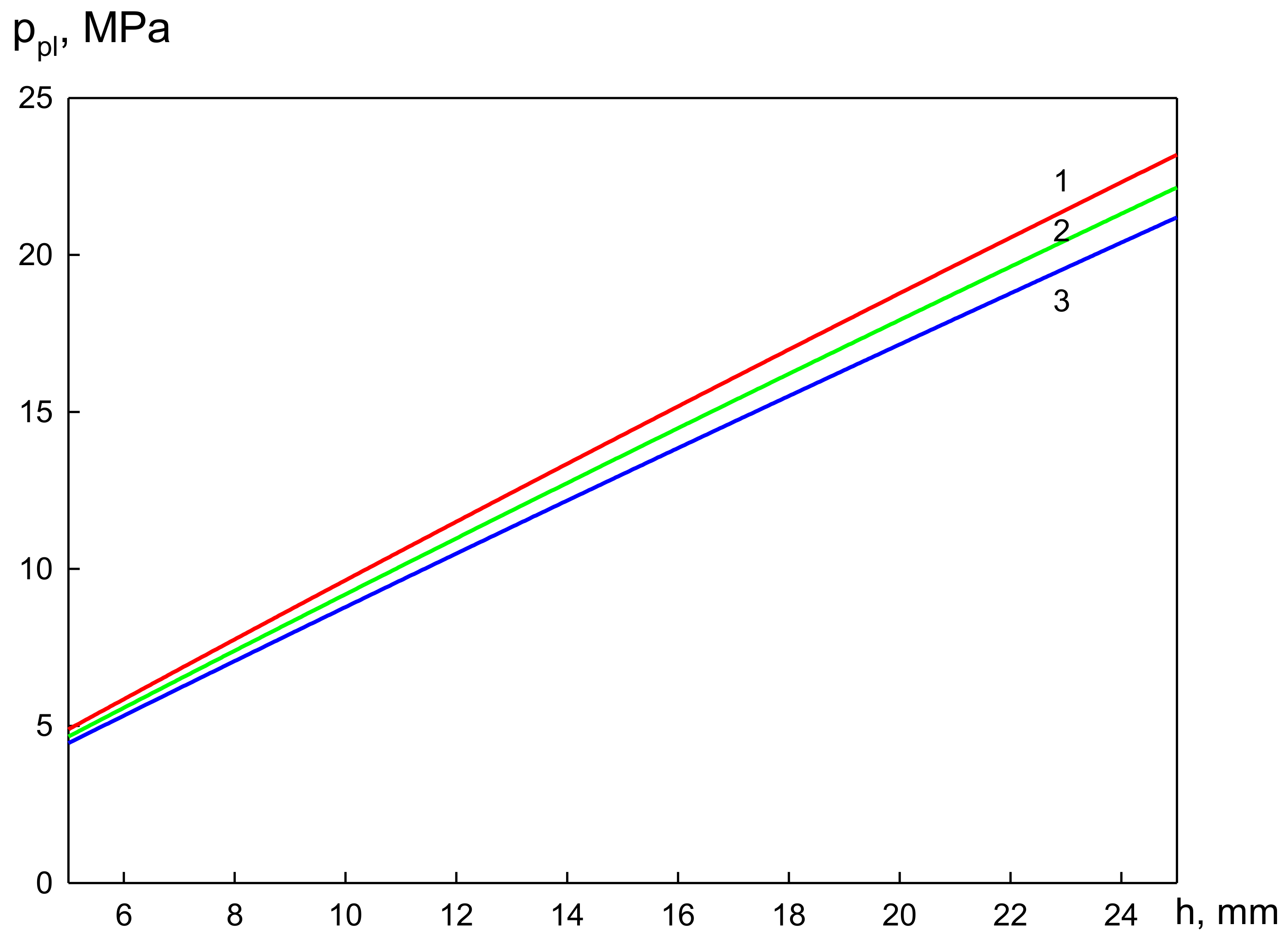
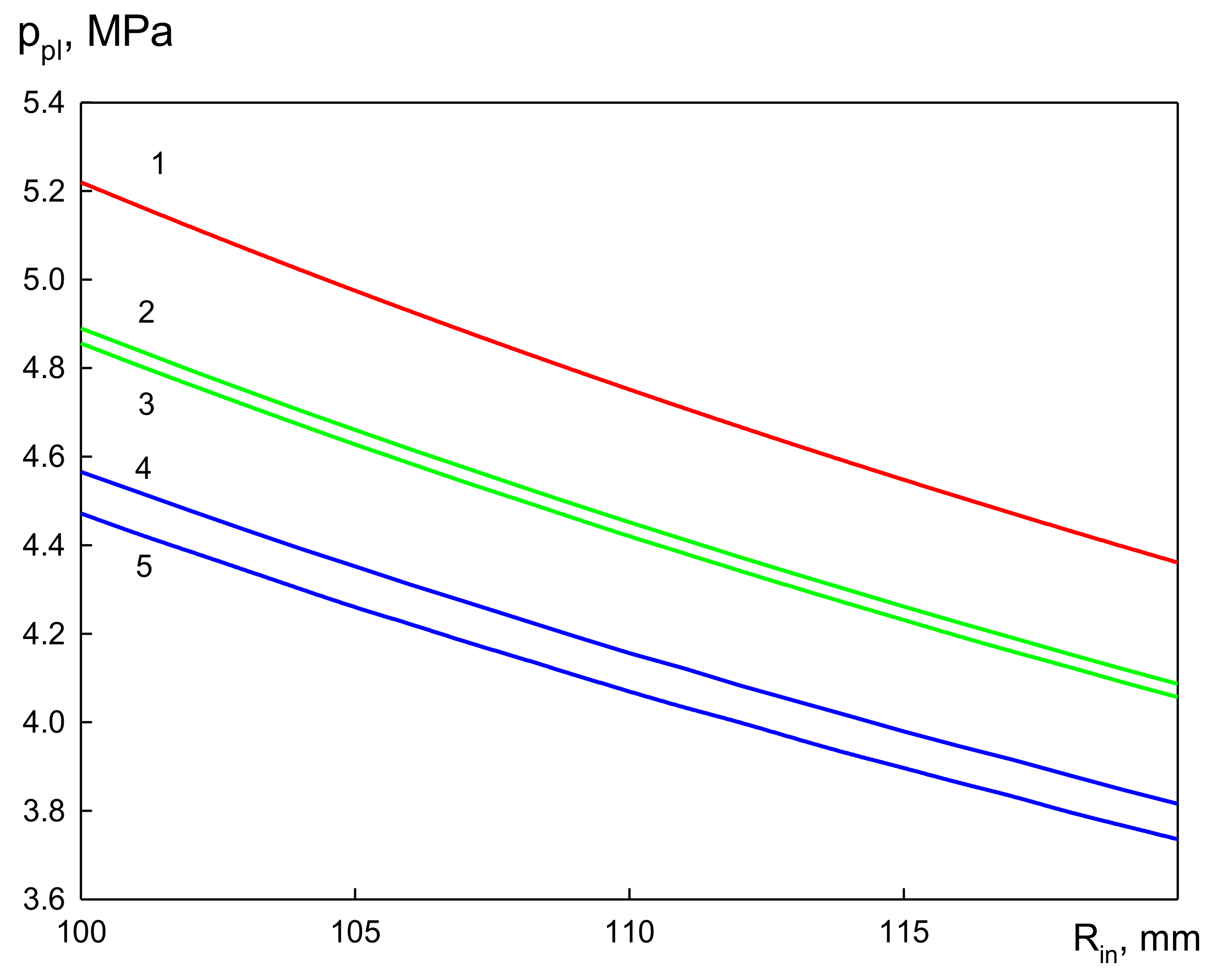
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saunders, E.A. Heat Exchanges: Selection, Design and Construction; Longman Scientific and Technical: New York, NY, USA, 1988. [Google Scholar]
- Northcutt, B.; Mudawar, I. Enhanced design of cross-flow microchannel heat exchanger module for high-performance aircraft gas turbine engines. J. Heat Transf. 2012, 134, 061801-1–061801-13. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Sang, Z. Theory solution of Hydraulic expansion tube-to-tube sheet joint residual contact pressure for power-hardening material. China Pet. Mach. 2007, 11, 24–28. [Google Scholar]
- Bouzid, A.H.; Mourad, A.H.I.; Domiaty, E.A. Influence of Bauschinger effect on the residual contact pressure of hydraulically expanded tube-to-tubesheet joints. Int. J. Press. Vessel. Pip. 2016, 146, 1–10. [Google Scholar] [CrossRef]
- Ying, H.; Xuesheng, W.; Qinzhu, C.; Jianfu, W. Bilinear Simplification of Material Model in Theoretical Calculation of Hydraulic Expansion. Mach. Des. Res. 2018, 34, 199–202. [Google Scholar]
- Law, M.; Bowie, G. Failure strain in high yield-to-tensile ratio line pipes. J. Pipeline Integr. 2006, 5, 25–36. [Google Scholar]
- Robertson, A.; Li, H.; Mackenzie, D. Plastic collapse of pipe bends under combined internal pressure and in-plane bending. Int. J. Press. Vessel. Pip. 2005, 82, 407–416. [Google Scholar] [CrossRef] [Green Version]
- Gajdos, L.; Sperl, M. Evaluating the integrity of pressure pipelines by fracture mechanics. INTECH Appl. Fract. Mech. 2012, 10, 283–310. [Google Scholar]
- Chemezov, D.; Bayakina, A.; Goremykin, V.; Prokofiev, A.; Pavlov, E.; Petrenko, A.; Sergeeva, M.; Gusenkov, M. Strain intensity of the steel pipe under the action of external tensile, compressive and combined loads. ISJ Theor. Appl. Sci. 2020, 2, 30–35. [Google Scholar] [CrossRef]
- Bergant, A.; Tijsseling, A.S.; Vítkovský, J.P.; Covas, D.I.; Simpson, A.R.; Lambert, M.F. Parameters affecting water-hammer wave attenuation, shape and timing, part 2: Case studies. J. Hydraul. Res. 2008, 46, 382–391. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.K.; Leis, B.N. Evaluation of burst pressure prediction models for line pipes. Int. J. Press. Vessel. Pip. 2012, 89, 85–97. [Google Scholar] [CrossRef]
- Zhu, X.K.; Leis, B.N. Theoretical and numerical predictions of burst pressure of pipelines. J. Press. Vessel. Technol. 2007, 129, 644–652. [Google Scholar] [CrossRef]
- Burkov, P.; Yan’nan, V.; Burkova, S. Stress–strain analysis of pipelines laid in permafrost. IOP Conf. Ser. Earth Environ. Sci. 2016, 43, 012080. [Google Scholar] [CrossRef] [Green Version]
- Chohan, R.K. Plastic deformation induced by pressure transients in fluid-filled pipes. Int. J. Press. Vessel. Pip. 1988, 33, 333–343. [Google Scholar] [CrossRef]
- Pleșcan, C.; Stanciu, M.D.; Szasz, M. The Effect of Internal Pressure on Radial Strain of Steel Pipe Subjected to Monotonic and Cyclic Loading. Materials 2019, 12, 2849. [Google Scholar] [CrossRef] [Green Version]
- Tomita, Y.; Shindo, A.; Kim, Y.S.; Michiura, K. Deformation behaviour of elastic-plastic tubes under external pressure and axial load. Int. J. Mech. Sci. 1986, 5, 263–274. [Google Scholar] [CrossRef]
- Chawla, N.; Shen, Y.L. Mechanical Behavior of Particle Reinforced Metal Matrix Composites. Adv. Eng. Mater. 2001, 3, 357–370. [Google Scholar] [CrossRef]
- Beffort, O.; Long, S.; Cayron, C.; Kuebler, J.; Buffat, P.A. Alloying effects on microstructure and mechanical properties of high volume fraction SiC-particle reinforced Al-MMCs made by squeeze casting infiltration. Compos. Sci. Technol. 2007, 67, 737–745. [Google Scholar] [CrossRef]
- Karabasov, Y.S. Advanced Materials; MISIS: Moscow, Russia, 2002; 736p. [Google Scholar]
- Orowan, E. Discussion on internal stresses. In Symposium on Internal Stresses in Metals and Alloys; Institute of Metals: London, UK, 1948; pp. 451–453. [Google Scholar]
- Ashby, M.F. Work hardening of dispersion-hardened crystals. Philos. Mag. 1966, 14, 1157–1178. [Google Scholar] [CrossRef]
- Ebeling, R.; Ashby, M.F. Dispersion hardening of copper single crystals. Philos. Mag. 1966, 13, 805–834. [Google Scholar] [CrossRef]
- Hirsch, P.B.; Hymphreys, F.J. Comment on “Dispersion hardening in metals” by E.W. Hart. Scr. Metall. 1973, 7, 259–265. [Google Scholar] [CrossRef]
- Hazzledine, P.M.; Hirsch, P.B. A coplanar Orowan loops model for dispersion hardening. Philos. Mag. 1974, 30, 1331–1351. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hirsch, P.B. Work-hardening and recovery of dispersion hardened alloys. Philos. Mag. 1976, 34, 373–390. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Stewart, A.T. Dislocation generation at SiO2 particles in an α-brass matrix on plastic deformation. Surf. Sci. 1972, 31, 389–421. [Google Scholar] [CrossRef]
- Hymphreys, F.J.; Martin, J.W. The effect of dispersed phases upon dislocation distributions in plastically deformed copper crystals. Philos. Mag. 1967, 16, 927–957. [Google Scholar] [CrossRef]
- Hymphreys, F.J.; Hirsch, P.B. The deformation of single crystals of copper and copper-zinc alloys containing alumina particles. II. Microstructure and dislocation-particle interactions. Proc. Phys. Soc. 1973, 318, 73–92. [Google Scholar]
- Matvienko, O.V.; Daneiko, O.I.; Kovalevskaya, T.A. Plastic deformation of copper-based alloy reinforced with incoherent nanoparticles. Russ. Phys. J. 2017, 60, 236–248. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Stress-stain state of pipe made of copper-based alloy strengthened with incoherent nanoparticles. Russ. Phys. J. 2017, 60, 562–569. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Dislocation structure of the pipe made of alloy reinforced with incoherent particles under uniform internal pressure. Russ. Phys. J. 2017, 60, 1233–1242. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T. Mathematical modeling of plastic deformation of a tube from dispersion-hardened aluminum alloy. MATEC Web Conf. 2018, 243, 00008. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Elastoplastic deformation of dispersion-hardened aluminum tube under external pressure. Russ. Phys. J. 2018, 61, 1520–1528. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Elastoplastic deformation of dispersion-hardened aluminum tube under external and internal pressure. Russ. Phys. J. 2019, 62, 720–728. [Google Scholar] [CrossRef]
- Daneyko, O.I.; Kovalevskaya, T.A. Temperature effect on stress–strain properties of dispersion-hardened crystalline materials with incoherent nanoparticles. Russ. Phys. J. 2019, 61, 1687–1694. [Google Scholar] [CrossRef]
- Kovalevskaya, T.A.; Daneyko, O.I. The influence of scale parameters of strengthening phase on plastic shear zone in heterophase alloys with incoherent nanoparticles. Russ. Phys. J. 2020, 62, 2247–2254. [Google Scholar] [CrossRef]
- Daneyko, O.I.; Kulaeva, N.A.; Kovalevskaya, T.A.; Kolupaeva, S.N. Investigation of thermal hardening of the FCC material containing strengthening particles with an L12 superstructure. Russ. Phys. J. 2015, 58, 336–342. [Google Scholar] [CrossRef]
- Chakrabarty, J. Theory of Plasticity; Mc Graw-Hill Book Company: New York, NY, USA; Hamburg, Germany; London, UK; Paris, France; Sydney, Australia; Tokyo, Japan, 1987; Volume VIII, 791p. [Google Scholar]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Strengthening particle size effect on residual stresses in dispersion-hardened alloy. Russ. Phys. J. 2018, 61, 962–973. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; McGraw Hill: New York, NY, USA, 2010; 567p. [Google Scholar]
- Kovalevskaya, T.A.; Vinogradova, I.V.; Popov, L.E. Mathematical Modeling of Plastic Deformation in Heterophase Alloys; TSU: Tomsk, Russia, 1992; 234p. [Google Scholar]
- Daneyko, O.I.; Kovalevskaya, T.A.; Matvienko, O.V. The influence of incoherent nanoparticles on thermal stability of aluminum alloys. Russ. Phys. J. 2018, 61, 1229–1235. [Google Scholar] [CrossRef]
- Kovalevskaya, T.; Daneyko, O.; Kulaeva, N.; Kolupaeva, S. Influence of the scale characteristics of the hardening phase with L12 superstructure on the evolution of deformation point defects. In AIP Conference Proceedings; AIP Publishing LLC: Tomsk, Russia, 2016; p. 040003. [Google Scholar] [CrossRef] [Green Version]
- Daneyko, O.I.; Kovalevskaya, T.A.; Kulaeva, N.A.; Kolupaeva, S.N.; Shalygina, T.A. Evolution of dislocation subsystem components during plastic deformation depending on parameters of strengthening phase with L12 superstructure. Russ. Phys. J. 2017, 60, 821–829. [Google Scholar] [CrossRef]
- Daneyko, O.I.; Kovalevskaya, T.A.; Kulaeva, N.A. Modeling of plastic deformation of dispersion-hardened materials with L12 superstructure particles. Russ. Phys. J. 2017, 60, 508–514. [Google Scholar] [CrossRef]
- Larikov, L.N.; Yurchenko, Y.F. Thermal Properties of Metals and Alloys; Naukova Dumka: Kiev, Ukraine, 1985; 312p. [Google Scholar]
- Polmear, L.J. Light Alloys: Metallurgy of Lights Metals; John Willey and Sons: Melbourne, Australia, 1995; 235p. [Google Scholar]
- Gorshkov, A.G.; Starovoitov, E.I.; Tarlakovskii, D.V. Theory of Elasticity and Plasticity; Fizmatlit: Moscow, Russia, 2002; 416p. [Google Scholar]
- Khrustalev, A.; Vorozhtsov, A.; Kazantseva, L.; Promakhov, V.; Kalashnikov, M.; Eskin, D.; Kurzina, I. Influence of scandium fluoride on the structure and phase composition of Al-Si alloy. MATEC Web Conf. 2018, 243, 00020. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T.; Khrustalyov, A.; Zhukov, I.; Vorozhtsov, A. Investigation of Stresses Induced Due to the Mismatch of the Coefficients of Thermal Expansion of the Matrix and the Strengthening Particle in Aluminium-Based Composites. Metals 2020. Unpublished. [Google Scholar]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Residual stresses induced by elastoplastic unloading in a tube made of dispersion-hardened alloy. Russ. Phys. J. 2018, 61, 730–742. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T. Mathematical modeling of nanodispersed hardening of FCC materials. Acta Metall. Sin. Engl. Lett. 2018, 31, 1297–1304. [Google Scholar] [CrossRef] [Green Version]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Stress–strain state of dispersion-hardened aluminum tube under external and internal pressure. Russ. Phys. J. 2020, 62, 1805–1812. [Google Scholar] [CrossRef]
- Chapra, S. Numerical Methods for Engineers; McGraw: New York, NY, USA, 2015; 518p. [Google Scholar]
| Hardening Phase Parameters | Material Constants |
|---|---|
| nm | MPa |
| nm | MPa |
| nm | MPa |
| nm | MPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matvienko, O.; Daneyko, O.; Kovalevskaya, T. Mathematical Modeling of Plastic Deformation of a Tube from Dispersion-Hardened Aluminum Alloy in an Inhomogeneous Temperature Field. Crystals 2020, 10, 1103. https://doi.org/10.3390/cryst10121103
Matvienko O, Daneyko O, Kovalevskaya T. Mathematical Modeling of Plastic Deformation of a Tube from Dispersion-Hardened Aluminum Alloy in an Inhomogeneous Temperature Field. Crystals. 2020; 10(12):1103. https://doi.org/10.3390/cryst10121103
Chicago/Turabian StyleMatvienko, Oleg, Olga Daneyko, and Tatiana Kovalevskaya. 2020. "Mathematical Modeling of Plastic Deformation of a Tube from Dispersion-Hardened Aluminum Alloy in an Inhomogeneous Temperature Field" Crystals 10, no. 12: 1103. https://doi.org/10.3390/cryst10121103





