A Combinatory Package for Diamond Anvil Cell Experiments
Abstract
:1. Introduction
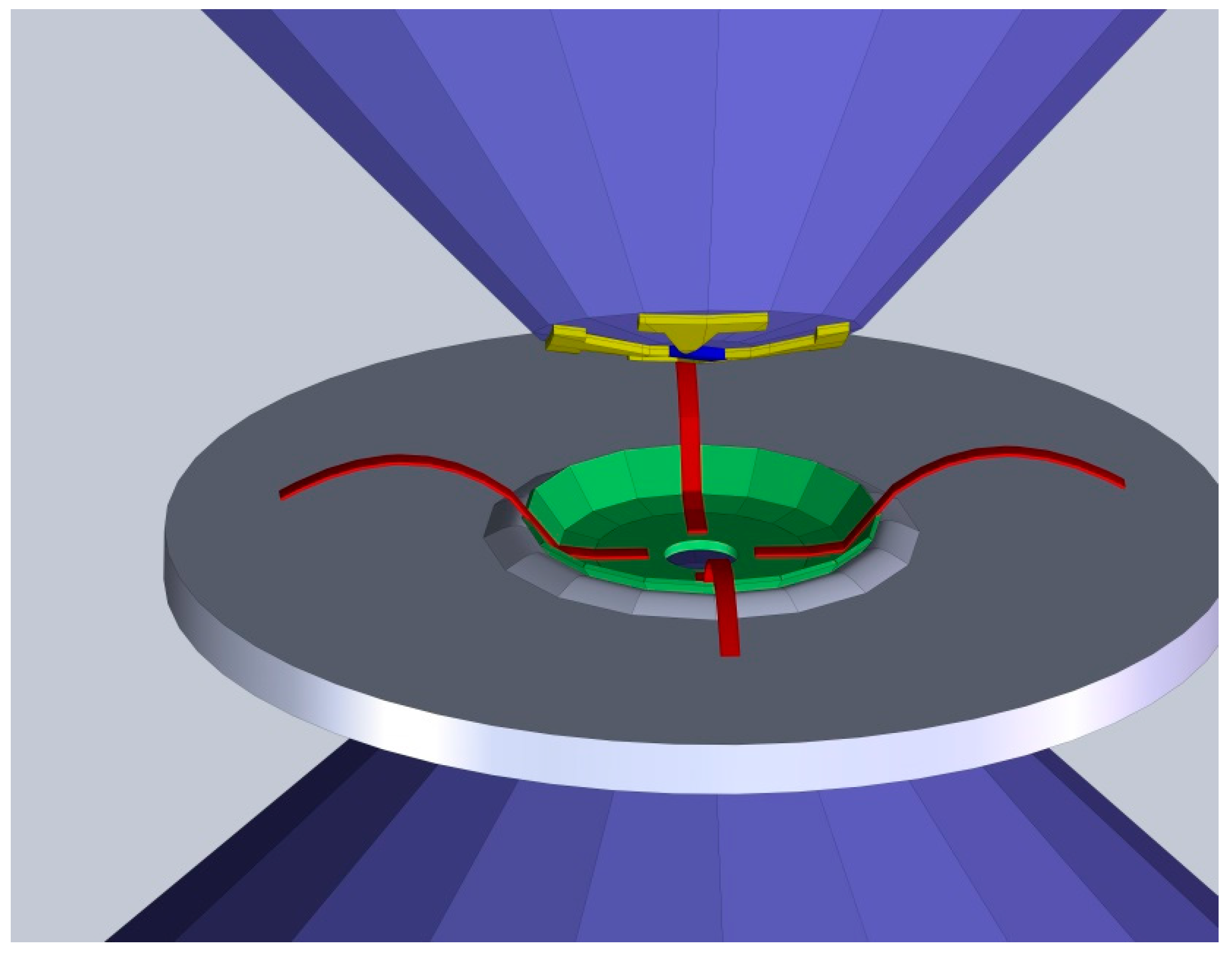
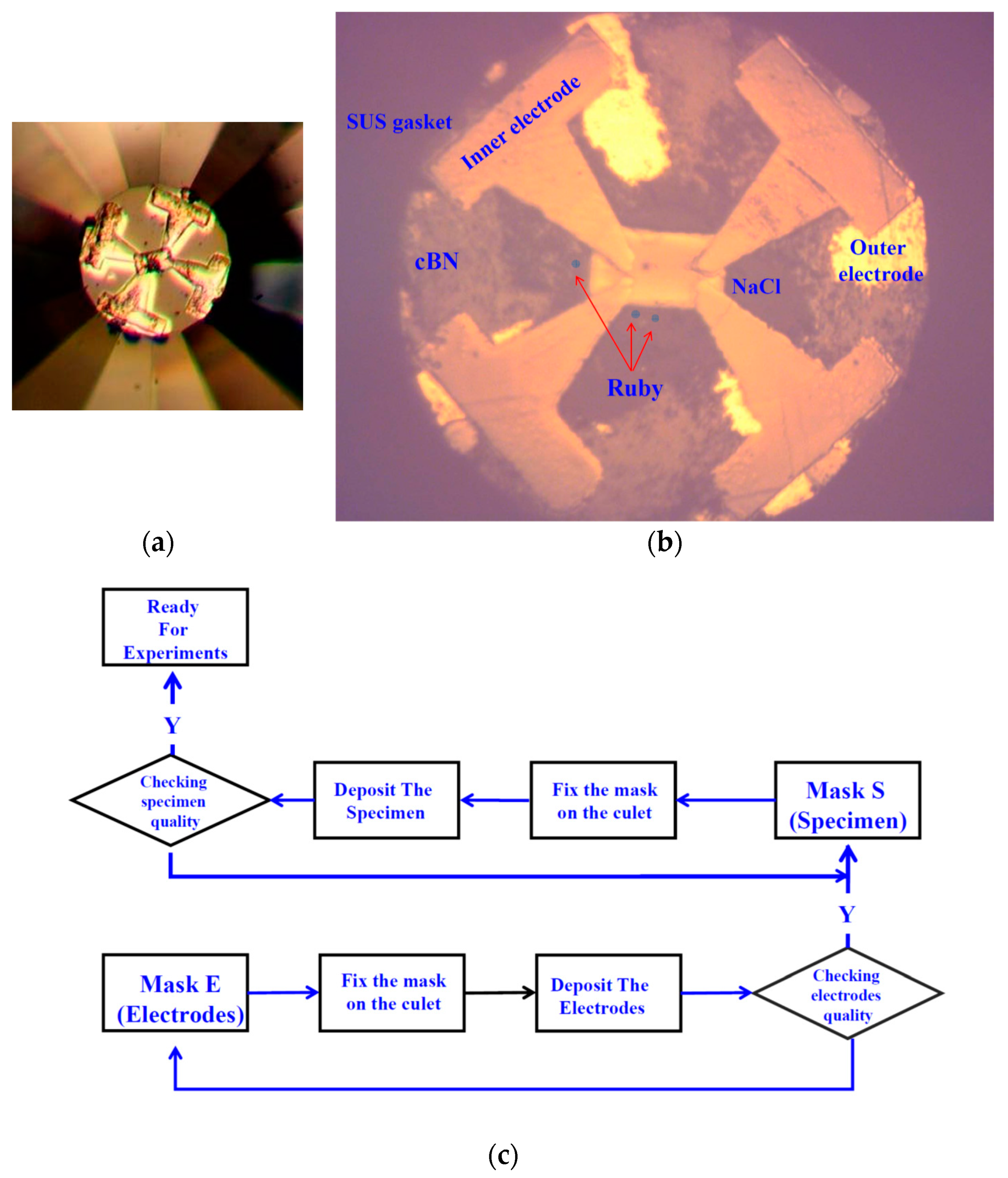
2. Experimental
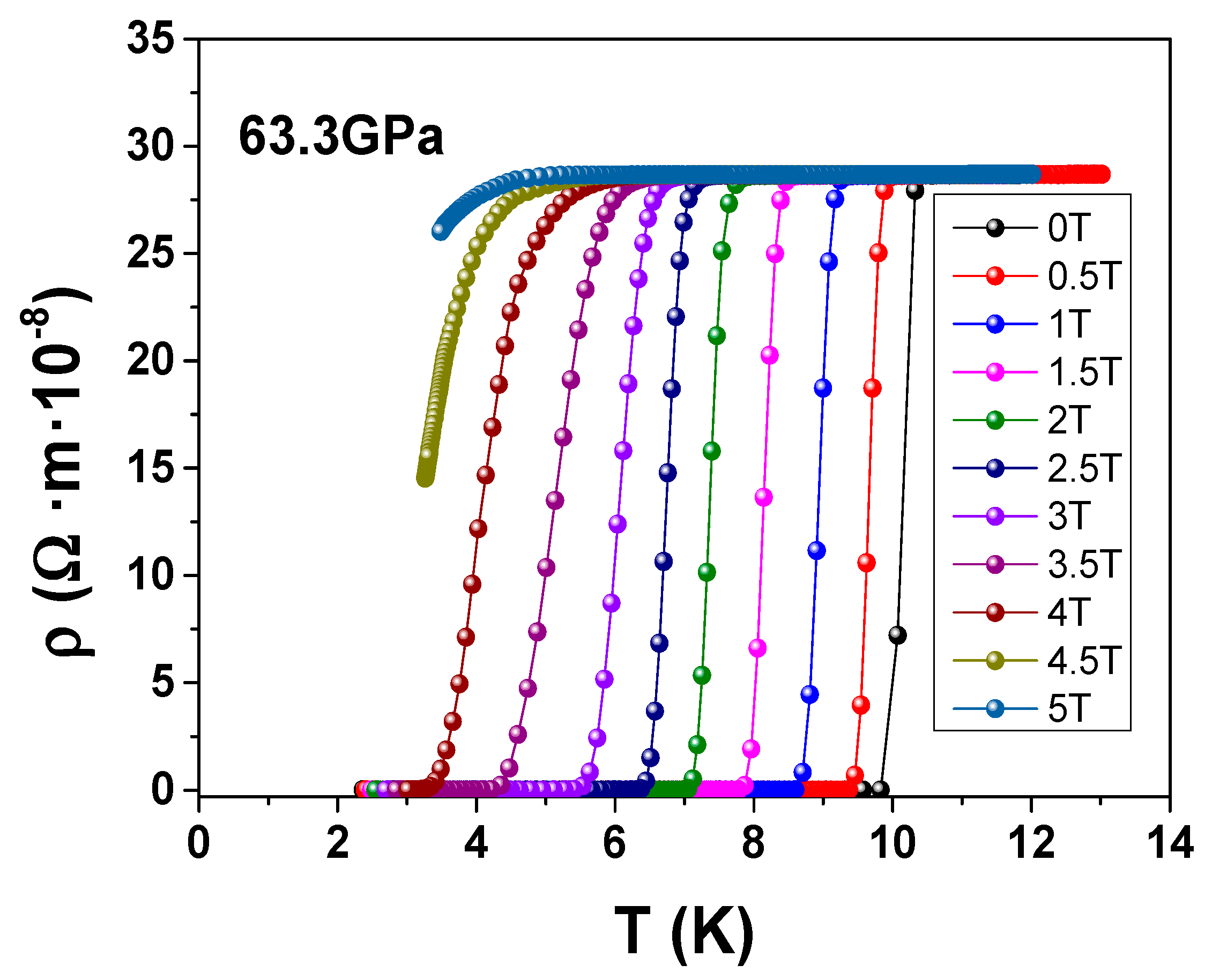
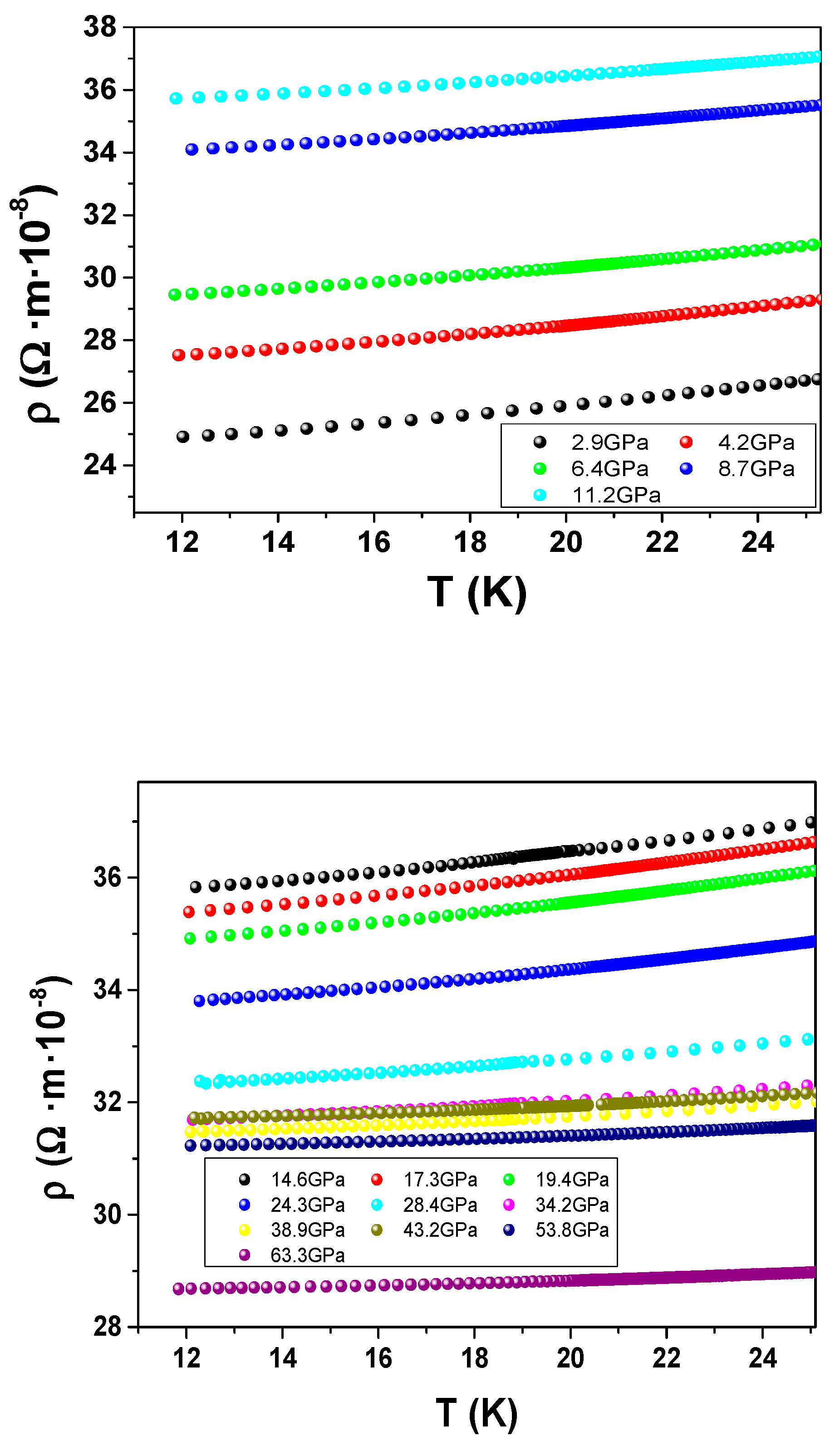
3. Results and Discussion
4. Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mao, H.-K.; Chen, X.-J.; Ding, Y.; Li, B.; Wang, L. Solids, liquids, and gases under high pressure. Rev. Mod. Phys. 2018, 90, 015007. [Google Scholar] [CrossRef] [Green Version]
- Schilling, J.S. Superconductivity in the alkali metals. High Press. Res. 2006, 26, 145–163. [Google Scholar] [CrossRef]
- Hamlin, J.J. Superconductivity in the metallic elements at high pressures. Phys. C Supercond. 2015, 514, 59–76. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, J.L.; Kong, P.P.; Zhang, S.J.; Yu, X.H.; Liu, Q.Q.; Li, X.; Yu, R.C.; Ahuja, R.; Yang, W.G.; et al. Superconductivity in Topological Insulator Sb2Te3 Induced by Pressure. Sci. Rep. 2013, 3, 2016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.; Semenok, D.V.; Troyan, I.A.; Ivanova, A.G.; Huang, X.; Oganov, A.R.; Cui, T. Superconductivity and equation of state of lanthanum at megabar pressures. Phys. Rev. B 2020, 102, 134510. [Google Scholar] [CrossRef]
- Zhang, J.L.; Zhang, S.J.; Weng, H.M.; Zhang, W.; Yang, L.X.; Liu, Q.Q.; Feng, S.M.; Wang, X.C.; Yu, R.C.; Cao, L.Z.; et al. Pressure-induced superconductivity in topological parent compound Bi2Te3. Proc. Natl. Acad. Sci. USA 2011, 108, 24–28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, C.; Han, Y.; Ma, Y.; White, A.; Liu, H.W.; Luo, J.; Li, M.; He, C.; Hao, A.; Huang, X.; et al. Accurate measurements of high pressure resistivity in a diamond anvil cell. Rev. Sci. Instrum. 2005, 76, 083912. [Google Scholar] [CrossRef]
- Kong, P.P.; Sun, F.; Xing, L.Y.; Zhu, J.L.; Zhang, S.J.; Li, W.M.; Liu, Q.Q.; Wang, X.C.; Feng, S.M.; Yu, X.H.; et al. Superconductivity in Strong Spin Orbital Coupling Compound Sb2Se3. Sci. Rep. 2015, 4, 6679. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsoi, G.; Stemshorn, A.K.; Vohra, Y.K.; Wu, P.M.; Hsu, F.C.; Huang, Y.L.; Wu, M.K.; Yeh, K.W.; Weir, S.T. High pressure superconductivity in iron-based layered compounds studied using designer diamonds. J. Phys. Condens. Matter 2009, 21, 232201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Welzel, O.P.; Grosche, F.M. Patterned anvils for high pressure measurements at low temperature. Rev. Sci. Instrum. 2011, 82, 33901. [Google Scholar] [CrossRef] [PubMed]
- Hemmes, H.; Driessen, A.; Griessen, R.; Gupta, M. Isotope effects and pressure dependence of the Tc of superconducting stoichiometric PdH and PdD synthesized and measured in a diamond anvil cell. Phys. Rev. B 1989, 39, 4110–4118. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. Solid Earth 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Balster, H.; Wittig, J. Pressure-induced lattice instability in fcc lanthanum at low temperature. J. Low Temp. Phys. 1975, 21, 377–414. [Google Scholar] [CrossRef]
- Tissen, V.G.; Ponyatovskii, E.G.; Nefedova, M.V.; Porsch, F.; Holzapfel, W.B. Effect of pressure on the superconducting Tc of lanthanum. Phys. Rev. B 1996, 53, 8238–8240. [Google Scholar] [CrossRef] [Green Version]
- Nixon, L.W.; Papaconstantopoulos, D.A.; Mehl, M.J. Electronic structure and superconducting properties of lanthanum. Phys. Rev. B 2008, 78, 214510. [Google Scholar] [CrossRef] [Green Version]
- Schlom, D.G.; Chen, L.-Q.; Eom, C.B.; Rabe, K.M.; Streiffer, S.K.; Triscone, J.-M. Strain Tuning of Ferroelectric Thin Films. Annu. Rev. Mater. Res. 2007, 37, 589–626. [Google Scholar] [CrossRef] [Green Version]
- Dubi, Y.; Meir, Y.; Avishai, Y. Nature of the superconductor–insulator transition in disordered superconductors. Nature 2007, 449, 876–880. [Google Scholar] [CrossRef] [PubMed]
- Holmes, A.T.; Jaccard, D.; Behr, G.; Inada, Y.; Onuki, Y. Unconventional superconductivity and non-Fermi liquid behaviour of ε-iron at high pressure. J. Phys. Condens. Matter 2004, 16, S1121–S1127. [Google Scholar] [CrossRef]


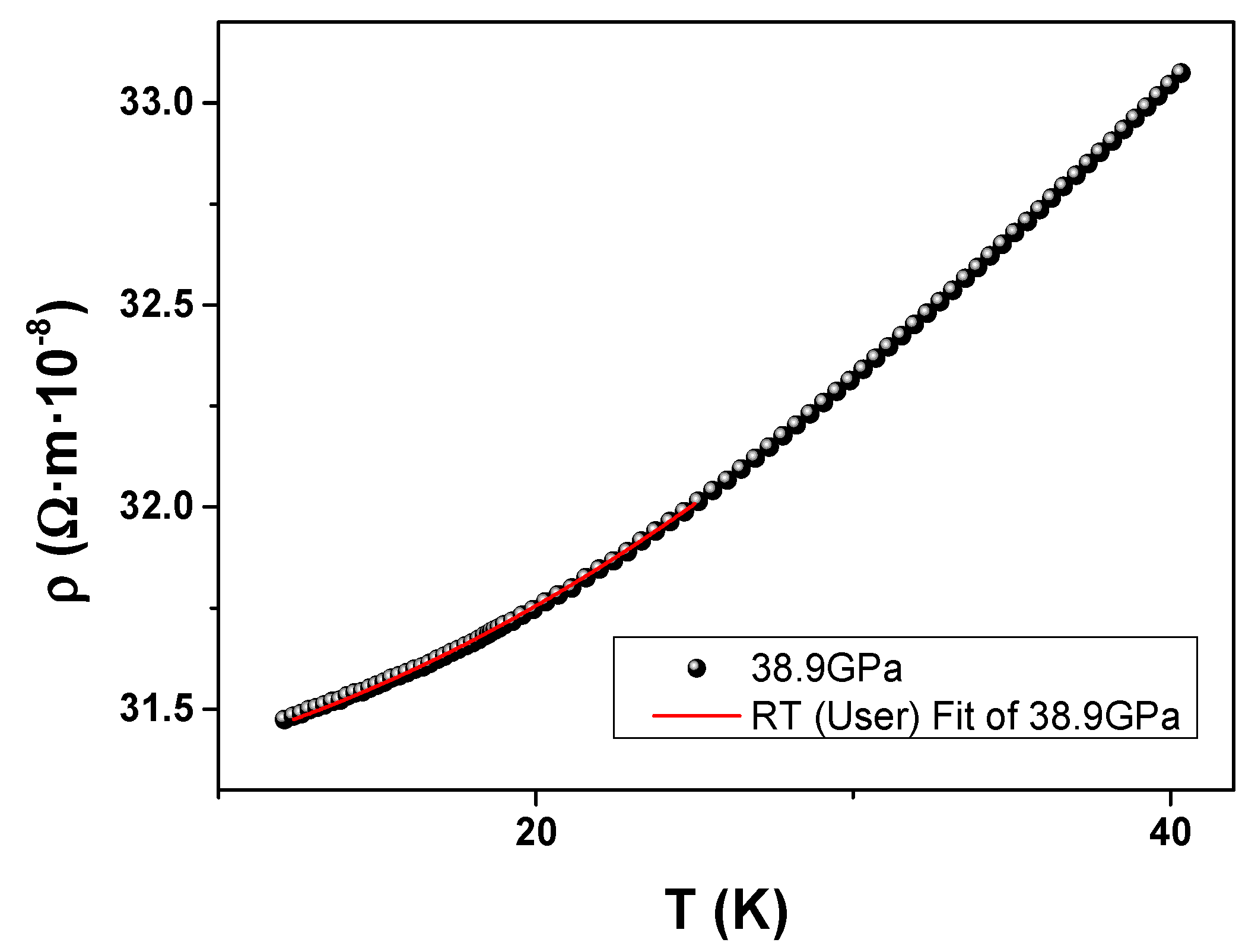

| Equation | |||
|---|---|---|---|
| Reduced Chi-Sqr | 2.67688 × 10−22 | ||
| Adj. R-Square | 0.99988 | ||
| Value | Standard Error | ||
| C22 | ρ0 | 3.13431 × 10−7 | 2.46144 × 10−11 |
| A | 5.57586 × 10−12 | 3.03352 × 10−13 | |
| n | 2.20043 | 0.01575 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; He, X.; Feng, S.; Zhang, S.; Zhang, C.; Ren, C.; Wang, X.; Jin, C. A Combinatory Package for Diamond Anvil Cell Experiments. Crystals 2020, 10, 1116. https://doi.org/10.3390/cryst10121116
Jia Y, He X, Feng S, Zhang S, Zhang C, Ren C, Wang X, Jin C. A Combinatory Package for Diamond Anvil Cell Experiments. Crystals. 2020; 10(12):1116. https://doi.org/10.3390/cryst10121116
Chicago/Turabian StyleJia, Yating, Xin He, Shaomin Feng, Sijia Zhang, Changling Zhang, Chongwen Ren, Xiancheng Wang, and Changqing Jin. 2020. "A Combinatory Package for Diamond Anvil Cell Experiments" Crystals 10, no. 12: 1116. https://doi.org/10.3390/cryst10121116
APA StyleJia, Y., He, X., Feng, S., Zhang, S., Zhang, C., Ren, C., Wang, X., & Jin, C. (2020). A Combinatory Package for Diamond Anvil Cell Experiments. Crystals, 10(12), 1116. https://doi.org/10.3390/cryst10121116





