Elastic Coefficients of ?-HMX as Functions of Pressure and Temperature from Molecular Dynamics
Abstract
:1. Introduction
2. Computational Details
2.1. Theoretical Background and System Preparation
2.2. Force Field and MD Simulation Details
2.3. Error Analysis
3. Results and Discussion
3.1. Isotherms and Isobars
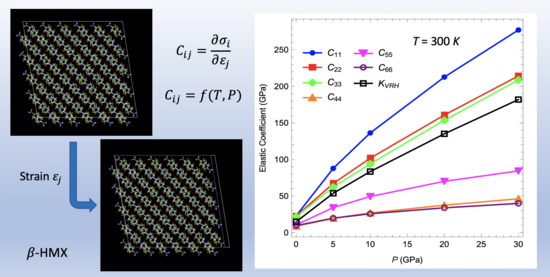
3.2. Elastic Coefficients
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HMX | 1,3,5,7-tetranitro-1,3,5,7-tetrazoctane |
| MD | Molecular Dynamics |
| NPT | isobaric-isothermal |
| NVT | isochoric-isothermal |
| DFT | density functional theory |
References
- Gibbs, T.; Popolato, A. LASL Explosive Property Data; University of California: Berkeley, CA, USA, 1980. [Google Scholar]
- Choi, C.S.; Boutin, H.P. A study of the crystal structure of β-cyclotetramethylene tetranitramine by neutron diffraction. Acta Crystallogr. B Struct. Cryst. Cryst. Chem. 1970, 26, 1235–1240. [Google Scholar] [CrossRef]
- Kohno, Y.; Maekawa, K.; Azuma, N.; Tsuchioka, T.; Hashizume, T.; Imamura, A. Ab initio calculations for a relationship between impact sensitivity and molecular structure in HMX polymorphs. Kogyo Kayako 1992, 53, 227–237. [Google Scholar]
- Cady, H.H.; Larson, A.C.; Cromer, D.T. The crystal structure of α-HMX and a refinement of the structure of β-HMX. Acta Crystallogr. 1963, 16, 617–623. [Google Scholar] [CrossRef]
- Cobbledick, R.E.; Small, R.W.H. The crystal structure of the δ-form of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (δ-HMX). Acta Crystallogr. B Struct. Cryst. Cryst. Chem. 1974, 30, 1918–1922. [Google Scholar] [CrossRef] [Green Version]
- Hooks, D.E.; Ramos, K.J.; Bolme, C.A.; Cawkwell, M.J. Elasticity of crystalline molecular explosives. Propellants Explos. Pyrotech. 2015, 40, 333–350. [Google Scholar] [CrossRef]
- Zaug, J.M. Elastic constants of β-HMX and Tantalum, equations of state of supercritical fluids and fluid mixtures and thermal transport determinations. In Proceedings of the Eleventh Detonation Symposium, Snowmass, CO, USA, 31 August–4 September 1998; p. 498. [Google Scholar]
- Stevens, L.L.; Eckhardt, C.J. The elastic constants and related properties of β-HMX determined by Brillouin scattering. J. Chem. Phys. 2005, 122, 174701. [Google Scholar] [CrossRef]
- Sun, B.; Winey, J.M.; Gupta, Y.M.; Hooks, D.E. Determination of second-order elastic constants of cyclotetramethylene tetranitramine (β-HMX) using impulsive stimulated thermal scattering. J. Appl. Phys. 2009, 106, 053505. [Google Scholar] [CrossRef]
- Menikoff, R.; Sewell, T.D. Fitting forms for isothermal data. High Press. Res. 2001, 21, 121–138. [Google Scholar] [CrossRef]
- Zaug, J.M.; Austin, R.A.; Armstrong, M.R.; Crowhurst, J.C.; Goldman, N.; Ferranti, L.; Saw, C.K.; Swan, R.A.; Gross, R.; Fried, L.E. Ultrafast dynamic response of single-crystal β-HMX (octahydro-1,3,5, 7-tetranitro-1,3,5,7-tetrazocine). J. Appl. Phys. 2018, 123, 205902. [Google Scholar] [CrossRef]
- Drouet, D.; Picart, D.; Bailly, P.; Bruneton, E. Plastic dissipation and hot-spot formation in HMX-based PBXs subjected to low velocity impact. Propellants Explos. Pyrotech. 2020, 45, 1–11. [Google Scholar] [CrossRef]
- Bower, A.F. Applied Mechanics of Solids; Taylor & Francis: Boca Raton, FL, USA, 2010; Available online: http://solidmechanics.org (accessed on 8 December 2020).
- Sewell, T.D.; Menikoff, R.; Bedrov, D.; Smith, G.D. A molecular dynamics simulation study of elastic properties of HMX. J. Chem. Phys. 2003, 119, 7417–7426. [Google Scholar] [CrossRef]
- Mathew, N.; Sewell, T. Pressure-dependent elastic coefficients of β-HMX from molecular simulations. Propellants Explos. Pyrotech. 2018, 43, 223–227. [Google Scholar] [CrossRef]
- Hall, P.G. Thermal decomposition and phase transitions in solid nitramines. Trans. Faraday Soc. 1971, 67, 556–562. [Google Scholar] [CrossRef]
- Myint, P.C.; Nichols, A.L. Thermodynamics of HMX polymorphs and HMX/RDX mixtures. Ind. Eng. Chem. Res. 2017, 56, 387–403. [Google Scholar] [CrossRef]
- Kroonblawd, M.P.; Austin, R.A. Sensitivity of pore collapse heating to the melting temperature and shear viscosity of HMX. Mech. Mater. 2021, 152, 103644. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. Available online: http://lammps.sandia.gov/ (accessed on 8 December 2020). [CrossRef] [Green Version]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Smith, G.D.; Bharadwaj, R.K. Quantum chemistry based force field for simulations of HMX. J. Phys. Chem. B 1999, 103, 3570–3575. [Google Scholar] [CrossRef]
- Bedrov, D.; Ayyagari, C.; Smith, G.D.; Sewell, T.D.; Menikoff, R.; Zaug, J.M. Molecular dynamics simulations of HMX crystal polymorphs using a flexible molecule force field. J. Comput. Aid. Mater. Des. 2001, 8, 77–85. [Google Scholar] [CrossRef]
- Bedrov, D.; Smith, G.D.; Sewell, T.D. Thermal conductivity of liquid octahydro-1,3,5,7-tetranitro-1,3, 5,7-tetrazocine (HMX) from molecular dynamics simulations. Chem. Phys. Lett. 2000, 324, 64–68. [Google Scholar] [CrossRef]
- Bedrov, D.; Smith, G.D.; Sewell, T.D. Temperature-dependent shear viscosity coefficient of octahydro-1,3, 5,7-tetranitro-1,3,5,7-tetrazocine (HMX): A molecular dynamics simulation study. J. Chem. Phys. 2000, 112, 7203–7208. [Google Scholar] [CrossRef]
- Kroonblawd, M.P.; Mathew, N.; Jiang, S.; Sewell, T.D. A generalized crystal-cutting method for modeling arbitrarily oriented crystals in 3D periodic simulation cells with applications to crystal-crystal interfaces. Comput. Phys. Commun. 2016, 207, 232–242. [Google Scholar] [CrossRef]
- Chitsazi, R.; Kroonblawd, M.P.; Pereverzev, A.; Sewell, T. A molecular dynamics simulation study of thermal conductivity anisotropy in β-octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (β-HMX). Modell. Simul. Mater. Sci. Eng. 2020, 28, 025008. [Google Scholar] [CrossRef]
- Zhao, P.; Lee, S.; Sewell, T.; Udaykumar, H.S. Tandem molecular dynamics and continuum studies of shock-induced pore collapse in TATB. Propellants Explos. Pyrotech. 2020, 45, 196–222. [Google Scholar] [CrossRef]
- Flyvbjerg, H.; Petersen, H.G. Error estimates on averages of correlated data. J. Chem. Phys. 1989, 91, 461–466. [Google Scholar] [CrossRef]
- Yoo, C.S.; Cynn, H. Equation of state, phase transition, decomposition of β-HMX (octahydro-1,3, 5,7-tetranitro-1,3,5,7-tetrazocine) at high pressures. J. Chem. Phys. 1999, 111, 10229–10235. [Google Scholar] [CrossRef]
- Gump, J.C.; Peiris, S.M. Isothermal equations of state of beta octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine at high temperatures. J. Appl. Phys. 2005, 97, 53513. [Google Scholar] [CrossRef]
- Olinger, B.; Roof, B.; Cady, H. The linear and volume compression of β-HMX and RDX to 9 GPa (90 kilobar). In Proceedings of the Symposium (International) on High Dynamic Pressures; Commissariat a l’Energie Atomique: Paris, France, 1978; pp. 3–8. [Google Scholar]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, G.; Liu, G.R.; De, S. Structures, mechanical properties, equations of state, and electronic properties of β-HMX under hydrostatic pressures: A DFT-D2 study. Phys. Chem. Chem. Phys. 2014, 16, 19972–19983. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, G.; Liu, G.R.; Grimme, S.; De, S. Predicting elastic properties of β-HMX from first-principles calculations. J. Phys. Chem. B 2015, 119, 5896–5903. [Google Scholar] [CrossRef]






| P | GPa | 5 GPa | 10 GPa | 20 GPa | 30 GPa |
|---|---|---|---|---|---|
| P | GPa | 5 GPa | 10 GPa | 20 GPa | 30 GPa |
|---|---|---|---|---|---|
| P | GPa | 5 GPa | 10 GPa | 20 GPa | 30 GPa |
|---|---|---|---|---|---|
| P | 5 GPa | 10 GPa | 20 GPa | 30 GPa |
|---|---|---|---|---|
| P | 5 GPa | 10 GPa | 20 GPa | 30 GPa |
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereverzev, A.; Sewell, T. Elastic Coefficients of ?-HMX as Functions of Pressure and Temperature from Molecular Dynamics. Crystals 2020, 10, 1123. https://doi.org/10.3390/cryst10121123
Pereverzev A, Sewell T. Elastic Coefficients of ?-HMX as Functions of Pressure and Temperature from Molecular Dynamics. Crystals. 2020; 10(12):1123. https://doi.org/10.3390/cryst10121123
Chicago/Turabian StylePereverzev, Andrey, and Tommy Sewell. 2020. "Elastic Coefficients of ?-HMX as Functions of Pressure and Temperature from Molecular Dynamics" Crystals 10, no. 12: 1123. https://doi.org/10.3390/cryst10121123
APA StylePereverzev, A., & Sewell, T. (2020). Elastic Coefficients of ?-HMX as Functions of Pressure and Temperature from Molecular Dynamics. Crystals, 10(12), 1123. https://doi.org/10.3390/cryst10121123