Correlation between Crystal Structure and Thermoelectric Properties of Sr1−xTi0.9Nb0.1O3−δ Ceramics
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
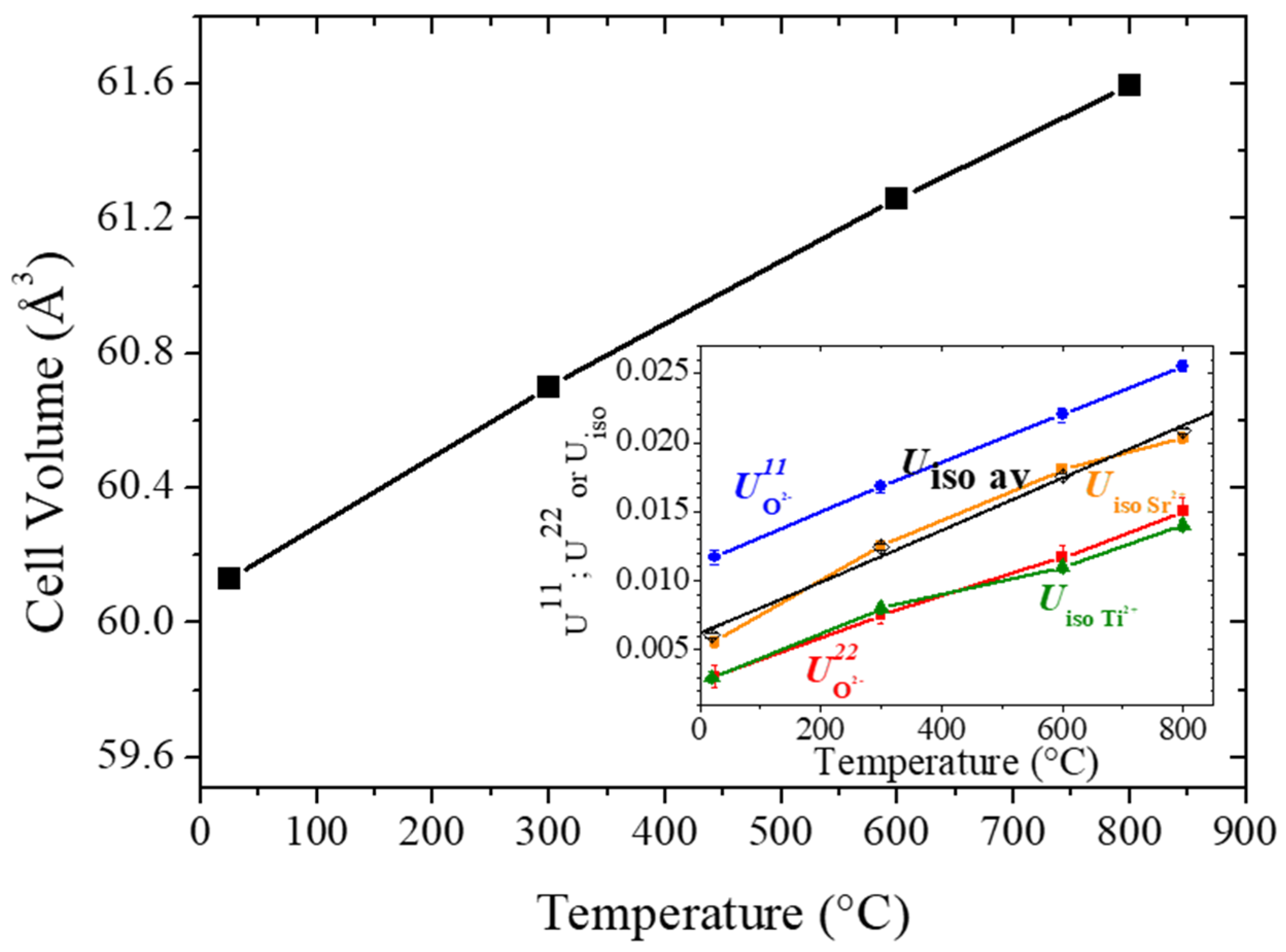
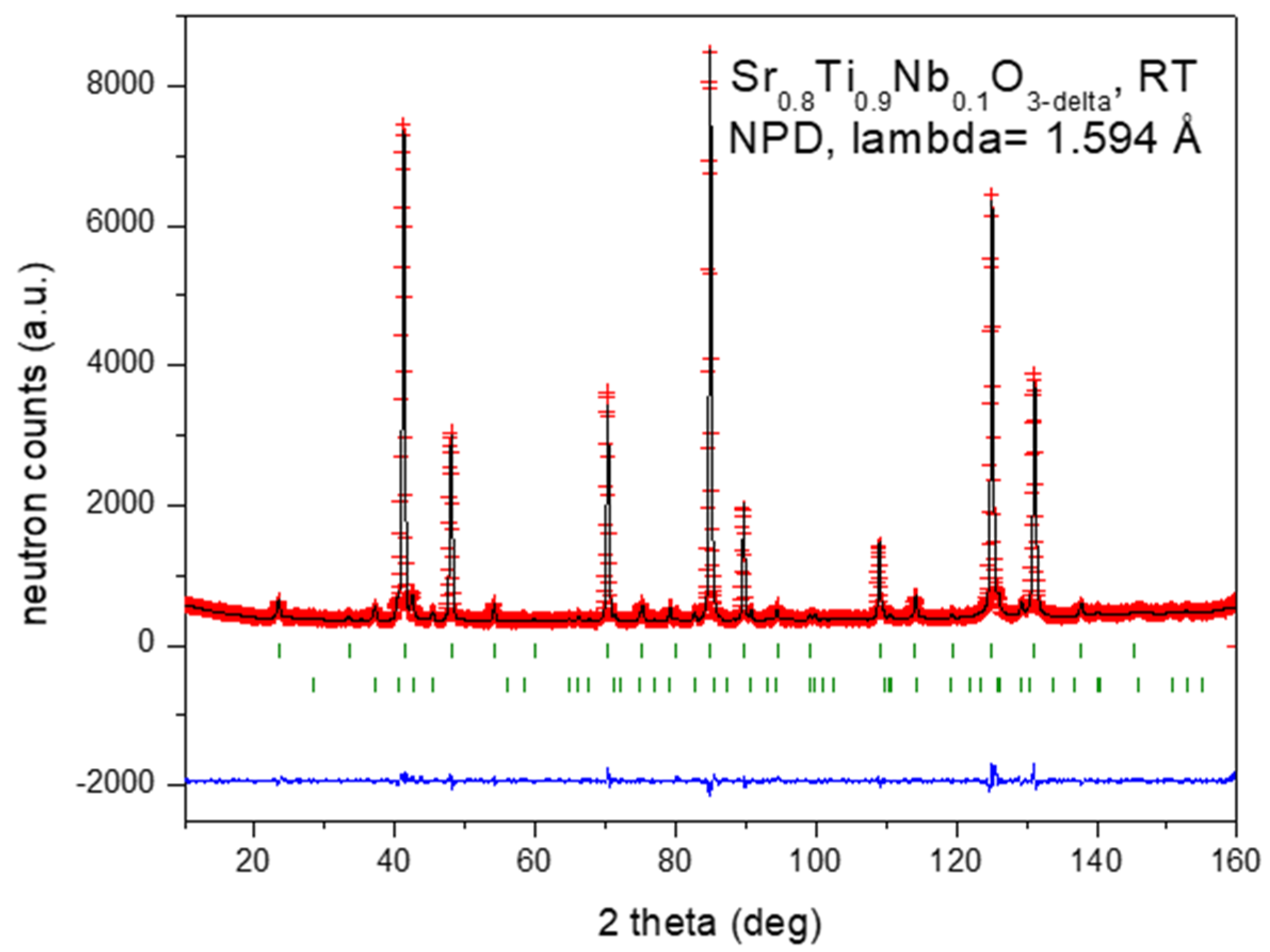
3.1. Structural Characterization by Neutron Powder Diffraction (NPD)
3.2. Analysis of the Anisotropic Displacement Parameters (ADPs)
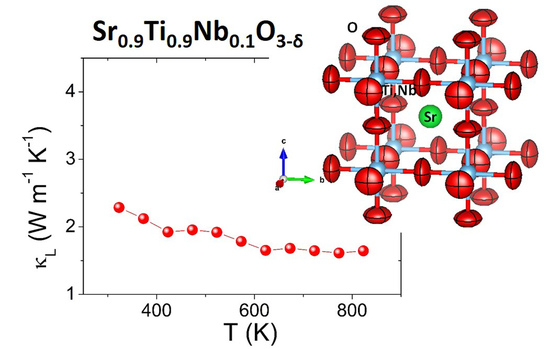
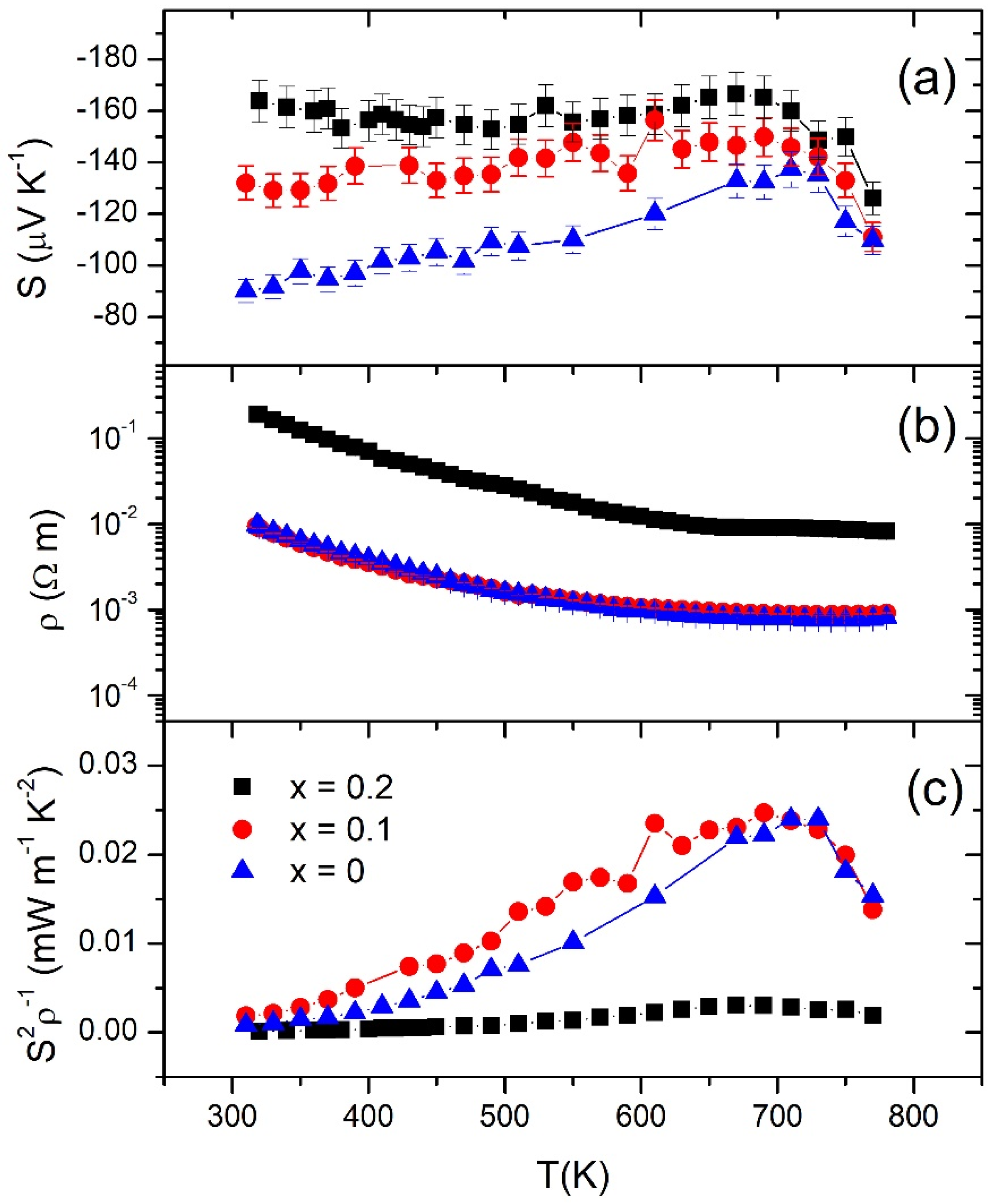
3.3. Thermoelectric Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Chen, G.; Tang, M.Y.; Yang, R.; Lee, H.; Wang, D.; Ren, Z.; Fleurial, J.P.; Gogna, P. New directions for low-dimensional thermoelectric materials. Adv. Mater. 2007, 19, 1043–1053. [Google Scholar] [CrossRef]
- Alam, H.; Ramakrishna, S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials. Nano Energy 2013, 2, 190–212. [Google Scholar] [CrossRef]
- Minnich, A.; Dresselhaus, M.; Ren, Z.; Chen, G. Bulk nanostructured thermoelectric materials: Current research and future prospects. Energy Environ. Sci. 2009, 2, 466–479. [Google Scholar] [CrossRef]
- Mohebali, M.; Liu, Y.; Tayebi, L.; Krasinski, J.S.; Vashaee, D. Thermoelectric figure of merit of bulk FeSi2–Si0.8Ge0.2 nanocomposite and a comparison with β-FeSi2. Renew. Energy 2015, 74, 940–947. [Google Scholar] [CrossRef]
- Twaha, S.; Zhu, J.; Yan, Y.; Li, B. A comprehensive review of thermoelectric technology: Materials, applications, modelling and performance improvement. Renew. Sustain. Energy Rev. 2016, 65, 698–726. [Google Scholar] [CrossRef]
- Majumdar, A. Thermoelectricity in Semiconductor Nanostructures. Science 2004, 303, 777–778. [Google Scholar] [CrossRef]
- Nolas, G.S.; Sharp, J.; Goldsmid, J. Thermoelectrics: Basic Principles and New Materials Developments; Springer Science & Business Media: Berlin, Germany, 2013; Volume 45. [Google Scholar]
- Sales, B.; Mandrus, D.; Williams, R.K. Filled skutterudite antimonides: A new class of thermoelectric materials. Science 1996, 272, 1325–1328. [Google Scholar] [CrossRef]
- Serrano-Sánchez, F.; Prado-Gonjal, J.; Nemes, N.M.; Biskup, N.; Varela, M.; Dura, O.J.; Martínez, J.; Fernández-Díaz, M.T.; Fauth, F.; Alonso, J.A. Low thermal conductivity in La-filled cobalt antimonide skutterudites with an inhomogeneous filling factor prepared under high-pressure conditions. J. Mater. Chem. A 2018, 6, 118–126. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-K.; Choi, S.-M.; Seo, W.-S.; Lim, Y.-S.; Lee, H.-L.; Kim, I.-H. Thermoelectric properties of Spark Plasma Sintered InxYbyLa0.3-x-yCo4Sb12 skutterudite system. Renew. Energy 2012, 42, 36–40. [Google Scholar] [CrossRef]
- Nolas, G.; Cohn, J.; Slack, G.; Schujman, S. Semiconducting Ge clathrates: Promising candidates for thermoelectric applications. Appl. Phys. Lett. 1998, 73, 178–180. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Bai, S.; Liu, Y.; Tang, Y.; Chen, L.; Zhao, X.; Zhu, T. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 2015, 6, 8144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kauzlarich, S.M.; Brown, S.R.; Snyder, G.J. Zintl phases for thermoelectric devices. Dalton Trans. 2007, 21, 2099–2107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Powell, A.V.; Vaqueiro, P. Chalcogenide thermoelectric materials. In Thermoelectric Materials and Devices; RSC Publishing: Cambridge, UK, 2016; p. 27. [Google Scholar]
- Guélou, G.; Vaqueiro, P.; Prado-Gonjal, J.; Barbier, T.; Hébert, S.; Guilmeau, E.; Kockelmann, W.; Powell, A.V. The impact of charge transfer and structural disorder on the thermoelectric properties of cobalt intercalated TiS2. J. Mater. Chem. C 2016, 4, 1871–1880. [Google Scholar] [CrossRef] [Green Version]
- Hebert, S.; Maignan, A. Thermoelectric oxides. In Functional Oxides; Wiley Online Library: Hoboken, NJ, USA, 2010; pp. 203–255. [Google Scholar]
- He, Y.; Day, T.; Zhang, T.; Liu, H.; Shi, X.; Chen, L.; Snyder, G.J. High Thermoelectric Performance in Non-Toxic Earth-Abundant Copper Sulfide. Adv. Mater. 2014, 26, 3974–3978. [Google Scholar] [CrossRef]
- An, T.-H.; Choi, S.-M.; Kim, I.-H.; Kim, S.-U.; Seo, W.-S.; Kim, J.-Y.; Park, C. Thermoelectric properties of a doped Mg2Sn system. Renew. Energy 2012, 42, 23–27. [Google Scholar] [CrossRef]
- Yin, Y.; Tudu, B.; Tiwari, A. Recent advances in oxide thermoelectric materials and modules. Vacuum 2017, 146, 356–374. [Google Scholar] [CrossRef]
- Weidenkaff, A.; Robert, R.; Aguirre, M.; Bocher, L.; Lippert, T.; Canulescu, S. Development of thermoelectric oxides for renewable energy conversion technologies. Renew. Energy 2008, 33, 342–347. [Google Scholar] [CrossRef]
- Wang, H.; Su, W.; Liu, J.; Wang, C. Recent development of n-type perovskite thermoelectrics. J. Mater. 2016, 2, 225–236. [Google Scholar] [CrossRef] [Green Version]
- Tritt, T.M.; Subramanian, M. Thermoelectric materials, phenomena, and applications: A bird’s eye view. Mrs Bull. 2006, 31, 188–198. [Google Scholar] [CrossRef] [Green Version]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and old concepts in thermoelectric materials. Angew. Chem. Int. Ed. 2009, 48, 8616–8639. [Google Scholar] [CrossRef] [PubMed]
- Okuda, T.; Nakanishi, K.; Miyasaka, S.; Tokura, Y. Large thermoelectric response of metallic perovskites: Sr1− xLaxTiO3 (0<~ x<~ 0. 1). Phys. Rev. B 2001, 63, 113104. [Google Scholar] [CrossRef]
- Popuri, S.R.; Scott, A.; Downie, R.; Hall, M.; Suard, E.; Decourt, R.; Pollet, M.; Bos, J.-W. Glass-like thermal conductivity in SrTiO3 thermoelectrics induced by A-site vacancies. Rsc Adv. 2014, 4, 33720–33723. [Google Scholar] [CrossRef] [Green Version]
- Blennow, P.; Hagen, A.; Hansen, K.K.; Wallenberg, L.R.; Mogensen, M. Defect and electrical transport properties of Nb-doped SrTiO3. Solid State Ion. 2008, 179, 2047–2058. [Google Scholar] [CrossRef]
- Kovalevsky, A.V.; Aguirre, M.H.; Populoh, S.; Patrício, S.G.; Ferreira, N.M.; Mikhalev, S.M.; Fagg, D.P.; Weidenkaff, A.; Frade, J.R. Designing strontium titanate-based thermoelectrics: Insight into defect chemistry mechanisms. J. Mater. Chem. A 2017, 5, 3909–3922. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, H.; Lei, W.; Sinclair, D.C.; Reaney, I.M. High-figure-of-merit thermoelectric La-doped A-site-deficient SrTiO3 ceramics. Chem. Mater. 2016, 28, 925–935. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.C.; Wang, C.L.; Su, W.B.; Liu, J.; Sun, Y.; Peng, H.; Mei, L.M. Doping effect of La and Dy on the thermoelectric properties of SrTiO3. J. Am. Ceram. Soc. 2011, 94, 838–842. [Google Scholar] [CrossRef]
- Wang, N.; Chen, H.; He, H.; Norimatsu, W.; Kusunoki, M.; Koumoto, K. Enhanced thermoelectric performance of Nb-doped SrTiO3 by nano-inclusion with low thermal conductivity. Sci. Rep. 2013, 3, 3449. [Google Scholar] [CrossRef]
- Muta, H.; Kurosaki, K.; Yamanaka, S. Thermoelectric properties of reduced and La-doped single-crystalline SrTiO3. J. Alloy. Compd. 2005, 392, 306–309. [Google Scholar] [CrossRef]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J.; Roisnel, T. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Mi, J.-L.; Christensen, M.; Nishibori, E.; Iversen, B.B. Multitemperature crystal structures and physical properties of the partially filled thermoelectric skutterudites M0.1Co4Sb12 (M= La, Ce, Nd, Sm, Yb, and Eu). Phys. Rev. B 2011, 84, 064114. [Google Scholar] [CrossRef]
- Kovalevsky, A.; Yaremchenko, A.; Populoh, S.; Weidenkaff, A.; Frade, J. Effect of A-site cation deficiency on the thermoelectric performance of donor-substituted strontium titanate. J. Phys. Chem. C 2014, 118, 4596–4606. [Google Scholar] [CrossRef]
- Koumoto, K.; Wang, Y.; Zhang, R.; Kosuga, A.; Funahashi, R. Oxide thermoelectric materials: A nanostructuring approach. Annu. Rev. Mater. Res. 2010, 40, 363–394. [Google Scholar] [CrossRef]
- Muta, H.; Kurosaki, K.; Yamanaka, S. Thermoelectric properties of rare earth doped SrTiO3. J. Alloy. Compd. 2003, 350, 292–295. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.; Li, Y.; Su, W.; Zhu, Y.; Li, J.; Mei, L. Influence of rare earth doping on thermoelectric properties of SrTiO3 ceramics. J. Appl. Phys. 2013, 114, 223714. [Google Scholar] [CrossRef]




| x | y | z | Uiso*/Ueq | Occ. (<1) | |
| Sr | 0.50000 | 0.50000 | 0.50000 | 0.0065(4)* | 0.9 |
| Ti | 0.00000 | 0.00000 | 0.00000 | 0.0028(6)* | 0.877(5) |
| Nb | 0.00000 | 0.00000 | 0.00000 | 0.0028(6)* | 0.123(5) |
| O1 | 0.50000 | 0.00000 | 0.00000 | 0.0085(5) | 0.95(1) |
| U11 | U22 | U33 | U12 | U13 | U23 | |
| O1 | 0.0035(7) | 0.0109(4) | 0.0109(4) | 0.00000 | 0.00000 | 0.00000 |
| Element | x | y | z | Uiso | Occ. (<1) |
|---|---|---|---|---|---|
| Sr | 0.5000 | 0.5000 | 0.5000 | 0.0040(4) | 0.8 |
| Ti | 0.0000 | 0.0000 | 0.0000 | 0.0007(8) | 0.875(3) |
| Nb | 0.0000 | 0.0000 | 0.0000 | 0.0007(8) | 0.125(3) |
| O1 | 0.5000 | 0.0000 | 0.0000 | 0.0046(2) | 0.832(6) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prado-Gonjal, J.; López, C.A.; Pinacca, R.M.; Serrano-Sánchez, F.; Nemes, N.M.; Dura, O.J.; Martínez, J.L.; Fernández-Díaz, M.T.; Alonso, J.A. Correlation between Crystal Structure and Thermoelectric Properties of Sr1−xTi0.9Nb0.1O3−δ Ceramics. Crystals 2020, 10, 100. https://doi.org/10.3390/cryst10020100
Prado-Gonjal J, López CA, Pinacca RM, Serrano-Sánchez F, Nemes NM, Dura OJ, Martínez JL, Fernández-Díaz MT, Alonso JA. Correlation between Crystal Structure and Thermoelectric Properties of Sr1−xTi0.9Nb0.1O3−δ Ceramics. Crystals. 2020; 10(2):100. https://doi.org/10.3390/cryst10020100
Chicago/Turabian StylePrado-Gonjal, J., C. A. López, R. M. Pinacca, F. Serrano-Sánchez, N. M. Nemes, O. J. Dura, J.L. Martínez, M.T. Fernández-Díaz, and J.A. Alonso. 2020. "Correlation between Crystal Structure and Thermoelectric Properties of Sr1−xTi0.9Nb0.1O3−δ Ceramics" Crystals 10, no. 2: 100. https://doi.org/10.3390/cryst10020100
APA StylePrado-Gonjal, J., López, C. A., Pinacca, R. M., Serrano-Sánchez, F., Nemes, N. M., Dura, O. J., Martínez, J. L., Fernández-Díaz, M. T., & Alonso, J. A. (2020). Correlation between Crystal Structure and Thermoelectric Properties of Sr1−xTi0.9Nb0.1O3−δ Ceramics. Crystals, 10(2), 100. https://doi.org/10.3390/cryst10020100