Hardness-Depth Relationship with Temperature Effect for Single Crystals—A Theoretical Analysis
Abstract
:1. Introduction
2. Hardness-Depth Relationship with Temperature Effect
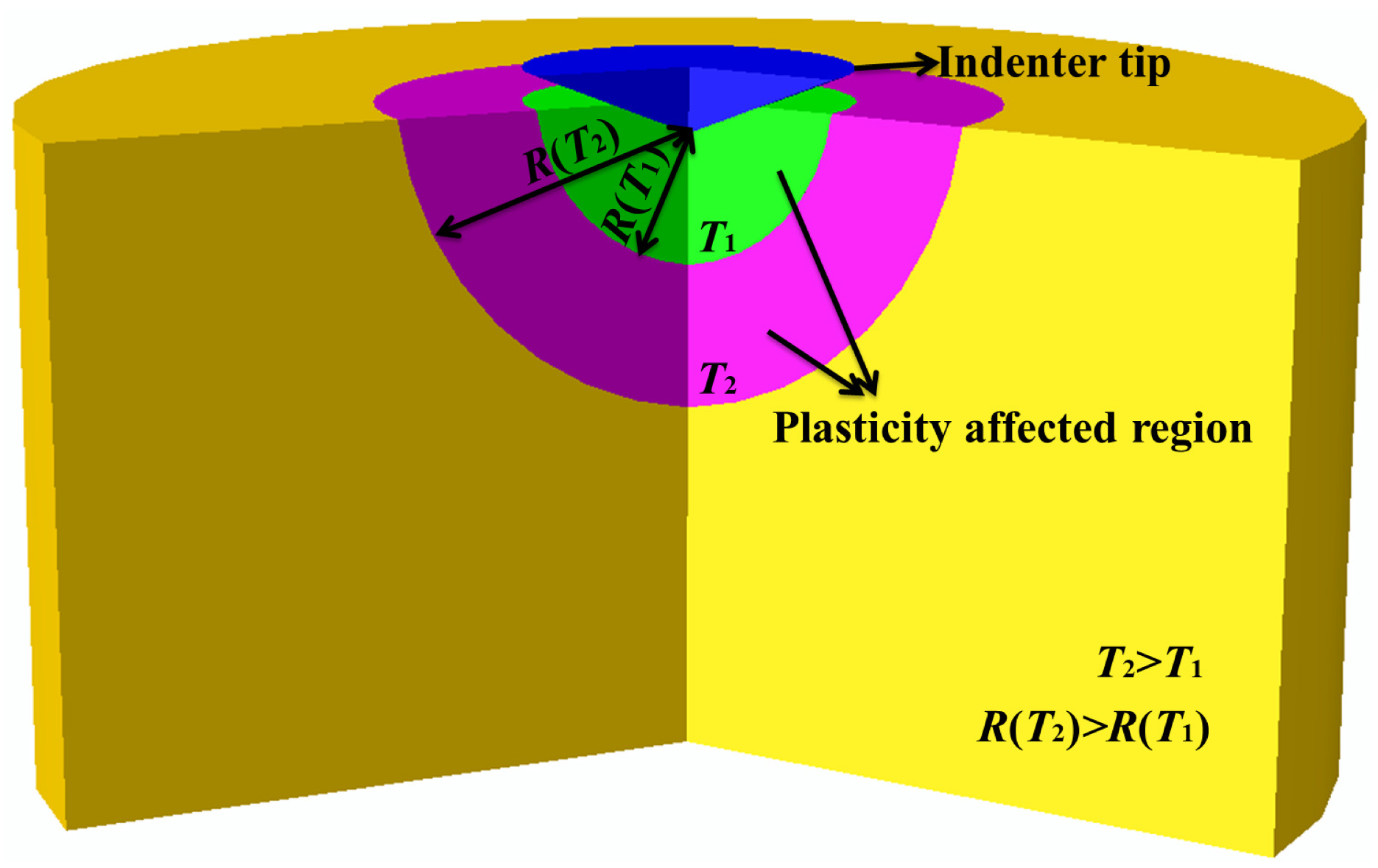
2.1. Model Development
2.2. Model Calibration
- (1)
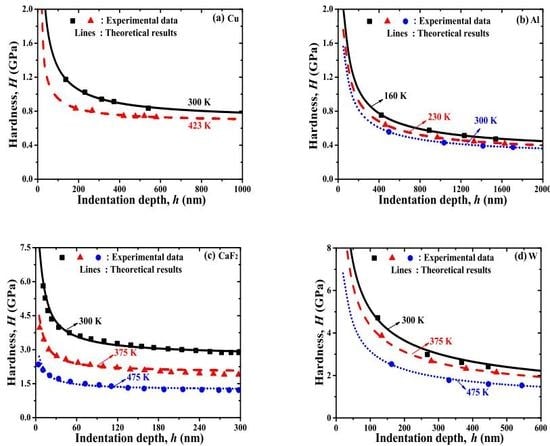
- First, conduct nano-indentation tests for single crystals at different temperatures to obtain the hardness-depth relationships, that is, the − h curves [33]. Hereafter, the symbol ∼ denotes the experimental data. It then follows from Equation (6) that the relationships are obtained by subtracting from .
- (2)
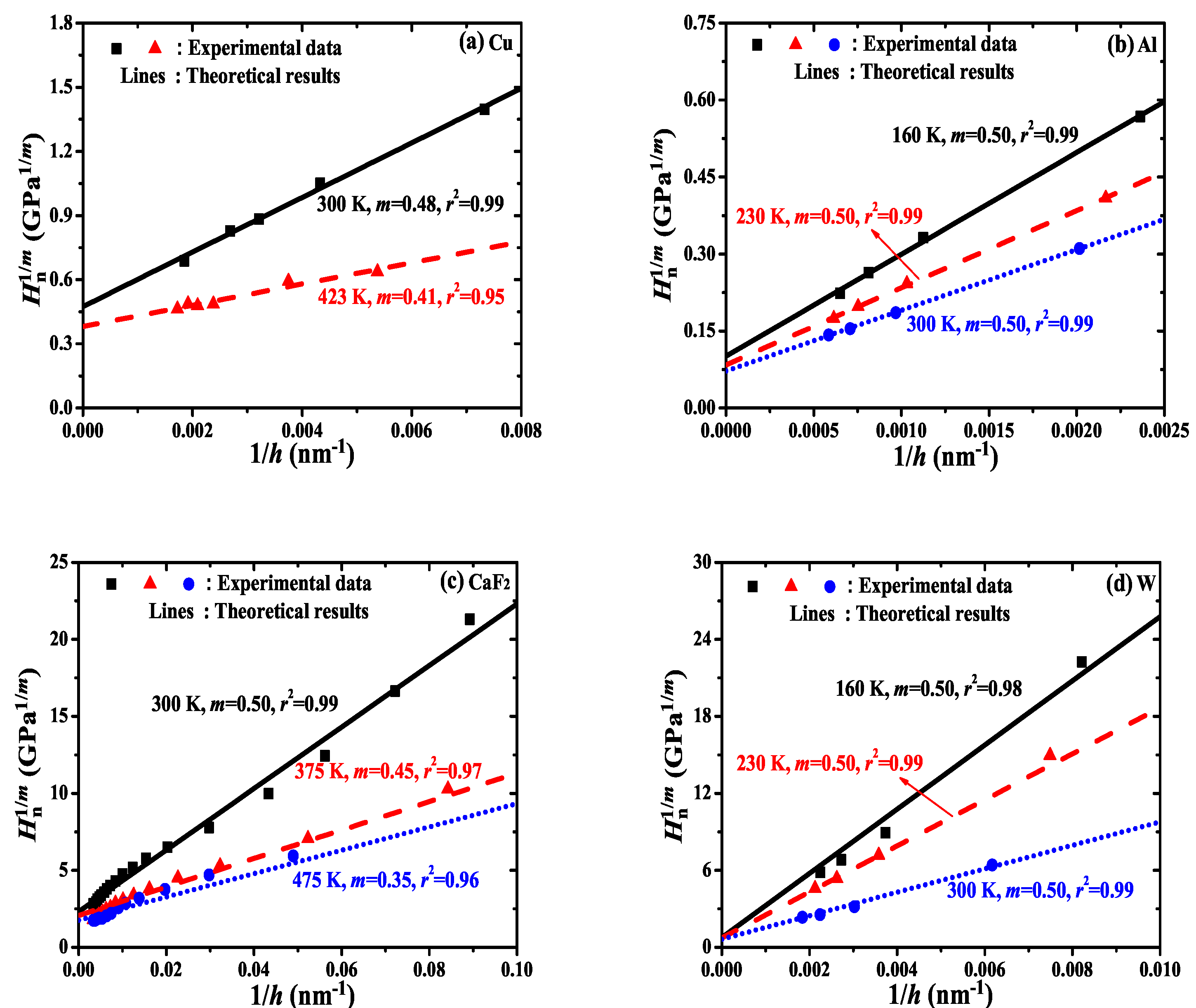
- Then, transform the − h relationships into the − curves. By adjusting parameter to approximately obtain a straight line with the determination coefficient . The slope and intercept with the vertical axis give and , respectively. It then yields the value of and .
- (3)
- (4)
- Finally, compare the fitted theoretical results with corresponding experimental data at different temperatures.
3. Experimental Verifications and Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, I.C.; Brandl, C.; Schwaiger, R. Thermally activated dislocation plasticity in body-centered cubic chromium studied by high-temperature nanoindentation. Acta Mater. 2017, 140, 107–115. [Google Scholar] [CrossRef]
- Chavoshi, S.Z.; Xu, S. Temperature-dependent nanoindentation response of materials. MRS Commun. 2018, 8, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, J.M.; Armstrong, D.E.J.; Heinz, W.; Schwaiger, R. High temperature nanoindentation: The state of the art and future challenges. Curr. Opin. Solid State Mater. Sci. 2015, 19, 354–366. [Google Scholar] [CrossRef] [Green Version]
- Duan, Z.C.; Hodge, A.M. High-temperature Nanoindentation: New Developments and Ongoing Challenges. Jom 2009, 61, 32–36. [Google Scholar] [CrossRef]
- Schuh, C.A.; Mason, J.K.; Lund, A.C. Quantitative insight into dislocation nucleation from high-temperature nanoindentation experiments. Nat. Mater. 2005, 4, 617–621. [Google Scholar] [CrossRef]
- Sawant, A.; Tin, S. High temperature nanoindentation of a Re-bearing single crystal Ni-base superalloy. Scr. Mater. 2008, 58, 275–278. [Google Scholar] [CrossRef]
- Harris, A.J.; Beake, B.D.; Armstrong, D.E.J.; Davies, M.I. Development of High Temperature Nanoindentation Methodology and its Application in the Nanoindentation of Polycrystalline Tungsten in Vacuum to 950 A degrees C. Exp. Mech. 2017, 57, 1115–1126. [Google Scholar] [CrossRef]
- Beake, B.D.; Harris, A.J.; Moghal, J.; Armstrong, D.E.J. Temperature dependence of strain rate sensitivity, indentation size effects and pile-up in polycrystalline tungsten from 25 to 950 degrees C. Mater. Des. 2018, 156, 278–286. [Google Scholar] [CrossRef]
- Zhang, Y.; Mohanty, D.P.; Seiler, P.; Siegmund, T.; Kruzic, J.J.; Tomar, V. High temperature indentation based property measurements of IN-617. Int. J. Plasticity 2017, 96, 264–281. [Google Scholar] [CrossRef]
- Maier, V.; Hohenwarter, A.; Pippan, R.; Kiener, D. Thermally activated deformation processes in body-centered cubic Cr-How microstructure influences strain-rate sensitivity. Scr. Mater. 2015, 106, 42–45. [Google Scholar] [CrossRef]
- Prasitthipayong, A.; Vachhani, S.J.; Tumey, S.J.; Minor, A.M.; Hosemann, R. Indentation size effect in unirradiated and ion-irradiated 800 H steel at high temperatures. Acta Mater. 2018, 144, 896–904. [Google Scholar] [CrossRef]
- Koch, S.; Abad, M.D.; Renhart, S.; Antrekowitsch, H.; Hosemann, P. A high temperature nanoindentation study of Al-Cu wrought alloy. Mater. Sci. Eng. Struct. Mater. Prop. Microstruct. Process. 2015, 644, 218–224. [Google Scholar] [CrossRef] [Green Version]
- Gibson, J.S.K.L.; Schroeders, S.; Zehnder, C.; Korte-Kerzel, S. On extracting mechanical properties from nanoindentation at temperatures up to 1000 degrees C. Extreme Mech. Lett. 2017, 17, 43–49. [Google Scholar] [CrossRef]
- Hangen, U.; Chen, C.L.; Richter, A. Mechanical Characterization of PM2000 Oxide-Dispersion-Strengthened Alloy by High Temperature Nanoindentation. Adv. Eng. Mater. 2015, 17, 1683–1690. [Google Scholar] [CrossRef]
- Javaid, F.; Johanns, K.E.; Patterson, E.A.; Durst, K. Temperature dependence of indentation size effect, dislocation pile-ups, and lattice friction in (001) strontium titanate. J. Am. Ceram. Soc. 2018, 101, 356–364. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.W.; Meza, L.; Greer, J.R. Cryogenic nanoindentation size effect in 001 -oriented face-centered cubic and body-centered cubic single crystals. Appl. Phys. Lett. 2013, 103. [Google Scholar] [CrossRef] [Green Version]
- Maughan, M.R.; Leonard, A.A.; Stauffer, D.D.; Bahr, D.F. The effects of intrinsic properties and defect structures on the indentation size effect in metals. Philos. Mag. 2017, 97, 1902–1920. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Karsten, D.; Bjom, B.; Mathias, G. Indentation size effect in metallic materials: Correcting for the size of the plastic zone. Scr. Mater. 2005, 52, 1093–1097. [Google Scholar]
- Qiu, X.; Huang, Y.; Nix, W.D.; Hwang, K.C.; Gao, H. Effect of intrinsic lattice resistance in strain gradient plasticity. Acta Mater. 2001, 49, 3949–3958. [Google Scholar] [CrossRef]
- Sadrabadi, P.; Durst, K.; Goeken, M. Study on the indentation size effect in CaF2: Dislocation structure and hardness. Acta Mater. 2009, 57, 1281–1289. [Google Scholar] [CrossRef]
- Lim, H.; Battaile, C.C.; Carroll, J.D.; Boyce, B.L.; Weinberger, C.R. A physically based model of temperature and strain rate dependent yield in BCC metals: Implementation into crystal plasticity. J. Mech. Phys. Solids 2015, 74, 80–96. [Google Scholar] [CrossRef] [Green Version]
- Durst, K.; Franke, O.; Bohner, A.; Goken, M. Indentation size effect in Ni-Fe solid solutions. Acta Mater. 2007, 55, 6825–6833. [Google Scholar] [CrossRef]
- Franke, O.; Trenkle, J.C.; Schuh, C.A. Temperature dependence of the indentation size effect. J. Mater. Res. 2010, 25, 1225–1229. [Google Scholar] [CrossRef]
- Chua, J.; Zhang, R.; Chaudhari, A.; Vachhani, S.J.; Kumar, A.S.; Tu, Q.; Wang, H. High-temperature nanoindentation size effect in fluorite material. Int. J. Mech. Sci. 2019, 159, 459–466. [Google Scholar] [CrossRef]
- Xiao, X.; Song, D.; Xue, J.; Chu, H.; Duan, H. A self-consistent plasticity theory for modeling the thermo-mechanical properties of irradiated FCC metallic polycrystals. J. Mech. Phys. Solids 2015, 78, 1–16. [Google Scholar] [CrossRef]
- Lu, C.; Deng, G.Y.; Tieu, A.K.; Su, L.H.; Zhu, H.T.; Liu, X.H. Crystal plasticity modeling of texture evolution and heterogeneity in equal channel angular pressing of aluminum single crystal. Acta Mater. 2011, 59, 3581–3592. [Google Scholar] [CrossRef]
- Kiner, D.; Hosemann, P.; Maloy, S.A.; Minor, A.M. In situ nanocompression testing of irradiated copper. Nat. Mater. 2011, 10, 608–613. [Google Scholar] [CrossRef] [Green Version]
- Terentyev, D.; Xiao, X.; Dubinko, A.; Bakaeva, A.; Duan, H. Dislocation-mediated strain hardening in tungsten: Thermo-mechanical plasticity theory and experimental validation. J. Mech. Phys. Solids 2015, 85, 1–15. [Google Scholar] [CrossRef]
- Brunner, D.; Glebovsky, V. The plastic properties of high-purity W single crystals. Mater. Lett. 2000, 42, 290–296. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I-Yield Criteria and Flow Rules for Porous Ductile Media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- David, T. A simple theory of static and dynamic hardness. Proc. R. Soc. A 1948, 192, 247–274. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Mekala, S.R. Analysis of Creep Transients in Calcium Fluoride Single Crystals following Stress Changes. Ph.D. Thesis, Friedrich-Alexander-University Erlangen-Nurnberg, Erlangen and Nuremberg, Bavaria, Germany, 2006. [Google Scholar]
- Xiao, X.; Terentyev, D.; Ruiz, A.; Zinovev, A.; Bakaev, A.; Zhurkin, E.E. High temperature nano-indentation of tungsten: Modelling and experimental validation. Mater. Sci. Eng. Struct. Mater. Prop. Microstruct. Process. 2019, 743, 106–113. [Google Scholar] [CrossRef]
- Christodoulou, N.; Jonas, J.J. Work hardening and rate sensitivity material coefficients for OFHC Cu and 99.99% A1. Acta Metall. 1984, 32, 1655–1668. [Google Scholar] [CrossRef]
- Durst, K.; Maier, V. Dynamic nanoindentation testing for studying thermally activated processes from single to nanocrystalline metals. Curr. Opin. Solid State Mater. Sci. 2015, 19, 340–353. [Google Scholar] [CrossRef]
- Lowrie, R.; Gonas, A.M. Single-Crystal Elastic Properties of Tungsten from 24 to 1800 C. J. Appl. Phys. 1967, 38, 4505. [Google Scholar] [CrossRef]



| Cu (N/A) | Al ([001]) | CaF2 ([111]) | W ([001]) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 300 K | 423 K | 160 K | 230 K | 300 K | 300 K | 375 K | 475 K | 160 K | 230 K | 300 K | |
| (GPa) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.20 | 0.60 | 0.00 | 3.05 | 2.58 | 2.18 |
| m | 0.48 | 0.41 | 0.50 | 0.50 | 0.50 | 0.50 | 0.45 | 0.35 | 0.50 | 0.50 | 0.50 |
| (GPa) | 0.474 | 0.381 | 0.101 | 0.084 | 0.072 | 2.320 | 2.070 | 1.750 | 0.750 | 0.716 | 0.627 |
| (GPa·nm) | 127.6 | 49.6 | 198.5 | 150.3 | 118.3 | 199.8 | 92.4 | 75.9 | 2503 | 1796 | 915 |
| 0.99 | 0.95 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.96 | 0.98 | 0.99 | 0.99 | |
| (GPa) | 0.699 | 0.673 | 0.318 | 0.290 | 0.268 | 1.523 | 1.390 | 1.220 | 0.866 | 0.846 | 0.792 |
| (nm) | 268 | 130 | 1965 | 1789 | 1643 | 86 | 45 | 43 | 3337 | 2508 | 1459 |
| Parameter | b (nm) | μ (GPa) | α |
|---|---|---|---|
| Value | 0.274 | with and | |
| Ref. | [29] | [38] | [35] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yu, L.; Xiao, X. Hardness-Depth Relationship with Temperature Effect for Single Crystals—A Theoretical Analysis. Crystals 2020, 10, 112. https://doi.org/10.3390/cryst10020112
Liu H, Yu L, Xiao X. Hardness-Depth Relationship with Temperature Effect for Single Crystals—A Theoretical Analysis. Crystals. 2020; 10(2):112. https://doi.org/10.3390/cryst10020112
Chicago/Turabian StyleLiu, Hao, Long Yu, and Xiazi Xiao. 2020. "Hardness-Depth Relationship with Temperature Effect for Single Crystals—A Theoretical Analysis" Crystals 10, no. 2: 112. https://doi.org/10.3390/cryst10020112
APA StyleLiu, H., Yu, L., & Xiao, X. (2020). Hardness-Depth Relationship with Temperature Effect for Single Crystals—A Theoretical Analysis. Crystals, 10(2), 112. https://doi.org/10.3390/cryst10020112