Interaction and Polarization Energy Relationships in σ-Hole and π-Hole Bonding
Abstract
:1. σ-Holes and π-Holes
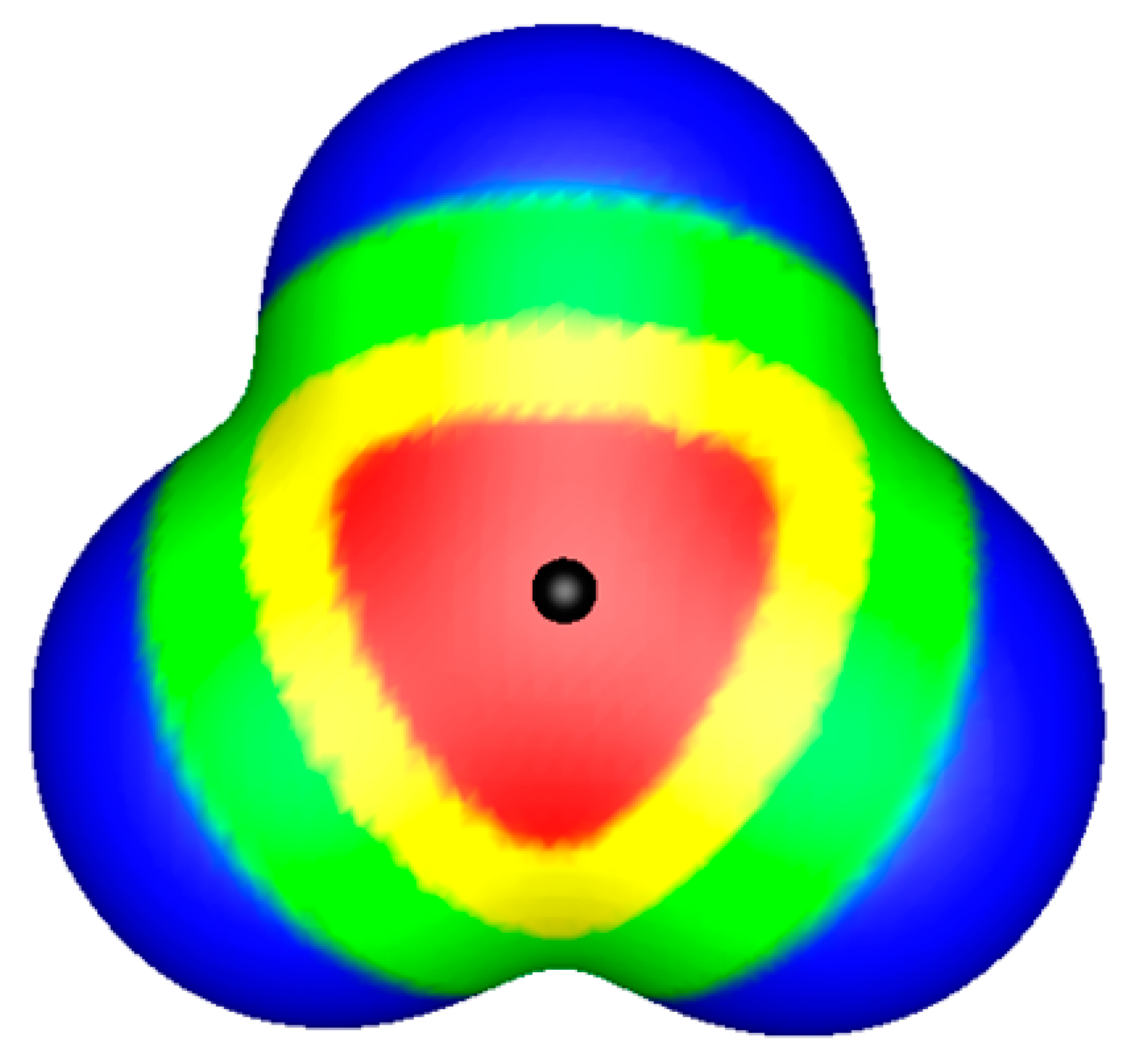
2. Molecular Electrostatic Potentials and Electric Fields
3. σ- and π-Hole Interactions
4. Polarization
5. Strengths of σ- and π-Hole Interactions
6. Present Results
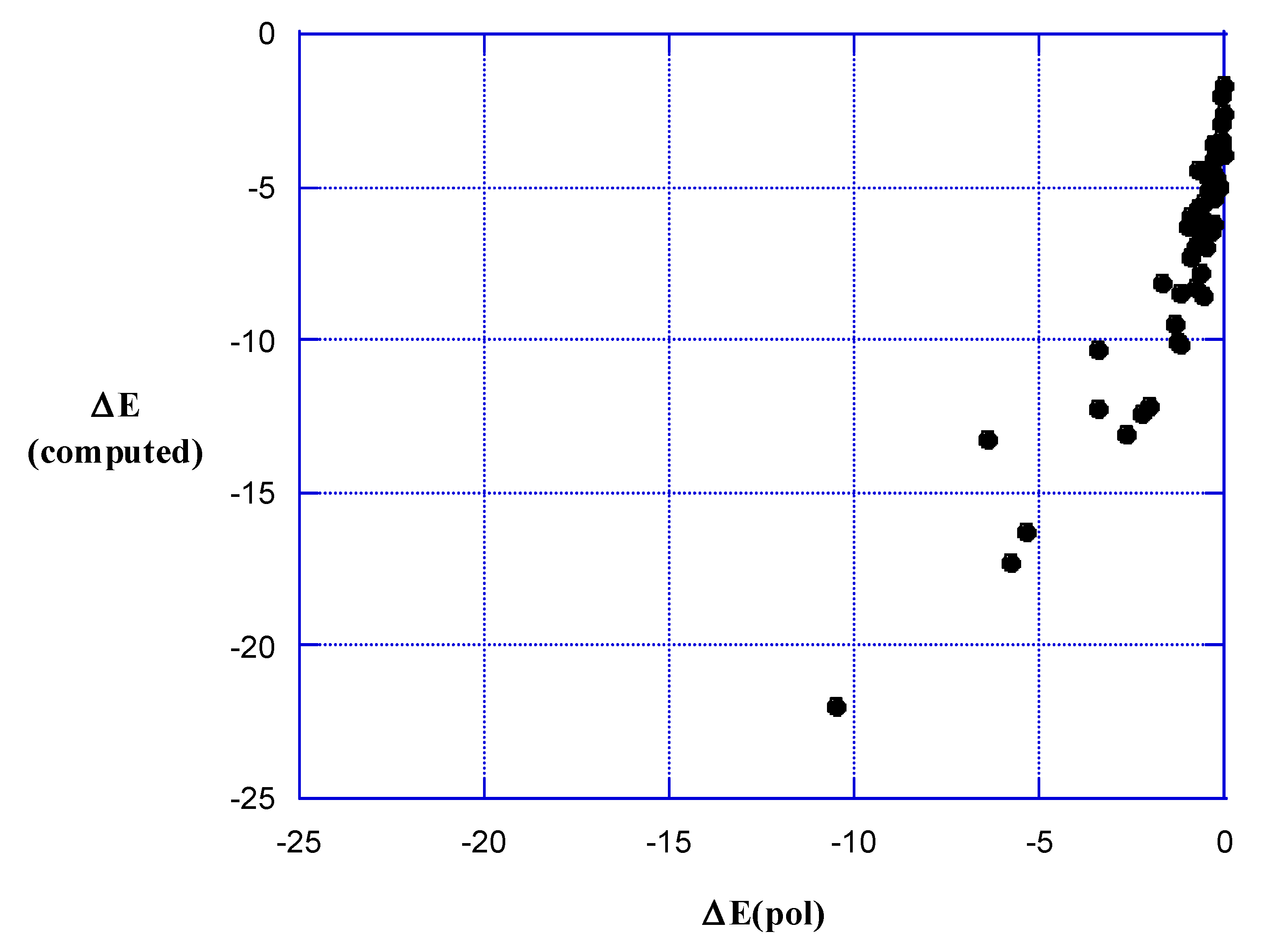
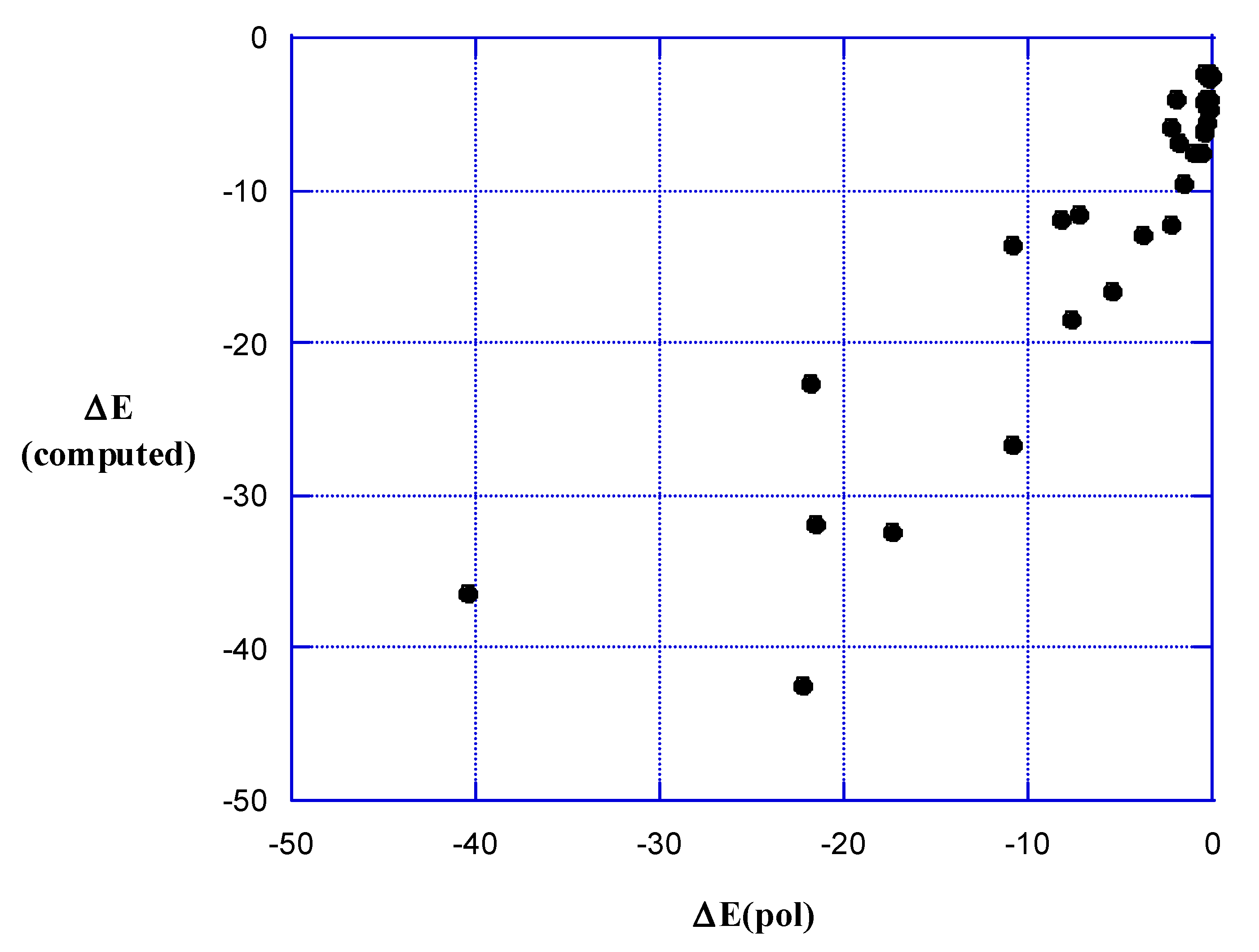
7. Polarization Energies
8. Discussion and Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Delgado-Barrio, G.; Prat, R.F. Deformed Hartree-Fock Solutions for Atoms. III. Convergent Iterative Process and Results for O−. Phys Rev. A 1975, 12, 2288–2297. [Google Scholar] [CrossRef]
- Bent, H.A. Structural Chemistry of Donor-Acceptor Interactions. Chem. Rev. 1968, 68, 587–648. [Google Scholar] [CrossRef]
- Stevens, E.D. Experimental Electron Density Distribution of Molecular Chlorine. Mol. Phys. 1979, 37, 27–45. [Google Scholar] [CrossRef]
- Guru Row, T.N.; Parthasarathy, R. Directional Preferences of Nonbonded Atomic Contacts with Divalent Sulfur in Terms of its Orbital Orientations. 2. S---S Interactions and Nonspherical Shape of Sulfur in Crystals. J. Am. Chem. Soc. 1981, 103, 477–479. [Google Scholar]
- Nyburg, S.C.; Faerman, C.H. A Revision of van der Waals Atomic Radii for Molecular Crystals: N, O, F, S, Cl, Se, Br and I Bonded to Carbon. Acta Cryst. B 1985, 41, 274–279. [Google Scholar] [CrossRef]
- Ramasubbu, N.; Parthasarathy, R. Stereochemistry of Incipient Electrophilic and Nucleophilic Reactions at Divalent Selenium Center: Electrophilic-Nucleophlic Pairing and Anisotropic Shape of Se in Se-Se Interactions. Phosphorus Sulfur. 1987, 31, 221–229. [Google Scholar] [CrossRef]
- Tsirelson, V.G.; Zou, P.F.; Tang, T.H.; Bader, R.F.W. Topological Definition of Crystal Structure: Determination of the Bonded Interactions in Solid Molecular Chlorine. Acta Cryst. A 1995, 51, 143–153. [Google Scholar] [CrossRef]
- Batsanov, S.S. Anisotropy of Atomic van der Waals Radii in the Gas Phase and Condensed Molecules. Struct. Chem. 2000, 11, 177–183. [Google Scholar] [CrossRef]
- Eramian, H.; Tian, Y.-H.; Fox, Z.; Beneberu, H.Z.; Kertesz, M. On the Anisotropy of van der Waals Atomic Radii of O, S, Se, F, Cl, Br and I. J. Phys. Chem. A 2013, 117, 14184–14190. [Google Scholar] [CrossRef]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen Bonding: The σ-Hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
- Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. σ-Holes, π-Holes and Electrostatically-Driven Interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Coppens, P. Experimental electron densities and chemical bonding. Angew. Chem. Int. Ed. 1977, 16, 32–40. [Google Scholar] [CrossRef]
- Feil, D. The electron density distribution in molecular crystals: Exploring the boundary between X-ray diffraction and quantum chemistry. Chem. Scr. 1986, 26, 395–408. [Google Scholar]
- Klein, C.L.; Stevens, E.D. Charge density studies of drug molecules. In Structure and Reactivity; Liebman, J.F., Greenberg, A., Eds.; VCH Publishers: New York, NY, USA, 1988; pp. 26–64. [Google Scholar]
- Stewart, R.F. On the mapping of electrostatic properties from Bragg diffraction data. Chem. Phys. Lett. 1979, 65, 335–342. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Molecular electrostatic potentials and chemical reactivity. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; VCH Publishers: New York, NY, USA, 1991; Volume 2, pp. 273–312. [Google Scholar]
- Politzer, P.; Daiker, K.C. Models for chemical reactivity. In The Force Concept in Chemistry; Deb, B.M., Ed.; Van Nostrand Reinhold: New York, NY, USA, 1981; pp. 294–387. [Google Scholar]
- Politzer, P.; Truhlar, D.G. (Eds.) Chemical Applications of Atomic and Molecular Electrostatic Potentials; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Stone, A.J.; Price, S.L. Some new ideas in the theory of intermolecular forces: Anisotropic atom-atom potentials. J. Phys. Chem. 1988, 92, 3325–3335. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Rablen, P.R. Comparison of atomic charges derived via different procedures. J. Comput. Chem. 1993, 14, 1504–1518. [Google Scholar] [CrossRef]
- Bachrach, S.M. Population analysis and electron densities from quantum mechanics. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; VCH Publishers: New York, NY, USA, 1994; Volume 5, pp. 171–227. [Google Scholar]
- Price, S.L. Applications of realistic electrostatic modelling to molecules in complexes, solids and proteins. J. Chem. Soc. Faraday Trans. 1996, 92, 2997–3008. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. Wires Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π-hole interactions. Chem. Phys. 2015, 16, 2496–2517. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. An overview of strengths and directionalities of noncovalent interactions: σ-Holes and π-holes. Crystals 2019, 9, 165. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The σ-hole revisited. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. σ-Hole interactions: Perspectives and misconceptions. Crystals 2017, 7, 212. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Murray, J.S. Halogen bonding: An interim discussion. Chem. Phys. 2013, 14, 278–294. [Google Scholar] [CrossRef]
- Benesi, H.A.; Hildebrand, J.H. A spectrophotometric investigation of the interaction of iodine with aromatic hydrocarbons. J. Am. Chem. Soc. 1949, 71, 2703–2707. [Google Scholar] [CrossRef]
- Hassel, O.; Romming, C. Direct structural evidence for weak charge transfer bonds in solids containing chemically saturated molecules. Quart. Rev. Chem. Soc. 1962, 16, 1–18. [Google Scholar] [CrossRef]
- Blackstock, S.C.; Lorand, J.P.; Kochi, J.K. Charge-transfer interactions of amines with tetrahalomethanes. J. Org. Chem. 1987, 52, 1451–1460. [Google Scholar] [CrossRef]
- Ramasubbu, N.; Parthasarathy, R.; Murray-Rust, P. Angular preferences of intermolecular forces around halogen centers: Preferred directions of approach of electrophiles and nucleophiles around carbon-halogen bond. J. Am. Chem. So. 1986, 108, 4308–4314. [Google Scholar] [CrossRef]
- Rosenfeld, R.E., Jr.; Parthasarathy, R.; Dunitz, J.D. Directional preferences of nonbonded atomic contacts with divalent sulfur. 1. Electrophiles and nucleophiles. J. Am. Chem. Soc. 1977, 99, 4860–4862. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Janjić, G.V.; Zarić, S.D. σ-Hole interactions of covalently- bonded nitrogen, phosphorus and arsenic: A survey of crystal structures. Crystal 2014, 4, 12–31. [Google Scholar] [CrossRef] [Green Version]
- Andree, S.N.L.; Sinha, A.S.; Aakeröy, C.B. Structural examination of halogen-bonded co-crystals of tritopic acceptors. Molecules 2018, 23, 163. [Google Scholar] [CrossRef]
- Shields, Z.P.-I.; Murray, J.S.; Politzer, P. Directional tendencies of halogen and hydrogen bonding. Intern. J. Quantum Chem. 2010, 110, 2823–2832. [Google Scholar] [CrossRef]
- Hennemann, M.; Murray, J.S.; Politzer, P.; Riley, K.E.; Clark, T. Polarization-induced σ-holes and hydrogen bonding. J. Mol. Model. 2012, 18, 2461–2469. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. σ-Hole bonding: A physical interpretation. Top. Curr. Chem. 2014, 358, 19–42. [Google Scholar]
- Politzer, P.; Murray, J.S.; Clark, T. Intermolecular interactions in crystals. In Intermolecular Interactions in Crystals: Fundamentals of Crystal Engineering; Novoa, J.J., Ed.; RSC Publishing: London, UK, 2017. [Google Scholar]
- Murray, J.S.; Politzer, P. Hydrogen bonding: A Coulombic σ-hole interaction. J. Indian Inst. Sci. 2019. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J. Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Bulat, F.A.; Toro-Labbé, A.; Brinck, T.; Murray, J.S.; Politzer, P. Quantitative analysis of molecular surfaces: Volumes, electrostatic potentials and average local ionization energies. J. Mol. Model. 2010, 16, 1679–1691. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Concha, M.C. σ-Hole bonding between like atoms. A fallacy of atomic charges. J. Mol. Model. 2008, 14, 659–665. [Google Scholar] [CrossRef]
- Solimannejad, M.; Malekani, M.; Alkorta, I. Cooperative and diminutive unusual weak bonding in F3CX---HMgH---Y and F3CX---Y---HMgH trimers (X = Cl, Br; Y = HCN and HNC). J. Phys. Chem. A 2010, 114, 12106–12111. [Google Scholar] [CrossRef]
- Politzer, P.; Riley, K.E.; Bulat, F.A.; Murray, J.S. Perspectives on halogen bonding and other σ-hole interactions: lex parsimoniae (Occam’s Razor). Comput. Chem. 2012, 998, 2–8. [Google Scholar] [CrossRef]
- Clark, T. Polarization, donor-acceptor interactions and covalent contributions in weak interactions: A clarification. J. Mol. Model. 2017, 23, 297. [Google Scholar] [CrossRef]
- Edwards, A.J.; Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Intermolecular interactions in molecular crystals: What’s in a name? Faraday Discuss. 2017, 203, 93–112. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Murray, J.S.; Clark, T. Mathematical modeling and physical reality in noncovalent interactions. J. Mol. Model. 2015, 21, 52. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. A unified view of halogen bonding, hydrogen bonding and other σ-hole interactions. In Noncovalent Forces; Scheiner, S., Ed.; Springer: Heidelberg, Germany, 2015; pp. 291–321. [Google Scholar]
- Clark, T.; Murray, J.S.; Politzer, P. A perspective on quantum mechanics and chemical concepts in describing noncovalent interactions. Phys. Chem. Chem. Phys. 2018, 20, 30076–30082. [Google Scholar] [CrossRef]
- Riley, K.E.; Hobza, P. Investigations into the nature of halogen bonding including symmetry adapted perturbation theory analyses. J. Chem. Theory Comput. 2008, 4, 232–242. [Google Scholar] [CrossRef]
- Solimannejad, M.; Gharabaghi, M.; Scheiner, S. SH---N and SH---P blue shifting H-bonds and and N---P interactions in complexes pairing HSN with amines and phosphines. J. Chem. Phys. 2011, 134, 24312. [Google Scholar] [CrossRef]
- Murray, J.S.; Shields, Z.P.-I.; Seybold, P.G.; Politzer, P. Intuitive and counterintuitive noncovalent interactions of aromatic π regions with the hydrogen and nitrogen of HCN. J. Comput. Sci. 2015, 10, 209–216. [Google Scholar] [CrossRef]
- Geronimo, I.; Singh, N.J.; Kim, K.S. Can electron-rich π systems bind anions? J. Chem. Theory Comput. 2011, 7, 825–829. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Weinstein, H. Theoretical treatment of multiple site reactivity in large molecules. Chem. Phys. Lett. 1975, 30, 441–447. [Google Scholar] [CrossRef]
- Bonaccorsi, R.; Scrocco, E.; Tomasi, J. A representation of the polarization term in the interaction energy between a molecule and a point-like charge. Theoret. Chim. Acta 1976, 43, 63–73. [Google Scholar] [CrossRef]
- Francl, M.M. Polarization correction to electrostatic potentials. J. Phys. Chem. 1985, 89, 428–433. [Google Scholar] [CrossRef]
- Orozco, M.; Luque, F.J. Generalization of the molecular electrostatic potential for the study of noncovalent interactions. In Molecular Electrostatic Potentials: Concepts and Applications; Murray, J.S., Sen, K., Eds.; Elsevier: Amsterdam, Holland, 1996; pp. 181–218. [Google Scholar]
- Alkorta, I.; Perez, J.J.; Villar, H.O. Molecular polarization maps as a tool for studies of intermolecular interactions and chemical reactivity. J. Mol. Graph. 1994, 12, 3–13. [Google Scholar] [CrossRef]
- Clark, T.; Murray, J.S.; Politzer, P. The σ-hole Coulombic interpretation of trihalide anion formation. Chem. Phys. Chem. 2018, 19, 3044–3049. [Google Scholar] [CrossRef]
- Brinck, T.; Borrfors, A.N. Electrostatics and polarization determine the strength of the halogen bond: A red card for charge transfer. J. Mol. Model. 2019, 25, 125. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Murray, J.S. Electrostatics and polarization in σ- and π-hole noncovalent interactions: An overview. Chem. Phys. Chem. 2019. [Google Scholar] [CrossRef]
- Riley, K.E.; Murray, J.S.; Politzer, P.; Concha, M.C.; Hobza, P. Br---O complexes as probes of factors affecting halogen bonding: Interactions of bromobenzenes and bromopyrimidines with acetone. J. Chem. Theory Comput. 2009, 5, 155–163. [Google Scholar] [CrossRef]
- Bundhun, A.; Ramasami, P.; Murray, J.S.; Politzer, P. Trends in σ-hole strengths and interactions of F3MX molecules (M = C, Si, Ge and X = F, Cl, Br, I). J. Mol. Model. 2013, 19, 2739–2746. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Jin, W.H. σ-Hole bond vs π-hole bond: A comparison based on halogen bond. Chem. Rev. 2016, 116, 5072–5104. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Explicit inclusion of polarizing electric fields in σ- and π-hole interactions. J. Phys. Chem. A 2019, 123, 10123–10130. [Google Scholar] [CrossRef]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B. Molecular Theory of Gases and Liquids; Wiley: New York, NY, USA, 1954; p. 852. [Google Scholar]
- NCSS 11 Statistical Software, version 2016; NCSS, LLC: Kaysville, UT, USA, 2016; Available online: https://www.ncss.com/software/ncss/ (accessed on 27 January 2020).
- Johnson, R.D., III (Ed.) NIST Computational Chemistry Comparison and Benchmark DataBase; NIST Standard Reference DataBase No. 101; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. Available online: https://cccbdb.nist.gov/ (accessed on 27 January 2020).
- Alvarez, S. A cartography of the van der Waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Wong, N.B.; Zheng, W.; Tian, A. Theoretical study on the blueshifting halogen bond. J. Phys. Chem. A 2004, 108, 1799–1805. [Google Scholar] [CrossRef]
- Murray, J.S.; Concha, M.S.; Lane, P.; Hobza, P.; Politzer, P. Blue shifts vs. red shifts in σ-hole bonding. J. Mol. Model. 2008, 14, 699–704. [Google Scholar] [CrossRef]
- Crews, P.; Jaspars, M.; Rodriguez, J. Organic Structure Analysis; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Couling, V.W.; Halliburton, B.W.; Keir, R.L.; Ritchie, G.L.D. Anisotropic molecular polarizabilities of HCHO, CH3CHO and CH3COCH3, Rayleigh depolarization ratios of HCHO and CH3CHO and first and second Kerr virial coefficients of CH3COCH. J. Phys. Chem. A 2001, 105, 4365–4370. [Google Scholar] [CrossRef]
- Hellmann, H. Einführung in die Quantenchemie; Deuticke: Leipzig, Germany, 1937. [Google Scholar]
- Feynman, R.P. Forces in molecules. Phys. Rev. 1939, 56, 340–343. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Halogen bonding and beyond: Factors influencing the nature of CN-R and SiN-R complexes with F-Cl and Cl2. Chem. Acc. 2012, 131, 1114. [Google Scholar] [CrossRef]
- Slater, J.C. Hellmann-Feynman and virial theorems in the Xα method. J. Chem. Phys. 1972, 57, 2389–2396. [Google Scholar] [CrossRef]
- Bader, R.F.W. Bond paths are not chemical bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef] [Green Version]
- Rahm, M.; Hoffmann, R. Distinguishing bonds. J. Am. Chem. Soc. 2016, 138, 3731–3744. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. A look at bonds and bonding. Struct. Chem. 2019, 30, 1153–1157. [Google Scholar] [CrossRef]
- Riley, K.E.; Murray, J.S.; Fanfrlίk, J.; Řezáč, J.; Solá, R.J.; Concha, M.C.; Ramos, F.M.; Politzer, P. Halogen bond tunability I: The effects of aromatic fluorine substitution on the strengths of halogen-bonding interactions involving chlorine, bromine and iodine. J. Mol. Model. 2011, 17, 3309–3318. [Google Scholar] [CrossRef]
- Metrangolo, P.; Murray, J.S.; Pilati, T.; Politzer, P.; Resnati, G.; Terraneo, G. Fluorine-centered halogen bonding: A factor in recognition phenomena and reactivity. Cryst. Growth Des. 2011, 11, 4238–4246. [Google Scholar] [CrossRef]




| Interaction | ΔE (kcal/mol) | VS,max (kcal/mol) | R (Å) | V(R) (kcal/mol) | ε(R) (au) | ΔE(pol) (kcal/mol) |
|---|---|---|---|---|---|---|
| FF---OH2 | −1.68 | 14.5 | 2.60 | 2.7 | 0.002549 | −0.02 |
| FF---O=CH2 | −2.04 | 14.5 | 2.54 | 2.8 | 0.002781 | −0.05 |
| H3C(Cl)Se---NCH | −2.58 | 8.8 | 3.19 | 1.8 | 0.001770 | −0.02 |
| HF2CBr---NCH | −2.97 | 16.5 | 3.12 | 3.1 | 0.003319 | −0.06 |
| HF2CBr---O=CH2 | −3.47 | 16.5 | 3.02 | 3.5 | 0.003856 | −0.09 |
| HCCH---NCH | −3.58 | 30.7 | 2.30 | 9.1 | 0.006834 | −0.26 |
| H2NH---NH3 | −3.62 | 25.5 | 2.28 | 7.7 | 0.005442 | −0.13 |
| NC-Cl---OH2 | −3.65 | 35.3 | 2.88 | 13.6 | 0.007823 | −0.19 |
| HF2CBr---NH3 | −3.67 | 16.5 | 3.06 | 3.3 | 0.003621 | −0.06 |
| H3C(Cl)Se---NH3 | −3.91 | 8.8 | 3.13 | 1.7 | 0.001990 | −0.02 |
| F3CBr---NCH | −3.92 | 24.1 | 3.04 | 7.1 | 0.005416 | −0.16 |
| F3CBr---O=CH2 | −4.04 | 24.1 | 2.94 | 7.8 | 0.006187 | −0.22 |
| F3CH---NCH | −4.13 | 31.2 | 2.33 | 12.6 | 0.007259 | −0.29 |
| F3CH---O=CH2 | −4.32 | 31.2 | 2.31 | 12.8 | 0.007431 | −0.32 |
| HOH---NCH | −4.41 | 43.4 | 2.11 | 15.2 | 0.01097 | −0.66 |
| F2(NC)P---NCH | −4.60 | 36.5 | 2.98 | 12.0 | 0.007417 | −0.30 |
| H3(F)Si---NCH | −4.67 | 34.1 | 2.91 | 12.2 | 0.008482 | −0.39 |
| HCCH---NH3 | −4.71 | 30.7 | 2.26 | 9.5 | 0.007218 | −0.23 |
| F3CBr---NH3 | −4.97 | 24.1 | 2.97 | 7.6 | 0.005923 | −0.16 |
| HF2CBr---NH2CH3 | −5.05 | 16.5 | 2.98 | 3.7 | 0.004098 | −0.13 |
| NC-Br---OH2 | −5.15 | 42.7 | 2.87 | 18.3 | 0.01112 | −0.40 |
| F3CH---NH3 | −5.33 | 31.2 | 2.28 | 13.1 | 0.007667 | −0.26 |
| HCCH---NH2CH3 | −5.51 | 30.7 | 2.17 | 10.3 | 0.008089 | −0.52 |
| NC-H---OH2 | −5.66 | 50.0 | 2.05 | 22.8 | 0.01439 | −0.66 |
| FCl---OH2 | −5.93 | 40.3 | 2.53 | 16.5 | 0.01396 | −0.62 |
| FCl---NCH | −5.96 | 40.3 | 2.60 | 15.4 | 0.01256 | −0.87 |
| F3As---NCH | −6.01 | 36.2 | 2.91 | 14.6 | 0.01044 | −0.60 |
| HF2CBr---NH(CH3)2 | −6.17 | 16.5 | 2.90 | 4.1 | 0.004658 | −0.25 |
| HCCH---NH(CH3)2 | −6.26 | 30.7 | 2.09 | 11.1 | 0.009099 | −0.95 |
| F3CH---NH2CH3 | −6.29 | 31.2 | 2.24 | 13.4 | 0.007994 | −0.51 |
| F3CBr---NH2CH3 | −6.42 | 24.1 | 2.88 | 8.2 | 0.006701 | −0.36 |
| Cl-Cl---NH3 | −6.48 | 24.1 | 2.55 | 8.9 | 0.009112 | −0.37 |
| (NC)2S---NCH | −6.65 | 43.8 | 2.92 | 17.0 | 0.01033 | −0.59 |
| HOH---NH3 | −6.96 | 43.4 | 1.97 | 17.1 | 0.01325 | −0.78 |
| F2(NC)P---NH3 | −6.98 | 36.5 | 2.73 | 14.7 | 0.01032 | −0.48 |
| H3FSi---NH3 | −7.26 | 34.1 | 2.56 | 16.8 | 0.01416 | −0.89 |
| F3CBr---NH(CH3)2 | −7.79 | 24.1 | 2.80 | 8.9 | 0.007504 | −0.65 |
| HOH---NH2CH3 | −8.13 | 43.4 | 1.91 | 18.1 | 0.01442 | −1.65 |
| (NC)2S---O=CH2 | −8.27 | 43.8 | 2.82 | 18.3 | 0.01156 | −0.79 |
| FBr---OH2 | −8.43 | 47.7 | 2.53 | 22.3 | 0.01908 | −1.16 |
| F3As---O=CH2 | −8.44 | 36.2 | 2.68 | 17.8 | 0.01407 | −1.16 |
| (NC)2S---NH3 | −8.56 | 43.8 | 2.86 | 17.8 | 0.01104 | −0.54 |
| F2(NC)P---NH2CH3 | −9.45 | 36.5 | 2.56 | 16.9 | 0.01305 | −1.35 |
| (NC)2S---NH2CH3 | −10.10 | 43.8 | 2.74 | 19.5 | 0.01267 | −1.28 |
| F3As---NH3 | −10.13 | 36.2 | 2.59 | 19.4 | 0.01611 | −1.16 |
| H3FSi---NH2CH3 | −10.35 | 34.1 | 2.34 | 21.1 | 0.02059 | −3.37 |
| FCl---NH3 | −12.18 | 40.3 | 2.27 | 21.8 | 0.02138 | −2.03 |
| F2(NC)P---NH(CH3)2 | −12.26 | 36.5 | 2.39 | 20.0 | 0.01713 | −3.38 |
| (NC)2S---NH(CH3)2 | −12.39 | 43.8 | 2.66 | 20.7 | 0.01393 | −2.24 |
| F3As---NH2CH3 | −13.10 | 36.2 | 2.51 | 21.1 | 0.01825 | −2.65 |
| H3FSi---NH(CH3)2 | −13.22 | 34.1 | 2.27 | 23.0 | 0.02358 | −6.41 |
| F3As---NH(CH3)2 | −16.29 | 36.2 | 2.41 | 23.5 | 0.02156 | −5.36 |
| FCl---NH2CH3 | −17.28 | 40.3 | 2.15 | 25.3 | 0.02697 | −5.78 |
| FCl---NH(CH3)2 | −21.96 | 40.3 | 2.09 | 27.4 | 0.03012 | −10.46 |
| π-Hole Molecule | Negative Site | ΔE (kcal/mol) | VS,max (kcal/mol) | R (Å) | V(R) (kcal/mol) | ε(R) (au) | ΔE(pol) (kcal/mol) |
|---|---|---|---|---|---|---|---|
| SeO2 | OCO | −2.36 | 35.4 | 3.19 | 10.5 | 0.007622 | −0.36 |
| SeO2 | CO | −2.42 | 35.4 | 3.44 | 8.5 | 0.005766 | −0.14 |
| Cl2C=O | CO | −2.55 | 22.8 | 3.16 | 3.9 | 0.003483 | −0.05 |
| Cl2C=O | OCO | −2.70 | 22.8 | 2.88 | 5.3 | 0.005104 | −0.16 |
| Cl2C=O | NCH | −3.99 | 22.8 | 2.89 | 5.2 | 0.005042 | −0.14 |
| FPO2 | OCO | −4.00 | 58.4 | 2.71 | 20.5 | 0.01795 | −1.99 |
| SO2 | NCH | −4.04 | 32.9 | 3.03 | 10.2 | 0.007796 | −0.33 |
| SeO2 | NCH | −4.14 | 35.4 | 3.08 | 11.6 | 0.008652 | −0.41 |
| FNO2 | NCH | −4.38 | 32.8 | 2.80 | 8.5 | 0.007202 | −0.28 |
| Cl3B | NCH | −4.46 | 24.0 | 2.84 | 6.7 | 0.006555 | −0.24 |
| F2C=O | NCH | −4.58 | 40.9 | 2.77 | 9.0 | 0.007798 | −0.33 |
| Cl2C=O | NH3 | −4.64 | 22.8 | 2.85 | 5.5 | 0.005332 | −0.13 |
| FNO2 | NH3 | −5.52 | 32.8 | 2.79 | 8.5 | 0.007301 | −0.24 |
| FPO2 | CO | −5.91 | 58.4 | 2.53 | 24.9 | 0.02326 | −2.24 |
| SO2 | NH3 | −6.00 | 32.9 | 2.83 | 12.3 | 0.01004 | −0.45 |
| F2C=O | NH3 | −6.14 | 40.9 | 2.67 | 10.0 | 0.008952 | −0.36 |
| F3B | NCH | −6.94 | 48.8 | 2.35 | 17.9 | 0.01836 | −1.85 |
| H3CPO2 | NCH | −7.59 | 47.6 | 2.68 | 14.8 | 0.01361 | −1.02 |
| SeO2 | NH3 | −7.62 | 35.4 | 2.87 | 14.0 | 0.01123 | −0.56 |
| SO2 | NH2CH3 | −9.52 | 32.9 | 2.59 | 15.6 | 0.01398 | −1.55 |
| H2Si=O | NCH | −11.55 | 43.4 | 2.18 | 30.7 | 0.03635 | −7.25 |
| FPO2 | NCH | −11.88 | 58.4 | 2.21 | 36.3 | 0.03868 | −8.21 |
| SeO2 | NH2CH3 | −12.23 | 35.4 | 2.58 | 18.8 | 0.01693 | −2.28 |
| SO2 | NH(CH3)2 | −12.93 | 32.9 | 2.43 | 18.7 | 0.01793 | −3.71 |
| F2Si=O | CO | −13.52 | 66.7 | 2.12 | 45.9 | 0.05101 | −10.76 |
| SeO2 | NH(CH3)2 | −16.66 | 35.4 | 2.42 | 22.4 | 0.02177 | −5.47 |
| H3CPO2 | NH3 | −18.41 | 47.6 | 2.05 | 32.9 | 0.04145 | −7.65 |
| F2Si=O | NCH | −22.58 | 66.7 | 2.01 | 53.4 | 0.06293 | −21.74 |
| H2Si=O | NH3 | −26.69 | 43.4 | 2.03 | 38.2 | 0.04925 | −10.80 |
| H2Si=O | NH2CH3 | −31.91 | 43.4 | 2.00 | 39.7 | 0.05195 | −21.46 |
| FPO2 | NH3 | −32.35 | 58.4 | 1.95 | 51.5 | 0.06246 | −17.37 |
| H2Si=O | NH(CH3)2 | −36.39 | 43.4 | 1.94 | 43.7 | 0.05916 | −40.36 |
| F2Si=O | NH3 | −42.38 | 66.7 | 1.95 | 58.2 | 0.07063 | −22.21 |
| Molecule | VS,min (kcal/mol) a | Polarizability, α (Å3) b |
|---|---|---|
| CO2 | −12.6 | 2.911 |
| CO | −14.0 | 1.953 |
| H2C=O | −30.2 | 2.77 |
| HCN | −32.2 | 2.593 |
| NH(CH3)2 | −39.1 | 5.447 |
| H2O | −39.6 | 1.501 |
| NH2CH3 | −42.9 | 3.754 |
| NH3 | −46.2 | 2.103 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murray, J.S.; Politzer, P. Interaction and Polarization Energy Relationships in σ-Hole and π-Hole Bonding. Crystals 2020, 10, 76. https://doi.org/10.3390/cryst10020076
Murray JS, Politzer P. Interaction and Polarization Energy Relationships in σ-Hole and π-Hole Bonding. Crystals. 2020; 10(2):76. https://doi.org/10.3390/cryst10020076
Chicago/Turabian StyleMurray, Jane S., and Peter Politzer. 2020. "Interaction and Polarization Energy Relationships in σ-Hole and π-Hole Bonding" Crystals 10, no. 2: 76. https://doi.org/10.3390/cryst10020076
APA StyleMurray, J. S., & Politzer, P. (2020). Interaction and Polarization Energy Relationships in σ-Hole and π-Hole Bonding. Crystals, 10(2), 76. https://doi.org/10.3390/cryst10020076





