Guided Optical Modes in Metal-Cladded Tunable Hyperbolic Metamaterial Slab Waveguides
Abstract
1. Introduction
2. Theoretical Model
2.1. THMM Slab Waveguide in Configuration A
2.2. THMM Slab Waveguide in Configuration B
3. Results and Discussion
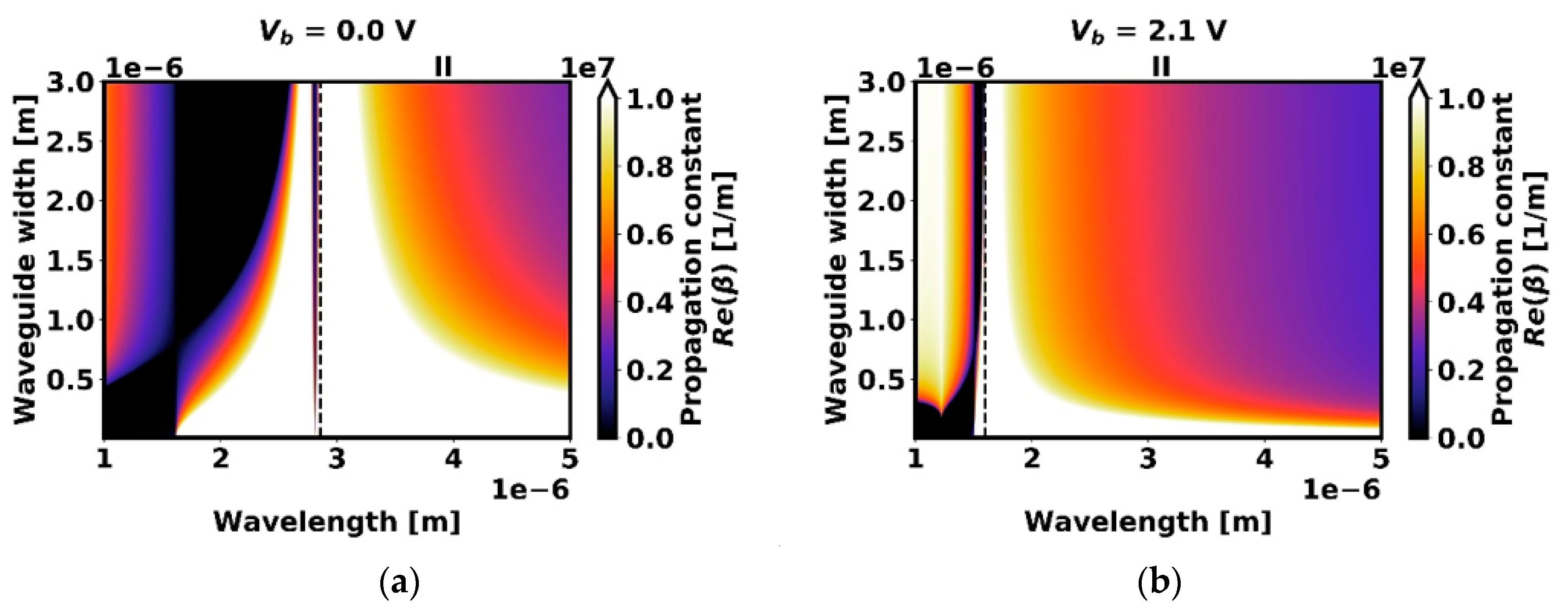
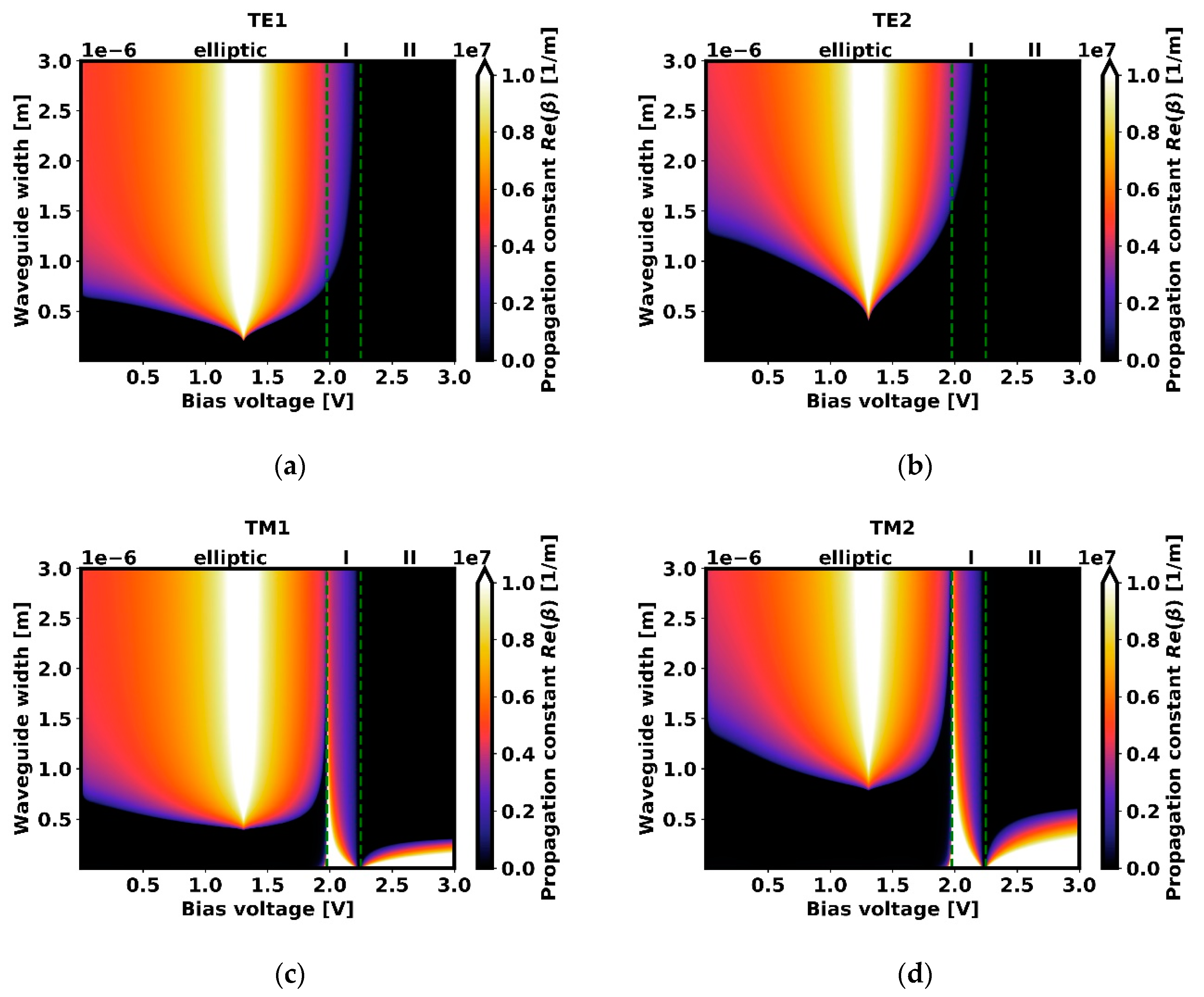
3.1. Results for Configuration A
3.2. Results for Configuration B
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and µ. Sov. Phys. Uspekhi. 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef]
- Shadrivov, I.V.; Sukhorukov, A.A.; Kivshar, Y.S. Beam shaping by a periodic structure with negative refraction. Appl. Phys. Lett. 2003, 82, 3820–3822. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 2005, 72. [Google Scholar] [CrossRef] [PubMed]
- Shamonina, E.; Solymar, L. Metamaterials: How the subject started. Metamaterials 2007, 1, 12–18. [Google Scholar] [CrossRef]
- Shadrivov, I.V.; Sukhorukov, A.A.; Kivshar, Y.S. Guided modes in negative-refractive-index waveguides. Phys. Rev. E 2003, 67, 57602. [Google Scholar] [CrossRef]
- Wu, B.-I.; Grzegorczyk, T.M.; Zhang, Y.; Kong, J.A. Guided modes with imaginary transverse wave number in a slab waveguide with negative permittivity and permeability. J. Appl. Phys. 2003, 93, 9386–9388. [Google Scholar] [CrossRef]
- He, Y.; Cao, Z.; Shen, Q. Guided optical modes in asymmetric left-handed waveguides. Opt. Commun. 2005, 245, 125–135. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, J. Analysis of Guided Modes in Asymmetric Left-Handed Slab Waveguides. Prog. Electromagn. Res. 2006, 62, 203–215. [Google Scholar] [CrossRef]
- D’Aguanno, G.; Mattiucci, N.; Scalora, M.; Bloemer, M.J. TE and TM guided modes in an air waveguide with negative-index-material cladding. Phys. Rev. E 2005, 71, 046603. [Google Scholar] [CrossRef]
- Wang, Z.H.; Xiao, Z.Y.; Li, S.P. Guided modes in slab waveguides with a left handed material cover or substrate. Opt. Commun. 2008, 281, 607–613. [Google Scholar] [CrossRef]
- Taya, S.A.; Qadoura, I.M. Guided modes in slab waveguides with negative index cladding and substrate. Opt. - Int. J. Light Electron Opt. 2013, 124, 1431–1436. [Google Scholar] [CrossRef]
- Lavoie, B.R.; Leung, P.M.; Sanders, B.C. Slow light with three-level atoms in metamaterial waveguides. Phys. Rev. A 2013, 88, 023860. [Google Scholar] [CrossRef]
- Tsakmakidis, K.L.; Boardman, A.D.; Hess, O. ‘Trapped rainbow’ storage of light in metamaterials. Nature 2007, 450, 397. [Google Scholar] [CrossRef]
- He, J.; He, S. Slow propagation of electromagnetic waves in a dielectric slab waveguide with a left-handed material substrate. Ieee Microw. Wirel. Compon. Lett. 2006, 16, 96–98. [Google Scholar] [CrossRef]
- Lu, W.T.; Huang, Y.J.; Casse, B.D.F.; Banyal, R.K.; Sridhar, S. Storing light in active optical waveguides with single-negative materials. Appl. Phys. Lett. 2010, 96, 211112. [Google Scholar]
- Zheng, G.; Ran, L. Light transmission along a slab waveguide with a core of anisotropic metamaterial. Opt. - Int. J. Light Electron Opt. 2008, 119, 591–595. [Google Scholar] [CrossRef]
- Jiang, T.; Zhao, J.; Feng, Y. Stopping light by an air waveguide with anisotropic metamaterial cladding. Opt. Express 2009, 17, 170. [Google Scholar] [CrossRef]
- Tang, T. Slow propagation of plasmonic modes in a symmetrical waveguide containing anisotropic metamaterial. Opt. - Int. J. Light Electron Opt. 2013, 124, 6119–6121. [Google Scholar] [CrossRef]
- Lu, W.T.; Sridhar, S. Slow light, open-cavity formation, and large longitudinal electric field on a slab waveguide made of indefinite permittivity metamaterials. Phys. Rev. A 2010, 82, 013811. [Google Scholar] [CrossRef]
- Neira, A.D.; Wurtz, G.A.; Zayats, A.V. Superluminal and stopped light due to mode coupling in confined hyperbolic metamaterial waveguides. Sci. Rep. 2015, 5, 17678. [Google Scholar] [CrossRef] [PubMed]
- Babicheva, V.E. Long-range propagation of plasmon and phonon polaritons in hyperbolic-metamaterial waveguides. J. Opt. 2017, 19, 124013. [Google Scholar] [CrossRef]
- Zeng, A.W.; Gao, M.X.; Guo, B. Slow light in a hyperbolic metamaterial waveguide cladded with arbitrary nonlinear dielectric materials. Appl. Phys. B 2018, 124, 146. [Google Scholar] [CrossRef]
- Babicheva, V.E.; Shalaginov, M.Y.; Ishii, S.; Boltasseva, A.; Kildishev, A.V. Finite-width plasmonic waveguides with hyperbolic multilayer cladding. Opt. Express 2015, 23, 9681. [Google Scholar] [CrossRef] [PubMed]
- Lyashko, E.I.; Maimistov, A.I. Linear guided waves in a hyperbolic planar waveguide. Dispersion relations. Quantum Electron. 2015, 45, 1050–1054. [Google Scholar] [CrossRef]
- Ishii, S.; Shalaginov, M.Y.; Babicheva, V.E.; Boltasseva, A.; Kildishev, A.V. Plasmonic waveguides cladded by hyperbolic metamaterials. Opt. Lett. 2014, 39, 4663. [Google Scholar] [CrossRef]
- He, Y.; He, S.; Yang, X. Optical field enhancement in nanoscale slot waveguides of hyperbolic metamaterials. Opt. Lett. 2012, 37, 2907. [Google Scholar] [CrossRef]
- Li, B.; He, Y.; He, S. Investigation of light trapping effect in hyperbolic metamaterial slow-light waveguides. Appl. Phys. Express 2015, 8, 082601. [Google Scholar] [CrossRef]
- Hu, H.; Ji, D.; Zeng, X.; Liu, K.; Gan, Q. Rainbow Trapping in Hyperbolic Metamaterial Waveguide. Sci. Rep. 2013, 3, 1249. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Kang, C.; Cheng, B.; Chen, L.; Yang, X.; Wang, J.; Li, W.; Wang, B. Tunable bulk polaritons of graphene-based hyperbolic metamaterials. Opt. Express 2014, 22, 14022. [Google Scholar] [CrossRef]
- Xiang, Y.; Guo, J.; Dai, X.; Wen, S.; Tang, D. Engineered surface Bloch waves in graphene-based hyperbolic metamaterials. Opt. Express 2014, 22, 3054. [Google Scholar] [CrossRef] [PubMed]
- Othman, M.A.K.; Guclu, C.; Capolino, F. Graphene-Dielectric Composite Metamaterials: Evolution from Elliptic to Hyperbolic Wavevector Dispersion and The Transverse Epsilon-Near-Zero Condition. J. Nanophotonics 2013, 7, 073089. [Google Scholar] [CrossRef]
- Hajian, H.; Ghobadi, A.; Dereshgi, S.A.; Butun, B.; Ozbay, E. Hybrid plasmon–phonon polariton bands in graphene–hexagonal boron nitride metamaterials [Invited]. J. Opt. Soc. Am. B 2017, 34, D29. [Google Scholar] [CrossRef]
- Bhuyan, M.S.A.; Uddin, M.N.; Bipasha, F.A.; Islam, M.M.; Hossain, S.S. A Review of Functionalized Graphene properties and its application. Int. J. Innov. Sci. Res. 2015, 17, 303–315. [Google Scholar]
- Guo, B.; Fang, L.; Zhang, B.; Gong, J.R. Graphene Doping: A Review. Insciences J. 2011, 1, 80–89. [Google Scholar] [CrossRef]
- Zhu, B.; Ren, G.; Zheng, S.; Lin, Z.; Jian, S. Nanoscale dielectric-graphene-dielectric tunable infrared waveguide with ultrahigh refractive indices. Opt. Express 2013, 21, 17089. [Google Scholar] [CrossRef] [PubMed]
- Sayem, A.A.; Mahdy, M.R.C.; Hasan, D.N.; Matin, M.A. Tunable slow light with graphene based hyperbolic metamaterial. In Proceedings of the 8th International Conference on Electrical and Computer Engineering, Piscataway, NJ, USA, 20–22 December 2014; IEEE: Dhaka, Bangladesh, 2014; pp. 230–233. [Google Scholar]
- Zhu, B.; Ren, G.; Gao, Y.; Yang, Y.; Wu, B.; Lian, Y.; Jian, S. Local Field Enhancement in Infrared Graphene- Dielectric Hyperbolic Slot Waveguides. IEEE Photonics Technol. Lett. 2015, 27, 276–279. [Google Scholar] [CrossRef]
- Tyszka-Zawadzka, A.; Janaszek, B.; Szczepański, P. Tunable slow light in graphene-based hyperbolic metamaterial waveguide operating in SCLU telecom bands. Opt. Express 2017, 25, 7263. [Google Scholar] [CrossRef] [PubMed]
- Choy, T.C. Effective Medium Theory: Principles and Applications, International Series of Monographs on Physics; 2nd ed.; Oxford University Press: Oxford, UK, 2016; ISBN 978-0-19-870509-3. [Google Scholar]
- Janaszek, B.; Tyszka-Zawadzka, A.; Szczepański, P. Tunable graphene-based hyperbolic metamaterial operating in SCLU telecom bands. Opt. Express 2016, 24, 24129. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s Functions for an Anisotropic, Non-Local Model of Biased Graphene. IEEE Trans. Antennas Propag. 2008, 56, 747–757. [Google Scholar] [CrossRef]
- Maharana, P.K.; Jha, R.; Palei, S. Sensitivity enhancement by air mediated graphene multilayer based surface plasmon resonance biosensor for near infrared. Sens. Actuators B Chem. 2014, 190, 494–501. [Google Scholar] [CrossRef]
- Gómez-Díaz, J.S.; Perruisseau-Carrier, J. Graphene-based plasmonic switches at near infrared frequencies. Opt. Express 2013, 21, 15490. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; Garcia de Abajo, F.J.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef]
- Zhao, X.; Zhu, L.; Yuan, C.; Yao, J. Tunable plasmon-induced transparency in a grating-coupled double-layer graphene hybrid system at far-infrared frequencies. Opt. Lett. 2016, 41, 5470. [Google Scholar] [CrossRef] [PubMed]
- Higuchi, M.; Takahara, J. Plasmonic interpretation of bulk propagating waves in hyperbolic metamaterial optical waveguides. Opt. Express 2018, 26, 1918. [Google Scholar] [CrossRef] [PubMed]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; ISBN 978-0-387-33150-8. [Google Scholar]
- Kaminow, I.P.; Mammel, W.L.; Weber, H.P. Metal-Clad Optical Waveguides: Analytical and Experimental Study. Appl. Opt. 1974, 13, 396. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.J.; Lu, W.T.; Sridhar, S. Nanowire waveguide made from extremely anisotropic metamaterials. Phys. Rev. A 2008, 77, 063836. [Google Scholar] [CrossRef]
- Satomura, Y.; Matsuhara, M.; Kumagai, N. Analysis of Electromagnetic-Wave Modes in Anisotropic Slab Waveguide. IEEE Trans. Microw. Theory Tech. 1974, 22, 86–92. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kieliszczyk, M.; Janaszek, B.; Tyszka-Zawadzka, A.; Szczepański, P. Guided Optical Modes in Metal-Cladded Tunable Hyperbolic Metamaterial Slab Waveguides. Crystals 2020, 10, 176. https://doi.org/10.3390/cryst10030176
Kieliszczyk M, Janaszek B, Tyszka-Zawadzka A, Szczepański P. Guided Optical Modes in Metal-Cladded Tunable Hyperbolic Metamaterial Slab Waveguides. Crystals. 2020; 10(3):176. https://doi.org/10.3390/cryst10030176
Chicago/Turabian StyleKieliszczyk, Marcin, Bartosz Janaszek, Anna Tyszka-Zawadzka, and Paweł Szczepański. 2020. "Guided Optical Modes in Metal-Cladded Tunable Hyperbolic Metamaterial Slab Waveguides" Crystals 10, no. 3: 176. https://doi.org/10.3390/cryst10030176
APA StyleKieliszczyk, M., Janaszek, B., Tyszka-Zawadzka, A., & Szczepański, P. (2020). Guided Optical Modes in Metal-Cladded Tunable Hyperbolic Metamaterial Slab Waveguides. Crystals, 10(3), 176. https://doi.org/10.3390/cryst10030176




