Study on Transformation Mechanism and Kinetics of α’ Martensite in TC4 Alloy Isothermal Aging Process
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Analysis
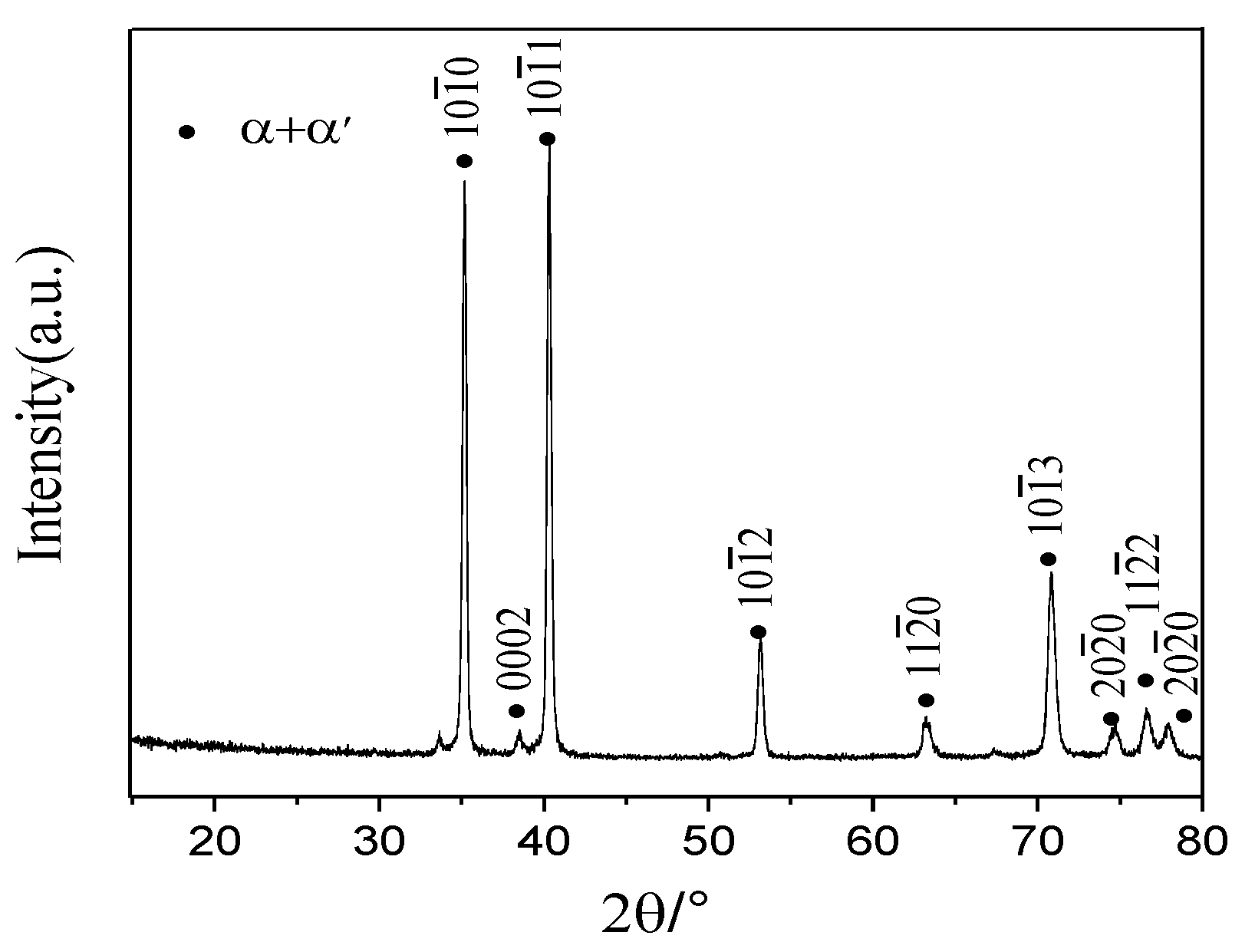
3.1. Solid Solution Preparation
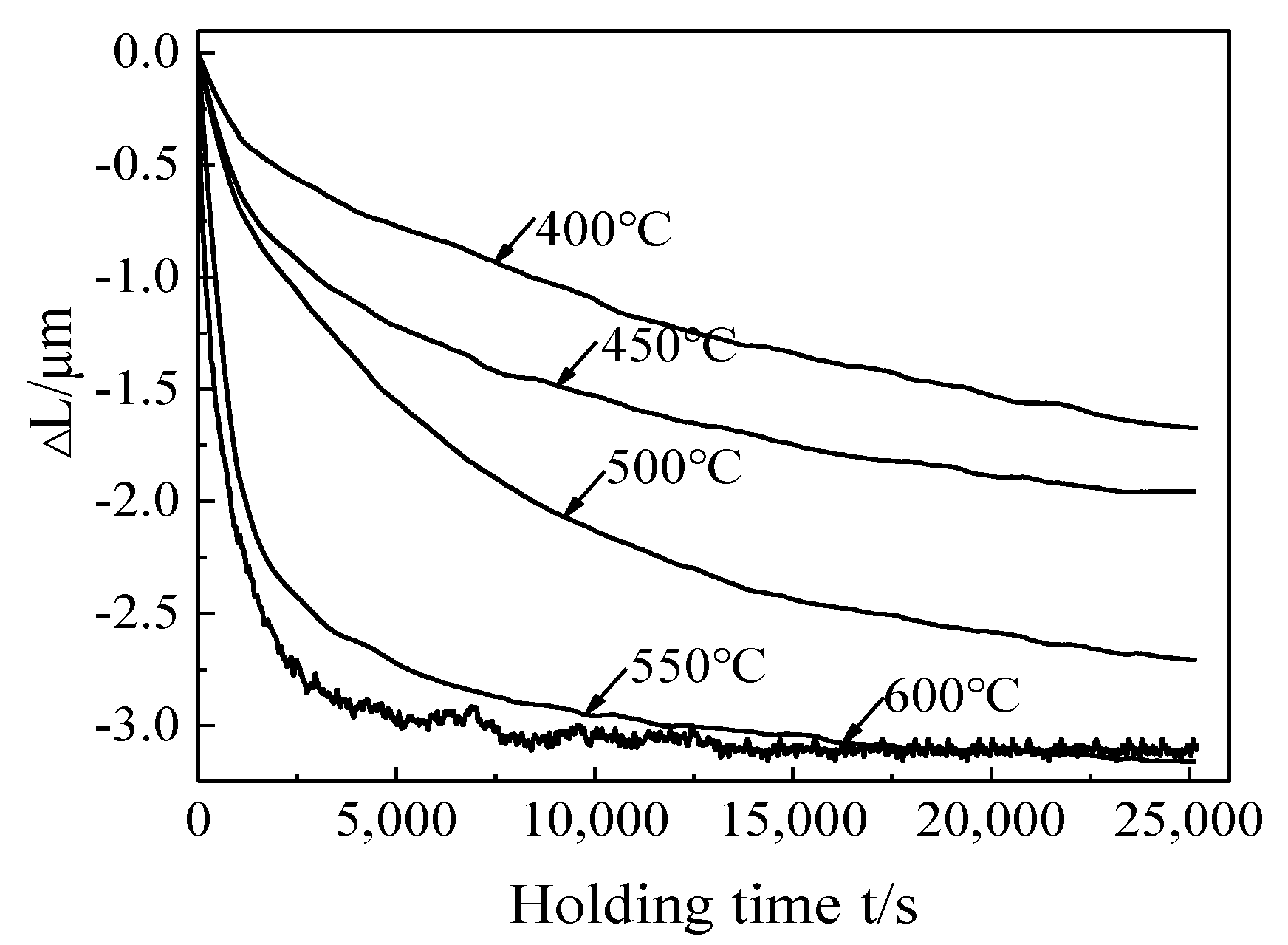
3.2. Phase Transformation Kinetic during Isothermal Aging
3.3. Microstructure Evolution During Isothermal Aging
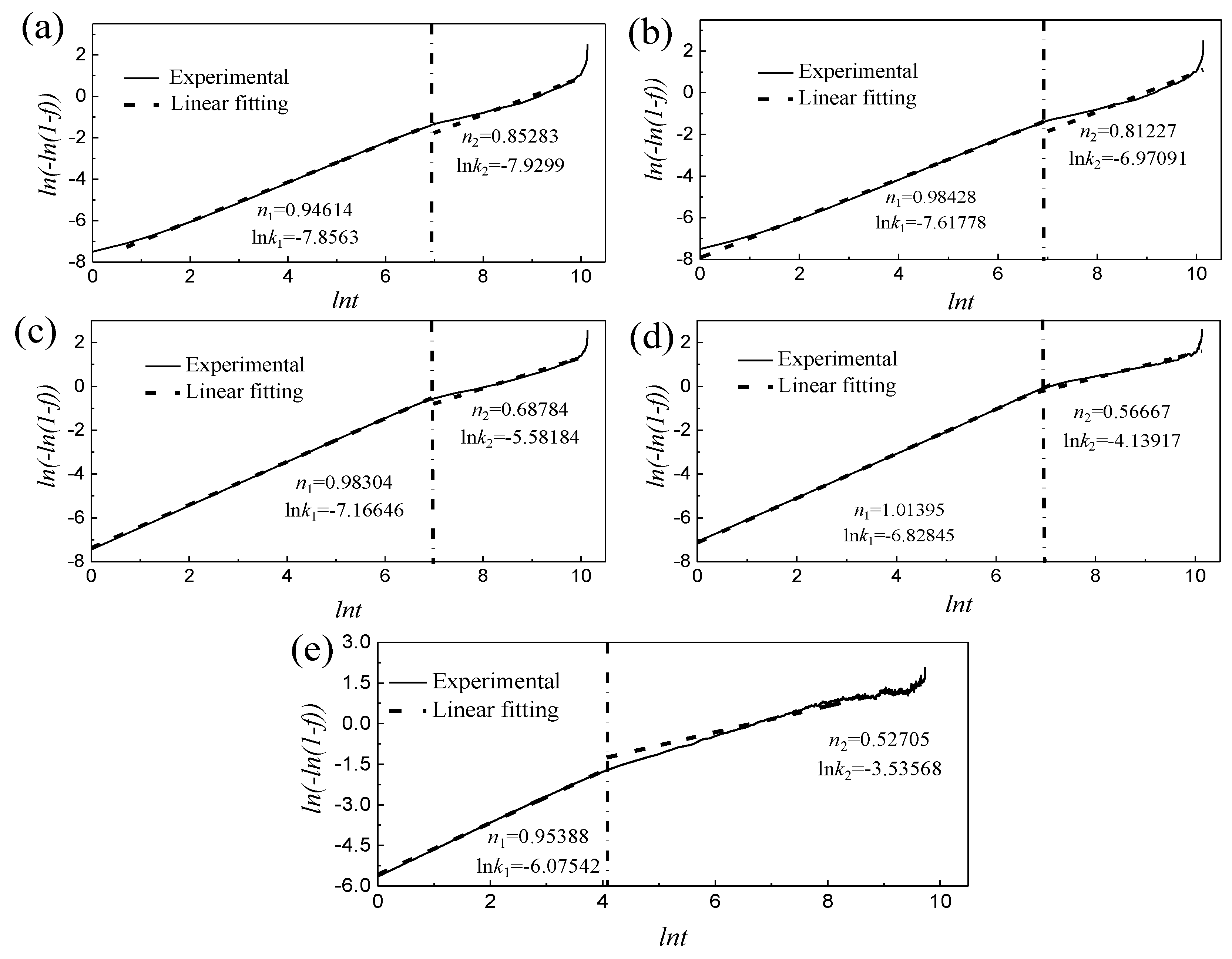
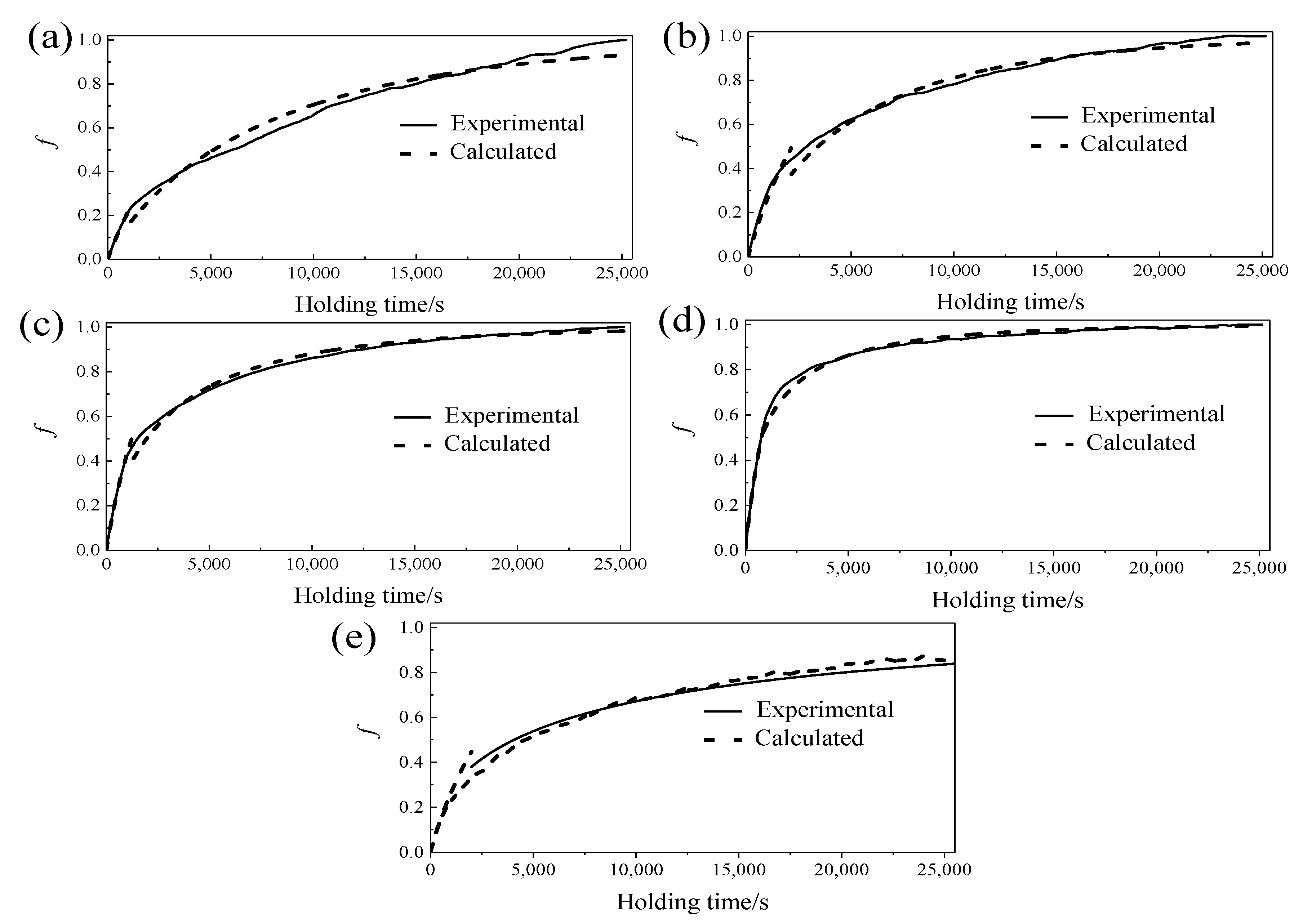
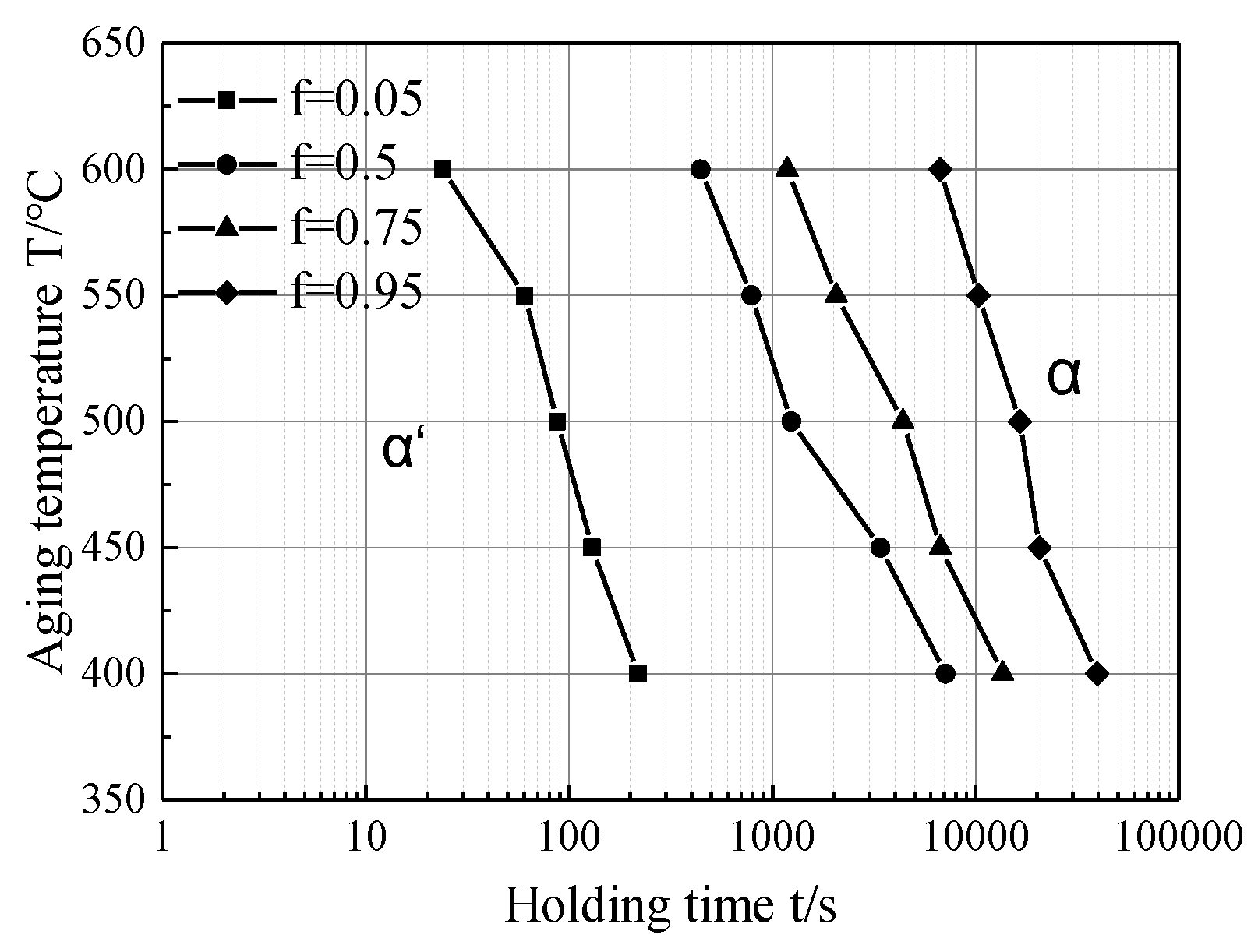
3.4. The Isothermal Aging Transformation Curve of Martensite
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oryshchenko, A.S.; Gorynin, I.V.; Leonov, V.P.; Kudryavtsev, A.S.; Mikhailov, V.I.; Chudakov, E.V. Marine titanium alloys: Present and future. Inorg. Mater. Appl. Res. 2015, 6, 571–579. [Google Scholar] [CrossRef]
- Zhang, L.C.; Chen, L.Y. A Review on Biomedical Titanium Alloys: Recent Progress and Prospect. Adv. Eng. Mater. 2019, 21, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Tarzimoghadam, Z.; Sandlöbes, S.; Pradeep, K.G.; Raabe, D. Microstructure Design and Mechanical Properties in a Near-α Ti-4Mo Alloy. Acta. Mater. 2015, 97, 291–304. [Google Scholar] [CrossRef]
- Li, C.L.; Zou, L.N.; Fu, Y.Y.; Ye, W.J.; Hui, S.X. Effect of Heat treatments on Microstructure and Property of a High Strength/Toughness Ti8V1.5Mo2Fe3Al Alloy. Mater. Sci. Eng. A 2014, 616, 207–213. [Google Scholar] [CrossRef]
- Li, C.; Chen, J.; Li, W.; He, J.J.; Qiu, W.; Ren, Y.J.; Chen, J.L.; Chen, J.H. Study on The Relationship Between Microstructure and Mechanical Property in a Metastable β Titanium Alloy. J. Alloys Compd. 2015, 627, 222–230. [Google Scholar] [CrossRef]
- Yu, W.X.; Li, M.Q.; Luo, J. Effect of deformation parameters on the precipitation mechanism of secondary phase under high temperature isothermal compression of Ti6Al4V alloy. Mater. Sci. Eng. A 2010, 527, 4210–4217. [Google Scholar] [CrossRef]
- Fu, J.; Ding, H.; Huang, Y.; Zhang, W.J.; Langdon, T.G. Influence of phase volume fraction on the grain refining of a Ti-6Al-4V alloy by high-pressure torsion. J. Mater. Res. Technol. 2014, 4, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Motyka, M.; Kubiak, K.; Sieniawski, J. Phase transformation and characterization of α+β titanium alloys. In Comprehensive Materials Processing, Materials Modeling and Characterization; Hashmi, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 2, pp. 7–36. [Google Scholar]
- Motyka, M.; Baran-Sadleja, A.; Sieniawski, J.; Wierzbinska, M.; Gancarczyk, K. Decomposition of deformed α’(α”) martensitic phase in Ti-6Al-4V alloy. Mater. Sci. Technol. 2019, 35, 260–272. [Google Scholar] [CrossRef]
- Ahmed, T.; Rack, H.J. Phase transformations during cooling in α+β titanium alloys. Mater. Sci. Eng. A 1998, 243, 206–211. [Google Scholar] [CrossRef]
- Gil Mur, F.X.; Rodríguez, D.; Planell, J.A. Influence of tempering temperature and time on the ed-Ti-6A1-4V martensite. J. Alloys Compd. 1996, 234, 287–289. [Google Scholar] [CrossRef]
- Gupta, R.K.; Anil Kumar, V.; Chhangani, S. Study on Variants of Solution Treatment and Aging Cycle of Titanium Alloy Ti6Al4V. J. Mater. Eng. Perform. 2016, 25, 1492–1501. [Google Scholar] [CrossRef]
- Shah, A.K.; Kulkarni, G.J.; Gopinathan, V. Determination of activation energy for α+β→β transformation in Ti-6AI-4V alloy by dilatometry. Scripta Metall. Mater. 1995, 32, 1353–1356. [Google Scholar] [CrossRef]
- Ming, L.C.; Manghnani, M.H.; Katahara, K.W. Phase Transformations in the Ti-V System under High Pressure up to 25 GPa. Acta Metall. 1981, 29, 479–485. [Google Scholar] [CrossRef]
- Katzarov, I.; Malinov, S.; Sha, W. Finite element modeling of the morphology of β to α phase transformation in Ti-6Al-4V alloy. Metall. Mater. Trans. A 2002, 33, 1027–1040. [Google Scholar] [CrossRef]
- Elmer, J.W.; Palmer, T.A.; Babu, S.S.; Specht, E.D. In Situ Observations of Lattice Expansion and Transformation Rates of α and β Phases in Ti6Al4V. Mater. Sci. Eng. A 2005, 391, 104–113. [Google Scholar] [CrossRef]
- Kherrouba, N.; Bouabdallah, M.; Badji, R.; Carron, D.; Amir, M. Beta to alpha transformation kinetics and microstructure of Ti6Al4V alloy during continuous cooling. Mater. Chem. Phys. 2016, 181, 462–469. [Google Scholar] [CrossRef]
- Mi, G.; Wei, Y.; Zhan, X.; Gu, C.; Yu, F. A coupled thermal and metallurgical model for welding simulation of Ti6Al4V alloy. J. Mater. Process. Technol. 2014, 214, 2434–2443. [Google Scholar] [CrossRef]
- Malinov, S.; Markovsky, P.; Sha, W.; Guo, Z. Resistivity study and computer modelling of the isothermal transformation kinetics of Ti6Al4V and Ti6Al2Sn4Zr2Mo0.08Si alloys. J. Alloy. Compd. 2001, 314, 181–192. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.B.; Lai, M.J.; Tang, B.; Kou, H.C.; Chang, H.; Zhu, Z.; Li, J.S.; Zhou, L. Non-isothermal phase transformation kinetics of phase in TB-13 titanium alloys. Mater. Sci. Eng. A 2010, 527, 5100–5104. [Google Scholar] [CrossRef]
- Elmer, J.W.; Palmer, T.A.; Babu, S.S.; Specht, E.D. Low Temperature Relaxation of Residual Stress in Ti-6Al-4V. Scr. Mater. 2005, 52, 1051–1056. [Google Scholar] [CrossRef]
- Charpentier, M.; Hazotte, A.; Daloz, D. Lamellar Transformation in near-γ TiAl Alloys-Quantitative Analysis of Kinetics and Microstructure. Mater. Sci. Eng. A 2008, 491, 321–330. [Google Scholar] [CrossRef]
- Malinov, S.; Sha, W. Modeling Thermodynamics, Kinetics, and Phase Transformation Morphology while Heat Treating Titanium alloys. JOM 2005, 57, 42–45. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Ma, N.; Chen, Q.; Zhang, F.; Chen, S.L.; Chang, Y.T. Predicting Phase Equilibrium, Phase Transformation, and Microstructure Evolution in Titanium Alloys. JOM 2005, 57, 32–39. [Google Scholar] [CrossRef]
- Sundar, G.; Hoyt, J.J. Effect of dislocations on the Langer-Schwartz model of nucleation and growth. J. Phys. Condens. Matter 1992, 4, 4359–4371. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.M. Aging Response of Laser Melting Deposited Ti6Al2Zr1Mo1V Alloy. Mater. Sci. Eng. A Struct. Mater. 2013, 560, 193–199. [Google Scholar] [CrossRef]
- Tang, B.; Kou, H.C.; Wang, Y.H.; Zhu, Z.S.; Zhang, F.S.; Li, J.S. Kinetics of orthorhombic martensite decomposition in TC21 alloy under isothermal conditions. J. Mater. Sci. 2012, 47, 521–529. [Google Scholar] [CrossRef]
- Blazquez, J.S.; Conde, C.F.; Conde, A. Non-isothermal Approach to Isokinetic Crystallization Processes: Application to the Nanocrystallization of HITPERM Alloys. Acta Mater. 2005, 53, 2305–2311. [Google Scholar] [CrossRef]
- Yu, H.; Li, W.; Zou, H.B.; Li, S.S.; Zhai, T.G.; Liu, L.G. Study on Non-Isothermal Transformation of Ti-6Al-4V in Solution Heating Stage. Metals 2019, 9, 968. [Google Scholar] [CrossRef] [Green Version]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Li, W.; Li, S.; Zou, H.; Zhai, T.; Liu, L. Study on Transformation Mechanism and Kinetics of α’ Martensite in TC4 Alloy Isothermal Aging Process. Crystals 2020, 10, 229. https://doi.org/10.3390/cryst10030229
Yu H, Li W, Li S, Zou H, Zhai T, Liu L. Study on Transformation Mechanism and Kinetics of α’ Martensite in TC4 Alloy Isothermal Aging Process. Crystals. 2020; 10(3):229. https://doi.org/10.3390/cryst10030229
Chicago/Turabian StyleYu, Hui, Wei Li, Songsong Li, Haibei Zou, Tongguang Zhai, and Ligang Liu. 2020. "Study on Transformation Mechanism and Kinetics of α’ Martensite in TC4 Alloy Isothermal Aging Process" Crystals 10, no. 3: 229. https://doi.org/10.3390/cryst10030229
APA StyleYu, H., Li, W., Li, S., Zou, H., Zhai, T., & Liu, L. (2020). Study on Transformation Mechanism and Kinetics of α’ Martensite in TC4 Alloy Isothermal Aging Process. Crystals, 10(3), 229. https://doi.org/10.3390/cryst10030229



