Microstructure Heredity of Inconel 718 Nickel-Based Superalloy during Preheating and Following Deformation
Abstract
1. Introduction
2. Experimental Procedures and Finite Element Model
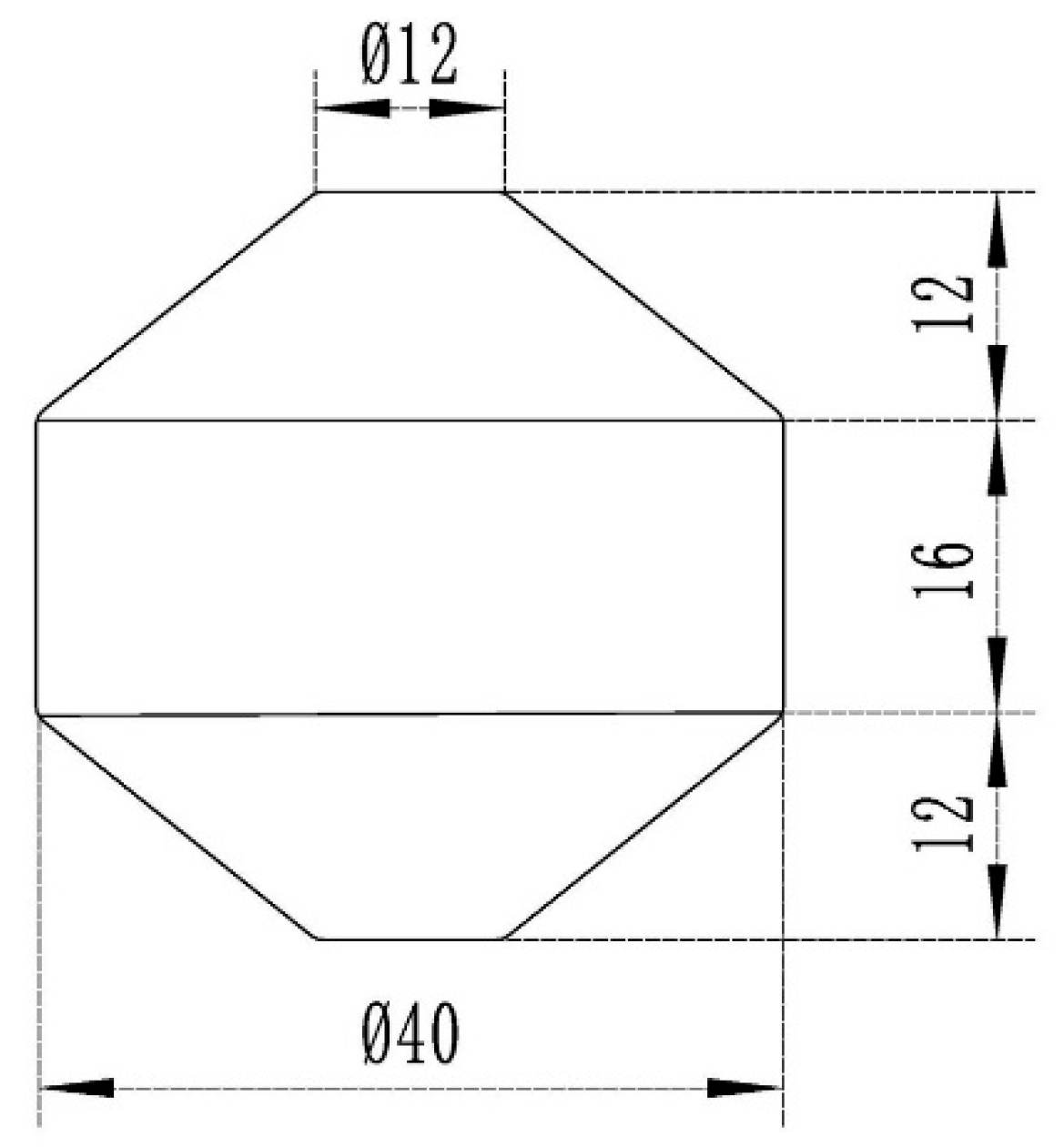
2.1. Experimental Procedures
2.2. Effective Strain Evaluation by FEM
3. Results and Discussion
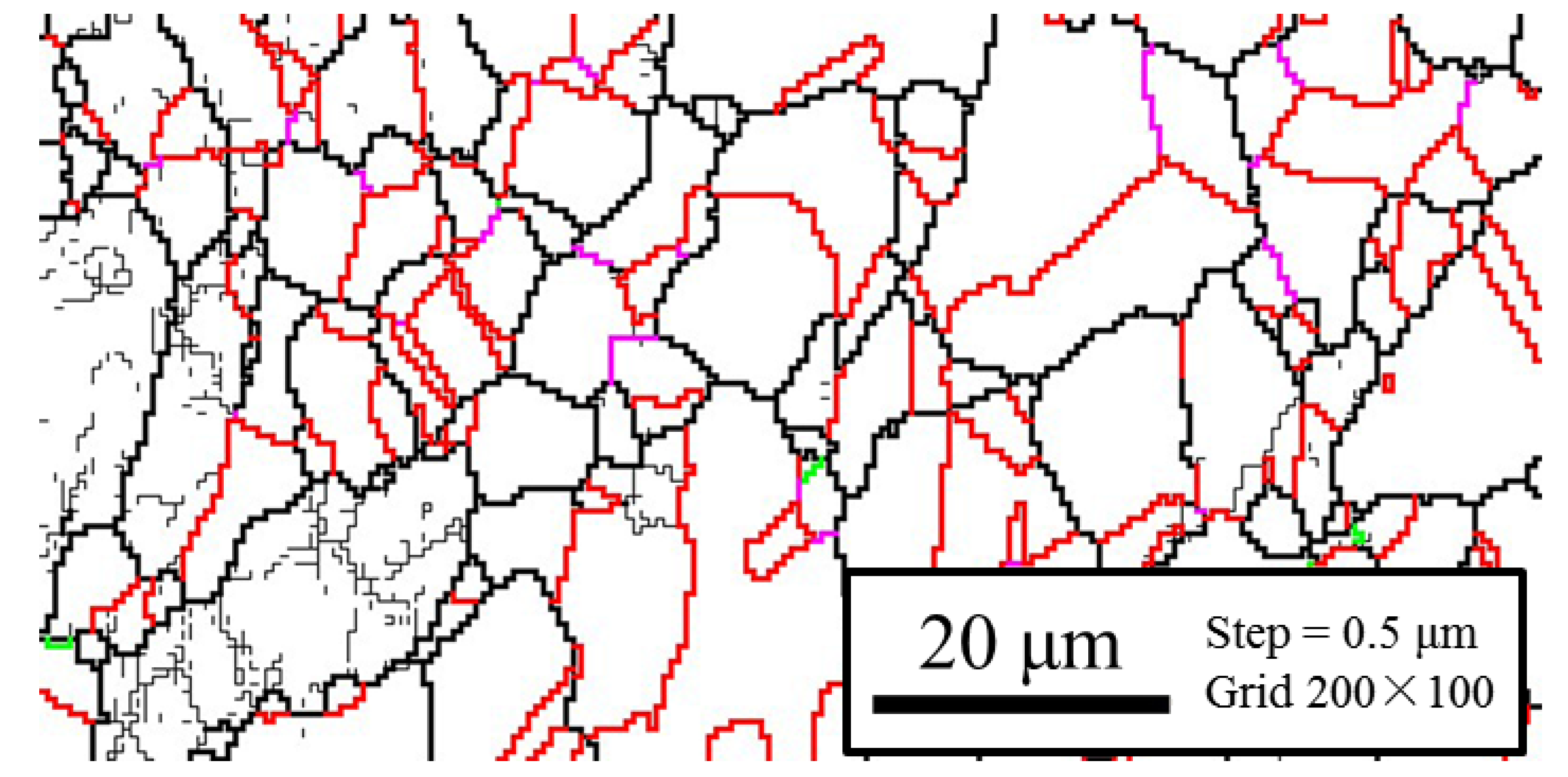
3.1. Initial Microstructure
3.2. Strain Distribution and Flow Behavior
3.3. Effect of Preheating Process on the Microstructure Evolution
3.4. Microstructure Evolution during Compression
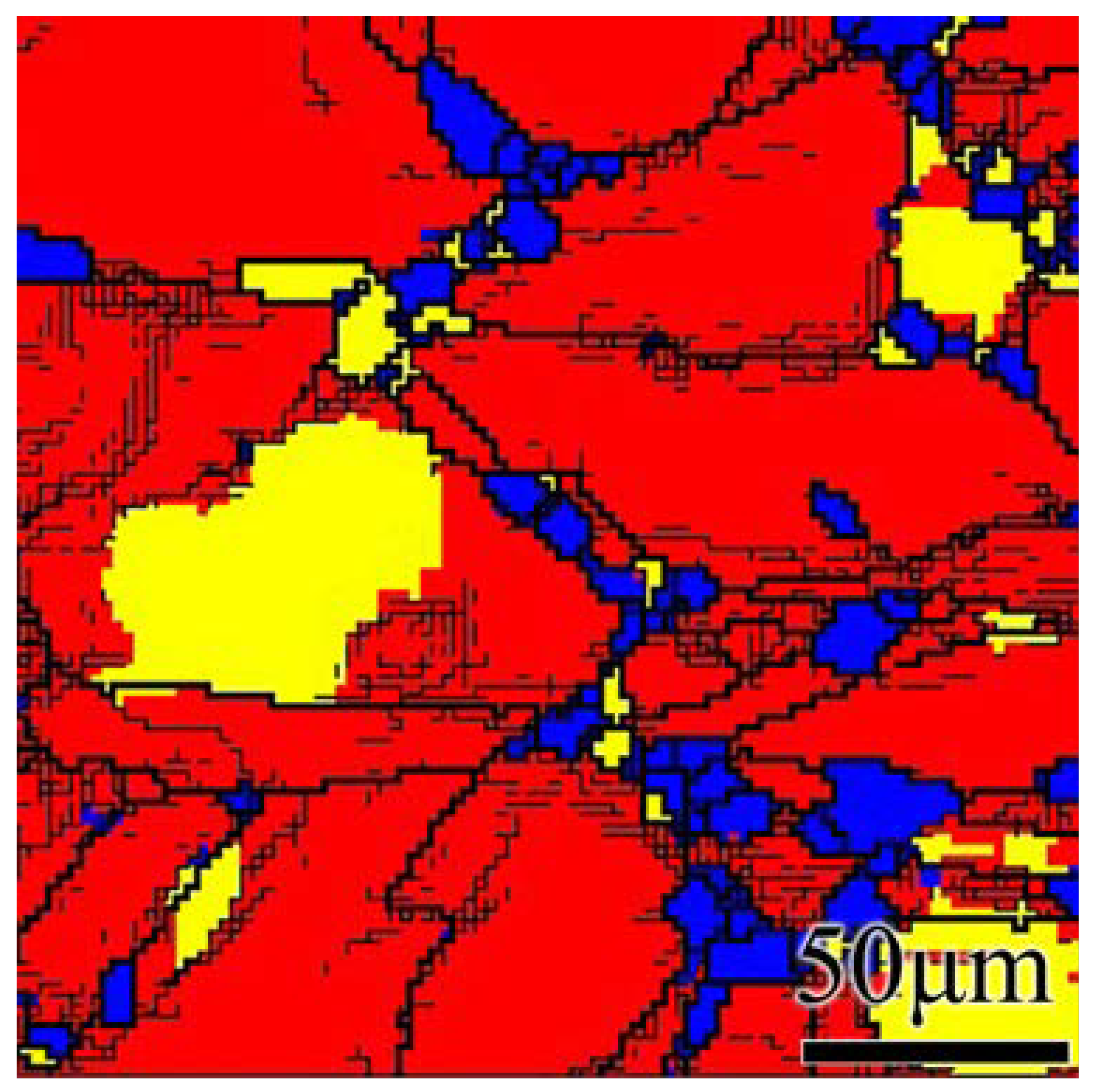
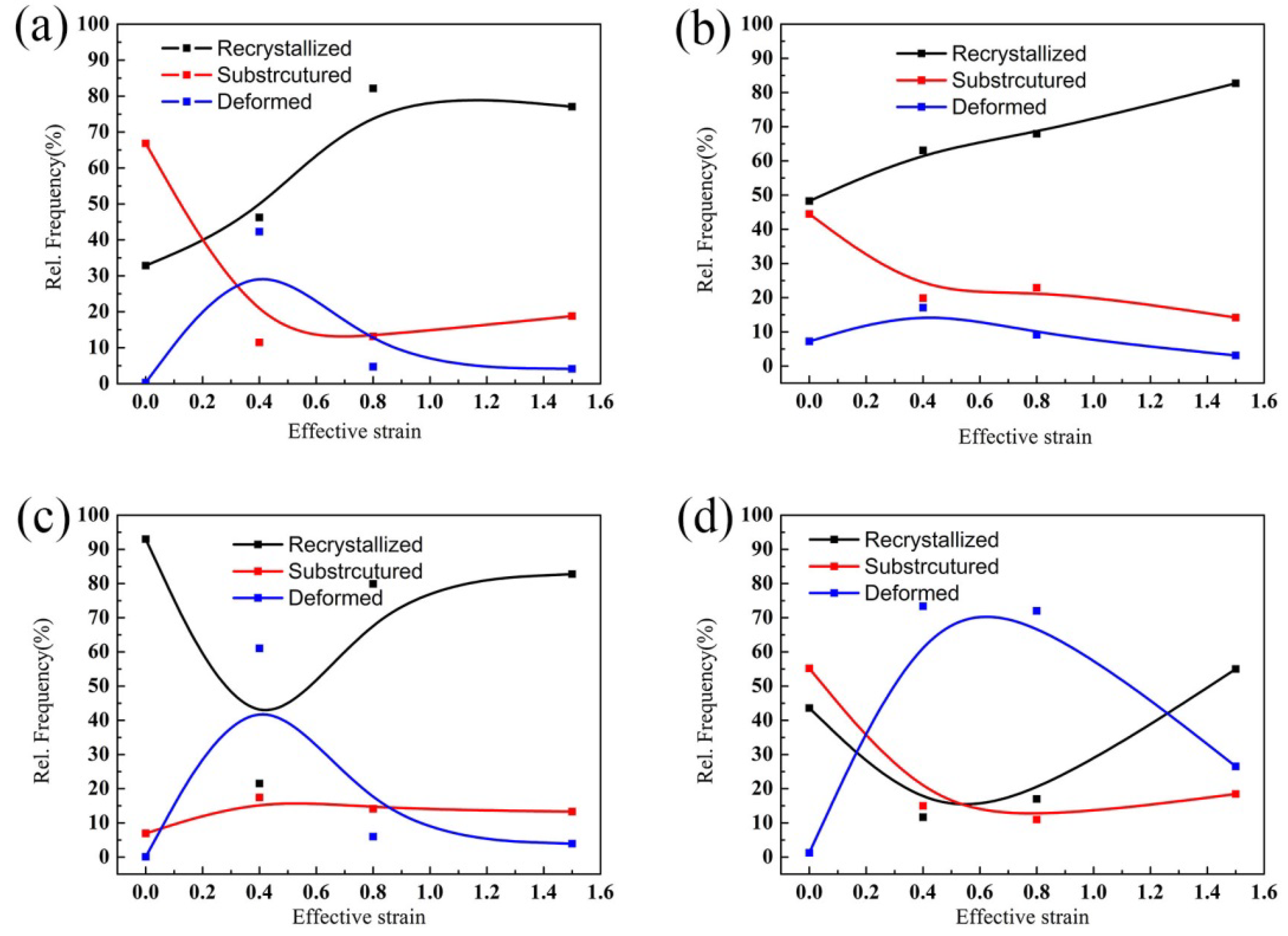
3.4.1. Volume Fraction of Recrystallized, Substructure and Deformed Grains
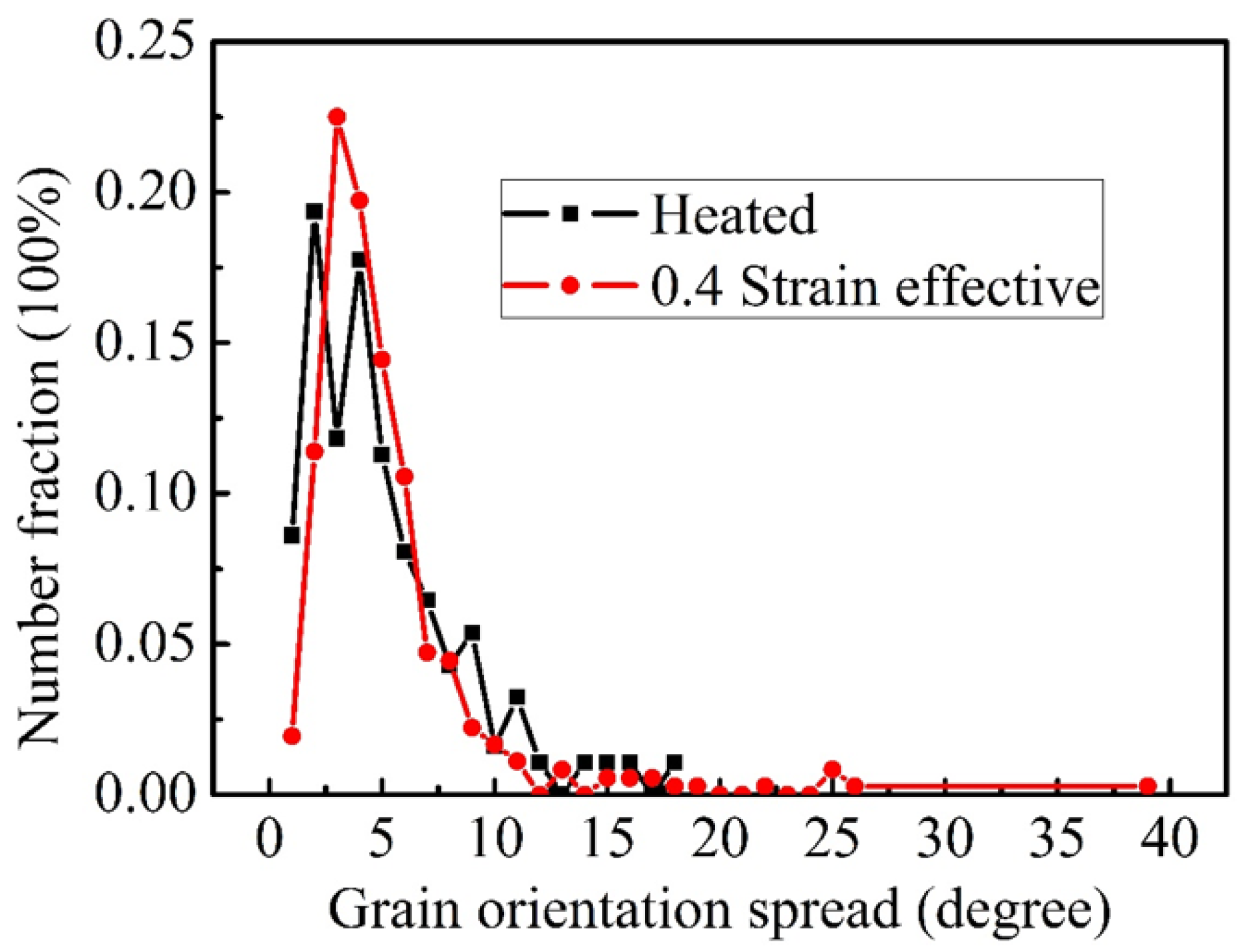
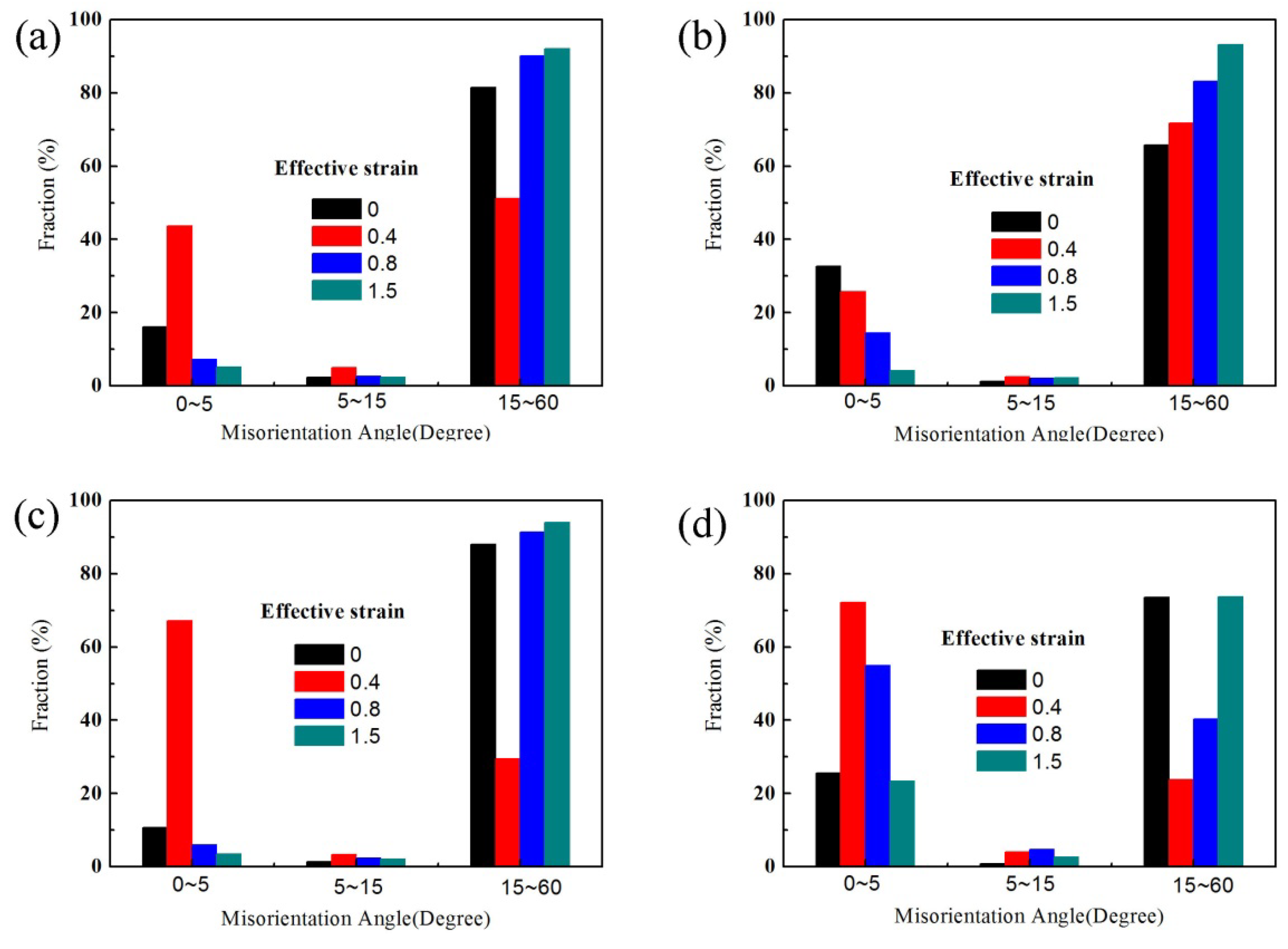
3.4.2. Misorientation Angle Distribution
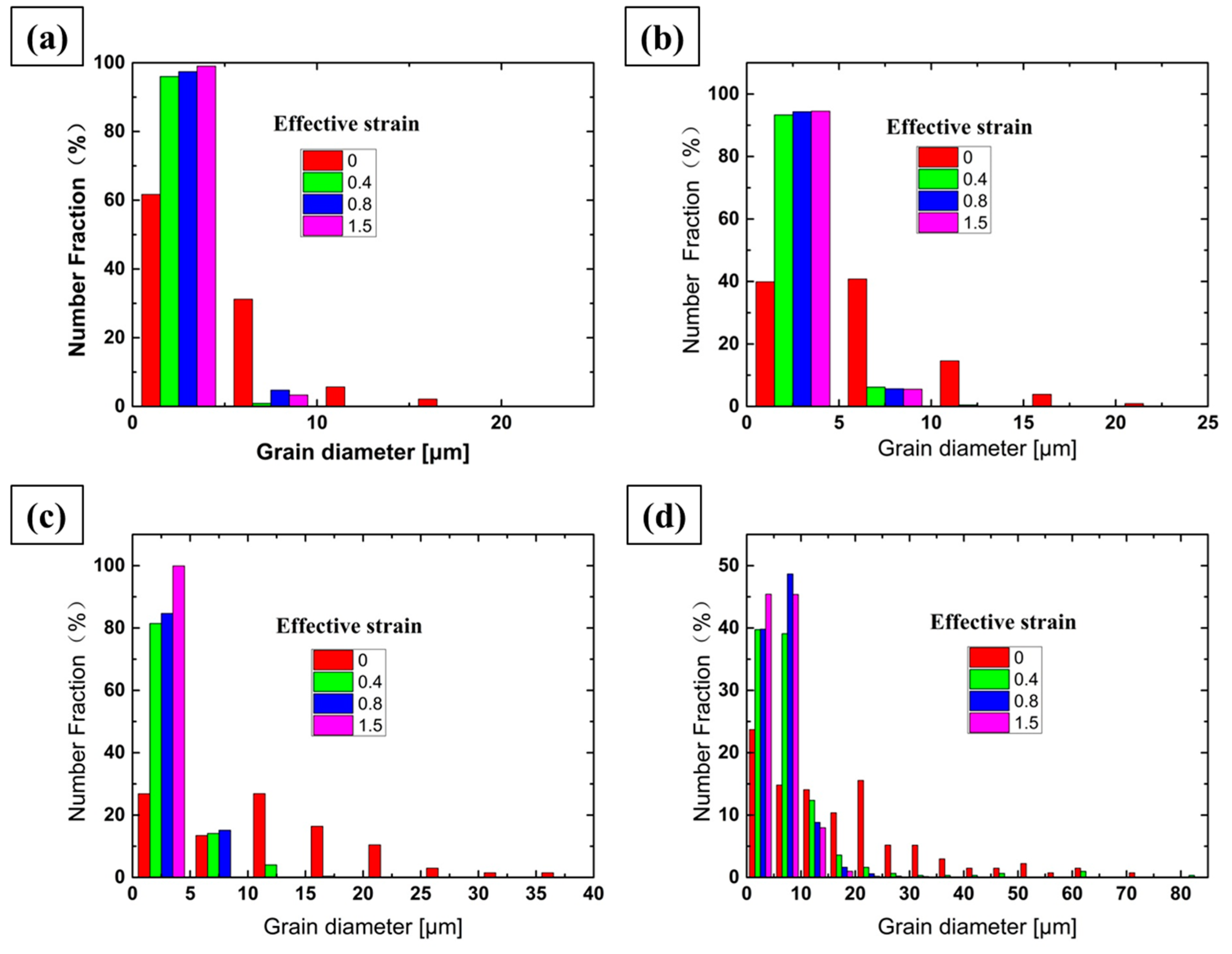
3.4.3. Grain size Distribution
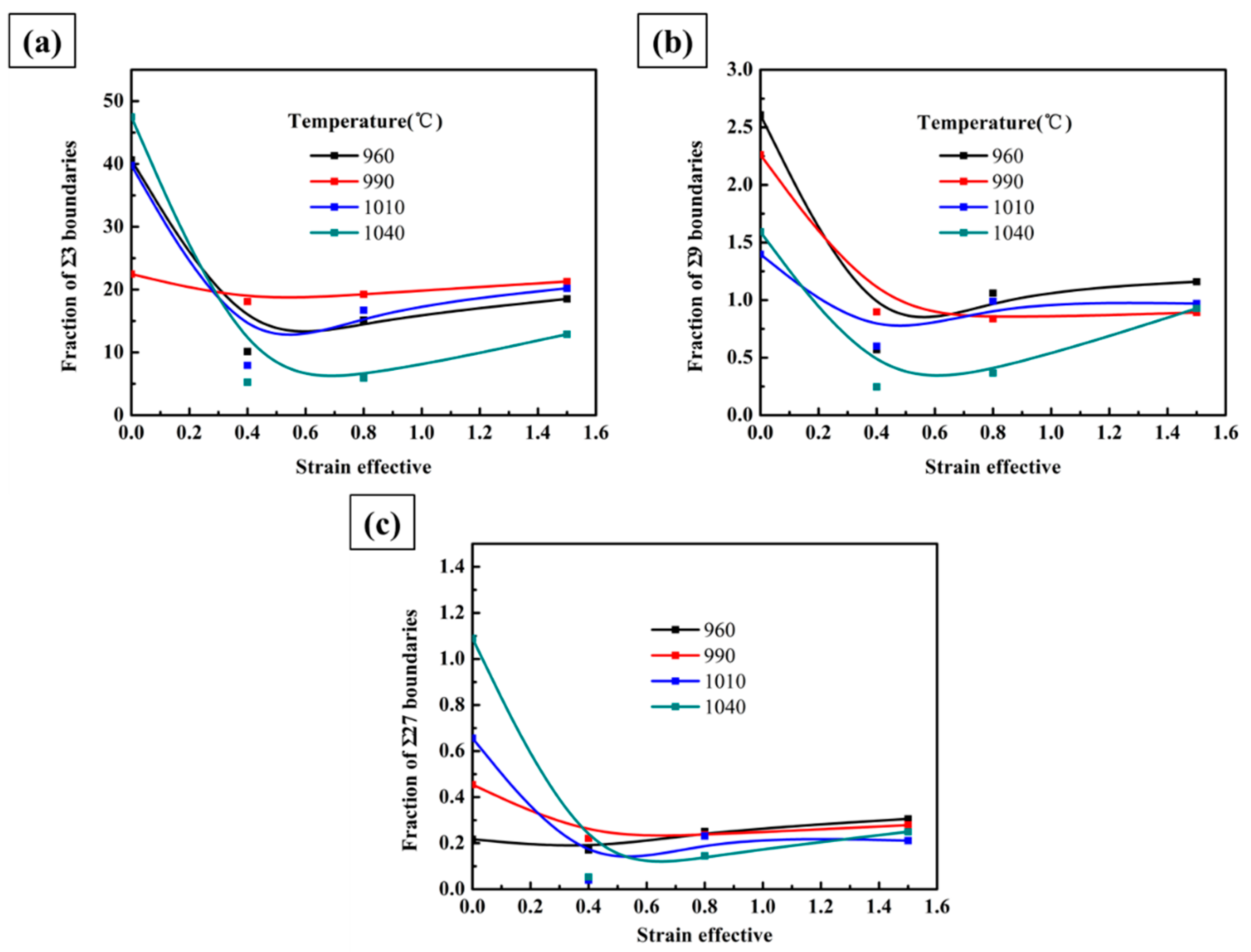
3.4.4. Twinning Grain Boundary
3.4.5. Effect of Temperature on the Deformation Mechanism
4. Conclusions
- (1)
- A continuous, increased effective strain can be obtained by double cone compressions, which is more convenient to investigate the microstructure heredity during hot deformation from zero to high strains.
- (2)
- Intense microstructure heredity can be found at 960~990 °C, which is much lower than the temperature needed for the dissolution of δ phases.
- (3)
- At the temperature lower than 990 °C, the volume fraction of recrystallized grain increases with effective strain increasing. At higher temperatures, the volume fraction of recrystallized grain decreases and then increases with the increase of effective strain. The unimodal grain diameter distribution can be obtained at lower strains at the low temperature. The fraction of twin boundaries decreases first and then increases with effective strain increasing.
- (4)
- The nucleation mechanism of DDRX and CDRX occurred simultaneously in the alloy during hot deformation, which was closely related to the grain size after the heating process. It was noted that CDRX was strengthened with the increase of grain size. The twin introduced deformation will be the primary deformation mode for alloys with a larger initial grain size.
Author Contributions
Funding
Conflicts of Interest
References
- Luo, Z.J.; Liu, D. Evaluation of IN718 disk-forging processes using the quality-loss function. J. Mater. Process. Technol. 1996, 59, 381–385. [Google Scholar] [CrossRef]
- Wei, X.; Zheng, W.; Song, Z.; Lei, T.; Yong, Q.; Xie, Q. Static recrystallization behavior of Inconel 718 alloy during thermal deformation. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2014, 29, 379–383. [Google Scholar] [CrossRef]
- Araujo, L.S.; Santos, D.S.D.; Godet, S.; Dille, J.; Pinto, A.L.; de Almeida, L.H. Analysis of Grain Boundary Character in a Fine-Grained Nickel-Based Superalloy 718. J. Mater. Eng. Perform. 2014, 23, 4130–4135. [Google Scholar] [CrossRef]
- Li, R.B.; Yao, M.; Liu, W.C.; He, X.C. Isolation and determination for δ, γ′ and γ″ phases in Inconel 718 alloy. Scr. Mater. 2002, 46, 635–638. [Google Scholar] [CrossRef]
- Sundararaman, M.; Mukhopadhyay, P.; Banerjee, S. Some aspects of the precipitation of metastable intermetallic phases in INCONEL 718. Metall. Trans. A 1992, 23, 2015–2028. [Google Scholar] [CrossRef]
- Devaux, A.; Eacute, L.N.; Molins, R.; Pineau, A.; Organista, A.; Guédou, J.Y.; Uginet, J.F.; Eacute, P.H. Gamma double prime precipitation kinetic in Alloy 718. Mater. Sci. Eng. A 2008, 486, 117–122. [Google Scholar] [CrossRef]
- Thomas, A.; El-Wahabi, M.; Cabrera, J.M.; Prado, J.M. High temperature deformation of Inconel 718. J. Mater. Process. Technol. 2006, 177, 469–472. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Prasad, Y.V.R.K.; Frazier, W.G.; Srinivasan, R. Microstructural modeling of metadynamic recrystallization in hot working of IN 718 superalloy. Mater. Sci. Eng. A 2000, 293, 198–207. [Google Scholar] [CrossRef]
- Nayan, N.; Gurao, N.P.; Murty, S.V.S.N.; Jha, A.K.; Pant, B.; George, K.M. Microstructure and micro-texture evolution during large strain deformation of Inconel alloy IN718. Mater. Charact. 2015, 110, 236–241. [Google Scholar] [CrossRef]
- Deng, D.; Wang, C.; Liu, Q.; Niu, T. Effect of standard heat treatment on microstructure and properties of borided Inconel 718. Trans. Nonferrous Metals Soc. China 2015, 25, 437–443. [Google Scholar] [CrossRef]
- Etas, P.J.P.K.; Osorio, L.A.R.; Mata, M.P.G.; Garza, M.D.L.; López, V.P. Influence of the Delta Phase in the Microstructure of the Inconel 718 subjected to “Delta-processing” Heat Treatment and Hot Deformed. Procedia Mater. Sci. 2015, 8, 1160–1165. [Google Scholar]
- Zouari, M.; Bozzolo, N.; Loge, R.E. Mean field modelling of dynamic and post-dynamic recrystallization during hot deformation of Inconel 718 in the absence of δ phase particles. Mater. Sci. Eng. A 2016, 655, 408–424. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wu, X.; Chen, X.; Chen, J.; Wen, D.; Zhang, J.; Li, L. EBSD study of a hot deformed nickel-based superalloy. J. Alloys Comp. 2015, 640, 101–113. [Google Scholar] [CrossRef]
- Makower, H.; Skurska, Z. Mater. In Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 1995; pp. 219–224. [Google Scholar]
- Wen, D.; Lin, Y.C.; Li, H.; Chen, X.; Deng, J.; Li, L. Hot deformation behavior and processing map of a typical Ni-based superalloy. Mater. Sci. Eng. A 2014, 591, 183–192. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, K.; Zhou, H.; Lu, Z.; Zhao, C.; Yang, X. Effect of strain rate on microstructure evolution of a nickel-based superalloy during hot deformation. Mater. Des. 2015, 80, 51–62. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, K.; Lu, Z.; Zhao, C.; Yang, X. Hot deformation behavior and processing map of a γ′-hardened nickel-based superalloy. Mater. Sci. Eng. A 2014, 604, 1–8. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, K.; Jiang, S.; Zhou, H.; Zhao, C.; Yang, X. Dynamic recrystallization behavior of a γ′-hardened nickel-based superalloy during hot deformation. J. Alloys Comp. 2015, 623, 374–385. [Google Scholar] [CrossRef]
- Yu, Q.Y.; Yao, Z.H.; Dong, J.X. Deformation and recrystallization behavior of a coarse-grain, nickel-base superalloy Udimet720Li ingot material. Mater. Charact. 2015, 107, 398–410. [Google Scholar] [CrossRef]
- Wang, J.; Dong, J.; Zhang, M.; Xie, X. Hot working characteristics of nickel-base superalloy 740H during compression. Mater. Sci. Eng. A 2013, 566, 61–70. [Google Scholar] [CrossRef]
- Ning, Y.; Yao, Z.; Li, H.; Guo, H.; Tao, Y.; Zhang, Y. High temperature deformation behavior of hot isostatically pressed P/M FGH4096 superalloy. Mater. Sci. Eng. A 2010, 527, 961–966. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, R.; Li, J.; Kou, H.; Li, H.; Chang, H.; Fu, H. Characterization of hot deformation behavior of Haynes230 by using processing maps. J. Mater. Process. Technol. 2009, 209, 4020–4026. [Google Scholar] [CrossRef]
- He, D.; Lin, Y.C.; Chen, M.; Chen, J.; Wen, D.; Chen, X. Effect of pre-treatment on hot deformation behavior and processing map of an aged nickel-based superalloy. J. Alloys Comp. 2015, 649, 1075–1084. [Google Scholar] [CrossRef]
- Detrois, M.; Helmink, R.C.; Tin, S. Hot deformation characteristics of a polycrystalline γ–γ′–δ ternary eutectic Ni-base superalloy. Mater. Sci. Eng. A 2013, 586, 236–244. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, C.; Ding, C.G.; Zhu, Q.; Qin, H.Y. Plastic deformation behavior and processing maps of a Ni-based superalloy. Mater. Des. 2015, 65, 575–584. [Google Scholar] [CrossRef]
- Huang, L.; Qi, F.; Hua, P.; Yu, L.; Liu, F.; Sun, W.; Hu, Z. Discontinuous Dynamic Recrystallization of Inconel 718 Superalloy during the Superplastic Deformation. Metall. Mater. Trans. A 2015, 46, 4276–4285. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, W.Z.; Zhen, L.; Zhang, X.M. Microstructure evolution during dynamic recrystallization of hot deformed superalloy 718. Mater. Sci. Eng. A 2008, 486, 321–332. [Google Scholar] [CrossRef]
- Zhang, J.M.; Gao, Z.Y.; Zhuang, J.Y.; Zhong, Z.Y.; Janschek, P. Strain-rate hardening behavior of superalloy IN718. J. Mater. Process. Technol. 1997, 70, 252–257. [Google Scholar] [CrossRef]
- Wang, Y.; Zhen, L.; Shao, W.Z.; Yang, L.; Zhang, X.M. Hot working characteristics and dynamic recrystallization of delta-processed superalloy 718. J. Alloys Comp. 2009, 474, 341–346. [Google Scholar] [CrossRef]
- Mandal, S.; Bhaduri, A.K.; Sarma, V.S. A Study on Microstructural Evolution and Dynamic Recrystallization during Isothermal Deformation of a Ti-Modified Austenitic Stainless Steel. Metall. Mater. Trans. A 2011, 42, 1062–1072. [Google Scholar] [CrossRef]
- Hrutkay, K.; Kaoumi, D. Tensile deformation behavior of a nickel based superalloy at different temperatures. Mater. Sci. Eng. A 2014, 599, 196–203. [Google Scholar] [CrossRef]
- Yu, D. Modeling high-temperature tensile deformation behavior of AZ31B magnesium alloy considering strain effects. Mater. Des. 2013, 51, 323–330. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Biswas, S.; Beausir, B.T.; Toth, L.S.; Suwas, S. Evolution of texture and microstructure during hot torsion of a magnesium alloy. Acta Mater. 2013, 61, 5263–5277. [Google Scholar] [CrossRef]
- Kovarik, L.; Unocic, R.R.; Li, J.; Sarosi, P.; Shen, C.; Wang, Y.; Mills, M.J. Microtwinning and other shearing mechanisms at intermediate temperatures in Ni-based superalloys. Prog. Mater. Sci. 2009, 54, 839–873. [Google Scholar] [CrossRef]
- Zong, Y.; Wen, D.; Liu, Z.; Shan, D. γ-Phase transformation, dynamic recrystallization and texture of a forged TiAl-based alloy based on plane strain compression at elevated temperature. Mater. Des. 2016, 91, 321–330. [Google Scholar] [CrossRef]
- Xu, S.; Liu, T.; Ding, X.; Zeng, W. Reducing the anisotropy of a pre-twinned hot-rolled Mg–3Al–1Zn alloy by plane-strain compression. Mater. Sci. Eng. A 2014, 592, 230–235. [Google Scholar] [CrossRef]
- Cheng, L.; Xue, X.; Tang, B.; Liu, D.; Li, J.; Kou, H.; Li, J. Deformation behavior of hot-rolled IN718 superalloy under plane strain compression at elevated temperature. Mater. Sci. Eng. A 2014, 606, 24–30. [Google Scholar] [CrossRef]
- Uranga, P.; Gutiérrez, I.; López, B. Determination of recrystallization kinetics from plane strain compression tests. Mater. Sci. Eng. A 2013, 578, 174–180. [Google Scholar] [CrossRef]
- Chen, X.; Lin, Y.C.; Wen, D.; Zhang, J.; He, M. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar] [CrossRef]
- Yoon, J.G.; Jeong, H.W.; Yoo, Y.S.; Hong, H.U. Influence of initial microstructure on creep deformation behaviors and fracture characteristics of Haynes 230 superalloy at 900 °C. Mater. Charact. 2015, 101, 49–57. [Google Scholar] [CrossRef]
- Semiatin, S.L.; Weaver, D.S.; Kramb, R.C.; Fagin, P.N.; Glavicic, M.G.; Goetz, R.L.; Frey, N.D.; Antony, M.M. Deformation and recrystallization behavior during hot working of a coarse-grain, nickel-base superalloy ingot material. Metall. Mater. Trans. A 2004, 35, 679–693. [Google Scholar] [CrossRef]
- Na, Y.S.; Yeom, J.T.; Park, N.K.; Lee, J.Y. Simulation of microstructures for Alloy 718 blade forging using 3D FEM simulator. J. Mater. Process. Technol. 2003, 141, 337–342. [Google Scholar] [CrossRef]
- Wang, J.; Liu, D.; Hu, Y.; Yang, Y.; Zhu, X. Effect of Grain Size Distribution on Processing Maps for Isothermal Compression of Inconel 718 Superalloy. J. Mater. Eng. Perform. 2016, 25, 677–686. [Google Scholar] [CrossRef]
- Muralidharan, G.; Thompson, R.G. Effect of second phase precipitation on limiting grain growth in alloy 718. Scr. Mater. 1997, 36, 755–761. [Google Scholar] [CrossRef]
- Monajati, H.; Taheri, A.K.; Jahazi, M.; Yue, S. Deformation characteristics of isothermally forged UDIMET 720 nickel-base superalloy. Metall. Mater. Trans. A 2005, 36, 895–905. [Google Scholar] [CrossRef]
- Song, K.; Aindow, M. Grain growth and particle pinning in a model Ni-based superalloy. Mater. Sci. Eng. A 2008, 479, 365–372. [Google Scholar] [CrossRef]
- Jin, Y.; Bernacki, M.; Agnoli, A.; Lin, B.; Rohrer, G.S.; Rollett, A.D.; Bozzolo, N. Evolution of the Annealing Twin Density during δ-Supersolvus Grain Growth in the Nickel-Based Superalloy Inconel™ 718. Metals 2016, 6, 5. [Google Scholar] [CrossRef]
- Allain, S.; Chateau, J.P.; Bouaziz, O.; Migot, S.; Guelton, N. Correlations between the calculated stacking fault energy and the plasticity mechanisms in Fe–Mn–C alloys. Mater. Sci. Eng. A 2004, 387, 158–162. [Google Scholar] [CrossRef]
- Randle, V. Twinning-related grain boundary engineering. Acta Mater. 2004, 52, 4067–4081. [Google Scholar] [CrossRef]
- Wu, K.; Liu, G.Q.; Hu, B.F.; Wang, C.Y.; Zhang, Y.W.; Tao, Y.; Liu, J.T. Effect of processing parameters on hot compressive deformation behavior of a new Ni–Cr–Co based P/M superalloy. Mater. Sci. Eng. A 2011, 528, 4620–4629. [Google Scholar] [CrossRef]
- Dehmas, M.; Lacaze, J.; Niang, A.; Viguier, B. TEM Study of High-Temperature Precipitation of Delta Phase in Inconel 718 Alloy. Adv. Mater. Sci. Eng. 2011, 2011, 123–126. [Google Scholar] [CrossRef]
- El-Danaf, E.; Kalidindi, S.R.; Doherty, R.D. Influence of grain size and stacking-fault energy on deformation twinning in fcc metals. Metall. Mater. Trans. A 1999, 30, 1223–1233. [Google Scholar] [CrossRef]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, D.; Ding, X.; Wang, H.; Wang, H.; Chen, J.; Yang, Y. Microstructure Heredity of Inconel 718 Nickel-Based Superalloy during Preheating and Following Deformation. Crystals 2020, 10, 303. https://doi.org/10.3390/cryst10040303
Wang J, Liu D, Ding X, Wang H, Wang H, Chen J, Yang Y. Microstructure Heredity of Inconel 718 Nickel-Based Superalloy during Preheating and Following Deformation. Crystals. 2020; 10(4):303. https://doi.org/10.3390/cryst10040303
Chicago/Turabian StyleWang, Jianguo, Dong Liu, Xiao Ding, Haiping Wang, Hai Wang, Jingqing Chen, and Yanhui Yang. 2020. "Microstructure Heredity of Inconel 718 Nickel-Based Superalloy during Preheating and Following Deformation" Crystals 10, no. 4: 303. https://doi.org/10.3390/cryst10040303
APA StyleWang, J., Liu, D., Ding, X., Wang, H., Wang, H., Chen, J., & Yang, Y. (2020). Microstructure Heredity of Inconel 718 Nickel-Based Superalloy during Preheating and Following Deformation. Crystals, 10(4), 303. https://doi.org/10.3390/cryst10040303




