Broadband Plasmonic Nanopolarizer Based on Different Surface Plasmon Resonance Modes in a Silver Nanorod
Abstract
:1. Introduction
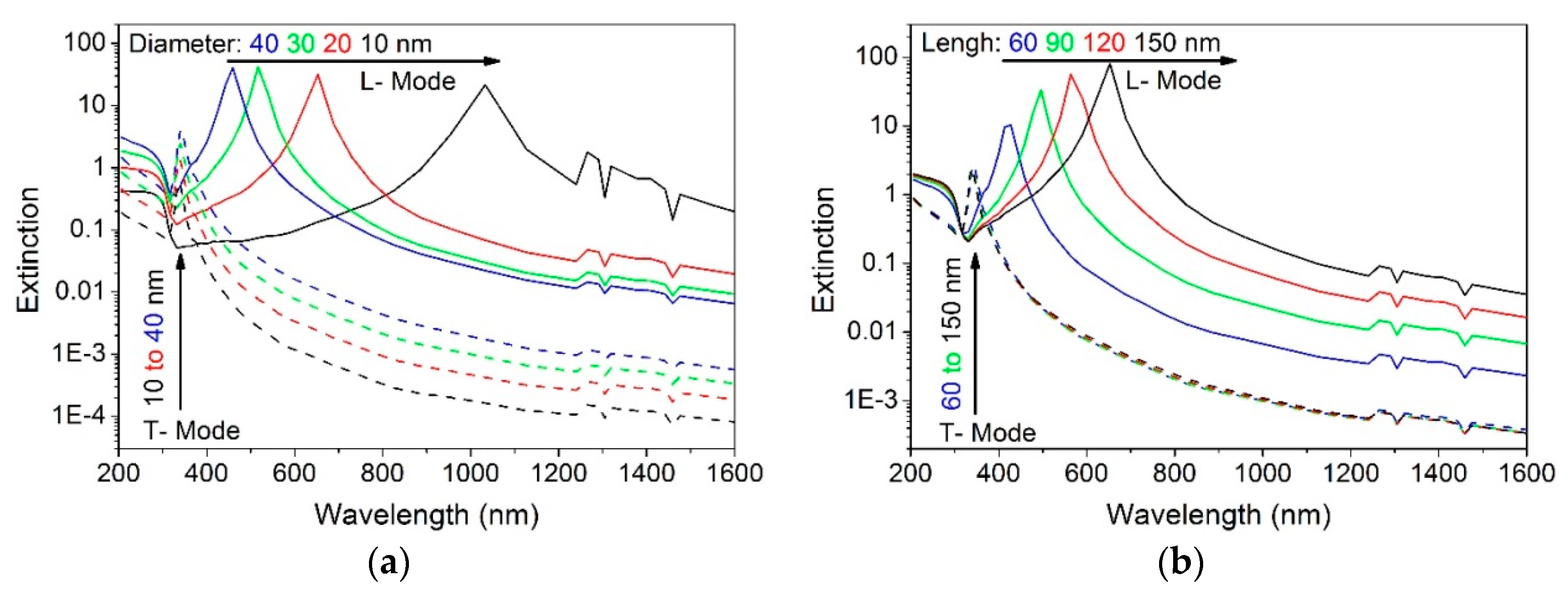
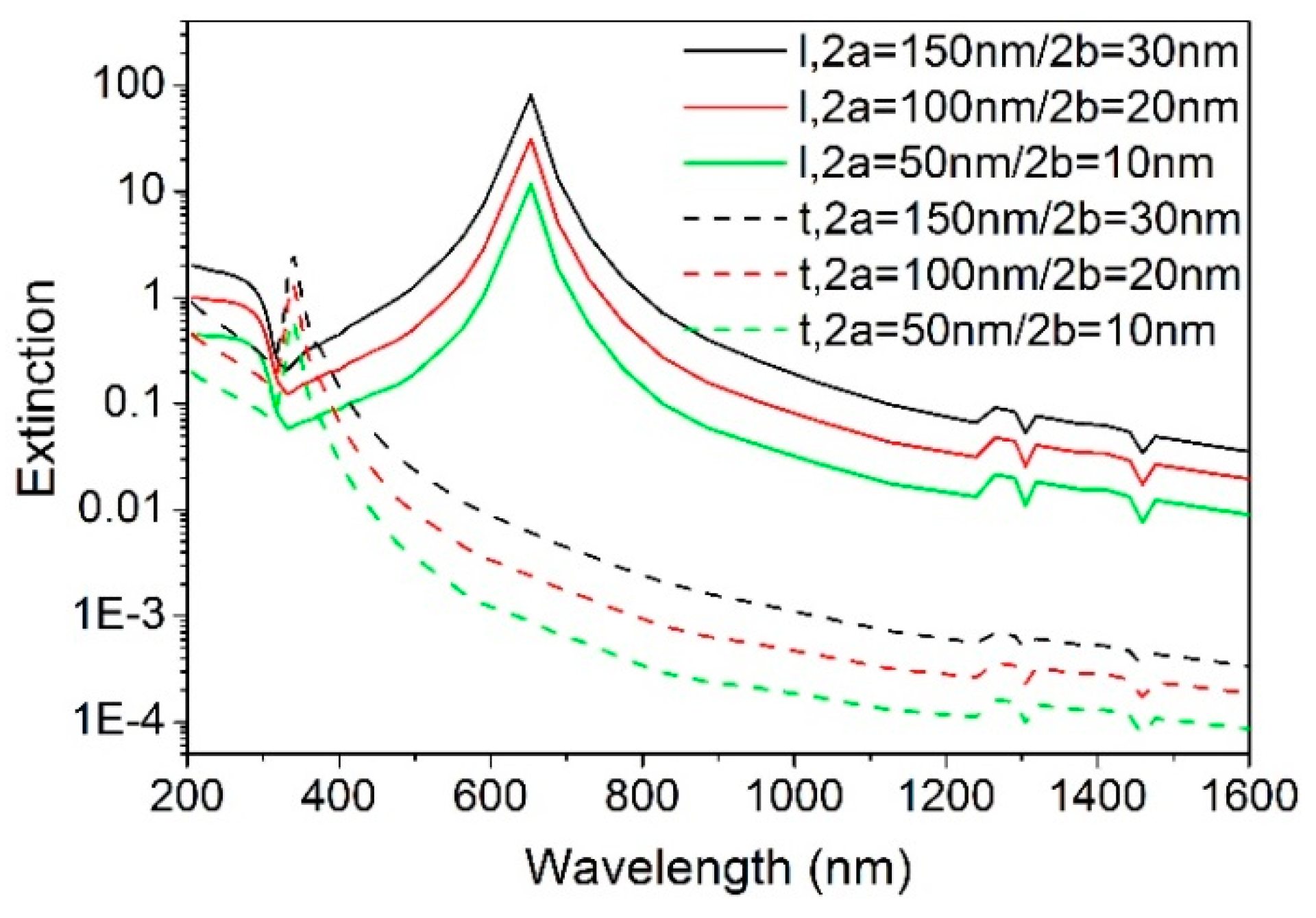
2. Extinction Properties of a Plasmonic Nanorod
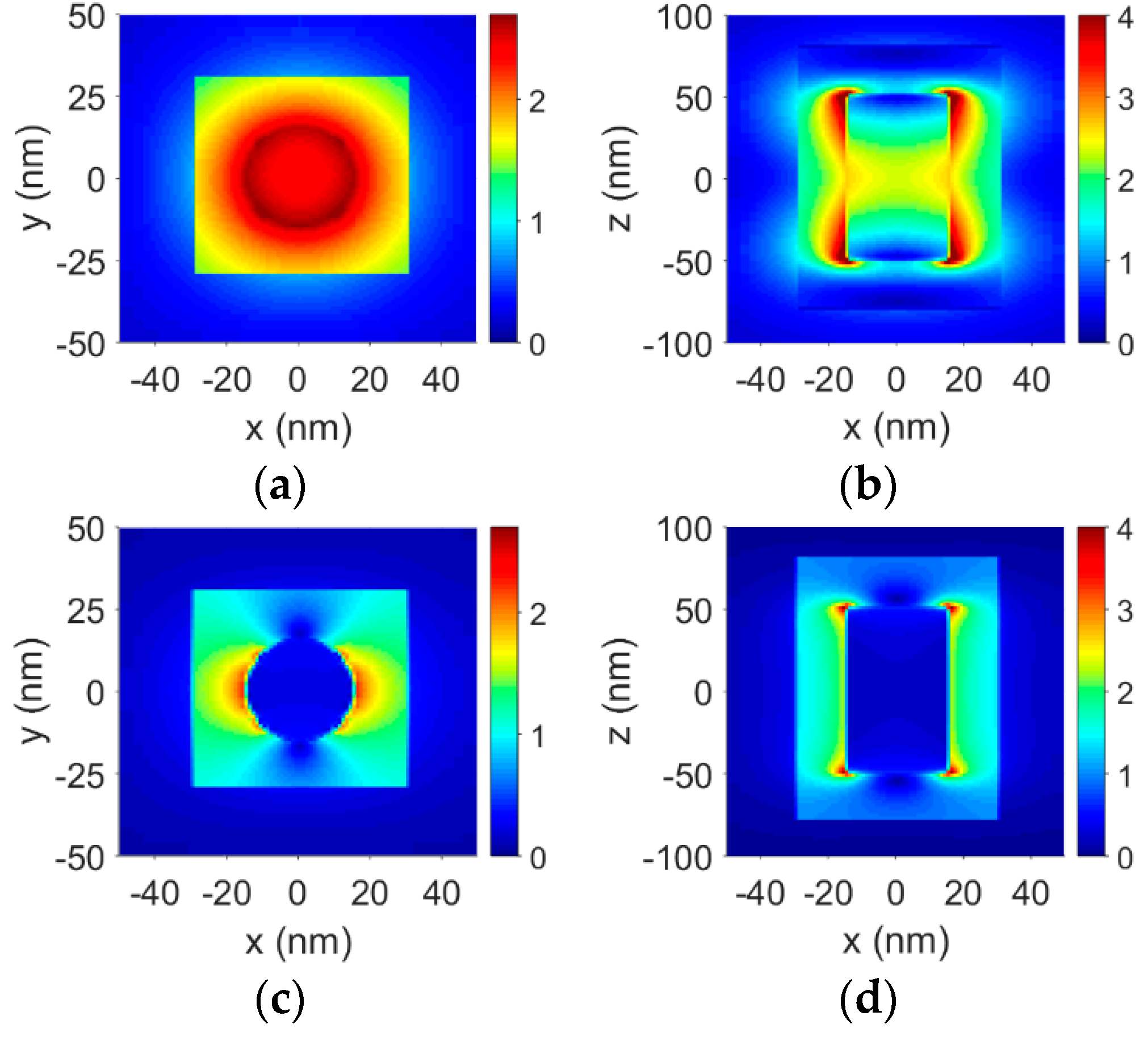
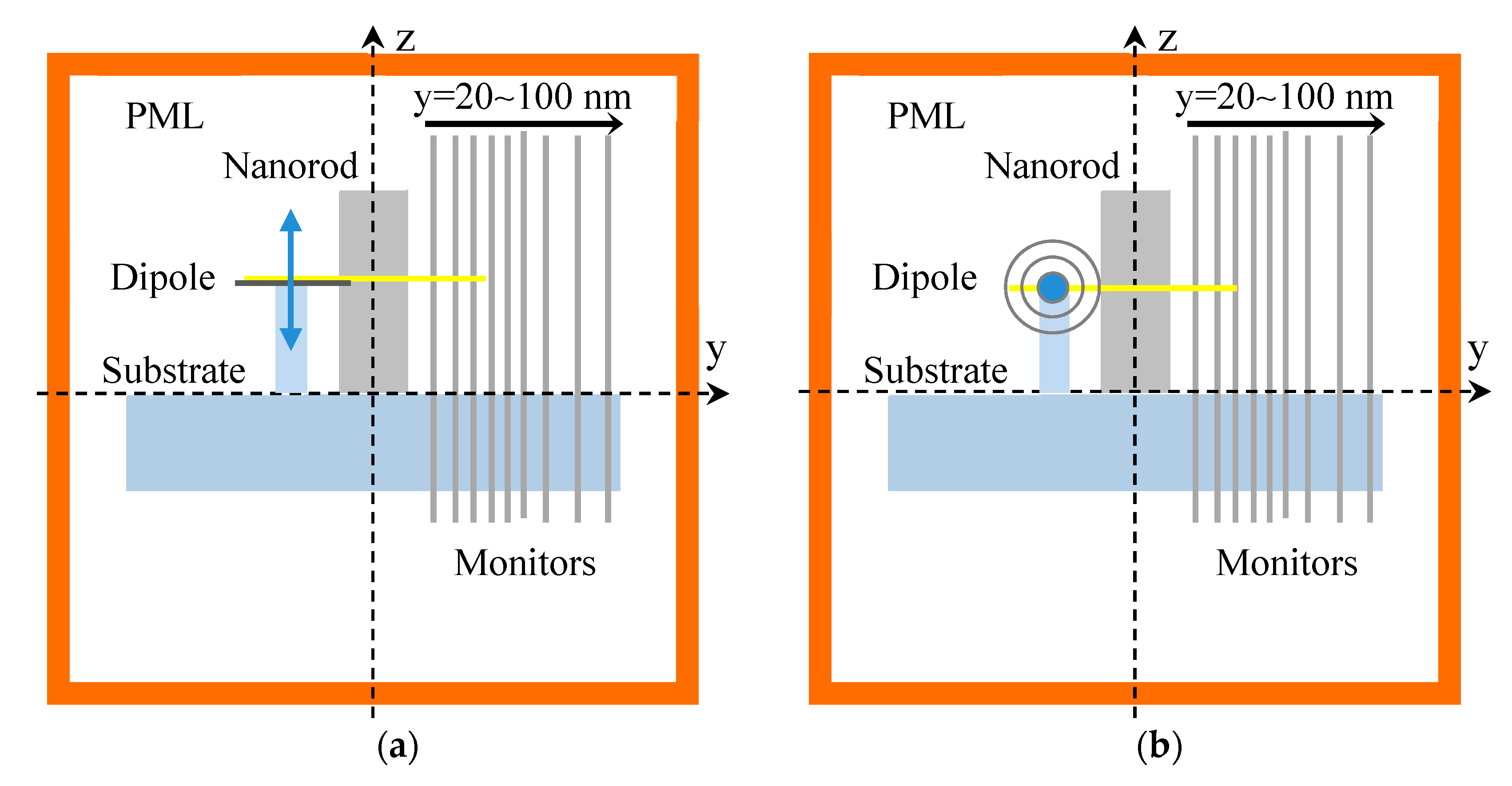
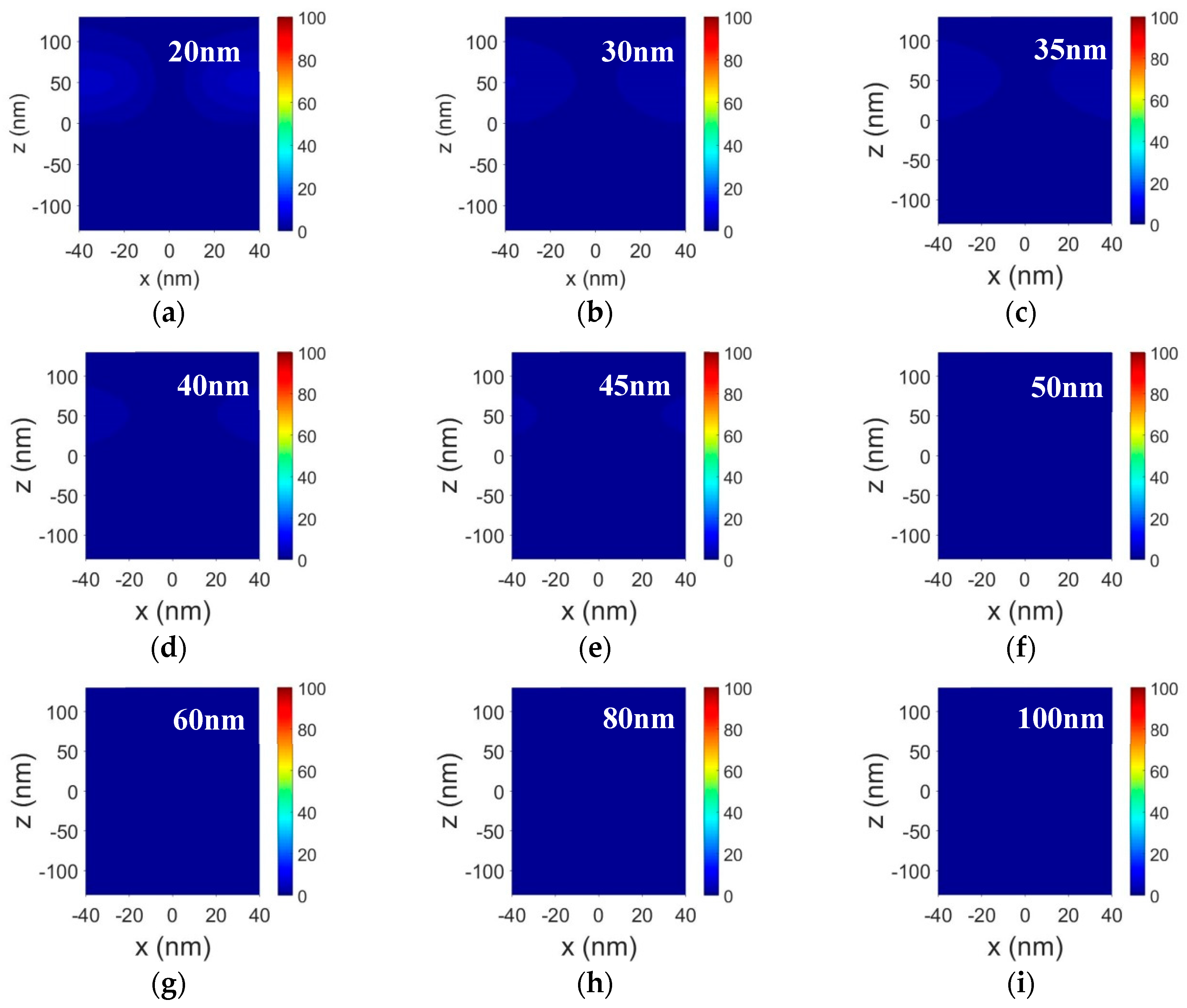
3. Simulation of Nanopolarization Characteristics in Near Field Region of the Plasmonic Nanorod
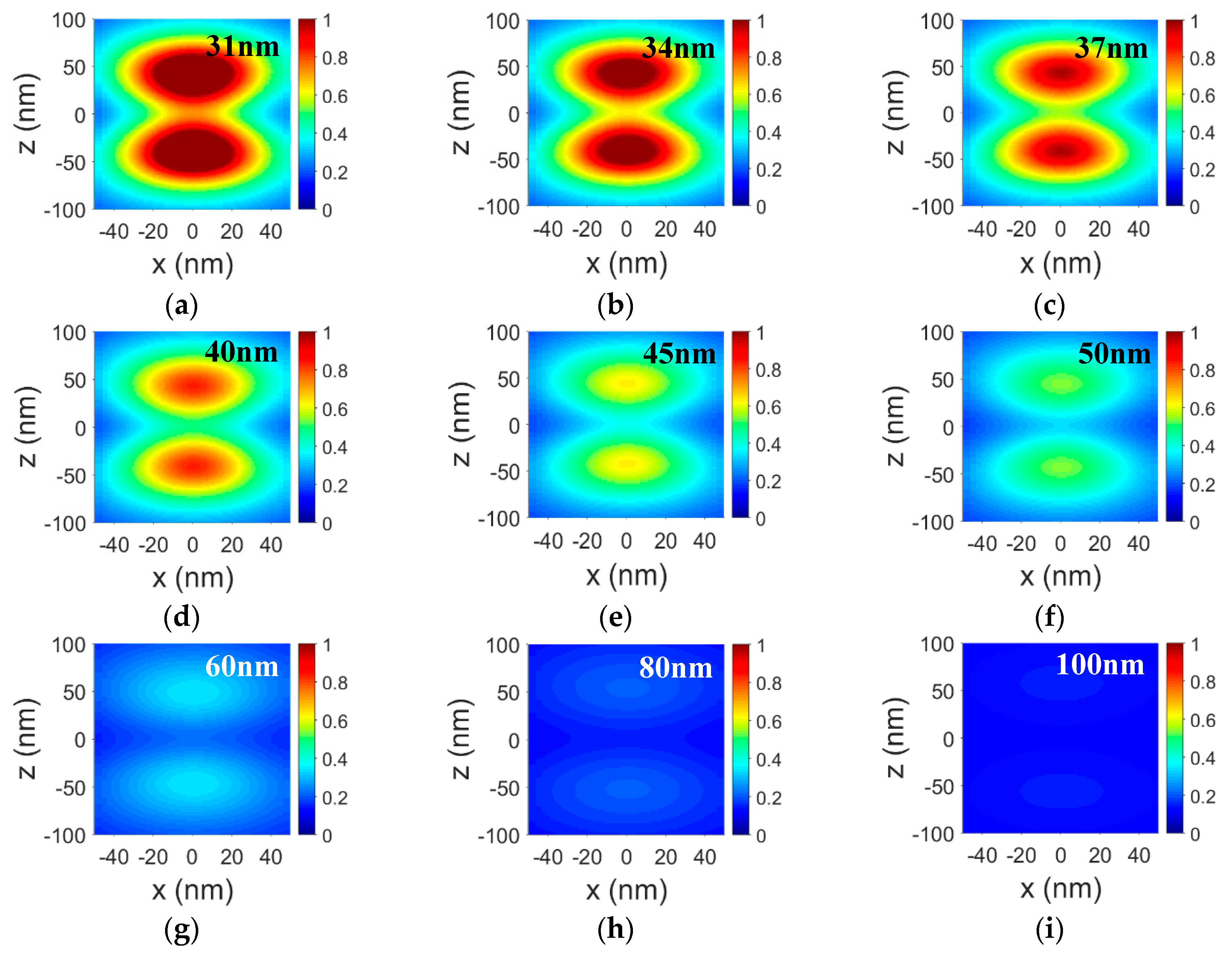
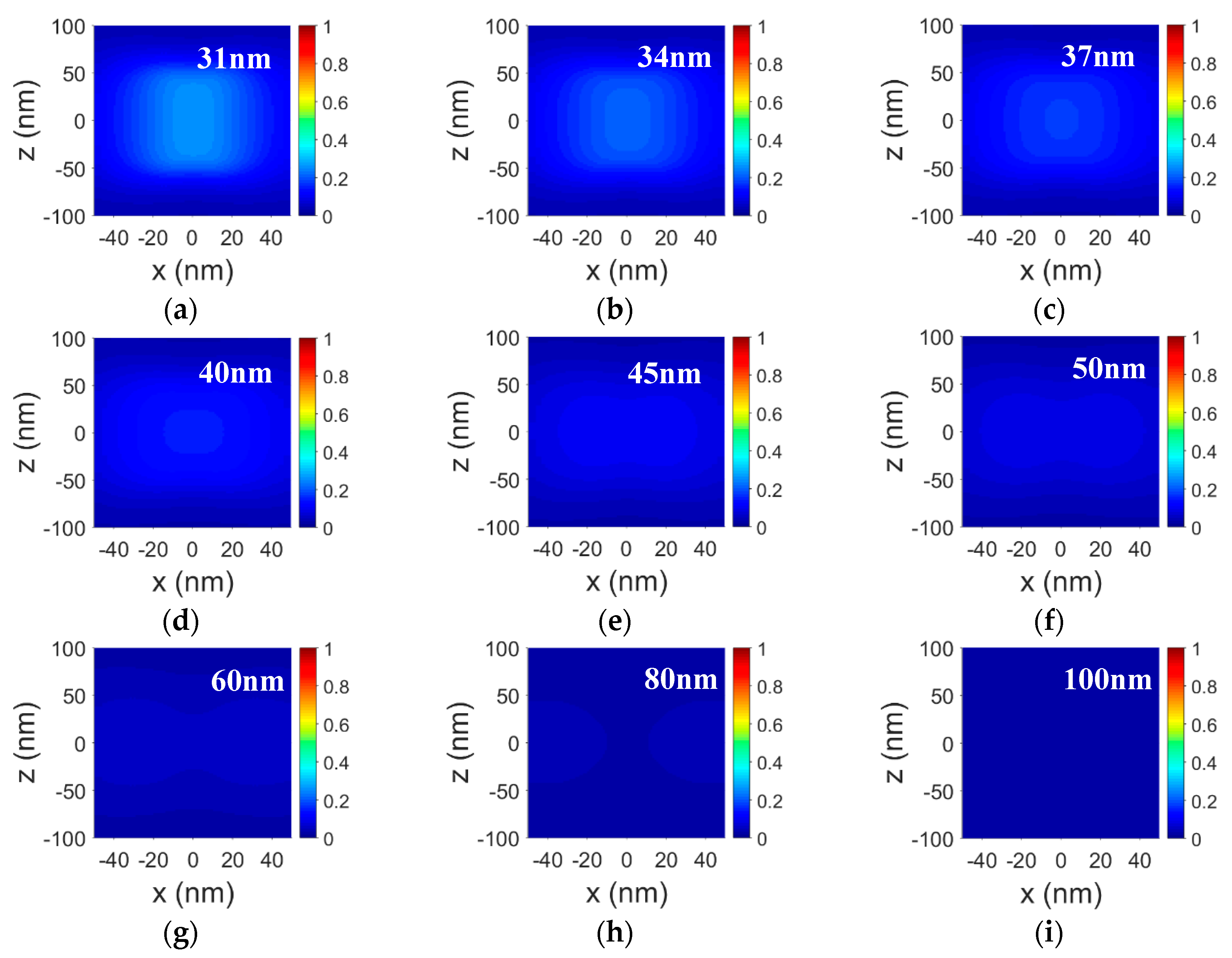
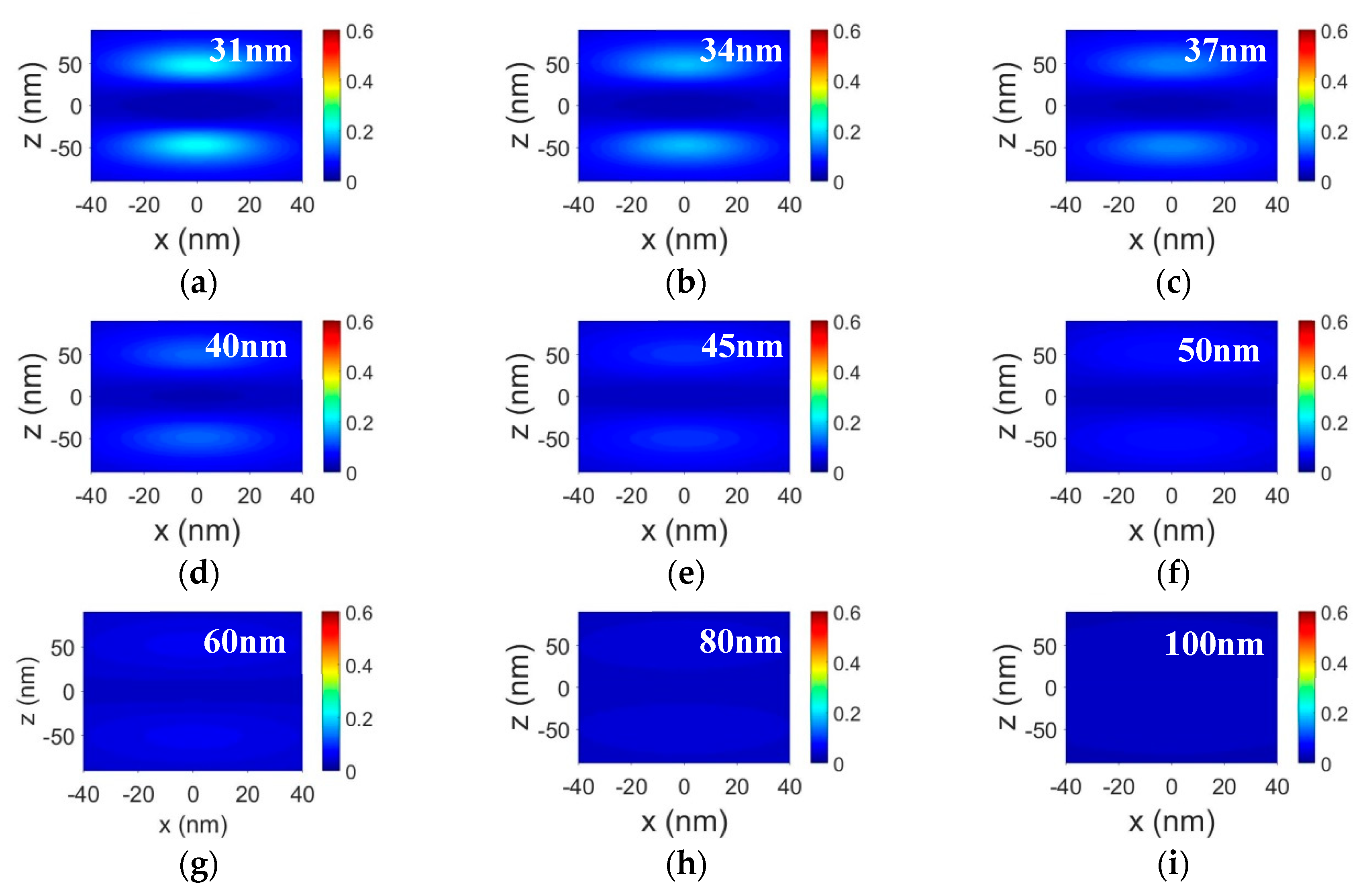
4. Tuning the Polarization Properties of the Plasmonic Nanopolarizer in Visible to Near Infrared Spectral Range
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goldstein, D. Polarized Light; Marcel Dekker: New York, NY, USA, 2003; pp. 497–538. [Google Scholar]
- Zhou, K.M.; Simpson, G.; Chen, X.F.; Zhang, L.; Bennion, I. High extinction ratio in-fiber polarizers based on 45 degrees tilted fiber Bragg gratings. Opt. Lett. 2005, 30, 1285–1287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Z.; Zhou, K.; Zhang, L. In-fiber linear polarizer based on UV-inscribed 45 degrees tilted grating in polarization maintaining fiber. Opt. Lett. 2012, 37, 3819–3821. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bao, Q.L.; Zhang, H.; Wang, B.; Ni, Z.H.; Lim, C.; Wang, Y.; Tang, D.Y.; Loh, K.P. Broadband graphene polarizer. Nat. Photonics 2011, 5, 411–415. [Google Scholar] [CrossRef]
- Dong, C.H.; Zou, C.L.; Ren, X.F.; Guo, G.C.; Sun, F.W. In-line high efficient fiber polarizer based on surface plasmon. Appl. Phys. Lett. 2012, 100, 041104. [Google Scholar] [CrossRef]
- Lu, Z.H.; Tang, Y.F.; Shen, Y.F.; Liu, X.H.; Zi, J. Polarization beam splitting in two-dimensional photonic crystals based on negative refraction. Phys. Lett. A. 2015, 346, 243–247. [Google Scholar] [CrossRef]
- Tagashira, K.; Yoshida, H.; Kubo, H.; Fujii, A.; Ozaki, M. Radial and azimuthal polarizer using a one-dimensional photonic crystal with a patterned liquid crystal defect layer. Appl. Phys. Express 2010, 3, 062002. [Google Scholar] [CrossRef]
- Sahani, P.; Vijaya, R. Polarizing properties of a 2D photonic crystal slab for simultaneous in-plane and out-of-plane light incidence. J. Phys. D Appl. Phys. 2018, 51, 355101. [Google Scholar] [CrossRef]
- Odoeze, J.A.H.; Hameed, M.F.O.; Shalaby, H.M.H.; Obayya, S.S.A. Si-core photonic crystal fiber transverse-electric pass polarizer. J. Opt. Soc. Am. B 2018, 35, 980–986. [Google Scholar] [CrossRef]
- Zhang, J.X.; Zhang, L.D.; Ye, C.H.; Chang, M.; Yan, Y.G.; Lu, Q.F. Polarization properties of ordered copper nanowire microarrays embedded in anodic alumina membrane. Chem. Phys. Lett. 2004, 400, 158–162. [Google Scholar] [CrossRef]
- Wang, J.J.; Zhang, W.; Deng, X.G.; Deng, J.D.; Liu, F.; Sciortino, P.; Chen, L. High-performance nanowire-grid polarizers. Opt. Lett. 2005, 30, 195–197. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.J.; Walters, F.; Deng, X.G.; Buonanno, M.; Tai, S.; Liu, X.M. Large flexible nanowire grid visible polarizer made by nanoimprint lithography. Appl. Phys. Lett. 2007, 90, 063001. [Google Scholar] [CrossRef]
- Wu, C.-L.; Sung, C.-K.; Yao, P.-H.; Chen, C.-H. Sub-15 nm linewidth gratings using roll-to-roll nanoimprinting and plasma trimming to fabricate flexible wire-grid polarizers with low colour shift. Nanotechnology 2013, 24, 265301. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.W.; Lee, K.J.; Magnusson, R. Ultra-sparse dielectric nanowire grids as wideband reflectors and polarizers. Opt. Express 2013, 23, 28849–28856. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liu, H.; Tian, J.; Song, Y.; Wang, L.; Song, J.; Zhang, G. Optical polarizers based on gold nanowires fabricated using colloidal gold nanoparticles. Nanotechnology 2008, 19, 285202. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liu, H.; Tian, J.; Song, Y.; Wang, L. Band-selective optical polarizer based on gold-nanowire plasmonic diffraction gratings. Nano Lett. 2008, 8, 2653–2658. [Google Scholar] [CrossRef] [PubMed]
- Rosenzveig, T.; Hermannsson, P.G.; Leosson, K. Modelling of polarization-dependent loss in plasmonic nanowire waveguides. Plasmonics 2010, 5, 75–77. [Google Scholar] [CrossRef]
- Sun, X.; Alam, M.Z.; Wagner, S.J.; Aitchison, J.S.; Mojahedi, M. Experimental demonstration of a hybrid plasmonic transverse electric pass polarizer for a silicon-on-insulator platform. Opt. Lett. 2012, 37, 4814–4816. [Google Scholar] [CrossRef]
- Alam, M.Z.; Aitchison, J.S.; Mojahedi, M. Compact and silicon-on-insulator-compatible hybrid plasmonic TE-pass polarizer. Opt. Lett. 2012, 37, 55–57. [Google Scholar] [CrossRef] [Green Version]
- Han, C.R.; Tam, W.Y. Plasmonic ultra-broadband polarizers based on Ag nano wire-slit arrays. Appl. Phys. Lett. 2015, 106, 081102. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.K.; Madaan, D.; Kapoor, A. High extinction ratio and short length surface plasmon polariton polarizer. IEEE Photonic. Technol. Lett. 2016, 28, 1541–1544. [Google Scholar] [CrossRef]
- Sun, X.; Mojahedi, M.; Aitchison, J.S. Hybrid plasmonic waveguide-based ultra-low insertion loss transverse electric-pass polarizer. Opt. Lett. 2016, 41, 4020–4023. [Google Scholar] [CrossRef] [PubMed]
- Shang, X.-J.; Zhai, X.; Wang, L.-L.; He, M.-D.; Li, Q.; Luo, X.; Duan, H.-G. Asymmetric transmission and polarization conversion of linearly polarized waves with bilayer L-shaped metasurfaces. Appl. Phys. Express 2017, 10, 052602. [Google Scholar] [CrossRef]
- Shang, X.-J.; Zhai, X.; Yue, J.; Luo, X.; Liu, J.-P.; Zhu, X.-P.; Duan, H.-G.; Wang, L.-L. Broad-band and high-efficiency polarization converters around 1550 nm based on composite structures. Opt. Express 2017, 25, 14406–14413. [Google Scholar] [CrossRef] [PubMed]
- Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.S.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef]
- Berini, P.; De Leon, I. Surface plasmon-polariton amplifiers and lasers. Nat. Photonics 2012, 6, 16–24. [Google Scholar] [CrossRef]
- Zhang, J.X.; Zhang, L.D. Nanostructures for surface plasmons. Adv. Opt. Photon. 2012, 4, 157–321. [Google Scholar] [CrossRef]
- Ma, R.M.; Oulton, R.F.; Sorger, V.J.; Zhang, X. Plasmon lasers: Coherent light source at molecular scales. Laser Photonics Rev. 2013, 7, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Saj, W.M. FDTD simulations of 2D plasmon waveguide on silver nanorods in hexagonal lattice. Opt. Express 2005, 13, 4818–4827. [Google Scholar] [CrossRef]
- Kim, M.; Mun, J.; Bae, D.; Jeon, G.; Go, M.C.; Rho, J.; Kim, J.K. Accordion-like plasmonic silver nanorod array exhibiting multiple electromagnetic responses. NPG Asia Mater. 2018, 10, 190–196. [Google Scholar] [CrossRef]
- Aspnes, D.E. Optical properties of thin films. Thin Solid Films 1982, 89, 249–262. [Google Scholar] [CrossRef]
- van de Hulst, H.C. Light Scattering by Small Particles; Dover: New York, NY, USA, 1981; pp. 63–84. [Google Scholar]
- Wang, J.; Zhang, C.; Zhang, J.; Song, H.; Wang, P.; Lu, Y.; Fei, G.; Xu, W.; Xu, W.; Zhang, L.; et al. Hybrid plasmonic cavity modes in arrays of gold nanotubes. Adv. Opt. Mater. 2017, 5, 1600731. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Zhang, J.; Fei, G.; Wang, J.; Jiang, K.; Wang, P.; Lu, Y.; Iorsh, I.; Xu, W.; Jia, J.; et al. Near-field coupling and resonant cavity modes in plasmonic nanorod metamaterials. Nanotechnology 2016, 27, 415708. [Google Scholar] [CrossRef] [Green Version]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1998; pp. 130–157. [Google Scholar]
- Lynch, D.W.; Hunter, W.R. Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Cambridge, MA, USA, 1985; pp. 350–357. [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Hu, L.; Hu, Z.; Wei, Y.; Zhang, W.; Zhang, L. Broadband Plasmonic Nanopolarizer Based on Different Surface Plasmon Resonance Modes in a Silver Nanorod. Crystals 2020, 10, 447. https://doi.org/10.3390/cryst10060447
Zhang J, Hu L, Hu Z, Wei Y, Zhang W, Zhang L. Broadband Plasmonic Nanopolarizer Based on Different Surface Plasmon Resonance Modes in a Silver Nanorod. Crystals. 2020; 10(6):447. https://doi.org/10.3390/cryst10060447
Chicago/Turabian StyleZhang, Junxi, Lei Hu, Zhijia Hu, Yongqing Wei, Wei Zhang, and Lide Zhang. 2020. "Broadband Plasmonic Nanopolarizer Based on Different Surface Plasmon Resonance Modes in a Silver Nanorod" Crystals 10, no. 6: 447. https://doi.org/10.3390/cryst10060447
APA StyleZhang, J., Hu, L., Hu, Z., Wei, Y., Zhang, W., & Zhang, L. (2020). Broadband Plasmonic Nanopolarizer Based on Different Surface Plasmon Resonance Modes in a Silver Nanorod. Crystals, 10(6), 447. https://doi.org/10.3390/cryst10060447





