On Directional Dendritic Growth and Primary Spacing—A Review
Abstract
:1. Introduction
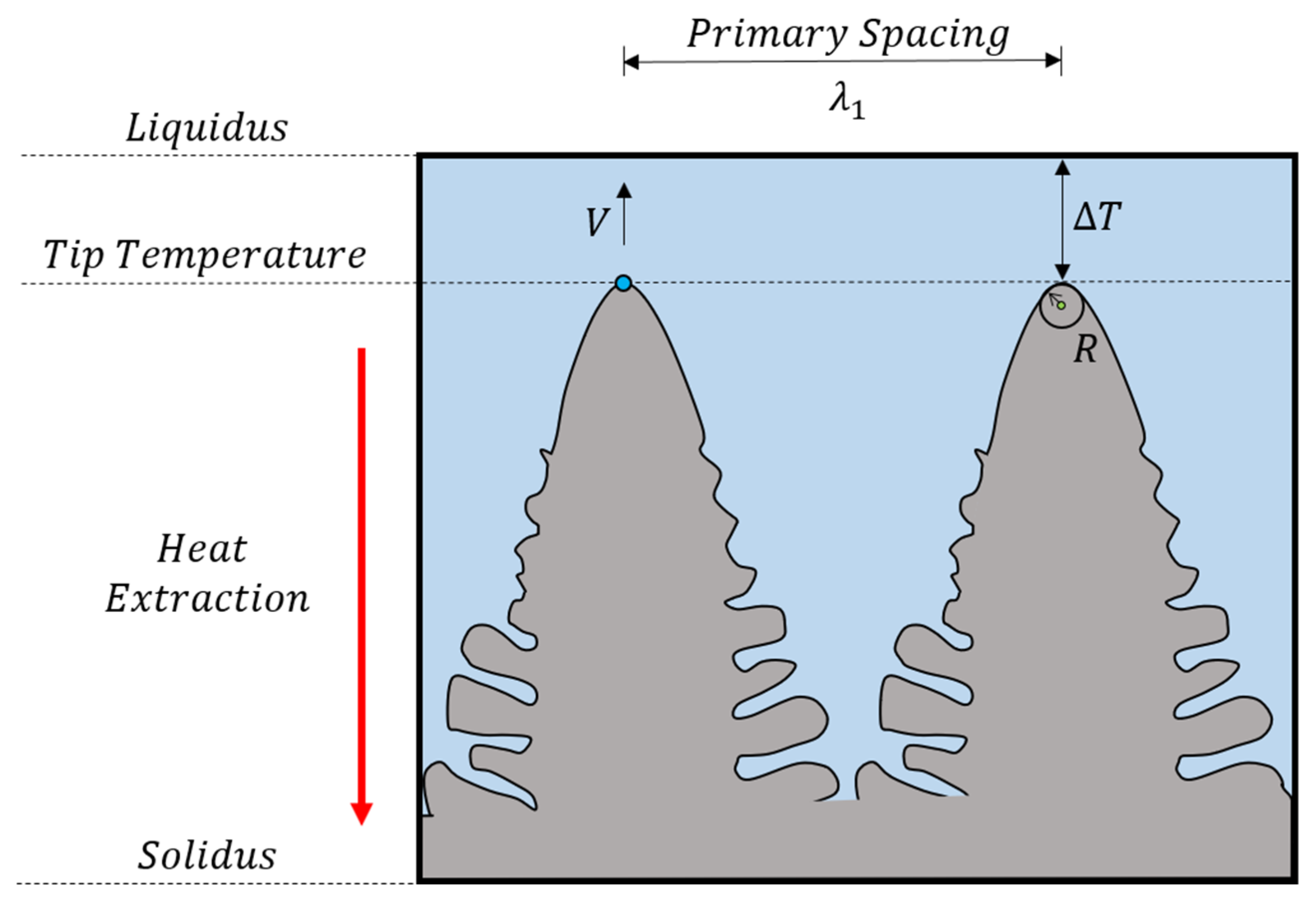
2. The Operating Point of a Dendrite Tip (1935–1999)
2.1. The Extremum Condition
2.2. The Marginal Stability Condition
2.3. The Microscopic Solvability Condition
2.4. A Test of Theory
3. Primary Spacing Selection in Directional Solidification (1979–2004)
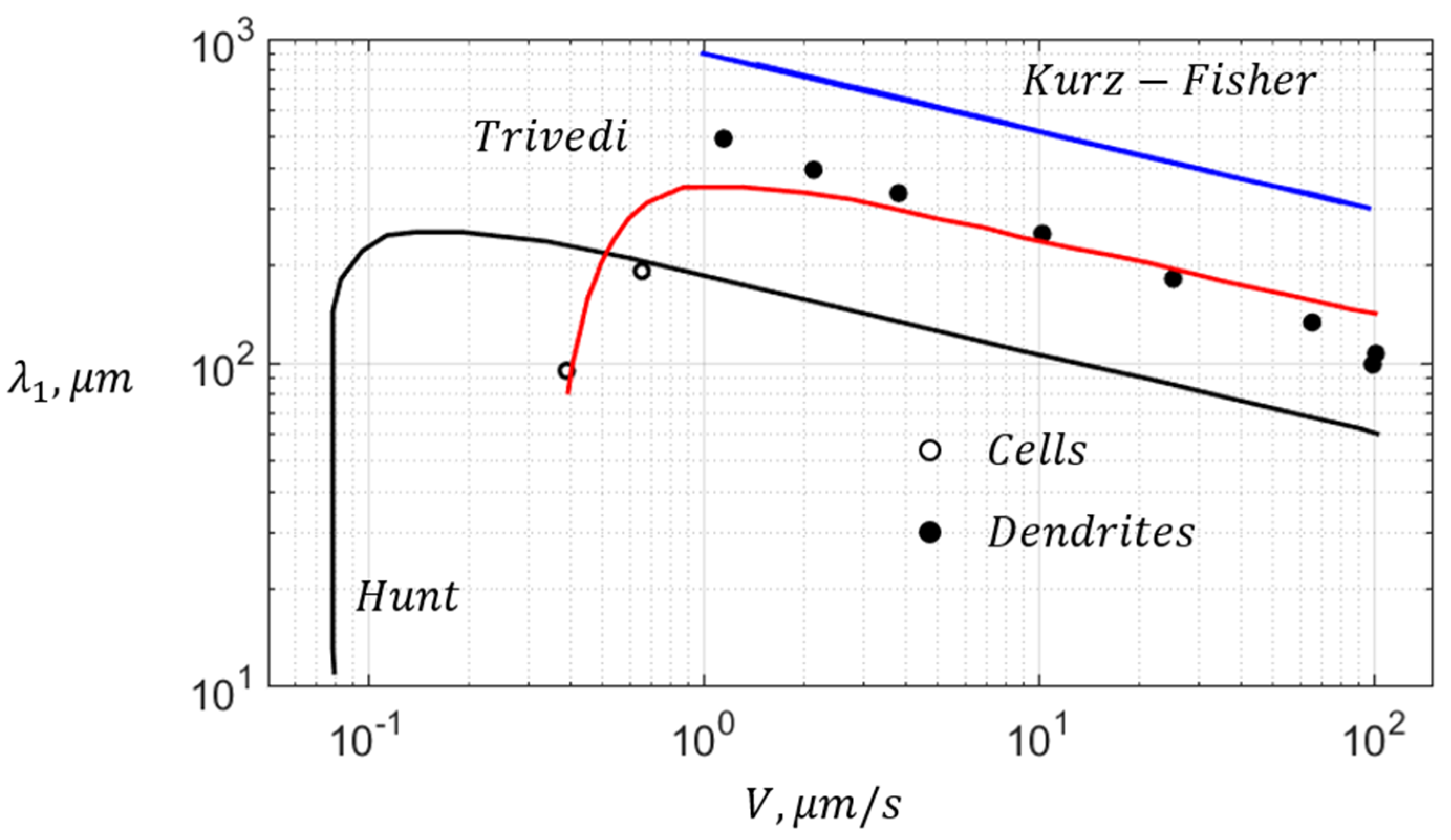
3.1. Early Primary Spacing Models
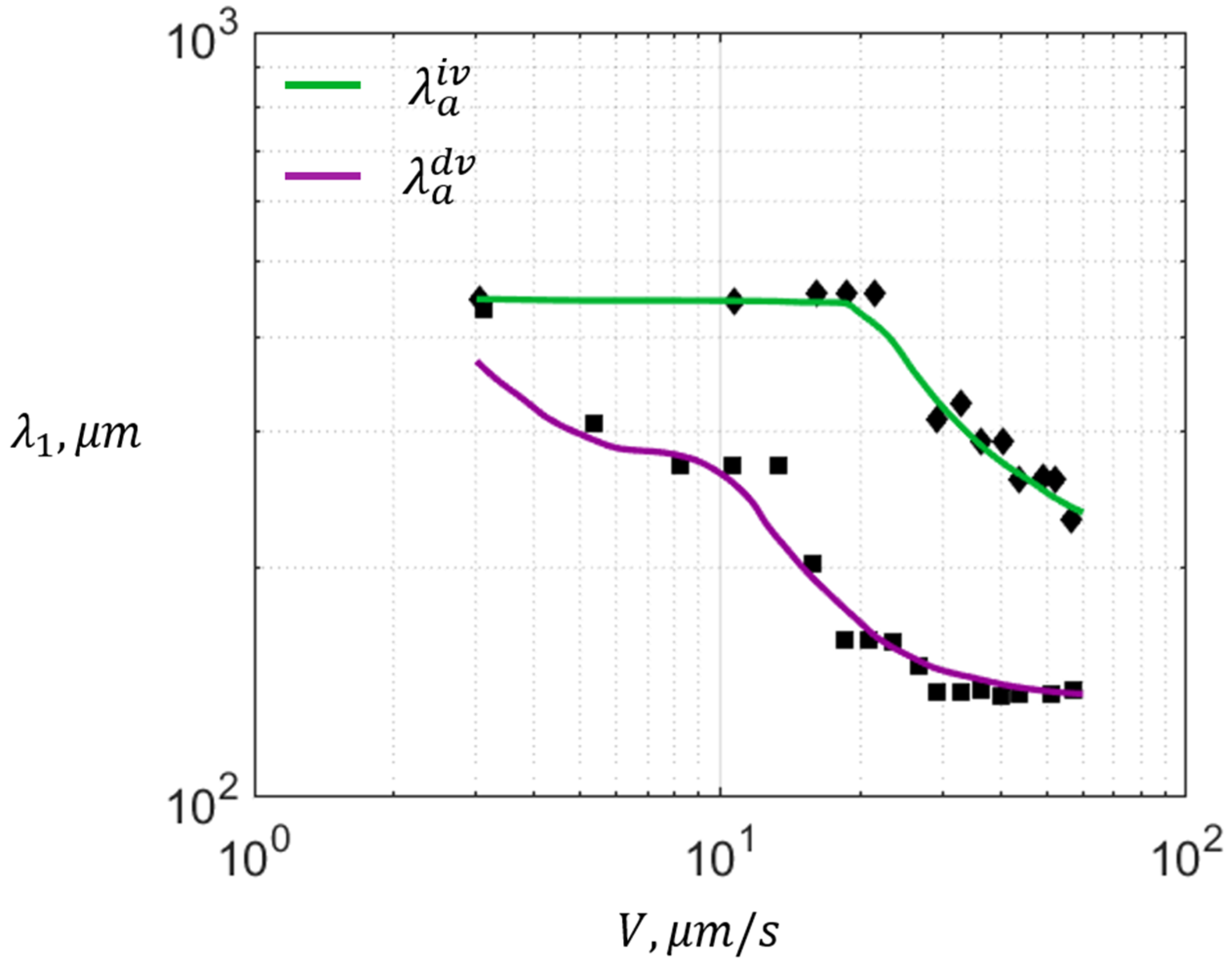
3.2. Precisely Controlled Experiments
3.3. An Improved Analytical Primary Spacing Model
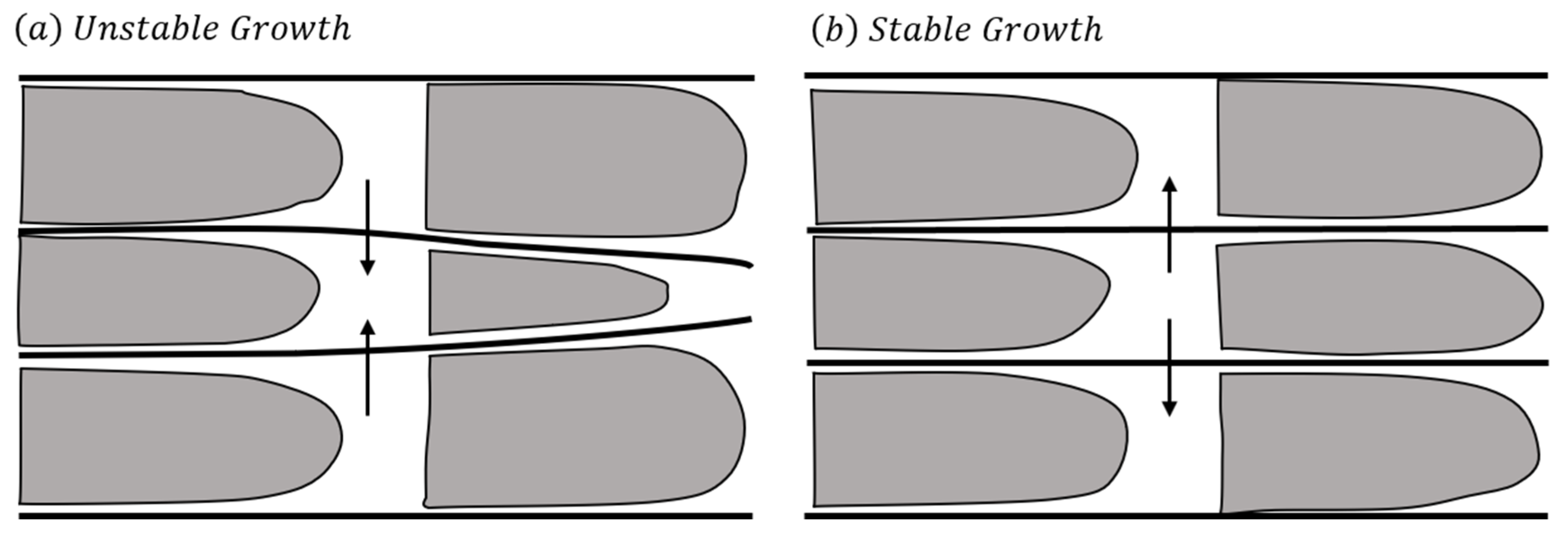
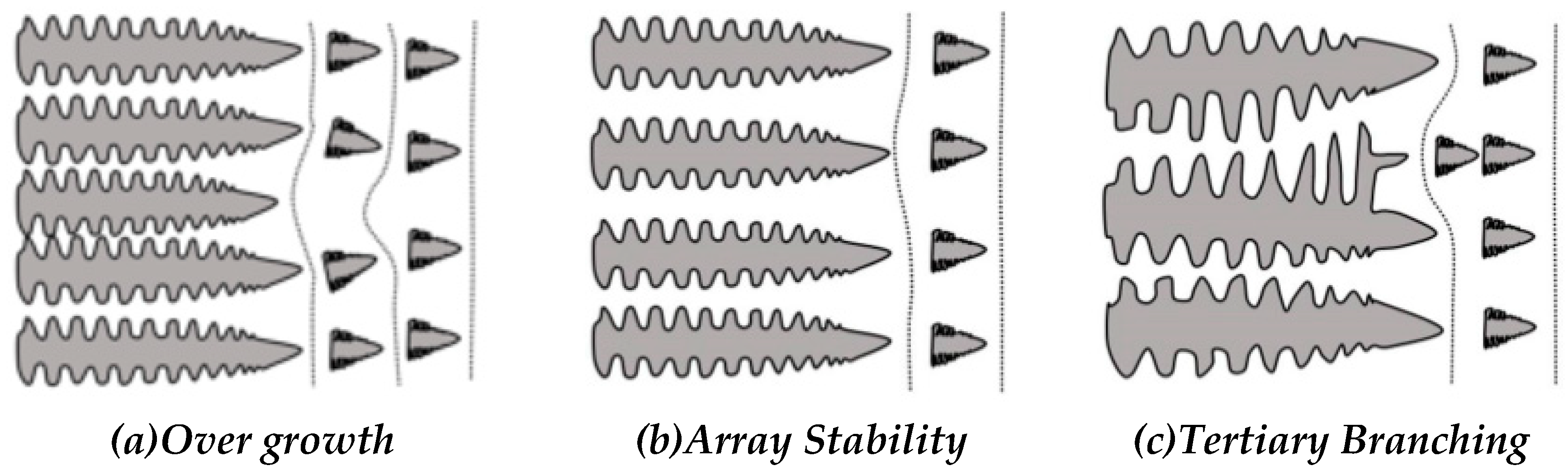
3.4. The Stable Range of Primary Spacing
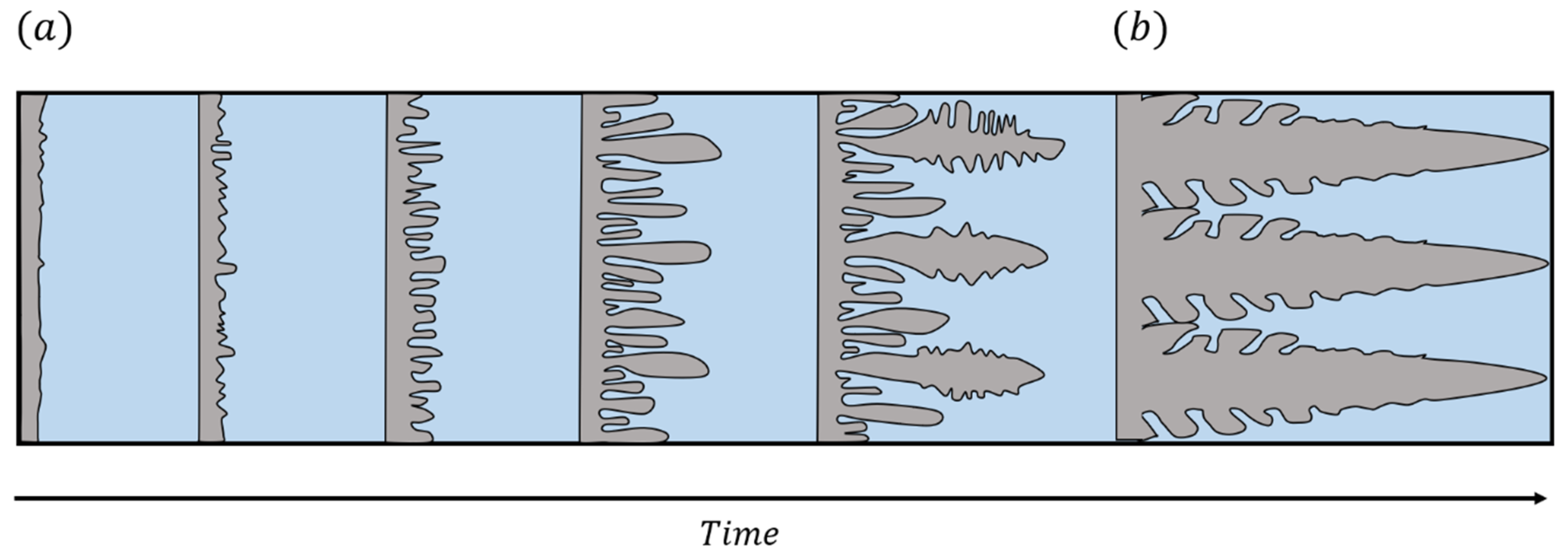
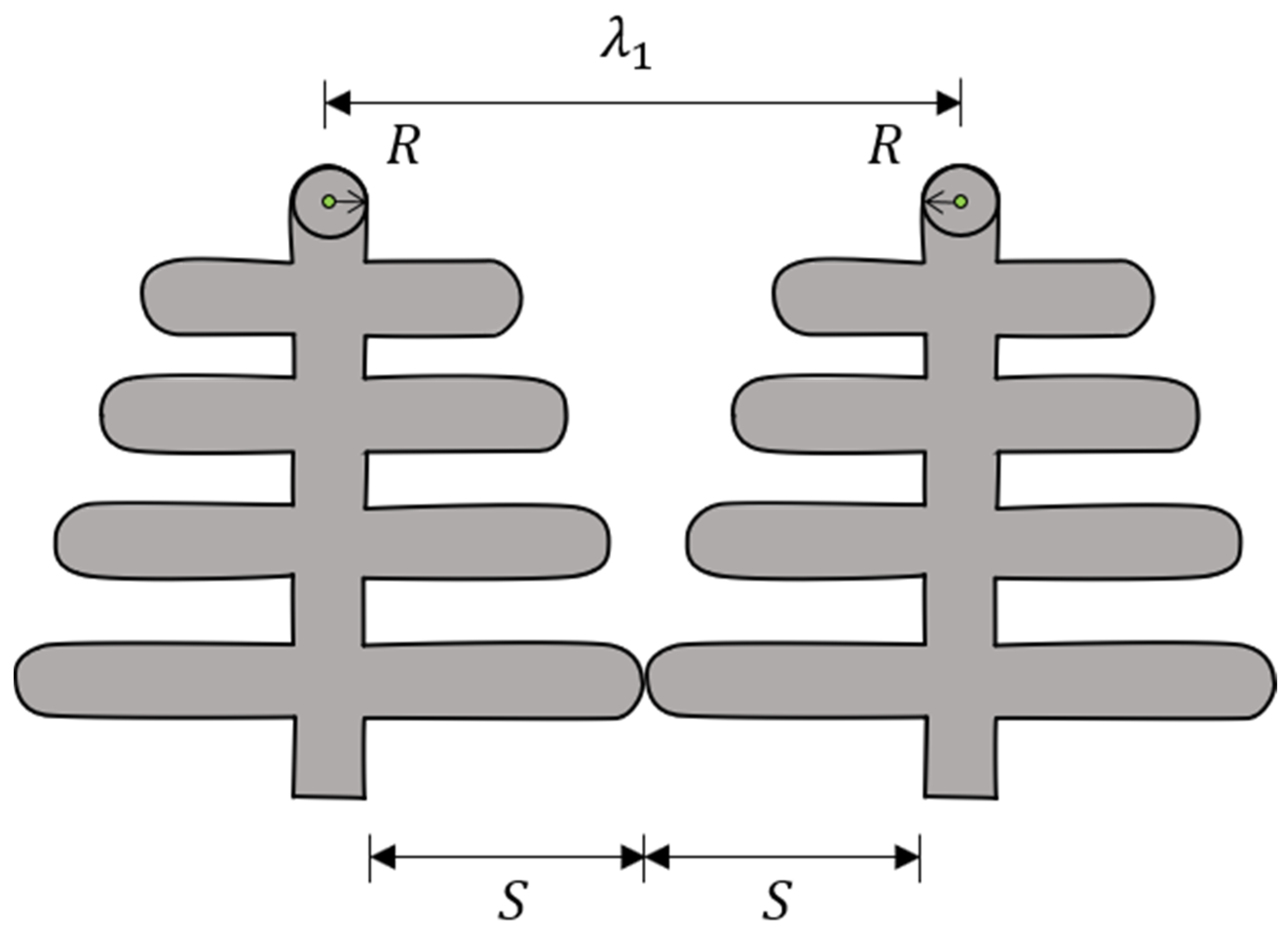
3.5. The First Numerical Primary Spacing Model
3.6. Understanding the Primary Spacing Selection Process
3.7. Delimiting the Wide Range of Stable Primary Spacings
3.8. Models Viewed as Complimentary to Hunt and Lu
4. Dendritic Growth Computational Modelling—Present Day
5. Dendritic Growth in Metallic Alloy Systems—Synchrotron X-ray and Neutron Source
6. Outlook
- providing a proper theoretical treatment of the mechanism/s behind the upper primary spacing stability bound under 3D growth conditions;
- determining the reason behind the history dependence of primary spacing distribution for a given set of growth conditions;
- investigating 3D lateral translation and providing a mechanism behind this phenomenon;
- understanding the relationship between strain and misorientation;
- quantifying the influence of convection within the melt on primary spacing variation;
- comparing microgravity experiments and PF modelling of diffusive directional dendritic growth with identical terrestrial experiments;
- reducing the influence of grid anisotropy in CA to enable quantitative modelling of micro-macroscopic scale phenomena;
- improving computational efficiency of PF modelling to facilitate larger scale simulations with convective melt flow;
- utilising synchrotron X-ray and neutron sources for further investigation into directional dendritic growth theory and ascertaining metallic phenomenological parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ivantsov, G. Diffusion Supercooling during the Solidification of a Binary Alloy. Dokl. Akad. Nauk SSSR 1951, 81, 179–182. [Google Scholar]
- Tiller, W.; Jackson, K.; Rutter, J.; Chalmers, B. The redistribution of solute atoms during the solidification of metals. Acta Metall. 1953, 1, 428–437. [Google Scholar] [CrossRef]
- Singer, H. Measurements of the three-dimensional shape of ice crystals in supercooled water. Phys. Rev. E 2006, 73, 051606. [Google Scholar] [CrossRef]
- McCartney, D.; Hunt, J. Measurements of cell and primary dendrite arm spacings in directionally solidified aluminium alloys. Acta Metall. 1981, 29, 1851–1863. [Google Scholar] [CrossRef]
- D’Souza, N.; Beanland, R.; Hayward, C.; Dong, H. Accuracy of composition measurement using X-ray spectroscopy in precipitate-strengthened alloys: Application to Ni-base superalloys. Acta Mater. 2011, 59, 1003–1013. [Google Scholar] [CrossRef]
- D’souza, N.; Dong, H. Solidification path in third-generation Ni-based superalloys, with an emphasis on last stage solidification. Scr. Mater. 2007, 56, 41–44. [Google Scholar] [CrossRef]
- Dong, H.; Wang, W.; Lee, P.D. Simulation of the thermal history dependence of primary spacing during directional solidification. Superalloys 2004 2004, 925–931. Available online: https://pdfs.semanticscholar.org/887e/23d1e65f07b748e0289c7f4b40d321a7162f.pdf (accessed on 20 July 2020).
- Welton, D.; D’Souza, N.; Kelleher, J.; Gardner, S.; Dong, Z.; West, G.; Dong, H. Discontinuous precipitation in Ni-base superalloys during solution heat treatment. Metall. Mater. Trans. A 2015, 46, 4298–4315. [Google Scholar] [CrossRef] [Green Version]
- Pang, H.T.; D’Souza, N.; Dong, H.; Stone, H.J.; Rae, C.M. Detailed Analysis of the Solution Heat Treatment of a Third-Generation Single-Crystal Nickel-Based Superalloy CMSX-10K®. Metall. Mater. Trans. A 2016, 47, 889–906. [Google Scholar] [CrossRef] [Green Version]
- Brundidge, C.; Van Drasek, D.; Wang, B.; Pollock, T. Structure refinement by a liquid metal cooling solidification process for single-crystal nickel-base superalloys. Metall. Mater. Trans. A 2012, 43, 965–976. [Google Scholar] [CrossRef]
- Hui, J.; Tiwari, R.; Wu, X.; Tewari, S.N.; Trivedi, R. Primary dendrite distribution and disorder during directional solidification of Pb-Sb alloys. Metall. Mater. Trans. A 2002, 33, 3499–3510. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Liu, L.; Yu, Z.; Zhang, W.; Zhang, J.; Fu, H. Influence of directional solidification variables on the microstructure and crystal orientation of AM3 under high thermal gradient. J. Mater. Sci. 2010, 45, 6101–6107. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, L. Solidification microstructure of directionally solidified superalloy under high temperature gradient. Rare Met. 2012, 31, 541–546. [Google Scholar] [CrossRef]
- Trivedi, R.; Mason, J. The effects of interface attachment kinetics on solidification interface morphologies. Metall. Trans. A 1991, 22, 235–249. [Google Scholar] [CrossRef]
- Liu, L.; Huang, T.; Qu, M.; Liu, G.; Zhang, J.; Fu, H. High thermal gradient directional solidification and its application in the processing of nickel-based superalloys. J. Mater. Process. Technol. 2010, 210, 159–165. [Google Scholar] [CrossRef]
- Ramsperger, M.; Singer, R.F.; Körner, C. Microstructure of the nickel-base superalloy CMSX-4 fabricated by selective electron beam melting. Metall. Mater. Trans. A 2016, 47, 1469–1480. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Ma, D.; Zhang, J.; Bogner, S.; Bührig-Polaczek, A. A high thermal gradient directional solidification method for growing superalloy single crystals. J. Mater. Process. Technol. 2014, 214, 3112–3121. [Google Scholar] [CrossRef]
- Brundidge, C.; Miller, J.; Pollock, T. Development of dendritic structure in the liquid-metal-cooled, directional-solidification process. Metall. Mater. Trans. A 2011, 42, 2723–2732. [Google Scholar] [CrossRef]
- Rezaei, M.; Kermanpur, A.; Sadeghi, F. Effects of withdrawal rate and starter block size on crystal orientation of a single crystal Ni-based superalloy. J. Cryst. Growth 2018, 485, 19–27. [Google Scholar] [CrossRef]
- Lamm, M.; Singer, R. The effect of casting conditions on the high-cycle fatigue properties of the single-crystal nickel-base superalloy PWA 1483. Metall. Mater. Trans. A 2007, 38, 1177–1183. [Google Scholar] [CrossRef]
- Wilson, B.; Cutler, E.; Fuchs, G. Effect of solidification parameters on the microstructures and properties of CMSX-10. Mater. Sci. Eng. A 2008, 479, 356–364. [Google Scholar] [CrossRef]
- Quaresma, J.M.; Santos, C.A.; Garcia, A. Correlation between unsteady-state solidification conditions, dendrite spacings, and mechanical properties of Al-Cu alloys. Metall. Mater. Trans. A 2000, 31, 3167–3178. [Google Scholar] [CrossRef]
- Goulart, P.R.; Spinelli, J.E.; Osório, W.R.; Garcia, A. Mechanical properties as a function of microstructure and solidification thermal variables of Al–Si castings. Mater. Sci. Eng. A 2006, 421, 245–253. [Google Scholar] [CrossRef]
- Osorio, W.R.; Goulart, P.R.; Garcia, A.; Santos, G.A.; Neto, C.M. Effect of dendritic arm spacing on mechanical properties and corrosion resistance of Al 9 Wt Pct Si and Zn 27 Wt Pct Al alloys. Metall. Mater. Trans. A 2006, 37, 2525–2538. [Google Scholar] [CrossRef] [Green Version]
- Whitesell, H.; Overfelt, R. Influence of solidification variables on the microstructure, macrosegregation, and porosity of directionally solidified Mar-M247. Mater. Sci. Eng. A 2001, 318, 264–276. [Google Scholar] [CrossRef]
- Elliott, A.; Pollock, T.; Tin, S.; King, W.; Huang, S.-C.; Gigliotti, M. Directional solidification of large superalloy castings with radiation and liquid-metal cooling: A comparative assessment. Metall. Mater. Trans. A 2004, 35, 3221–3231. [Google Scholar] [CrossRef]
- Melo, M.; Rizzo, E.; Santos, R. Predicting dendrite arm spacing and their effect on microporosity formation in directionally solidified Al-Cu alloy. J. Mater. Sci. 2005, 40, 1599–1609. [Google Scholar] [CrossRef]
- Yue, Q.; Liu, L.; Yang, W.; Huang, T.; Zhang, J.; Fu, H.; Zhao, X. Influence of withdrawal rate on the porosity in a third-generation Ni-based single crystal superalloy. Prog. Nat. Sci. Mater. Int. 2017, 27, 236–243. [Google Scholar] [CrossRef]
- Yang, X. Simulation of Stray Grain Formation in Single Crystal Ni-Based Superalloy Turbine Blades. Ph.D. Thesis, Imperial College London (University of London), London, UK, 2005. [Google Scholar]
- Giamei, A.F.; Kear, B. On the nature of freckles in nickel base superalloys. Metall. Trans. 1970, 1, 2185–2192. [Google Scholar] [CrossRef]
- Matache, G.; Stefanescu, D.; Puscasu, C.; Alexandrescu, E. Dendritic segregation and arm spacing in directionally solidified CMSX-4 superalloy. Int. J. Cast Met. Res. 2016, 29, 303–316. [Google Scholar] [CrossRef]
- Stanford, N.; Djakovic, A.; Shollock, B.; McLean, M.; D’Souza, N.; Jennings, P. Defect grains in the melt-back region of CMSX-4 single crystal seeds. Superalloys 2004, 2004, 719–726. [Google Scholar]
- Tiryakioğlu, M. On the statistical distribution of primary and secondary dendrite arm spacing in cast metals. Mater. Sci. Technol. 2019, 35, 509–511. [Google Scholar] [CrossRef]
- Ghosh, S.; Ma, L.; Ofori-Opoku, N.; Guyer, J.E. On the primary spacing and microsegregation of cellular dendrites in laser deposited Ni–Nb alloys. Model. Simul. Mater. Sci. Eng. 2017, 25, 065002. [Google Scholar] [CrossRef]
- Santos, G.; Goulart, P.R.; Couto, A.A.; Garcia, A. Primary dendrite arm spacing effects upon mechanical properties of an Al–3wt% cu–1wt% li alloy. In Properties and Characterization of Modern Materials; Springer: Singapore, 2017; pp. 215–229. [Google Scholar]
- Tschopp, M.A.; Miller, J.D.; Oppedal, A.L.; Solanki, K.N. Evaluating local primary dendrite arm spacing characterization techniques using synthetic directionally solidified dendritic microstructures. Metall. Mater. Trans. A 2015, 46, 4610–4628. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Miller, J.D.; Oppedal, A.L.; Solanki, K.N. Characterizing the local primary dendrite arm spacing in directionally solidified dendritic microstructures. Metall. Mater. Trans. A 2014, 45, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Li, J.; Wang, J.; Zhou, Y. Phase field modeling the selection mechanism of primary dendritic spacing in directional solidification. Acta Mater. 2012, 60, 1957–1964. [Google Scholar] [CrossRef]
- Trivedi, R.; Mazumder, P.; Tewari, S. The effect of convection on disorder in primary cellular and dendritic arrays. Metall. Mater. Trans. A 2002, 33, 3763–3775. [Google Scholar] [CrossRef]
- Ma, D.; Sahm, P.R. Primary spacing in directional solidification. Metall. Mater. Trans. A 1998, 29, 1113–1119. [Google Scholar] [CrossRef]
- Gandin, C.A.; Eshelman, M.; Trivedi, R. Orientation dependence of primary dendrite spacing. Metall. Mater. Trans. A 1996, 27, 2727–2739. [Google Scholar] [CrossRef]
- Ivantsov, G. Temperature field around a spherical, cylindrical, and needle-shaped crystal, growing in a pre-cooled melt. Dokl. Akad. Nauk SSSR 1947, 58, 567–569. [Google Scholar]
- Temkin, D. Growth rate of the needle-crystal formed in a supercoled melt. Dokl. Akad. Nauk SSSR 1960, 132, 1307–1310. [Google Scholar]
- Amar, M.B.; Pomeau, Y. Theory of dendritic growth in a weakly undercooled melt. EPL 1986, 2, 307. [Google Scholar] [CrossRef]
- Hunt, J.D. Solidification and Casting of Metals; The Metals Society: London, UK, 1979; pp. 3–9. [Google Scholar]
- Kurz, W.; Fisher, D. Dendrite growth at the limit of stability: Tip radius and spacing. Acta Metall. 1981, 29, 11–20. [Google Scholar] [CrossRef]
- Trivedi, R. Interdendritic spacing: Part II. A comparison of theory and experiment. Metall. Mater. Trans. A 1984, 15, 977–982. [Google Scholar] [CrossRef]
- Han, S.H.; Trivedi, R. Primary spacing selection in directionally solidified alloys. Acta Metall. Mater. 1994, 42, 25–41. [Google Scholar] [CrossRef]
- Hunt, J.; Lu, S.-Z. Numerical modeling of cellular/dendritic array growth: Spacing and structure predictions. Metall. Mater. Trans. A 1996, 27, 611–623. [Google Scholar] [CrossRef]
- Bouchard, D.; Kirkaldy, J.S. Prediction of dendrite arm spacings in unsteady-and steady-state heat flow of unidirectionally solidified binary alloys. Metall. Mater. Trans. B 1997, 28, 651–663. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J.; Trivedi, R. Progress in modelling solidification microstructures in metals and alloys: Dendrites and cells from 1700 to 2000. Int. Mater. Rev. 2019, 64, 311–354. [Google Scholar] [CrossRef]
- Kurz, W.; Rappaz, M.; Trivedi, R. Progress in modelling solidification microstructures in metals and alloys. Part II: Dendrites from 2001 to 2018. Int. Mater. Rev. 2020, 1–47. Available online: https://iom3.tandfonline.com/action/doSearch?AllField=2020&SeriesKey=yimr20&pageSize=10&subjectTitle=&startPage=2 (accessed on 16 July 2020). [CrossRef]
- Papapetrou, A. Untersuchungen über dendritisches Wachstum von Kristallen. Z. für Krist.-Cryst. Mater. 1935, 92, 89–130. [Google Scholar] [CrossRef]
- Horvay, G.; Cahn, J. Dendritic and spheroidal growth. Acta Metall. 1961, 9, 695–705. [Google Scholar] [CrossRef]
- Zener, C. Kinetics of the decomposition of austenite. Trans. AIME 1946, 167, 550–595. [Google Scholar]
- Hillert, M. The role of interfacial energy during solid-state phase transformations. Jernkontorets Ann. 1957, 141, 757–789. [Google Scholar]
- Bolling, G.; Tiller, W. Growth from the melt. III. Dendritic growth. J. Appl. Phys. 1961, 32, 2587–2605. [Google Scholar] [CrossRef]
- Kotler, G.; Tarshis, L. An extension to the analysis of dendritic growth in pure systems. J. Cryst. Growth 1969, 5, 90–98. [Google Scholar] [CrossRef]
- Trivedi, R. Growth of dendritic needles from a supercooled melt. Acta Metall. 1970, 18, 287–296. [Google Scholar] [CrossRef]
- Trivedi, R. The role of interfacial free energy and interface kinetics during the growth of precipitate plates and needles. Metall. Trans. 1970, 1, 921. [Google Scholar]
- Nash, G.E. Capillarity-Limited Steady-State Dendritic Growth. Part 1. Theoretical Development; Naval Research Lab: Washington, DC, USA, 1974. [Google Scholar]
- Jackson, K.; Hunt, J. Transparent compounds that freeze like metals. Acta Metall. 1965, 13, 1212–1215. [Google Scholar] [CrossRef]
- Jackson, K.; Uhlmann, D.R.; Hunt, J. On the nature of crystal growth from the melt. J. Cryst. Growth 1967, 1, 1–36. [Google Scholar] [CrossRef]
- Glicksman, M.; Schaefer, R.; Ayers, J. Dendritic growth-a test of theory. Metall. Trans. A 1976, 7, 1747–1759. [Google Scholar] [CrossRef]
- Chopra, M.; Glicksman, M.; Singh, N. Dendritic solidification in binary alloys. Metall. Trans. A 1988, 19, 3087–3096. [Google Scholar] [CrossRef]
- Huang, S.-C.; Glicksman, M. Overview 12: Fundamentals of dendritic solidification—I. Steady-state tip growth. Acta Metall. 1981, 29, 701–715. [Google Scholar] [CrossRef]
- Oldfield, W. Computer model studies of dendritic growth. Mater. Sci. Eng. 1973, 11, 211–218. [Google Scholar] [CrossRef]
- Langer, J.; Müller-Krumbhaar, J. Stability effects in dendritic crystal growth. J. Cryst. Growth 1977, 42, 11–14. [Google Scholar] [CrossRef]
- Langer, J.; Müller-Krumbhaar, H. Theory of dendritic growth—I. Elements of a stability analysis. Acta Metall. 1978, 26, 1681–1687. [Google Scholar] [CrossRef]
- Mullins, W.W.; Sekerka, R.F. Morphological stability of a particle growing by diffusion or heat flow. J. Appl. Phys. 1963, 34, 323–329. [Google Scholar] [CrossRef]
- Mullins, W.W.; Sekerka, R. Stability of a planar interface during solidification of a dilute binary alloy. J. Appl. Phys. 1964, 35, 444–451. [Google Scholar] [CrossRef]
- Trivedi, R.; Kurz, W. Dendritic growth. Int. Mater. Rev. 1994, 39, 49–74. [Google Scholar] [CrossRef]
- Bensimon, D.; Pelcé, P.; Shraiman, B.I. Dynamics of curved fronts and pattern selection. J. Phys. 1987, 48, 2081–2087. [Google Scholar] [CrossRef]
- Ben-Jacob, E.; Goldenfeld, N.; Langer, J.; Schön, G. Dynamics of interfacial pattern formation. Phys. Rev. Lett. 1983, 51, 1930. [Google Scholar] [CrossRef]
- Brower, R.C.; Kessler, D.A.; Koplik, J.; Levine, H. Geometrical approach to moving-interface dynamics. Phys. Rev. Lett. 1983, 51, 1111. [Google Scholar] [CrossRef]
- Meiron, D.I. Selection of steady states in the two-dimensional symmetric model of dendritic growth. Phys. Rev. A 1986, 33, 2704. [Google Scholar] [CrossRef] [Green Version]
- Barbieri, A.; Hong, D.C.; Langer, J.S. Velocity selection in the symmetric model of dendritic crystal growth. Phys. Rev. A 1987, 35, 1802–1808. [Google Scholar] [CrossRef]
- Pelce, P.; Pomeau, Y. Dendrites in the small undercooling limit. In Dynamics of Curved Fronts; Academic Press: Boston, UK, 1988; pp. 327–340. [Google Scholar]
- Kessler, D.A.; Levine, H. Stability of Dendritic Crystals. Phys. Rev. Lett. 1986, 57, 3069–3072. [Google Scholar] [CrossRef]
- Ben-Jacob, E.; Garik, P. The formation of patterns in non-equilibrium growth. Nature 1990, 343, 523. [Google Scholar] [CrossRef] [Green Version]
- Muschol, M.; Liu, D.; Cummins, H. Surface-tension-anisotropy measurements of succinonitrile and pivalic acid: Comparison with microscopic solvability theory. Phys. Rev. A 1992, 46, 1038. [Google Scholar] [CrossRef]
- Glicksman, M.; Winsa, E.; Hahn, R.; Lograsso, T.; Tirmizi, S.; Selleck, M. Isothermal dendritic growth—A proposed microgravity experiment. Metall. Trans. A 1988, 19, 1945–1953. [Google Scholar] [CrossRef]
- LaCombe, J.; Koss, M.; Fradkov, V.; Glicksman, M. Three-dimensional dendrite-tip morphology. Phys. Rev. E 1995, 52, 2778. [Google Scholar] [CrossRef]
- Glicksman, M.E.; Koss, M.B.; Bushnell, L.T.; Lacombe, J.C.; Winsa, E.A. Dendritic growth of succinonitrile in terrestrial and microgravity conditions as a test of theory. ISIJ Int. 1995, 35, 604–610. [Google Scholar] [CrossRef]
- Glicksman, M.; Koss, M.; Winsa, E. Dendritic growth velocities in microgravity. Phys. Rev. Lett. 1994, 73, 573. [Google Scholar] [CrossRef]
- Tennenhouse, L.; Koss, M.; LaCombe, J.; Glicksman, M. Use of microgravity to interpret dendritic growth kinetics at small supercoolings. J. Cryst. Growth 1997, 174, 82–89. [Google Scholar] [CrossRef]
- Koss, M.; LaCombe, J.; Tennenhouse, L.; Glicksman, M.; Winsa, E. Dendritic growth tip velocities and radii of curvature in microgravity. Metall. Mater. Trans. A 1999, 30, 3177–3190. [Google Scholar] [CrossRef]
- Lee, Y.-W.; Smith, R.N.; Glicksman, M.E.; Koss, M.B. Effects of buoyancy on the growth of dendritic crystals. Annu. Rev. Heat Transf. 1996, 7, 59–139. [Google Scholar] [CrossRef]
- Bower, T.F.; Brody, H.; Flemings, M.C. Measurements of solute redistribution in dendritic solidification. AIME Met. Soc. Trans. 1966, 236, 624–634. [Google Scholar]
- Burden, M.; Hunt, J. Cellular and dendritic growth. II. J. Cryst. Growth 1974, 22, 109–116. [Google Scholar] [CrossRef]
- Trivedi, R. Theory of dendritic growth during the directional solidification of binary alloys. J. Cryst. Growth 1980, 49, 219–232. [Google Scholar] [CrossRef]
- Mason, J.T.; Verhoeven, J.; Trivedi, R. Primary dendrite spacing I. Experimental studies. J. Cryst. Growth 1982, 59, 516–524. [Google Scholar] [CrossRef]
- Somboonsuk, K.; Mason, J.; Trivedi, R. Interdendritic spacing: Part I. Experimental studies. Metall. Mater. Trans. A 1984, 15, 967–975. [Google Scholar] [CrossRef]
- Venugopalan, D.; Kirkaldy, J. Theory of cellular solidification of binary alloys with applications to succinonitrile-salol. Acta Metall. 1984, 32, 893–906. [Google Scholar] [CrossRef]
- Eshelman, M.; Seetharaman, V.; Trivedi, R. Cellular spacings—I. Steady-state growth. Acta Metall. 1988, 36, 1165–1174. [Google Scholar] [CrossRef]
- Somboonsuk, K.; Trivedi, R. Dynamical studies of dendritic growth. Acta Metall. 1985, 33, 1051–1060. [Google Scholar] [CrossRef]
- Trivedi, R.; Somboonsuk, K. Pattern formation during the directional solidification of binary systems. Acta Metall. 1985, 33, 1061–1068. [Google Scholar] [CrossRef]
- Amar, M.B.; Moussallam, B. Absence of selection in directional solidification. Phys. Rev. Lett. 1988, 60, 317. [Google Scholar] [CrossRef] [PubMed]
- Dombre, T.; Hakim, V. Saffman-Taylor fingers and directional solidification at low velocity. Phys. Rev. A 1987, 36, 2811. [Google Scholar] [CrossRef] [PubMed]
- Quested, P.; McLean, M. Solidification morphologies in directionally solidified superalloys. Mater. Sci. Eng. 1984, 65, 171–180. [Google Scholar] [CrossRef]
- Chopra, M.; Tewari, S. Growth-speed dependence of primary arm spacings in directionally solidified Pb-10 Wt Pct Sn. Metall. Trans. A 1991, 22, 2467–2474. [Google Scholar] [CrossRef]
- Warren, J.A.; Langer, J. Stability of dendritic arrays. Phys. Rev. A 1990, 42, 3518. [Google Scholar] [CrossRef]
- Warren, J.A.; Langer, J. Prediction of dendritic spacings in a directional-solidification experiment. Phys. Rev. E 1993, 47, 2702. [Google Scholar] [CrossRef]
- Ding, G.; Huang, W.; Lin, X.; Zhou, Y. Prediction of average spacing for constrained cellular/dendritic growth. J. Cryst. Growth 1997, 177, 281–288. [Google Scholar] [CrossRef]
- Hunt, J. A numerical analysis of time dependent isolated dendritic growth for conditions near the steady state. Acta Metall. Mater. 1990, 38, 411–418. [Google Scholar] [CrossRef]
- Hunt, J. A numerical analysis of dendritic and cellular growth of a pure material investigating the transition from “array” to “isolated” growth. Acta Metall. Mater. 1991, 39, 2117–2133. [Google Scholar] [CrossRef]
- Lu, S.-Z.; Hunt, J. A numerical analysis of dendritic and cellular array growth: The spacing adjustment mechanisms. J. Cryst. Growth 1992, 123, 17–34. [Google Scholar] [CrossRef]
- McCartney, D.; Hunt, J. A numerical finite difference model of steady state cellular and dendritic growth. Metall. Mater. Trans. A 1984, 15, 983–994. [Google Scholar] [CrossRef]
- Hunt, J.; McCartney, D. Numerical finite difference model for steady state cellular array growth. Acta Metall. 1987, 35, 89–99. [Google Scholar] [CrossRef]
- Lu, S.-Z.; Hunt, J.; Gilgien, P.; Kurz, W. Cellular and dendritic growth in rapidly solidified AlFe and AlCu alloys. Acta Metall. Mater. 1994, 42, 1653–1660. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Hunt, J.; Thomas, R. Microscopical Modelling of Binary/Multicomponent Alloys. In Proceedings of the Fourth Decennial International Conference on Solidification Processing, Sheffield, UK, 7–10 July 1997. [Google Scholar]
- Hunt, J. Pattern formation in solidification. Sci. Technol. Adv. Mater. 2001, 2, 147–155. [Google Scholar] [CrossRef]
- Weidong, H.; Xingguo, G.; Yaohe, Z. Primary spacing selection of constrained dendritic growth. J. Cryst. Growth 1993, 134, 105–115. [Google Scholar] [CrossRef]
- Ding, G.; Huang, W.; Huang, X.; Lin, X.; Zhou, Y. On primary dendritic spacing during unidirectional solidification. Acta Mater. 1996, 44, 3705–3709. [Google Scholar] [CrossRef]
- Weidong, H. Non-steady state process and interface pattern selection of a single-phase alloy during unidirectional solidification. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 1989. [Google Scholar]
- Losert, W.; Shi, B.; Cummins, H.; Warren, J.A. Spatial period-doubling instability of dendritic arrays in directional solidification. Phys. Rev. Lett. 1996, 77, 889. [Google Scholar] [CrossRef]
- Wan, X.; Han, Q.; Hunt, J. Different growth regimes during directional dendritic growth. Acta Mater. 1997, 45, 3975–3979. [Google Scholar] [CrossRef]
- Esaka, H. Dendrite growth and spacing in succinonitrile-acetone alloys. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 1986. [Google Scholar]
- Losert, W.; Mesquita, O.; Figueiredo, J.; Cummins, H. Direct measurement of dendritic array stability. Phys. Rev. Lett. 1998, 81, 409. [Google Scholar] [CrossRef]
- Losert, W.; Shi, B.; Cummins, H. Evolution of dendritic patterns during alloy solidification: From the initial instability to the steady state. Proc. Natl. Acad. Sci. USA 1998, 95, 439–442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bouchard, D.; Kirkaldy, J. Scaling of intragranuiar dendritic microstructure in ingot solidification. Metall. Mater. Trans. B 1996, 27, 101–113. [Google Scholar] [CrossRef]
- Kirkaldy, J.; Venugopalan, D. Pattern selection relations for deep-rooted binary alloy cells. Scr. Metall. 1989, 23, 1603–1608. [Google Scholar] [CrossRef]
- Spencer, B.J.; Huppert, H.E. On the solidification of dendritic arrays: An asymptotic theory for the directional solidification of slender needle crystals. Acta Mater. 1997, 45, 1535–1549. [Google Scholar] [CrossRef]
- Spencer, B.; Huppert, H. On the solidification of dendritic arrays: Selection of the tip characteristics of slender needle crystals by array interactions. Acta Mater. 1998, 46, 2645–2662. [Google Scholar] [CrossRef] [Green Version]
- Ma, D. Modeling of primary spacing selection in dendrite arrays during directional solidification. Metall. Mater. Trans. B 2002, 33, 223–233. [Google Scholar] [CrossRef]
- Ma, D. Response of primary dendrite spacing to varying temperature gradient during directional solidification. Metall. Mater. Trans. B 2004, 35, 735–742. [Google Scholar] [CrossRef]
- Aveson, J.; Reinhart, G.; Goddard, C.; Nguyen-Thi, H.; Mangelinck-Noël, N.; Tandjaoui, A.; Davenport, J.; Warnken, N.; Di Gioacchino, F.; Lafford, T. On the Deformation of Dendrites During Directional Solidification of a Nickel-Based Superalloy. Metall. Mater. Trans. A 2019, 50, 5234–5241. [Google Scholar] [CrossRef] [Green Version]
- Siredey, N.; Boufoussi, M.B.; Denis, S.; Lacaze, J. Dendritic growth and crystalline quality of nickel-base single grains. J. Cryst. Growth 1993, 130, 132–146. [Google Scholar] [CrossRef]
- Husseini, N.S.; Kumah, D.P.; Jian, Z.Y.; Torbet, C.J.; Arms, D.A.; Dufresne, E.M.; Pollock, T.M.; Jones, J.W.; Clarke, R. Mapping single-crystal dendritic microstructure and defects in nickel-base superalloys with synchrotron radiation. Acta Mater. 2008, 56, 4715–4723. [Google Scholar] [CrossRef]
- Van Hoose, J.; Grugel, R.; Tewari, S.; Brush, L.; Erdmann, R.; Poirier, D.R. Observation of Misoriented Tertiary Dendrite Arms During Controlled Directional Solidification in Aluminum-7 Wt pct Silicon Alloys. Metall. Mater. Trans. A 2012, 43, 4724–4731. [Google Scholar] [CrossRef]
- D’Souza, N.; Newell, M.; Devendra, K.; Jennings, P.; Ardakani, M.; Shollock, B. Formation of low angle boundaries in Ni-based superalloys. Mater. Sci. Eng. A 2005, 413, 567–570. [Google Scholar] [CrossRef]
- Newell, M.; Devendra, K.; Jennings, P.; D’Souza, N. Role of dendrite branching and growth kinetics in the formation of low angle boundaries in Ni–base superalloys. Mater. Sci. Eng. A 2005, 412, 307–315. [Google Scholar] [CrossRef]
- Newell, M.; D’Souza, N.; Green, N. Formation of low angle boundaries in Ni-based superalloys. Int. J. Cast Met. Res. 2009, 22, 66–69. [Google Scholar] [CrossRef]
- Aveson, J.; Tennant, P.; Foss, B.; Shollock, B.; Stone, H.; D’Souza, N. On the origin of sliver defects in single crystal investment castings. Acta Mater. 2013, 61, 5162–5171. [Google Scholar] [CrossRef]
- Hallensleben, P.; Scholz, F.; Thome, P.; Schaar, H.; Steinbach, I.; Eggeler, G.; Frenzel, J. On crystal mosaicity in single crystal Ni-based superalloys. Crystals 2019, 9, 149. [Google Scholar] [CrossRef] [Green Version]
- Bogdanowicz, W.; Krawczyk, J.; Paszkowski, R.; Sieniawski, J. Primary crystal orientation of the thin-walled area of single-crystalline turbine blade airfoils. Materials 2019, 12, 2699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huo, M.; Liu, L.; Yang, W.; Hu, S.; Sun, D.; Su, H.; Zhang, J.; Fu, H. Dendrite growth and defects formation with increasing withdrawal rates in the rejoined platforms of Ni-based single crystal superalloys. Vacuum 2019, 161, 29–36. [Google Scholar] [CrossRef]
- Ananth, R.; Gill, W.N. Dendritic growth in microgravity and forced convection. J. Cryst. Growth 1997, 179, 263–276. [Google Scholar] [CrossRef]
- Das, S.K.; Gill, W.N. Foced convection heat and momentum transfer to dendritic structures (parabolic cylinders and paraboloids of revolution). Int. J. Heat Mass Transf. 1984, 27, 1345–1356. [Google Scholar]
- KIND, M.; GILL, W.N.; ANANTH, R. The growth of ice dendrites under mixed convection conditions. Chem. Eng. Commun. 1987, 55, 295–312. [Google Scholar] [CrossRef]
- Tirmizi, S.H.; Gill, W.N. Effect of natural convection on growth velocity and morphology of dendritic ice crystals. J. Cryst. Growth 1987, 85, 488–502. [Google Scholar] [CrossRef]
- Ananth, R.; Gill, W.N. Dendritic growth with thermal convection. J. Cryst. Growth 1988, 91, 587–598. [Google Scholar] [CrossRef]
- Lee, Y.-W.; Ananth, R.; Gill, W.N. Selection of a length scale in unconstrained dendritic growth with convection in the melt. J. Cryst. Growth 1993, 132, 226–230. [Google Scholar] [CrossRef]
- Beckermann, C.; Diepers, H.-J.; Steinbach, I.; Karma, A.; Tong, X. Modeling melt convection in phase-field simulations of solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Lipton, J.; Glicksman, M.; Kurz, W. Dendritic growth into undercooled alloy metals. Mater. Sci. Eng. 1984, 65, 57–63. [Google Scholar] [CrossRef]
- Trivedi, R.; Kurz, W. Theory of microstructural development during rapid solidification. In Science and Technology of the Undercooled Melt; Springer: Dordrecht, The Netherlands, 1986; pp. 260–267. [Google Scholar]
- Yuan, L.; Lee, P.D.; Djambazov, G.; Pericleous, K. Numerical simulation of the effect of fluid flow on solute distribution and dendritic morphology. Int. J. Cast Met. Res. 2009, 22, 204–207. [Google Scholar] [CrossRef]
- Yuan, L.; Lee, P.D. Dendritic solidification under natural and forced convection in binary alloys: 2D versus 3D simulation. Modell. Simul. Mater. Sci. Eng. 2010, 18, 055008. [Google Scholar] [CrossRef]
- Zhu, M.F.; Lee, S.Y.; Hong, C.P. Modified cellular automaton model for the prediction of dendritic growth with melt convection. PhRvE 2004, 69, 061610. [Google Scholar] [CrossRef]
- Zhu, M.-F.; Dai, T.; Lee, S.-Y.; Hong, C.-P. Modeling of solutal dendritic growth with melt convection. Comput. Math. Appl. 2008, 55, 1620–1628. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Heinrich, J.; Poirier, D.R. Numerical modeling of fluid–particle interactions. Comput. Methods Appl. Mech. Eng. 2006, 195, 5780–5796. [Google Scholar] [CrossRef]
- Yang, X.L.; Dong, H.B.; Wang, W.; Lee, P.D. Microscale simulation of stray grain formation in investment cast turbine blades. Mater. Sci. Eng. A 2004, 386, 129–139. [Google Scholar] [CrossRef]
- Yang, X.; Ness, D.; Lee, P.D.; D’Souza, N. Simulation of stray grain formation during single crystal seed melt-back and initial withdrawal in the Ni-base superalloy CMSX4. Mater. Sci. Eng. A 2005, 413–414, 571–577. [Google Scholar] [CrossRef]
- Lee, P.D.; Chirazi, A.; Atwood, R.C.; Wang, W. Multiscale modelling of solidification microstructures, including microsegregation and microporosity, in an Al–Si–Cu alloy. Mater. Sci. Eng. A 2004, 365, 57–65. [Google Scholar] [CrossRef]
- Wang, W.; Kermanpur, A.; Lee, P.D.; McLean, M. Simulation of dendritic growth in the platform region of single crystal superalloy turbine blades. JMatS 2003, 38, 4385–4391. [Google Scholar]
- Sun, Q.Y.; Ren, Y.; Liu, D.-R. Numerical investigations of freckles in directionally solidified nickel-based superalloy casting with abrupt contraction in cross section. Results Phys. 2019, 12, 1547–1558. [Google Scholar] [CrossRef]
- Chen, R.; Xu, Q.; Liu, B. Cellular automaton simulation of three-dimensional dendrite growth in Al–7Si–Mg ternary aluminum alloys. Comput. Mater. Sci. 2015, 105, 90–100. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhao, J. Dendritic microstructure formation in a directionally solidified Al–11.6 Cu–0.85 Mg alloy. J. Cryst. Growth 2014, 391, 52–58. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Perspectives for cellular automata for the simulation of dendritic solidification–A review. Comput. Mater. Sci. 2014, 95, 213–220. [Google Scholar] [CrossRef]
- Dong, H.; Yang, X.; Lee, P.; Wang, W. Simulation of equiaxed growth ahead of an advancing columnar front in directionally solidified Ni-based superalloys. J. Mater. Sci. 2004, 39, 7207–7212. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.-J. Phase-field simulation of three-dimensional dendrites: Is microscopic solvability theory correct? J. Cryst. Growth 1997, 174, 54–64. [Google Scholar] [CrossRef]
- Takaki, T.; Shimokawabe, T.; Ohno, M.; Yamanaka, A.; Aoki, T. Unexpected selection of growing dendrites by very-large-scale phase-field simulation. J. Cryst. Growth 2013, 382, 21–25. [Google Scholar] [CrossRef]
- Kobayashi, R.; Warren, J.; Carter, W. Mathematical models for solidification and grain boundary formation. Achmodels Chem. 1998, 135, 287–295. [Google Scholar]
- Amoorezaei, M.; Gurevich, S.; Provatas, N. Orientation selection in solidification patterning. Acta Mater. 2012, 60, 657–663. [Google Scholar] [CrossRef]
- Eiken, J. Dendritic growth texture evolution in Mg-based alloys investigated by phase-field simulation. Int. J. Cast Met. Res. 2009, 22, 86–89. [Google Scholar] [CrossRef]
- Tourret, D.; Karma, A. Growth competition of columnar dendritic grains: A phase-field study. Acta Mater. 2015, 82, 64–83. [Google Scholar] [CrossRef]
- Takaki, T.; Ohno, M.; Shimokawabe, T.; Aoki, T. Two-dimensional phase-field simulations of dendrite competitive growth during the directional solidification of a binary alloy bicrystal. Acta Mater. 2014, 81, 272–283. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wang, Y.; Wang, J. Phase-field study of competitive dendritic growth of converging grains during directional solidification. Acta Mater. 2012, 60, 1478–1493. [Google Scholar] [CrossRef]
- Amoorezaei, M.; Gurevich, S.; Provatas, N. Spacing characterization in Al–Cu alloys directionally solidified under transient growth conditions. Acta Mater. 2010, 58, 6115–6124. [Google Scholar] [CrossRef] [Green Version]
- Gurevich, S.; Karma, A.; Plapp, M.; Trivedi, R. Phase-field study of three-dimensional steady-state growth shapes in directional solidification. Phys. Rev. E 2010, 81, 011603. [Google Scholar] [CrossRef]
- Bergeon, N.; Tourret, D.; Chen, L.; Debierre, J.-M.; Guérin, R.; Ramirez, A.; Billia, B.; Karma, A.; Trivedi, R. Spatiotemporal dynamics of oscillatory cellular patterns in three-dimensional directional solidification. Phys. Rev. Lett. 2013, 110, 226102. [Google Scholar] [CrossRef] [Green Version]
- Greenwood, M.; Haataja, M.; Provatas, N. Crossover scaling of wavelength selection in directional solidification of binary alloys. Phys. Rev. Lett. 2004, 93, 246101. [Google Scholar] [CrossRef] [Green Version]
- Steinbach, I. Effect of interface anisotropy on spacing selection in constrained dendrite growth. Acta Mater. 2008, 56, 4965–4971. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, B.; Hou, H.; Chen, W.; Wang, M. Phase-field simulation for the evolution of solid/liquid interface front in directional solidification process. J. Mater. Sci. Technol. 2019, 35, 1044–1052. [Google Scholar] [CrossRef]
- Takaki, T.; Fukuoka, T.; Tomita, Y. Phase-field simulation during directional solidification of a binary alloy using adaptive finite element method. J. Cryst. Growth 2005, 283, 263–278. [Google Scholar] [CrossRef] [Green Version]
- Gurevich, S.; Amoorezaei, M.; Montiel, D.; Provatas, N. Evolution of microstructural length scales during solidification of magnesium alloys. Acta Mater. 2012, 60, 3287–3295. [Google Scholar] [CrossRef]
- Montiel, D.; Gurevich, S.; Ofori-Opoku, N.; Provatas, N. Characterization of late-stage equiaxed solidification of alloys. Acta Mater. 2014, 77, 183–190. [Google Scholar] [CrossRef]
- Echebarria, B.; Karma, A.; Gurevich, S. Onset of sidebranching in directional solidification. Phys. Rev. E 2010, 81, 021608. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Beckermann, C. Effect of solid–liquid density change on dendrite tip velocity and shape selection. J. Cryst. Growth 2009, 311, 4447–4453. [Google Scholar] [CrossRef]
- Galenko, P.; Abramova, E.; Jou, D.; Danilov, D.; Lebedev, V.; Herlach, D.M. Solute trapping in rapid solidification of a binary dilute system: A phase-field study. Phys. Rev. E 2011, 84, 041143. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Danilova, E.V.; Steinbach, I.; Medvedev, D.; Galenko, P.K. Diffuse-interface modeling of solute trapping in rapid solidification: Predictions of the hyperbolic phase-field model and parabolic model with finite interface dissipation. Acta Mater. 2013, 61, 4155–4168. [Google Scholar] [CrossRef]
- Wang, H.; Liu, F.; Ehlen, G.; Herlach, D. Application of the maximal entropy production principle to rapid solidification: A multi-phase-field model. Acta Mater. 2013, 61, 2617–2627. [Google Scholar] [CrossRef]
- Wang, H.; Kuang, W.; Zhang, X.; Liu, F. A hyperbolic phase-field model for rapid solidification of a binary alloy. J. Mater. Sci. 2015, 50, 1277–1286. [Google Scholar] [CrossRef]
- Mullis, A. Prediction of the operating point of dendrites growing under coupled thermosolutal control at high growth velocity. Phys. Rev. E 2011, 83, 061601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akamatsu, S.; Plapp, M. Eutectic and peritectic solidification patterns. Curr. Opin. Solid State Mater. Sci. 2016, 20, 46–54. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, R.; Warren, J.A.; Carter, W.C. A continuum model of grain boundaries. Phys. D Nonlinear Phenom. 2000, 140, 141–150. [Google Scholar] [CrossRef]
- Steinbach, I.; Pezzolla, F.; Nestler, B.; Seeßelberg, M.; Prieler, R.; Schmitz, G.J.; Rezende, J.L. A phase field concept for multiphase systems. Phys. D Nonlinear Phenom. 1996, 94, 135–147. [Google Scholar] [CrossRef]
- Vanherpe, L.; Moelans, N.; Blanpain, B.; Vandewalle, S. Bounding box algorithm for three-dimensional phase-field simulations of microstructural evolution in polycrystalline materials. Phys. Rev. E 2007, 76, 056702. [Google Scholar] [CrossRef] [Green Version]
- Eiken, J.; Böttger, B.; Steinbach, I. Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application. Phys. Rev. E 2006, 73, 066122. [Google Scholar] [CrossRef]
- Choudhury, A.; Nestler, B. Grand-potential formulation for multicomponent phase transformations combined with thin-interface asymptotics of the double-obstacle potential. Phys. Rev. E 2012, 85, 021602. [Google Scholar] [CrossRef] [PubMed]
- Moelans, N. A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater. 2011, 59, 1077–1086. [Google Scholar] [CrossRef] [Green Version]
- Ohno, M. Quantitative phase-field modeling of nonisothermal solidification in dilute multicomponent alloys with arbitrary diffusivities. Phys. Rev. E 2012, 86, 051603. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Steinbach, I. Phase-field model with finite interface dissipation: Extension to multi-component multi-phase alloys. Acta Mater. 2012, 60, 2702–2710. [Google Scholar] [CrossRef]
- Tiaden, J.; Nestler, B.; Diepers, H.-J.; Steinbach, I. The multiphase-field model with an integrated concept for modelling solute diffusion. Phys. D Nonlinear Phenom. 1998, 115, 73–86. [Google Scholar] [CrossRef]
- Bottger, B.; Eiken, J.; Steinbach, I. Multi phase-field approach for alloy solidification. Phys Rev E 2006, 73, 066122–1. [Google Scholar]
- Steinbach, I.; Pezzolla, F. A generalized field method for multiphase transformations using interface fields. Phys. D Nonlinear Phenom. 1999, 134, 385–393. [Google Scholar] [CrossRef]
- Steinbach, I.; Apel, M. Multi phase field model for solid state transformation with elastic strain. Phys. D: Nonlinear Phenom. 2006, 217, 153–160. [Google Scholar] [CrossRef]
- Kim, S.G. A phase-field model with antitrapping current for multicomponent alloys with arbitrary thermodynamic properties. Acta Mater. 2007, 55, 4391–4399. [Google Scholar] [CrossRef]
- Ofori-Opoku, N.; Provatas, N. A quantitative multi-phase field model of polycrystalline alloy solidification. Acta Mater. 2010, 58, 2155–2164. [Google Scholar] [CrossRef]
- Yamanaka, A.; Aoki, T.; Ogawa, S.; Takaki, T. GPU-accelerated phase-field simulation of dendritic solidification in a binary alloy. J. Cryst. Growth 2011, 318, 40–45. [Google Scholar] [CrossRef]
- Shimokawabe, T.; Aoki, T.; Takaki, T.; Endo, T.; Yamanaka, A.; Maruyama, N.; Nukada, A.; Matsuoka, S. Peta-Scale Phase-Field Simulation for Dendritic Solidification on the TSUBAME 2.0 Supercomputer. In Proceedings of the 2011 International Conference for High Performance Computing, Networking, Storage and Analysis, Seattle, WA, USA, 12–18 November 2011; ACM: New York, NY, USA, 2011; p. 3. [Google Scholar]
- Takaki, T.; Sakane, S.; Ohno, M.; Shibuta, Y.; Shimokawabe, T.; Aoki, T. Primary arm array during directional solidification of a single-crystal binary alloy: Large-scale phase-field study. Acta Mater. 2016, 118, 230–243. [Google Scholar] [CrossRef] [Green Version]
- Takaki, T. Phase-field modeling and simulations of dendrite growth. ISIJ Int. 2014, 54, 437–444. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, R. Modeling and numerical simulations of dendritic crystal growth. Phys. D Nonlinear Phenom. 1993, 63, 410–423. [Google Scholar] [CrossRef]
- Bergeon, N.; Ramirez, A.; Chen, L.; Billia, B.; Gu, J.; Trivedi, R. Dynamics of interface pattern formation in 3D alloy solidification: First results from experiments in the DECLIC directional solidification insert on the International Space Station. J. Mater. Sci. 2011, 46, 6191–6202. [Google Scholar] [CrossRef]
- Tourret, D.; Debierre, J.-M.; Song, Y.; Mota, F.L.; Bergeon, N.; Guerin, R.; Trivedi, R.; Billia, B.; Karma, A. Oscillatory cellular patterns in three-dimensional directional solidification. Phys. Rev. E 2015, 92, 042401. [Google Scholar] [CrossRef] [Green Version]
- Bergeon, N.; Trivedi, R.; Billia, B.; Echebarria, B.; Karma, A.; Liu, S.; Weiss, C.; Mangelinck, N. Necessity of investigating microstructure formation during directional solidification of transparent alloys in 3D. Adv. Space Res. 2005, 36, 80–85. [Google Scholar] [CrossRef]
- Ramirez, A.; Chen, L.; Bergeon, N.; Billia, B.; Gu, J.; Trivedi, R. In Situ and Real Time Characterization of Interface Microstructure in 3D Alloy Solidification: BENCHMARK Microgravity Experiments in the DECLIC-Directional Solidification Insert on ISS; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2012; p. 012087. [Google Scholar]
- Sturz, L.; Zimmermann, G.; Rex, S.; Mathes, M.; Kauerauf, B. Analysis of diffusive cellular patterns in directional solidification of bulk samples. Metall. Mater. Trans. A 2004, 35, 239–246. [Google Scholar] [CrossRef]
- Rex, S.; Kauerauf, B.; Zimmermann, G. Directional solidification of cellular arrays in a transparent organic alloy. Adv. Space Res. 2002, 29, 511–520. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, S.; Wei, M.; Peng, L.; Wu, Y.; Ji, Y.; Chen, L.-Q.; Liu, X. Coupling in situ synchrotron X-ray radiography and phase-field simulation to study the effect of low cooling rates on dendrite morphology during directional solidification in Mg–Gd alloys. J. Alloy. Compd. 2020, 815, 152385. [Google Scholar] [CrossRef]
- Yang, M.; Xiong, S.; Guo, Z. Dendrite Morphology and Growth Orientation of Magnesium Alloys: Simulation by Phase-Field and 3-D Characterization by Synchrotron X-Ray Tomography. In Magnesium Technology 2016; Springer: Cham, Switzerland, 2016; pp. 35–39. [Google Scholar]
- Chen, Y.; Li, D.Z.; Billia, B.; Nguyen-Thi, H.; Qi, X.B.; Xiao, N.M. Quantitative phase-field simulation of dendritic equiaxed growth and comparison with in situ observation on Al–4 wt.% Cu alloy by means of synchrotron X-ray radiography. ISIJ Int. 2014, 54, 445–451. [Google Scholar] [CrossRef] [Green Version]
- Mathiesen, R.H.; Arnberg, L.; Mo, F.; Weitkamp, T.; Snigirev, A. Time resolved x-ray imaging of dendritic growth in binary alloys. Phys. Rev. Lett. 1999, 83, 5062. [Google Scholar] [CrossRef]
- Mathiesen, R.; Arnberg, L.; Nguyen-Thi, H.; Billia, B. In situ x-ray video microscopy as a tool in solidification science. JOM 2012, 64, 76–82. [Google Scholar] [CrossRef]
- Shuai, S.; Guo, E.; Phillion, A.; Callaghan, M.D.; Jing, T.; Lee, P.D. Fast synchrotron X-ray tomographic quantification of dendrite evolution during the solidification of MgSn alloys. Acta Mater. 2016, 118, 260–269. [Google Scholar] [CrossRef]
- Cai, B.; Wang, J.; Kao, A.; Pericleous, K.; Phillion, A.; Atwood, R.; Lee, P. 4D synchrotron X-ray tomographic quantification of the transition from cellular to dendrite growth during directional solidification. Acta Mater. 2016, 117, 160–169. [Google Scholar] [CrossRef]
- Cai, B.; Karagadde, S.; Yuan, L.; Marrow, T.; Connolley, T.; Lee, P. In situ synchrotron tomographic quantification of granular and intragranular deformation during semi-solid compression of an equiaxed dendritic Al–Cu alloy. Acta Mater. 2014, 76, 371–380. [Google Scholar] [CrossRef]
- Bogno, A.; Nguyen-Thi, H.; Reinhart, G.; Billia, B.; Baruchel, J. Growth and interaction of dendritic equiaxed grains: In situ characterization by synchrotron X-ray radiography. Acta Mater. 2013, 61, 1303–1315. [Google Scholar] [CrossRef]
- Azeem, M.; Lee, P.; Phillion, A.; Karagadde, S.; Rockett, P.; Atwood, R.; Courtois, L.; Rahman, K.; Dye, D. Revealing dendritic pattern formation in Ni, Fe and Co alloys using synchrotron tomography. Acta Mater. 2017, 128, 241–248. [Google Scholar] [CrossRef] [Green Version]
- Winick, H. Fourth generation light sources. In Proceedings of the 1997 Particle Accelerator Conference (Cat. No. 97CH36167), Vancouver, BC, Canada, 12–16 May 1997; IEEE: New York, NY, USA, 1997; pp. 37–41. [Google Scholar]
- Eriksson, M.; van der Veen, J.F.; Quitmann, C. Diffraction-limited storage rings–a window to the science of tomorrow. J. Synchrotron Radiat. 2014, 21, 837–842. [Google Scholar] [CrossRef]
- Cereser, A.; Strobl, M.; Hall, S.A.; Steuwer, A.; Kiyanagi, R.; Tremsin, A.S.; Knudsen, E.B.; Shinohara, T.; Willendrup, P.K.; da Silva Fanta, A.B. Time-of-flight three dimensional neutron diffraction in transmission mode for mapping crystal grain structures. Sci. Rep. 2017, 7, 9561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kardjilov, N.; Manke, I.; Hilger, A.; Strobl, M.; Banhart, J. Neutron imaging in materials science. Mater. Today 2011, 14, 248–256. [Google Scholar] [CrossRef]
- Frei, G.; Lehmann, E.; Mannes, D.; Boillat, P. The neutron micro-tomography setup at PSI and its use for research purposes and engineering applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 605, 111–114. [Google Scholar] [CrossRef]
- Tremsin, A.; McPhate, J.; Vallerga, J.; Siegmund, O.; Hull, J.; Feller, W.; Lehmann, E. Detection efficiency, spatial and timing resolution of thermal and cold neutron counting MCP detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 604, 140–143. [Google Scholar] [CrossRef]
- Tremsin, A.; McPhate, J.; Vallerga, J.; Siegmund, O.; Hull, J.; Feller, W.; Lehmann, E. High-resolution neutron radiography with microchannel plates: Proof-of-principle experiments at PSI. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 605, 103–106. [Google Scholar] [CrossRef]
- Peetermans, S.; Lehmann, E. Simultaneous neutron transmission and diffraction contrast tomography as a non-destructive 3D method for bulk single crystal quality investigations. J. Appl. Phys. 2013, 114, 124905. [Google Scholar] [CrossRef] [Green Version]
- Peetermans, S.; King, A.; Ludwig, W.; Reischig, P.; Lehmann, E. Cold neutron diffraction contrast tomography of polycrystalline material. Analyst 2014, 139, 5765–5771. [Google Scholar] [CrossRef]
- Nenchev, B.; Strickland, J.; Tassenberg, K.; Perry, S.; Gill, S.; Dong, H. Automatic Recognition of Dendritic Solidification Structures: DenMap. J. Imaging 2020, 6, 19. [Google Scholar] [CrossRef] [Green Version]
- Strickland, J.; Nenchev, B.; Dong, H. Applications of Pattern Recognition for Dendritic Microstructures; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; p. 012057. [Google Scholar]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strickland, J.; Nenchev, B.; Dong, H. On Directional Dendritic Growth and Primary Spacing—A Review. Crystals 2020, 10, 627. https://doi.org/10.3390/cryst10070627
Strickland J, Nenchev B, Dong H. On Directional Dendritic Growth and Primary Spacing—A Review. Crystals. 2020; 10(7):627. https://doi.org/10.3390/cryst10070627
Chicago/Turabian StyleStrickland, Joel, Bogdan Nenchev, and Hongbiao Dong. 2020. "On Directional Dendritic Growth and Primary Spacing—A Review" Crystals 10, no. 7: 627. https://doi.org/10.3390/cryst10070627
APA StyleStrickland, J., Nenchev, B., & Dong, H. (2020). On Directional Dendritic Growth and Primary Spacing—A Review. Crystals, 10(7), 627. https://doi.org/10.3390/cryst10070627




