Investigation of Statistical Metal-Insulator Transition Properties of Electronic Domains in Spatially Confined VO2 Nanostructure
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
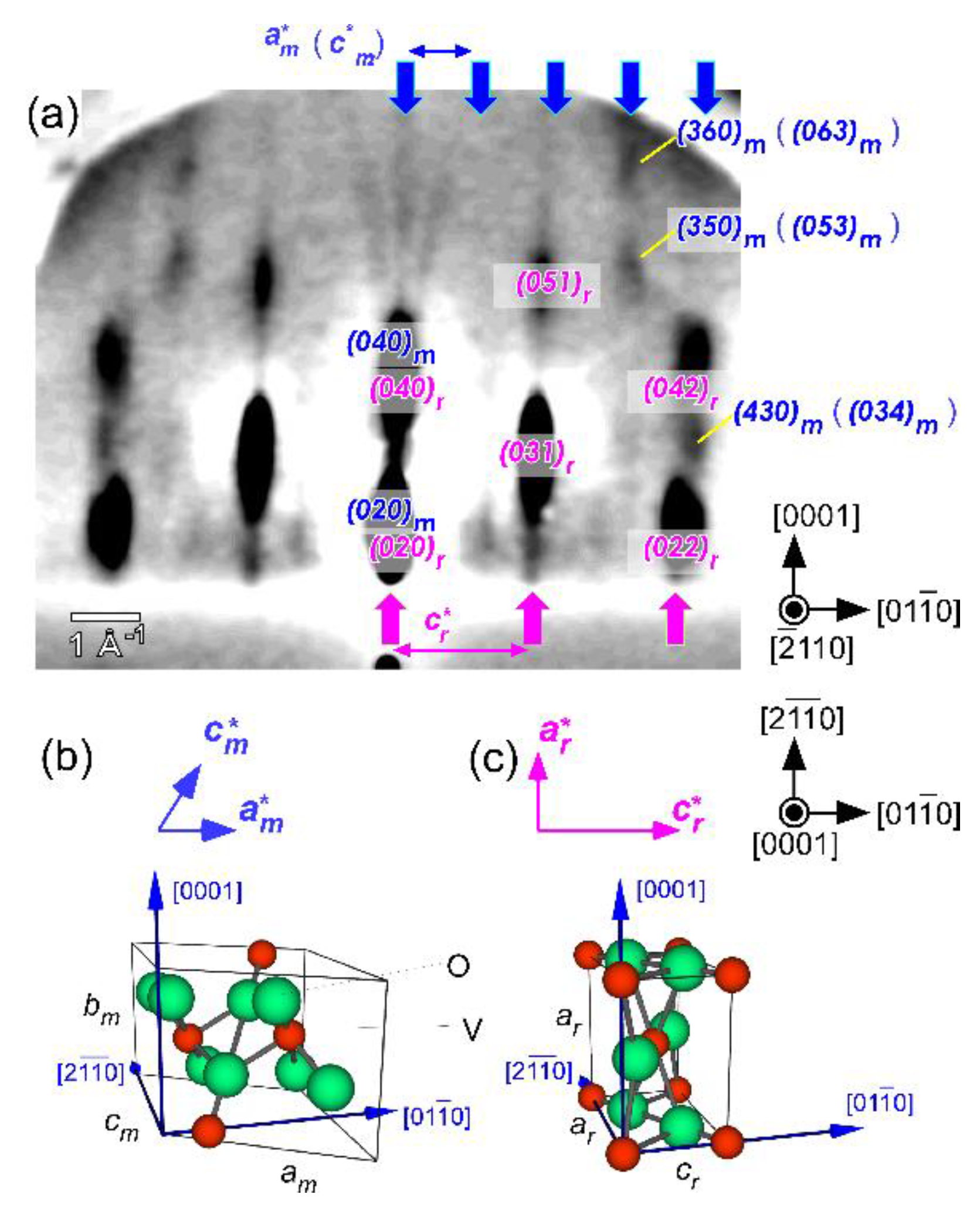
3.1. Phase-Separated VO2 Structure
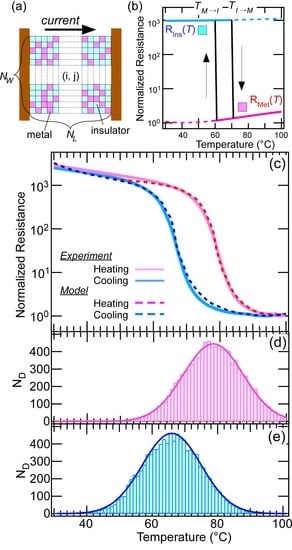
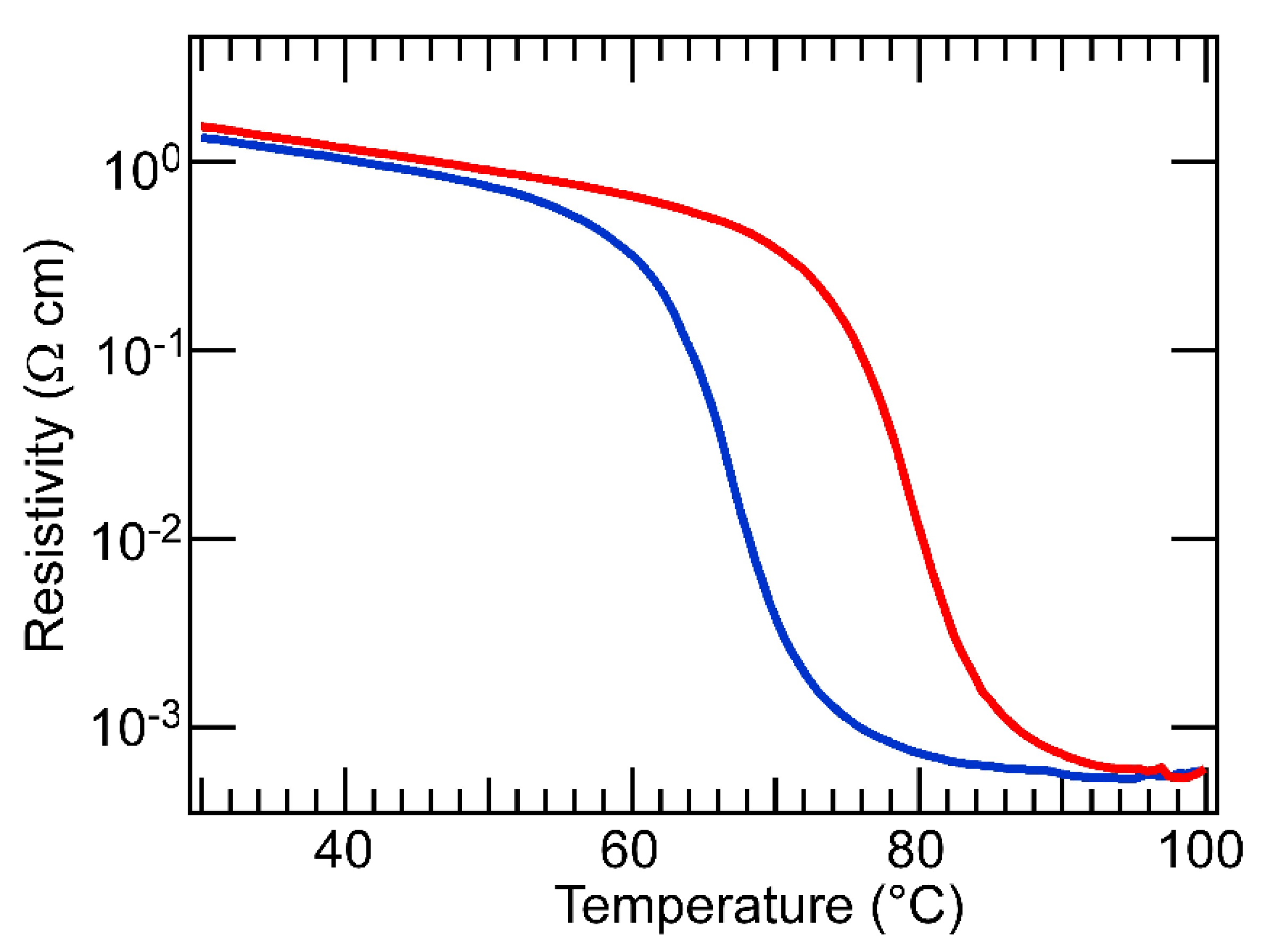
3.2. Transport Properties in the Phase-Separated VO2
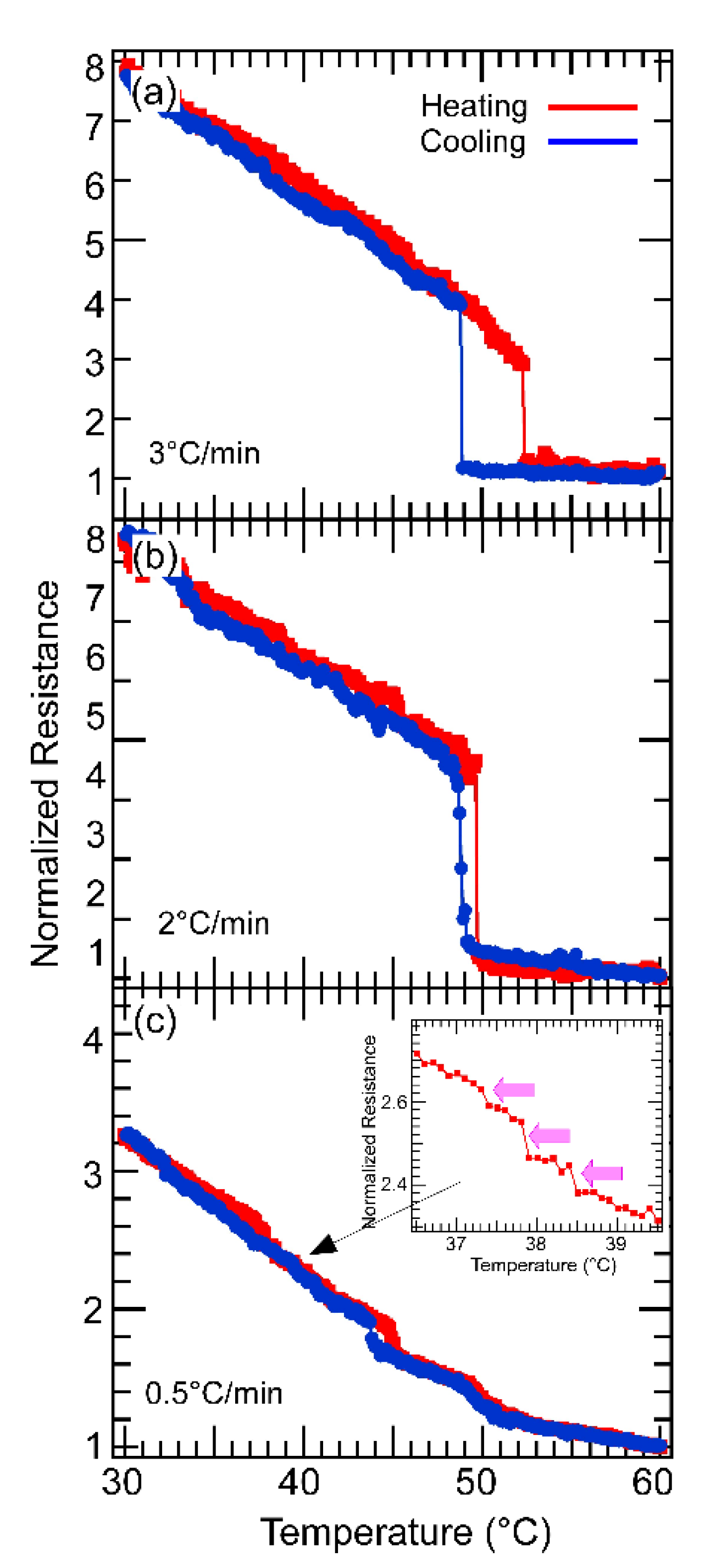
3.3. Domain Dynamics of VO2 Domains: The Effect of the Temperature-Sweep-Rate
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Morin, E.J. Oxides Which Show a Metal-to-Insulator Transition at the Neel Temperature. Phys. Rev. Lett. 1959, 3, 34. [Google Scholar] [CrossRef]
- Eyert, V. The metal-insulator transitions of VO2: A band theoretical approach. Ann. Phys. 2002, 11, 650–702. [Google Scholar] [CrossRef]
- Yang, Z.; Ko, C.; Ramanathan, S. Oxide Electronics Utilizing Ultrafast Metal-Insulator Transitions. Annu. Rev. Mater. Res. 2011, 41, 337–367. [Google Scholar] [CrossRef]
- Cavalleri, A.; Tóth, C.; Siders, C.W.; Squier, J.A.; Raksi, F.; Forget, P.; Kieffer, J.C. Femtosecond Structural Dynamics in VO2 during an Ultrafast Solid-Solid Phase Transition. Phys. Rev. Lett. 2001, 87, 237401. [Google Scholar] [CrossRef] [PubMed]
- Kübler, C.; Ehrke, H.; Huber, R.; Lopez, R.; Halabica, A.; Haglund, R.F.; Leitenstorfer, A. Coherent Structural Dynamics and Electronic Correlations during an Ultrafast Insulator-to-Metal Phase Transition in VO2. Phys. Rev. Lett. 2007, 99, 116401. [Google Scholar] [CrossRef]
- Kim, H.-T.; Chae, B.-G.; Youn, D.-H.; Maeng, S.-L.; Kim, G.; Kang, K.-Y.; Lim, Y.-S. Mechanism and Observation of Mott Transition in VO2-Based Two- and Three-Terminal Devices. New J. Phys. 2004, 6, 52. [Google Scholar] [CrossRef]
- Stefanovich, G.; Pergament, A.; Stefanovich, D. Electronical Switching and Mott Transition in VO2. J. Phys. Condens. Matter 2000, 12, 8837–8845. [Google Scholar] [CrossRef]
- Strelcov, E.; Lilach, Y.; Kolmakov, A. Gas Sensor Based on Metal-Insulator Transition in VO2 Nanowire Thermistor. Nano Lett. 2009, 9, 2322–2326. [Google Scholar] [CrossRef]
- Yajima, T.; Nishimura, T.; Toriumi, T. Positive-bias gate-controlled metal–insulator transition in ultrathin VO2 channels with TiO2 gate dielectronics. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef]
- Pellegrino, L.; Manca, N.; Kanki, T.; Tanaka, H.; Biasotti, M.; Bellingeri, E.; Siri, A.S.; Multistate, D. Multistate Memory Devices Based on Free-Standing VO2/TiO2 Microstructures Driven by Joule Self-Heating. Adv. Mater. 2012, 24, 2929–2934. [Google Scholar] [CrossRef]
- Shukla, N.; Thathachary, A.V.; Agrawal, A.; Paik, H.; Aziz, A.; Schlopp, D.G.; Gupta, S.K.; Engel-Herbert, R.; Datta, S. A Steep-Slope Transistor Based on Abrupt Electronic Phase Transition. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- IEEE. The International Roadmap for Devices and Systems. 2020. Available online: https://irds.ieee.org/ (accessed on 7 July 2020).
- Tsuji, Y.; Kanki, T.; Murakami, Y.; Tanaka, H. Single-step metal-insulator transition in thin film-based vanadium dioxide nanowires with a 20 nm electrode gap. Appl. Phys. Express 2019, 12, 025003. [Google Scholar] [CrossRef]
- Ueda, H.; Kanki, T.; Tanaka, H. Manipulation of metal-insulator transition characteristics in aspect ratio-controlled VO2 micro-scale thin films on TiO2 (001) substrates. Appl. Phys. Lett. 2013, 102, 153106. [Google Scholar] [CrossRef]
- Qazilbash, M.M.; Brehm, M.; Chae, B.G.; Ho, P.C.; Andreev, G.O.; Kim, B.J.; Yun, S.J.; Balatsky, A.V.; Maple, M.B.; Keilmann, F.; et al. Mott Transition in VO2 Revealed by Infrared Spectroscopy and Nano-Imaging. Science 2007, 318, 1750–1753. [Google Scholar] [CrossRef]
- He, X.; Xu, T.; Xu, X.; Zeng, Y.; Xu, J.; Sun, L.; Wang, C.; Xing, H.; Wu, B.; Lu, A.; et al. In Situ Atom Scale Visualization of Domain Wall Dynamics in VO2 Insulator-Metal Phase Transition. Sci. Rep. 2015, 4, 6544. [Google Scholar] [CrossRef]
- Takami, H.; Kawatani, K.; Ueda, H.; Fujiwara, K.; Kanki, T.; Tanaka, H. Tuning metal-insulator transition by one dimensional alignment of giant electronic domains in artificially size-controlled epitaxial VO2 wires. Appl. Phys. Lett. 2012, 101, 263111. [Google Scholar] [CrossRef]
- Tsubota, S.; Hattori, A.N.; Nakamura, T.; Azuma, Y.; Majima, Y.; Tanaka, H. Enhancement of discrete changes in resistivity in engineered VO2 heterointerface nanowall wire. Appl. Phys. Express 2017, 10, 115001. [Google Scholar] [CrossRef]
- Kawatani, K.; Kanki, T.; Tanaka, H. Formation mechanism of a microscale domain and effect on transport properties in strained VO2 thin films on TiO2 (001). Phys. Rev. B 2014, 90, 054203. [Google Scholar] [CrossRef]
- Kawatani, K.; Takami, H.; Kanki, T.; Tanaka, H. Metal-insulator transition with multiple micro-scaled avalanches in VO2 thin film on TiO2 (001) substrates. Appl. Phys. Lett. 2012, 100, 173112. [Google Scholar] [CrossRef]
- Wu, J.; Gu, Q.; Guiton, B.S.; Leom, N.P.; Ouyang, L.; Park, H. Strain-Induced Self Organization of Metal-Insulator Domains in Single-Crystalline VO2 Nanobeams. Nano Lett. 2006, 6, 2313–2317. [Google Scholar] [CrossRef]
- Wu, J.; Gu, Q.; Guiton, B.S.; Leon, N.P.; Ouyang, L.; Park, H. Surface-Stress-Induced Mott Transition and Nature of Associated Spatial Phase Transition in Single Crystalline VO2 Nanowires. Nano Lett. 2009, 9, 3392–3397. [Google Scholar]
- Zhang, S.; Chou, J.Y.; Lauhon, L.J. Direct Correlation of Structural Domain Formation with the Metal Insulator Transition in a VO2 Nanobeam. Nano Lett. 2009, 9, 4527–4532. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Ertekin, E.; Srinivasan, V.; Fan, W.; Huang, S.; Zheng, H.; Yim, J.W.L.; Khanal, D.R.; Ogletree, D.F.; Grossman, J.C.; et al. Strain engineering and one-dimensional organization of metal–insulator domains in single-crystal vanadium dioxide beams. Nat. Nanotechnol. 2009, 4, 732–737. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Fan, W.; Zheng, H.; Wu, J. Thermoelectronic Effect across the Metal−Insulator Domain Walls in VO2 Microbeams. Nano Lett. 2009, 9, 4001–4006. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H.; Takami, H.; Kanki, T.; Hattori, A.N.; Fujiwara, K. Artificial three dimensional oxide nanostructures for high performance correlated oxide nanoelectronics. Jpn. J. Appl. Phys. 2014, 53, 05FA10. [Google Scholar] [CrossRef]
- Kanki, T.; Kawatani, K.; Takami, H.; Tanaka, H. Direct observation of giant metallic domain evolution driven by electric bias in VO2 thin films on TiO2 (001) substrate. Appl. Phys. Lett. 2012, 101, 243118. [Google Scholar] [CrossRef]
- Sohn, A.; Kanki, T.; Sakai, K.; Tanaka, H.; Kim, D.-W. Fractal Nature of Metallic and Insulating Domain Configurations in a VO2 Thin Film Revealed by Kelvin Probe Force Microscopy. Sci. Rep. 2015, 5, 10417. [Google Scholar] [CrossRef]
- Dagotto, E.; Hotta, T.; Moreo, A. Colossal magnetoresistant materials: The key role of phase separation. Phys. Rep. 2001, 344, 1–153. [Google Scholar] [CrossRef]
- Uehara, M.; Mori, S.; Chen, C.H.; Cheong, S.-W. Percolative phase separation underlies colossal magnetoresistance in mixed-valent manganites. Nature 1999, 399, 560–563. [Google Scholar] [CrossRef]
- Ward, T.Z.; Liang, S.; Fuchigami, K.; Yin, L.F.; Dagotto, E.; Plummer, E.W.; Shen, J. Reemergent Metal-Insulator Transitions in Manganites Exposed with Spatial Confinement. Phys. Rev. Lett. 2008, 100, 247204. [Google Scholar] [CrossRef]
- Preziosi, D.; Lopez-Mir, L.; Li, X.; Cornelissen, T.; Lee, J.H.; Trier, F.; Bouzehouane, K.; Valencia, S.; Gloter, A.; Barthélémy, A.; et al. Direct Mapping of Phase Separation across the Metal-Insulator Transition of NdNiO3. Nano Lett. 2018, 18, 2226–2232. [Google Scholar] [CrossRef] [PubMed]
- Mattoni, G.; Zubko, P.; Maccherozzi, F.; Torren, A.J.H.; Boltje, D.B.; Hadjimichael, M.; Manca1, N.; Catalano, S.; Gibert, M.; Liu, Y.; et al. Striped nanoscale phase separation at the metal-insulator transition of heteroepitaxial nickelates. Nat. Commun. 2016, 93, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Trier, F.; Cornelissen, T.; Preziosi, D.; Bouzehouane, K.; Fusil, S.; Valencia, S.; Bibes, M. Imaging and Harnessing Percolation at the Metal–Insulator Transition of NdNiO3 Nanogaps. Nano Lett. 2019, 19, 7801–7805. [Google Scholar] [CrossRef] [PubMed]
- Hattori, A.N.; Fujiwara, Y.; Fujiwara, K.; Nguyen, T.V.A.; Nakamura, T.; Ichimiya, M.; Ashida, M.; Tanaka, H. Identification of Giant Mott Phase Transition of Single Electronic Nanodomain in Manganite nanowall wire. Nano Lett. 2015, 15, 4322–4328. [Google Scholar] [CrossRef] [PubMed]
- Rakshit, R.; Hattori, A.N.; Naitoh, Y.; Shima, H.; Akinaga, H.; Tanaka, H. Three-dimensional Nanoconfinement Supports Verwey Transition in Fe3O4 Nanowire at 10 nm length scale. Nano Lett. 2019, 19, 5003–5010. [Google Scholar] [CrossRef]
- Fan, W.; Cao, J.; Seidel, J.; Gu, Y.; Yim, J.W.; Barrett, C.; Yu, K.M.; Ji, J.; Ramesh, R.; Chen, L.Q.; et al. Large kinetic asymmetry in the metal-insulator transition nucleated at localized and extended defects. Phys. Rev. B 2011, 83, 235102. [Google Scholar] [CrossRef]
- Wei, J.; Wang, Z.; Chen, W.; Cobden, D.H. New aspects of the metal-insulator transition in single-domain vanadium dioxide nanobeams. Nat. Nanotechnol. 2009, 4, 420–424. [Google Scholar] [CrossRef]
- Yoon, J.; Kim, H.; Chen, X.; Tamura, N.; Mun, B.S.; Park, C.; Ju, H. Controlling the Temperature and Speed of the Phase Transition of VO2 Microcrystals. ACS Appl. Mater. Interfaces 2016, 8, 2280–2286. [Google Scholar] [CrossRef]
- Oike, H.; Suda, M.; Kamitani, M.; Ueda, A.; Mori, H.; Tokura, Y.; Yamamoto, H.M.; Kagawa, F. Size effects on supercooling phenomena in strongly correlated electron systems: IrTe2 and θ−(BEDT−TTF)2 RbZn (SCN)4. Phys. Rev. B 2018, 97, 085102. [Google Scholar] [CrossRef]
- Lopez, R.; Haynes, T.E.; Boatner, L.A. Size effects in the structural phase transition of VO2 nanoparticles. Phys. Rev. B 2002, 65, 224113. [Google Scholar] [CrossRef]
- Naitoh, Y.; Tsukagoshi, K.; Murata, K.; Mizutani, W. A Reliable Method for Fabricating sub-10 nm Gap Junctions Without Using Electron Beam Lithography. E-J. Surf. Sci. Nanotechnol. 2003, 1, 41–44. [Google Scholar] [CrossRef]
- Bollobas, B. Modern Graph Theory (Graduate Texts in Mathematics); Springer: Berlin, Germany, 1998. [Google Scholar]
- Okimura, K.; Sakai, J. Changes in Lattice Parameters of VO2 Films Grown on c-Plane Al2O3 Substrates across Metal–Insulator Transition. Jpn. J. Appl. Phys. 2009, 48, 045504. [Google Scholar] [CrossRef]
- Kawakubo, T.; Nakagawa, T. Phase Transition in VO2. J. Phys. Soc. Jpn. 1964, 19, 517–519. [Google Scholar] [CrossRef]
- Peggs, I.P. Thermal Expansion 6; Plenum Press: New York, NY, USA, 1978; pp. 191–201. [Google Scholar]
- Yang, Y.; Lee, K.; Zobel, M.; Maćković, M.; Unruh, T.; Spiecker, E.; Schmuki, P. Formation of Highly Ordered VO2 Nanotubular/Nanoporous Layers and Their Supercooling Effect in Phase Transitions. Adv. Mater. 2012, 24, 1571–1575. [Google Scholar] [CrossRef] [PubMed]
- In the simulation in Figs. 5(c–e), = 8 °C, Tcenter = 77 °C in heating (IMT) process and = 9 °C, Tcenter = 65 °C in the cooling (MIT) process were used.
- Kagawa, F.; Oike, H. Quenching of Charge and Spin Degrees of Freedom in Condensed Matter. Adv. Mater. 2017, 29, 1601979. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef]
- Mellan, T.A.; Wang, H.; Schwingenschlögl, U.; Crau-Crespo, R. Origin of the transition entropy in vanadium dioxide. Phys. Rev. B 2019, 99, 064113. [Google Scholar] [CrossRef]
- Wang, M.; Xue, Y.; Cui, Z.; Zhang, R. Size-Dependent Crystal Transition Thermodynamics of Nano-VO2 (M). J. Phys. Chem. C 2018, 122, 8621–8627. [Google Scholar] [CrossRef]
- Whittaker, L.; Jaye, C.; Fu, Z.; Fischer, D.A.; Banerjee, S. Depressed Phase Transition in Solution-Grown VO2 Nanostructure. J. Am. Chem. Soc. 2009, 131, 8884–8894. [Google Scholar] [CrossRef]
- Chena, S.; Ma, H.; Dai, J.; Yi, X. Nanostructured vanadium dioxide thin films with low phase transition temperature. Appl. Phys. Lett. 2007, 90, 101117. [Google Scholar] [CrossRef]
- Dai, L.; Cao, C.; Gao, Y.; Luo, H. Synthesis and phase transition behavior of undoped VO2 with a strong nano-size effect. Sol. Energy Mater. Sol. Cells 2011, 95, 712–715. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hattori, A.N.; Osaka, A.I.; Hattori, K.; Naitoh, Y.; Shima, H.; Akinaga, H.; Tanaka, H. Investigation of Statistical Metal-Insulator Transition Properties of Electronic Domains in Spatially Confined VO2 Nanostructure. Crystals 2020, 10, 631. https://doi.org/10.3390/cryst10080631
Hattori AN, Osaka AI, Hattori K, Naitoh Y, Shima H, Akinaga H, Tanaka H. Investigation of Statistical Metal-Insulator Transition Properties of Electronic Domains in Spatially Confined VO2 Nanostructure. Crystals. 2020; 10(8):631. https://doi.org/10.3390/cryst10080631
Chicago/Turabian StyleHattori, Azusa N., Ai I. Osaka, Ken Hattori, Yasuhisa Naitoh, Hisashi Shima, Hiroyuki Akinaga, and Hidekazu Tanaka. 2020. "Investigation of Statistical Metal-Insulator Transition Properties of Electronic Domains in Spatially Confined VO2 Nanostructure" Crystals 10, no. 8: 631. https://doi.org/10.3390/cryst10080631
APA StyleHattori, A. N., Osaka, A. I., Hattori, K., Naitoh, Y., Shima, H., Akinaga, H., & Tanaka, H. (2020). Investigation of Statistical Metal-Insulator Transition Properties of Electronic Domains in Spatially Confined VO2 Nanostructure. Crystals, 10(8), 631. https://doi.org/10.3390/cryst10080631