Three-Dimensional CA-LBM Model of Silicon Facet Formation during Directional Solidification
Abstract
1. Introduction
2. Materials and Methods
2.1. LBM Model
2.2. CA Model
2.2.1. Model for the Growth
2.2.2. Remelting Calculation
2.2.3. Model for the Capture
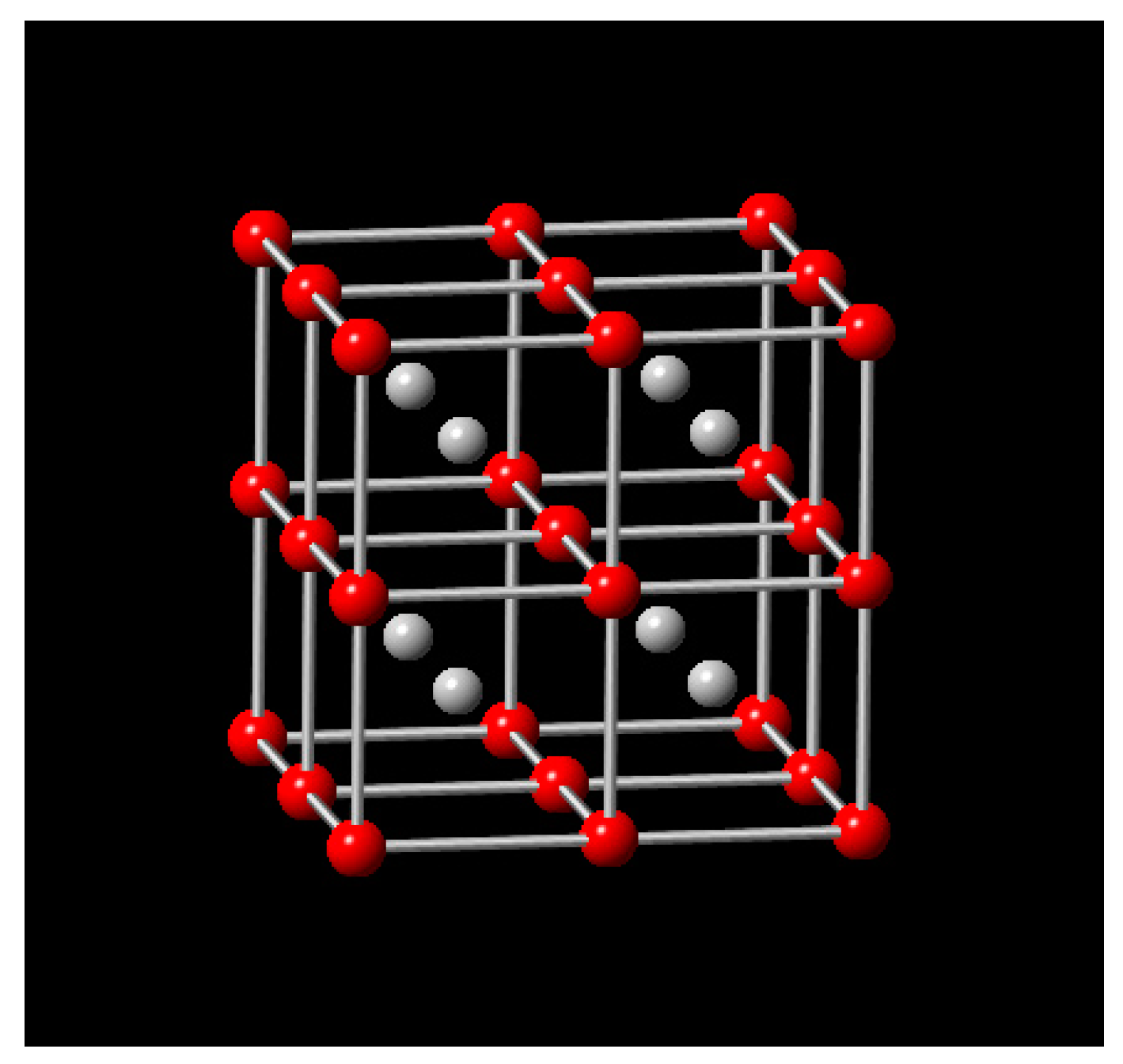
2.3. The Physical Parameters of Silicon Melt
3. Results and Discussion
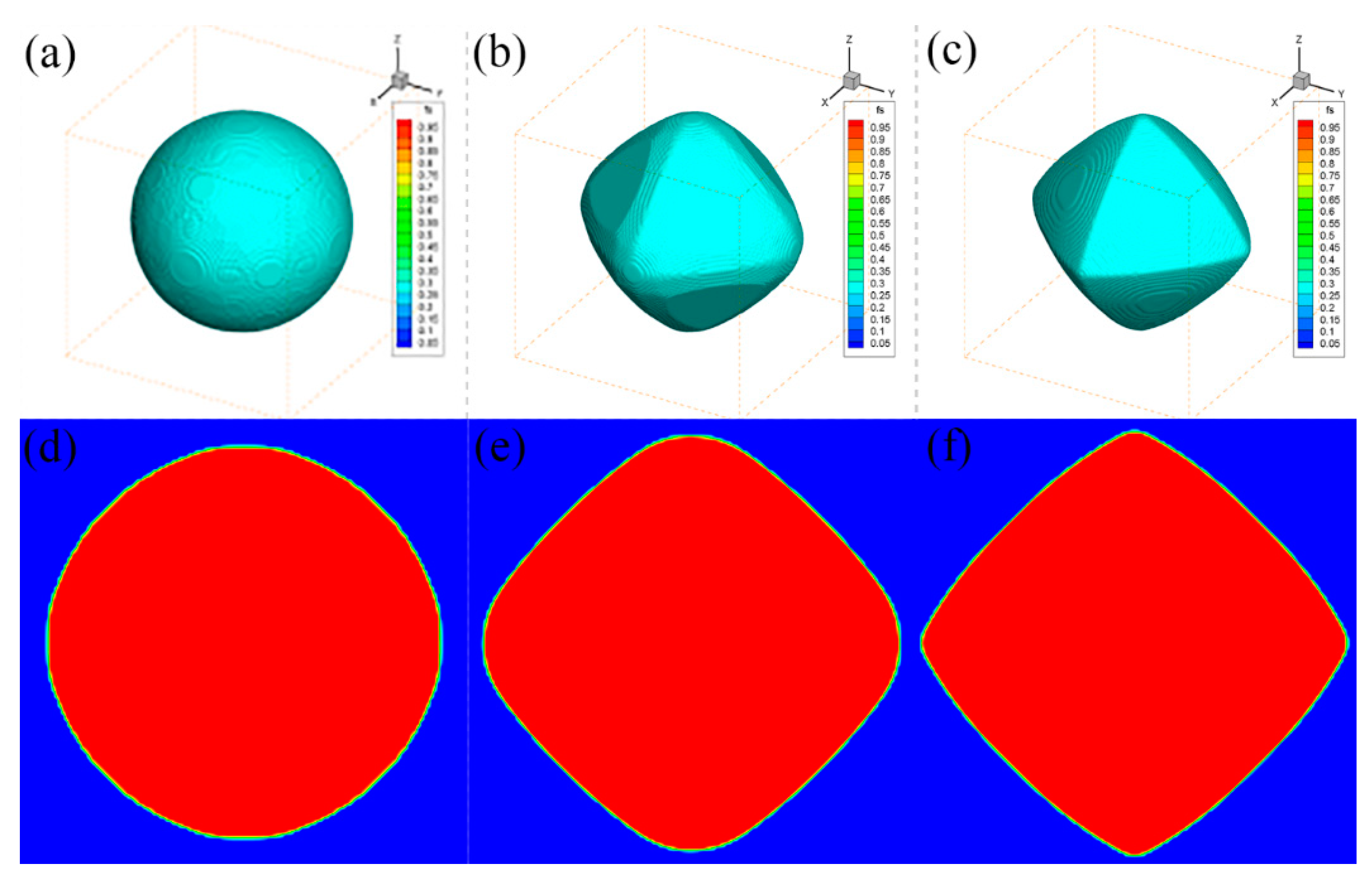
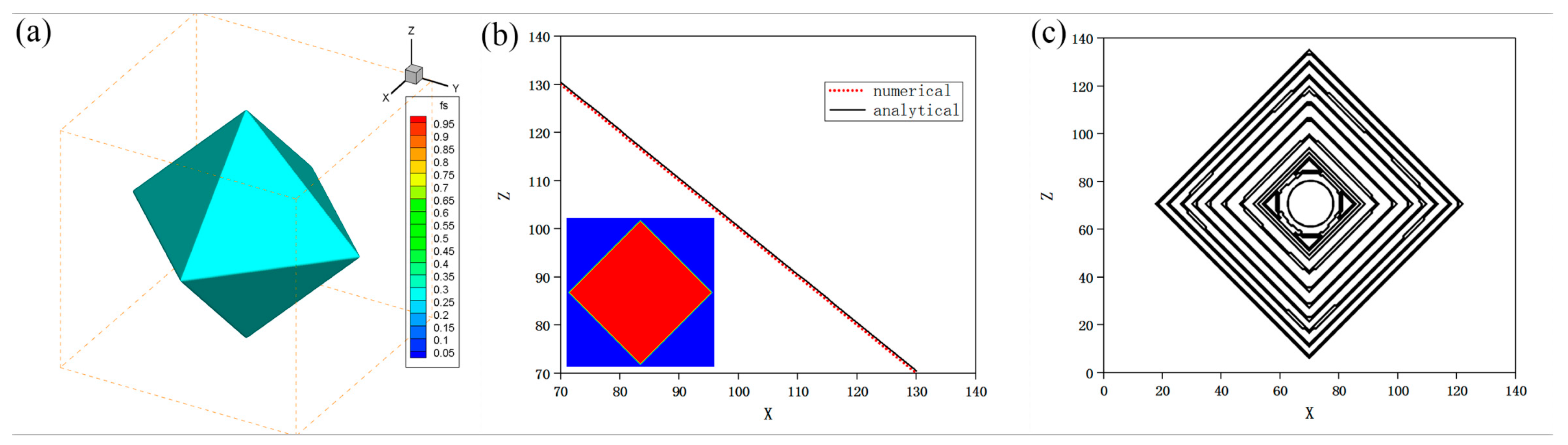
3.1. Anisotropy of Interfacial Free Energy
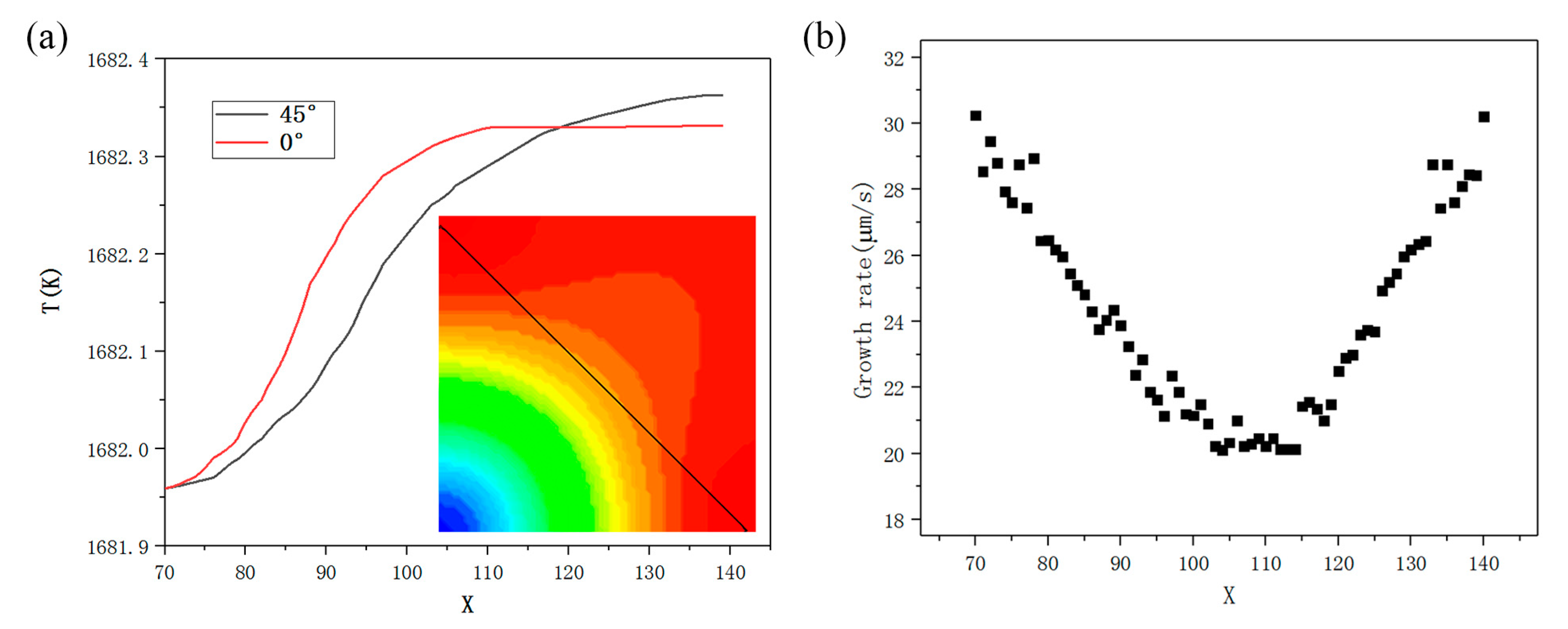
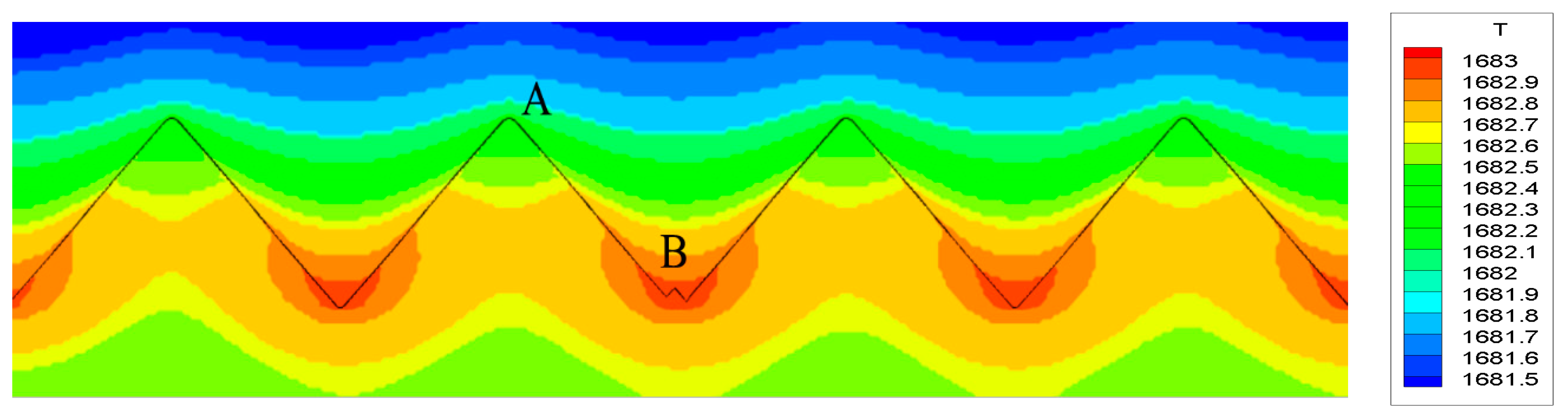
3.2. Simulations for Facet Formation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Steinbach, I.; Apel, M.; Rettelbach, T.; Franke, D. Numerical simulations for silicon crystallization processes—Examples from ingot and ribbon casting. Sol. Energy Mater. Sol. Cells 2002, 72, 59–68. [Google Scholar] [CrossRef]
- Vizman, D.; Friedrich, J.; Müller, G. Comparison of the predictions from 3D numerical simulation with temperature distributions measured in Si Czochralski melts under the influence of different magnetic fields. J. Cryst. Growth 2001, 230, 73–80. [Google Scholar] [CrossRef]
- Kalaev, V.V.; Lukanin, D.P.; Zabelin, V.A.; Makarov, Y.N.; Virbulis, J.; Dornberger, E.; Von Ammon, W. Calculation of bulk defects in CZ Si growth: Impact of melt turbulent fluctuations. J. Cryst. Growth 2003, 250, 203–208. [Google Scholar] [CrossRef]
- Liu, L.; Kakimoto, K. Partly three-dimensional global modeling of a silicon Czochralski furnace. I. Principles, formulation and implementation of the model. Int. J. Heat Mass Transf. 2005, 48, 4481–4491. [Google Scholar] [CrossRef]
- Habler, C.; Stollwerck, G.; Koch, W.; Krumbe, W.; Muller, A.; Franke, D.; Rettelbach, T. Multicrystalline silicon for solar cells: Process development by numerical simulation. Adv. Mater. 2001, 13, 1815–1819. [Google Scholar]
- Jackson, K.A. Crystal growth kinetics. Mater. Sci. Eng. 1984, 65, 7–13. [Google Scholar] [CrossRef]
- Lin, H.K.; Chen, H.Y.; Lan, C.W. Phase field modeling of facet formation during directional solidification of silicon film. J. Cryst. Growth 2014, 385, 134–139. [Google Scholar] [CrossRef]
- Lin, H.K.; Lan, C.W. Three-dimensional phase field modeling of silicon thin-film growth during directional solidification: Facet formation and grain competition. J. Cryst. Growth 2014, 401, 740–747. [Google Scholar] [CrossRef]
- Chen, G.Y.; Lan, C.W. Understanding the facet formation mechanisms of Si thin-film solidification through three-dimensional phase-field modeling. J. Cryst. Growth 2016, 474, 166–170. [Google Scholar] [CrossRef]
- Zhi, C.; Chen, C.L.; Hao, L.M. Numerical simulation of facet dendrite growth. Trans. Nonferrous Met. Soc. China 2008, 18, 938–943. [Google Scholar]
- Lian, Q.; Liu, W.; Li, R.; Yan, W.; Liu, C.; Zhang, Y.; Wang, L.; Chen, H. Numerical simulation of multi-crystalline silicon crystal growth using a macro-micro coupled method during the directional solidifification process. Appl. Sci. 2016, 7, 21. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Li, R.; Wang, J.; Wang, L.X.; Yan, W.B.; Liu, C.C.; Chen, H.J. Cellular automaton modeling of the transition of multi-crystalline silicon from a planar faceted front to equiaxed growth. Appl. Sci. 2017, 7, 13. [Google Scholar]
- Chen, R.; Xu, Q.; Liu, B. Cellular automaton simulation of three-dimensional dendrite growth in Al–7Si–Mg ternary aluminum alloys. Comput. Mater. Sci. 2015, 105, 90–100. [Google Scholar] [CrossRef]
- Nastac, L. Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys. Acta Mater. 1999, 47, 4253–4262. [Google Scholar] [CrossRef]
- Fujiwara, K.; Obinata, Y.; Ujihara, T.; Usami, N.; Sazaki, G.; Nakajima, K. Grain growth behaviors of polycrystalline silicon during melt growth processes. J. Cryst. Growth. 2004, 266, 441–448. [Google Scholar] [CrossRef]
- Fujiwara, K.; Obinata, Y.; Ujihara, T.; Usami, N.; Sazaki, G.; Nakajima, K. In-situ observations of melt growth behavior of polycrystalline silicon. J. Cryst. Growth. 2004, 262, 124–129. [Google Scholar] [CrossRef]
- Lei, W.; Xin, L.; Meng, W.; Huang, W. Orientation selection of equiaxed dendritic growth by three-dimensional cellular automaton model. Physical B 2012, 407, 2471–2475. [Google Scholar]
- Qiu, S.; Wen, S.; Fang, M.; Zhang, L.; Gan, C.; Jiang, D.; Tan, Y.; Li, J.; Luo, X. Process parameters inflfluenceI. Vacuum 2016, 125, 40–47. [Google Scholar] [CrossRef]
- Desai, P.D. Thermodynamic properties of iron and silicon. J. Phys. Chem. Ref. Date 1986, 15, 967–983. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The growth of crystals and the equilibrium structure of their surfaces. Philos. Trans. R. Soc. Lond. A 1951, 243, 299–358. [Google Scholar]


| Property | Value |
|---|---|
| Melting temperature, Tmel (T) | 1683 |
| Density of silicon solid, ρs (kg·m−3) | 2330 − 2.19 × 10−2T |
| Density of silicon melt, ρm (kg·m−3) | 2330 − 2.19 × 10−2T − 1.21 × 10−5T2 |
| Thermal diffusivity of silicon solid, as (m2/s) | 9.6 × 10−6 |
| Thermal diffusivity of melt, a1 (m2/s) | 2.134 × 10−5 |
| Molar liquid heat capacity, cp (j mol−1k−1) | 26.6 |
| Molar melting entropy, Δsf (j mol−1k−1) | 29.8 |
| Molar latent heat, ΔHf (j/mol) | 4.444 × 104 |
| Liquidus slope, m (K/mass%) | −0.7637 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Li, R.; Chen, H. Three-Dimensional CA-LBM Model of Silicon Facet Formation during Directional Solidification. Crystals 2020, 10, 669. https://doi.org/10.3390/cryst10080669
Ma W, Li R, Chen H. Three-Dimensional CA-LBM Model of Silicon Facet Formation during Directional Solidification. Crystals. 2020; 10(8):669. https://doi.org/10.3390/cryst10080669
Chicago/Turabian StyleMa, Wang, Ri Li, and Hongjian Chen. 2020. "Three-Dimensional CA-LBM Model of Silicon Facet Formation during Directional Solidification" Crystals 10, no. 8: 669. https://doi.org/10.3390/cryst10080669
APA StyleMa, W., Li, R., & Chen, H. (2020). Three-Dimensional CA-LBM Model of Silicon Facet Formation during Directional Solidification. Crystals, 10(8), 669. https://doi.org/10.3390/cryst10080669




