Study on Lamb Waves in a Composite Phononic Crystal Plate
Abstract
:1. Introduction
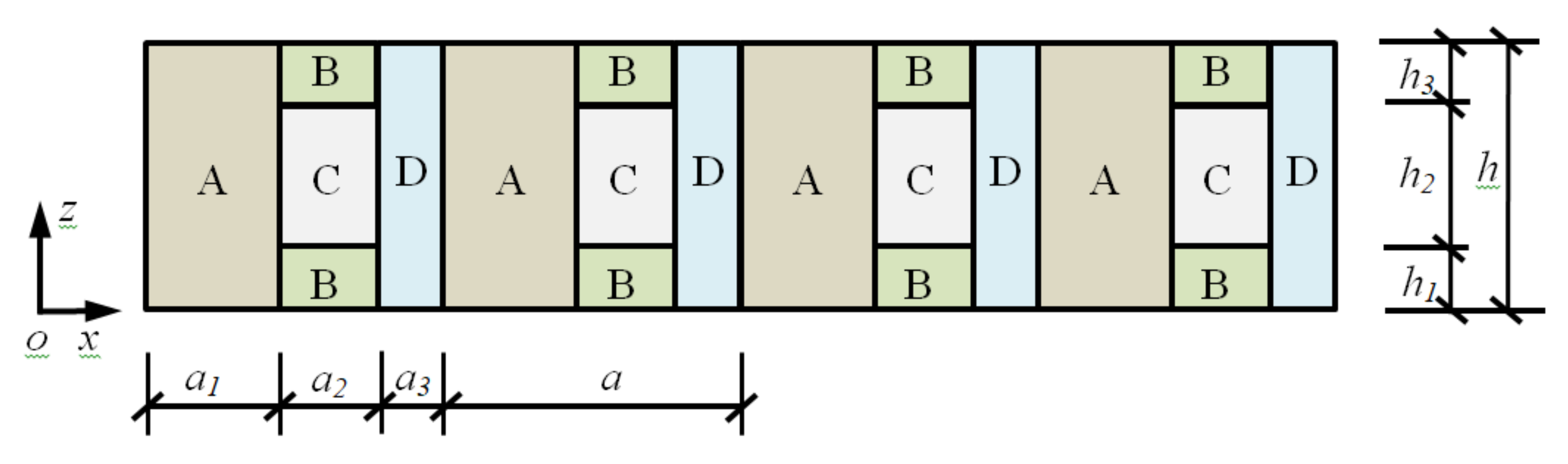
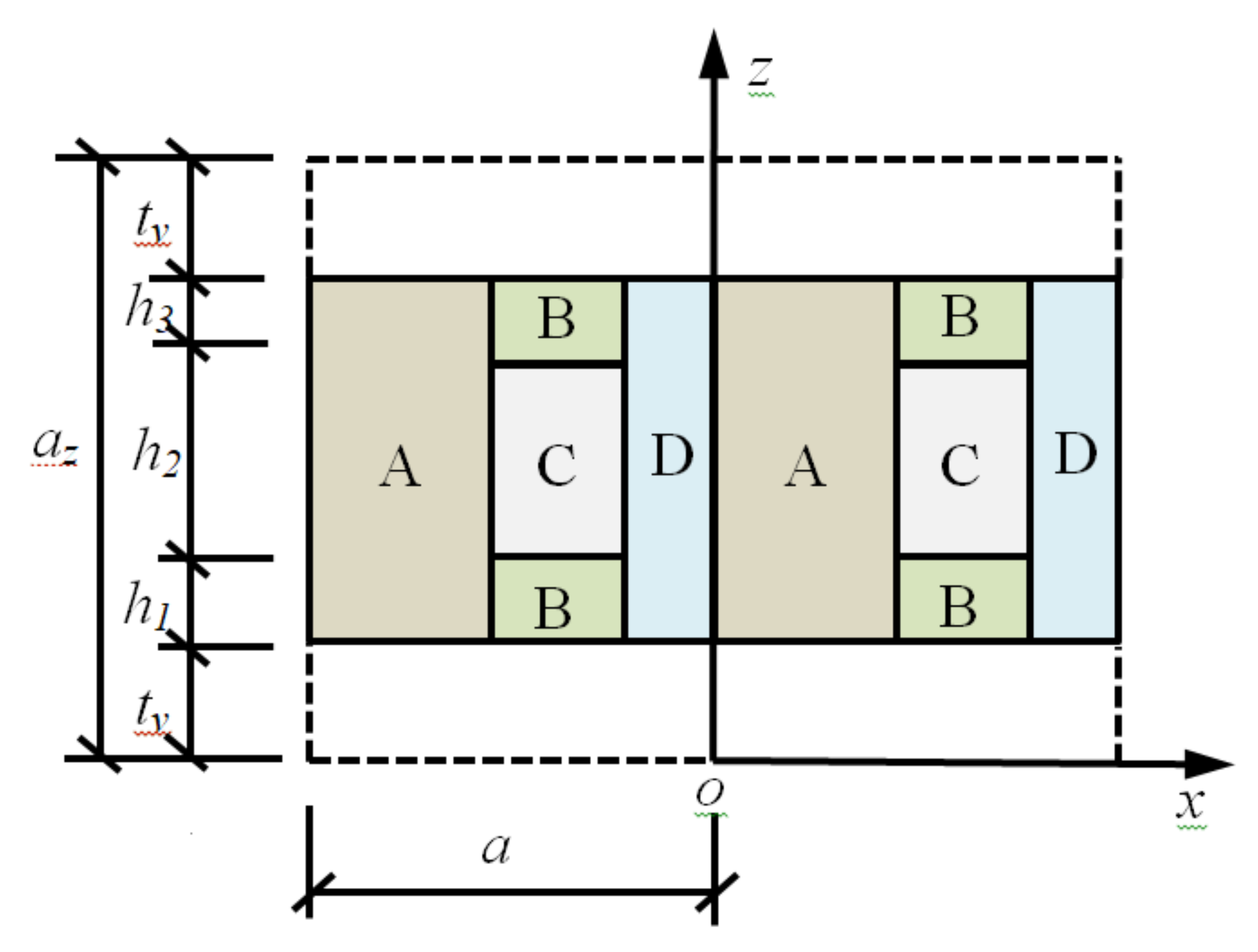
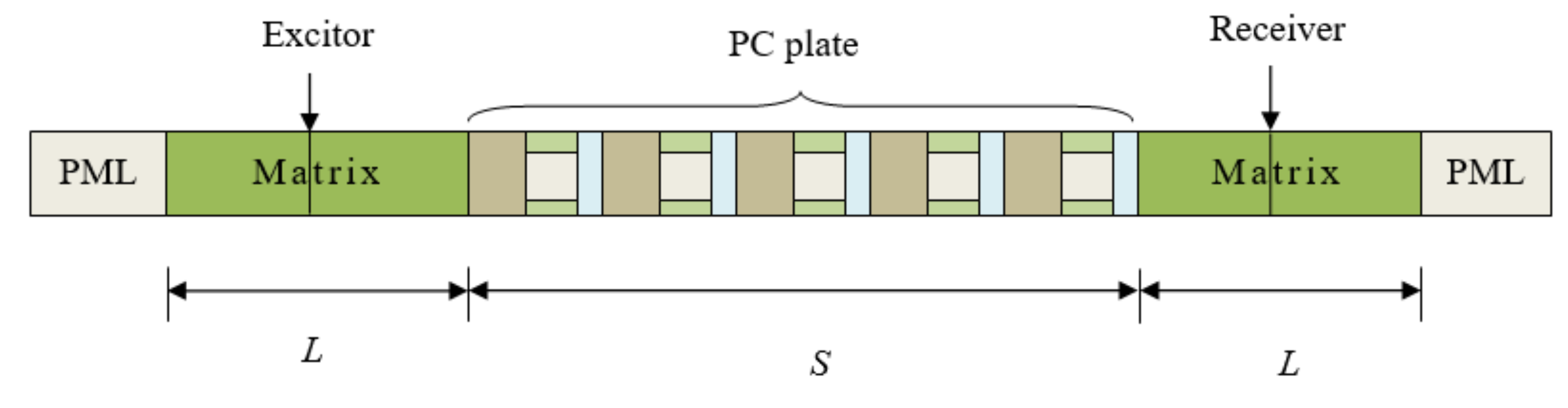
2. Formulation of the Problem
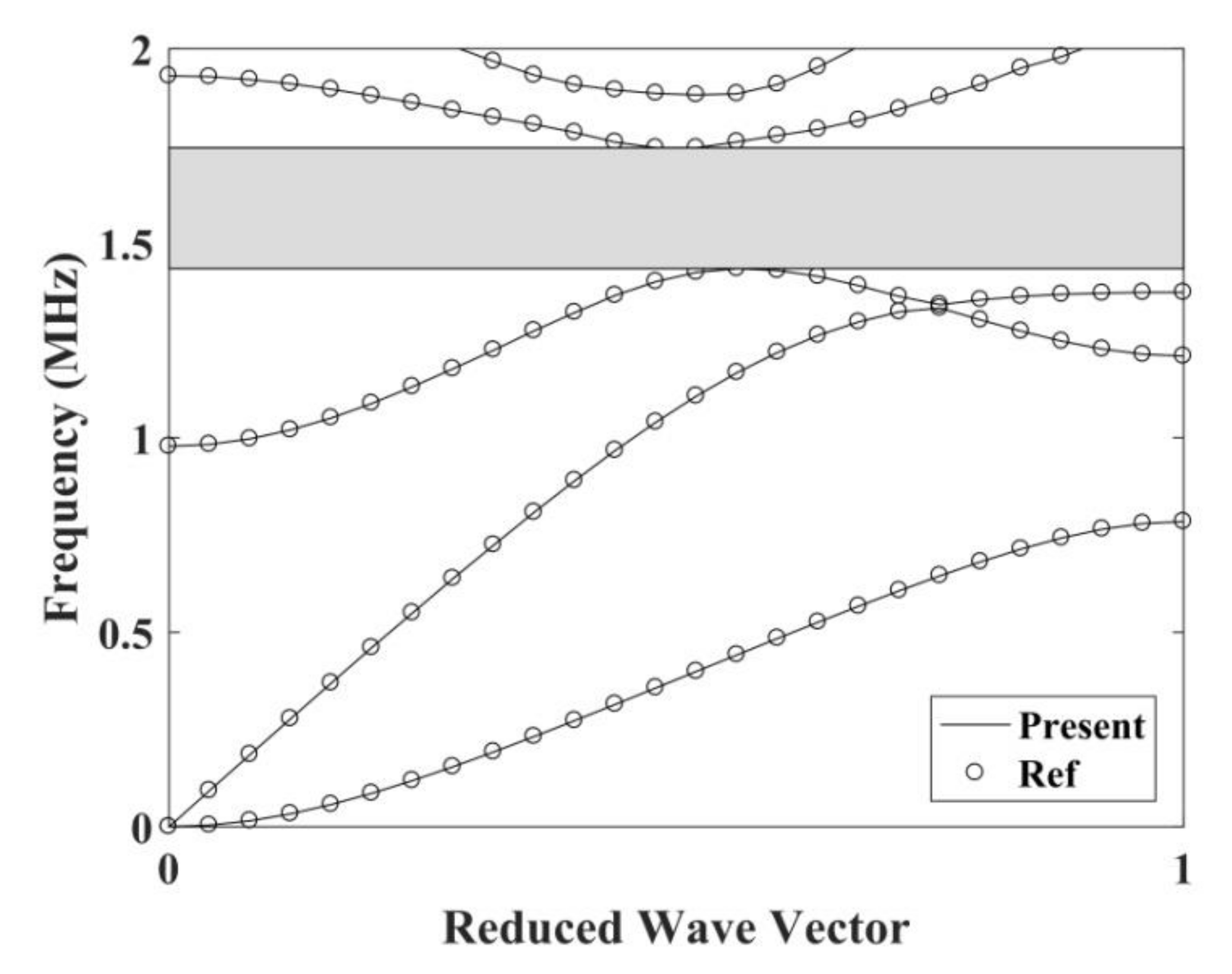
3. Numerical Results
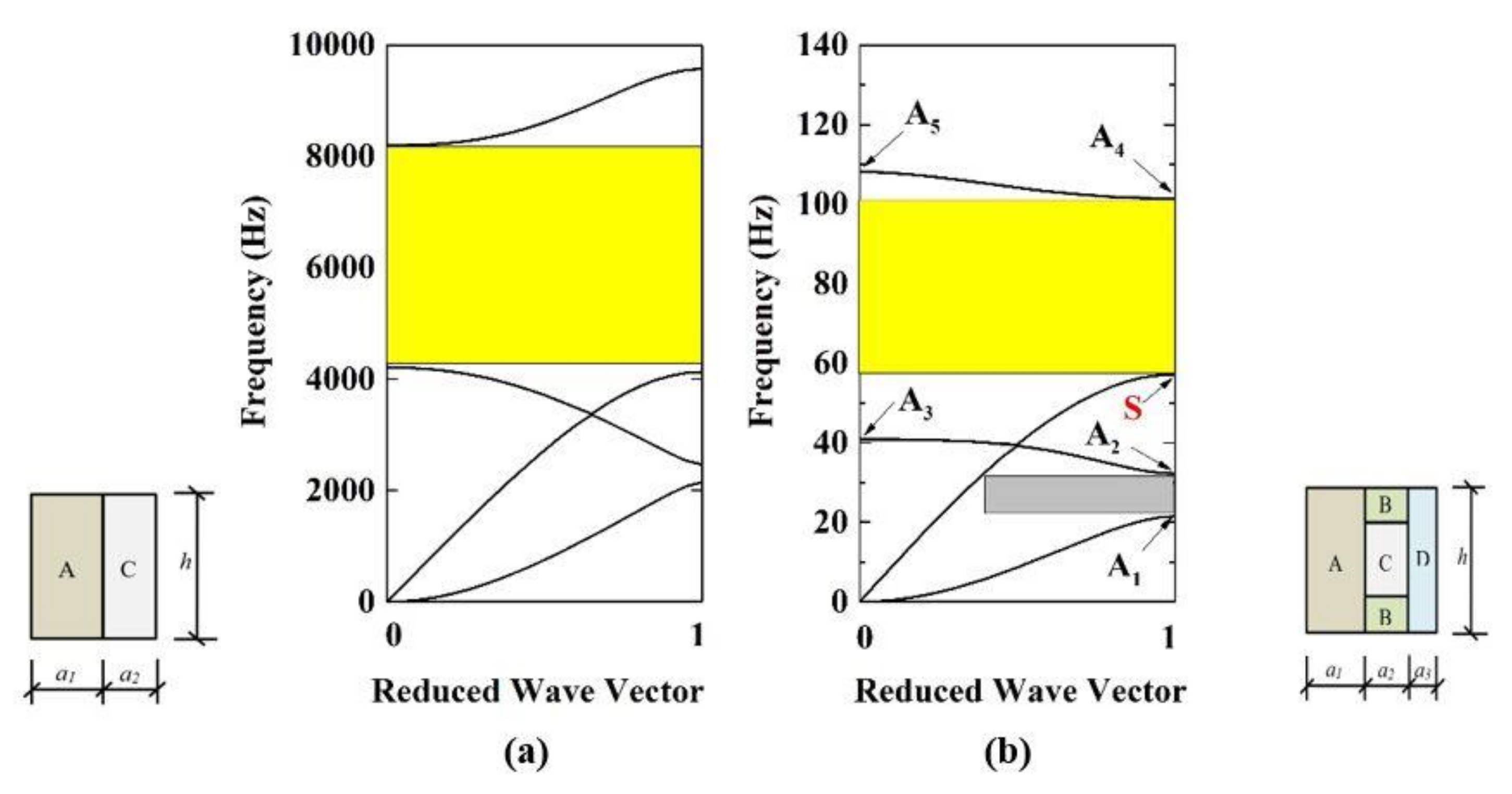
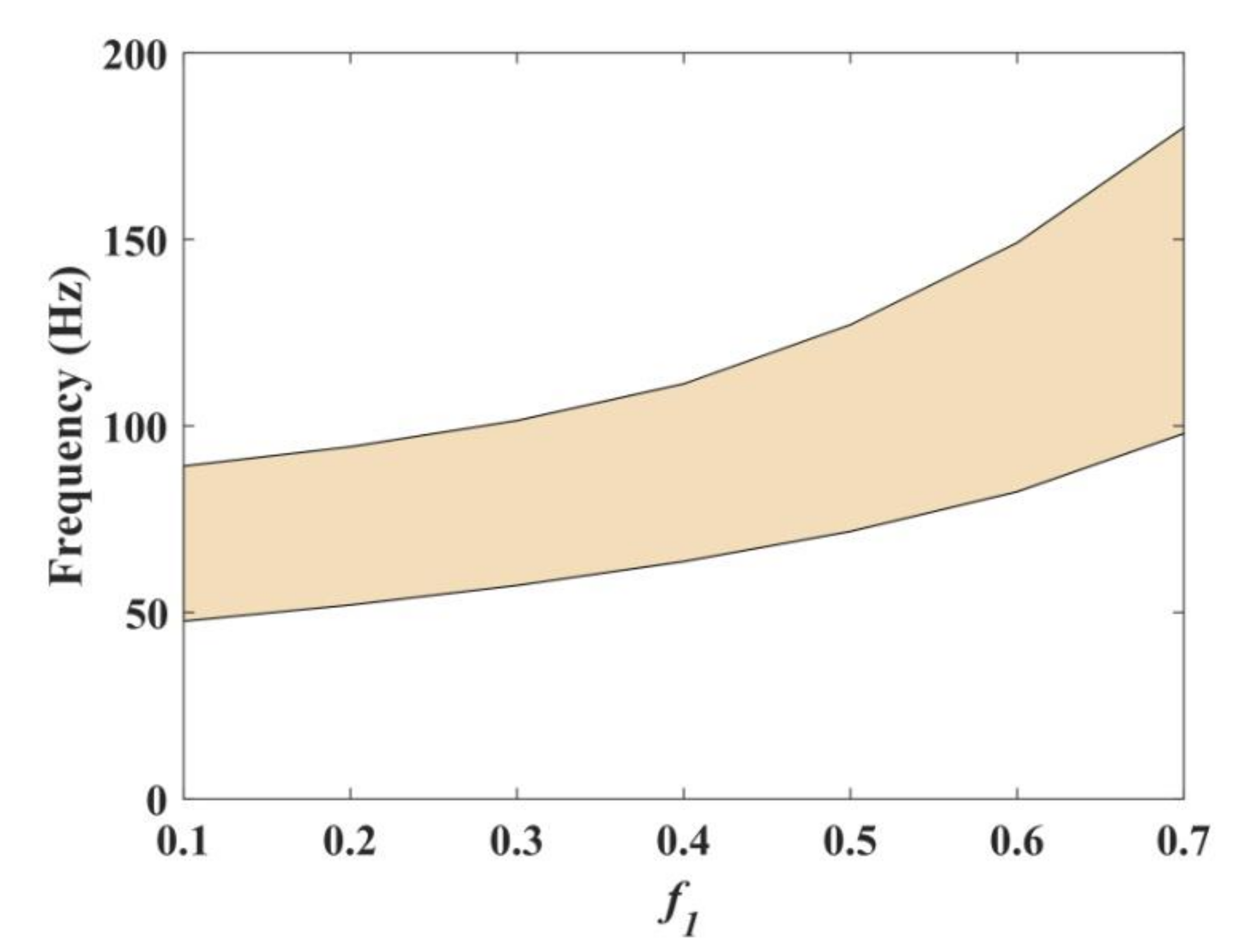
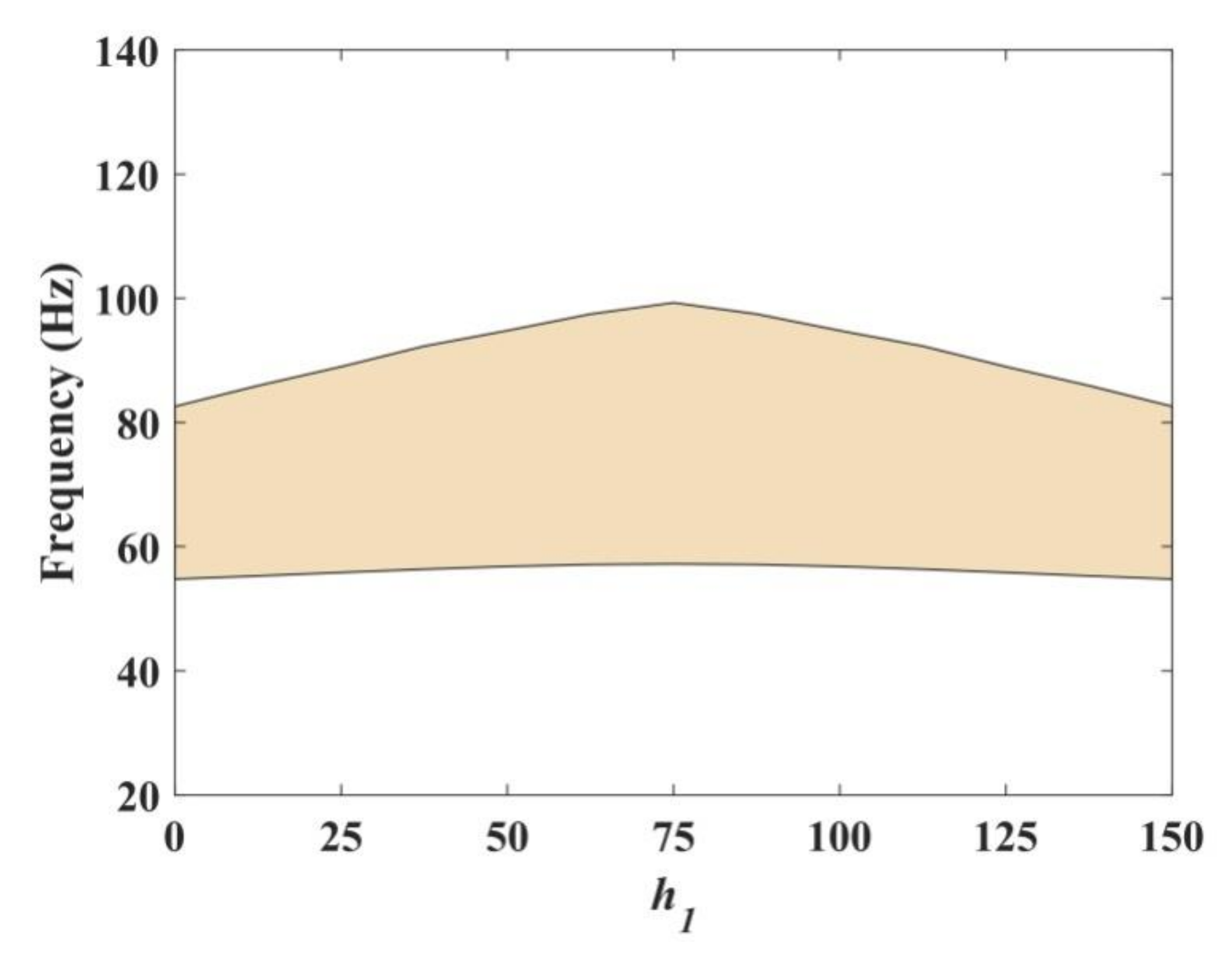
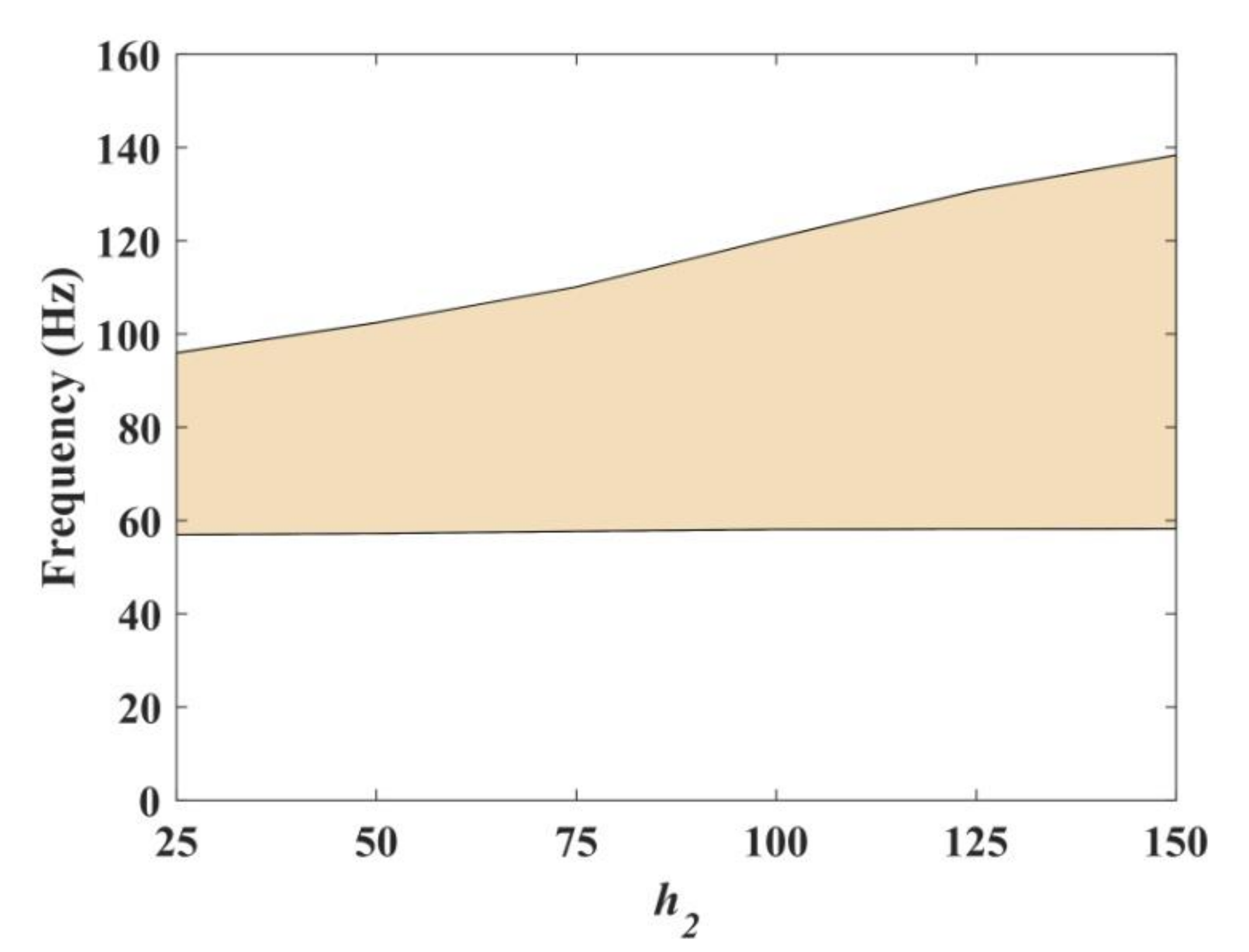
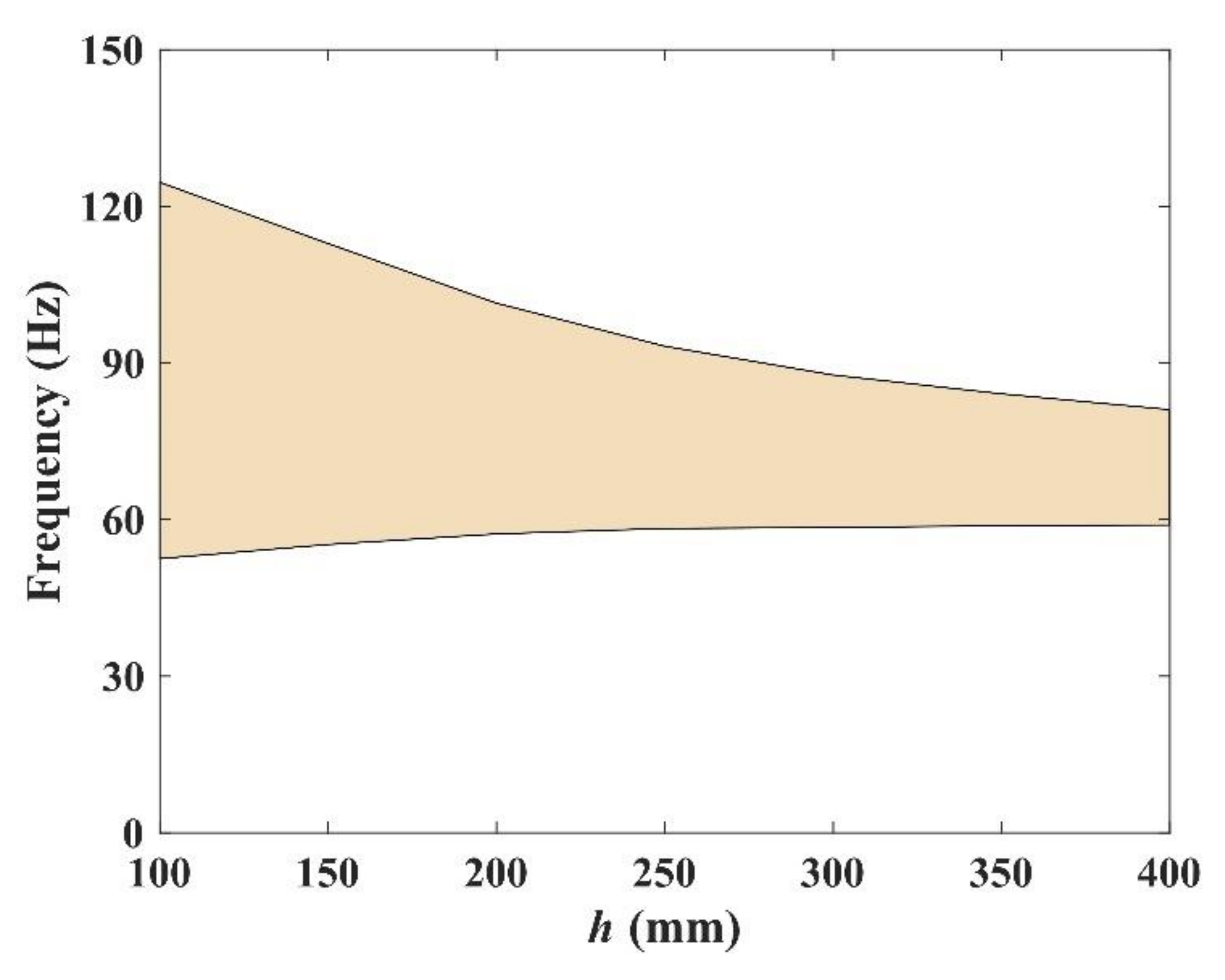
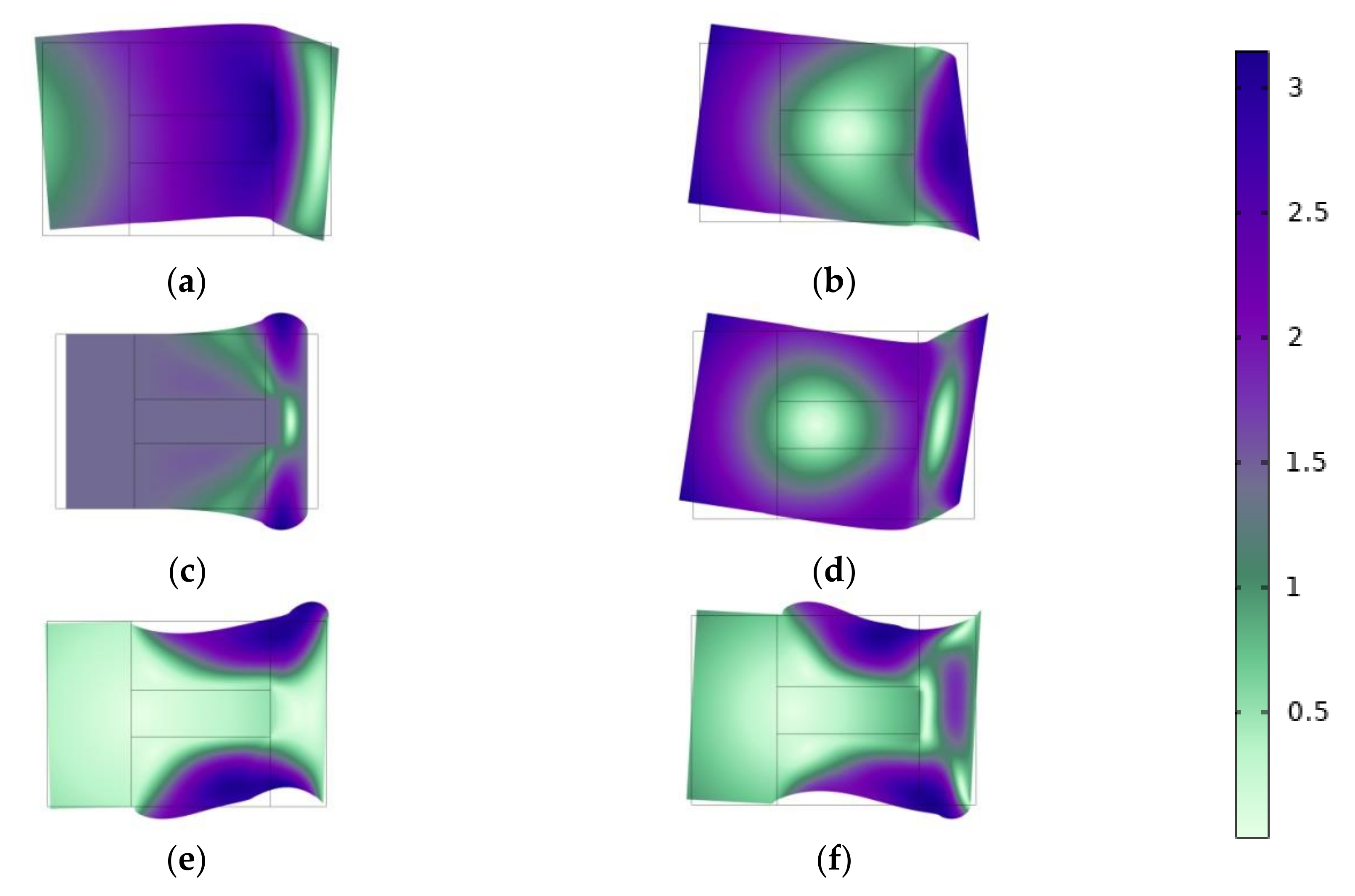
3.1. Influence of Geometric Parameters on Band Gaps
3.2. Influence of Magnetic Field on Band Gaps
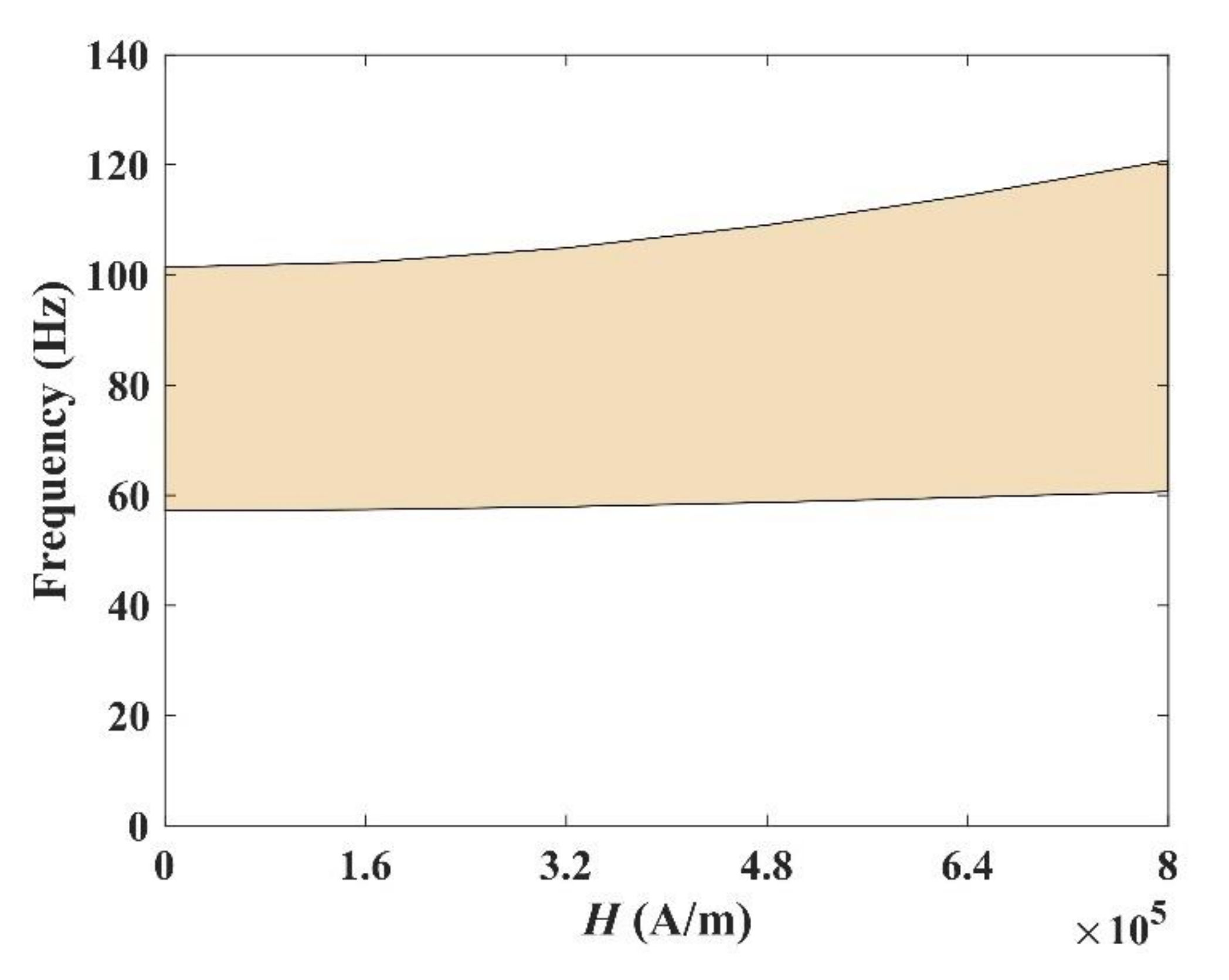
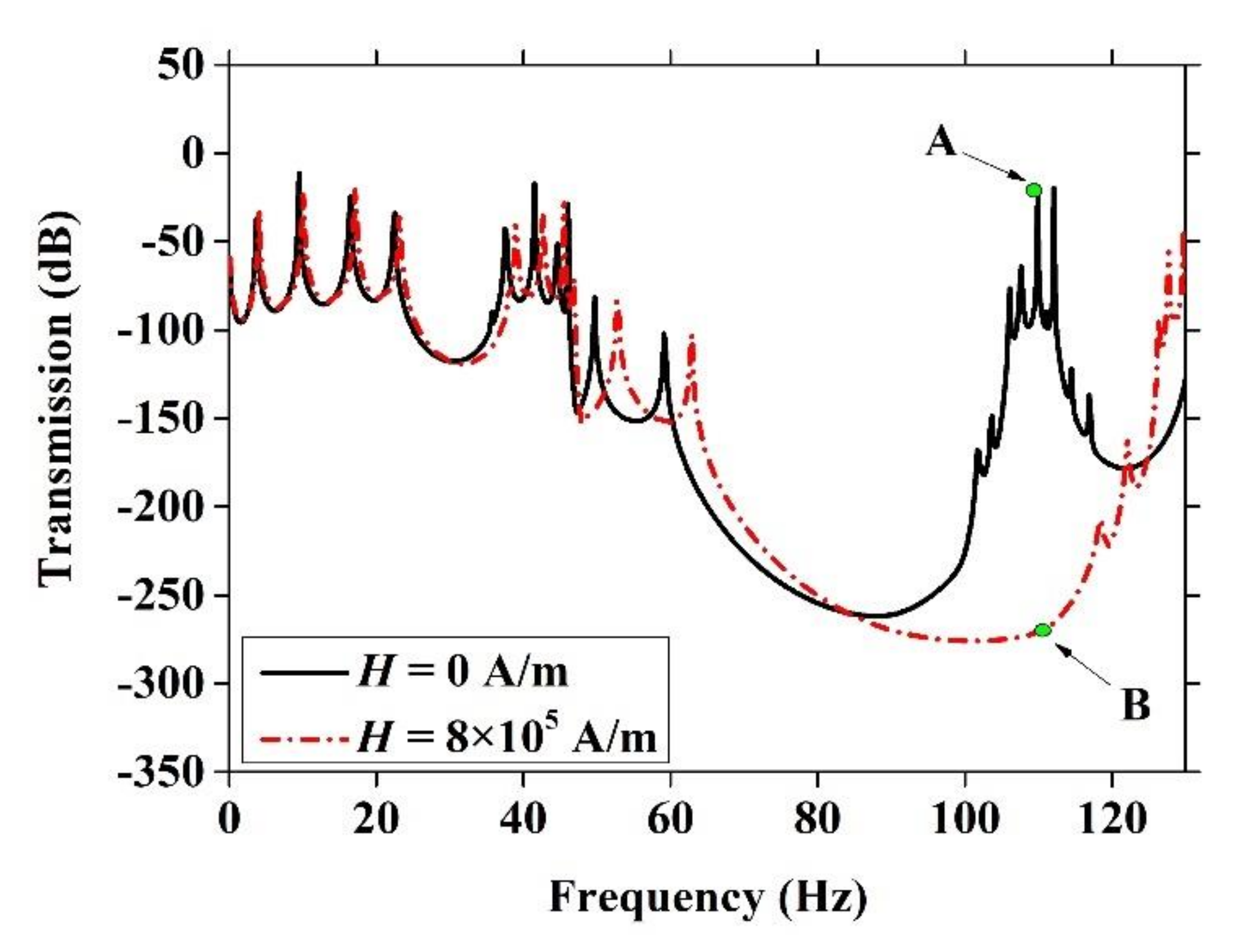
3.3. Influence of Period Number n and Magnetic Field Intensity H on Attenuation Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, Y.-J.; Yu, Y.-J.; Zuo, Y.-Y.; Qiu, L.-L.; Dong, M.-M.; Ye, J.-T.; Yang, J. Band gap and experimental study in phononic crystals with super-cell structure. Results Phys. 2019, 13, 102200. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, G.-J.; Gao, N.-S.; Li, L.-Z.; Lei, H.-X.; Yu, M.-R. Flexural vibration bandgaps of the multiple local resonance elastic metamaterial plates with irregular resonators. Appl. Acoust. 2020, 159, 107115. [Google Scholar] [CrossRef]
- Kushwaha, M.-S.; Halevi, P.; Dobrzynsi, L. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-Y.; Zhang, X.; Mao, Y. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Guo, T.; Yang, X.-W.; Geng, Q.; Li, Z.; Li, Y.-M.; Wang, X.; Zhang, H. Anisotropic phononic crystal structure with low-frequency bandgap and heat flux manipulation. Sci. China Phys. Mech. Astron. 2020, 63, 224711. [Google Scholar] [CrossRef]
- Graczykowski, B.; EI Sachat, A.; Reparaz, J.-S.; Sledzinska, M.; Wagner, M.-R.; Chavez-Angel, E.; Wu, Y.; Volz, S.; Wu, Y.; Alzina, F.; et al. Thermal conductivity and air-mediated losses in periodic porous silicon membranes at high temperatures. Nat. Commun. 2017, 8, 415. [Google Scholar] [CrossRef]
- An, X.-Y.; Fan, H.-L.; Zhang, C.-Z. Elastic wave and vibration bandgaps in two-dimensional acoustic metamaterials with resonators and disorders. Wave Motion 2018, 80, 69–81. [Google Scholar] [CrossRef]
- Oudich, M.; Yong, L.; Assouar, B.-M. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 1–10. [Google Scholar] [CrossRef]
- Sukhovich, A.; Merheb, B.; Muralidharan, K.; Vasseur, J.-O.; Pennec, Y.; Deymier, P.-A.; Page, J.-H. Experimental and theoretical evidence for subwavelength imaging in phononic crystals. Phys. Rev. Lett. 2019, 102, 154301. [Google Scholar] [CrossRef]
- Hou, Z.-L.; Assouar, B.-M. Modeling of Lamb wave propagation in plate with two-dimensional phononic crystal layer coated on uniform substrate using plane-wave-expansion method. Phys. Lett. A 2008, 372, 2091–2097. [Google Scholar] [CrossRef]
- Graczykowski, B.; Vogel, N.; Bley, K.; Butt, H.-J.; Fytas, G. Multiband hypersound filtering in two-dimensional colloidal crystals: Adhesion, resonances, and periodicity. Nano Lett. 2020, 20, 1883–1889. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.-W.; Wu, F.-G.; Zhang, X.; Hou, Z.-L. Lamb wave band gaps in locally resonant phononic crystal strip waveguides. Phys. Lett. A 2012, 376, 579–583. [Google Scholar] [CrossRef]
- Hedayatrasa, S.; Abhary, K.; Uddin, M. Numerical study and topology optimization of 1D periodic biomaterial phononic crystal plates for bandgaps of low order Lamb waves. Ultrasonics 2015, 57, 104–124. [Google Scholar] [CrossRef]
- Chen, J.-J.; Han, X. The propagation of Lamb waves in one-dimensional phononic crystal plates bordered with symmetric uniform layers. Phys. Lett. A 2010, 374, 3243–3246. [Google Scholar] [CrossRef]
- Chen, J.-J.; Xia, Y.-J.; Han, X.; Zhang, H.-B. Lamb waves in phononic crystal slabs: Truncated plane parallels to the axis of periodicity. Ultrasonics 2012, 52, 920–924. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.-B.; Chen, J.-J.; Han, X. Lamb wave band gaps in a homogenous plate with periodic tapered surface. J. Appl. Phys. 2012, 112, 054503. [Google Scholar] [CrossRef]
- Zhu, Y.-F.; Yuan, Y.; Zou, X.-Y.; Cheng, J.-C. Piezoelectric-sensitive mode of lamb wave in one-dimensional piezoelectric phononic crystal plate. Wave Motion 2015, 54, 66–75. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, T.-T.; Liu, J.-P.; Wang, Y.-S.; Laude, V. Guiding and splitting Lamb waves in coupled-resonator elastic waveguides. Compos. Struct. 2018, 206, 588–593. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.-J.; Wu, B.; Su, Y.-P.; Liu, D.-Y.; Chen, W.-Q.; Bao, R.-H. Tunable flexural wave band gaps in a prestressed elastic beam with periodic smart resonators. Mech. Adv. Mater. Struct. 2019, 1–8. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, H.-Y.; Wu, B.; Chen, W.-Q.; Balogun, O. Tunable band gaps and transmission behavior of SH waves with oblique incident angle in periodic dielectric elastomer laminates. Int. J. Mech. Sci. 2018, 146, 81–90. [Google Scholar] [CrossRef]
- Gao, N.-S.; Hou, H.; Mu, Y.-H. Low frequency acoustic properties of bilayer membrane acoustic metamaterial with magnetic oscillator. Theor. Appl. Mech. Lett. 2017, 7, 252–257. [Google Scholar] [CrossRef]
- Chen, Q.-L.; Elbanna, A. Tension-induced tunable corrugation in two-phase soft composites: Mechanisms and implications. Extreme Mech. Lett. 2015, 4, 26–37. [Google Scholar] [CrossRef]
- Farshad, M.; Benine, A. Magnetoactive elastomer composites. Polym. Test. 2004, 23, 347–353. [Google Scholar] [CrossRef]
- Elhajjar, R.; Law, C.-T.; Pegoretti, A. Magnetostrictive polymer composites: Recent advances in materials, structures and properties. Progr. Mater. Sci. 2018, 97, 204–229. [Google Scholar] [CrossRef]
- Perales-Martínez, I.-A.; Palacios-Pineda, L.-M.; Lozano-Sánchez, L.-M. Enhancement of a magnetorheological PDMS elastomer with carbonyl iron particles. Polym. Test. 2017, 57, 78–86. [Google Scholar] [CrossRef]
- Winger, J.; Schümann, M.; Kupka, A.; Odenbach, S. Influence of the particle size on the magnetorheological effect of magnetorheological elastomers. J. Magn. Magn. Mater. 2019, 481, 176–182. [Google Scholar] [CrossRef]
- Sun, S.-S.; Yang, J.; Yildirim, T.-J.; Ning, D.-H.; Zhu, X.-J.; Du, H.-P.; Zhang, S.-W.; Nakano, M.; Li, W.-H. A magnetorheological elastomer rail damper for wideband attenuation of rail noise and vibration. J. Intell. Mater. Syst. Struct. 2020, 31, 220–228. [Google Scholar] [CrossRef] [Green Version]
- Mikhailov, V.-P.; Bazinenkov, A.-M. Active vibration isolation platform on base of magnetorheological elastomers. J. Magn. Magn. Mater. 2017, 431, 266–268. [Google Scholar] [CrossRef]
- Xu, Z.-L.; Wu, F.-G.; Guo, Z.-N. Shear-wave band gaps tuned in two-dimensional phononic crystals with magnetorheological material. Solid State Commun. 2013, 154, 43–45. [Google Scholar] [CrossRef]
- Xu, Z.-L.; Tong, J.; Wu, F.-G. Magnetorheological elastomer vibration isolation of tunable three-dimensional locally resonant acoustic metamaterial. Solid State Commun. 2018, 271, 51–55. [Google Scholar] [CrossRef]
- Wen, X.-X.; Yu, G.-J.; Wang, L.-Y.; Zhu, S.-J. Band Gap Vibration Isolation of Phononic Crystals Based on Magnetorheological Elastomers. J. Synth. Cryst. 2018, 47, 102–108. [Google Scholar]
- Liu, S.-G.; Zhao, Y.-C.; Zhao, D. Bandgap and transmission spectrum characteristics of multilayered acoustic metamaterials with magnetorheological elastomer. Acta Phys. Sin. 2019, 68, 234301. [Google Scholar]
- Bellan, C.; Bossis, G. Field dependence of viscoelastic properties of mr elastomers. Int. J. Mod. Phys. B 2002, 16, 2447–2453. [Google Scholar] [CrossRef]
- Davis, L.-C. Model of magnetorheological elastomers. J. Appl. Phys. 1999, 85, 3348–3351. [Google Scholar] [CrossRef]
- Jolly, M.-R.; Carlson, J.-D.; Munoz, B.-C. The magnetoviscoelastic response of elastomer composites consisting of ferrous particles embedded in a polymer matrix. J. Intell. Mater. Syst. Struct. 1996, 7, 613–622. [Google Scholar] [CrossRef]
- Wang, G.; Wen, J.-h.; Liu, Y.-Z.; Yu, D.-L.; Zhao, H.-G. Research on the vibration band gaps of one dimensional viscoelastic periodic structure. Chin. J. Mech. Eng. 2004, 40, 47–50. [Google Scholar] [CrossRef]







| Material | |||
|---|---|---|---|
| Concrete | 30 | 0.2 | 2500 |
| Steel | 210.6 | 0.3 | 7780 |
| Rubber | 0.47 | 1300 |
| a/mm 300 | a1/mm 90 | a2/mm 150 | a3/mm 60 |
|---|---|---|---|
| h1/mm | h2/mm | h3/mm | |
| 75 | 50 | 75 | 27% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Zhao, P.; Ding, Y.; Ding, B.; Du, J.; Ma, T.; Wang, J. Study on Lamb Waves in a Composite Phononic Crystal Plate. Crystals 2020, 10, 799. https://doi.org/10.3390/cryst10090799
Yuan L, Zhao P, Ding Y, Ding B, Du J, Ma T, Wang J. Study on Lamb Waves in a Composite Phononic Crystal Plate. Crystals. 2020; 10(9):799. https://doi.org/10.3390/cryst10090799
Chicago/Turabian StyleYuan, Lili, Peng Zhao, Yong Ding, Benjie Ding, Jianke Du, Tingfeng Ma, and Ji Wang. 2020. "Study on Lamb Waves in a Composite Phononic Crystal Plate" Crystals 10, no. 9: 799. https://doi.org/10.3390/cryst10090799







