1. Introduction
Flat optical components are interesting to realize in- or out- coupling elements in applications such as near-to-eye displays, head-up displays, and virtual or augmented reality systems [
1,
2,
3,
4]. Reflective diffraction gratings based on chiral liquid crystal (CLC) are particularly suitable for these applications, due to their unique properties, such as polarization selectivity, high diffraction efficiency, and large reflection angles [
5,
6,
7,
8,
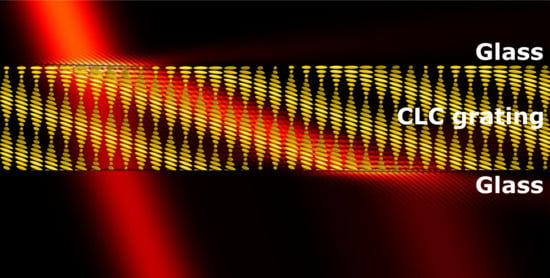
9]. In a CLC the liquid crystal (LC), director self-organizes into a periodic helical structure. Due to this periodicity, a photonic band-gap is formed and circularly polarized light is efficiently reflected in a wavelength range that depends on the helical pitch and refractive indices of the material. To make a reflective grating, CLC is deposited on top of a substrate with patterned photo-alignment [
5]. The alignment direction is periodically rotating along the
x-axis, as depicted in
Figure 1a. Thanks to the self-organization of the CLC, very small grating periods and, therefore, larger diffraction angles, can be easily achieved. In literature, gratings with a period as small as 440 nm and an efficiency of ≈90% have been reported [
10], proving the huge potential of these components.
However, the structure and diffraction properties of reflective gratings need to be thoroughly investigated and understood in order to reach this potential. In general, there is an agreement that, when CLC is combined with a periodic photo-alignment pattern at the confining substrate, a so called “slanted” structure is formed. The inclination angle (
) of the planes with equal phase depends on the period of the grating (
) (see
Figure 1a,c). Due to this inclination, the reflection band shifts towards shorter wavelengths as
increases, similarly to a planar CLC layer with light incident at an oblique angle [
11,
12,
13]. This was theoretically investigated in [
14,
15], assuming that the director in the bulk remains parallel to the substrate and the helical axis is perpendicular to the substrate (see
Figure 1c). However, no experimental results were provided in this work. A more thorough investigation was carried out in [
10], where the helical axis was assumed to be inclined, and in [
16], where the LC director was assumed to be tilted over a constant polar angle
. Numerical simulations of polarization properties and angular dependency of diffraction efficiency were supported by a limited amount of experimental data in [
10], providing evidence that the helical axis was indeed inclined in the studied configuration (
nm,
nm). However, no investigation of the spectral properties was provided and questions about the response at large angles of incidence (AOIs) remained unanswered, as only a limited range of incident angles was considered (
). Looking into this oblique incidence is important, since it is known that a polarization independent reflection (so-called full reflection band) appears in CLC at very large AOIs [
17]. Questions remain as to what extent the inclination angle in CLC gratings is equivalent to the AOI in a planar CLC and whether a similar full reflection band is observed at smaller angles of incidence for the CLC gratings with a large inclination of the helical axis.
Following the previous investigation that was carried out in our group [
9], we derived expressions for the LC director angles in the bulk of the reflective grating with inclined helix. Differently from previous research [
10,
14,
15,
16], we took into account that the LC director in CLC grating is at an angle with respect to the surface and this angle varies as a function of
x and
y. We implemented these angles into a numerical model and carried out calculations of the transmission spectra and intensity distributions for a wide range of AOIs and different polarizations. The results were compared with simulations for a CLC grating with vertical helical axis and for a planar CLC layer at equivalent AOIs. We also fabricated a CLC grating with a period
nm and helical pitch
nm to compare the numerical results with experimental measurements and validate the accuracy of the model. In this paper, the fabrication and characterization method of reflective CLC gratings is described. The analytical formulas for the LC director angles in such gratings are derived and the results of both measurements and simulations are compared.
3. Results
The experimentally measured and simulated transmission spectra for incident plane waves with TE polarization (along the z-axis) are compared in
Figure 2 for five AOIs in glass. The incidence is defined by
the angle with the helical axis, according to the convention of
Figure 1a. The left
Figure 2a shows the experimentally obtained spectra. The shaded area marks the range in which the characteristics of the polarizers are not optimal.
The incident light suffers from partial reflections at the glass/air interface and there is some scattering loss. As a result, the experimentally measured transmission remains below 90%. Note that, in order to experimentally obtain a given AOI in glass, the AOI in air has to be adapted, according to Snell’s law of refraction. The AOI in air with respect to the surface normal, for the five spectra is 0°, 11°, 21°, 33°, and 44°.
Figure 2b shows simulated transmission spectra according to the director distribution defined by Equation (
4), thus corresponding to an unperturbed helix with an inclined helical axis.
Figure 2c on the other hand shows simulated transmission spectra according to the director defined by Equation (
6), with the director remaining parallel to the substrates.
For the three sets of spectra, we can see a similar blue shift and a similar narrowing of the band gap when the AOI is increased. However, there is a striking difference between the simulations for the inclined helix (
Figure 2b) and the simulations for helix with planar director (
Figure 2c). For the inclined helix, the transmission decreases well below 50% for wavelengths close to the long wavelength edge of the band gap, for
below 51°. For the helix with planar director, the transmission stays ≈50% for all of the AOIs.
Figure 3,
Figure 4 and
Figure 5 show the spectral transmission for six different polarizations and five different angles of incidence
, as obtained from measurements (a) and numerical simulations for CLC grating with inclined helix (b) and for a standard planar CLC layer, with director independent of the x-coordinate (c). In all of the graphs, the angle of incidence is expressed with respect to the helical axis (
). In order to do that, for measurements and simulations of CLC grating with inclined helical axis, AOI is adjusted by adding the inclination angle
to the angles of incidence
used in the measurements (a) and simulations of CLC grating (b). In case of planar CLC layer
=
(c). This is only correct in a first approximation, since the refractive indices of the LC and of the glass substrate are different. There is some refraction at the boundaries and the relative angle between the k-vector and the helical axis is slightly different from the case of the inclined helix. This effect is not taken into account. The aim of planar CLC layer simulation is to investigate the role of the relative angle between the helical axis and propagation vector of the light.
For the measurements presented in
Figure 3,
Figure 4 and
Figure 5a, the same remarks apply as in
Figure 2a. In the shaded area the polarizer and the broadband quarter waveplate are not within the specifications. The values are not corrected for reflections at the glass/air interfaces and, therefore, remain below 90%. The angles of incidence reported on the graph refer to the angles in glass.
Figure 3 shows the transmission in the three cases for circularly polarized light. As expected, for right-handed circularly polarized (RHCP) light, the transmission is close to 0% in the reflection band region for all AOIs
. For left-handed circularly polarized (LHCP) light, the transmission is close to 100%. Both experimentally and in the simulation for a CLC grating with inclined helix, a clear dip in transmission spectrum appears for LHCP at
= 45°, which corresponds to
= 21°. In case of the planar structure, the LHCP transmission keeps decreasing as AOI increases further.
Apart from the circular polarizations, we also investigated the transmission for four different linear polarizations: TM (1 0 0), TE (0 0 1), +45° (1 0 1), and −45° (−1 0 1). In
Figure 4, the transmission for incident TM and TE polarizations are compared. The general tendency is that the transmission in the band gap is wavelength dependent: for TM polarization, the transmission in the band gap increases with wavelength, while it decreases for TE polarization. Close to the long wavelength band edge, the transmission for TE is much lower than for TM polarization. For a linear polarization at +45° the transmission is lower near the two band edges, while, for −45°, the transmission is lower near the center of the band gap. This incident polarization dependency of the shape of the reflection band was already observed in the literature for a planar CLC layer [
20].
Apart from the transmission simulations for incident plane waves, we also simulated the distribution of the electric field intensity with a Gaussian beam with
(
) and a fixed wavelength. The graph in
Figure 6a shows the simulated transmission curves for −45° polarization. For
nm both the CLC grating with inclined helix and the planar CLC have low transmission (
Figure 6a). The field intensity distribution represented in
Figure 6b for this case shows indeed that most of the light is reflected. For
nm the transmission for the CLC grating with inclined helix is almost equal to 100% as can be seen in
Figure 6a. For the same wavelength, the transmission for the planar CLC is still very low, because the wavelength is within the band gap.
Figure 6c indicates that part of the light goes straight through, while the other part is first diffracted into the CLC layer at a large AOI, then travels inside the layer and at the other side is diffracted again into the vertical direction, being shifted by a distance of about 30
.
4. Discussion
First, we investigate the difference between the two configurations (inclined helix and vertical helix) that have been discussed in literature. Comparison with the experimental spectra in
Figure 2a shows a very good agreement with
Figure 2b, and not with
Figure 2c. This indicates that the director distribution in our devices, consisting of a periodic grating at the interfaces filled with CLC, matches very well with the model of the inclined helix, described by Equation (
4). This also indicates that the theoretical model (based on spherical trigonometry), neglecting the parallel CLC layer formed at the interface, is sufficiently accurate to describe the experimental structure. Therefore, in all of the simulations for CLC gratings we focused on the inclined helix model and no longer considered the standing helix gratings. For the simulation that was based on the vertical helix, the band edge wavelengths correspond to the experiment, but the spectral distribution is very different, in particular for larger angles of incidence.
When analyzing the transmission spectra in the
Figure 3,
Figure 4 and
Figure 5, we can observe that there is a good agreement between the cases (a) and (b) for all polarizations and all angles
. The band gap (best observed for right-handed circularly polarized (RHCP) light) shifts to the blue for larger angles of incidence. For wavelengths above 800 nm the correspondence is less good, as could be expected from limitations in the experimental setup mentioned before. In the experiments, the transmission remains above 10%, which may be due to imperfections in the layers (loss of polarization). The link between the simulations (b) and (c) is also clear, indicating that the relative angle between light propagation and helical axis is important. However, there are also several important differences, induced by the presence of a grating structure. The most striking difference is that the reflection band is much smaller for the inclined helix structure than for the planar CLC for the same
(the short band-edge is at the same position, but the long band-edge occurs at a shorter wavelength). This is particularly true for the larger angles of incidence (e.g., for RHCP with
the long band-edge is at
nm for the CLC grating and at
nm for the planar CLC). For the planar CLC layer the bandgap is becoming wider for larger AOI, as described in the literature [
11,
12,
13]. However, for the CLC grating with inclined helix, the bandgap is becoming narrower with increasing AOI. Another difference is that the side lobes of the reflection band are further apart from each other for the planar CLC.
The position of side lobes of the reflection band in
Figure 3,
Figure 4 and
Figure 5, corresponds very well between the measurement (a) and simulations (b). However, in the measured spectra, these side lobes are less strong than in the simulations, which could be related to the resolution of the spectro-photometer or small imperfections in the CLC structure, especially at the edges of the device, where photo-alignment is not strong enough. The oscillation of these side lobes, as explained in [
20], gets faster at shorter wavelengths, since the normalized spacing (
) between two maxima is a constant for fixed cell thickness and AOI. According to this work, the spacing between maxima also increases with larger AOI. This explains why, in the case of an unpatterned planar CLC (c) we have slower oscillations than in the measured (a) and the simulated CLC grating with inclined helix (b), as the AOI (with respect to the substrate normal) in the case of planar CLC is larger than for the CLC grating, for the same angle
.
It is well known that the transmission spectrum of a planar CLC for linearly polarized light strongly depends on the orientation of the polarization [
21]. This is indeed observed in the simulations of
Figure 4c and even more in
Figure 5c. Additionally, the measured and simulated transmission spectra for a CLC grating with inclined helix strongly depend on the orientation of linearly polarized light. If the transmission spectra for two orthogonal polarizations are averaged out (RHCP and LHCP, TM, and TE, or +45° and −45°), the same spectrum, corresponding to the transmission for unpolarized light, is obtained.
The transmission spectra for LHCP light incident on a CLC grating with inclined helix (
Figure 3) reveal that a reflection band for LHCP (in addition to the band for RHCP light) appears at
(
). This is in agreement with the angle that was obtained in the literature, at which the full reflection band appears in unpatterned planar CLC layers [
17].
Even though we see stronger reflection for LHCP at
, the reflection band for this polarization is not fully developed, because the layer is too thin [
20,
22]. That is because this mode (which is a Bloch mode in the periodic structure of the CLC) is evanescent with a small imaginary part and, therefore, a thick layer is required for full reflection. To check this, we carried out simulations for LHCP light for a CLC grating with inclined helix with a three times larger thickness. The results of the simulations, as presented in
Figure 7, confirm that, for the larger thickness, the transmission drops to ≈0%.
In literature, it is shown that the reflection band for LHCP for planar CLC typically appears more or less in the middle of the selective reflection band [
20]. Here, we find that, for the CLC grating with an inclined helix, the reflection band for LHCP light appears closer to the long wavelength edge of the (narrower) selective reflection band for RHCP light (Figure
3). We consider simulations with Gaussian beam in order to understand the origin of the narrowing of the selective reflection band for the CLC grating with inclined helix. From
Figure 6b we find that the angle with the normal for the first diffraction order (reflected or transmitted) into air,
, is found from the grating equation with
:
with
the angle of incidence with respect to surface normal and
= 1.5 the refractive index of the glass substrate.
This allows for understanding why, for the CLC grating with inclined helix, the transmission increases from a low value to almost 100%, while, for the planar CLC, the transmission remains low over a much wider reflection band. The cut-off wavelength for reflection in the CLC grating corresponds to the wavelength at which the first diffraction order, according to the grating equation, is subjected to total internal reflection in the CLC layer. From the grating equation (Equation (
7)), we find:
The cut-off wavelength for
in our case is, for example, given by:
From the experimental and numerical data, we can indeed observe that, for (), the transmission increases to a high level near nm. This explains why, in a CLC grating with an inclined helix, the reflection band for LHCP is situated closer to the long wavelength edge of the selective reflection, as light with larger wavelengths is transmitted due to the limitation imposed by the grating equation. In the conventional planar CLC, the angle of the reflected light is equal to and there is no restriction related to diffraction, giving rise to a broader selective reflection band. In fact, for a CLC grating with an inclined helix, the LHCP reflection band completely disappears for larger AOIs, because of the limitation imposed by the grating equation.
The angle of propagation in the CLC grating with an inclined helix at the cut-off wavelength can be estimated from the critical angle for total internal reflection between the CLC and glass interface. From the simulations, we observe the propagation angle of 68° at 674 nm, which corresponds to the critical angle for total internal reflection between glass (
) and CLC with average refractive index
. In a CLC grating with an inclined helix, light with wavelength 700 nm (above the cut-off value) is efficiently coupled into the CLC layer at an angle with the normal to the substrate of ≈70°, as can be seen in
Figure 6c. Taking into account that the inclination axis of the helical axis is
, the propagation is practically perpendicular to the helical axis of the CLC.
This is the first demonstration of efficient large-angle forward diffraction based on CLC with an inclined helical axis. Circularly polarized light is coupled into the CLC layer. When considering the ray propagation in the COMSOL simulation, it appears as if refraction occurs in the opposite direction than expected from the contrast in refractive index: although both refractive indices of the LC (1.54 and 1.74) are higher than that of the substrate (1.50), the light in the CLC makes a larger angle () with the normal than the light in the substrate (). This effect is entirely due to the periodicity of the structure near the surface of the layer.
The optical behavior of a CLC grating with an inclined helix can be understood by considering three layers: two linear gratings (one near the top substrate and one near the bottom substrate) that are responsible for diffraction, and a homogeneous CLC layer in which only certain Bloch modes can propagate. We show here that very high diffraction efficiency is not only observed when light is reflected, but it can also take place when light is propagating in the CLC itself, leading to a lateral displacement of the beam. We are the first to demonstrate this efficient lateral shift of light in a CLC layer with inclined helix, according to our knowledge.
The excellent agreement with experimental transmission spectra shows that the inclined helix model accurately describes the behavior of reflective CLC gratings, in contrast to the previously suggested vertical helix model [
14,
15]. Even though a similar configuration was suggested by [
10], here we provide a complete description of the LC director orientation in the CLC grating with inclined helix. We also investigate the spectral response of CLC grating with inclined helix at large AOIs and observe the appearance of the reflection band for LHCP light.