Hardness, Young’s Modulus and Elastic Recovery in Magnetron Sputtered Amorphous AlMgB₁₄ Films

Abstract

We report optical and mechanical properties of hard aluminum magnesium boride films magnetron sputtered from a stoichiometric AlMgB₁₄ ceramic target onto Corning^® 1737 Glass and Si (100) wafers. High target sputtering rf-power and sufficiently short target-to-substrate distance appeared to be critical processing conditions. Amorphous AlMgB₁₄ films demonstrate very strong indentation size effect (ISE): exceptionally high nanohardness H = 88 GPa and elastic Young’s modulus $E^{*}$ = 517 GPa at 26 nm of the diamond probe penetration depth and almost constant values, respectively, of about 35 GPa and 275 GPa starting at depths of about 2–3% of films’ thickness. For comparative analysis of elastic strain to failure index $H/E^{*}$, resistance to plastic deformation ratio $H^3/E^{*2}$ and elastic recovery ratio $W_{\mathrm{e}}$ were obtained in nanoindentation tests performed in a wide range of loading forces from 0.5 to 40 mN. High authentic numerical values of H = 50 GPa and $E^{*}$ = 340 GPa correlate with as low as only 10% of total energy dissipating through the plastic deformations.

1. Introduction

For the first time, aluminum magnesium boride was sintered in 1970 in Carborundum Company by V.I. Matkovich and J. Economy. Small black AlMgB₁₄ crystals were prepared by heating a mixture of aluminum, magnesium and boron at a temperature of 900 °C. Their structure was determined as a 3D network formed from icosahedral B₁₂ groups within the orthorhombic unit cell with the dimensions a = 10.313 Å, b = 8.115 Å, and c = 5.848 Å [1]. Results obtained in succeeding works on AlMgB14 can be divided into three main groups. True stoichiometry Al_0.75Mg_0.78B₁₄, thermoelectric, electronic and optical properties were reported between the 1970s and 1990s (see references in Ref. [2]). Next, in 1993 Higashi et al. and later in 2000 Cook et al. from Iowa have reported exceptional hardness of AlMgB₁₄ crystals as high as, respectively, 27.4–28.3 GPa [3] and 32–35 GPa [2]. Lastly in 2003, the same Iowa group took an important step in exploration of AlMgB₁₄ fabricating superhard self-lubricating (hereinafter BAM) films. They used pulsed laser deposition (PLD) technique to obtain films which hardness ranged from 45 to 51 GPa [4].

Recently, we succeeded in deposition of high quality amorphous BAM films by an RF magnetron sputtering method which can easily be scaled up for industrial use. High sputtering power of ceramic AlMgB₁₄ target, moderately low substrate temperature, and a short target-to-substrate distance enabled high-energy ballistic impact regime of adatoms’ motion thus leading to an enhanced hardness by 25% and Young’s modulus by 60%, compared to PLD-made films. Correct stoichiometry and compositional in-depth homogeneity governed superior mechanical properties of magnetron sputtered films [5]. Correlative theoretical and experimental elaboration of high power pulsed magnetron sputtering (HPPMS) of AlYB₁₄ films acknowledged the ability to form icosahedral boron-rich phases below the bulk synthesis temperatures [6]. Matching results of ab initio molecular dynamics calculations of elastic properties with nanoindentation measurements of Young’s modulus proved the predictive power of the HPPMS technique to sinter amorphous boride coatings [7].

Both amorphous AlMgB₁₄ films obtained by pulsed laser deposition [4] and magnetron sputtering [5] exhibit a strong indentation size effect (ISE). This is the exceptionally high parameters of nanohardness H and elastic Young’s modulus $E^{*}$ at the tens-of-nanometer-scale of penetration depth of a diamond probe and their very steep decrease to the constant values at depths of about 2–3% of the film’s thickness. Still the general necessity remains to authenticate these results. Herein, we examined additional mechanical parameters: elastic strain to failure index $H/E^{*}$, resistance to plastic deformation ratio $H^3/E^{*2}$, and elastic recovery ratio $W_{\mathrm{e}}$. Maximum values of calculated parameter $H^3/E^{*2}$ and measured $W_{\mathrm{e}}$ as high as 90% always match the peak values of hardness H and elastic modulus $E^{*}$. Therefore, we relate ISE to a very low portion of total energy dissipating through the plastic deformations at shallow indenter prints.

2. Materials and Methods

The details of RF magnetron sputtering of ultra-hard AlMgB₁₄ coatings were published elsewhere [5]. In brief, a batch of BAM films was deposited onto Si(100) wafers and Corning^® 1737 glass by sputtering of a stoichiometric AlMgB₁₄ ceramic target. The target was manufactured via the grinding and subsequent spark plasma sintering of Al (99.97%), Mg (99.8%), and B (99%) powders [8]. The ultimate pressure in vacuum chamber was better than 3 × 10⁻⁷ Torr, films deposition was carried out at 7 mTorr of Ar-gas pressure. In-depth uniformity, smooth surface and ultimate hardness of BAM films were achieved at optimum processing conditions: distance of 25 mm between 1 inch 50 W RF powered magnetron and substrates kept on the heater at 250–350 °C. Typical film size was 10 × 10 mm², deposition rate was 0.44 nm/s. Films’ roughness was checked with KLA-Tencor P-15 stylus profiler. It does not exceed the roughness of Corning^® 1737 glass and Si wafers as the substrates.

All films sintered at different temperatures varied from room temperature up to 550 °C and appeared to be X-ray amorphous. BAM films onto Si wafers do not exhibit themselves with any XRD pattern (recorded with a Siemens D-5000 powder diffractometer) even in a magnifying log-scale. Θ-2Θ scan of 0.4 μm thick BAM/Si film in the main frame of Figure 1 contains only Si(100) wafer’s Bragg reflections. In insets, the selected area electron diffraction (SAED, performed on a FEI Tecnai T20 TEM) pattern and HRTEM image also attest amorphous structure of 2.12-μm-thick BAM/Si film.

Optical dispersion was evaluated from the transmission spectrum of BAM films onto glass substrate recorded at normal light incidence with a Fourier transform infrared spectrometer Nicolet 5700 in the range 0.3–2.5 μm. The spectrum was normalized to the spectrum of the bare glass substrate. Unpolarized backscattered micro-Raman spectra of AlMgB₁₄ films onto Si(100) wafers were collected with a confocal Thermo Scientific Nicolet Almega XR Dispersive Raman Spectrometer at room temperature using 785 nm and 532 nm laser pumping. NHT S/N 06-0134 and TTX-NHT2 S/N 01-05821 nanoindentation instruments with Berkovich three-sided diamond pyramid tips were employed to measure hardness H and effective Young’s modulus $E^{*}=E/\left(1-{\nu }^2\right)$. In calculation we used ν = 0.25 as a Poisson’s ratio for AlMgB₁₄ films. Abrasion BAM films’ properties were characterized using CSM Instruments SA micro-scratch tester S/N 01-03079 with the diamond Rockwell C indenter of 200-μm radius.

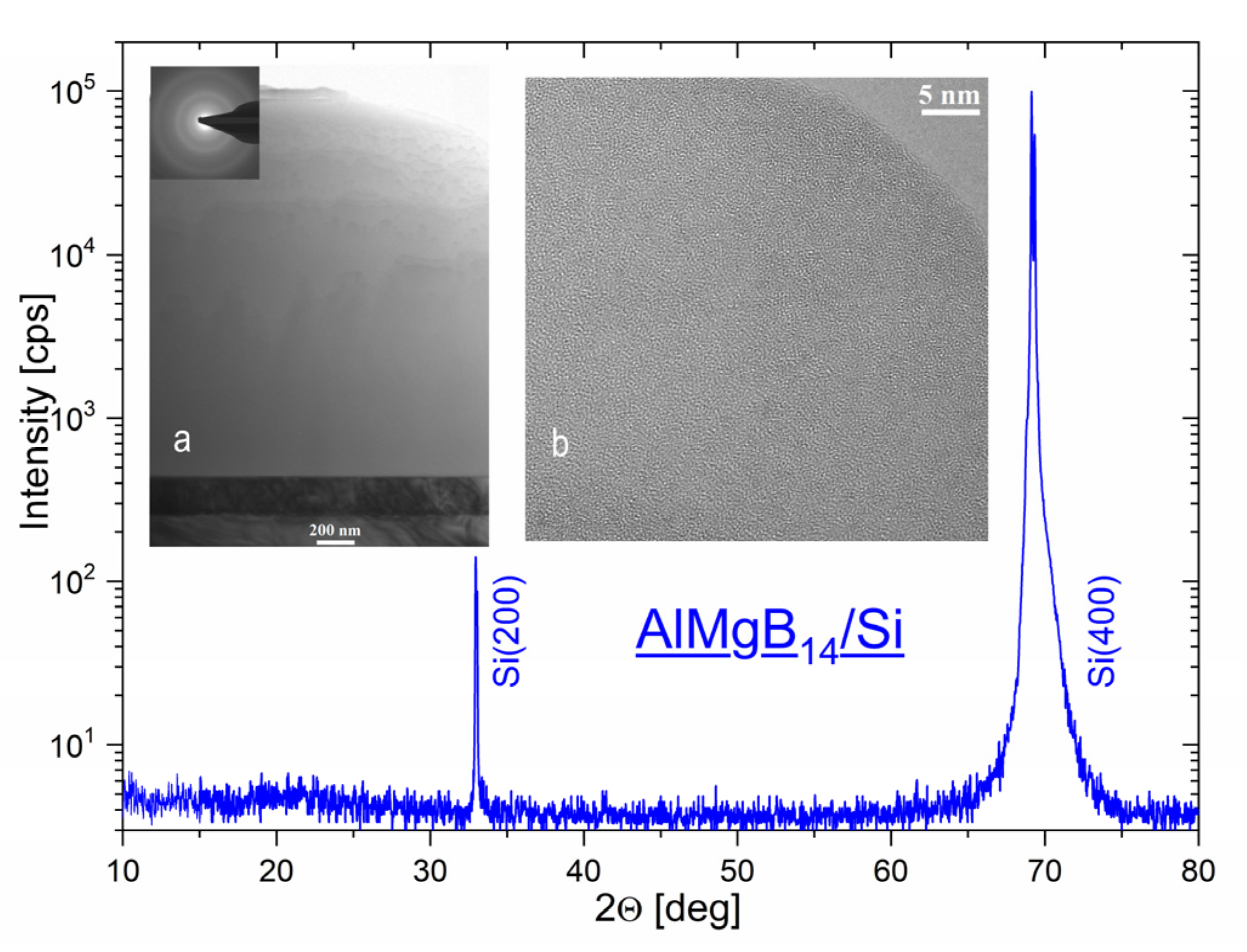
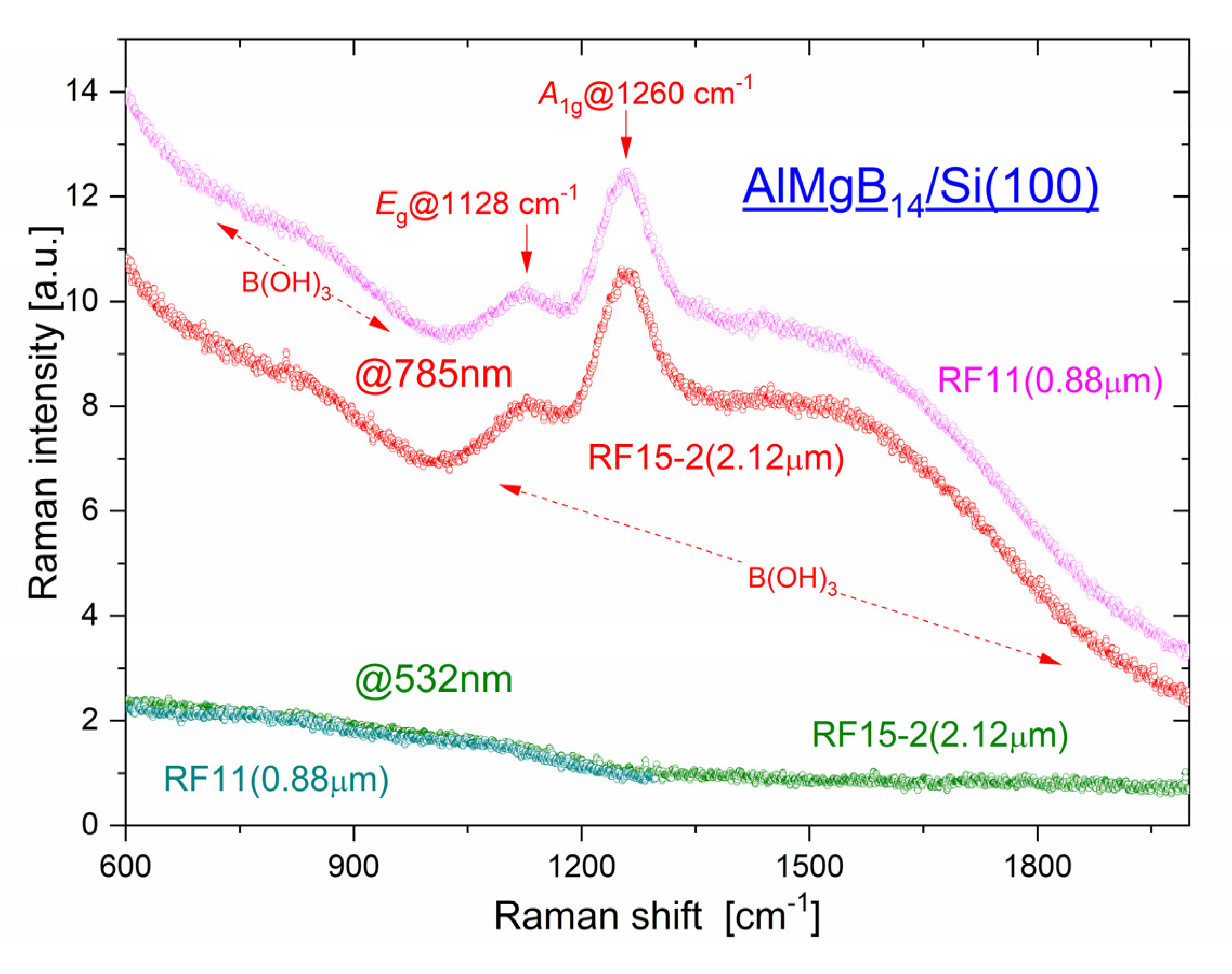
3. Results and Discussion

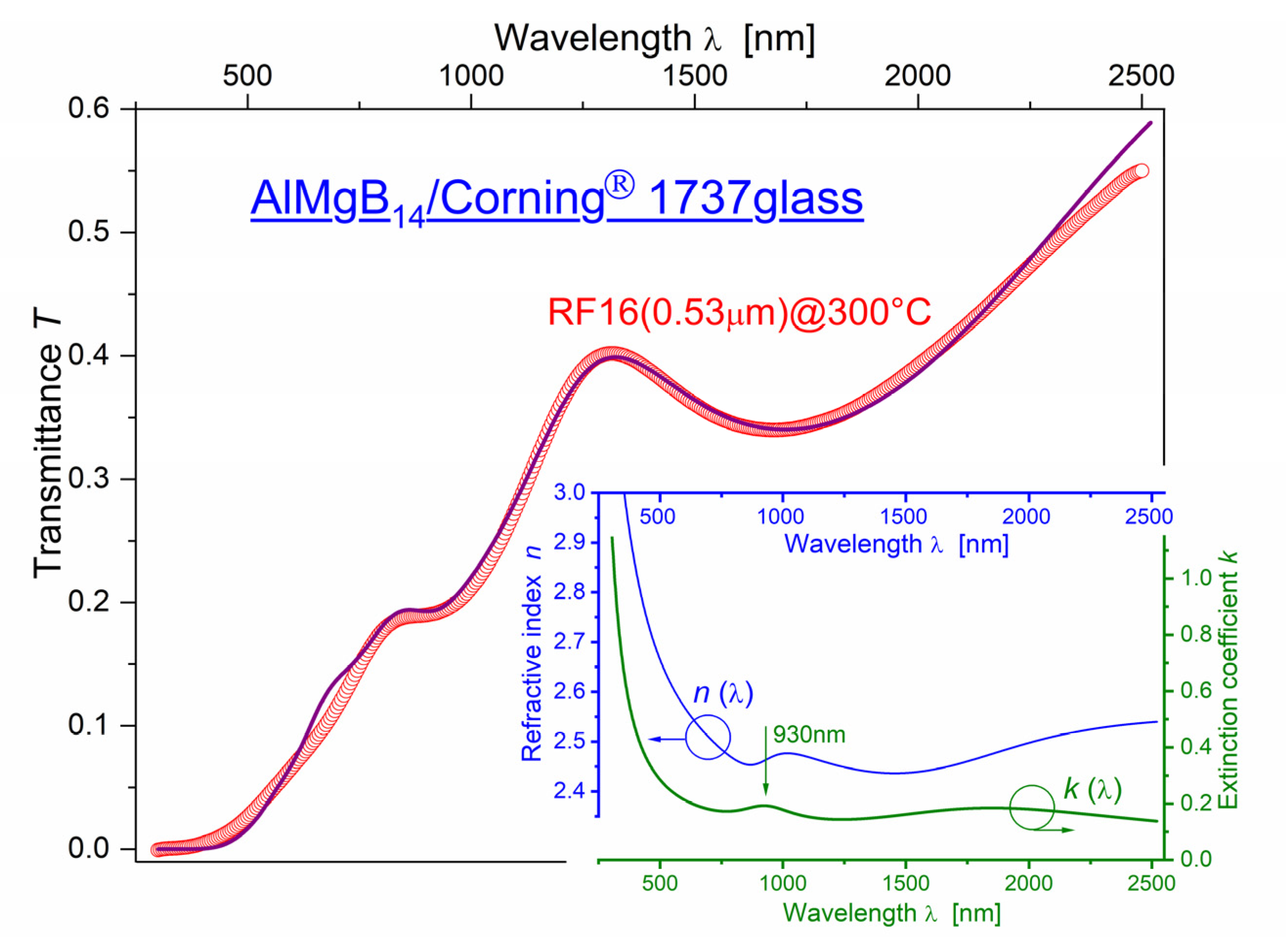
3.1. Optical Properties

Circular symbols in Figure 2 display optical transmission spectrum of 0.53-μm-thick film onto transparent Corning^® 1737 glass substrate. It has a semiconductor-type character. The absorption edge lies around 310 nm (bandgap is 4 eV) and specific resistivity $\rho =1 \mathsf{\Omega } \mathrm{cm}$.

Observed spectrum features we modeled with a commonly used Swanepoel [9] formula (follows afterward in Appendix A). Theoretical solid line in Figure 2 firmly fits to the experimental spectrum. A good agreement with the experimental results was achieved presenting complex refractive index with three Sellmeier-type electric dipole resonances, Equation (1):

$$\begin{array}{c}{\left(n-ik\right)}^2=1+\frac{4.85}{1-{\left(270\mathrm{nm}/\lambda \right)}^2+i\times 0.34\left(270\mathrm{nm}/\lambda \right)}\\ +\frac{0.1}{1-{\left(930\mathrm{nm}/\lambda \right)}^2+i\times 0.3\left(930\mathrm{nm}/\lambda \right)}\\ +\frac{0.5}{1-{\left(1800\mathrm{nm}/\lambda \right)}^2+i\times 0.8\left(1800\mathrm{nm}/\lambda \right)} \end{array}$$

(1)

Inset to Figure 2 shows a wavelength dispersion of refractive index n(λ) and extinction coefficient k(λ) calculated with Equation (1). Within the explored 0.3–2.5 μm range, they distinctly reveal dipole resonance at 930 nm. It manifests itself as a hump in extinction coefficient k(λ) and as a derivative-type curve of the real part of refractive index n(λ) correspondent to Kramers–Kronig relations.

Figure 3 presents unpolarized backscattered micro-Raman spectra for two RF15-2(2.12 μm) and RF11(0.88 μm) BAM films prepared onto Si(100), respectively, at 250 °C and 300 °C. Red/magenta and green/cyan color symbols depict spectra obtained at 785 nm and 532 nm laser light pumping, correspondingly.

Since the structure of AlMgB₁₄ films is completely amorphous, the Raman spectra do not contain any narrow lines. There are two broad bands with maxima at 1128 cm⁻¹ and 1260 cm⁻¹. Following Ref. [10] we attribute them, respectively, to intra-icosahedral B-B vibration E_g modes and to predominantly inter-icosahedral B-B vibration A_1g modes. The shoulder around 840 cm⁻¹ and the broad band ranging from 1030 up to 2000 cm⁻¹ can rely upon Raman and IR active vibrations in the molecule of orthorhombic boric acid [11]. Molecular vibrations of boric acid together with E_g and A_1g icosahedral B-B vibrational modes can be ascribed to the subtle optical resonance absorption at λ = 930 nm revealed in inset to Figure 2.

Three (OH)⁻¹ groups surround B³⁺ atom and form a planar trigonal molecular configuration. Strong hydrogen bonds between hydroxyl groups build a stable layer of B(OH)₃ molecules whereas only weak van der Waal’s forces link two adjacent layers to each other at the distance of 0.318 nm. Easily sheared multilayered B(OH)₃ structure governs unique lubrication properties of crystalline boric acid [12]. These nanometer-thick B(OH)₃ surface layers make BAM films slicker than Teflon ^TM [13]. Mechanical properties of AlMgB₁₄ films are not affected by boric acid since its hardness and elastic modulus are as low as 1.2 GPa and 15 GPa, correspondingly [14]. Due to ultra-high hardness and slipperiness, BAM films have great potential for a wide range of diverse applications for MEMS devices, wear-resistant and low-friction transparent coatings, metal dies, measuring tools and gauges.

3.2. Nanoindentation

Nanoindentation tests of AlMgB₁₄ films on Si(100) wafers were conducted applying a load to Berkovich diamond pyramid tip from 0.5 up to 40 mN. The measurements were carried out applying a multiple simple matrix 2×2 indentations to exclude spurious notches and collect reliable data sufficient for statistical averaging. A new diamond probe adjustment was performed every time for the next 2×2 indentations. To eliminate a role of Si substrate, penetration depth of the diamond indenter did not exceed 10–15% of films’ thickness. Typical loading L(h) (ascending) and unloading L_↓(h) (descending) force curves are shown in Figure 4. The area between the loading and unloading curve represents the energy dissipated in BAM film due to plastic deformation whereas the area under the unloading curve defines recovered work of elastic forces.

Load-displacement curves are used to determine three main parameters that characterize hard AlMgB₁₄ films: hardness H, effective Young’s modulus $E^{*}=E/\left(1-{\nu }^2\right)$ and elastic recovery ratio $W_{\mathrm{e}}$. H and $E^{*}$ are calculated as per the Oliver and Pharr method fitting L_↓(h) = A(h − h_res)^m dependence to the experimental unloading force curve [15]. Elastic recovery ratio is defined as a ratio of areas under unloading L_↓(h) and loading L_↑(h) curves, Equation (2):

$$W_{\mathrm{e}}={{\displaystyle \int }}_{h_{\mathrm{res}}}^{h_{\max }}dh·L_{\downarrow }\left(h\right)/{{\displaystyle \int }}_0^{h_{\max }}dh·L_{\uparrow }\left(h\right)$$

(2)

From ascertained values of H and $E^{*}$, we calculate dimensionless elastic strain index $H/E^{*}$ and the ratio $H^3/E^{*2}$ measured in GPa. It is commonly assumed that a material with high $H/E^{*}$ ratio like 0.1 possesses a better wear resistance than a material with a low ratio $H/E^{*}~ 0.01$. Parameter $H^3/E^{*2}$ controls the resistance of the coating to plastic deformation. Really, to initiate plastic deformation, loading force should exceed the critical value $L_{\mathrm{cr}}=0.78 r^2{H}^3/E^{*2}$ [16]. Therefore, plasticity is reduced in materials with higher hardness and lower modulus. The next paragraph presents all the above mentioned mechanical parameters measured in BAM films at different loading forces.

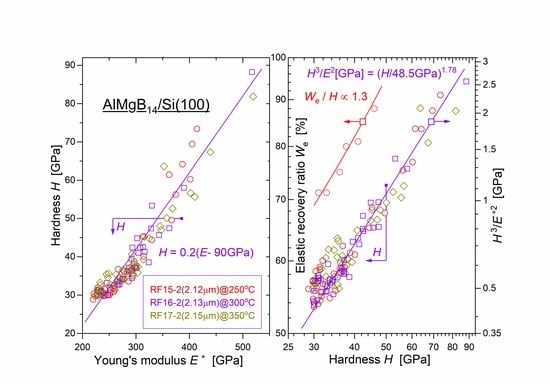
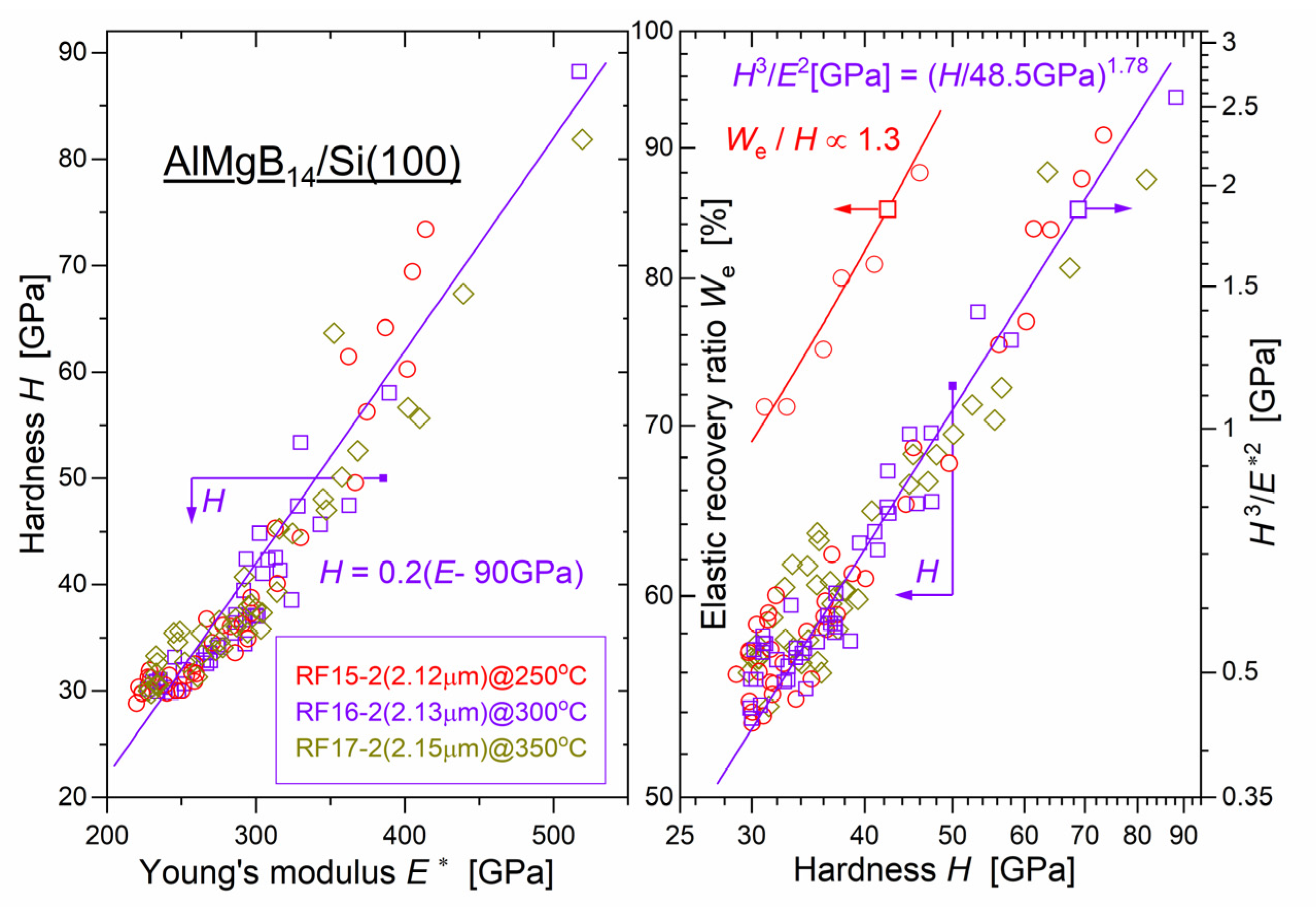
3.3. Hardness and Young’s Modulus

Symbols in Figure 5 present experimental data for hardness H and Young’s modulus $E^{*}$ collected for all the indentations made at different loading forces L in three AlMgB₁₄ films fabricated within the optimal temperature range 250–350 °C.

Measurements performed at too shallow notches exhibit severe noise, seem much less reproducible and hence yield big scattering of H and $E^{*}$ data. To find reliable range of the loading force that guaranties authentic results, we have performed the nanohardness test of blank 300 μm thick Si(100) wafer used as a substrate for BAM films deposition (see results are also shown in Figure 5). At loading forces above 2 mN, both measured hardness 13 GPa and Young’s modulus 173 GPa are very close to the hardness H = 10.5–13 GPa and modulus $E^{*}$ = 130–185 GPa reported in the literature for different directions in Si single crystals [17,18,19]. Uncertain values of hardness δH = 10 GPa and modulus δE = ± 32 GPa obtained for Si serve as an estimate accuracy of indentation tests at weak loading forces. Despite big scattering of the data observed at shallow indentations, a strong indentation size effect (ISE) is readily seen in Figure 5. Both hardness H and modulus $E^{*}$ sharply increase at weak loads L ~ 0.5–2 mN (small h ~ 20–50 nm) reaching the peak values of 88 GPa and 517 GPa, correspondingly. At stronger loading forces 2–5 mN, H and $E^{*}$ data become less scattered and depth dependent. This “veritable” L interval starts from 2% and continues to 15% of the relative film thickness indenter’s penetration depth without any indication of Si substrate contribution to H and $E^{*}$.

3.4. Plastic and Elastic Parts of the Indentation Work

In Figure 6, we drew dependencies of the nanohardness H upon the elastic modulus $E^{*}$, resistance to plastic deformation ratio $H^3/E^{*2}$ and elastic recovery ratio $W_{\mathrm{e}}$ vs. H obtained at different loading forces L. This plot composed of a complete set of the same, as in Figure 5, H and $E^{*}$ data.

For all three films grown at “favorable” 250–350 °C temperatures, hardness H vs. modulus $E^{*}$ data form the most dense track along the straight line for which the slope yields high a value of elastic strain index $H/E^{*}$ = 0.2. The dependence of resistance to plastic deformation ratio $H^3/E^{*2}$ upon the nanohardness H follows the power law $H^3/E^{*2}\left[\mathrm{GPa}\right] ={\left(H/48.5\mathrm{GPa}\right)}^{1.78}$. High hardness is always accompanied with very high values of $W_{\mathrm{e}}$ growing as $H^{1.3}$ to become higher than 90%.

When load weakens (L < 2 mN), scattering of H and $E^{*}$ data quickly grows. It happens because the energy dissipating through the plastic deformations suddenly decreases at shallow prints and the shape of load-displacement curves experiences severe distortions. Therefore, the most reliable results for elastic strain index $H/E^{*}$ and $H^3/E^{*2}$ ratio are marked in Figure 6 with the straight lines pointed towards H < 50 GPa. Indentation size effect (ISE) manifests a strong reduction of the main mechanical parameters. It is readily seen in Figure 5 and Figure 6 when the penetration depth of a diamond probe h increasing from 28 to 330 nm. Namely: H becomes reduced by 66%, $E^{*}$ by 56%, resistance to plastic deformation ratio $H^3/E^{*2}$ is diminished by 83%, and elastic recovery $W_{\mathrm{e}}$ decreases from 90 ± 5% down to 71 ± 1%.

Strong ISE, wide spread of mechanical properties of BAM films and their correlation with hardness resemble results reported by J. Musil for nanocomposite titanium, zirconium and chromium nitride coatings sputtered at different deposition conditions [20,21]. Similar to AlMgB₁₄, these films in an amorphous state exhibit superhardness $\left(H\ge 40 \mathrm{GPa}\right)$, hardness and elastic modulus grow at weak loads whereas energy dissipating through the plastic deformations decreases ($W_{\mathrm{e}}$ increases up to about 85% for films with H ≈ 70 GPa), H(L) and $E^{*}\left(L\right)$ values become constant at higher loads L demonstrating independence on substrate properties. In Figure 6, linear dependence $H=0.2\left(E-90\mathrm{GPa}\right)$ and power law $H^3/E^{*2}\left[\mathrm{GPa}\right] ={\left(H/48.5\mathrm{GPa}\right)}^{1.78}$ obtained for BAM films accord J. Musil’s conclusion on the general character of these relations for numerous oxides, carbides and nitrides prepared by magnetron sputtering under different deposition conditions [22].

Scratch tests performed with AlMgB₁₄ films on Si(100) and Corning^® 1737 glass substrates enable determination of the second critical loads L_c2 when side chips and peelings of coating appear inside the indenter’s track. Corresponding L_c2 values were used to obtain film-substrate interfacial adhesion strength equal to 18.4 J/m² and 6.4 J/m² for BAM film on Si(100) and glass substrate, correspondingly (see the details in Ref. [23] and [24]).

4. Conclusions

Optical properties of amorphous magnetron sputtered AlMgB₁₄ films are characterized by constan in near IR values of refractive index n = 2.5 and extinction coefficient k = 0.2 as well as two bands of Raman-active intra- and inter-icosahedral boron–boron vibrations. Nanoindentation tests displayed a strong indentation size effect (ISE): exceptionally high values of hardness H and Young’s modulus $E^{*}$ at the tens-of-nm-scale of indenter penetration depth and a very steep decrease to almost constant parameters at depths which are only 2–3% of films’ thickness. Peak values of H and $E^{*}$ correspond to the maximum values of calculated resistance to plastic deformation ratio $H^3/E^{*2}$ and elastic recovery ratio $W_{\mathrm{e}}=90\%$. We arrived at the conclusion that ISE is a natural attribute of anomalous low energy dissipated through the plastic deformations at shallow indenter’s prints.

5. Patents

Protective BAM coatings sputtered onto glass exhibit a hardness that is 1.5 times higher than in Gorilla^® Glass at loads above 15 mN and up to 5 times higher at low mN-range loads (see Ref. [24] and patents [25,26]).