Abstract
The existing kinetic models often consider the influence of a single factor alone on the chemical reaction and this is insufficient to completely describe the decomposition reaction of solids. Therefore, the existing kinetic models were improved using the pore structure model. The proposed model was verified using the thermal decomposition experiment on calcium carbonate. The equation has been modified as . This led to the conclusion that the pore structure, generated during the thermal decomposition of calcite, has an important influence on the decomposition kinetics. The existing experimental data show that the improved model, with random pores as the main body, reasonably describes the thermal decomposition process of calcite.
1. Introduction
Calcium carbonate is a crystal mineral with a large reserve and wide distribution in nature and has a wide range of applications in metallurgy, chemical industry, construction, and more [1,2,3,4,5,6]. The prediction and identification of the thermal decomposition mechanism are important for kinetic studies in order to expand the practical applications of calcium carbonate and its decomposition products [7,8,9,10,11]. The factors that influence the thermal decomposition of calcium carbonate, such as heat transfer, mass transfer, chemical reaction, etc. have been proposed in the last century [12,13,14,15,16]. In order to better apply calcium carbonate and its products to industrial production, it is necessary to know the dependence of reaction rate on temperature under different conditions, and express it in mathematical form by using kinetic model.
In the past few decades, there have been many studies on the thermal decomposition kinetics of calcium carbonate. Ingraham and his collaborators studied the thermal decomposition mechanism of calcium carbonate using the kinetic models by changing the partial pressure of carbon dioxide in the process. The results were found to conform to the diffusion model, they also found that the particle size of the sample had a significant effect on the decomposition rate, while the inert impurities had little effect [17]. However, the potential that the change of decomposition mechanism might be caused by the change of thermal decomposition conditions, was not considered in their study. The partial pressure of carbon dioxide during the thermal decomposition of calcium carbonate is a minor factor in comparison with the heat conduction and geometry of the sample that was discovered by Calvo et al. by changing the experimental conditions of thermal decomposition [18]. This indicates that there may be some factors influencing the thermal decomposition process of calcium carbonate, that have no influence on the reaction mechanism, while some factors have a greater influence on the reaction process and may even change the reaction mechanism. Beruto and Search studied the thermal decomposition of calcite and found that the rate limiting step conforms to the chemical reaction mechanism [19,20]. Although they noted in their paper that the diffusion of gaseous products may also be a rate limiting step, they did not consider the two in relation to each other. Bouineau et al. used Mampel’s model to show the strong influence of sample purity on the chemical reaction under isothermal and isobaric conditions, but did not illustrate whether the influence of impurities will change the reaction mechanism [21]. Chen et al. determined the decomposition reaction model of calcium carbonate using the model-free and model fitting methods. The model for the thermal decomposition of calcium carbonate was proposed to be R2 [22] which can be expressed as:
where is the model of R2, α is the conversion percentage.
Although there are several functional mechanisms to describe the decomposition reaction of solids, they are obtained on the basis of a single influencing factor [23]. The model functions used for the thermal decomposition of calcium carbonate include the random nucleation and subsequent growth model (A), contraction model (R), diffusion model (D), etc. [8,24,25]. Those model functions can be described as follows, respectively.
In Equations (2)–(5), represents the random nucleation and subsequent growth model (A) (n = 1 in this paper), contraction model (R) (n = 2, and n = 3 in this paper) and diffusion model (Equation (4) is two-dimensional diffusion (D2), and Equation (5) represents cylindrical symmetric diffusion (D4)), respectively. Where is the kinetic model indexes and α is the conversion percentage.
Because the formation of a random pore structure, which is attributed to the liberation of gas during the thermal decomposition of calcium carbonate, was supposed to have a definite influence on the decomposition process [26,27]. Mulokozi and Lugwisha also showed that the heterogeneous reaction is not describable by a single-phase [28]. It can be seen that the thermal decomposition reaction of calcium carbonate may involve several reaction processes. Currently, the theoretical and experimental studies on the random pore model are used to investigate the kinetics of the coke gasification reaction but rarely used in similar studies of other substances [29,30,31]. Based on the summary and analysis of the existing research, we hope to construct a kinetic mechanism function containing multiple reaction processes. Therefore, the random pore model was incorporated into the kinetic model for the thermal decomposition of calcium carbonate in order to obtain a better result.
In this work, the relative errors of some model functions in the literature have been calculated. It was concluded that the R model suitably describes the thermal decomposition reaction of calcium carbonate. In order to test this, the improved model function was further proposed. The experiments in the previous work were repeated to verify the model. It was concluded that the improved model function was more accurate, both in describing the thermal decomposition of experimental process, and activation energy.
2. Kinetic Model
As the thermal decomposition experiment of calcium carbonate was performed under non-isothermal conditions, the kinetic parameters of the reaction were solved by Achar–Brindley–Sharp–Wentdworth (ABSW) for differential non-isothermal equations [32].
where is the temperature at any time t, is the pre-exponential factor, is the activation energy of the reaction, is the conversion percentage at any temperature, and is the heating rate.
This simplifies to a linear equation
The conversion percentage at any temperature can be expressed as
where, is the initial mass of the samples, is the sample mass at temperature , and is the final mass of the samples.
The linear relationship between and can be obtained from Equation (2). This method was used to obtain the activation energy (by slash of against ) and pre-exponential factor (by intercept of against ) as well.
Due to the formation of pores as a result of carbon dioxide liberation during the thermal decomposition of calcium carbonate, the random pore model, interface reaction model, and diffusion model were introduced for combinatorial optimization [4,22,30,33]. Based on the theory of Šesták for the kinetic model of accommodation function [34,35,36], the following multifaceted model function was established.
where is the real kinetic mechanism function of the accommodation function in Šesták’s theory, is the random pore model (as a modified function in this article), is the accommodation function, and are the kinetic model indexes, and is the pore structure parameters of the product [35]. In this paper, is used for the calculation in place of .
The multifaceted pattern function is tested using the test deviation method described in the literature to verify the matching degree of the function [30].
where is the relative error, is the experimental value, is the value calculated from the model, is the maximum conversion of the experiment, and N is the number of data points.
3. Experimental Details
In this work, one of the samples (No.1) was MKBL0094V supplied by Sigma-Aldrich (St. Louis, MO, USA). The other samples (No.2, No.3) were natural calcite obtained from Guilin, Guangxi, China, with the same characteristics except for the particle size. The images in Figure 1 were obtained using the field emission scanning electron microscopy (FESEM, ZEISS-ΣIGMA HD, Carl Zeiss AG, Jena, Germany). The size distribution of the samples was analyzed using the laser particle size analyzer (LPSA) under dry conditions (better size in China). Sample No.1 was regularly shaped with uniform particle size and no debris on the surface, as seen from Figure 1a. According to Figure 1b,c, the shapes of samples No.2 and No.3 were irregular with non-uniform particle sizes and debris on the surface of the samples. From Figure 1d–f, the average volume of samples was found to be 18.21 μm3 (No.1), 22.63 μm3 (No.2), and 109.6 μm 3 (No.3). Figure 2 was obtained using the XRD instrument (PANalytical X, RigakuD/max-Ra with CuKα, λ = 0.15418 nm). All the samples were found to be calcite crystal.
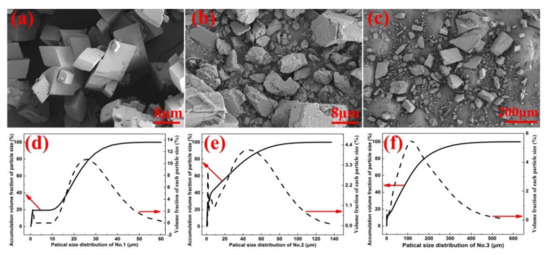
Figure 1.
(a) SEM of analytically pure calcium carbonate (No.1); (b) SEM of calcite crystal power (No.2); (c) SEM of calcite power (No.3); (d–f) Particle size distribution and accumulation volume fraction of the particle size for No.1, 2 and 3.
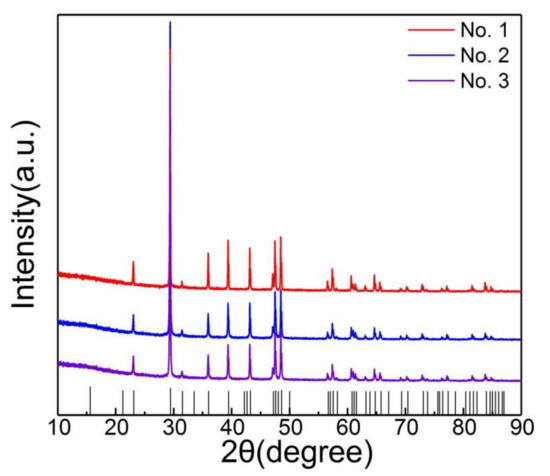
Figure 2.
XRD of the three samples.
The differential thermal analysis was performed on the prepared samples (the sample mass was 5 mg). The STA 449F3 equipment manufactured by NETZSCH in Germany was used for the analysis. The heating system of the experiment is presented in Figure 3. The flow rate of high purity argon was 30 mL/min. Before the formal experiment, a blank test was conducted without sample to correct the baseline. The tests were repeated twice to ensure accurate results.
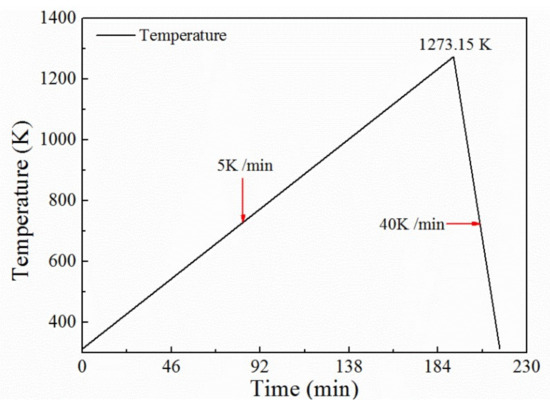
Figure 3.
Heating system of the thermogravimetry (TG) experiment.
4. Results and Discussion
4.1. Comparison with Other Models
Figure 4a,b shows the curves for the thermal decomposition conversion of calcium carbonate and the conversion rate against temperature under the atmosphere of argon. Since the thermogravimetry (TG) data have significantly higher precision than the differential scanning calorimetry (DSC) data [37], these two curves were transformed using the experiment for TG curves based on the definition of α. Figure 4b shows the results after smoothing the curves and eliminating the experimental background. The adjacent-averaging method was used for smoothing the curves. Both the parameters of the method were found to be 79. All the experiments were repeated twice to ensure the accuracy of this method.
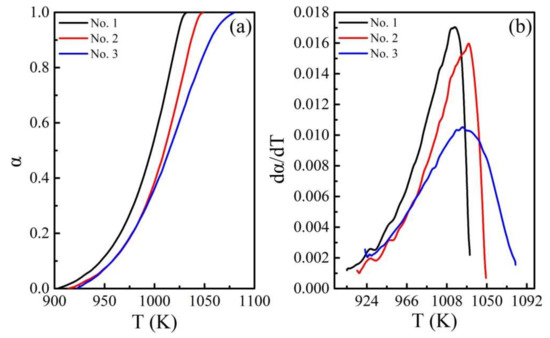
Figure 4.
The conversion (a) rate curves (b) for the thermal decomposition of calcium carbonate under the argon atmosphere.
Figure 4 clearly shows the gradual increase in the initial decomposition temperature of the three samples. There is a significant difference in the rate curves of the samples within the corresponding temperature range, which may be attributed to the presence of dislocation and small amounts of impurities in the natural calcium carbonate, and the inconsistency in the particle size during the conduction of heat [38].
There have been several studies on calcium carbonate among which the kinetic studies on the thermal decomposition of calcium carbonate are extensively reported. Some model functions were selected from the literature to compare with the multifaceted model function [4,15,17,22,24,39,40]. The experiments mentioned in the previous section were repeated in the comparative studies of the different models for the thermal decomposition of calcium carbonate.
Figure 5a–c gives a comparison between the multifaceted model function and the model function mentioned in the literature to analyze the suitability of the model for the thermal decomposition of calcite at a heating rate of 5 K/min using the given error analysis function. The solid black line in the figure is the theoretical value calculated by the multifaceted model function. The solid purple line represents the experimental value, and the dashed lines of different colors represent the theoretical values calculated from the model functions mentioned in the literature. It is seen from the figure that the two solid lines match better than the dashed lines for the three samples.
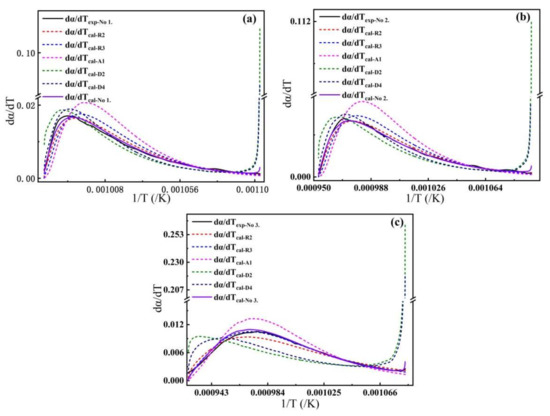
Figure 5.
The relative error curves of the models corresponding to samples No.1, No.2, and No.3, respectively (a–c).
Table 1 shows the kinetic parameters and relative errors calculated from the model function involved in the comparison ( is the multifaceted function model developed in this paper). From the data in Table 1, it is intuitively seen that the multifaceted model function has a better fit.

Table 1.
Kinetic parameters and relative errors obtained from different models.
4.2. Calculation of Activation Energy
The data for sample No.1 (Figure 4) and Equation (9) were substituted into Equation (6). The optimal parameters were optimized as = 2, = 4, and = 50. Therefore, the activation energy and pre-exponential factor were solved by substituting Equation (9) into Equation (7). It can be seen from Figure 6a,b that the calculated results of the multifaceted model function have a good fitting effect on both and . The detailed data are shown in Table 2 (Heating rate is 5 K/min). The activation energy values are found to conform with the values mentioned in the literature [18,28].
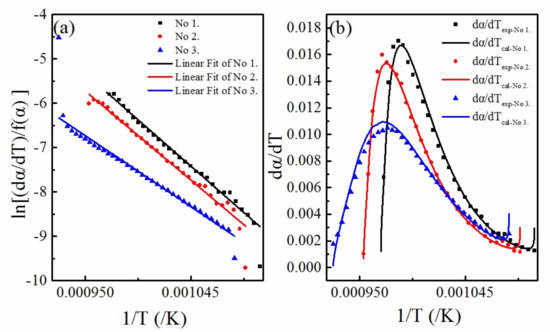
Figure 6.
(a) The fitting of curves of against
; (b) The relative error curves of the experimental and calculated values.

Table 2.
The related parameters calculated for the multifaceted model.
The application of the above parameters on sample No.3 increased the relative error. Thus, the values of the parameters were adjusted to obtain better results. In fact, the accuracy of the multifaceted model is obvious from the calculated data.
In order to verify the applicability of the multifaceted model, the experiments were performed under different heating rates. The specific experiment and calculation steps are mentioned in Section 3 and Section 4.2.
Figure 7 shows the relative error curves of the theoretical and experimental values at different heating rates. The experiment values were found to agree with the theoretically calculated values.
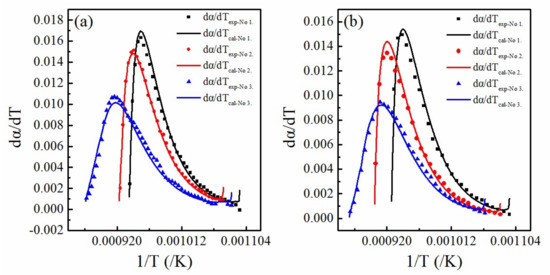
Figure 7.
The relative error curves under different heating rate (a) The heating rate is 10 K/min; (b) The heating rate is 15 K/min.
Table 3 illustrates the corresponding data in detail. Table 2 and Table 3 show that the parameters obtained from each sample under different heating rates are consistent with the calculated values. Additionally, the activation energy and pre-exponential factors were found to be independent of the heating rate.

Table 3.
Kinetic parameters under different heating rates.
It can be seen from the multifaceted model established by us that the relative error between the theoretical calculation value of the multifaceted model and the experimental value is smaller than other models, which indicates that the multifaceted model can better describe the experimental results. At the same time, the thermal decomposition activation energy of calcite, solved by the multifaceted model, is closer to the values (the activation energy for the thermal decomposition of calcite in nitrogen is about 170 kJ/mol) reported in the literature [18,28,41]. This indicates that the multifaceted model is more consistent with both the actual situation in predicting the experimental process and the activation energy for the thermal decomposition of calcite, compared with other models.
4.3. Rationality of the Multifaceted Model
According to Figure 5, the theoretical values calculated from the interface model (R) agree well with the experimental data obtained for the thermal decomposition of calcium carbonate. The relative error data in Table 1 also indicates the accuracy of the interface model in describing the thermal decomposition behavior of calcium carbonate, which is also consistent with the literature [22,42,43]. Although the calculated data in Table 1 indicate a relatively larger value for the relative error between the theoretical and experimental values of the diffusion model, it is seen from Figure 5 that the diffusion model partly describes the thermal decomposition process of calcium carbonate with consistency [17]. Figure 8 shows the electron microscope images for the thermal decomposition of calcium carbonate. These images clearly capture the pore structure information of the product. This indicates that the formation of pores in the reaction process cannot be neglected. Therefore, the interface model, diffusion model, and random pore model were combined to obtain a multifaceted model function that accurately describes the thermal decomposition process of calcium carbonate. Figure 8a,b indicate the pore structure of the product to be similar to a regular pore stacking structure. However, the pore structure in Figure 8c appears disordered, which indicates that the kinetic information shows a variation that is exactly consistent with the change in values mentioned above. Deutsch proposed that the mesoporosity affects the reaction characteristics [44], which confirms the inference in this study. There are electron microscope images for the thermal decomposition of calcium carbonate in the literature. The interface information on the reaction [45] product micro-crystals, and pore information is consistent with the literature [46], which strongly confirms the conjecture drawn in this study.
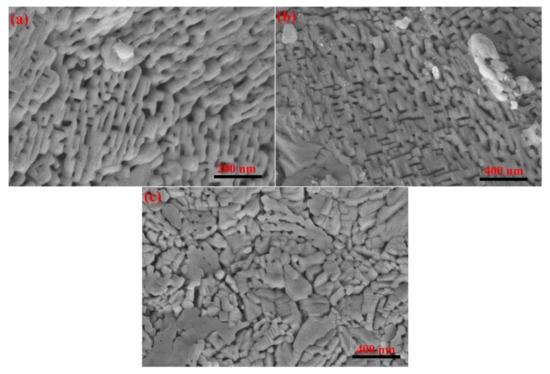
Figure 8.
Pores formed by the decomposition of calcium carbonate at the heating rate of 5 K/min (a) SEM of calcium oxide from analytically pure calcium carbonate; (b) SEM of calcium oxide from calcite crystal powder (No.2); (c) SEM of calcium oxide from calcite powder (No.3).
The random pore model can be improved by directly modifying the pore structure parameters or exponential factors, or by the incorporation of additional parameters [29,30,47,48]. Thus, the values of n changes in the multifaceted model while remains constant. As a matter of fact, there are many mechanisms in the calcite thermal decomposition process, during which, different mechanisms interact to form the final experimental results. The values of the kinetic parameters n, m and actually represent the result of the interactions between different mechanism functions. Under the same conditions, although there are differences between No.1 and No.2, the kinetic parameters did not change, indicating that the slight differences between No.1 and No.2 could not affect the thermal decomposition mechanism. The samples of No.2 and No.3 had the same condition expect for the different particle size, which indicated that the particle size of the sample had a great influence on the thermal decomposition mechanism of calcite during the thermal decomposition process, which would lead to the change of kinetic parameters.
5. Conclusions
In this work, a multifaceted rate-determining mechanism model for the thermal decomposition of calcium carbonate was proposed and verified with an objective to nullify the defects in the literature. The equation: was proposed. Firstly, the optimal parameters of the kinetic parameters of , and were found to be 2, 4, and 50, respectively. As the particle size increases, the reaction process can be accurately described by adjusting the parameters of the multifaceted model. The kinetic parameters upon adjustment of , and were 4, 4, and 50, respectively. The comparative study of the multifaceted model and the partially suitable models for the thermal decomposition of calcium carbonate was carried out. The multifaceted model was found to describe the thermal decomposition of calcium carbonate better than other models. The experimental data under different heating rates were calculated. The results show that the activation energy of a sample is consistent with the corresponding pre-exponential factor, which does not vary with the change in the heating rate and is thus reasonable. Finally, the multifaceted model, interface model, and diffusion model were analyzed. This explained the reasonable rationality of the multifaceted model containing pore.
Author Contributions
J.Z.: Writing—original draft, Z.L. and Q.W.: Writing—review and editing, J.H. and L.T.: methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 51634004 and Grant No. 51874169) and Graduate Education Reform and Science Technology Innovation Entrepreneurship Project of University of Science and Technology Liaoning (Grant No. LKDYC201801) are gratefully acknowledged.
Acknowledgments
Thanks to analysis and Testing Center of School of Materials and Metallurgy, Liaoning University of Science and Technology for the support of this experiment.
Conflicts of Interest
The authors declare no competing financial interests.
References
- Momenzadeh, L.; Moghtaderi, B.; Buzzi, O.; Liu, X.; Sloan, S.W.; Murch, G.E. The thermal conductivity decomposition of calcite calculated by molecular dynamics simulation. Comput. Mater. Sci. 2018, 141, 170–179. [Google Scholar] [CrossRef]
- Du, H.; Steinacher, M.; Borca, C.; Huthwelker, T.; Murello, A.; Stellacci, F.; Amstad, E. Amorphous CaCO3: Influence of the Formation Time on Its Degree of Hydration and Stability. J. Am. Chem. Soc. 2018, 140, 14289–14299. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Alfredsson, V.; Tropsch, J.; Ettl, R.; Nylander, T. Formation of CaCO3 deposits on hard surfaces--effect of bulk solution conditions and surface properties. ACS Appl. Mater. Interfaces 2013, 5, 4035–4045. [Google Scholar] [CrossRef] [PubMed]
- Valverde, J.M.; Sanchez-Jimenez, P.E.; Perez-Maqueda, L.A. Limestone Calcination Nearby Equilibrium: Kinetics, CaO Crystal Structure, Sintering and Reactivity. J. Phys. Chem. C 2015, 119, 1623–1641. [Google Scholar] [CrossRef]
- Escardino, A.; Garcia-Ten, J.; Feliu, C.; Gozalbo, A. Calcium carbonate thermal decomposition in white-body wall tile during firing. II. Influence of body thickness and calcite content. Ceram. Int. 2012, 38, 3141–3147. [Google Scholar] [CrossRef]
- Escardino, A.; García-Ten, J.; Feliu, C.; Moreno, A. Calcium carbonate thermal decomposition in white-body wall tile during firing. I. Kinetic study. J. Eur. Ceram. Soc. 2010, 30, 1989–2001. [Google Scholar] [CrossRef]
- Bennadji, H.; Khachatryan, L.; Lomnicki, S.M. Kinetic Modeling of Cellulose Fractional Pyrolysis. Energy Fuels 2018, 32, 3436–3446. [Google Scholar] [CrossRef]
- Sánchez-Jiménez, P.E.; Perejón, A.; Pérez-Maqueda, L.A.; Criado, J.M. New Insights on the Kinetic Analysis of Isothermal Data: The Independence of the Activation Energy from the Assumed Kinetic Model. Energy Fuels 2014, 29, 392–397. [Google Scholar] [CrossRef]
- Tan, G.; Wang, Q.; Zheng, H.; Zhao, W.; Zhang, S.; Liu, Z. Concept of variable activation energy and its validity in nonisothermal kinetics. J. Phys. Chem. A 2011, 115, 5517–5524. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Mehl, M.; Pitz, W.J.; Kukkadapu, G.; Wagnon, S.; Zhang, K. Multi-fuel surrogate chemical kinetic mechanisms for real world applications. Phys. Chem. Chem. Phys. 2018, 20, 10588–10606. [Google Scholar] [CrossRef]
- Zhou, D.G.; David, J.W. Model Dependence of the Activation Energy Derived from Nonisothermal Kinetic Data. J. Phys. Chem. A 2004, 108, 19. [Google Scholar] [CrossRef]
- Satterfield, C.N.; Feakes, F. Kinetics of the thermal decomposition of calcium carbonate. AICHE J. 1959, 115–122. [Google Scholar] [CrossRef]
- Maitra, S.; Choudhury, A.; Das, H.S.; Pramanik, M.J. Effect of compaction on the kinetics of thermal decomposition of dolomite under non-isothermal condition. J. Mater. Sci. 2005, 40, 4749–4751. [Google Scholar] [CrossRef]
- Rao, T.R. Kinetics of calcium carbonate decomposition. Chem. Eng. Technol. 1996, 19, 373–377. [Google Scholar] [CrossRef]
- Criado, J.M.; Ortega, A. A study of the influence of particle size on the thermal decomposition of CaCO3 by means of constant rate thermal analysis. Thermochim. Acta 1992, 195, 163–167. [Google Scholar] [CrossRef]
- Chinyama, M.P.M.; Lockwood, F.C.; Yousif, S.Y.A.; Kandamby, N. Modelling of calcium carbonate decomposition in cement plant precalciners. J. Energy Inst. 2008, 81, 19–24. [Google Scholar] [CrossRef]
- Ingraham, T.R.; Marier, P. Kinetic studies on the thermal decomposition of calcium carbonate. Can. J. Chem. Eng. 1963, 41, 170–173. [Google Scholar] [CrossRef]
- Calvo, E.G.; Arranz, M.A.; Letón, P. Effects of impurities in the kinetics of calcite decomposition. Thermochim. Acta 1990, 170, 7–11. [Google Scholar] [CrossRef]
- Beruto, D.; Searcy, A.W. Use of the Langmuir method for kinetic studies of decomposition reactions: Calcite (CaCO3). J. Chem. Soc. Faraday Trans. Phys. Chem. Condens. Phases 1974, 70, 2145. [Google Scholar] [CrossRef]
- Beruto, D.T.; Vecchiattini, R.; Giordani, M. Solid products and rate-limiting step in the thermal half decomposition of natural dolomite in a CO2 (g) atmosphere. Thermochim. Acta 2003, 405, 183–194. [Google Scholar] [CrossRef]
- Bouineau, V.; Pijolat, M.; Soustelle, M. Characterisation of the chemical reactivity of a CaCO3 powder for its decomposition. J. Eur. Ceram. Soc. 1998, 18, 1319–1324. [Google Scholar] [CrossRef]
- Chen, H.; Liu, N. Application of Non-Arrhenius Equations in Interpreting Calcium Carbonate Decomposition Kinetics: Revisited. J. Am. Ceram. Soc. 2010, 93, 548–553. [Google Scholar] [CrossRef]
- Brown, D.D.; Galwey, M.E. Comprehensive Chemical Kinetics; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Georgieva, V.; Vlaev, L.; Gyurova, K. Non-Isothermal Degradation Kinetics of CaCO3 from Different Origin. J. Chem. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Maitra, S.; Bandyopadhyay, N.; Das, S.; Pal, A.J.; Pramanik, J. Non-Isothermal Decomposition Kinetics of Alkaline Earth Metal Carbonates. J. Am. Ceram. Soc. 2007, 90, 1299–1303. [Google Scholar] [CrossRef]
- Beruto, D.; Searcy, A.W. Calcium oxides of high reactivity. Nature 1976, 263, 221–222. [Google Scholar] [CrossRef]
- Bertrand, G. Kinetics of endothermic decomposition reactions. 2. Effect of the solid and gaseous products. Comments. J. Phys. Chem. 1978, 82, 2536–2537. [Google Scholar] [CrossRef]
- Mulokozi, A.M.; Lugwisha, E. New aspects of the decomposition kinetics of calcite. Thermochim. Acta 1992, 194, 375–383. [Google Scholar] [CrossRef]
- Zhang, J.-L.; Wang, G.-W.; Shao, J.-G.; Zuo, H.-B. A Modified Random Pore Model for the Kinetics of Char Gasification. BioResources 2014, 9, 3497–3507. [Google Scholar] [CrossRef]
- Wang, G.W.; Zhang, J.L.; Shao, J.G.; Liu, Z.J.; Wang, H.Y.; Li, X.Y.; Zhang, P.C.; Geng, W.W.; Zhang, G.H. Experimental and modeling studies on CO2 gasification of biomass chars. Energy 2016, 114, 143–154. [Google Scholar] [CrossRef]
- Lahijani, P.; Zainal, Z.A.; Mohamed, A.R.; Mohammadi, M. Co-gasification of tire and biomass for enhancement of tire-char reactivity in CO2 gasification process. Bioresour. Technol. 2013, 138, 124–130. [Google Scholar] [CrossRef]
- Sharp, J.H.; Wentworth, S.A. Kinetic analysis of thermogravimetric data. Anal. Chem. 2002, 41, 2060–2062. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Wang, H.; Chen, X.; Dai, W.; Fu, X. The mechanism of photodriven oxidation of CO over anatase and rutile TiO2 investigated from the hydrogen adsorption behavior. Appl. Catal. B Environ. 2020, 277, 119169. [Google Scholar] [CrossRef]
- Šesták, J. Diagnostic limits of phenomenological kinetic models introducing the accommodation function. J. Therm. Anal. 1990, 36, 1997–2007. [Google Scholar] [CrossRef]
- Sestak, J.; Malek, J. Diagnostic limits of phenomenological models of heterogeneous reactions and thermal analysis kinetics. Solid State Ionics 1993, 65, 245–254. [Google Scholar] [CrossRef]
- Gorbachev, V.M. A method for determining the starting temperature of the thermal effect. J. Therm. Anal. 1980, 19, 377–380. [Google Scholar] [CrossRef]
- Sanders, J.P.; Gallagher, P.K. Kinetic analyses using simultaneous TG/DSC measurements. J. Therm. Anal. Calorim. 2005, 82, 659–664. [Google Scholar] [CrossRef]
- Thomas, J.M.; Renshaw, G.D. Influence of dislocations on the thermal decomposition of calcium carbonate. J. Chem. Soc. A Inorg. Phys. Theor. 1967, 2058–2061. [Google Scholar] [CrossRef]
- Dollimore, D.; Evans, T.A.; Lee, Y.F.; Pee, G.P.; Wilburn, F.W. The significance of the onset and final temperatures in the kinetic analysis of TG curves. Thermochim. Acta 1992, 196, 255–265. [Google Scholar] [CrossRef]
- Dollimore, D.; Tong, P.; Alexander, K.S. The kinetic interpretation of the decomposition of calcium carbonate by use of relationships other than the Arrhenius equation. Thermochim. Acta 1996, 283, 13–27. [Google Scholar] [CrossRef]
- Maciejewski, M. Computational aspects of kinetic analysis. Thermochimica Acta. 2000, 355, 145–154. [Google Scholar] [CrossRef]
- Britton, H.T.S.; Gregg, S.J.; Winsor, G.W. The calcination of dolomite. Part I—The kinetics of the thermal decomposition of calcite and of magnesite. Trans. Faraday Soc. 1952, 48, 63–69. [Google Scholar] [CrossRef]
- Hills, A.W.D. The mechanism of the thermal decomposition of calcium carbonate. Chem. Eng. Sci. 1968, 23, 297–320. [Google Scholar] [CrossRef]
- Deutsch, Y.; Heller-Kallai, L. Decarbonation and recarbonation of calcites heated m CO2. Thermochim. Acta 1991, 182, 77–89. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Ruiz-Agudo, E.; Luque, A.; Rodriguez-Navarro, A.B.; Ortega-Huertas, M. Thermal decomposition of calcite: Mechanisms of formation and textural evolution of CaO nanocrystals. Am. Mineral. 2009, 94, 578–593. [Google Scholar] [CrossRef]
- Escardino, A.; Garcia-Ten, J.; Feliu, C. Kinetic study of calcite particle (powder) thermal decomposition: Part I. J. Eur. Ceram. Soc. 2008, 28, 3011–3020. [Google Scholar] [CrossRef]
- Fei, H.; Hu, S.; Xiang, J.; Sun, L.; Zhang, A.; Fu, P.; Wang, B.; Chen, G. Modified Random Pore Model Study on Coal Char Reactions under O2/CO2 Atmosphere. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010. [Google Scholar] [CrossRef]
- Cai, J.; Wang, S.; Kuang, C. A Modified Random Pore Model for Carbonation Reaction of CaO-based Limestone with CO2 in Different Calcination-carbonation Cycles. Energy Procedia 2017, 105, 1924–1931. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).