LiNbO3-Tm3+ Crystal. Material for Optical Cooling
Abstract
1. Introduction
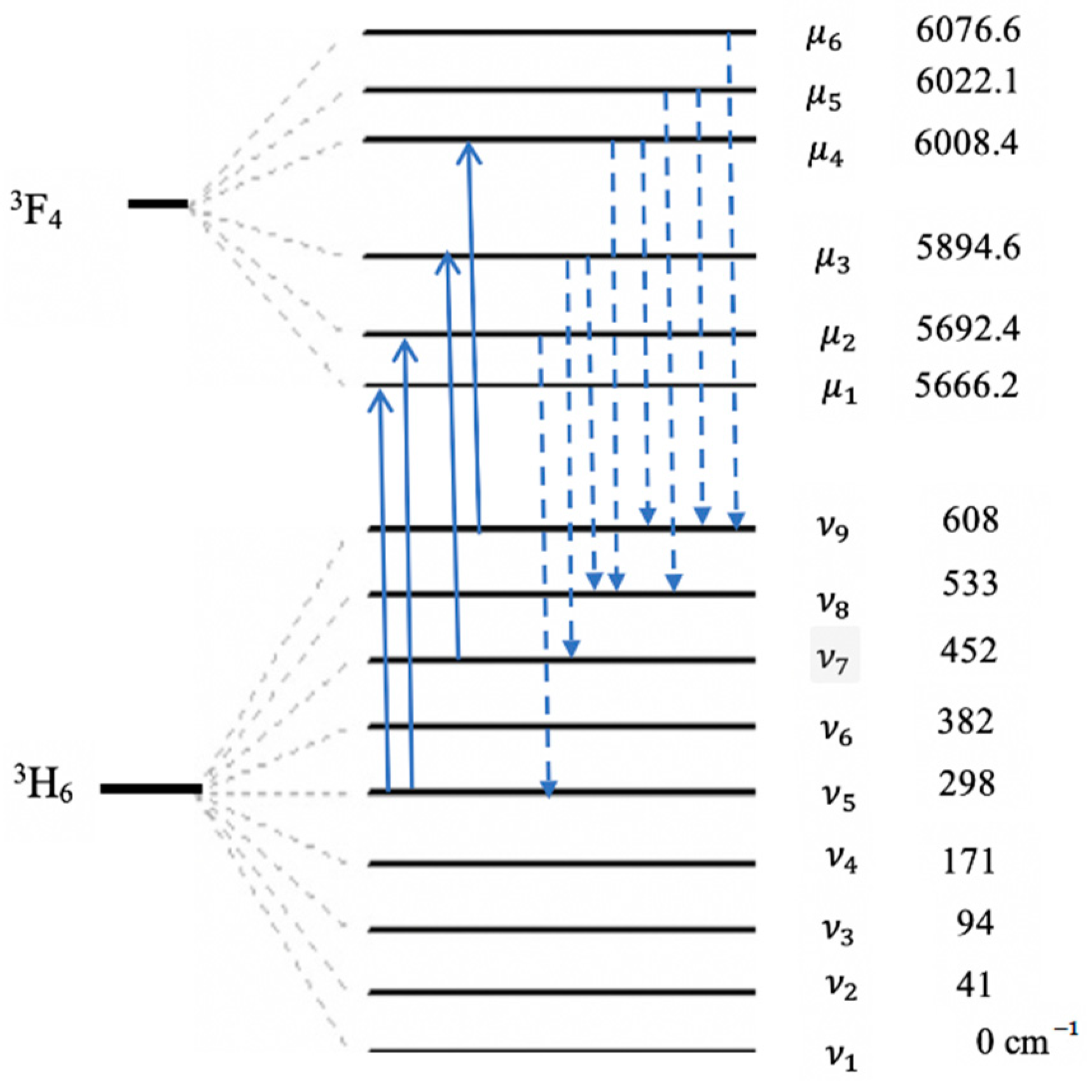
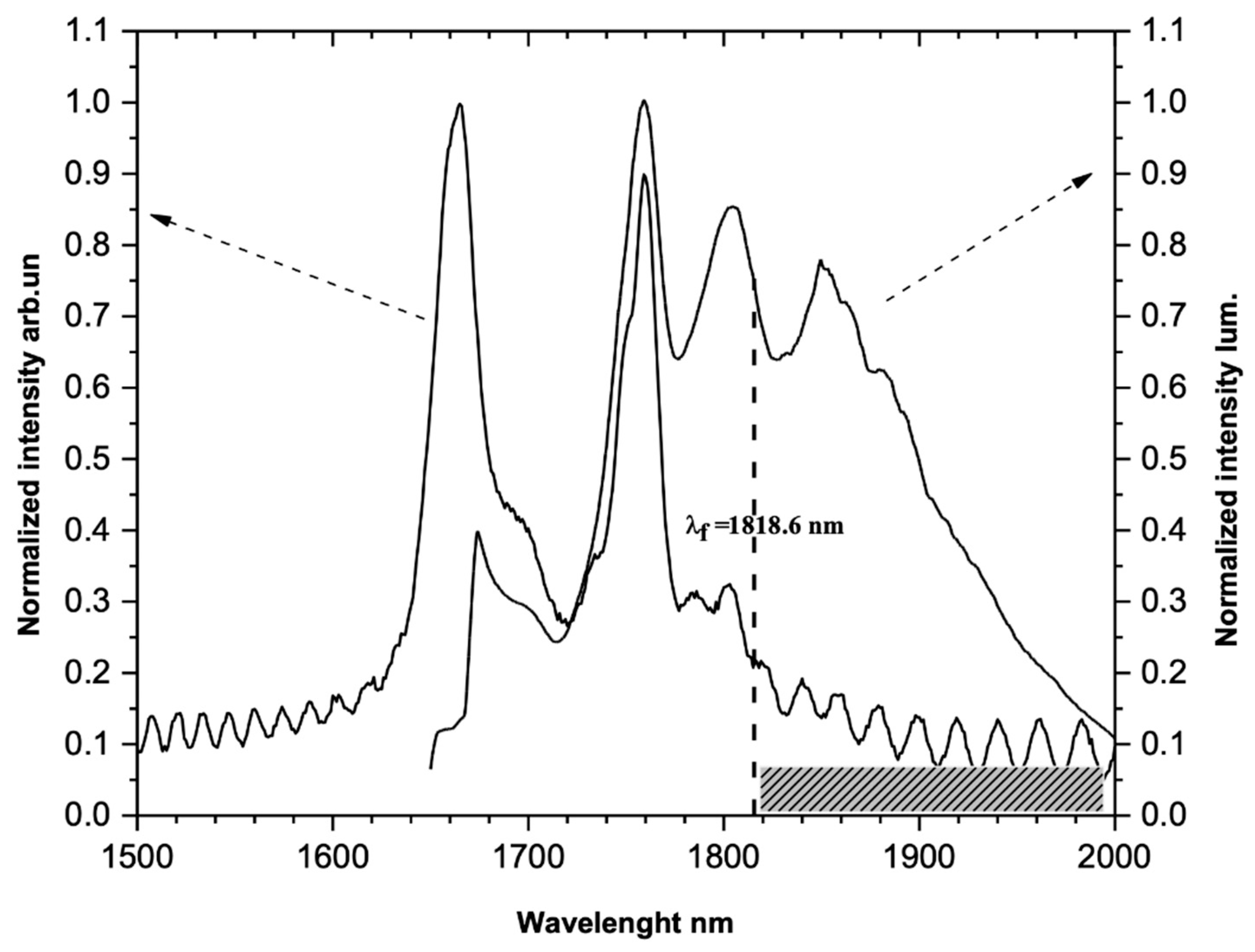
2. Possibilities of Using the LN-Tm3+ Crystal in Optical Cooling Systems
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cordova-Plaza, A.; Digonnet, M.; Shaw, H.J. Miniature CW and active internally Q-switched Nd: MgO:LiNbO3 lasers. IEEE J. Quantum Electron. 1987, 23, 262–266. [Google Scholar] [CrossRef]
- Lallier, E.; Pocholle, J.P.; Papuchon, M.; de Micheli, M.; Li, M.J.; He, Q.; Ostrowsky, D.B.; Grezes-Besset, C.; Pelletier, E. Nd:MgO:LiNbO3 waveguide laser and amplifier. Opt. Lett. 1990, 15, 682–684. [Google Scholar] [PubMed]
- Ruan, X.L.; Kaviany, M. Enhanced laser cooling rare-earth-ion-doped nanocrystalline powder. Phys. Rev. B 2006, 73, 155422. [Google Scholar] [CrossRef]
- Garcia-Adeva, A.J.; Balda, R.; Fernandez, J. Upconversion cooling Er-doped low-phonon fluorescent solids. Phys. Rev. B 2009, 79, 033110. [Google Scholar] [CrossRef]
- Nemova, G.; Kashyap, R. Laser cooling of solids. Rep. Prog. Phys. 2010, 73, 086501. [Google Scholar] [CrossRef]
- Babajanyan, V.G. Spectroscopic study of the expected optical cooling effect of LiNbO3:Er3+ crystal. Laser Phys. 2013, 23, 126002. [Google Scholar] [CrossRef]
- Demirkhanyan, G.G.; Kokanyan, E.P.; Demirkhanyan, H.G.; Sardar, D.; Aillerie, M. Crystal LiNbO3-Ho3+: Material for optical cooling. J. Contemp. Phys. (Armen. Acad. Sci.) 2016, 51, 28–34. [Google Scholar] [CrossRef]
- Zhang, R.; Li, H.; Zhang, P.; Hang, Y.; Xu, J. Efficient 1856nm emission from Tm,Mg:LiNbO3 laser. Opt. Express 2013, 21, 020990–020998. [Google Scholar] [CrossRef] [PubMed]
- Kokanyan, E.P.; Demirkhanyana, G.G.; Demirkhanyan, H.G. Spectroscopic properties of LiNbO3:Tm3+ crystal in the 1650-1970nm wavelength range. J. Contem. Phys. (Armen. Acad. Sci.) 2018, 53, 227–233. [Google Scholar] [CrossRef]
- Melgard, S.D.; Seletskiy, D.V.; Di Lieto, A.; Tonelli, M.; Sheik-Bahae, M. Optical refrigeration to 119K, below national institute of standards and technology cryogenic temperature. Opt. Lett. 2013, 38, 1588–1590. [Google Scholar] [CrossRef] [PubMed]
- Patterson, W.; Bigotta, S.; Sheik-Bahae, M.; Parisi, D.; Tonelli, M.; Epstein, R. Anti-Stokes luminescence cooling of Tm3+ doped BaY2F8. Opt. Express 2008, 16, 1704–1710. [Google Scholar] [CrossRef] [PubMed]

| λex, nm | Transition | 1S, 10−21 cm2 | 2 α, 10−26 cm3 | 3Ni/N0 | 4 cm2 | 5 ξabs, 10−3% |
|---|---|---|---|---|---|---|
| 1822 | 0.9298 | 0.087 | 0.022 | 0.174 | 1.0 | |
| 1826 | 1.1059 | 0.104 | 0.022 | 0.208 | 1.2 | |
| 1829 | 0.1143 | 0.007 | 0.015 | 0.014 | 0.1 | |
| 1837 | 0.1695 | 0.024 | 0.032 | 0.048 | 0.4 | |
| 1847 | 0.0831 | 0.005 | 0.015 | 0.001 | <0.1 | |
| 1852 | 0.8259 | 0.048 | 0.015 | 0.096 | 0.4 | |
| 1854 | 0.7892 | 0.232 | 0.068 | 0.464 | 8.4 | |
| 1863 | 0.1627 | 0.048 | 0.068 | 0.096 | 1.7 | |
| 1865 | 0.3191 | 0.031 | 0.022 | 0.062 | 0.4 | |
| 1883 | 1.0080 | 0.201 | 0.045 | 0.402 | 4.8 | |
| 1892 | 0.8978 | 0.180 | 0.045 | 0.306 | 4.3 | |
| 1908 | 0.3850 | 0.056 | 0.032 | 0.112 | 1.0 | |
| 1918 | 0.0938 | 0.014 | 0.032 | 0.028 | 0.2 | |
| 1938 | 1.5134 | 0.150 | 0.022 | 0.048 | 1.8 | |
| 1948 | 1.6029 | 0.160 | 0.022 | 0.320 | 1.9 | |
| 1967 | 1.0154 | 0.071 | 0.015 | 0.142 | 0.6 | |
| 1977 | 0.9514 | 0.049 | 0.015 | 0.098 | 0.5 |
| Transition | λem, nm | 1S, 10−21 cm2 | 2 A, s−1 | 3Ni/N0 | 4, % |
|---|---|---|---|---|---|
| 1820 | 0.1191 | 17.5 | 0.367 | 0.60 | |
| 1822 | 0.9298 | 136.3 | 0.065 | 0.85 | |
| 1826 | 1.1059 | 161.0 | 0.071 | 1.07 | |
| 1829 | 0.1143 | 16.6 | 0.051 | 0.08 | |
| 1837 | 0.1695 | 24.3 | 0.123 | 0.28 | |
| 1847 | 0.0831 | 11.7 | 0.065 | 0.07 | |
| 1852 | 0.7259 | 101.3 | 0.071 | 0.67 | |
| 1854 | 0.7892 | 109.8 | 0.323 | 3.32 | |
| 1863 | 0.1627 | 22.3 | 0.367 | 0.77 | |
| 1865 | 0.3191 | 43.6 | 0.123 | 0.05 | |
| 1883 | 1.0080 | 133.8 | 0.323 | 4.05 | |
| 1892 | 0.8978 | 117.5 | 0.367 | 4.30 | |
| 1892 | 0.0324 | 4.2 | 0.123 | 0.05 | |
| 1908 | 0.3850 | 49.1 | 0.323 | 1.49 | |
| 1918 | 0.0938 | 11.8 | 0.367 | 0.41 | |
| 1938 | 1.5134 | 184.3 | 0.323 | 5.58 | |
| 1948 | 1.6029 | 192.2 | 0.367 | 6.60 | |
| 1967 | 1.0154 | 118.3 | 0.323 | 3.58 |
| ASL | , nm) | ||||||||||
| , nm | Transition | (1822) | (1826) | (1829) | (1837) | (1847) | (1852) | (1854) | (1863) | ||
| 1820 | 0.231 | 0.589 | 0.082 | 0.394 | 0.178 | 1.332 | 5.528 | 1.770 | |||
| 1822 | - | 0.632 | 0.088 | 3.174 | 1.263 | 1.429 | 5.948 | 1.902 | |||
| 1826 | - | - | 0.111 | 0.534 | 0.241 | 1.801 | 7.488 | 2.395 | |||
| 1829 | - | - | - | 0.040 | 0.018 | 0.135 | 0.560 | 0.179 | |||
| 1837 | - | - | - | - | 0.063 | 0.471 | 1.959 | 0.627 | |||
| 1847 | - | - | - | - | - | 0.118 | 0.490 | 0.157 | |||
| 1852 | - | - | - | - | - | - | 4.689 | 1.500 | |||
| 1854 | - | - | - | - | - | - | - | 7.431 | |||
| , | 0.231 | 1.221 | 0.281 | 4.142 | 1.763 | 5.286 | 26.662 | 15.961 | |||
| ASL | (, nm) | ||||||||||
| ,nm | Transition | (1865) | (1883) | (1892) | (1908) | (1918) | (1938) | (1948) | (1967) | (1977) | |
| 1820 | 1.247 | 8.970 | 9.343 | 4.092 | 1.343 | 1.709 | 1.961 | 8.506 | 14.552 | ||
| 1822 | 1.341 | 9.652 | 10.053 | 4.403 | 1.445 | 1.839 | 2.104 | 9.152 | 15.657 | ||
| 1826 | 1.689 | 12.151 | 12.654 | 5.543 | 1.819 | 2.314 | 2.644 | 11.521 | 19.757 | ||
| 1829 | 0.126 | 0.908 | 0.946 | 0.414 | 0.136 | 0.173 | 0.045 | 0.861 | 1.474 | ||
| 1837 | 0.442 | 3.180 | 3.311 | 1.450 | 0.476 | 0.606 | 0.693 | 3.015 | 5.156 | ||
| 1847 | 0.110 | 0.795 | 0.828 | 0.363 | 0.119 | 0.151 | 0.173 | 0.754 | 1.289 | ||
| 1852 | 1.057 | 7.608 | 7.924 | 3.471 | 1.139 | 1.449 | 1.656 | 7.214 | 12.341 | ||
| 1854 | 5.239 | 37.701 | 39.264 | 17.198 | 5.645 | 7.181 | 8.205 | 35.746 | 61.155 | ||
| 1863 | 1.215 | 8.744 | 9.106 | 3.989 | 1.309 | 1.666 | 1.903 | 8.290 | 14.184 | ||
| 1865 | - | 0.568 | 0.591 | 0.259 | 0.085 | 0.108 | 0.124 | 0.538 | 0.921 | ||
| 1883 | - | - | 47.897 | 20.980 | 6.886 | 8.760 | 10.009 | 43.606 | 74.601 | ||
| 1892 | - | - | - | 20.876 | 6.851 | 8.717 | 9.960 | 43.390 | 74.233 | ||
| 1892 | - | - | - | 0.259 | 0.085 | 0.108 | 0.124 | 0.538 | 0.921 | ||
| 1908 | - | - | - | - | 2.533 | 3.222 | 3.682 | 16.043 | 27.446 | ||
| 1918 | - | - | - | - | - | 0.887 | 1.013 | 4.414 | 7.552 | ||
| 1938 | - | - | - | - | - | 13.790 | 60.079 | 102.784 | |||
| 1948 | - | - | - | - | - | - | - | 71.061 | 121.572 | ||
| 1967 | - | - | - | - | - | - | - | - | 65.944 | ||
| , | 12.466 | 90.277 | 141.917 | 83.297 | 29.871 | 38.89 | 58.086 | 324.728 | 621.539 | ||
| 1822 | 1.7 |
| 1826 | 2.4 |
| 1829 | 0.2 |
| 1837 | 0.2 |
| 1847 | 0.3 |
| 1852 | 3.3 |
| 1854 | 3.0 |
| 1863 | 0.3 |
| 1865 | 2.6 |
| 1883 | 8.7 |
| 1892 | 8.3 |
| 1908 | 4.8 |
| 1918 | 1.0 |
| 1938 | 4.2 |
| 1948 | 16.4 |
| 1967 | 19.0 |
| 1977 | 22.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokanyan, N.; Mkhitaryan, N.; Demirkhanyan, G.; Kumar, A.; Aillerie, M.; Sardar, D.; Kokanyan, E. LiNbO3-Tm3+ Crystal. Material for Optical Cooling. Crystals 2021, 11, 50. https://doi.org/10.3390/cryst11010050
Kokanyan N, Mkhitaryan N, Demirkhanyan G, Kumar A, Aillerie M, Sardar D, Kokanyan E. LiNbO3-Tm3+ Crystal. Material for Optical Cooling. Crystals. 2021; 11(1):50. https://doi.org/10.3390/cryst11010050
Chicago/Turabian StyleKokanyan, Ninel, Nune Mkhitaryan, Gagik Demirkhanyan, Ajith Kumar, Michel Aillerie, Dhiraj Sardar, and Edvard Kokanyan. 2021. "LiNbO3-Tm3+ Crystal. Material for Optical Cooling" Crystals 11, no. 1: 50. https://doi.org/10.3390/cryst11010050
APA StyleKokanyan, N., Mkhitaryan, N., Demirkhanyan, G., Kumar, A., Aillerie, M., Sardar, D., & Kokanyan, E. (2021). LiNbO3-Tm3+ Crystal. Material for Optical Cooling. Crystals, 11(1), 50. https://doi.org/10.3390/cryst11010050





