Hybrid Graphene-Based Photonic-Plasmonic Biochemical Sensor with a Photonic and Acoustic Cavity Structure
Abstract
:1. Introduction
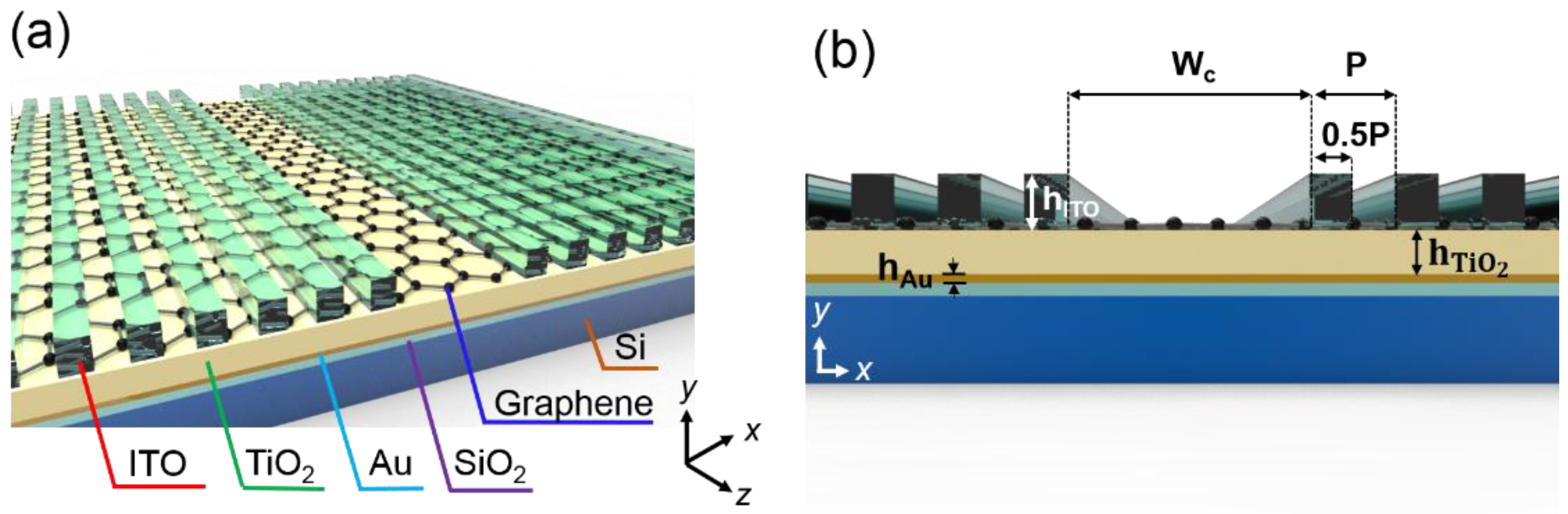
2. Device Design and Materials
2.1. The Design of the Biochemical Sensor
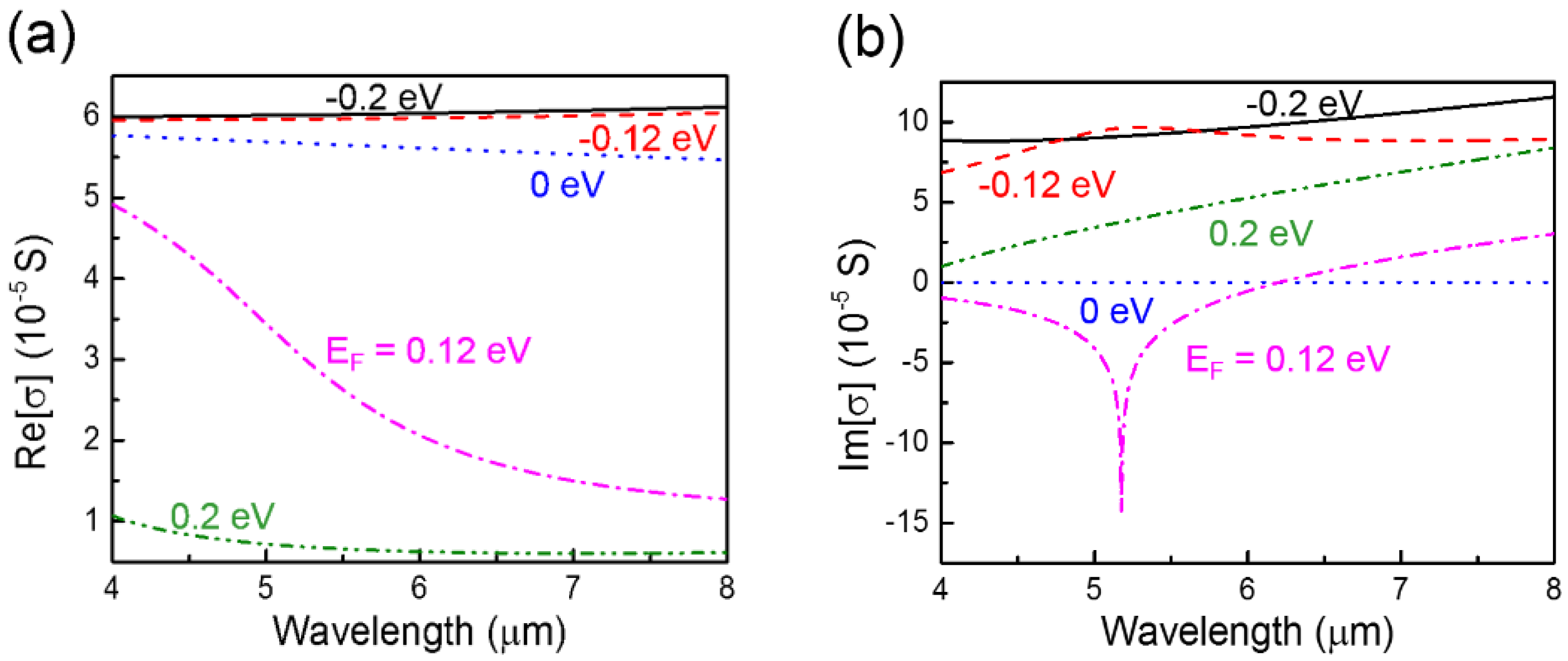
2.2. Complex Conductivity of Graphene
2.3. Dielectric Functions of Biochemical Analytes
3. Results and Discussion
3.1. Optical Results
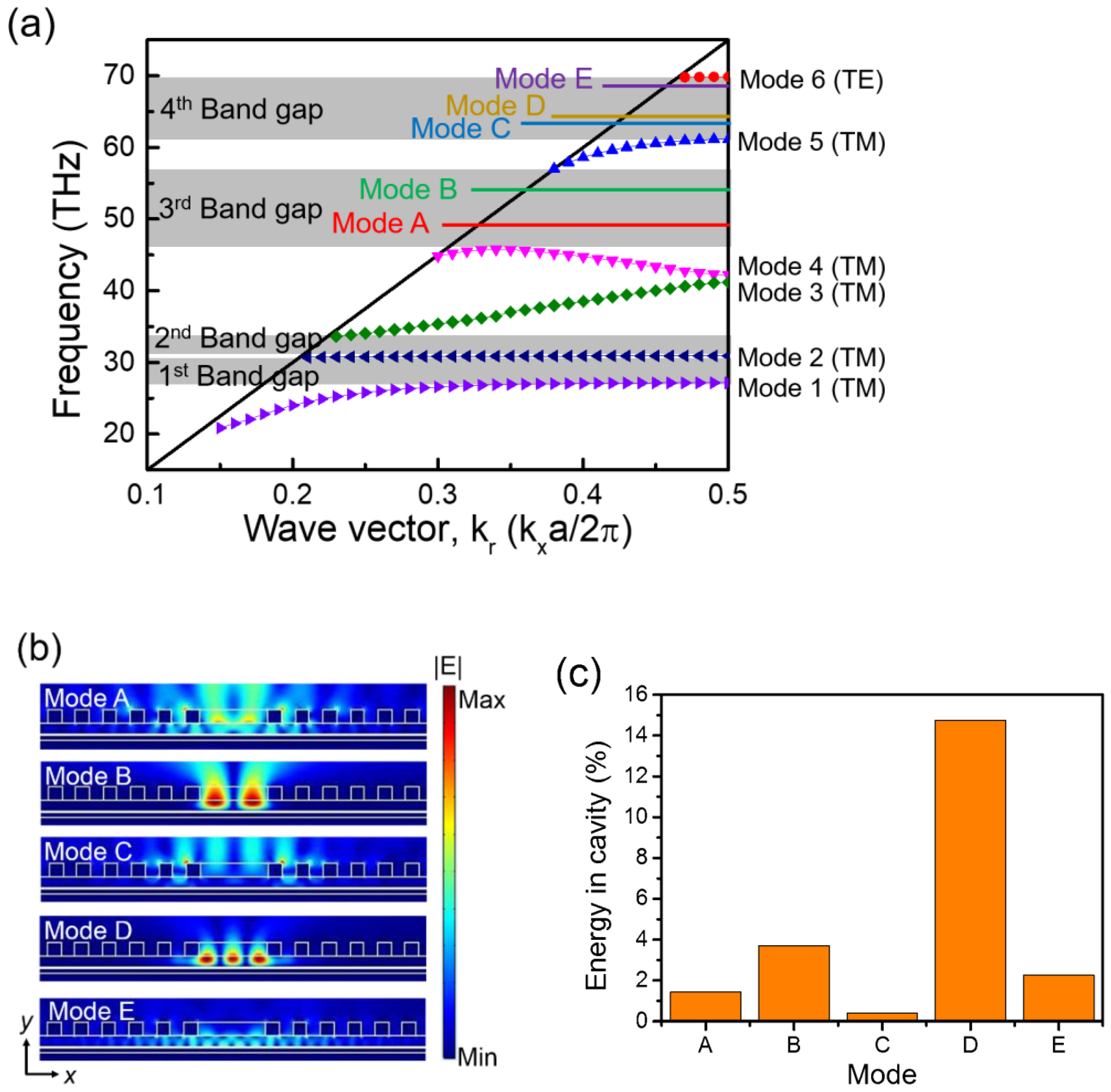
3.1.1. Modal Analysis for Perfect PTC and Defect Structure
3.1.2. Detection of Molecular Fingerprints and Sensing Performance Evaluation
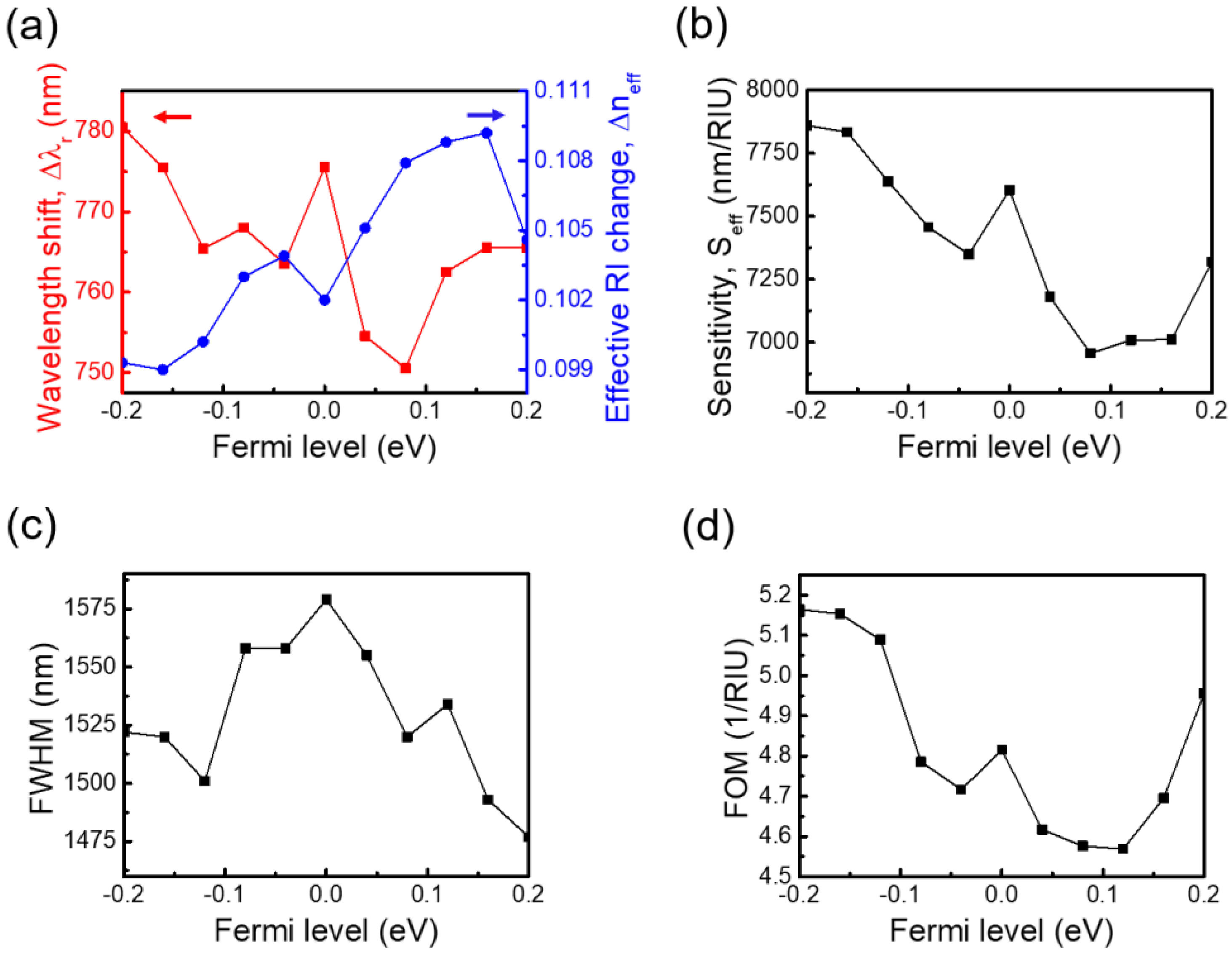
3.1.3. Effect of Graphene’s Tunability on the Sensing Performance
3.2. Accoustic Results
3.2.1. Band Diagram and Defect Modes
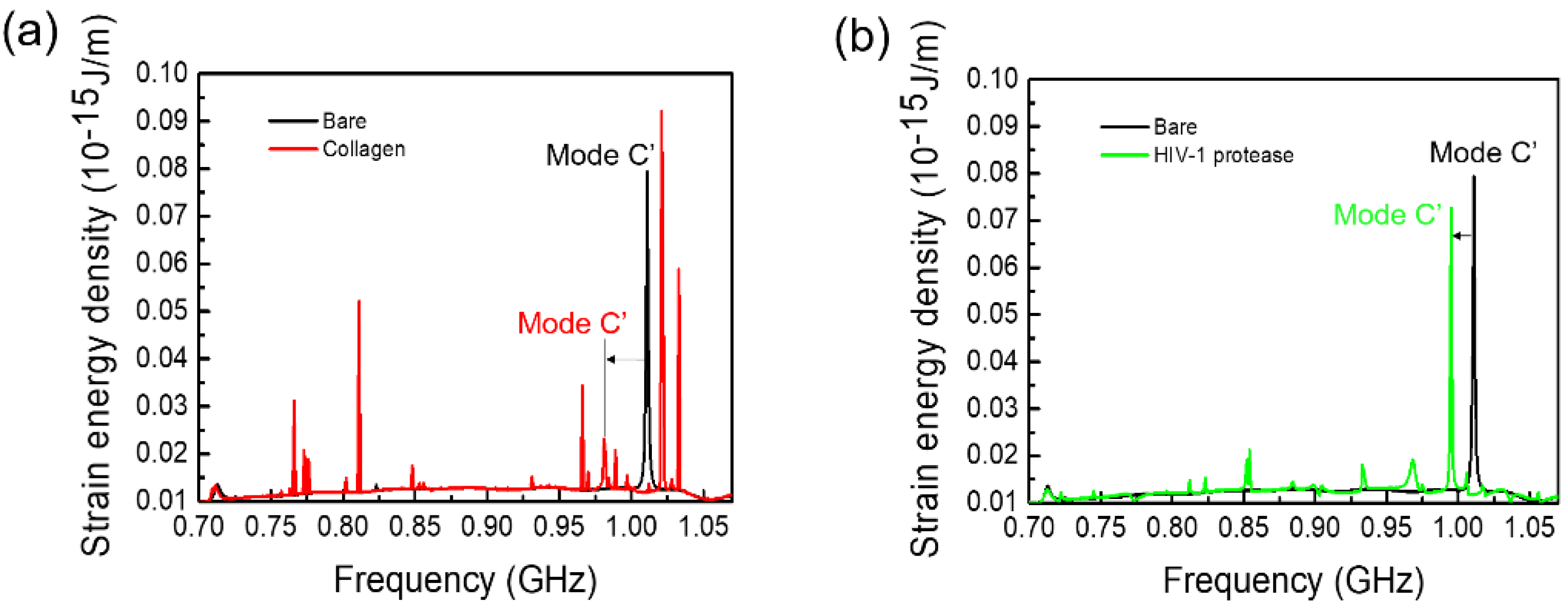
3.2.2. Acoustic Sensing of Proteins
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alvarez-Ordóñez, A.; Prieto, M. Fourier Transform Infrared Spectroscopy in Food Microbiology; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; Garcia de Abajo, F.J.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef] [Green Version]
- Hong, Q.; Luo, J.; Wen, C.; Zhang, J.; Zhu, Z.; Qin, S.; Yuan, X. Hybrid metal-graphene plasmonic sensor for multi-spectral sensing in both near- and mid-infrared ranges. Opt. Express 2019, 27, 35914–35924. [Google Scholar] [CrossRef]
- Isaac, T.H.; Barnes, W.L.; Hendry, E. Determining the terahertz optical properties of subwavelength films using semiconductor surface plasmons. Appl. Phys. Lett. 2008, 93, 241115. [Google Scholar] [CrossRef] [Green Version]
- Autore, M.; Li, P.; Dolado, I.; Alfaro-Mozaz, F.J.; Esteban, R.; Atxabal, A.; Casanova, F.; Hueso, L.E.; Alonso-González, P.; Aizpurua, J.; et al. Boron nitride nanoresonators for phonon-enhanced molecular vibrational spectroscopy at the strong coupling limit. Light Sci. Appl. 2018, 7, 17172. [Google Scholar] [CrossRef]
- Spadavecchia, J.; Barras, A.; Lyskawa, J.; Woisel, P.; Laure, W.; Pradier, C.M.; Boukherroub, R.; Szunerits, S. Approach for plasmonic based DNA sensing: Amplification of the wavelength shift and simultaneous detection of the plasmon modes of gold nanostructures. Anal. Chem. 2013, 85, 3288–3296. [Google Scholar] [CrossRef]
- Li, J.; Ye, J.; Chen, C.; Hermans, L.; Verellen, N.; Ryken, J.; Jans, H.; Van Roy, W.; Moshchalkov, V.V.; Lagae, L.; et al. Biosensing using diffractively coupled plasmonic crystals: The figure of merit revisited. Adv. Opt. Mater. 2014, 3, 176–181. [Google Scholar] [CrossRef]
- Semenyshyn, R.; Hentschel, M.; Stanglmair, C.; Teutsch, T.; Tarin, C.; Pacholski, C.; Giessen, H.; Neubrech, F. In vitro monitoring conformational changes of polypeptide monolayers using infrared plasmonic nanoantennas. Nano Lett. 2018, 19, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Adato, R.; Altug, H. Dual-band perfect absorber for multispectral plasmon-enhanced infrared spectroscopy. ACS Nano 2012, 6, 7998–8006. [Google Scholar] [CrossRef] [PubMed]
- Farmer, D.B.; Avouris, P.; Li, Y.; Heinz, T.F.; Han, S.J. Ultrasensitive plasmonic detection of molecules with graphene. ACS Photonics 2016, 3, 553–557. [Google Scholar] [CrossRef]
- Chen, S.; Autore, M.; Li, J.; Li, P.; Alonso-Gonzalez, P.; Yang, Z.; Martin-Moreno, L.; Hillenbrand, R.; Nikitin, A.Y. Acoustic graphene plasmon nanoresonators for field-enhanced infrared molecular spectroscopy. ACS Photonics 2017, 4, 3089–3097. [Google Scholar] [CrossRef] [Green Version]
- Lee, I.-H.; Yoo, D.; Avouris, P.; Low, T.; Oh, S.-H. Graphene acoustic plasmon resonator for ultrasensitive infrared spectroscopy. Nat. Nanotechnol. 2019, 14, 313. [Google Scholar] [CrossRef] [PubMed]
- Vasić, B.; Isić, G.; Gajić, R. Localized surface plasmon resonances in graphene ribbon arrays for sensing of dielectric environment at infrared frequencies. J. Appl. Phys. 2013, 113, 013110. [Google Scholar] [CrossRef]
- Wang, B.; Dündar, M.A.; Nötzel, R.; Karouta, F.; He, S.; van der Heijden, R.W. Photonic crystal slot nanobeam slow light waveguides for refractive index sensing. Appl. Phys. Lett. 2010, 97, 151105. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.-N.; Chung, Y.-C.; Chiu, H.-T.; Hsu, J.-C.; Lin, Y.-F.; Kuo, C.-T.; Chang, Y.-W.; Chen, C.-Y.; Lin, T.-R. Dual photonic-phononic crystal slot nanobeam with gradient cavity for liquid sensing. Crystals 2020, 10, 421. [Google Scholar] [CrossRef]
- Amoudache, S.; Pennec, Y.; Rouhani, B.D.; Khater, A.; Lucklum, R.; Tigrine, R. Simultaneous sensing of light and sound velocities of fluids in a two-dimensional phoXonic crystal with defects. J. Appl. Phys. 2014, 115, 134503. [Google Scholar] [CrossRef]
- Liang, F.; Clarke, N.; Patel, P.; Loncar, M.; Quan, Q. Scalable photonic crystal chips for high sensitivity protein detection. Opt. Express 2013, 21, 32306–32312. [Google Scholar] [CrossRef]
- Rodriguez, G.A.; Markov, P.; Cartwright, A.P.; Choudhury, M.H.; Afzal, F.O.; Cao, T.; Halimi, S.I.; Retterer, S.T.; Kravchenko, I.I.; Weiss, S.M. Photonic crystal nanobeam biosensors based on porous silicon. Opt. Express 2019, 27, 9536–9549. [Google Scholar] [CrossRef]
- Qiao, Q.; Xia, J.; Lee, C.; Zhou, G. Applications of photonic crystal nanobeam cavities for sensing. Micromachines 2018, 9, 541. [Google Scholar] [CrossRef] [Green Version]
- Aly, A.H.; Mohamed, D.; Zaky, Z.A.; Matar, Z.S.; Abd El-Gawaad, N.S.; Shalaby, A.S.; Tayeboun, F.; Mohaseb, M. Novel biosensor detection of tuberculosis based on photonic band gap materials. Mater. Res. 2021, 24, e20200483. [Google Scholar] [CrossRef]
- Panda, A.; Devi, P.P. Photonic crystal biosensor for refractive index based cancerous cell detection. Opt. Fiber Technol. 2020, 54, 102123. [Google Scholar] [CrossRef]
- Chakravarty, S.; Chen, X.; Tang, N.; Lai, W.-C.; Zou, Y.; Yan, H.; Chen, R.T. Review of design principles of 2D photonic crystal microcavity biosensors in silicon and their applications. Front. Optoelectron. 2016, 9, 206–224. [Google Scholar] [CrossRef]
- Liu, T.L.; Russell, K.J.; Cui, S.; Hu, E.L. Two-dimensional hybrid photonic/plasmonic crystal cavities. Opt. Express 2014, 22, 8219–8225. [Google Scholar] [CrossRef] [PubMed]
- Cheng, P.-J.; Huang, Z.-T.; Li, J.-H.; Chou, B.-T.; Chou, Y.-H.; Lo, W.-C.; Chen, K.-P.; Lu, T.-C.; Lin, T.-R. High-performance plasmonic nanolasers with a nanotrench defect cavity for sensing applications. ACS Photonics 2018, 5, 2638–2644. [Google Scholar] [CrossRef]
- Yang, C.-S.; Chung, Y.-C.; Cheng, Y.-S.; Hsu, Y.-C.; Chen, C.-F.; Huang, N.-N.; Chen, H.-C.; Liu, C.-H.; Hsu, J.-C.; Lin, Y.-F.; et al. Electrically tunable plasmonic biosensors based on cavity-coupled structure with graphene. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4601208. [Google Scholar] [CrossRef]
- Lucklum, R.; Li, J.; Zubtsov, M. 1D and 2D phononic crystal sensors. Procedia Eng. 2010, 5, 436–439. [Google Scholar] [CrossRef] [Green Version]
- Lucklum, R.; Ke, M.; Zubtsov, M. Two-dimensional phononic crystal sensor based on a cavity mode. Sens. Actuators B Chem. 2012, 171, 271–277. [Google Scholar] [CrossRef]
- Oseev, A.; Mukhin, N.; Lucklum, R.; Zubtsov, M.; Schmidt, M.-P.; Steinmann, U.; Fomin, A.; Kozyrev, A.; Hirsch, S. Study of liquid resonances in solid-liquid composite periodic structures (phononic crystals)—Theoretical investigations and practical application for in-line analysis of conventional petroleum products. Sens. Actuators B Chem. 2018, 257, 469–477. [Google Scholar] [CrossRef]
- Lucklum, R.; Mukhin, N.; Rouhani, B.D.; Pennec, Y. Phononic crystal sensors: A new class of resonant sensors—chances and challenges for the determination of liquid properties. Front. Mech. Eng. 2021, 7, 705194. [Google Scholar] [CrossRef]
- Khateib, F.; Mehaney, A.; Amin, R.M.; Aly, A.H. Ultra-sensitive acoustic biosensor based on a 1D phononic crystal. Phys. Scr. 2020, 95, 075704. [Google Scholar] [CrossRef]
- Lucklum, R.; Zubtsov, M.; Oseev, A. Phoxonic crystals—a new platform for chemical and biochemical sensors. Anal. Bioanal. Chem. 2013, 405, 6497–6509. [Google Scholar] [CrossRef]
- Amoudache, S.; Moiseyenko, R.; Pennec, Y.; Rouhani, B.D.; Khater, A.; Lucklum, R.; Tigrine, R. Optical and acoustic sensing using Fano-like resonances in dual phononic and photonic crystal plate. J. Appl. Phys. 2016, 119, 114502. [Google Scholar] [CrossRef] [Green Version]
- Ma, T.X.; Wang, Y.S.; Zhang, C.; Su, X.X. Theoretical research on a two-dimensional phoxonic crystal liquid sensor by utilizing surface optical and acoustic waves. Sens. Actuators A Phys. 2016, 242, 123–131. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® Modeling Software. Available online: https://www.comsol.com/ (accessed on 16 August 2021).
- Emani, N.K.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Graphene: A dynamic platform for electrical control of plasmonic resonance. Nanophotonics 2015, 4, 214–223. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, P.; Yang, C.-S.; Lyu, T.; Tian, F.; Kou, R.; Zhang, H.; Watanabe, K.; Taniguchi, T.; Wang, F. Quantum-critical conductivity of the Dirac fluid in graphene. Science 2019, 364, 158–167. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Llatser, I.; Kremers, C.; Cabellos-Aparicio, A.; Jornet, J.M.; Alarcón, E.; Chigrin, D.N. Graphene-based nano-patch antenna for terahertz radiation. Photonics Nanostruct.-Fundam. Appl. 2012, 10, 353–358. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Kats, M.A.; Genevet, P.; Yu, N.; Song, Y.; Kong, J.; Capasso, F. Broad electrical tuning of graphene-loaded plasmonic antennas. Nano Lett. 2013, 13, 1257–1264. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, T.; Wang, H.; Zhang, C.; Deotare, P.B.; Agrawal, A.; Lezec, H.J. Surface plasmon polariton laser based on a metallic trench Fabry-Perot resonator. Sci. Adv. 2017, 3, e1700909. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Chiao, Y.A.; Wang, Y.; Voorhees, A.; Han, H.C.; Lindsey, M.L.; Jin, Y.F. Mathematical modeling of left ventricular dimensional changes in mice during aging. Yang T, Chiao Y A, Wang Y; et al. Mathematical modeling of left ventricular dimensional changes in mice during aging. BMC Syst. Biol. 2012, 6, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.-F. Application of Finite Element Method in Protein Normal Mode Analysis. Master’s Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 2013. [Google Scholar]



| Mode | Analyte | λb (nm) | λa (nm) | Δλr (nm) | neff,b | neff,a | Δneff | FWHM | Seff (nm/RIU) | FOM (1/RIU) |
|---|---|---|---|---|---|---|---|---|---|---|
| B | Protein | 5464 | 6227 | 763 | 1.039 | 1.148 | 0.109 | 1534 | 7000 | 4.56 |
| B | CBP | 5464 | 6787 | 1323 | 1.039 | 1.237 | 0.198 | 1520 | 6682 | 4.40 |
| D | Protein | 4680 | 4975 | 295 | 1.253 | 1.356 | 0.103 | 124 | 2864 | 23.1 |
| D | CBP | 4680 | 5263 | 583 | 1.253 | 1.447 | 0.194 | 149 | 3005 | 20.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-S.; Cheng, Y.-S.; Hsu, Y.-C.; Chung, Y.-C.; Hung, J.-T.; Liu, C.-H.; Hsu, J.-C.; Chen, C.-Y.; Yang, C.-R.; Li, Y.-T.; et al. Hybrid Graphene-Based Photonic-Plasmonic Biochemical Sensor with a Photonic and Acoustic Cavity Structure. Crystals 2021, 11, 1175. https://doi.org/10.3390/cryst11101175
Yang C-S, Cheng Y-S, Hsu Y-C, Chung Y-C, Hung J-T, Liu C-H, Hsu J-C, Chen C-Y, Yang C-R, Li Y-T, et al. Hybrid Graphene-Based Photonic-Plasmonic Biochemical Sensor with a Photonic and Acoustic Cavity Structure. Crystals. 2021; 11(10):1175. https://doi.org/10.3390/cryst11101175
Chicago/Turabian StyleYang, Chan-Shan, Yi-Sheng Cheng, Young-Chou Hsu, Yi-Cheng Chung, Jing-Ting Hung, Chien-Hao Liu, Jin-Chen Hsu, Cheng-Ying Chen, Chii-Rong Yang, Yu-Tai Li, and et al. 2021. "Hybrid Graphene-Based Photonic-Plasmonic Biochemical Sensor with a Photonic and Acoustic Cavity Structure" Crystals 11, no. 10: 1175. https://doi.org/10.3390/cryst11101175









