Porosity Distribution Simulation and Impure Inclusion Analysis of Porous Crystal Layer Formed via Polythermal Process
Abstract
:1. Introduction
2. Theory
3. Experiment
3.1. Materials
3.2. Apparatus and Procedure
4. Results and Discussion
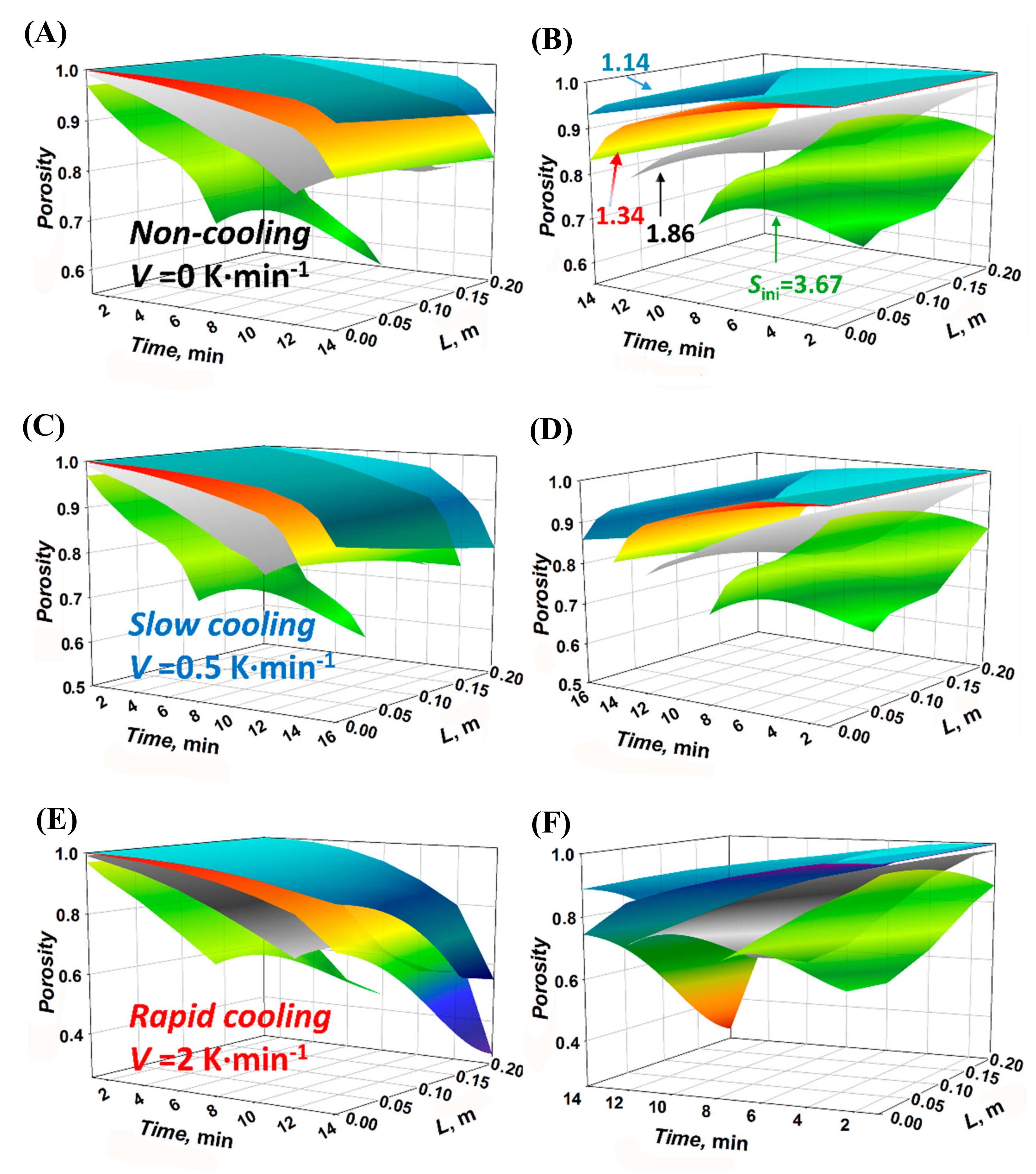
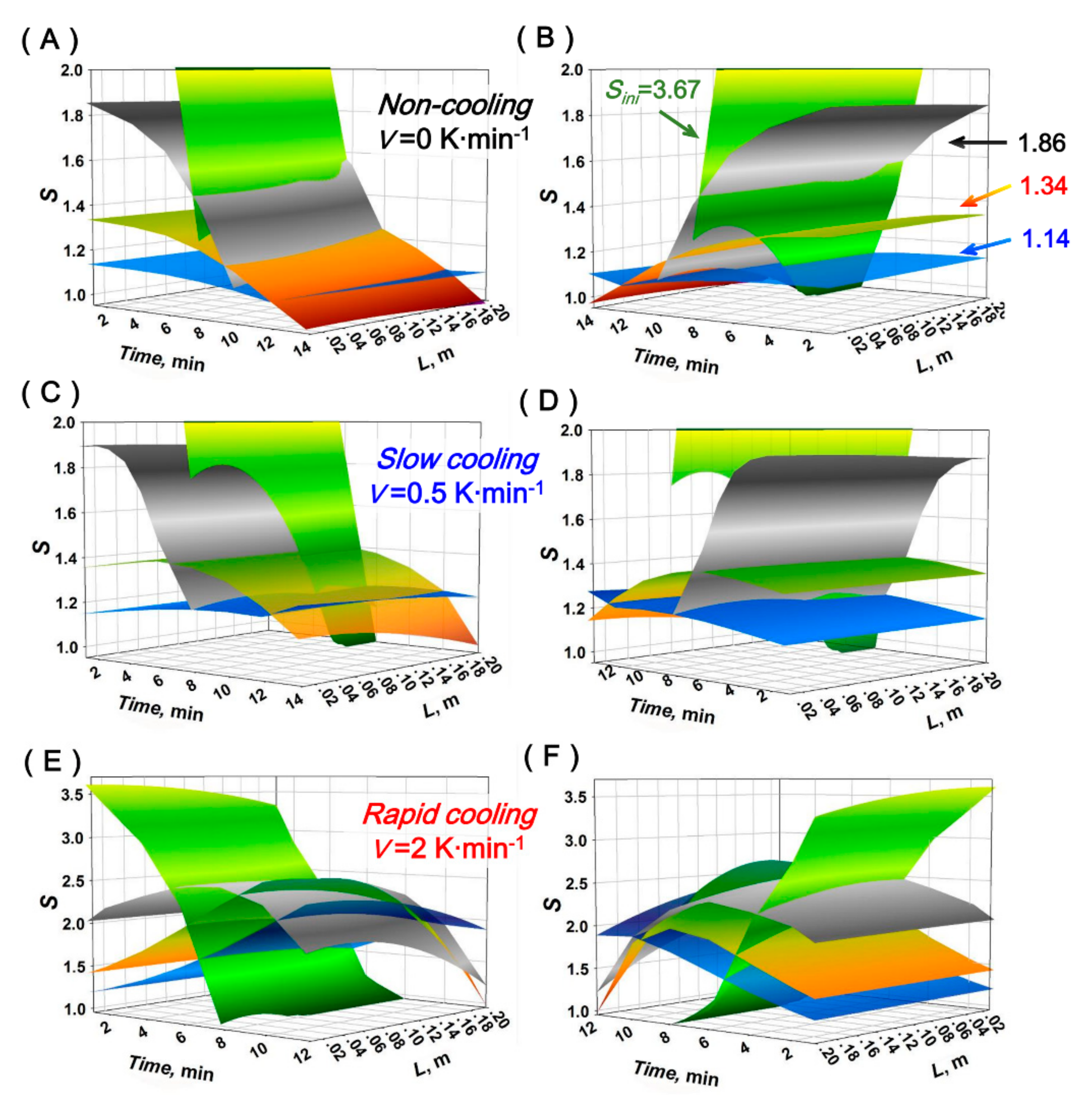
4.1. Formation Process of the Porous Crystal Layer
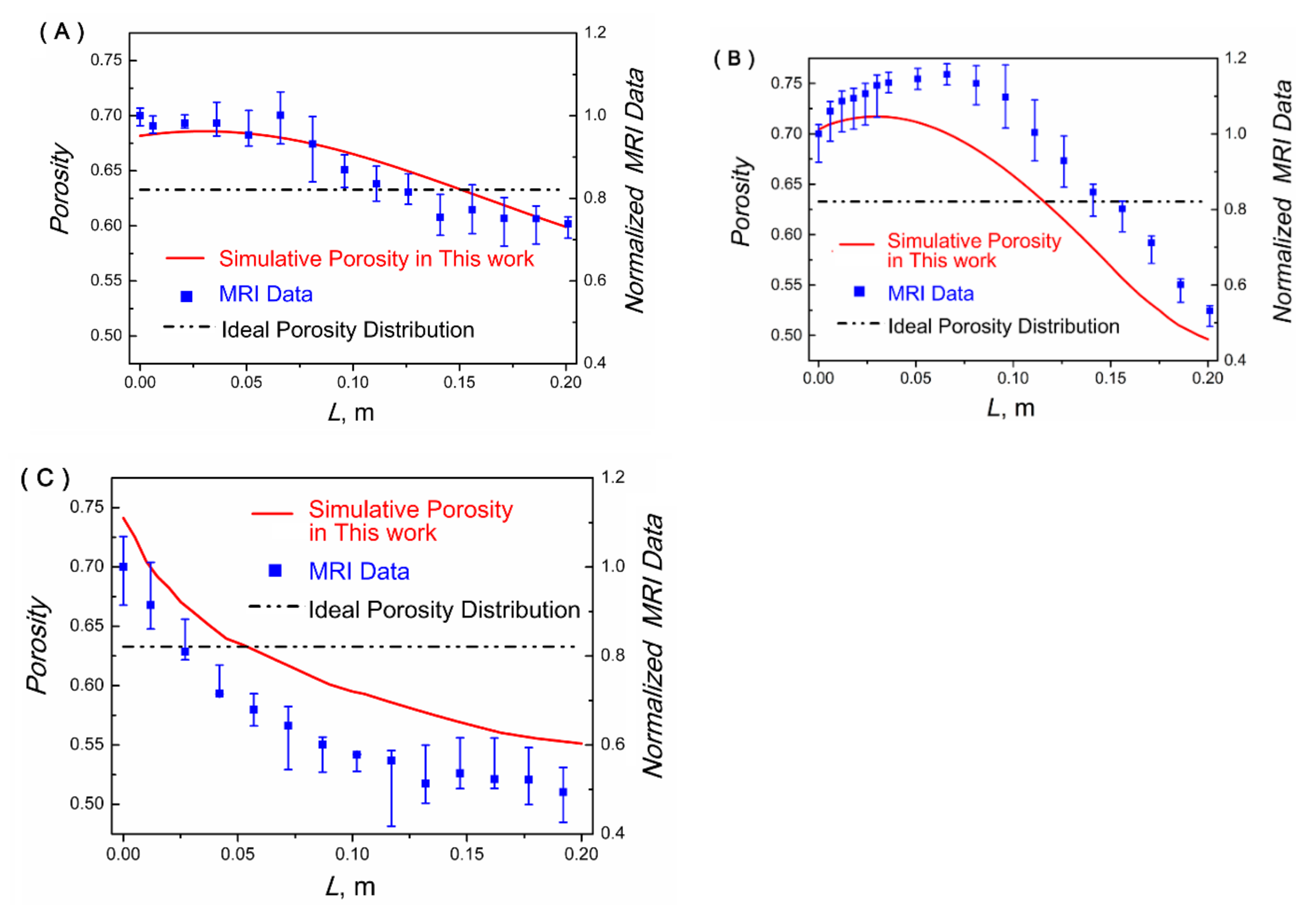
4.2. Porosity Distribution (PD) of the Crystal Layer
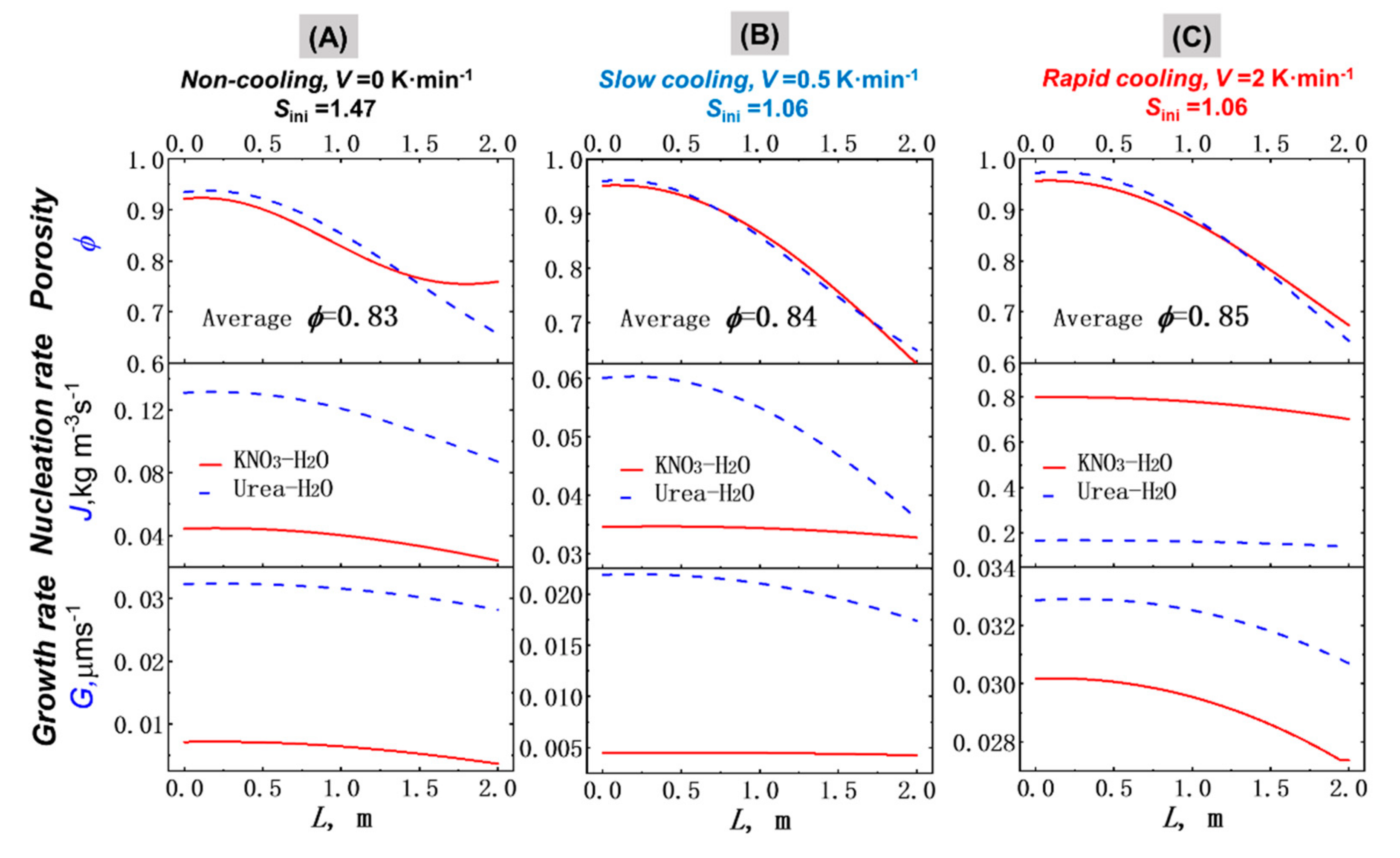
4.3. The Inclusion and the Separation Property Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ulrich, J.; Jones, M.J. Industrial Crystallization. Chem. Eng. Res. Des. 2004, 82, 1567–1570. [Google Scholar] [CrossRef]
- Sha, Z.L.; Yin, Q.X.; Chen, J.X. Industrial Crystallization: Trends and Challenges. Chem. Eng. Technol. 2013, 36, 1286. [Google Scholar] [CrossRef]
- Jiang, X.B.; Hou, B.H.; He, G.H.; Wang, J.K. Falling film melt crystallization (I): Model development, experimental validation of crystal layer growth and impurity distribution process. Chem. Eng. Sci. 2012, 84, 120–133. [Google Scholar] [CrossRef]
- Jiang, X.; Hou, B.; He, G.; Wang, J. Falling film melt crystallization (II): Model to simulate the dynamic sweating using fractal porous media theory. Chem. Eng. Sci. 2013, 91, 111–121. [Google Scholar] [CrossRef]
- Jiang, X.; Xiao, W.; He, G. Falling film melt crystallization (III): Model development, separation effect compared to static melt crystallization and process optimization. Chem. Eng. Sci. 2014, 117, 198–209. [Google Scholar] [CrossRef]
- Gilbert, S.W. Melt Crystallization—Process Analysis and Optimization. AIChE J. 1991, 37, 1205–1218. [Google Scholar] [CrossRef]
- Yazdanpanah, N.; Myerson, A.; Trout, B. Mathematical Modeling of Layer Crystallization on a Cold Column with Recirculation. Ind. Eng. Chem. Res. 2016, 55, 5019–5029. [Google Scholar] [CrossRef]
- Kalista, B.; Shin, H.; Cho, J.; Jang, A. Current development and future prospect review of freeze desalination. Desalination 2018, 447, 167–181. [Google Scholar] [CrossRef]
- Ding, S.; Huang, X.; Yin, Q.; Dong, Y.; Bai, Y.; Wang, T.; Hao, H. Heat transfer and its effect on growth behaviors of crystal layers during static layer melt crystallization. Chem. Eng. Sci. 2021, 233, 116390. [Google Scholar] [CrossRef]
- Meng, S.; Hsu, Y.-C.; Ye, Y.; Chen, V. Submerged membrane distillation for inland desalination applications. Desalination 2015, 361, 72–80. [Google Scholar] [CrossRef]
- Ye, W.; Lin, J.; Tækker Madsen, H.; Gydesen Søgaard, E.; Hélix-Nielsen, C.; Luis, P.; Van der Bruggen, B. Enhanced performance of a biomimetic membrane for Na2CO3 crystallization in the scenario of CO2 capture. J. Membr. Sci. 2016, 498, 75–85. [Google Scholar] [CrossRef] [Green Version]
- Jia, S.; Jing, B.; Hong, W.; Gao, Z.; Gong, J.; Wang, J.; Rohani, S. Purification of 2,4-dinitrochlorobenzene using layer melt crystallization: Model and experiment. Sep. Purif. Technol. 2021, 270, 118806. [Google Scholar] [CrossRef]
- Chen, X.D.; Wu, W.D.; Chen, P. An analytical relationship of concentration-dependent interfacial solute distribution coefficient for aqueous layer freeze concentration. AIChE J. 2015, 61, 1334–1344. [Google Scholar] [CrossRef]
- Zhou, L.; Su, M.; Benyahia, B.; Singh, A.; Barton, P.I.; Trout, B.L.; Myerson, A.S.; Braatz, R.D. Mathematical modeling and design of layer crystallization in a concentric annulus with and without recirculation. AIChE J. 2013, 59, 1308–1321. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Hou, B.; Wang, J.; Yin, Q.; Zhang, M. Model to Simulate the Structure of a Crystal Pillar and Optimize the Separation Efficiency in Melt Crystallization by Fractal Theory and Technique. Ind. Eng. Chem. Res. 2011, 50, 10229–10245. [Google Scholar] [CrossRef]
- Nakahara, M.; Nomura, K.; Koizumi, T. Purification Rate of Uranyl Nitrate Hexahydrate Crystal for Transuranium Elements on Isothermal Sweating Phenomenon. Ind. Eng. Chem. Res. 2010, 49, 11661–11666. [Google Scholar] [CrossRef]
- Eisenbart, F.J.; Ulrich, J. Solvent-aided layer crystallization—Case study glycerol–water. Chem. Eng. Sci. 2015, 133, 24–29. [Google Scholar] [CrossRef]
- Jo, J.H.; Ernest, T.; Kim, K.J. Treatment of TNT red water by layer melt crystallization. J. Hazard. Mater. 2014, 280, 185–190. [Google Scholar] [CrossRef]
- Ding, S.; Huang, X.; Yin, Q.; Wang, N.; Wang, T.; Dong, Y.; Chen, Y.; Hao, H. Static layer melt crystallization: Effects of impurities on the growth behaviors of crystal layers. Sep. Purif. Technol. 2021, 279, 119764. [Google Scholar] [CrossRef]
- Peterson, T.D. A refined technique for measuring crystal size distributions in thin section. Contrib. Miner. Petrol. 1996, 124, 395–405. [Google Scholar] [CrossRef]
- Zieg, M.J.; Marsh, B.D. Crystal size distributions and scaling laws in the quantification of igneous textures. J. Petrol. 2002, 43, 85–101. [Google Scholar] [CrossRef]
- Yu, B.; Liu, W. Fractal analysis of permeabilities for porous media. AIChE J. 2004, 50, 46–57. [Google Scholar] [CrossRef]
- Zheng, Q.; Yu, B.M.; Wang, S.F.; Luo, L. A diffusivity model for gas diffusion through fractal porous media. Chem. Eng. Sci. 2012, 68, 650–655. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; He, G. Fractal slice model analysis for effective thermal conductivity and temperature distribution of porous crystal layer via layer crystallization. Cryst. Res. Technol. 2013, 48, 574–581. [Google Scholar] [CrossRef]
- Zhu, F.; Cui, S.; Gu, B. Fractal analysis for effective thermal conductivity of random fibrous porous materials. Phys. Lett. A 2010, 374, 4411–4414. [Google Scholar] [CrossRef]
- Cai, J.; Perfect, E.; Cheng, C.L.; Hu, X. Generalized modeling of spontaneous imbibition based on Hagen-Poiseuille flow in tortuous capillaries with variably shaped apertures. Langmuir ACS J. Surf. Colloids 2014, 30, 5142–5151. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Cai, J.C.; Yu, B.M. A Discussion of the Effect of Tortuosity on the Capillary Imbibition in Porous Media. Transp. Porous. Media 2011, 89, 251–263. [Google Scholar] [CrossRef]
- Cai, J.C.; Hu, X.Y.; Standnes, D.C.; You, L.J. An analytical model for spontaneous imbibition in fractal porous media including gravity. Colloid Surf. A Physicochem. Eng. Asp. 2012, 414, 228–233. [Google Scholar] [CrossRef]
- Power, G.; Hou, G.; Kamaraju, V.K.; Morris, G.; Zhao, Y.; Glennon, B. Design and optimization of a multistage continuous cooling mixed suspension, mixed product removal crystallizer. Chem. Eng. Sci. 2015, 133, 125–139. [Google Scholar] [CrossRef]
- Zhao, Y.; Kamaraju, V.K.; Hou, G.; Power, G.; Donnellan, P.; Glennon, B. Kinetic identification and experimental validation of continuous plug flow crystallization. Chem. Eng. Sci. 2015, 133, 106–115. [Google Scholar] [CrossRef]
- Hou, G.; Power, G.; Barrett, M.; Glennon, B.; Morris, G.; Zhao, Y. Development and Characterization of a Single Stage Mixed-Suspension, Mixed-Product-Removal Crystallization Process with a Novel Transfer Unit. Cryst. Growth Des. 2014, 14, 1782–1793. [Google Scholar] [CrossRef]
- Tang, S.W.; Li, Z.J.; Chen, E.; Shao, H.Y. Non-steady state migration of chloride ions in cement pastes at early age. RSC Adv. 2014, 4, 48582–48589. [Google Scholar] [CrossRef]
- Carpenter, K.; Bahadur, V. Saltwater icephobicity: Influence of surface chemistry on saltwater icing. Sci. Rep. 2015, 5, 17563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.; Li, S.; Li, S. Purification of 2-Pyrrolidone by Falling Film Melt Crystallization. Ind. Eng. Chem. Res. 2021, 60, 13286–13292. [Google Scholar] [CrossRef]
- Xu, P.; Mujumdar, A.S.; Yu, B. Fractal Theory on Drying: A Review. Dry. Technol. 2008, 26, 640–650. [Google Scholar] [CrossRef]
- Luo, L.A.; Yu, B.M.; Cai, J.C.; Mei, M.F. Symmetry is not always prefect. Int. J. Heat Mass Transf. 2010, 53, 5022–5024. [Google Scholar] [CrossRef]
- Yu, B.M.; Li, B.W. Fractal-like tree networks reducing the thermal conductivity. Phys. Rev. E 2006, 73, 066302. [Google Scholar] [CrossRef]
- Prat, M.; Veran-Tissoires, S.; Vorhauer, N.; Metzger, T.; Tsotsas, E. Fractal Phase Distribution and Drying: Impact on Two-Phase Zone Scaling and Drying Time Scale Dependence. Dry. Technol. 2012, 30, 1129–1135. [Google Scholar] [CrossRef] [Green Version]
- Mei, M.; Yu, B.; Zou, M.; Luo, L. A numerical study on growth mechanism of dropwise condensation. Int. J. Heat Mass Transf. 2011, 54, 2004–2013. [Google Scholar] [CrossRef]
- Lu, D.; Li, P.; Xiao, W.; He, G.; Jiang, X. Simultaneous recovery and crystallization control of saline organic wastewater by membrane distillation crystallization. AIChE J. 2017, 63, 2187–2197. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Song, Y.; Zhao, Y.; Zhao, J.; Wang, D. Fractal analysis and its impact factors on pore structure of artificial cores based on the images obtained using magnetic resonance imaging. J. Appl. Geophys. 2012, 86, 70–81. [Google Scholar] [CrossRef]
- Jiang, X.; Hou, B.; Zhao, Y.; Wang, J.; Zhang, M. Kinetics Study on the Liquid Entrapment and Melt Transport of Static and Falling-Film Melt Crystallization. Ind. Eng. Chem. Res. 2012, 51, 5037–5044. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Hou, B. Coarse crystal layer growth and liquid entrapment study with gradient freeze technology. Cryst. Res. Technol. 2012, 47, 649–657. [Google Scholar] [CrossRef]
- Moreno, F.L.; Hernández, E.; Raventós, M.; Robles, C.; Ruiz, Y. A process to concentrate coffee extract by the integration of falling film and block freeze-concentration. J. Food Eng. 2014, 128, 88–95. [Google Scholar] [CrossRef]
- Fukui, K.; Fujikawa, T.; Satone, H.; Yamamoto, T.; Maeda, K.; Kuramochi, H. Application of solute distribution theory to melt crystallization of fatty acids. Chem. Eng. Sci. 2015, 133, 24–29. [Google Scholar] [CrossRef]
- Kobari, M.; Kubota, N.; Hirasawa, I. Simulation of metastable zone width and induction time for a seeded aqueous solution of potassium sulfate. J. Cryst. Growth 2010, 312, 2734–2739. [Google Scholar] [CrossRef]
- Sangwal, K. On the interpretation of metastable zone width in anti-solvent crystallization. Cryst. Res. Technol. 2010, 45, 909–919. [Google Scholar] [CrossRef]
- Kashchiev, D.; Borissova, A.; Hammond, R.B.; Roberts, K.J. Effect of cooling rate on the critical undercooling for crystallization. J. Cryst. Growth 2010, 312, 698–704. [Google Scholar] [CrossRef]
- Khaddour, I.; Rocha, F. Metastable zone width for secondary nucleation and secondary nucleation inside the metastable zone. Cryst. Res. Technol. 2011, 46, 373–382. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Myerson, A. Handbook of Industrial Crystallization; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Cogoni, G.; Grosso, M.; Baratti, R.; Romagnoli, J.A. Time evolution of the PSD in crystallization operations: An analytical solution based on Ornstein-Uhlenbeck process. Aiche J. 2012, 58, 3731–3739. [Google Scholar] [CrossRef]
- Mydlarz, J.; Jones, A.G. On the estimation of size-dependent crystal growth rate functions in MSMPR crystallizers. Chem. Eng. J. 1993, 53, 125–135. [Google Scholar] [CrossRef]
- Jiang, X.; Ruan, X.; Xiao, W.; Lu, D.; He, G. A novel membrane distillation response technology for nucleation detection, metastable zone width measurement and analysis. Chem. Eng. Sci. 2015, 134, 671–680. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Y.; Li, Z.; Li, X.; Xiao, W.; He, G.; Wu, X.; Jiang, X. Porosity Distribution Simulation and Impure Inclusion Analysis of Porous Crystal Layer Formed via Polythermal Process. Crystals 2021, 11, 1347. https://doi.org/10.3390/cryst11111347
Meng Y, Li Z, Li X, Xiao W, He G, Wu X, Jiang X. Porosity Distribution Simulation and Impure Inclusion Analysis of Porous Crystal Layer Formed via Polythermal Process. Crystals. 2021; 11(11):1347. https://doi.org/10.3390/cryst11111347
Chicago/Turabian StyleMeng, Yingshuang, Zhonghua Li, Xiangcun Li, Wu Xiao, Gaohong He, Xuemei Wu, and Xiaobin Jiang. 2021. "Porosity Distribution Simulation and Impure Inclusion Analysis of Porous Crystal Layer Formed via Polythermal Process" Crystals 11, no. 11: 1347. https://doi.org/10.3390/cryst11111347






