Study and Analysis of Simple and Precise of Contact Resistance Single-Transistor Extracting Method for Accurate Analytical Modeling of OTFTs Current-Voltage Characteristics: Application to Different Organic Semiconductors
Abstract
:1. Introduction
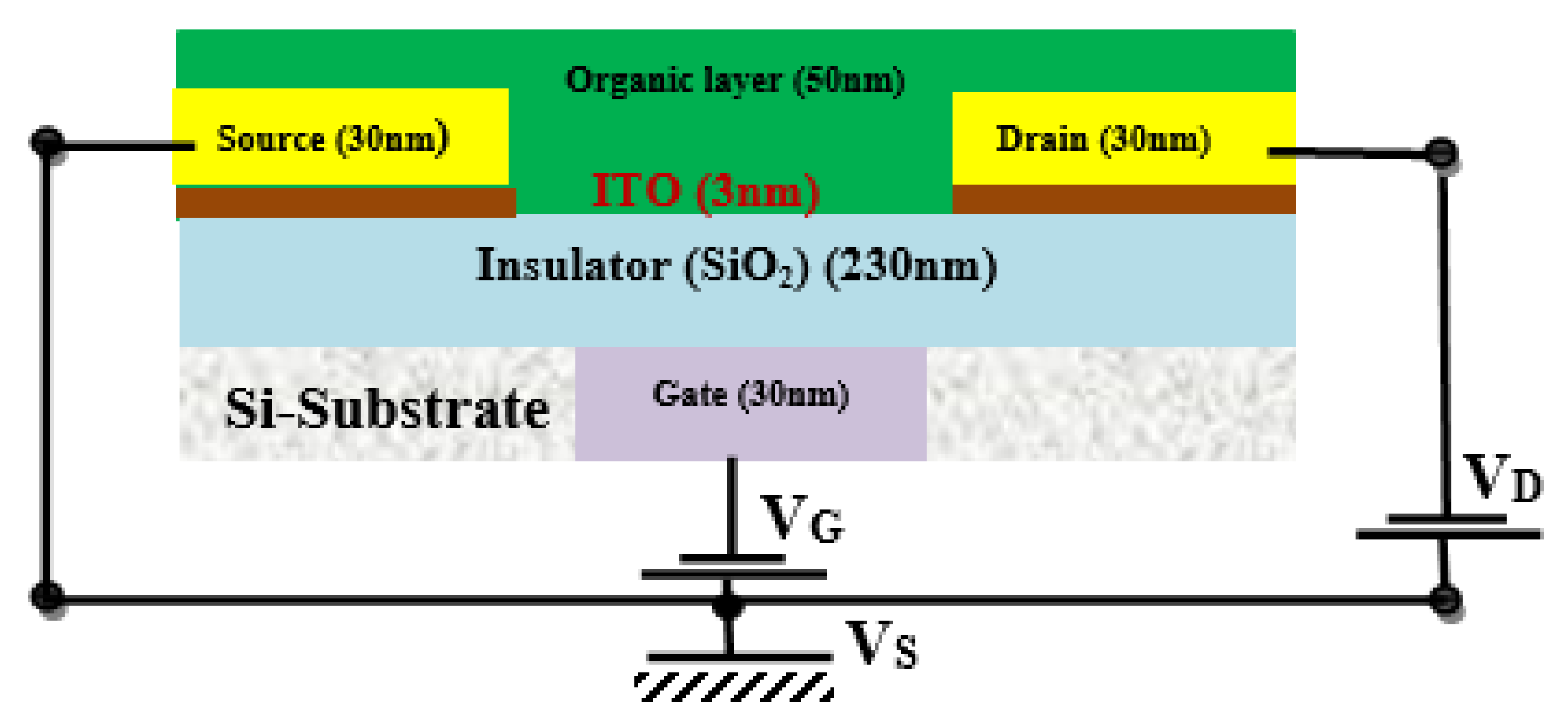
2. Experimental Details
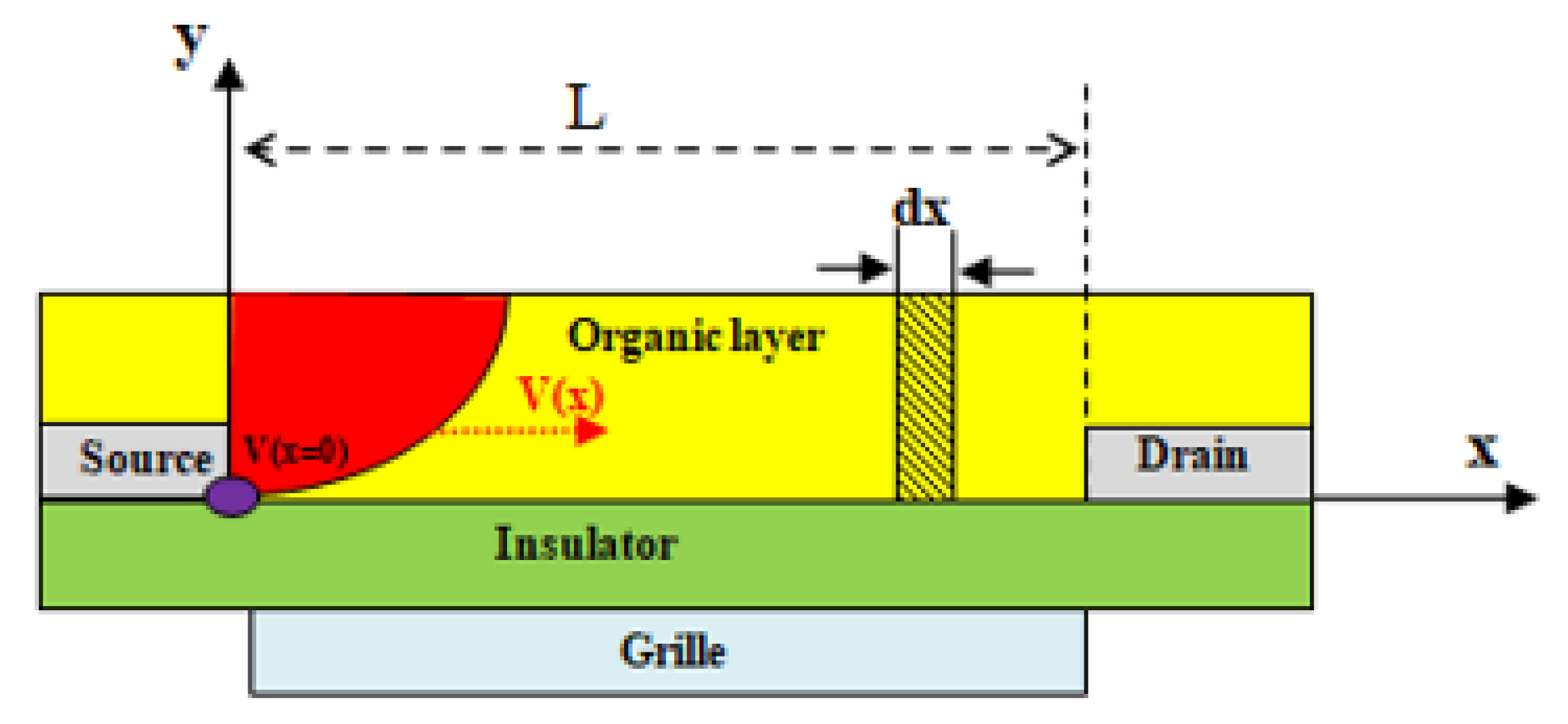
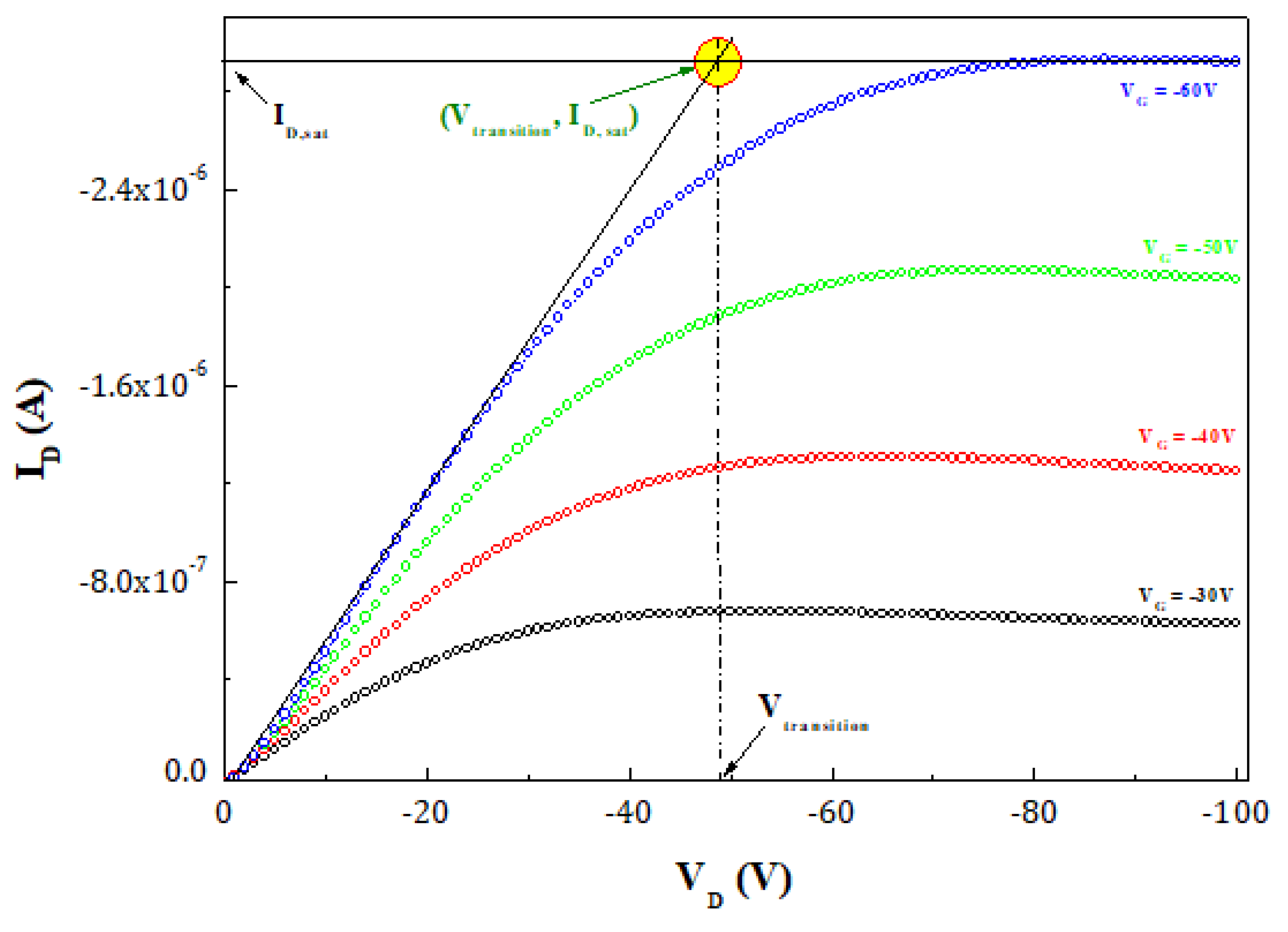
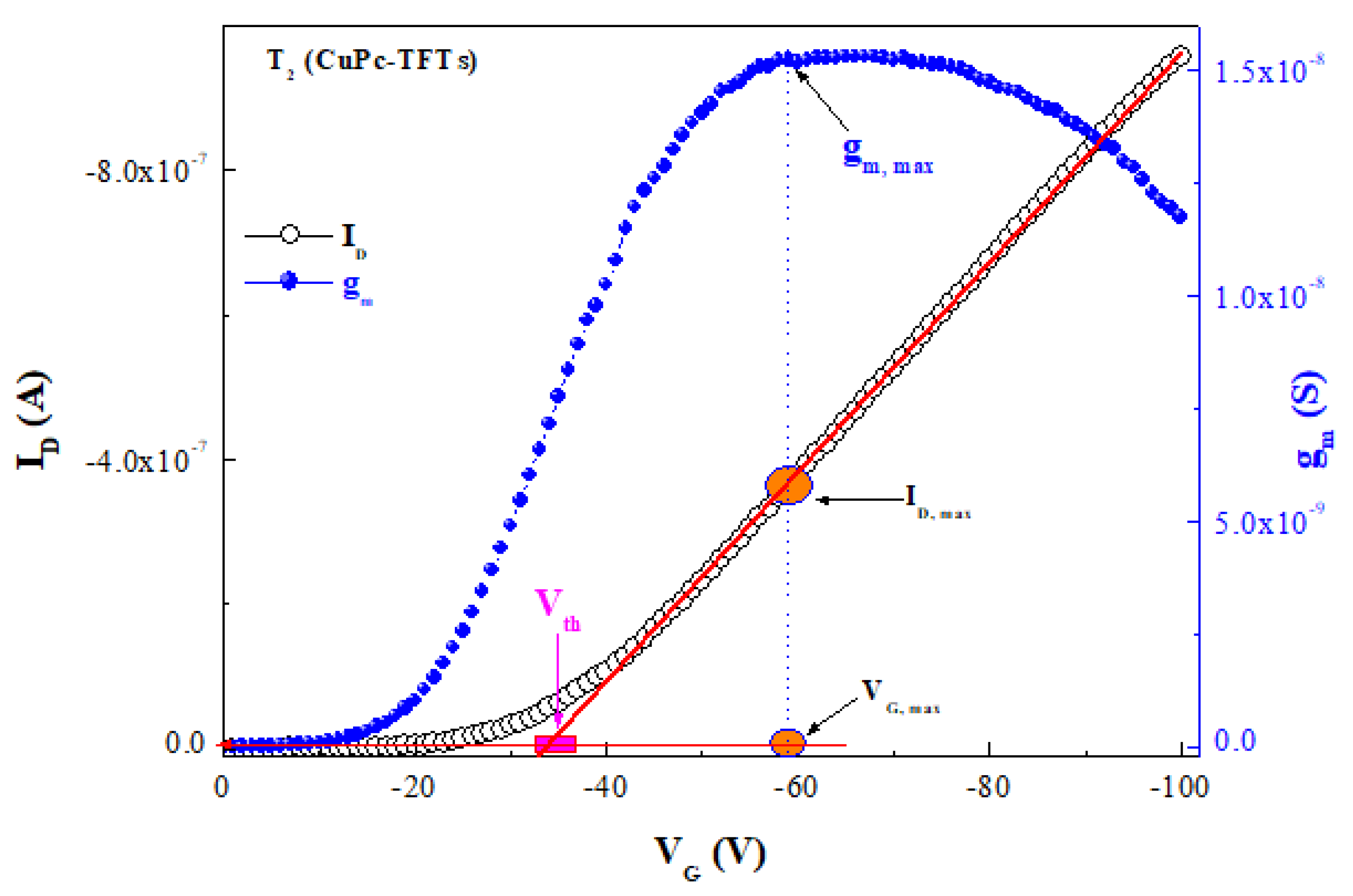
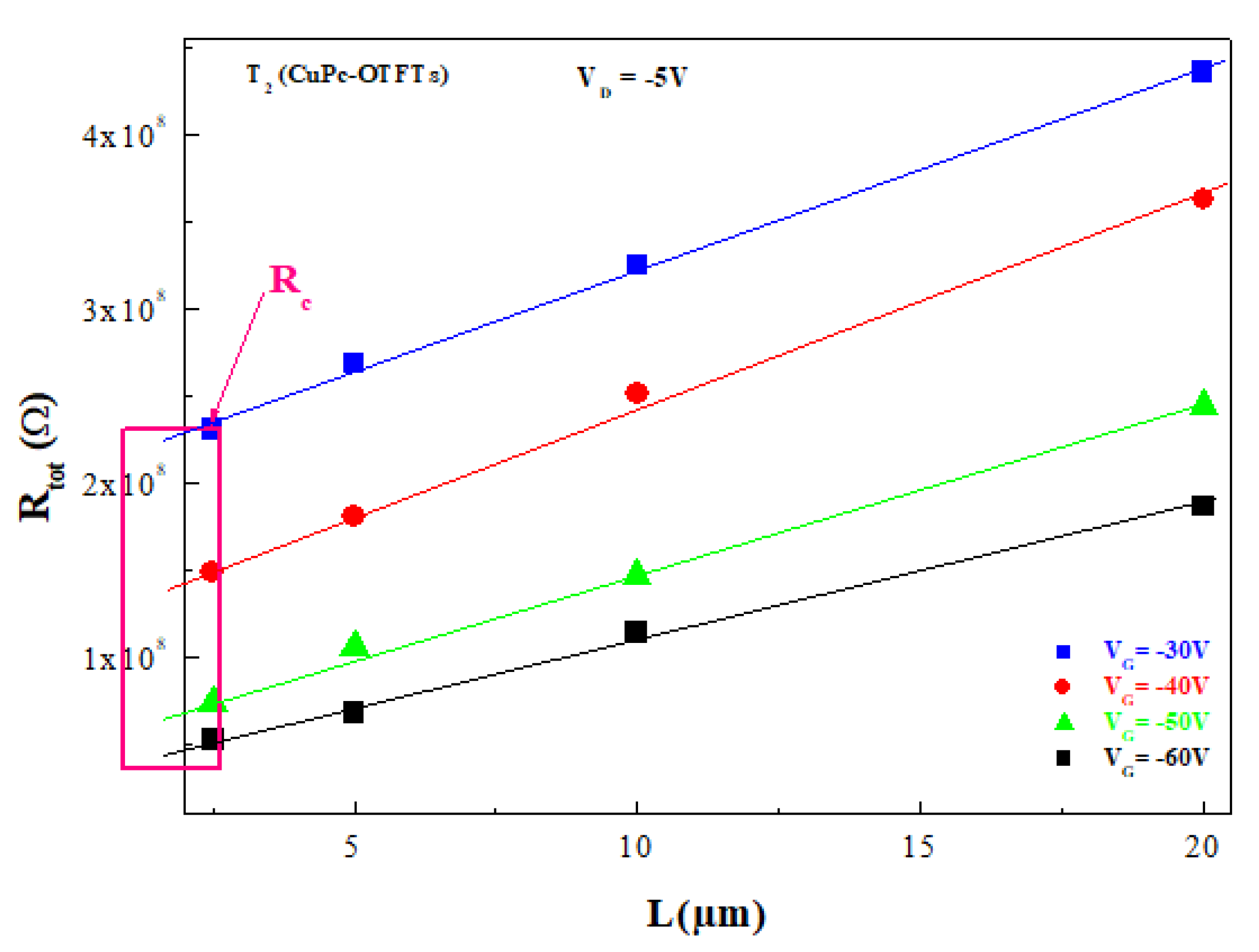
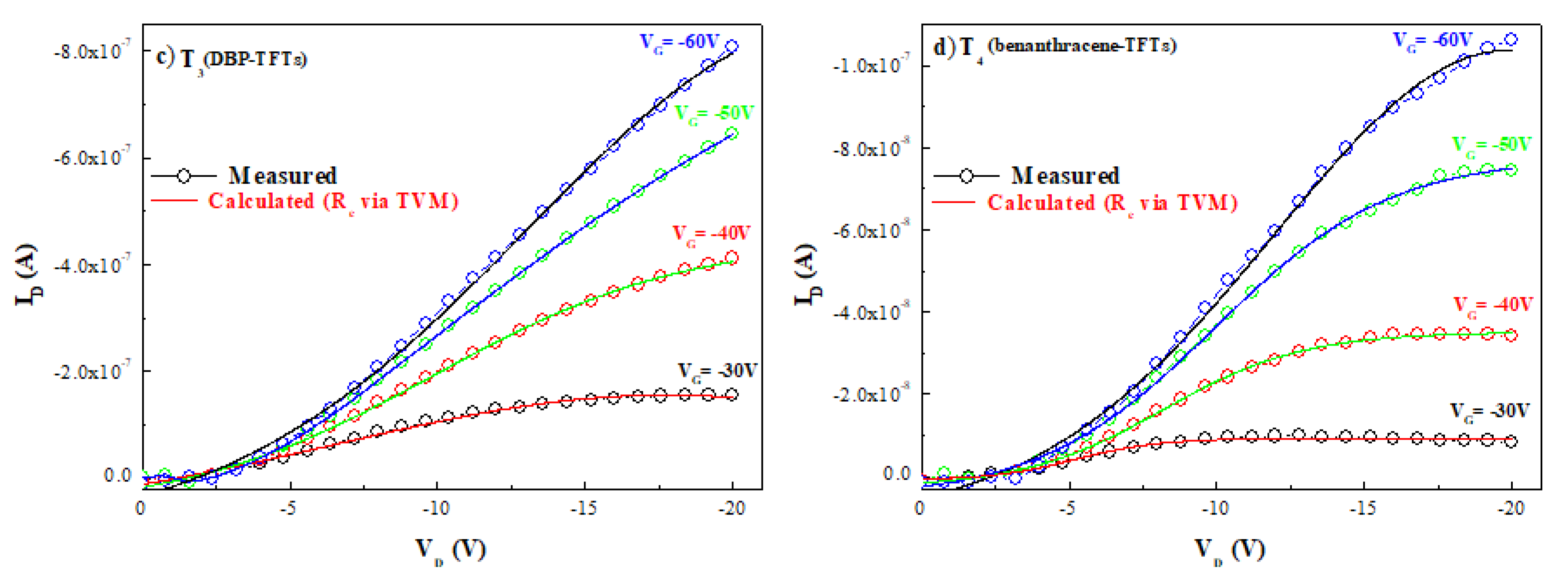
3. Results and Discussion
4. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kabe, R.; Adachi, C. Organic long persistent luminescence. Nature 2017, 550, 384–387. [Google Scholar] [CrossRef]
- Lia, J.H.; Tang, W.; Wang, Q.; Sun, W.J.; Zhang, Q.; Guo, X.J.; Wang, X.B.; Yan, F. Solution-processable organic and hybrid gate dielectrics for printed electronics. Mater. Sci. Eng. R. Rep. 2018, 127, 1–36. [Google Scholar] [CrossRef]
- Geffroy, B.; le Roy, P.; Prat, C. Organic light-emitting diode (OLED) technology: Materials, devices and display technologies. Polym. Int. 2006, 55, 572–582. [Google Scholar] [CrossRef]
- Wageh, S. Light Emitting Devices Based on CdSe Nanoparticles Capped with Mercaptoacetic Acid. IEEE J. Quantum Electron. 2014, 50, 741–748. [Google Scholar] [CrossRef]
- Eder, F.; Klauk, H.; Halik, M.; Zschieschang, U.; Schmid, G.; Dehm, C. Organic electronics on paper. Appl. Phys. Lett. 2004, 84, 2673–2675. [Google Scholar] [CrossRef]
- Wageh, S.; Raïssi, M.; Berthelot, T.; Al-Ghamdi, A.A.; Abusorrah, A.M.; Boukhili, W.; Al-Hartomy, O.A. Silver Nanowires Digital Printing for Inverted Flexible Semi-Transparent Solar Cells. Adv. Eng. Mater. 2021, 23, 2001305. [Google Scholar] [CrossRef]
- Alam, M.W.; Wang, Z.; Naka, S.; Okada, H. Performance Enhancement of Top-Contact Pentacene-Based Organic Thin-Film Transistors with Bilayer WO3/Au Electrodes. Jpn. J. Appl. Phys. 2013, 21, 03BB08. [Google Scholar] [CrossRef]
- Wageh, S.; Raïssi, M.; Berthelot, T.; Laurent, M.; Rousseau, D.; Abusorrah, A.M.; Al-Hartomy, O.A.; Al-Ghamdi, A.A. Digital printing of a novel electrode for stable flexible organic solar cells with a power conversion efficiency of 8.5%. Sci. Rep. 2021, 11, 14212. [Google Scholar] [CrossRef] [PubMed]
- Borchert, J.W.; Peng, B.; Letzkus, F.; Burghartz, J.N.; Chan, P.K.L.; Zojer, K.; Ludwigs, S.; Klauk, H. Small contact resistance and high-frequency operation of flexible low-voltage inverted coplanar organic transistors. Nat. Commun. 2019, 10, 1119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoth, C.N.; Schilinsky, P.; Choulis, S.A.; Brabec, C.J. Printing Highly Efficient Organic Solar Cells. Nano Lett. 2008, 8, 2806–2813. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.W.; Wang, S.; Naka, S.; Okada, H. Top Contact Pentacene Based Organic Thin Film Transistor with Bi-layer TiO2Electrodes. J. Photopolym. Sci. Technol. 2012, 26, 659–664. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.H.; Kim, K.S.; Ji, Y.J.; Kang, J.E.G.; Yeom, Y. Silicon nitride deposited by laser assisted plasma enhanced chemical vapor deposition for next generation organic electronic device. Appl. Surf. Sci. 2021, 541, 148313. [Google Scholar] [CrossRef]
- Kelley, T.W.; Baude, P.F.; Gerlach, C.; Ender, D.E.; Muyres, D.; Haase, M.A.; Vogel, D.E.; Theiss, S.D. Recent Progress in Organic Electronics: Materials, Devices, and Processes. Chem. Mater. 2004, 16, 4413–4422. [Google Scholar] [CrossRef]
- Natali, D. Fundamentals of Organic Electronic Devices, Organic Flexible Electronics Fundamentals, Devices, and Applications Woodhead Publishing Series in Electronic and Optical Materials; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–25. [Google Scholar]
- Borchert, J.W.; Weitz, R.T.; Ludwigs, S.; Klauk, H. A Critical Outlook for the Pursuit of Lower Contact Resistance in Organic Transistors. Adv. Mater. 2021, 35, 2104075. [Google Scholar] [CrossRef] [PubMed]
- Hagen, K.; Jackson, T.N. Pentacene organic thin-film transistors and ICs. Solid State Technol. 2000, 43, 63–64. [Google Scholar]
- Katz, H.E.; Huang, J. Thin-Film Organic Electronic Devices. Annu. Rev. Mater. Res. 2009, 39, 71–92. [Google Scholar] [CrossRef] [Green Version]
- Torsi, L.; Dodabalapur, A.; Sabbatini, L.; Zambonin, P.G. Multi-parameter gas sensors based on organic thin-film-transistors. Sens. Actuators B 2000, 67, 312–316. [Google Scholar] [CrossRef]
- Boukhili, W.; Mahdouani, M.; Bourguiga, R.; Puigdollers, J. Experimental study and analytical modeling of the channel length influence on the electrical characteristics of small-molecule thin-film transistors. Superlattices Microstruct. 2015, 83, 224–236. [Google Scholar] [CrossRef] [Green Version]
- Boukhili, W.; Mahdouani, M.; Erouel, M.; Puigdollers, J.; Bourguiga, R. Reversibility of humidity effects in pentacene based organic thin-film transistor: Experimental data and electrical modeling. Synth. Met. 2015, 199, 303–309. [Google Scholar] [CrossRef] [Green Version]
- Boukhili, W.; Mahdouani, M.; Bourguiga, R.; Puigdollers, J. Temperature dependence of the electrical properties of organic thin-film transistors based on tetraphenyldibenzoperiflanthene deposited at different substrate temperatures: Experiment and modeling. Microelectron. Eng. 2016, 150, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Mahdouani, M.; Boukhili, W.; Bourguiga, R. Negative output differential resistance effect in organic thin film transistors based on pentacene: Characterization and modeling Mater. Today Commun. 2017, 13, 367–377. [Google Scholar] [CrossRef]
- Boukhili, W.; Mahdouani, M.; Bourguiga, R.; Puigdollers, J. Characterization and modeling of organic thin-film transistors based π-conjugated small molecule tetraphenyldibenzoperiflanthene: Effects of channel length. Microelectron. Eng. 2016, 160, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Boukhili, W.; Tozlu, C.; Mahdouani, M.; Erten-Ela, S.; Bourguiga, R. Illumination and dipole layer effects on the density of state distribution in n-type organic thin film phototransistors based on naphthalene bis-benzimidazole: Experiment and modeling. Microelectron. Eng. 2017, 179, 37–47. [Google Scholar] [CrossRef]
- Fan, C.L.; Lin, Y.Z.; Lee, W.D.; Wang, S.J.; Huang, C.H. Improved pentacene growth continuity for enhancing the performance of pentacene-based organic thin-film transistors. Org. Electron. 2012, 13, 2924–2928. [Google Scholar] [CrossRef]
- Marinkovic, M.; Belaineh, D.; Wagner, V.; Knipp, D. On the origin of contact resistances of organic thin film transistors. Adv. Mater. 2012, 24, 4005. [Google Scholar] [CrossRef]
- Natali, D.; Caironi, M. Charge Injection in Solution-Processed Organic Field-Effect Transistors: Physics, Models and Characterization Methods. Adv. Mater. 2012, 24, 1357–1387. [Google Scholar] [CrossRef] [PubMed]
- Al-Ghamdi, A.; Boukhili, W.; Wageh, S. Contact resistance corrected-electrical characteristics with channel length effects in π-conjugated small-molecule benzanthracene organic thin film transistors. Synth. Met. 2021, 273, 116670. [Google Scholar] [CrossRef]
- Natali, D.; Fumagalli, L.; Sampietro, M. Modeling of organic thin film transistors: Effect of contact resistances. J. Appl. Phys. 2007, 101, 014501. [Google Scholar] [CrossRef]
- Neamen, D.A. Semiconductor Physics and Devices: Basic Principles, 4th ed.; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- Pesavento, P.V.; Chesterfield, R.J.; Newman, C.R.; Frisbie, C.D. Gated four-probe measurements on pentacene thin-film transistors: Contact resistance as a function of gate voltage and temperature. J. Appl. Phys. 2004, 96, 7312. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wang, S.D.; Yan, Y.; Tsukagoshi, K. Transition-Voltage Method for Estimating Contact Resistance in Organic Thin-Film Transistors. IEEE Electron. Device Lett. 2010, 31, 509–511. [Google Scholar] [CrossRef]
- Jinhuo, C.; Jiaxing, H.; Yunlong, Z. A novel method to analyze the contact resistance effect on OTFTs. J. Semicond. 2012, 33, 124005. [Google Scholar]
- Lai, S.; Cosseddu, P.; Bonfiglio, A. A method for direct contact resistance evaluation in low voltage coplanar organic field-effect transistors. Appl. Phys. Lett. 2017, 110, 153304. [Google Scholar] [CrossRef]
- Takagaki, S.; Yamada, H.; Noda, K. Extraction of contact resistance and channel parameters from the electrical characteristics of a single bottom-gate/top-contact organic transistor. Jpn. J. Appl. Phys. 2016, 55, 03DC07. [Google Scholar] [CrossRef]
- Torricelli, F.; Ghittorelli, M.; Colalongo, L.; Kovacs-Vajna, Z.M. Single-transistor method for the extraction of the contact and channel resistances in organic field-effect transistors. Appl. Phys. Lett. 2014, 104, 093303. [Google Scholar] [CrossRef] [Green Version]
- Necliudov, P.V.; Shur, M.S.; Gundlach, D.J.; Jackson, T.N. Contact resistance extraction in pentacene thin film transistors. Solid-State Electron. 2003, 47, 259–262. [Google Scholar] [CrossRef]
- Horowitz, G.; Hajlaoui, R.; Fichou, D.; el Kassmi, A. Gate voltage dependent mobility of oligothiophene field-effect transistors. J. Appl. Phys. 1999, 85, 6. [Google Scholar] [CrossRef]
- Simonetti, O.; Giraudet, L.; Maurel, T.; Nicolas, J.L.; Belkhir, A. Organic transistor model with nonlinear injection: Effects of uneven source contact on apparent mobility and threshold voltage. Org. Electron. 2010, 11, 1381–1393. [Google Scholar] [CrossRef]
- Bolognesi, A.; Berliocchi, M.; Manenti, M.; Carlo, A.D.; Lugli, P.; Lmimouni, K.; Dufour, C. Effects of grain boundaries, field-dependent mobility, and interface trap States on the electrical Characteristics of pentacene TFT. IEEE Trans. Electron. Devices 2004, 51, 1997. [Google Scholar] [CrossRef]
- Haddock, J.N.; Zhang, X.; Zheng, S.; Zhang, Q.; Marder, S.R.; Kippelen, B. A comprehensive study of short channel effects in organic field-effect transistors. Org. Electron. 2006, 7, 45–54. [Google Scholar] [CrossRef]
- Jung, K.D.; Kim, Y.C.; Park, B.G.; Shin, H.; Lee, J.D. Modeling and parameter extraction for the series resistance in thin-film transistors. IEEE Trans. Electron. Devices 2009, 56, 431–440. [Google Scholar] [CrossRef]



| Organic Semiconductors | Device Abbreviation Name |
|---|---|
| Pentacene | T1 (Pentacene-TFTs) |
| Copper phthalocyanine (CuPc) | T2 (CuPc-TFTs) |
| Tetraphenyldibenzoperiflanthene (DBP) | T3 (DBP-TFTs) |
| Benzanthracene | T4 (Benzanthracene-TFTs) |
| Method Name | Abbreviation | Number of Transistor | Required Parameters | Required Measurement |
|---|---|---|---|---|
| Transfer line method | TLM | set of transistors: various channel lengths | Total resistance Mobility Threshold voltage | ID-VD of multiple OTFTs |
| Transition voltage method | TVM | Single transistor | Threshold voltage | ID-VD of single OTFTs |
| Parameters Device | Vaa (V) | γ | Vth (V) | |
|---|---|---|---|---|
| T1 | 1.22 | 1.11 | 7.7 × 10–6 | −36 |
| T2 | 0.98 | 1.85 | 2.6 × 10–6 | −37.75 |
| T3 | 1.74 | 1.29 | 7.8 × 10–7 | −42.5 |
| T4 | 1.35 | 1.03 | 2.73 × 10–7 | −45.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, N.A. Study and Analysis of Simple and Precise of Contact Resistance Single-Transistor Extracting Method for Accurate Analytical Modeling of OTFTs Current-Voltage Characteristics: Application to Different Organic Semiconductors. Crystals 2021, 11, 1448. https://doi.org/10.3390/cryst11121448
Alghamdi NA. Study and Analysis of Simple and Precise of Contact Resistance Single-Transistor Extracting Method for Accurate Analytical Modeling of OTFTs Current-Voltage Characteristics: Application to Different Organic Semiconductors. Crystals. 2021; 11(12):1448. https://doi.org/10.3390/cryst11121448
Chicago/Turabian StyleAlghamdi, Noweir Ahmad. 2021. "Study and Analysis of Simple and Precise of Contact Resistance Single-Transistor Extracting Method for Accurate Analytical Modeling of OTFTs Current-Voltage Characteristics: Application to Different Organic Semiconductors" Crystals 11, no. 12: 1448. https://doi.org/10.3390/cryst11121448
APA StyleAlghamdi, N. A. (2021). Study and Analysis of Simple and Precise of Contact Resistance Single-Transistor Extracting Method for Accurate Analytical Modeling of OTFTs Current-Voltage Characteristics: Application to Different Organic Semiconductors. Crystals, 11(12), 1448. https://doi.org/10.3390/cryst11121448





