Next Article in Journal
Contact-Mediated Nucleation of Subcooled Droplets in Melt Emulsions: A Microfluidic Approach
Previous Article in Journal
Numerical Modeling of High Conversion Efficiency FTO/ZnO/CdS/CZTS/MO Thin Film-Based Solar Cells: Using SCAPS-1D Software
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 11
Issue 12
10.3390/cryst11121472
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Principle of Maximal Simplicity for Modular Inorganic Crystal Structures

by
Sergey V. Krivovichev
1,2
1
Nanomaterials Centre, Kola Science Centre, Russian Academy of Sciences, 184209 Murmansk, Russia
2
Department of Crystallography, Institute of Earth Sciences, St. Petersburg State University, 199034 Saint Petersburg, Russia
Crystals 2021, 11(12), 1472; https://doi.org/10.3390/cryst11121472
Submission received: 7 November 2021 / Revised: 20 November 2021 / Accepted: 23 November 2021 / Published: 26 November 2021
(This article belongs to the Section Inorganic Crystalline Materials)
Browse Figures
Versions Notes

Abstract

:
Modularity is an important construction principle of many inorganic crystal structures that has been used for the analysis of structural relations, classification, structure description and structure prediction. The principle of maximal simplicity for modular inorganic crystal structures can be formulated as follows: in a modular series of inorganic crystal structures, the most common and abundant in nature and experiments are those arrangements that possess maximal simplicity and minimal structural information. The latter can be quantitatively estimated using information-based structural complexity parameters. The principle is applied for the modular series based upon 0D (lovozerite family), 1D (biopyriboles) and 2D (spinelloids and kurchatovite family) modules. This principle is empirical and is valid for those cases only, where there are no factors that may lead to the destabilization of simplest structural arrangements. The physical basis of the principle is in the relations between structural complexity and configurational entropy sensu stricto (which should be distinguished from the entropy of mixing). It can also be seen as an analogy of the principle of least action in physics.

1. Introduction

Modularity is an important property of complex natural and artificial networks, including biological, social and technological systems [1,2]. Many natural objects can be decomposed into modules that are recurrent and can be observed as building units in homologous series of structures. For inorganic crystal structures, it was first used by Taylor and West [3] for the chondrodite series, and since then, the concept of modular construction has been used for the analysis of a large variety of structural families [4], including silicates [5,6,7,8,9,10,11,12], sulfosalts [13,14,15,16,17,18], chalcogenides [19,20,21], complex oxides [22,23,24,25,26,27], carbonates [28,29,30,31], borates [32,33] and sulfates [34,35,36,37]. Two crystal structures are usually considered to belong to the same type of modular (or polysomatic) series if they are built from similar modules that have different sizes and/or different combinations. The description of modular components is a useful tool, not only for the analysis of relations between structure types but also for the prediction of unknown structures based upon the same structural principles [4]. Theoretically, modules of the same series can be recombined in an infinite number of ways, leading to an infinite number of possible structures. In this paper, we suggest that only a few structures of the same modular kind are stable and can be observed as abundant structures in nature. In contrast to biological systems, inorganic crystal structures lack functionality and their stability and abundance are governed by thermodynamic (and sometimes kinetic) factors, including entropic restrictions. It is widely recognized that more complex structures possess lower entropies compared to their less complex counterparts. Therefore, in the non-living world of inorganic crystals, which are governed by thermodynamics, complexity is an important parameter that has strong relations to the entropy of the crystal structures. Imposing complexity restrictions upon the endless sequence of modular structures may shed light upon the abundance of particular members of a modular series and the rarity or absence of others. This aspect is of particular importance for minerals, whose origin and sustainability are generally related to large periods of geological time. In this study, we analyzed modular crystal structures of minerals relative to the complexity of their modular construction, though the methodology and the results of our analysis are applicable to synthetic inorganic structures as well.
In order to formulate quantitative restrictions upon the complexity of modular series, we suggest using methods that are based upon Shannon information theory, which have been widely applied to the studies of complexity of graphs and networks previously [38,39,40]. In fact, crystal structures can be considered as networks with atoms and chemical bonds serving as nodes and edges, respectively. The condition of periodicity that is implied by the crystalline state means that crystalline networks are three-periodic (we do not consider the superspace approach for modulated structures and quasicrystals here) and, therefore, can be characterized by the quotient graphs, which are finite graphs that are associated with the bonding networks inside reduced crystallographic unit cells [41,42]. The Shannon information content of quotient graphs reflects their complexity and can be used as a universal complexity measure for any crystal structure that can be described by its unit cell content [43]. The information-based measures of structural complexity have been recognized as useful for a variety of purposes, from formal crystal structure classifications to the studies of metastable crystallization [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. At least from the theoretical point of view, these measures are directly related to the configurational entropies of crystals [59,60], which is important in the context of the present study.
The paper is organized as follows. First, we formulate basic principles of our analysis of modular series with the procedure of the calculation of structural complexity parameters. The next three sections are devoted to the application of the formulated methodology to the mineral structures with 0-, 1- and 2-dimensional modules (herein the dimensionality of a module is defined as the number of dimensions in which the module has an infinite extension). In the sixth section, we formulate the principle of maximal simplicity for modular inorganic crystal structures that can be seen as a ‘crystallographic’ principle of least action. However, in contrast to mechanics [61], where variational principles can be formulated in the form of equations, the principle of maximal simplicity is empirical by nature, though substantiated by the quantitative metrics of structural complexity.

2. Methodology

The crystallographic analysis of modular series starts with the identification of a sequence of homologous structures that are based upon the same principles. It is remarkable that such an identification can be made without knowledge of the structural details, i.e., atom coordinates. Taking as an example the classical chondrodite series (now known as the humite series) studied by Taylor and West [3], it is noteworthy that the crystallographic relations between their members with the general formula Mg2nSinO4n•Mg(OH,F)2 were recognized before the advent of X-ray crystal structure analysis, simply from the ratios between the crystallographic axes that were revealed using goniometric measurements. In particular, Penfield and Howe [62] observed that the c/b and c/a values for the series change in progressive order depending upon the n value, whereas the b/a ratio remains almost unchanged. This observation was reconsidered by Barlow and Pope [63], but the crystal–chemical mechanisms were outlined by Taylor and West [3] only after the crystal structure of olivine was determined by Bragg and Brown [64].
The general scheme of the analysis of a modular series is given in Figure 1. After the series is identified, one has to elaborate on the structure-building principles that govern the construction of members of the series. The application of these principles provides the route to deriving all possible atomic arrangements, the number of which is usually infinite. However, it is often possible to outline the dependence of Shannon information contents of the modules or whole structures from the parameter of homology (which is equal to n for the humite series cited above, for example). Imposing some crystallographic limitations (e.g., upon the number of symmetry-independent identical modules) provides additional restrictions upon the structural diversity. Finally, the comparison of the theoretical multitude of modular structures with their occurrence and abundance in nature provides important insight into the ‘natural selection’ of atomic arrangements, which is the final purpose of our work.
The calculation of structural complexity parameters follows the methodology that was formulated previously in [43,44,65]. The two basic quantities are the amounts of structural Shannon information per atom (strIG, in bit per atom) and per unit cell (strIG,total, in bit per cell), which are calculated using the following equations:
I G str = − ∑ i = 1 k p i log 2 p i
I G , t o t a l str = − v ∑ i = 1 k p i log 2 p i
where k is the number of different crystallographic orbits (crystallographic Wyckoff sites) in the structure, and
pi = mi/v
where mi is a multiplicity of a crystallographic orbit (i.e., the number of atoms of a specific Wyckoff site in the reduced unit cell) and v is the total number of atoms in the reduced unit cell. The calculations of structural complexity parameters were done by means of the TOPOSPro software [66]. We note that the quantities that are defined by Equations (1) and (2) take into account the atoms only, without considering the complexity of the bonding networks in a crystal structure. Since, in this work, we analyze the crystal structures based upon the same modules, i.e., with the same bonding networks, but in different spatial combinations, the consideration of bonds is not of primary importance. However, in other cases, bonding networks can be taken into account by including the bond midpoints in the analysis [44] or by the identification of various degrees of freedom [57].
From the two parameters given by Equations (1) and (2), the Shannon information amount per atom (strIG) is the most sensitive to symmetry [43,55], whereas the notion of complexity implies both the symmetry and size of the system (the lower the symmetry and the larger the size, the more complex the system). In contrast, the strIG,total parameter combines (through multiplication) both symmetry (strIG) and size (v) of the unit cell and, therefore, is more appropriate for the analysis of structural complexity.

3. Structures Built from 0D Modules: The Lovozerite Family

The lovozerite family contains several minerals and inorganic compounds that can be described in terms of pseudo-cubic modules containing a six-membered silicate tetrahedral chain with a chair-like conformation (Figure 2a). The structure-building principles and complexity of the family were discussed in detail in [67,68,69,70,71]. Here we provide the basic description of the construction principles and the general structural features of the family.
The following characteristics are essential for understanding the modular nature of the family:
1. The pseudo-cubic module (Figure 2a) can be considered as a cube that is split into eight octant cubes, from which, six are populated by SiO4 tetrahedra (white cubes), whereas the other two (black cubes) located along the body diagonal of the cube are vacant (Figure 2b).
2. The analysis of structural arrangements within the known members of the family reveals the two possible modes of the modular linkages: either by sharing whole faces (Figure 2c) or by sharing half-faces (Figure 2d). In any case, black octant cubes should not share common edges or faces with each other (corner sharing is allowed).
3. The arrangement of the modules should fill space without gaps or overlaps, i.e., should form a tiling of 3D space with equal cubes.
4. Taking the requirement that all modules are symmetrically equivalent (as derived from the empirical observations), there are only seven possible next-neighbor arrangements of cubes around a central cube that fulfill the properties 2 and 3 mentioned above (we do not delve deep into technical details here, since they are provided in [70]). From them, one arrangement allows for three possible tilings each, whereas another one allows for two possible arrangements; therefore, the total number of possible tilings is equal to ten (Figure 3, Figure 4 and Figure 5). Each tiling has its symbolic notation indicated in Figure 3, Figure 4 and Figure 5 (see [70] for more details). Formally speaking, the tiling 00112 has two symmetrically independent modules; therefore, the strict number of tilings that fulfill criterion 4 is nine.
It is remarkable that the number of possible theoretical members of the modular series is finite in this case, which is a consequence of the requirement of the crystallographic equivalence of all modules. Were this requirement absent, the number of possible structures would be infinite.
Table 1 provides the space groups, approximate unit cell parameters and structural complexity values for the nine possible lovozerite-type structures. The complexity parameters were calculated by taking into account the Si and O atoms only.
The comparison of the data compiled in Table 1 with empirical observations indicates that the simplest arrangements are those that are observed more often, both in nature and in experiments. The 0000 arrangement corresponding to the minimal structural information is typical for nine out of eleven natural members of the lovozerite group [69,72] and also is most frequently observed in synthetic compounds [68]. The 1111 tiling, which is second in simplicity, is more rare and is encountered in nature in the crystal structure of imandrite (Na6Ca1.5Fe3+Si6O18 [73,74]), as well as in the number of synthetic compounds [68]. Next in simplicity is the 0101 structure type, which is unknown in minerals, but was observed for synthetic Na5(Na0.5+xCa0.5-x)2(NdxCa1-x)2(Si6O18) [75]. Among the other theoretical members of the family listed in Table 1, only the 00111b member was observed in reality as the mineral koashvite (Na6CaTiSi6O18 [76]), whereas all other members have not been found so far. Thus, out of the ten (or nine) possible modular arrangements, only four have been observed either in nature or experimentally. It is remarkable that the structure type 00111a is slightly less complex (352 bit) than the koashvite type 00111b (368 bit), which points to the possibility of its future synthesis or discovery in nature.

4. Structures Built from 1D Modules: Biopyriboles

Biopyriboles are probably the most common mineralogical example of modular structures due to the high importance of two large supergroups, namely, pyroxenes and amphiboles, as rock-forming Earth minerals. Their polysomatic features have been widely discussed and investigated (see, e.g., classical papers by Thompson [5] and Veblen [6]).
The basic structural unit of biopyriboles is a chain of corner-sharing SiO4 tetrahedra, as shown in Figure 6a. The chains of this type may have different multiplicities M: M = 1 corresponds to a single chain (observed in pyroxenes; Figure 6a), M = 2 to a double chain (characteristic for amphiboles; Figure 6b), M = 3 for a triple chain (Figure 6c), etc. The chemical formula of the chain is the function of M and can be written as [Si2MO5M+1].
In the crystal structures of biopyriboles, two silicate chains are linked to one central chain consisting of edge-sharing octahedra (Figure 6d). The resulting one-dimensional unit is identified as an I-beam [5]. For each value of M observed in nature, there are two possible basic structure types, namely, monoclinic and triclinic. In monoclinic structure types, all I-beams have the same orientation. In the structure types with orthorhombic symmetry, the I-beams are parallel, but their orientations alternate. Three basic types of biopyribole structure topologies are shown in Figure 7. In terms of the I-beam directions, the monoclinic topology (Figure 7a) can be described as …+ + + +… or (+), since all I-beams have the same orientation (‘+’ or ‘−’). There are two orthorhombic topologies, …+ − + − + −… or (+ −) and … + + − − + + − −… or (+ + − −), as shown in Figure 7b and Figure 7c, respectively.
There are four major points concerning the complexity of biopyriboles: (i) In all three basic topologies, there is only one crystallographically independent I-beam unit (in the structures with reduced symmetry, the topological symmetry does not change). (ii) The value of M in known biopyriboles never exceeds three (the observations of higher M values are known from transmission electron microscopy (TEM) studies as faulting structures [6]). (iii) Most common bipyriboles are pyroxenes and amphiboles with M = 1 and 2, respectively; minerals with M = 3 (jimthompsonite, clinojimthompsonite, chesterite) are very rare. (iv) Only one case of a structure with mixed values of M is known, which is a rare mineral chesterite containing I-beams based upon double (M = 2) and triple (M = 3) silicate chains.
Table 2 lists structural complexity parameters for several representatives of basic topological structure types of bipyriboles that possess symmetries that are identical to their topological groups. For the monoclinic (+) structure types, an increase in the M value by unity results in the increase of total complexity by ~100 bits; therefore, one may expect that a structure with M = 4 would have strIG,total ~ 350 bits. For the (+ + – –) and (+ –) structure types, an increase in M by the value of 1 corresponds to the addition of ~480 and ~200 bits to the total complexities, respectively. From the viewpoint of structural complexity, a monoclinic bipyribole with M = 4 and strIG,total ~350 bits does not seem impossible, yet it has never been observed in natural or synthetic materials accessible for X-ray diffraction studies. Furthermore, the crystal structure of jimthompsonite with M = 3 and total complexity of 255 bits is not extremely complex, yet the mineral is very rare. Its complexity and rarity can be compared with enstatite (M = 1; strIG,total ~ 266 bits), which is slightly more complex but much more common in nature. It seems that there are natural complexity limits upon the complexity of chains and not the complexity of whole structures.
It can be shown that, for multiple chains occurring in biopyriboles, the strIG,total value depends differently upon M for even and odd M values.
For odd M values:
strIG,total = (7M + 1)log2(7M + 1) − (7M + 1)
For even M values:
strIG,total = (7M + 1)log2(7M + 1) − 9M
The application of Equation (5) to M = 3 and 4 results in strIG,total values equal to ~76 and 105 bits per repeating unit, respectively. This level of information processing is therefore unfavorable for biopyribole silicate chains, and the most stable and abundant structures are those with M = 1 and 2 and the complexity of chains not exceeding ~50 bits per repeating unit.
Thus, for the biopyribole modular series, the most abundant are members with M values of 1 and 2, which correspond to the lowest levels of structural complexity.

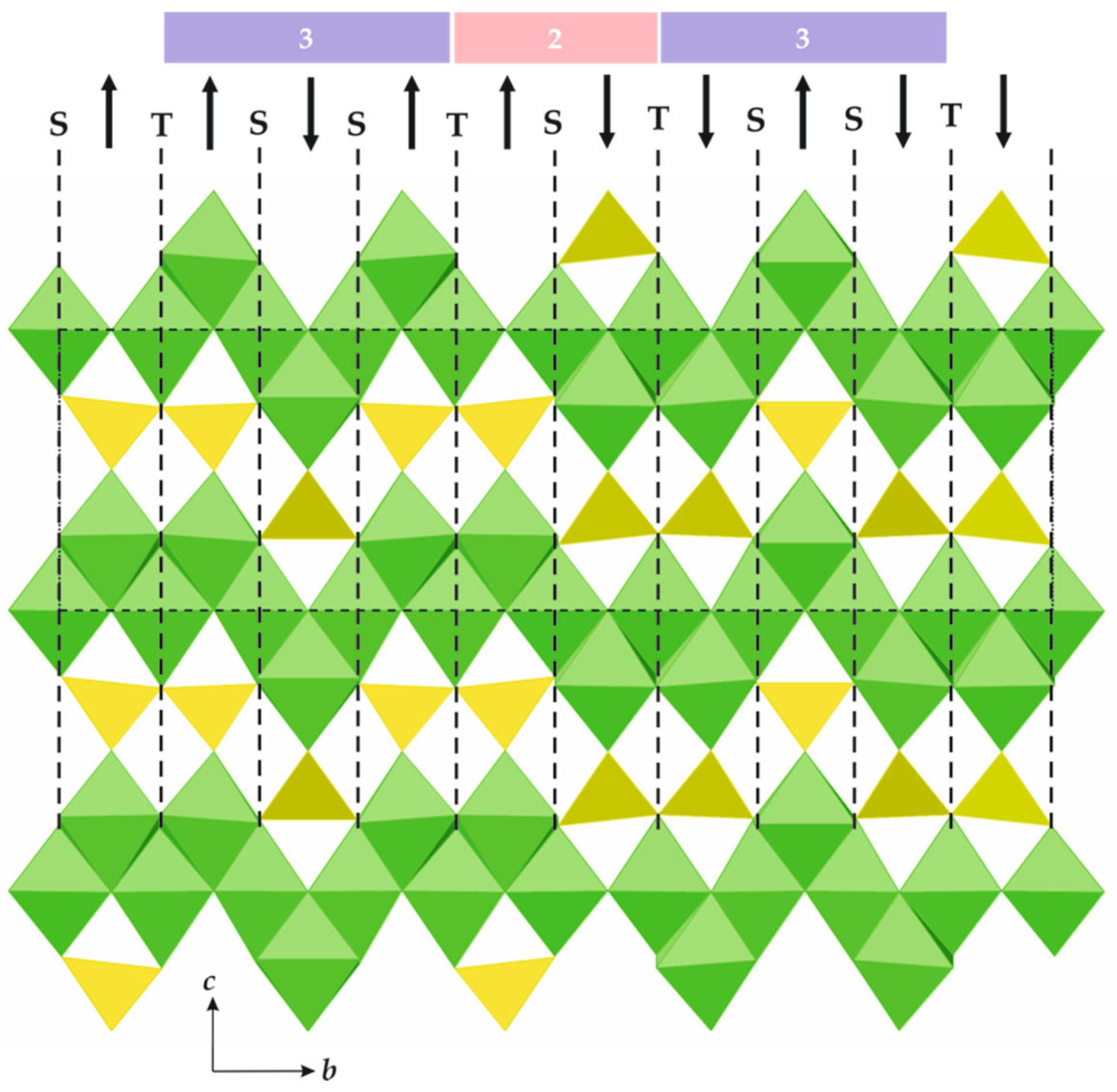
5. Structures Built from 2D Modules: Spinelloids and the Kurchatovite Family

5.1. Spinelloids

The M2SiO4 silicates (M = Mg, Fe) with spinel-related structures are believed to be important phases in the Earth’s upper mantle [77]. The formation of wadsleyite (β-(Mg,Fe)2SiO4) marks the beginning of the mantle transition zone, within which it transforms into ringwoodite (γ-(Mg,Fe)2SiO4) at 17.5 GPa (~520 km depth). Whereas ringwoodite has a spinel-type structure, wadsleyite belongs to the spinelloid family that was studied and classified by Hyde et al. [78] and Horiuchi et al. [79]. Below, we briefly outline the basic structural principles for the family and provide their complexity analysis, followed by an analysis of their abundance.
The general formula of spinelloid structures is M2TO4, where M and T are cations in octahedral and tetrahedral coordinations, respectively. The ideal crystal structure of spinel, namely, M2TO4, is based upon cubic close packing of O atoms with M and T in octahedral and tetrahedral interstices, respectively. Figure 8a shows the crystal structure of spinel projected along [110]. It can be considered as being built up with spinel modules, as shown in Figure 8b (in Figure 8a, the borders of the modules are indicated by dashed lines). In ideal spinel, the modules with ‘up’ (↑) and ‘down’ (↓) orientations alternate. The border between two modules with opposite orientations is identified as S, whereas the border between two modules with the same orientation (↑↑ or ↓↓) is identified as T. In fact, the T-plane can be considered as a local chemical twinning plane. Figure 9 shows the crystal structure of ‘wadsleyite-II’ (Mg2SiO4) that has the sequence of modules ... ↓(↑↑↓↑↑↓↓↑↓↓)↑…, where square brackets indicate the unit cell content along the direction of module stacking. Thus, the sequence of borders (or Hyde symbol) is [TSSTSTSSTS] or [TS2TS]2. The number of spinel modules in between the two T planes is given as n or m. These numbers correspond to the widths of the spinel-like blocks (inside which only S-borders are allowed) along the direction of the module stacking. For instance, in ‘wadsleyite-II’, the (n, m) numbers are (3, 2, 3, 2) or simply (3, 2). Table 3 provides the full classification of the spinelloid structures that are known today (modified after Hyde et al. [78]), including those that are observed in high-pressure mineral and synthetic phases.
The structure-building rules for spinelloids are therefore as follows: their structures are built up via the alternation of differently oriented spinel modules that can be described by the sequence of numbers corresponding to the amounts of spinel modules between the two T planes. It is obvious that there is an infinite number of theoretically possible spinelloid structures. For example, one could imagine (and rationally construct) the structure with the sequence (4, 8, 2, 3) that would correspond to the Hyde symbol [TSSSSTSSSSSSSSTSSTSSS] = [TS4TS8TS2TS3].
However, the analysis of the data that is shown in Table 3 reveals two important observations: (i) The values of n and m in observed spinelloids never exceed 3, and all possible (n, m) combinations with n ≤ 3 and m ≤ 3 have representatives in the real world. (ii) The number of the spinel blocks of different thicknesses does not exceed 2 (this is why only two numbers, n and m, are needed to characterize the sequence; sequences like (2, 1, 3) have not been observed). Why does nature restrict its structures to conform with the two restrictions indicated above? The only reasonable explanation is in the tendency to form less complex and more entropically rich structural arrangements.
Further analysis revealed that, among the spinelloids listed in Table 3, spinel itself (or ringwoodite and ahrensite) is the structurally simplest phase (19 bits), which explains its commonness and frequent occurrence in nature (the spinel group consists of 56 different mineral species [90]). Wadsleyite and its Fe analog asimowite (79 bits) are thought to be extremely important phases in the Earth’s mantle, and have been intensively investigated over the last fifty years [83,84].
However, the phase that is second (35 bits) in simplicity (ε-phase or poirierite) is less common and had only recently been described in nature as nanometer-scale lamellae in ringwoodite crystals from shocked meteorites [80]. Despite its structural simplicity, this phase is energetically unfavorable for the following reasons. The transition from the olivine structure based upon hexagonal closest packing to that of spinel (based upon cubic closest packing) requires shear mechanisms, as predicted by Hyde et al. [78] and first observed by Madon and Poirier [91]. Poirierite, which is a (1, 1) spinelloid with the module sequence [↑] (or equivalent [↓]) and the sequence of borders [T], is the first phase that forms as a result of shear transformations. This silicate phase with the formula M2(SiO3)O (M = Mg, Fe) contains one-periodic (or einer in the Liebau’s [92] notation) chains of corner-sharing SiO4 tetrahedra, which is quite atypical for silicate crystal chemistry (though it has been known for germanates [93]). The single periodicity of this chain results in the close distance between Si4+ ions in adjacent tetrahedra, which, in turn, generates strong electrostatically repulsive forces that make this arrangement energetically unstable. This example shows that structural simplicity is not the only factor that governs structural abundance in modular series. However, in the absence of structure-destabilizing factors, it achieves primary importance.
All other spinelloid structures listed in Table 3 possess more than 100 bits of structural information per reduced unit cell and have not been observed in nature, though they were prepared under experimental conditions. No other spinelloid structure types of the modular series have been observed so far.

5.2. Kurchatovite Family

Kurchatovite and clinokurchatovite are two polymorphs of CaMgB2O5 with modular crystal structures based upon two-dimensional blocks [33]. The blocks are built up from diborate B2O5 groups, and Ca2+ and Mg2+ cations in seven- and sixfold coordination, respectively (Figure 10). Detailed analysis of geometrical parameters of the adjacent blocks by Pankova et al. [33] revealed that symmetrically different diborate groups have different degrees of conformation in terms of the δ angles between the planes of two BO3 triangles sharing a common O atom, featuring two discrete sets of the δ values of ca. 55° (B’ blocks) and 34° (B” blocks). The blocks may have two different orientations, ‘+’ and ‘−’, which are related by the 180° rotation along the direction perpendicular to the block’s planes (similarly to those observed in biopyriboles). The stacking of the blocks in clinokurchatovite can be described as …(+B’)(+B”)(+B’)(+B”)… or [(+B’)(+B”)], whereas in kurchatovite, it is more complex and corresponds to the sequence …(+B’)(+B”)(+B’)(−B’)(−B”)(−B’)(+B’)(+B”)(+B’)(−B’)(−B”)(−B’)… or [(+B’)(+B”)(+B’)(−B’)(−B”)(−B’)]. The B’:B” ratios for clinokurchatovite and kurchatovite are 1:1 and 2:1, respectively.
The description of kurchatovite and clinokurchatovite in terms of the B’ and B” blocks with different orientations allowed for formulating two empirical rules that govern the modular construction of the series: (i) the B” blocks are always surrounded by the B’ blocks of the same directionality (i.e., of the same sign); (ii) the B’ blocks may occur in two combinations: either surrounded by two B” blocks of the same sign or by one B” block of the same sign and one B’ block of the opposite sign.
Pankova et al. [33] derived the following eight triplets that satisfy the (i) and (ii) conditions:
I (+B’)(+B”)(+B’)V (+B”)(+B’)(−B’)
II (−B’)(−B”)(−B’)VI (−B’)(+B’)(+B”)
III (+B”)(+B’)(+B”)VII (−B”)(−B’)(+B’)
IV (−B”)(−B’)(−B”)VIII (+B’)(−B’)(−B”)
The number of symbolic sequences that may contain these triplets is obviously infinite and the sequences may be both periodic and aperiodic. In order to produce a sequence that satisfies the rules, two triplets should overlap in two symbols: two right symbols of the first (preceding) one and two left symbols of the second (following) one. Thus, all of the triplets can be split into the following ten overlapping pairs (Figure 11a): I–III, II–IV, I–V, II–VII, III–I, IV–II, V–VIII, VI–I, VII–VI and VIII–II.
The relations between the triplets can be visualized using de Brujin diagram [94,95,96], as shown in Figure 11b. The arrow lines in the diagram indicate the only ‘legal’ sequences of triplets: any realizable symbolic sequence is produced by the loop of arrows starting and ending at the same triplet.
The possible symbolic sequences that are generated by the diagram are as follows:
1. The sequences I↔III, III↔I, II↔IV and IV↔II (Figure 11c) produce the sequence of modules corresponding to the crystal structure of clinokurchatovite. This is the simplest structure possible in this group, which contains two blocks within its identity period (e.g., [(+B’)(+B”)]).
2. Starting from triplet I and going to triplet V and so forth results in the following six-membered sequence …→VI→[I→V→VIII→II→VII→VI]→I→… (Figure 11d), which corresponds exactly to the six-membered sequence of blocks that are observed in the crystal structure of kurchatovite.
3. An infinite number of periodic and aperiodic sequences can be obtained by inserting any even subsequence from the sequences I↔III and II↔IV into the six-membered sequence of triplets given above. For instance, the sequence [I→V→VIII→II→(IV→II)→VII→VI] is produced by inserting the (IV→II) element into the sequence [I→V→VIII→II→VII→VI] after the triplet II. However, all such derivative sequences are at least two blocks longer than the sequence that produces the kurchatovite structure.
Therefore, the symbolic analysis resulted in the following conclusion: given the rules (i) and (ii), the sequences of blocks that are observed in the crystal structures of clinokurchatovite and kurchatovite contain the minimal number of blocks per identity period. All other sequences are either aperiodic or contain at least two more blocks within their identity periods.
The information-based structural complexity parameters of the two minerals are equal to 300 bits for clinokurchatovite and 1027 bits for kurchatovite. The two structures possess the minimal lengths of symbolic sequences that can be produced by means of the diagram shown in Figure 11b. All other ‘legal’ sequences will be at least two symbols longer, which will correspond to the insertion of two additional blocks into the structure, leading to arrangements that are more complex than those observed in kurchatovite and clinokurchatovite. Therefore, only the simplest possible members of the kurchatovite family (which is theoretically infinite) are observed in nature or can be synthesized under laboratory conditions.

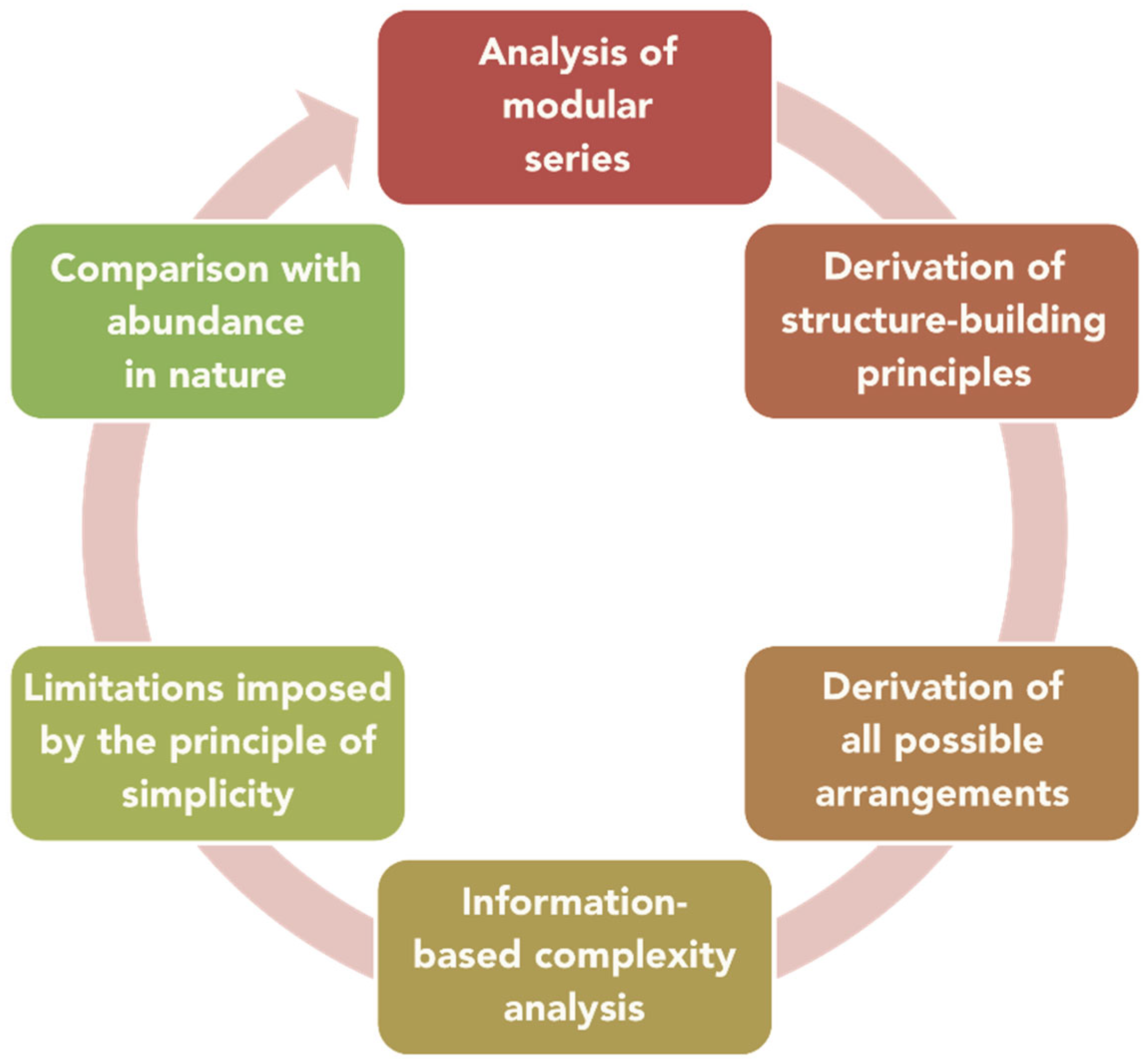
6. The Principle of Maximal Simplicity (Minimal Information)

The principle of maximal simplicity for modular inorganic crystal structures can be formulated as follows:
In a modular series of inorganic crystal structures, those that are most common and abundant in nature and experiments are those arrangements that possess maximal simplicity and minimal structural information.
This principle is empirical and is valid for those cases only where there are no structure-destabilizing factors, such as one observed for the (1, 1) spinelloid (poirierite). The influence of such factors depends upon the scale of the modules; for atomic-scale modules, it is of high importance (in fact, single atoms may hypothetically be considered as modules as well), but, for modules of larger size, the relevance of structural destabilization decreases and the principle of maximal simplicity plays the primary role.
The physical basis of the principle is in the relations between structural complexity and configurational entropy sensu stricto (which should be distinguished from the entropy of mixing). In turn, configurational entropy, in general, correlates positively with vibrational entropy, and the sum of the two kinds of entropy constitutes the major contribution to this thermodynamic quantity. Thus, the principle can be re-phrased in favor of the abundance of highly entropic and less complex structures. It can also be seen as an analogy of the principle of least action in physics that had always been considered as a principle of economy in (or of) nature, expressed by Pierre Louis Maupertuis (1748) as: ‘Nature is thrifty in all its actions’. In his Principia, Isaac Newton noted that ‘Nature does nothing in vain, and more is in vain when less will serve; for Nature is pleased with simplicity, and affects not the pomp of superfluous causes’ (1687). The principle of minimal action corresponds to the group of variational principles in physics that are usually expressed analytically through the minimization of some function (e.g., energy or distance). It is rather doubtful that the principle of maximal simplicity in modular series may have a universal analytical expression since the crystal structures are complex systems that involve a whole range of atomic species and their interactions.

7. Concluding Remarks

The principle of maximal simplicity in modular crystal structures can also be expressed in terms of information: complex structures require higher levels of information storage and processing. The complexity of inorganic crystal structures is governed by thermodynamic and kinetic factors, in contrast to living organisms, where the systems are adapted to perform a particular function. The functionality that is observed in organisms requires a much higher level of structural complexity and modularity that involve molecular structures consisting of billions of atoms. The absence of functionality in minerals defines their passive behavior relative to information, which has no material carrier but rather is stored in the chemical composition and structural and microstructural features. This is why Shannon information theory is more suitable for the description of the chemical and structural complexity of inorganic systems, where syntactic information dominates (if not completely replaces) semantic information [97]. The latter is the kind of information that is meaningful to the system, for instance, in terms of its functionality. The principle of maximal simplicity formulated here most likely has no analogs in living systems, where semantic information plays a dominant role. The important difference between the living and non-living systems is also the one between systems close to and far from thermodynamic equilibrium. It may be hypothesized that functioning in the far-from-equilibrium state requires a much high level of complexity than homeostatic existence with low dynamic activity.

Funding

This research was funded by the Russian Science Foundation (grant 19-17-00038) regarding the complexity analysis part and by the Russian Foundation for Basic Research (grant 21-011-44141) regarding the comparison of living and non-living structures part.

Acknowledgments

I am grateful to two anonymous reviewers for thoughtful and useful reviews that improved the manuscript essentially.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Schlosser, G.; Wagner, D.P. (Eds.) Modularity in Development and Evolution; University of Chicago Press: Chicago, IL, USA, 2004. [Google Scholar]
  2. Callebaut, W.; Raskin-Gutman, D. (Eds.) Modularity: Understanding the Development and Evolution of Natural Complex Systems; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
  3. Taylor, W.H.; West, J. The crystal structure of the chondrodite series. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1928, 117, 517–532. [Google Scholar] [CrossRef]
  4. Ferraris, G.; Makovicky, E.; Merlino, S. Crystallography of Modular Materials; Oxford University Press (OUP): Oxford, UK, 2008. [Google Scholar]
  5. Thompson, J.B. Biopyriboles and polysomatic series. Am. Mineral. 1978, 63, 239–249. [Google Scholar]
  6. Veblen, D.R. Polysomatism and polysomatic series: A review and applications. Am. Mineral. 1991, 76, 801–826. [Google Scholar]
  7. Merlino, S.; Zvyagin, B.B. Modular features of sapphirine-type structures. Z. Kristallogr. Cryst. Mater. 1998, 213, 513–521. [Google Scholar] [CrossRef]
  8. Zvyagin, B.B.; Merlino, S. The pyroxene-spinel polysomatic system. Z. Krist.-Cryst. Mater. 2003, 218, 210–220. [Google Scholar] [CrossRef]
  9. Ferraris, G.; Gula, A. Polysomatic aspects of microporous minerals—Heterophyllosilicates, palysepioles and rhodesite-related structures. Rev. Mineral. Geochem. 2005, 57, 69–104. [Google Scholar] [CrossRef]
  10. Ferraris, G. Modular structures—The paradigmatic case of the heterophyllosilicates. Z. Krist.-Cryst. Mater. 2008, 223, 76–84. [Google Scholar] [CrossRef]
  11. Nespolo, M.; Aroyo, M.I. The modular structure of pyroxenes. Eur. J. Miner. 2016, 28, 189–203. [Google Scholar] [CrossRef]
  12. Nespolo, M.; Bouznari, K. Modularity of crystal structures: A unifying model for the biopyribole–palysepiole series. Eur. J. Miner. 2017, 29, 369–383. [Google Scholar] [CrossRef]
  13. Makovicky, E. The building principles and classification of bismuth-lead sulphosalts and related compounds. Fortschr. Miner. 1981, 59, 137–190. [Google Scholar]
  14. Makovicky, E. The building principles and classification of sulphosalts based on the SnS archetype. Fortschr. Miner. 1985, 63, 45–89. [Google Scholar]
  15. Makovicky, E. Rod-based sulphosalt structures derived from the SnS and PbS archetypes. Eur. J. Miner. 1993, 5, 545–592. [Google Scholar] [CrossRef]
  16. Skowron, A.; Brown, I.D. Crystal chemistry and structures of lead–antimony sulfides. Acta Crystallogr. Sect. B Struct. Sci. 1994, 50, 524–538. [Google Scholar] [CrossRef]
  17. Makovicky, E. Modular crystal chemistry of sulphosalts and other complex sulphides. In Modular Aspects of Minerals; Mineralogical Society of Great Britain and Ireland: Middlesex, UK, 1997; pp. 237–271. [Google Scholar] [CrossRef]
  18. Makovicky, E. Modular Crystal Chemistry of Thallium Sulfosalts. Minerals 2018, 8, 478. [Google Scholar] [CrossRef] [Green Version]
  19. Neuhausen, C.; Rocker, F.; Tremel, W. Modular metal chalcogenide chemistry: Secondary building blocks as a basis of the silicate-type framework structure of CsLiU(PS4)2. Z. Anorg. Allg. Chem. 2012, 638, 405–410. [Google Scholar] [CrossRef]
  20. Cook, N.J.; Ciobanu, C.; Liu, W.; Slattery, A.; Wade, B.P.; Mills, S.J.; Stanley, C.J. Polytypism and Polysomatism in Mixed-Layer Chalcogenides: Characterization of PbBi4Te4S3 and Inferences for Ordered Phases in the Aleksite Series. Minerals 2019, 9, 628. [Google Scholar] [CrossRef] [Green Version]
  21. Cook, N.J.; Ciobanu, C.L.; Slattery, A.D.; Wade, B.P.; Ehrig, K. The Mixed-Layer Structures of Ikunolite, Laitakarite, Joséite-B and Joséite-A. Minerals 2021, 11, 920. [Google Scholar] [CrossRef]
  22. Hejny, C.; Armbruster, T. Polysomatism in högbomite: The crystal structures of 10T, 12H, 14T, and 24R polysomes. Am. Mineral. 2002, 87, 277–292. [Google Scholar] [CrossRef]
  23. Armbruster, T. Revised nomenclature of högbomite, nigerite, and taaffeite minerals. Eur. J. Mineral. 2002, 14, 389–395. [Google Scholar] [CrossRef] [Green Version]
  24. David, R.; Pautrat, A.; Kabbour, H.; Sturza, M.; Curelea, S.; André, G.; Pelloquin, D.; Mentré, O. BaCoO3n[BaCo8O11] modular intergrowths: Singularity of the n = 2 term. Chem. Mater. 2011, 23, 5191–5199. [Google Scholar] [CrossRef]
  25. Armbruster, T.; Lazić, B.; Reznitsky, L.Z.; Sklyarov, E.V. Kyzylkumite, Ti2V3+O5(OH): New structure type, modularity and revised formula. Miner. Mag. 2013, 77, 33–44. [Google Scholar] [CrossRef]
  26. Pakhomova, A.S.; Krivovichev, S.V.; Yudintsev, S.V.; Stefanovsky, S.V. Polysomatism and structural complexity: Structure model for murataite-8C, a complex crystalline matrix for the immobilization of high-level radioactive waste. Eur. J. Miner. 2016, 28, 205–214. [Google Scholar] [CrossRef]
  27. Kahlenberg, V.; Krüger, H.; Tribus, M. Structural systematics of SFCA-I type solid-solutions in the system CaO–Fe2O3–FeO–Al2O3. Phys. Chem. Miner. 2021, 48, 1–15. [Google Scholar] [CrossRef]
  28. Meng, D.; Wu, X.; Han, Y.; Meng, X. Polytypism and microstructures of the mixed-layer member B2S, CaCe3(CO3)4F3 in the bastnaesite-(Ce)–synchysite-(Ce) series. Earth Planet. Sci. Lett. 2002, 203, 817–828. [Google Scholar] [CrossRef]
  29. Siidra, O.; Nekrasova, D.; Depmeier, W.; Chukanov, N.; Zaitsev, A.; Turner, R. Hydrocerussite-related minerals and materials: Structural principles, chemical variations and infrared spectroscopy. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2018, 74, 182–195. [Google Scholar] [CrossRef]
  30. Capitani, G. HRTEM investigation of bastnäsite–parisite intergrowths from Mount Malosa (Malawi): Ordered sequences, polysomatic faults, polytypic disorder, and a new parisite-(Ce) polymorph. Eur. J. Mineral. 2019, 31, 429–442. [Google Scholar] [CrossRef]
  31. Capitani, G. Synchysite-(Ce) from Cinquevalli (Trento, Italy): Stacking Disorder and the Polytypism of (Ca,REE)-Fluorcarbonates. Minerals 2020, 10, 77. [Google Scholar] [CrossRef] [Green Version]
  32. Yamnova, N.A.; Zubkova, N.; Dimitrova, O.V.; Mochenova, N.N. Crystal structure of a new synthetic calcium pentaborate, Ca2[B5O8(OH)]2 · [B(OH)3] · H2O, and modular crystal chemistry of pentaborates with polar boron-oxygen layers. Crystallogr. Rep. 2009, 54, 800–813. [Google Scholar] [CrossRef]
  33. Pankova, Y.A.; Krivovichev, S.V.; Pekov, I.V.; Grew, E.S.; Yapaskurt, V.O. Kurchatovite and Clinokurchatovite, Ideally CaMgB2O5: An Example of Modular Polymorphism. Minerals 2018, 8, 332. [Google Scholar] [CrossRef] [Green Version]
  34. Galuskin, E.V.; Gfeller, F.; Armbruster, T.; Galuskina, I.O.; Vapnik, Y.; Murashko, M.; Włodyka, R.; Dzierzanowski, P. New minerals with a modular structure derived from hatrurite from the pyrometamorphic Hatrurim Complex. Part I. Nabimusaite, KCa12(SiO4)4(SO4)2O2F, from larnite rocks of Jabel Harmun, Palestinian Autonomy, Israel. Mineral. Mag. 2015, 79, 1061–1072. [Google Scholar] [CrossRef]
  35. Gorelova, L.A.; Vergasova, L.P.; Krivovichev, S.V.; Avdontseva, E.Y.; Moskaleva, S.V.; Karpov, G.A.; Filatov, S.K. Bubnovaite, K2Na8 Ca(SO4)6, a new mineral species with modular structure from the Tolbachik volcano, Kamchatka peninsula, Russia. Eur. J. Miner. 2016, 28, 677–686. [Google Scholar] [CrossRef]
  36. Galuskin, E.V.; Gfeller, F.; Galuskina, I.O.; Armbruster, T.; Krzątała, A.; Vapnik, Y.; Kusz, J.; Dulski, M.; Gardocki, M.; Gurbanov, A.G.; et al. New minerals with a modular structure derived from hatrurite from the pyrometamorphic rocks. Part III. Gazeevite, BaCa6(SiO4)2(SO4)2O, from Israel and the Palestine Autonomy, South Levant, and from South Ossetia, Greater Caucasus. Miner. Mag. 2017, 81, 499–513. [Google Scholar] [CrossRef]
  37. Galuskina, I.O.; Gfeller, F.; Galuskin, E.V.; Armbrüster, T.; Vapnik, Y.; Dulski, M.; Gardocki, M.; Jeżak, L.; Murashko, M. New minerals with modular structure derived from hatrurite from the pyrometamorphic rocks. Part IV: Dargaite, BaCa12(SiO4)4(SO4)2O3, from Nahal Darga, Palestinian Autonomy. Miner. Mag. 2018, 83, 81–88. [Google Scholar] [CrossRef]
  38. Rashevsky, N. Life, information theory, and topology. Bull. Math. Biophys. 1955, 17, 229–235. [Google Scholar] [CrossRef]
  39. Trucco, E. A note on the information content of graphs. Bull. Math. Biol. 1956, 18, 129–135. [Google Scholar] [CrossRef]
  40. Bonchev, D.; Rouvray, D.H. (Eds.) Complexity in Chemistry, Biology, and Ecology; Springer: New York, NY, USA, 2005. [Google Scholar]
  41. Chung, S.J.; Hahn, T.; Klee, W.E. Nomenclature and generation of three-periodic nets: The vector method. Acta Crystallogr. Sect. A Found. Crystallogr. 1984, 40, 42–50. [Google Scholar] [CrossRef] [Green Version]
  42. Klee, W.E. Crystallographic nets and their quotient graphs. Cryst. Res. Technol. 2004, 39, 959–968. [Google Scholar] [CrossRef]
  43. Krivovichev, S. Topological complexity of crystal structures: Quantitative approach. Acta Crystallogr. Sect. A Found. Crystallogr. 2012, 68, 393–398. [Google Scholar] [CrossRef] [PubMed]
  44. Krivovichev, S. Structural complexity of minerals: Information storage and processing in the mineral world. Miner. Mag. 2013, 77, 275–326. [Google Scholar] [CrossRef]
  45. Olds, T.A.; Plášil, J.; Kampf, A.R.; Simonetti, A.; Sadergaski, L.R.; Chen, Y.-S.; Burns, P.C. Ewingite: Earth’s most complex mineral. Geology 2017, 45, 1007–1010. [Google Scholar] [CrossRef]
  46. Krivovichev, S.V.; Hawthorne, F.C.; Williams, P.A. Structural complexity and crystallization: The Ostwald sequence of phases in the Cu2(OH)3Cl system (botallackite–atacamite–clinoatacamite). Struct. Chem. 2016, 28, 153–159. [Google Scholar] [CrossRef]
  47. Plášil, J. Mineralogy, Crystallography and Structural Complexity of Natural Uranyl Silicates. Minerals 2018, 8, 551. [Google Scholar] [CrossRef] [Green Version]
  48. Plášil, J. Structural complexity of uranophane and uranophane-β: Implications for their formation and occurrence. Eur. J. Miner. 2018, 30, 253–257. [Google Scholar] [CrossRef]
  49. Plášil, J. Uranyl-oxide hydroxy-hydrate minerals: Their structural complexity and evolution trends. Eur. J. Miner. 2018, 30, 237–251. [Google Scholar] [CrossRef]
  50. Plášil, J.; Petříček, V.; Majzlan, J. A commensurately modulated structure of parabutlerite, FeIIISO4(OH)·2H2O. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2017, 73, 856–862. [Google Scholar] [CrossRef] [PubMed]
  51. Huskić, I.; Novendra, N.; Lim, D.-W.; Topić, F.; Titi, H.M.; Pekov, I.V.; Krivovichev, S.V.; Navrotsky, A.; Kitagawa, H.; Friščić, T. Functionality in metal-organic framework minerals: Proton conductivity, stability and potential for polymorphism. Chem. Sci. 2019, 10, 4923–4929. [Google Scholar] [CrossRef] [Green Version]
  52. Gurzhiy, V.V.; Kuporev, I.V.; Kovrugin, V.M.; Murashko, M.N.; Kasatkin, A.V.; Plášil, J. Crystal Chemistry and Structural Complexity of Natural and Synthetic Uranyl Selenites. Crystals 2019, 9, 639. [Google Scholar] [CrossRef] [Green Version]
  53. Gurzhiy, V.V.; Plášil, J. Structural complexity of natural uranyl sulfates. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2019, 75, 39–48. [Google Scholar] [CrossRef] [Green Version]
  54. Majzlan, J. Processes of metastable-mineral formation in oxidation zones and mine waste. Miner. Mag. 2020, 84, 367–375. [Google Scholar] [CrossRef] [Green Version]
  55. Krivovichev, S.V.; Krivovichev, V.G. The Fedorov–Groth law revisited: Complexity analysis using mineralogical data. Acta Crystallogr. Sect. A Found. Adv. 2020, 76, 429–431. [Google Scholar] [CrossRef]
  56. Krivovichev, S.V. Feldspar polymorphs: Diversity, complexity, stability. Zap. RMO Proc. Russ. Miner. Soc. 2020, 149, 16–66. [Google Scholar] [CrossRef]
  57. Hornfeck, W. On an extension of Krivovichev’s complexity measures. Acta Crystallogr. Sect. A Found. Adv. 2020, 76, 534–548. [Google Scholar] [CrossRef] [PubMed]
  58. Zolotarev, A.A.; Krivovichev, S.V.; Cámara, F.; Bindi, L.; Zhitova, E.S.; Hawthorne, F.; Sokolova, E. Extraordinary structural complexity of ilmajokite: A multilevel hierarchical framework structure of natural origin. IUCrJ 2020, 7, 121–128. [Google Scholar] [CrossRef] [Green Version]
  59. Krivovichev, S.V. Structural complexity and configurational entropy of crystalline solids. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 274–276. [Google Scholar] [CrossRef]
  60. Kaußler, C.; Kieslich, G. crystIT: Complexity and configurational entropy of crystal structures via information theory. J. Appl. Crystallogr. 2021, 54, 306–316. [Google Scholar] [CrossRef]
  61. Gray, C.; Karl, G.; Novikov, V. The Four Variational Principles of Mechanics. Ann. Phys. 1996, 251, 1–25. [Google Scholar] [CrossRef]
  62. Penfield, S.L.; Howe, W.T.H., IV. Ueber die chemische Zusammensetzung des Chondrodits, Humits und Klinohumits. Z. Krist.-Cryst. Mater. 1894, 23, 78–98. [Google Scholar] [CrossRef]
  63. Barlow, W.; Pope, W.J. CLXVIII—A development of the atomic theory which correlates chemical and crystalline structure and leads to a demonstration of the nature of valency. J. Chem. Soc. Trans. 1906, 89, 1675–1744. [Google Scholar] [CrossRef] [Green Version]
  64. Bragg, W.L.; Brown, G.B. XXX. Die Struktur des Olivins. Z. Kristallogr. 1926, 63, 538–556. [Google Scholar] [CrossRef]
  65. Krivovichev, S.V. Which inorganic structures are the most complex? Angew. Chem. Int. Ed. 2014, 53, 654–661. [Google Scholar] [CrossRef]
  66. Blatov, V.A.; Shevchenko, A.P.; Proserpio, D.M. Applied Topological Analysis of Crystal Structures with the Program Package ToposPro. Cryst. Growth Des. 2014, 14, 3576–3586. [Google Scholar] [CrossRef]
  67. Chernitsova, N.M.; Pudovkina, Z.V.; Voronkov, A.A.; Kapustin, Y.L.; Pyatenko, Y.A. New crystal chemical family of lovozerite. Zap. Vseross. Mineral. Obshch. 1975, 104, 18–27. [Google Scholar]
  68. Malinovsky, Y.A.; Burzlaff, H.; Rothammel, W. Structures of the lovozerite type—A quantitative investigation. Acta Crystallogr. Sect. B Struct. Sci. 1993, 49, 158–164. [Google Scholar] [CrossRef]
  69. Pekov, I.V.; Krivovichev, S.V.; Zolotarev, A.; Yakovenchuk, V.N.; Armbruster, T.; Pakhomovsky, Y.A. Crystal chemistry and nomenclature of the lovozerite group. Eur. J. Miner. 2009, 21, 1061–1071. [Google Scholar] [CrossRef] [Green Version]
  70. Krivovichev, S.V. Local approach and the theory of lovozerite structures. Proc. Steklov Inst. Math. 2015, 288, 105–116. [Google Scholar] [CrossRef]
  71. Shevchenko, V.Y.; Krivovichev, S.V.; Mackay, A.L. Cellular automata and local order in the structural chemistry of the lovozerite group minerals. Glas. Phys. Chem. 2010, 36, 1–9. [Google Scholar] [CrossRef]
  72. Grey, I.E.; MacRae, C.M.; Gus Mummemmemme, W.; Pring, A. Townendite, Na8ZrSi6O18, a new uranium-bearing lovozerite group mineral from the Ilímaussaq alkaline complex, Southern Greenland. Am. Mineral. 2010, 95, 646–650. [Google Scholar] [CrossRef]
  73. Khomyakov, A.P.; Chernitsova, N.M.; Sandomirskaya, S.M.; Vasil’eva, G.L. Imandrite, a new mineral of the lovozerite family. Mineral. Zh. 1979, 1, 89–93. (In Russian) [Google Scholar]
  74. Chernitsova, N.M.; Pudovkina, Z.V.; Voronkov, A.A.; Ilyukhin, V.V.; Pyatenko, Y.A. Imandrite Na12Ca3Fe2[Si6O18]2 as a rep-resentative of a new branch in the lovozerite structural family. Dokl. Akad. Nauk SSSR 1980, 252, 618–621. [Google Scholar]
  75. Tamazyan, R.A.; Malinovskii, Y.A. Crystal structure and microtwinning of Na5(Na0.5+xCa0.5-x)2(NdxCa1-x)2(Si6O18). Kristallografiya 1989, 34, 310–315. [Google Scholar]
  76. Chernitsova, N.M.; Pudovkina, Z.A.; Voronkov, A.A.; Pyatenko, Y.A. Crystal structure of koashvite (Na6(Ca,Mn)1+0.5x(Fex3+Ti1-x)[Si6O18]. Mineral. Zh. 1980, 2, 40–44. [Google Scholar]
  77. Frost, D.J. The Upper Mantle and Transition Zone. Elements 2008, 4, 171–176. [Google Scholar] [CrossRef]
  78. Hyde, B.G.; White, T.J.; O’Keeffe, M.; Johnson, A.W.S. Structures related to those of spinel and the β-phase, and a possible mechanism for the transformation olivine—Spinel. Z. Kristallogr. 1982, 160, 53–62. [Google Scholar] [CrossRef]
  79. Horiuchi, H.; Horioka, K.; Morimoto, N. Spinelloid: A systematics of spinel-related structures obtained under high-pressure conditions. J. Miner. Soc. Jpn. 1980, 14, 253–264. [Google Scholar] [CrossRef]
  80. Tomioka, N.; Bindi, L.; Okuchi, T.; Miyahara, M.; Iitaka, T.; Li, Z.; Kawatsu, T.; Xie, X.; Purevjav, N.; Tani, R.; et al. Poirierite, a dense metastable polymorph of magnesium iron silicate in shocked meteorites. Commun. Earth Environ. 2021, 2, 1–8. [Google Scholar] [CrossRef]
  81. Ma, C.; Sahl, K.; Tillmanns, E. Nickel alumosilicate, phase I. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1975, 31, 2137–2139. [Google Scholar] [CrossRef]
  82. Ma, C.; Tillmanns, E. Nickel alumosilicate, phase II. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1975, 31, 2139–2141. [Google Scholar] [CrossRef]
  83. Moore, P.; Smith, J. Crystal structure of β-Mg2SiO4: Crystal-chemical and geophysical implications. Phys. Earth Planet. Inter. 1970, 3, 166–177. [Google Scholar] [CrossRef]
  84. Bindi, L.; Brenker, F.E.; Nestola, F.; Koch, T.E.; Prior, D.J.; Lilly, K.; Krot, A.N.; Bizzarro, M.; Xie, X. Discovery of asimowite, the Fe-analog of wadsleyite, in shock-melted silicate droplets of the Suizhou L6 and the Quebrada Chimborazo 001 CB3.0 chondrites. Am. Miner. 2019, 104, 775–778. [Google Scholar] [CrossRef]
  85. Horioka, K.; Takahashi, K.I.; Morimoto, N.; Horiuchi, H.; Akaogi, M.; Akimoto, S.I. Structure of nickel aluminosilicate (phase IV): A high-pressure phase related to spinel. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1981, 37, 635–638. [Google Scholar] [CrossRef]
  86. Smyth, J.R.; Kawamoto, T. Wadsleyite II: A new high pressure hydrous phase in the peridotite-H2O system. Earth Planet. Sci. Lett. 1997, 146, E9–E16. [Google Scholar] [CrossRef]
  87. Horioka, K.; Nishiguchi, M.; Morimoto, N.; Horiuchi, H.; Akaogi, M.; Akimoto, S.I. Structure of nickel aluminosilicate (phase V): A high-pressure phase related to spinel. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1981, 37, 638–640. [Google Scholar] [CrossRef]
  88. Sasaki, S.; Prewitt, C.T.; Sato, Y.; Ito, E. Single-crystal X-ray study of γ-Mg2SiO4. J. Geophys. Res. Solid Earth 1982, 87, 7829–7832. [Google Scholar] [CrossRef]
  89. Ma, C.; Tschauner, O.; Beckett, J.R.; Liu, Y.; Rossman, G.R.; Sinogeikin, S.V.; Smith, J.S.; Taylor, L.A. Ahrensite, γ-Fe2SiO4, a new shock-metamorphic mineral from the Tissint meteorite: Implications for the Tissint shock event on Mars. Geochim. Cosmochim. Acta 2016, 184, 240–256. [Google Scholar] [CrossRef] [Green Version]
  90. Bosi, F.; Biagioni, C.; Pasero, M. Nomenclature and classification of the spinel supergroup. Eur. J. Mineral. 2019, 31, 183–192. [Google Scholar] [CrossRef] [Green Version]
  91. Madon, M.; Poirier, J.P. Transmission electron microscope observation of α, β and γ (Mg, Fe)2SiO4 in shocked meteorites: Planar defects and polymorphic transitions. Phys. Earth Planet. Inter. 1983, 33, 31–44. [Google Scholar] [CrossRef]
  92. Liebau, F. Structural Chemistry of Silicates: Structure, Bonding, and Classification; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
  93. Pushcharovsky, D.Y. Structural Mineralogy of Silicates and Their Synthetic Analogues; Nedra: Moscow, Russia, 1986. (In Russian) [Google Scholar]
  94. Sutner, K. De Bruijn graph and linear cellular automata. Complex Syst. 1991, 5, 19–30. [Google Scholar]
  95. Krivovichev, S.V. Algorithmic crystal chemistry: A cellular automata approach. Crystallogr. Rep. 2012, 57, 10–17. [Google Scholar] [CrossRef]
  96. Shevchenko, V.; Krivovichev, S.V.; Tananaev, I.G.; Myasoedov, B.F. Cellular automata as models of inorganic structures self-assembly (Illustrated by uranyl selenate). Glas. Phys. Chem. 2013, 39, 1–10. [Google Scholar] [CrossRef]
  97. Kolchinsky, A.; Wolpert, D.H. Semantic information, autonomous agency and non-equilibrium statistical physics. Interface Focus 2018, 8, 20180041. [Google Scholar] [CrossRef]
Crystals 11 01472 g001 550
Figure 1. The complexity analysis of modular series of inorganic crystal structures.
Figure 1. The complexity analysis of modular series of inorganic crystal structures.
Crystals 11 01472 g001
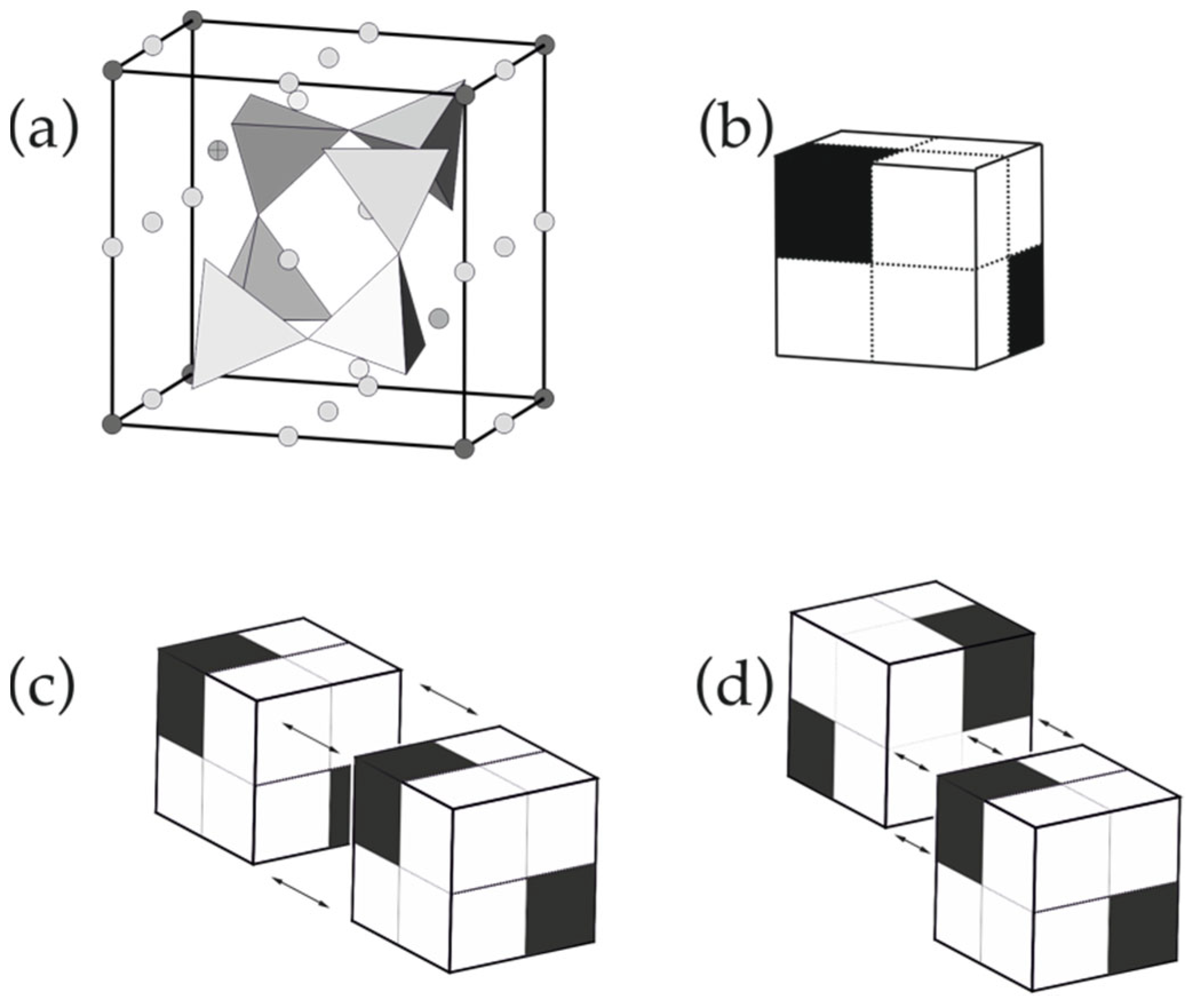
Crystals 11 01472 g002 550
Figure 2. The pseudo-cubic module in the lovozerite-type structures (a); the schematic representation of SiO4 tetrahedra is shown in polyhedral mode, whereas all other atoms are shown as spheres (b); white cubes are occupied by SiO4 tetrahedra, whereas black cubes are vacant, and the two possible models of modular linkages through a whole face (c) and a half-face (d). Modified after [70].
Figure 2. The pseudo-cubic module in the lovozerite-type structures (a); the schematic representation of SiO4 tetrahedra is shown in polyhedral mode, whereas all other atoms are shown as spheres (b); white cubes are occupied by SiO4 tetrahedra, whereas black cubes are vacant, and the two possible models of modular linkages through a whole face (c) and a half-face (d). Modified after [70].
Crystals 11 01472 g002
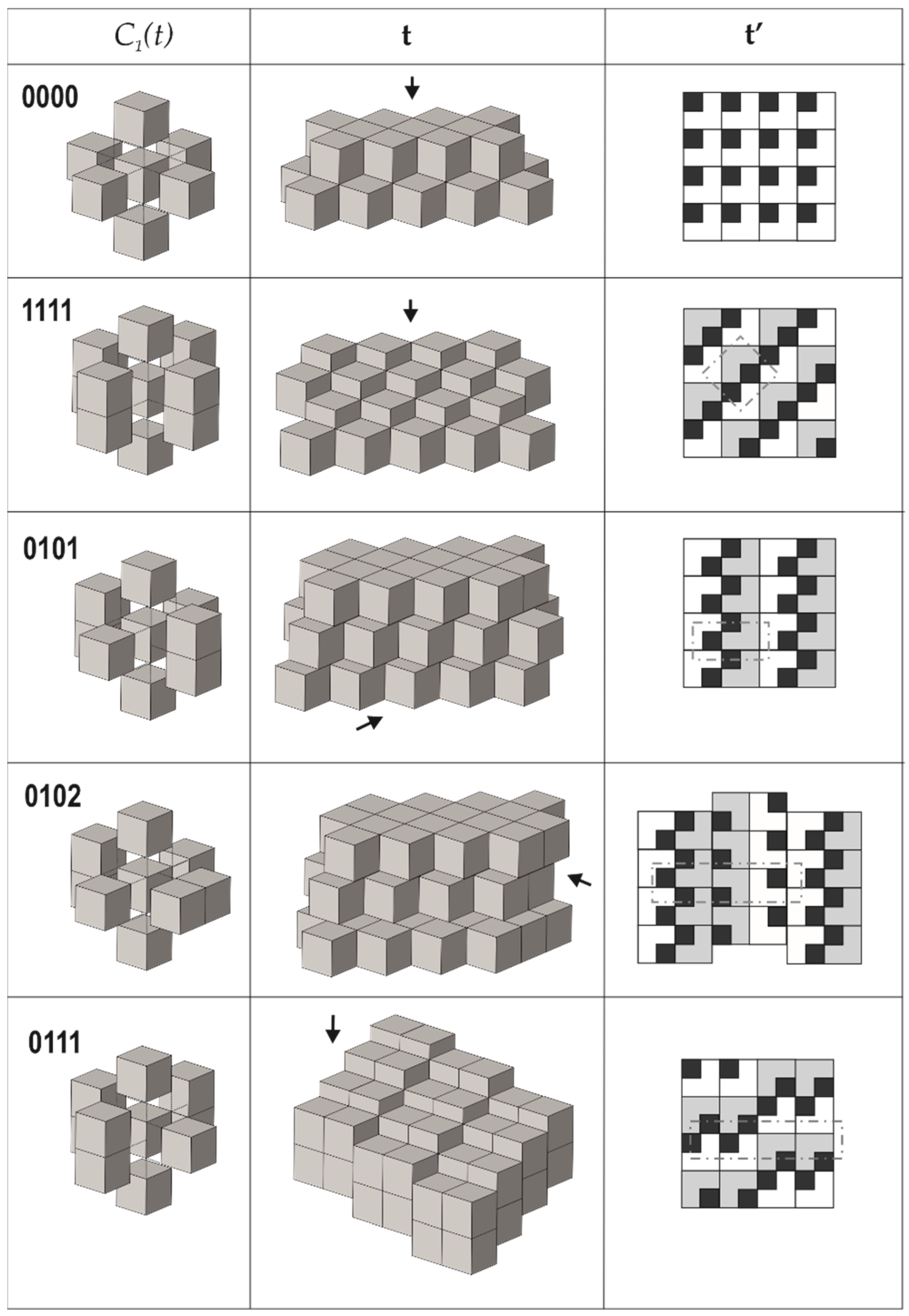
Crystals 11 01472 g003 550
Figure 3. Arrangements of the pseudo-cubic modules in lovozerite-type structures. Legend: C1(t)—the arrangement of modules around a central one; t—the general view of the tiling; t’—the view of the tiling from the direction indicated by the arrow, along with the scheme of arrangement of black cubes (the modules shown in grey are elevated relative to the white modules by 1/2a, where a is the edge length of the module); dot-and-dash lines outline the unit cell contours. Modified after [70].
Figure 3. Arrangements of the pseudo-cubic modules in lovozerite-type structures. Legend: C1(t)—the arrangement of modules around a central one; t—the general view of the tiling; t’—the view of the tiling from the direction indicated by the arrow, along with the scheme of arrangement of black cubes (the modules shown in grey are elevated relative to the white modules by 1/2a, where a is the edge length of the module); dot-and-dash lines outline the unit cell contours. Modified after [70].
Crystals 11 01472 g003
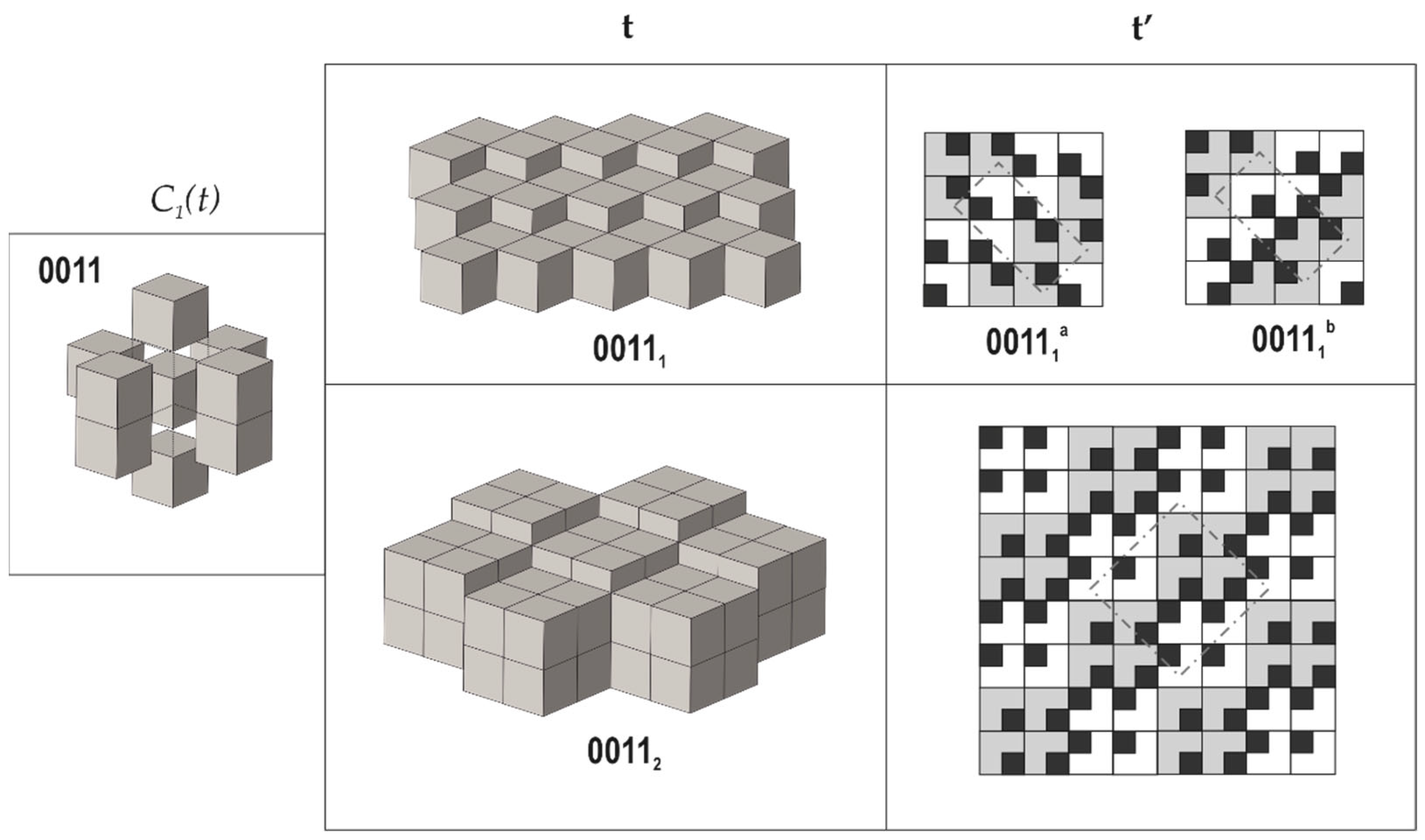
Crystals 11 01472 g004 550
Figure 4. Arrangements of the pseudo-cubic modules in lovozerite-type structures with 0011 local environment. Legend as in Figure 3. Modified after [70].
Figure 4. Arrangements of the pseudo-cubic modules in lovozerite-type structures with 0011 local environment. Legend as in Figure 3. Modified after [70].
Crystals 11 01472 g004
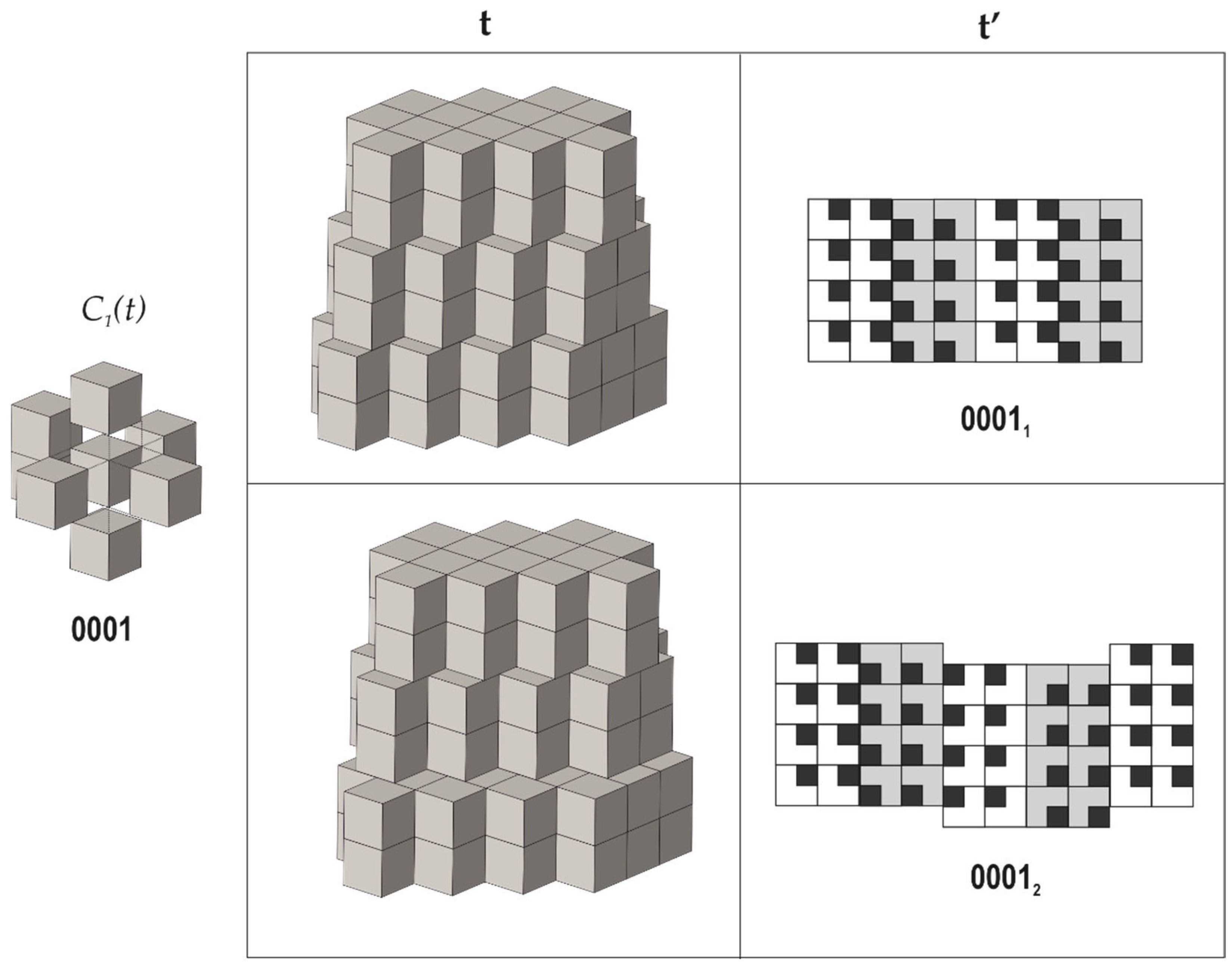
Crystals 11 01472 g005 550
Figure 5. Arrangements of the pseudo-cubic modules in lovozerite-type structures with 0001 local environment. Legend as in Figure 3. Modified after [70].
Figure 5. Arrangements of the pseudo-cubic modules in lovozerite-type structures with 0001 local environment. Legend as in Figure 3. Modified after [70].
Crystals 11 01472 g005
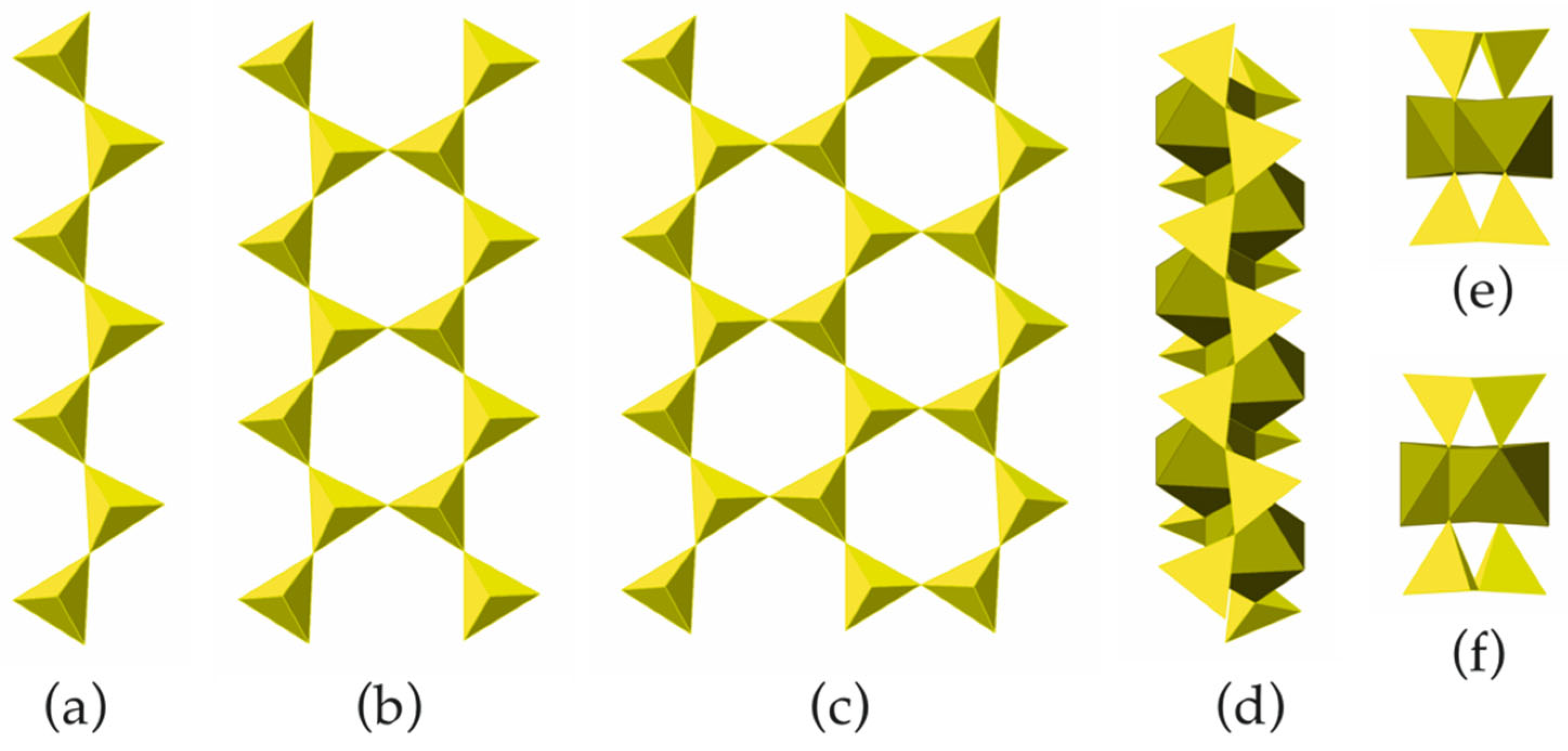
Crystals 11 01472 g006 550
Figure 6. The members of the [Si2MO5M+1] chains with M = 1 (a), 2 (b) and 3 (c); the I-beam viewed perpendicular to its extension (d) and two views of the I-beam parallel to its extension featuring two possible orientations (e,f).
Figure 6. The members of the [Si2MO5M+1] chains with M = 1 (a), 2 (b) and 3 (c); the I-beam viewed perpendicular to its extension (d) and two views of the I-beam parallel to its extension featuring two possible orientations (e,f).
Crystals 11 01472 g006
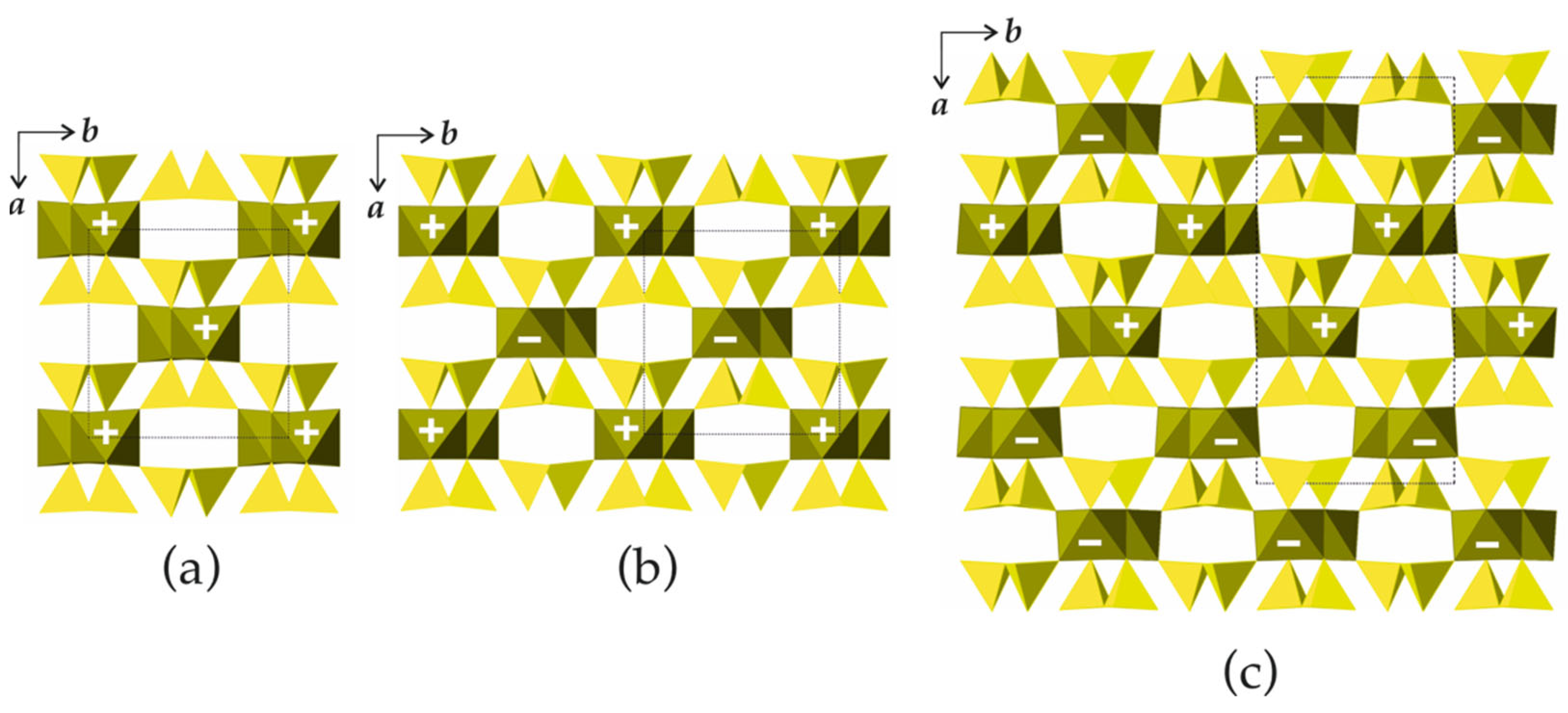
Crystals 11 01472 g007 550
Figure 7. Schematic representation of bipyribole structure types with M = 1 (pyroxenes): the (+) (a), (+ –) (b) and (+ + – –) (c) topological types. Legend: chains of octahedra are in dark-green, Si tetrahedra are in yellow.
Figure 7. Schematic representation of bipyribole structure types with M = 1 (pyroxenes): the (+) (a), (+ –) (b) and (+ + – –) (c) topological types. Legend: chains of octahedra are in dark-green, Si tetrahedra are in yellow.
Crystals 11 01472 g007
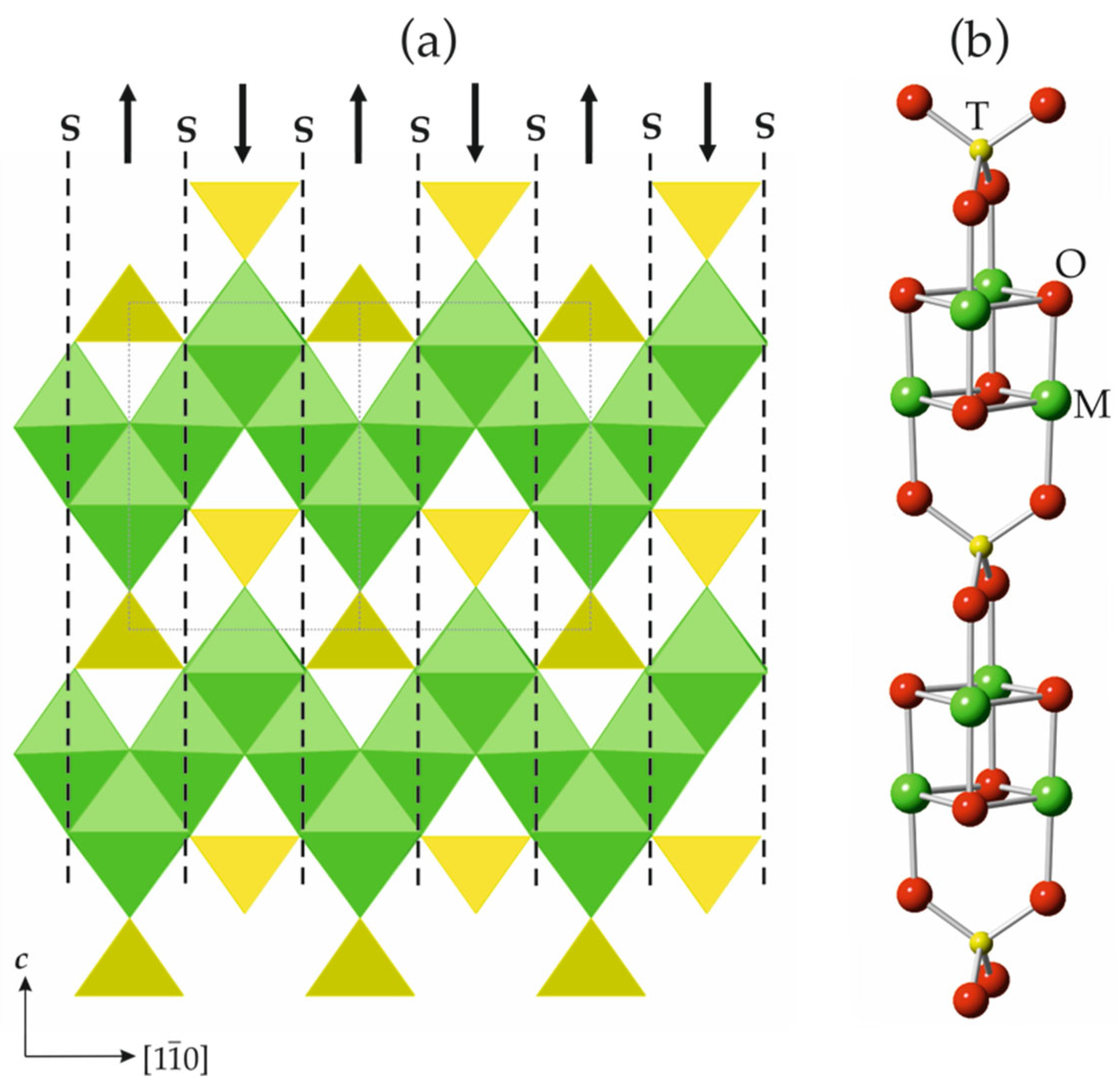
Crystals 11 01472 g008 550
Figure 8. The crystal structure of spinel projected along [110] (a) and the ball-and-stick representation of a spinel module (b). The dashed lines outline the contours of the modules, whereas the arrows indicate their orientation. The T- and M-centered polyhedra in (a) are shown in yellow and green, respectively.
Figure 8. The crystal structure of spinel projected along [110] (a) and the ball-and-stick representation of a spinel module (b). The dashed lines outline the contours of the modules, whereas the arrows indicate their orientation. The T- and M-centered polyhedra in (a) are shown in yellow and green, respectively.
Crystals 11 01472 g008
Crystals 11 01472 g009 550
Figure 9. The crystal structure of ‘wadsleyite-II’, featuring borders and orientations of spinel modules. The numbers above provide the widths of the spinel blocks in terms of the numbers of modules between the two T-planes.
Figure 9. The crystal structure of ‘wadsleyite-II’, featuring borders and orientations of spinel modules. The numbers above provide the widths of the spinel blocks in terms of the numbers of modules between the two T-planes.
Crystals 11 01472 g009
Crystals 11 01472 g010 550
Figure 10. The slices of the crystal structures of clinokurchatovite (a,b) and kurchatovite (c,d), which consist of diborate groups. The dot-and-dash lines in (a) and (c) indicate the relative positions of the B’ and B” of different orientations (distinguished by the ‘+’ and ‘−’ signs). After [33].
Figure 10. The slices of the crystal structures of clinokurchatovite (a,b) and kurchatovite (c,d), which consist of diborate groups. The dot-and-dash lines in (a) and (c) indicate the relative positions of the B’ and B” of different orientations (distinguished by the ‘+’ and ‘−’ signs). After [33].
Crystals 11 01472 g010
Crystals 11 01472 g011 550
Figure 11. An illustration of the rule of overlapping triplets using the example of the I–V pair (a), the diagram of relations between the triplets (b) and the parts of the diagram that result in the generation of clinokurchatovite (c) and kurchatovite (d) structures. See the text for details. After [33].
Figure 11. An illustration of the rule of overlapping triplets using the example of the I–V pair (a), the diagram of relations between the triplets (b) and the parts of the diagram that result in the generation of clinokurchatovite (c) and kurchatovite (d) structures. See the text for details. After [33].
Crystals 11 01472 g011
Table
Table 1. Space groups, unit cell parameters and structural complexity values (in bits/cell) for the ten possible lovozerite-type structures.
Table 1. Space groups, unit cell parameters and structural complexity values (in bits/cell) for the ten possible lovozerite-type structures.
TypeSpace GroupUnit Cell 1strIG,total (Si + O)
0000R 3 ¯ ma × a × a48
1111Pmnn21/2a × 21/2a × a140
0101P21/ca × a × 2a; β = 90o172
0102P41a × a × 4a440
0111B21/a2a × a × 2a; β = 90o440
00111aPbnn21/2a × 23/2a × a352
00111bPmnb21/2a × 23/2a × a368
00112Pnmn23/2a × 23/2a × a912 2
00011P21/ca × a × 4a; β = 90o440
00012P4122a × a × 8a1072
1 a—edge length of a pseudo-cubic module. 2 This arrangement has two symmetry-independent modules.
Table
Table 2. Total structural complexities for basic biopyribole structure types.
Table 2. Total structural complexities for basic biopyribole structure types.
MSpace GroupMineral NameChemical FormulastrIG,total
Monoclinic structure types with the (+) sequence
1C2/cDiopsideCaMg(Si2O6)50
2C2/mTremoliteCa2Mg5(Si4O11)2(OH)2152
3C2/cClinojimthompsoniteMg5(Si6O16)(OH)2255
Orthorhombic structure types with the (+ + – –) sequence
1PbcaEnstatiteMg2(Si2O6)266
2PnmaAnthophylliteMg7(Si4O11)2(OH)2743
3PbcaJimthompsoniteMg5(Si6O16)(OH)21229
Orthorhombic structure types with the (+ –) sequence
1PbcnProtoenstatiteMg2(Si2O6)101
2PnnmProtoanthophylliteMg7(Si8O22)(OH)2317
Structure types with mixed M values
2, 3Cmc21ChesteriteMg17(Si4O11)2(Si6O16)2(OH)61185
Table
Table 3. Total structural complexities for basic spinelloid structure types.
Table 3. Total structural complexities for basic spinelloid structure types.
PhaseOSHSn, mSpace GroupstrIG,total (bits/Cell)ExampleRef.
ε(↑)[T](1, 1)Pmma35ε-Mg2SiO4 poirierite[80]
I(↑↑↑↓)[T2S2](3, 1)Pmma213(Ni10.3Al7.7)(Al3.6Si2.4)O32[81]
II(↑↑↑↓↓↓)[T2S]2(2, 1)Imma141(Ni17Al7)(Al6.9Si5.1)O48[82]
III(↑↑↓↓)[TS]2(2, 2)Imma79β-Mg2SiO4 wadsleyite[83]
(2, 2)Imma79β-Fe2SiO4 asimowite[84]
IV(↑↑↓↑↑↓↓↑↓↓)[TS2TS]2(3, 2)Imma279Ni3Al2SiO8[85]
Imma279Mg2SiO4 ‘wadsleyite II’[86]
V(↑↑↓)[TS2](3, 3)Pmma144Ni3Al2SiO8[87]
Spinel(↑↓)[S]-Fd 3 ¯ m19γ-Mg2SiO4 ringwoodite[88]
-Fd 3 ¯ m19γ-Fe2SiO4 ahrensite[89]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Krivovichev, S.V. The Principle of Maximal Simplicity for Modular Inorganic Crystal Structures. Crystals 2021, 11, 1472. https://doi.org/10.3390/cryst11121472

AMA Style

Krivovichev SV. The Principle of Maximal Simplicity for Modular Inorganic Crystal Structures. Crystals. 2021; 11(12):1472. https://doi.org/10.3390/cryst11121472

Chicago/Turabian Style

Krivovichev, Sergey V. 2021. "The Principle of Maximal Simplicity for Modular Inorganic Crystal Structures" Crystals 11, no. 12: 1472. https://doi.org/10.3390/cryst11121472

APA Style

Krivovichev, S. V. (2021). The Principle of Maximal Simplicity for Modular Inorganic Crystal Structures. Crystals, 11(12), 1472. https://doi.org/10.3390/cryst11121472

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop