Tuning Charge Order in (TMTTF)2X by Partial Anion Substitution
Abstract
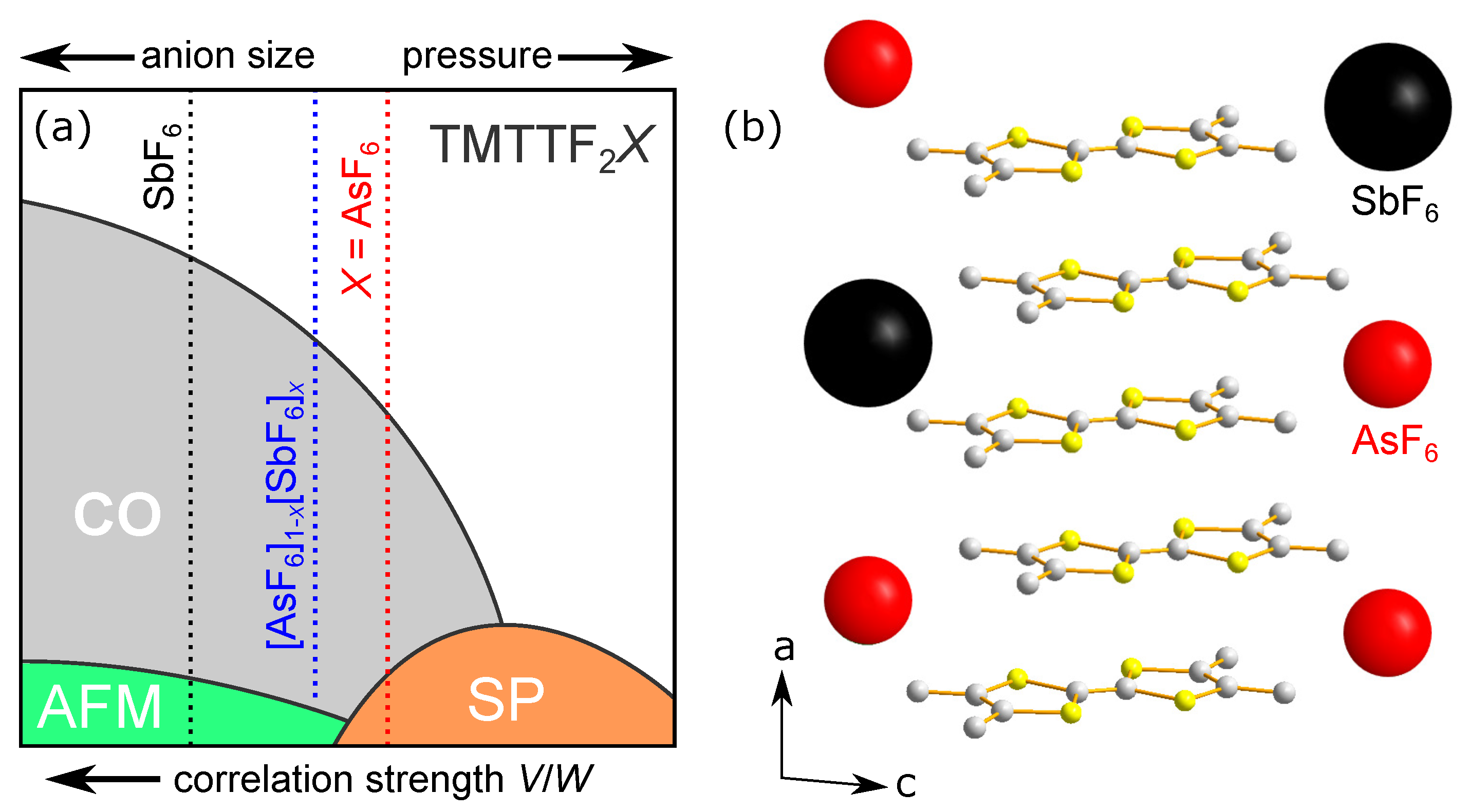
:1. Introduction
2. Materials and Experiments
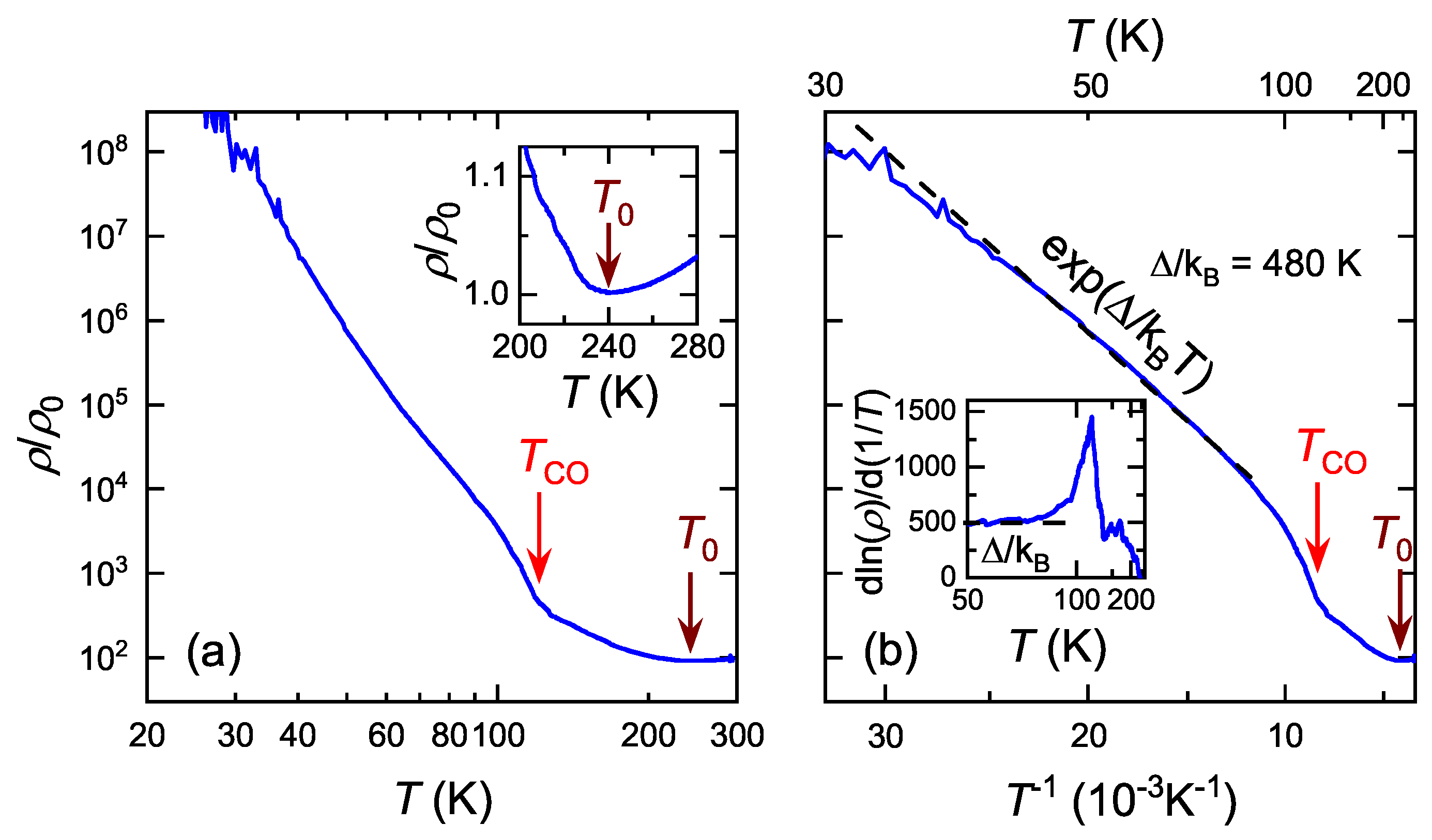
3. Results and Analysis
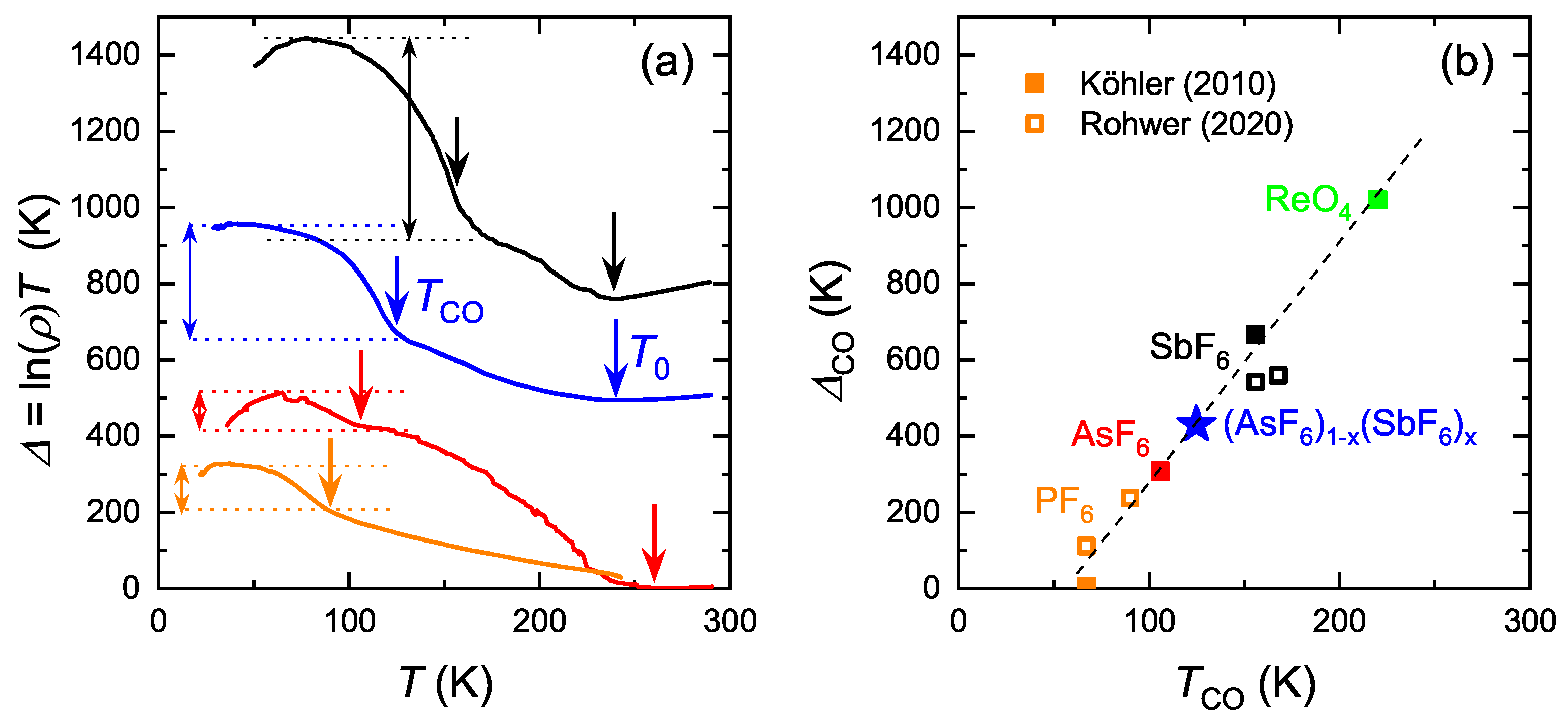
3.1. Universal Relation between Charge Gap and Transition Temperature
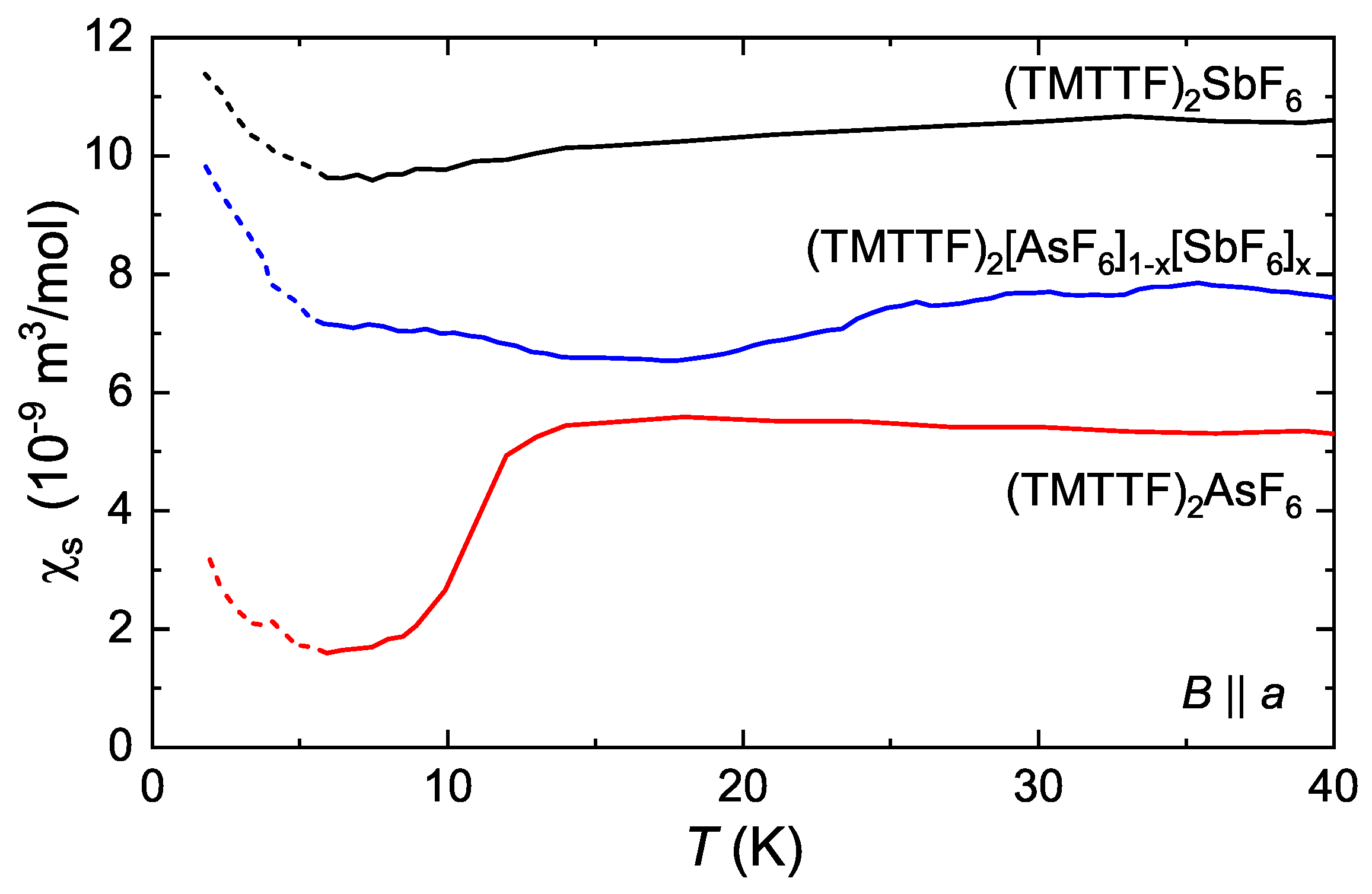
3.2. Charge Disproportionation Determined by Vibrational Spectroscopy
4. Discussion and Outlook
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dressel, M.; Dumm, M.; Knoblauch, T.; Masino, M. Comprehensive Optical Investigations of Charge Order in Organic Chain Compounds (TMTTF)2X. Crystals 2012, 2, 528–578. [Google Scholar] [CrossRef] [Green Version]
- Fukuyama, H. Physics of Molecular Conductors. J. Phys. Soc. Jpn. 2006, 75, 51001. [Google Scholar] [CrossRef]
- Seo, H.; Merino, J.; Yoshioka, H.; Ogata, M. Theoretical Aspects of Charge Ordering in Molecular Conductors. J. Phys. Soc. Jpn. 2006, 75, 51009. [Google Scholar] [CrossRef] [Green Version]
- Chow, D.S.; Zamborszky, F.; Alavi, B.; Tantillo, D.J.; Baur, A.; Merlic, C.A.; Brown, S.E. Charge Ordering in the TMTTF Family of Molecular Conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar] [CrossRef] [Green Version]
- Zamborszky, F.; Yu, W.; Raas, W.; Brown, S.E.; Alavi, B.; Merlic, C.A.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 81103. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Zhang, F.; Zamborszky, F.; Alavi, B.; Baur, A.; Merlic, C.A.; Brown, S.E. Electron-lattice coupling and broken symmetries of the molecular salt (TMTTF)2SbF6. Phys. Rev. B 2004, 70, 121101. [Google Scholar] [CrossRef] [Green Version]
- Dumm, M.; Salameh, B.; Abaker, M.; Montgomery, L.K.; Dressel, M. Magnetic and optical studies of spin and charge ordering in (TMTTF)2AsF6. J. Phys. IV 2004, 114, 57–60. [Google Scholar] [CrossRef] [Green Version]
- Dumm, M.; Abaker, M.; Dressel, M. Mid-infrared response of charge-ordered quasi-1D organic conductors (TMTTF)2X. J. Phys. IV 2005, 131, 55–58. [Google Scholar] [CrossRef]
- Dumm, M.; Abaker, M.; Dressel, M.; Montgomery, L.K. Charge Order in (TMTTF)2PF6 Investigated by Infrared Spectroscopy. J. Low Temp. Phys. 2006, 142, 613–616. [Google Scholar] [CrossRef]
- Pashkin, A.; Dressel, M.; Ebbinghaus, S.; Hanfland, M.; Kuntscher, C. Pressure-induced structural phase transition in the Bechgaard-Fabre salts. Synth. Met. 2009, 159, 2097–2100. [Google Scholar] [CrossRef]
- Pashkin, A.; Dressel, M.; Hanfland, M.; Kuntscher, C.A. Deconfinement transition and dimensional crossover in the Bechgaard-Fabre salts: Pressure- and temperature-dependent optical investigations. Phys. Rev. B 2010, 81, 125109. [Google Scholar] [CrossRef] [Green Version]
- Knoblauch, T.; Dressel, M. Charge disproportionation in (TMTTF)2X (X = PF6, AsF6 and SbF6) investigated by infrared spectroscopy. Phys. Status Solidi C 2012, 9, 1158–1160. [Google Scholar] [CrossRef]
- Oka, Y.; Matsunaga, N.; Nomura, K.; Kawamoto, A.; Yamamoto, K.; Yakushi, K. Charge Order in (TMTTF)2TaF6 by Infrared Spectroscopy. J. Phys. Soc. Jpn. 2015, 84, 114709. [Google Scholar] [CrossRef]
- Pustogow, A.; Peterseim, T.; Kolatschek, S.; Engel, L.; Dressel, M. Electronic correlations versus lattice interactions: Interplay of charge and anion orders in (TMTTF)2X. Phys.Rev. B 2016, 94, 195125. [Google Scholar] [CrossRef]
- Rösslhuber, R.; Rose, E.; Ivek, T.; Pustogow, A.; Breier, T.; Geiger, M.; Schrem, K.; Untereiner, G.; Dressel, M. Structural and Electronic Properties of (TMTTF)2X Salts with Tetrahedral Anions. Crystals 2018, 8, 121. [Google Scholar] [CrossRef] [Green Version]
- Parkin, S.S.P.; Coulon, C.; Jérome, D.; Fabre, J.M.; Giral, L. Substitution of TMTSeF with TMTTF in (TMTSeF)2ClO4: High pressure studies. J. Phys. France 1983, 44, 603–607. [Google Scholar] [CrossRef] [Green Version]
- Ilakovac, V.; Ravy, S.; Pouget, J.P.; Lenoir, C.; Boubekeur, K.; Batail, P.; Babic, S.D.; Biskup, N.; Korin-Hamzic, B.; Tomic, S.; et al. Enhanced charge localization in the organic alloys [(TMTSF)1−x(TMTTF)x]2ReO4. Phys. Rev. B 1994, 50, 7136–7139. [Google Scholar] [CrossRef]
- Tomic, S.; Auban-Senzier, P.; Jérome, D. Charge localization in [(TMTTF)0.5(TMTSF)0.5]2ReO4: A pressure study. Synth. Met. 1999, 103, 2197–2198. [Google Scholar] [CrossRef]
- Naito, T.; Miyamoto, A.; Kobayashi, H.; Kato, R.; Kobayashi1, A. Superconducting Transition Temperature of the Organic Alloy System. κ-[(BEDT-TTF)1−x(BEDT-STF)x]2Cu[N(CN)2]Br. Chem. Lett. 1992, 21, 119–122. [Google Scholar] [CrossRef]
- Kawamoto, A.; Taniguchi, H.; Kanoda, K. Superconductor-Insulator Transition Controlled by Partial Deuteration in BEDT-TTF Salt. J. Am. Chem. Soc. 1998, 120, 10984–10985. [Google Scholar] [CrossRef]
- Sasaki, J.; Kawamoto, A.; Kumagai, K.I. Magnetic Properties of the alloy of κ-(BEDT-TTF)2(1−X)(BEDSe-TTF)2XCu[N(CN)2]Br. Synth. Met. 2003, 137, 1249–1250. [Google Scholar] [CrossRef]
- Sushko, Y.V.; Leontsev, S.O.; Korneta, O.B.; Kawamoto, A. SQUID-magnetometry study of the P-T phase diagram of κ-[(BEDT-TTF)1−x(BEDSe-TTF)x]2Cu[N(CN)2]Br. J. Low Temp. Phys. 2006, 142, 563–566. [Google Scholar] [CrossRef]
- Kobayashi, T.; Ihara, Y.; Kawamoto, A. Modification of local electronic state by BEDT-STF doping to κ-(BEDT-TTF)2Cu[N(CN)2]Br salt studied by 13C NMR spectroscopy. Phys. Rev. B 2016, 93, 94515. [Google Scholar] [CrossRef]
- Saito, Y.; Minamidate, T.; Kawamoto, A.; Matsunaga, N.; Nomura, K. Site-specific 13C NMR study on the locally distorted triangular lattice of the organic conductor κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2018, 98, 205141. [Google Scholar] [CrossRef] [Green Version]
- Yesil, E.; Imajo, S.; Nomoto, T.; Yamashita, S.; Akutsu, H.; Nakazawa, Y. Variation of Electronic Heat Capacity of κ-(BEDT-TTF)2Cu[N(CN)2]Br Induced by Partial Substitution of Donor Layers. J. Phys. Soc. Jpn. 2020, 89, 73701. [Google Scholar] [CrossRef]
- Pustogow, A.; Saito, Y.; Löhle, A.; Sanz Alonso, M.; Kawamoto, A.; Dobrosavljević, V.; Dressel, M.; Fratini, S. Rise and fall of Landau’s quasiparticles while approaching the Mott transition. Nat. Commun. 2021, 12, 1571. [Google Scholar] [CrossRef]
- Pustogow, A.; Rösslhuber, R.; Tan, Y.; Uykur, E.; Böhme, A.; Wenzel, M.; Saito, Y.; Löhle, A.; Hübner, R.; Kawamoto, A.; et al. Low-temperature dielectric anomaly arising from electronic phase separation at the Mott insulator-metal transition. NPJ Quantum Mater. 2021, 6, 9. [Google Scholar] [CrossRef]
- Saito, Y.; Rösslhuber, R.; Löhle, A.; Sanz Alonso, M.; Wenzel, M.; Kawamoto, A.; Pustogow, A.; Dressel, M. Chemical tuning of molecular quantum materials κ-[(BEDT-TTF)1−x(BEDT-STF)x]2Cu2(CN)3: From the Mott-insulating quantum spin liquid to metallic Fermi liquid. J. Mater. Chem. C 2021, 9, 10841–10850. [Google Scholar] [CrossRef]
- Saito, Y.; Löhle, A.; Kawamoto, A.; Pustogow, A.; Dressel, M. Pressure-Tuned Superconducting Dome in Chemically-Substituted κ-(BEDT-TTF)2Cu2(CN)3. Crystals 2021, 11, 817. [Google Scholar] [CrossRef]
- Joo, N.; Auban-Senzier, P.; Pasquier, C.R.; Jérome, D.; Bechgaard, K. Impurity-controlled superconductivity/spin density wave interplay in the organic superconductor: (TMTSF)2ClO4. EPL 2005, 72, 645–651. [Google Scholar] [CrossRef]
- Faltermeier, D.; Barz, J.; Dumm, M.; Dressel, M.; Drichko, N.; Petrov, B.; Semkin, V.; Vlasova, R.; Meźière, C.; Batail, P. Bandwidth-controlled Mott transition in κ-(BEDT-TTF)2Cu[N(CN)2]BrxCl1−x: Optical studies o. Phys. Rev. B 2007, 76, 165113. [Google Scholar] [CrossRef] [Green Version]
- Dumm, M.; Faltermeier, D.; Drichko, N.; Dressel, M.; Mézière, C.; Batail, P. Bandwidth-controlled Mott transition in κ-(BEDT-TTF)2Cu[N(CN)2]BrxCl1−x: Optical studies of correlated carriers. Phys. Rev. B 2009, 79, 195106. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, Y.; Maesato, M.; Tomeno, S.; Kimura, Y.; Saito, G.; Nakamura, Y.; Kishida, H.; Kitagawa, H. Partial Substitution of Ag(I) for Cu(I) in Quantum Spin Liquid κ-(ET)2Cu2(CN)3, Where ET Is Bis(ethylenedithio)tetrathiafulvalene. Inorg. Chem. 2019, 58, 4820–4827. [Google Scholar] [CrossRef]
- Kitou, S.; Zhang, L.; Nakamura, T.; Sawa, H. Complex changes in structural parameters hidden in the universal phase diagram of the quasi-one-dimensional organic conductors (TMTTF)2X (X = NbF6, AsF6, PF6, and Br). Phys. Rev. B 2021, 103, 184112. [Google Scholar] [CrossRef]
- Yu, W.; Zamborszky, F.; Alavi, B.; Baur, A.; Merlic, C.A.; Brown, S.E. Influence of charge order on the ground states of TMTTF molecular salts. J. Phys. IV France 2004, 114, 35–40. [Google Scholar] [CrossRef] [Green Version]
- Voloshenko, I.; Herter, M.; Beyer, R.; Pustogow, A.; Dressel, M. Pressure-dependent optical investigations of Fabre salts in the charge-ordered state. J. Phys. Condens. Matter 2017, 29, 115601. [Google Scholar] [CrossRef]
- Köhler, B.; Rose, E.; Dumm, M.; Untereiner, G.; Dressel, M. Comprehensive transport study of anisotropy and ordering phenomena in quasi-one-dimensional (TMTTF)2X salts (X = PF6, AsF6, SbF6, BF4, ClO4, ReO4). Phys. Rev. B 2011, 84, 035124. [Google Scholar] [CrossRef] [Green Version]
- Meneghetti, M.; Bozio, R.; Zanon, I.; Pecile, C.; Ricotta, C.; Zanetti, M. Vibrational behavior of molecular constituents of organic superconductors: TMTSF, its radical cation and the sulphur analogs TMTTF and TMTTF+. J. Chem. Phys. 1984, 80, 6210. [Google Scholar] [CrossRef]
- Rohwer, A.; Dressel, M.; Nakamura, T. Deuteration Effects on the Transport Properties of (TMTTF)2X Salts. Crystals 2020, 10, 1085. [Google Scholar] [CrossRef]
- Merino, J.; McKenzie, R.H. Superconductivity Mediated by Charge Fluctuations in Layered Molecular Crystals. Phys. Rev. Lett. 2001, 87, 237002. [Google Scholar] [CrossRef] [Green Version]
- Drichko, N.; Dressel, M.; Kuntscher, C.; Pashkin, A.; Greco, A.; Merino, J.; Schlueter, J. Electronic properties of correlated metals in the vicinity of a charge-order transition: Optical spectroscopy of α-(BEDT-TTF)2MHg(SCN)4 (M = NH4, Rb, Tl). Phys. Rev. B 2006, 74, 235121. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, S.; Dressel, M.; Sun, Y.; Greco, A.; Schlueter, J.A.; Gard, G.L.; Drichko, N. Bandwidth Tuning Triggers Interplay of Charge Order and Superconductivity in Two-Dimensional Organic Materials. Phys. Rev. Lett. 2010, 105, 206402. [Google Scholar] [CrossRef] [Green Version]
- Pustogow, A.; Saito, Y.; Rohwer, A.; Schlueter, J.A.; Dressel, M. Coexistence of charge order and superconductivity in β′′-(BEDT-TTF)2SF5CH2CF2SO3. Phys. Rev. B 2019, 99, 140509. [Google Scholar] [CrossRef] [Green Version]
- Imajo, S.; Akutsu, H.; Akutsu-Sato, A.; Morritt, A.L.; Martin, L.; Nakazawa, Y. Effects of electron correlations and chemical pressures on superconductivity of β′′-type organic compounds. Phys. Rev. Res. 2019, 1, 33184. [Google Scholar] [CrossRef] [Green Version]
- Imajo, S.; Akutsu, H.; Kurihara, R.; Yajima, T.; Kohama, Y.; Tokunaga, M.; Kindo, K.; Nakazawa, Y. Anisotropic Fully Gapped Superconductivity Possibly Mediated by Charge Fluctuations in a Nondimeric Organic Complex. Phys. Rev. Lett. 2020, 125, 177002. [Google Scholar] [CrossRef]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pustogow, A.; Dizdarevic, D.; Erfort, S.; Iakutkina, O.; Merkl, V.; Untereiner, G.; Dressel, M. Tuning Charge Order in (TMTTF)2X by Partial Anion Substitution. Crystals 2021, 11, 1545. https://doi.org/10.3390/cryst11121545
Pustogow A, Dizdarevic D, Erfort S, Iakutkina O, Merkl V, Untereiner G, Dressel M. Tuning Charge Order in (TMTTF)2X by Partial Anion Substitution. Crystals. 2021; 11(12):1545. https://doi.org/10.3390/cryst11121545
Chicago/Turabian StylePustogow, Andrej, Daniel Dizdarevic, Sebastian Erfort, Olga Iakutkina, Valentino Merkl, Gabriele Untereiner, and Martin Dressel. 2021. "Tuning Charge Order in (TMTTF)2X by Partial Anion Substitution" Crystals 11, no. 12: 1545. https://doi.org/10.3390/cryst11121545
APA StylePustogow, A., Dizdarevic, D., Erfort, S., Iakutkina, O., Merkl, V., Untereiner, G., & Dressel, M. (2021). Tuning Charge Order in (TMTTF)2X by Partial Anion Substitution. Crystals, 11(12), 1545. https://doi.org/10.3390/cryst11121545







