Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C
Abstract
:1. Introduction
2. Materials and Methods
2.1. Investigated Specimens
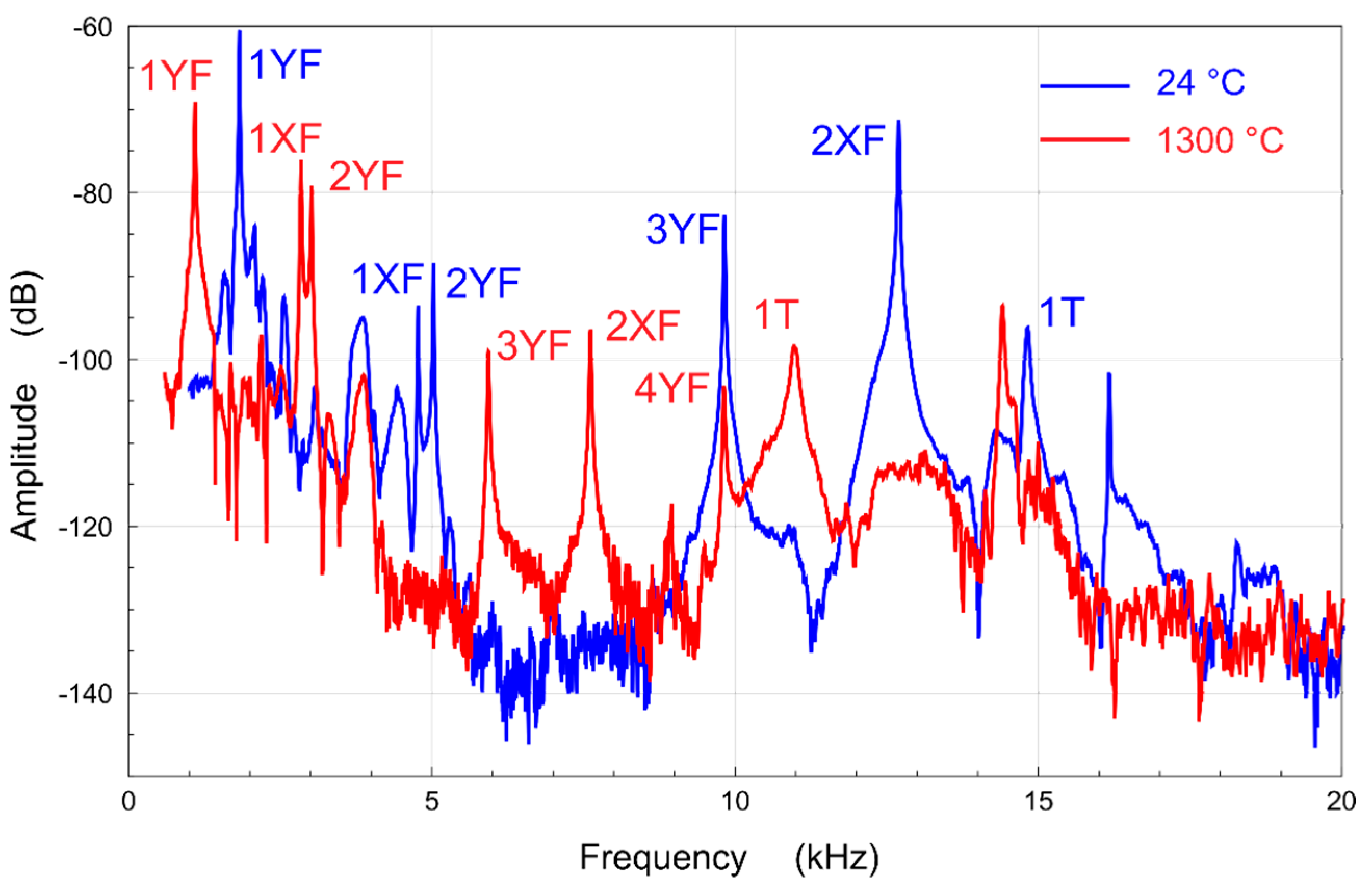
2.2. Measurement of Elastic Constants
2.3. Measurement of Material Density and Thermal Expansion
2.4. Measurement of the Temperature Dependence of γ′-Volume Fraction
3. Results
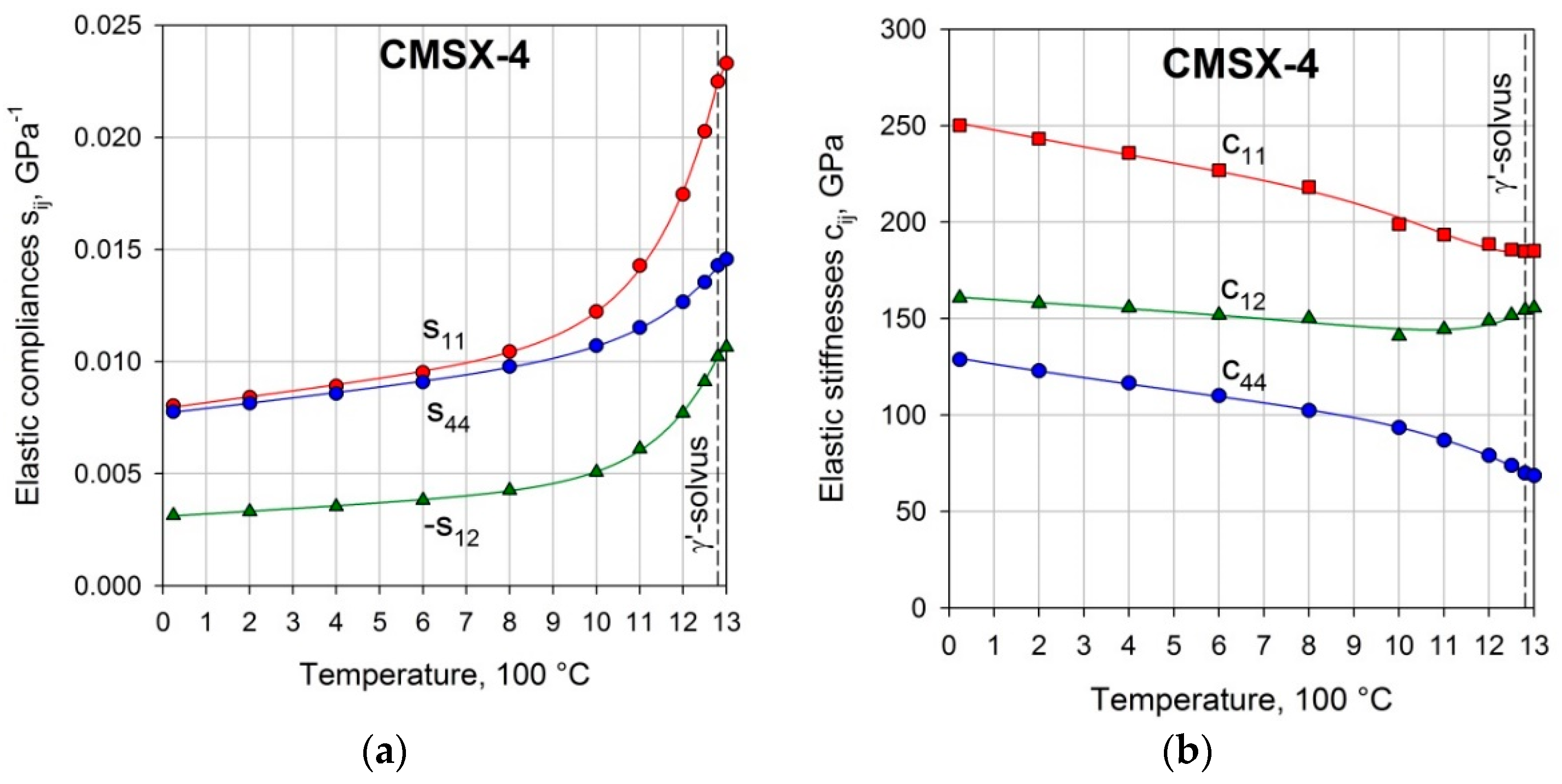
3.1. Temperature Dependence of Elastic Constants of Superalloy CMSX-4
3.2. Temperature Dependence of Elastic Constants of the Matrix Alloy
3.3. Calculation of Elastic Constants for the γ′-Phase
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| T, °C | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | - | 0.0238 | 0.0329 | 0.0425 | 0.053 | 0.0641 | ||
| 100 | 0.076 | 0.088 | 0.1 | 0.113 | 0.125 | 0.138 | 0.15 | 0.16 | 0.176 | 0.19 |
| 200 | 0.203 | 0.217 | 0.23 | 0.245 | 0.258 | 0.272 | 0.286 | 0.3 | 0.314 | 0.329 |
| 300 | 0.342 | 0.355 | 0.368 | 0.382 | 0.396 | 0.41 | 0.424 | 0.438 | 0.451 | 0.464 |
| 400 | 0.479 | 0.494 | 0.508 | 0.523 | 0.537 | 0.552 | 0.567 | 0.581 | 0.596 | 0.61 |
| 500 | 0.625 | 0.639 | 0.653 | 0.667 | 0.682 | 0.697 | 0.712 | 0.727 | 0.743 | 0.758 |
| 600 | 0.774 | 0.79 | 0.806 | 0.822 | 0.839 | 0.856 | 0.873 | 0.89 | 0.906 | 0.924 |
| 700 | 0.941 | 0.958 | 0.975 | 0.993 | 1.01 | 1.03 | 1.05 | 1.06 | 1.08 | 1.1 |
| 800 | 1.12 | 1.14 | 1.15 | 1.17 | 1.19 | 1.21 | 1.23 | 1.25 | 1.27 | 1.29 |
| 900 | 1.31 | 1.33 | 1.35 | 1.38 | 1.4 | 1.42 | 1.44 | 1.46 | 1.49 | 1.51 |
| 1000 | 1.53 | 1.56 | 1.58 | 1.61 | 1.63 | 1.66 | 1.68 | 1.71 | 1.74 | 1.76 |
| 1100 | 1.79 | 1.82 | 1.85 | 1.88 | 1.91 | 1.94 | 1.97 | 2.01 | 2.04 | 2.07 |
| 1200 | 2.11 | 2.15 | 2.18 | 2.22 | 2.26 | 2.3 | 2.35 | 2.39 | 2.44 | 2.47 |
| 1300 | 2.5 | 2.52 |
References
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Shalin, R.E.; Svetlov, I.L.; Kachanov, E.B.; Toloraya, V.N.; Gavrilin, O.S. Single-Crystals of Nickel-Base Superalloys; Mashinistroeniye: Moscow, Russia, 1997. [Google Scholar]
- Ghosh, R.N.; Curtis, R.V.; McLean, M. Creep deformation of single crystal superalloys—Modelling the crystallographic anisotropy. Acta Metall. Mater. 1990, 38, 1977–1992. [Google Scholar] [CrossRef]
- Méric, L.; Poubanne, P.; Cailletaud, G. Single Crystal Modeling for Structural Calculations: Part 1—Model Presentation. J. Eng. Mater. Technol. 1991, 113, 162–170. [Google Scholar] [CrossRef]
- Meéric, L.; Cailletaud, G. Single Crystal Modeling for Structural Calculations: Part 2—Finite Element Implementation. J. Eng. Mater. Technol. 1991, 113, 171–182. [Google Scholar] [CrossRef]
- Tinga, T. Multiscale Modelling of Single Crystal Superalloys for Gas Turbine Blades. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 7 May 2009. [Google Scholar] [CrossRef]
- Zhou, N.; Shen, C.; Mills, M.; Wang, Y. Contributions from elastic inhomogeneity and from plasticity to γ′ rafting in single-crystal Ni–Al. Acta Mater. 2008, 56, 6156–6173. [Google Scholar] [CrossRef]
- Link, T.; Epishin, A.; Fedelich, B. Inhomogeneity of misfit stresses in nickel-base superalloys: Effect on propagation of matrix dislocation loops. Philos. Mag. 2009, 89, 1141–1159. [Google Scholar] [CrossRef]
- Cottura, M.; Appolaire, B.; Finel, A.; Le Bouar, Y. Coupling the Phase Field Method for diffusive transformations with dislocation density-based crystal plasticity: Application to Ni-based superalloys. J. Mech. Phys. Solids 2016, 94, 473–489. [Google Scholar] [CrossRef]
- Böttger, B.; Apel, M.; Budnitzki, M.; Eiken, J.; Laschet, G.; Zhou, B. Calphad coupled phase-field model with mechano-chemical contributions and its application to rafting of γ′ in CMSX-4. Comput. Mater. Sci. 2020, 184, 109909. [Google Scholar] [CrossRef]
- Krivko, A.I.; Epishin, A.I.; Svetlov, I.L.; Samoilov, A.I. Elastic properties of single crystals of nickel alloys. Strength Mater. 1988, 20, 214–223. [Google Scholar] [CrossRef]
- Svetlov, I.L.; Epishin, A.I.; Krivko, A.I.; Samoilov, A.I.; Odintsev, I.N.; Andreev, A.P. Anisotropy of Poisson ratio of nickel-base alloy single-crystals. Dokl. Akad. Nauk SSSR 1988, 302, 1372–1375. [Google Scholar]
- Epishin, A.I.; Lisovenko, D.S. Extreme values of the Poisson’s ratio of cubic crystals. Tech. Phys. 2016, 61, 1516–1524. [Google Scholar] [CrossRef]
- Schneider, W. Hochtemperaturkriechverhalten und Mikrostruktur der einkristallinen Nickelbasis-Superlegierung CMSX-4 bei Temperaturen von 800 °C bis 1100 °C. Ph.D. Thesis, University of Erlangen-Nuremberg, Erlangen-Nuremberg, Germany, 1993. [Google Scholar]
- Hermann, W.; Sockel, H.; Han, J.; Bertram, A. Elastic properties and determination of elastic constants of nickel-base superalloys by a free-free beam technique. In Proceedings of the Superalloys 1996, Seven Springs Mountain Resort, Champion, PA, USA, 22–26 September 1996; Kissinger, R.D., Deye, D.J., Anton, D.L., Cetel, A.D., Nathal, M.V., Pollock, T.M., Woodford, D.A., Eds.; TMS: Warrendale, PA, USA, 2000; pp. 229–238. [Google Scholar] [CrossRef]
- Siebörger, D.; Knake, H.; Glatzel, U. Temperature dependence of the elastic moduli of the nickel-base superalloy CMSX-4 and its isolated phases. Mater. Sci. Eng. A 2001, 298, 26–33. [Google Scholar] [CrossRef]
- Demtröder, K.; Eggeler, G.; Schreuer, J. Influence of microstructure on macroscopic elastic properties and thermal expansion of nickel-base superalloys ERBO/1 and LEK94. Mater. Werkst. 2015, 46, 563–576. [Google Scholar] [CrossRef]
- Le Graverend, J.-B.; Cormier, J.; Gallerneau, F.; Kruch, S.; A Mendez, J. Highly non-linear creep life induced by a short close γ′-solvus overheating and a prior microstructure degradation on a nickel-based single crystal superalloy. Mater. Des. 2014, 56, 990–997. [Google Scholar] [CrossRef]
- Epishin, A.; Fedelich, B.; Link, T.; Feldmann, T.; Svetlov, I.L. Pore annihilation in a single-crystal nickel-base superalloy during hot isostatic pressing: Experiment and modelling. Mater. Sci. Eng. A 2013, 586, 342–349. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Fedelich, B.; Svetlov, I.L.; Golubovskiy, E.R. Hot isostatic pressing of single-crystal nickel-base superalloys: Mechanism of pore closure and effect on mechanical properties. In Proceedings of the of Eurosuperalloys 2014, Giens, France, 12–16 May 2014; Guedou, J.Y., Ed.; EDP: Les Ulis, France, 2014; Volume 14, p. 8003. [Google Scholar] [CrossRef] [Green Version]
- Epishin, A.; Fedelich, B.; Nolze, G.; Schriever, S.; Feldmann, T.; Ijaz, M.F.; Viguier, B.; Poquillon, D.; Le Bouar, Y.; Ruffini, A.; et al. Creep of Single Crystals of Nickel-Based Superalloys at Ultra-High Homologous Temperature. Met. Mater. Trans. A 2018, 49, 3973–3987. [Google Scholar] [CrossRef] [Green Version]
- Tien, J.K.; Copley, S.M. The effect of uniaxial stress on the periodic morphology of coherent gamma prime precipitates in nickel-base superalloy crystals. Met. Mater. Trans. A 1971, 2, 215–219. [Google Scholar] [CrossRef]
- Pineau, A. Influence of uniaxial stress on the morphology of coherent precipitates during coarsening-elastic energy considerations. Acta Met. 1976, 24, 559–564. [Google Scholar] [CrossRef]
- Svetlov, I.; Golovko, B.; Epishin, A.; Abalakin, N. Diffusional mechanism of γ′-phase particles coalescence in single crystals of nickel-base superalloys. Scr. Met. Mater. 1992, 26, 1353–1358. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. Rafting in Superalloys. Met. Mater. Trans. A 1996, 27, 513–530. [Google Scholar] [CrossRef]
- Nazmy, M.; Epishin, A.; Link, T.; Stäubli, M. A review of degradation in single crystal nickel based superalloys. Energy Mater. 2006, 1, 263–268. [Google Scholar] [CrossRef]
- Fedelich, B.; Epishin, A.; Link, T.; Klingelhöffer, H.; Künecke, G.; Portella, P.D. Rafting during high temperature deformation in a single crystal superalloy: Experiments and modeling. In Proceedings of the Superalloys 2012, Seven Springs Mountain Resort, Champion, PA, USA, 9–13 September 2012; Huron, E.S., Reed, R.C., Hardy, M.C., Mills, M.J., Montero, R.E., Portella, P.D., Telesman, J., Eds.; TMS: Warrendale, PA, USA, 2012; pp. 491–500. Available online: https://www.tms.org/Superalloys/10.7449/2012/Superalloys_2012_491_500.pdf (accessed on 1 October 2020).
- Titus, M.S.; Suzuki, A.; Pollock, T.M. High Temperature creep of new L12 containing cobalt-base superalloys. In Proceedings of the Superalloys 2012, Seven Springs Mountain Resort, Champion, PA, USA, 9–13 September 2012; Huron, E.S., Reed, R.C., Hardy, M.C., Mills, M.J., Montero, R.E., Portella, P.D., Telesman, J., Eds.; TMS: Warrendale, PA, USA, 2012; pp. 823–832. Available online: https://www.tms.org/Superalloys/10.7449/2012/Superalloys_2012_823_832.pdf (accessed on 1 October 2020).
- Epishin, A.; Petrushin, N.; Nolze, G.; Gerstein, G.; Maier, H.J. Investigation of the γ′-Strengthened Quaternary Co-Based Alloys Co-Al-W-Ta. Met. Mater. Trans. A 2018, 49, 4042–4057. [Google Scholar] [CrossRef]
- Fisher, E. On the elastic moduli of nickel rich Ni-Al alloy single crystals. Scr. Met. 1986, 20, 279–284. [Google Scholar] [CrossRef]
- Kuhn, H.-A.; Sockel, H.G. Contributions of the Different Phases of Two Nickel-Base Superalloys to the Elastic Behaviour in a Wide Temperature Range. Phys. Status Solidi 1990, 119, 93–105. [Google Scholar] [CrossRef]
- Fahrmann, M.; Hermann, W.; Boegli, A.; Pollock, T.; Sockel, H. Determination of matrix and precipitate elastic constants in (γ–γ′) Ni-base model alloys, and their relevance to rafting. Mater. Sci. Eng. A 1999, 260, 212–221. [Google Scholar] [CrossRef]
- Ichitsubo, T.; Koumoto, D.; Hirao, M.; Tanaka, K.; Osawa, M.; Yokokawa, T.; Harada, H. Elastic anisotropy of rafted Ni-base superalloy at high temperatures. Acta Mater. 2003, 51, 4863–4869. [Google Scholar] [CrossRef]
- Dye, D.; Coakley, J.; Vorontsov, V.A.; Stone, H.J.; Rogge, R. Elastic moduli and load partitioning in a single-crystal nickel superalloy. Scr. Mater. 2009, 61, 109–112. [Google Scholar] [CrossRef]
- Harris, K.; Erickson, G.L.; Sikkenga, S.L.; Brentnall, W.D.; Aurrecoechea, J.M.; Kubarych, K.G. Development of two rhenium containing superalloys for single crystal blade and directionally solidified vane applications in advanced turbine engines. J. Mater. Eng. Perform. 1993, 2, 481–487. [Google Scholar] [CrossRef]
- Brückner, U.; Epishin, A.; Link, T. Local X-ray diffraction analysis of the structure of dendrites in single-crystal nickel-base superalloys. Acta Mater. 1997, 45, 5223–5231. [Google Scholar] [CrossRef]
- Brückner, U.; Epishin, A.; Link, T.; Dressel, K. The influence of the dendritic structure on the γ/γ′-lattice misfit in the single-crystal nickel-base superalloy CMSX-4. Mater. Sci. Eng. A 1998, 247, 23–31. [Google Scholar] [CrossRef]
- Förster, F. Ein neues Messverfahren zur Bestimmung des Elastizitätsmoduls und der Dämpfung. Z. Metallkunde 1937, 29, 109–115. [Google Scholar]
- ASTM International. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Sonic Resonance. Revision 13. ASTM E1875. Available online: https://www.astm.org/Standards/E1875.htm (accessed on 1 December 2020).
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth & Heinemann: Oxford, UK, 2000; Volume 1. [Google Scholar]
- Abaqus/Standard. 3ds.com. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/abaqusstandard/ (accessed on 1 February 2021).
- Link, T.; Epishin, A.; Gottwald, A.; Wichmann, T. Quantitative analysis of the structure of single crystal superalloys. In Proceedings of the Fortschritte in der Metallographie, 37 Metallographie-Tagung, Berlin, Germany, 17–19 September 2003; Portella, P.D., Ed.; Werkstoff-Informationsges: Frankfurt, Germany, 2004; pp. 257–262. [Google Scholar]
- Cormier, J.; Milhet, X.; Mendez, J. Effect of very high temperature short exposures on the dissolution of the γ′ phase in single crystal MC2 superalloy. J. Mater. Sci. 2007, 42, 7780–7786. [Google Scholar] [CrossRef]
- Tiley, J.; Viswanathan, G.; Hwang, J.; Shiveley, A.; Banerjee, R. Evaluation of gamma prime volume fractions and lattice misfits in a nickel base superalloy using the external standard X-ray diffraction method. Mater. Sci. Eng. A 2010, 528, 32–36. [Google Scholar] [CrossRef]
- Glatzel, U. Microstructure and Internal Strains of Undeformed and Creep Deformed Samples of a Nickel-Base Superalloy; Verlag Dr. Köster: Berlin, Germany, 1994. [Google Scholar]
- Hemmersmeier, U.; Feller-Kniepmeier, M. Element distribution in the macro- and microstructure of nickel base superalloy CMSX-4. Mater. Sci. Eng. A 1998, 248, 87–97. [Google Scholar] [CrossRef]
- Roebuck, B.; Cox, D.; Reed, R. The temperature dependence of γ′ volume fraction in a Ni-based single crystal superalloy from resistivity measurements. Scr. Mater. 2001, 44, 917–921. [Google Scholar] [CrossRef]
- Caron, P. High γ′ Solvus New Generation Nickel-Based Superalloys for Single Crystal Turbine Blade Applications. In Proceedings of the Superalloys 2000, Seven Springs Mountain Resort, Champion, PA, USA, 17–21 September 2000; Pollock, T.M., Kissinger, R.D., Bowman, R.R., Green, K.A., McLean, M., Olson, S., Schirra, J.J., Eds.; TMS: Warrendale, PA, USA, 2000; pp. 737–746. [Google Scholar] [CrossRef] [Green Version]
- Mackay, R.; Gabb, T.P.; Garg, A.; Rogers, R.B.; Nathal, M. Influence of composition on microstructural parameters of single crystal nickel-base superalloys. Mater. Charact. 2012, 70, 83–100. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Klingelhöffer, H.; Fedelich, B.; Brückner, U.; Portella, P. New technique for characterization of microstructural degradation under creep: Application to the nickel-base superalloy CMSX-4. Mater. Sci. Eng. A 2009, 510–511, 262–265. [Google Scholar] [CrossRef]
- IMAGE J. Available online: https://imagej.nih.gov/ij/ (accessed on 5 December 2020).
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Morris, P.R. Elastic constants of polycrystals. Int. J. Eng. Sci. 1970, 8, 49–61. [Google Scholar] [CrossRef]
- Matthies, S.; Humbert, M. On the Principle of a Geometric Mean of Even-Rank Symmetric Tensors for Textured Polycrystals. J. Appl. Crystallogr. 1995, 28, 254–266. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Springer: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Thomson, W. Elements of a mathematical theory of elasticity. Philos. Trans. R. Soc. Lond. 1856, 146, 481–498. [Google Scholar] [CrossRef]
- Sutcliffe, S. Spectral Decomposition of the Elasticity Tensor. J. Appl. Mech. 1992, 59, 762–773. [Google Scholar] [CrossRef]
- Mehrabadi, M.M.; Cowin, S.C. eigentensors of linear anisotropic elastic materials. Q. J. Mech. Appl. Math. 1990, 43, 15–41. [Google Scholar] [CrossRef]
- Walpole, L.J. Fourth-rank tensors of the thirty-two crystal classes: Multiplication tables. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1984, 391, 149–179. [Google Scholar] [CrossRef]
- Matthies, S.; Humbert, M. The Realization of the Concept of a Geometric Mean for Calculating Physical Constants of Polycrystalline Materials. Phys. Status Solidi 1993, 177, K47–K50. [Google Scholar] [CrossRef]
- Brückner, U.; Epishin, A.; Nolze, G. Determination of the sign of the γ/γ′-misfit in nickel-base superalloys by use of spectral impure Cu(Cr) radiation. Scr. Mater. 1997, 36, 1279–1282. [Google Scholar] [CrossRef]


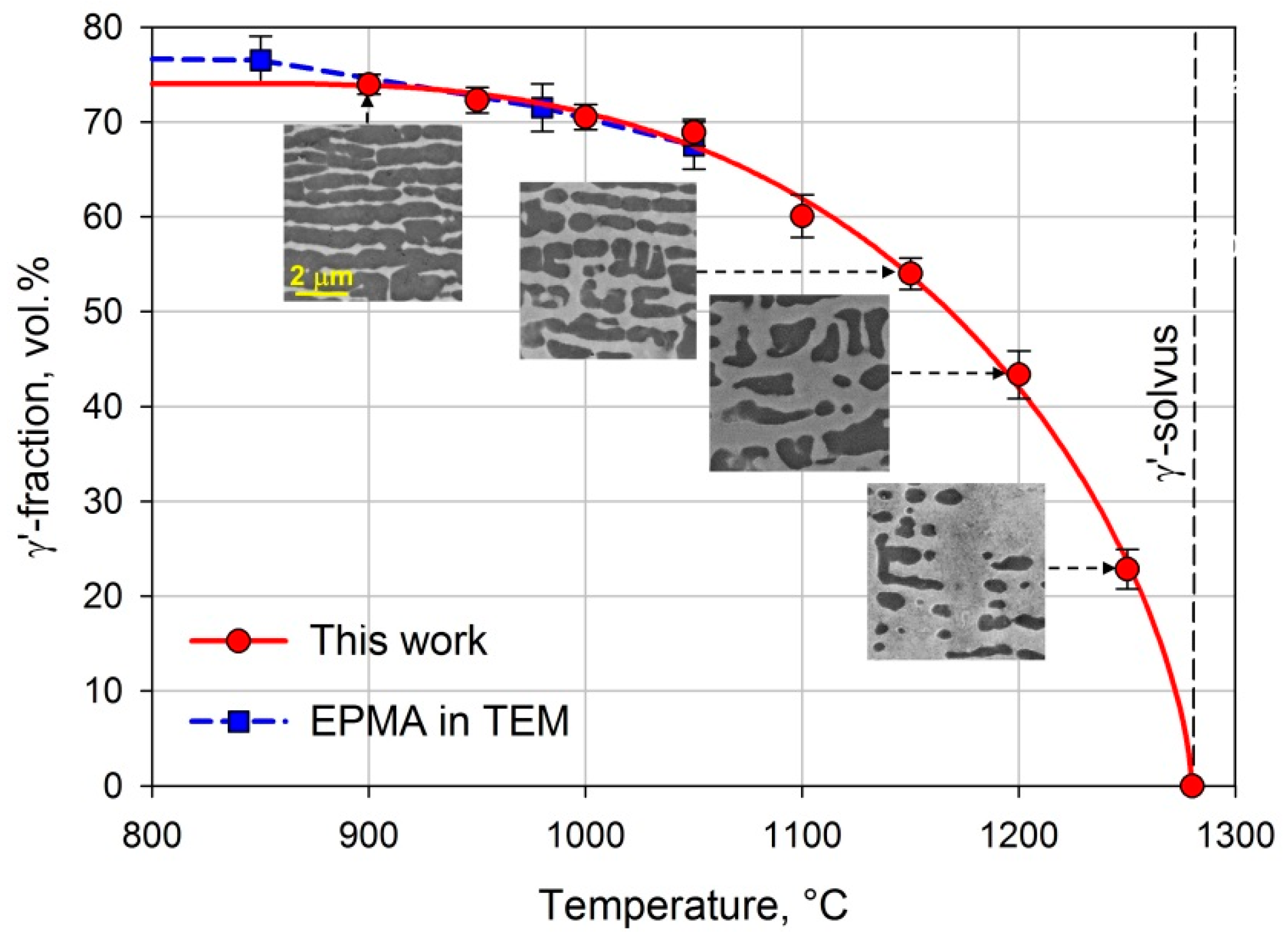




| T, °C | 900 | 950 | 1000 | 1050 | 1100 | 1150 | 1200 | 1250 | 1280 |
|---|---|---|---|---|---|---|---|---|---|
| 74.0 | 72.3 | 70.5 | 68.9 | 60.1 | 54.0 | 43.4 | 22.8 | 0 |
| T, °C | 24 | 200 | 400 | 600 | 800 | 1000 | 1100 | 1200 | 1250 | 1280 | 1300 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 250 | 243 | 236 | 227 | 218 | 199 | 193 | 189 | 186 | 185 | 185 | |
| 161 | 158 | 155 | 152 | 150 | 141 | 144 | 149 | 152 | 154 | 156 | |
| 129 | 123 | 117 | 110 | 102 | 93 | 87 | 79 | 74 | 70 | 69 |
| Elastic Compliances of Superalloy CMSX-4 | ||||
|---|---|---|---|---|
| , GPa−1 | a, 10−3 GPa−1 | b, 10−6 GPa−1 °C−1 | c, 10−6 GPa−1 | d, 10−6 °C−1 |
| 7.90 | 2.58 | 2.10 | 6.71 | |
| 3.08 | 1.17 | 0.886 | 6.84 | |
| 7.68 | 2.30 | 2.11 | 5.82 | |
| Elastic Compliances of Matrix | ||||
|---|---|---|---|---|
| , GPa−1 | a, 10−3 GPa−1 | b, 10−6 GPa−1 °C−1 | c, 10−6 GPa−1 | d, 10−6 °C−1 |
| 7.49 | 4.44 | 1.05 | 7.10 | |
| − | 2.90 | 2.12 | 0.399 | 7.31 |
| 7.19 | 2.89 | 3.26 | 5.43 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Epishin, A.; Fedelich, B.; Finn, M.; Künecke, G.; Rehmer, B.; Nolze, G.; Leistner, C.; Petrushin, N.; Svetlov, I. Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C. Crystals 2021, 11, 152. https://doi.org/10.3390/cryst11020152
Epishin A, Fedelich B, Finn M, Künecke G, Rehmer B, Nolze G, Leistner C, Petrushin N, Svetlov I. Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C. Crystals. 2021; 11(2):152. https://doi.org/10.3390/cryst11020152
Chicago/Turabian StyleEpishin, Alexander, Bernard Fedelich, Monika Finn, Georgia Künecke, Birgit Rehmer, Gert Nolze, Claudia Leistner, Nikolay Petrushin, and Igor Svetlov. 2021. "Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C" Crystals 11, no. 2: 152. https://doi.org/10.3390/cryst11020152






