Luminescence Intensity Ratio Thermometry with Er³⁺: Performance Overview

Abstract

The figures of merit of luminescence intensity ratio (LIR) thermometry for Er³⁺ in 40 different crystals and glasses have been calculated and compared. For calculations, the relevant data has been collected from the literature while the missing data were derived from available absorption and emission spectra. The calculated parameters include Judd–Ofelt parameters, refractive indexes, Slater integrals, spin–orbit coupling parameters, reduced matrix elements (RMEs), energy differences between emitting levels used for LIR, absolute, and relative sensitivities. We found a slight variation of RMEs between hosts because of variations in values of Slater integrals and spin–orbit coupling parameters, and we calculated their average values over 40 hosts. The calculations showed that crystals perform better than glasses in Er³⁺-based thermometry, and we identified hosts that have large values of both absolute and relative sensitivity.

1. Introduction

The measurements of temperature, one of seven fundamental physical quantities, can be classified according to the nature of contact between the measurement object and instrument to invasive (where there is direct contact, e.g., thermocouples, thermistors), semi-invasive (where measuring object is altered in a way to enable contactless measurements), and non-invasive (where the temperature is estimated remotely, e.g., optical pyrometers) [1]. The first type necessarily perturbs the temperature of measurement objects which limits its use in microscopic objects. In addition, such approaches are difficult to implement on moving objects or in harsh environments, for example, in high-intensity electromagnetic fields, radioactive, or chemically challenging surroundings. Thus, the current market of thermometers, accounting for more than 80% of all sensors [2], demands methods that allow for remote or microscopic measurements. Among many perspective optical semi-invasive techniques, luminescence thermometry which uses thermographic phosphors has drawn the largest attention [3,4]. The thermographic phosphor probe can be incorporated within the measured object or on its surface, on macroscale to nanoscale sizes, or can be mounted on the surface of the fiber-optic cables and bring to proximity of measuring objects. Luminescent thermometry has found a range of valuable applications, from engineering to biomedical [5], and, currently, it is a widely researched topic with an exponentially increasing number of published research papers [6].

Presently, many types of materials are used for the construction of thermometry probes. These include rare-earth and transition metal activated phosphors, semiconductor quantum dots, organic dyes, and metal-organic complexes, carbon dots, and luminescent polymers. Among the rare-earth crystals are by far the most exploited type [5], usually exploited in the so-called luminescence intensity ratio (LIR, sometimes called fluorescence intensity ratio (FIR) or labeled as Δ) temperature read-out scheme that is based on the temperature-dependent intensity ratio of emissions from the thermally coupled excited levels of rare-earth ions.

The Er³⁺ is considered to be workhorse in LIR-based luminescence thermometry. LIR read-out is obtained with both downshifting and up-conversion emissions, the latter most frequently sensitized by Yb³⁺. The popularity of Er³⁺ in luminescence thermometry is a consequence of its efficient emission and ~700 cm⁻¹ energy difference between its thermally coupled ⁴S_3/2 and ²H_11/2 levels. Such energy difference is ideal for thermometry in the physiological range of temperatures (30–50 °C) since it provides the maximal sensitivity of measurement in this range (~ 1.1%K⁻¹ at 303 K). To increase sensitivity, in recent times, the emission from the Er^{3+ 4}F_7/2 level is used for LIR considering the higher energy difference between ⁴F_7/2 and ⁴S_3/2 levels compared to the energy difference between ²H_11/2 and ⁴S_3/2 levels [7]. This Er³⁺ LIR variant has perspective applications at high temperatures and greatly widens the sensor’s operating temperature range.

Since Er³⁺ can activate many hosts there are many investigations of luminescence thermometry using emissions of this ion. These studies are lengthy and cumbersome involving material synthesis and characterizations, measurements of emission spectra at various temperatures, complex data fitting and analysis, and evaluation of thermometric performance. Therefore, to alleviate this problem, the theoretical prediction of Er³⁺ thermometric performance in different hosts may be useful as a guide for the host selection.

Our previous research has demonstrated that LIR and figures of merit of luminescence thermometry can be predicted by a theoretical model that involves the famous Judd–Ofelt (JO) theory with the high matching to experimental data [6,8]. JO theory explains and predicts the intensities of the trivalent rare-earth ions’ (RE³⁺) f-f electronic transitions, and its parameters include all phenomenological mechanisms responsible for the line strengths observed in both absorption and emission spectra.

Here, we aimed to perform the theoretical analysis of Er³⁺ emissions involved in the LIR thermometry, linking the temperature sensing performance of materials (LIR absolute and relative sensitivities) with their composition and structural properties. For this extensive analysis we have selected 40 different materials in crystal and glass form, and collected the relevant data from the literature. The refractive index values were calculated from Sellmeier’s equation (where available). The energy level positions are given for each host. For 16 hosts, the reduced matrix elements (RMEs) are recalculated from the Slater integrals and spin–orbit (s–o) parameters. The relation between material properties, JO parameters, Slater integrals, and s–o parameters is provided.

2. Methods

2.1. Luminescence Intensity Ratio Method

Out of all the luminescence temperature read-out methods the LIR has been the most frequently investigated since it is simple, requires inexpensive equipment, and, most importantly, is ratiometric and self-referenced [7]. The temperature read-out is not affected by fluctuations in excitation power. The most interesting materials for LIR thermometry are trivalent lanthanides, as they have sharp emission lines and plenty to choose from, from ultraviolet (UV) to near-infrared (NIR) spectral regions. LIR is defined as the ratio of two emissions that varies with temperature [9]. In the case of two energy levels separated by < 2000 cm⁻¹, it is said that they are thermally coupled, as the higher energy level can be effectively populated by the thermal energy. The ratio of populations of optical centers in the energetically higher (H) and lower (L) levels is then proportional to the Boltzmann distribution: N_H/N_L~exp(−ΔE/kT), where ΔE is the energy difference between the levels of interest, k = 0.695 cm⁻¹ K⁻¹ is the Boltzmann constant, and T is the temperature. As the intensities are proportional to the population, the equation for LIR for the Boltzmann thermometer is:

$$LIR\left(T\right)=\frac{I_H\left(T\right)}{I_L\left(T\right)}=B\times \exp \left(-\frac{\mathsf{\Delta }E}{kT}\right)$$

(1)

where B is the temperature invariant parameter that depends only on the host.

The thermometer’s performance is estimated by the absolute ($S_a$) and relative ($S_r$) sensitivities, and temperature resolution ($\mathsf{\Delta }T$) given by [10]:

$$S_a=\left|\frac{\partial LIR}{\partial T}\right|,S_r=\frac{S_a}{LIR}·100\%,\mathsf{\Delta }T=\frac{{\sigma }_a}{S_a}=\frac{{\sigma }_r}{S_r}$$

(2)

where σ_a and σ_r are the absolute and relative uncertainties in measurement of LIR, presented as standard deviations.

For the temperature dependence of LIR given by Equation (1), sensitivities have the following form:

$$S_a=\frac{\mathsf{\Delta }E}{k{T}^2}B\exp \left(-\frac{\mathsf{\Delta }E}{kT}\right),S_r=\frac{\mathsf{\Delta }E}{k{T}^2}·100\%$$

(3)

The absolute sensitivity reaches maximum at $T=\mathsf{\Delta }E/2k$ with the value of [8]:

$$S_{amax}=\frac{4Bk}{e^2\mathsf{\Delta }E}$$

(4)

where e = 2.718 is a number (the natural logarithm base).

The ideal situation for LIR is the Boltzmann luminescence thermometer since it is easily calibrated with the well-known and simple theory. According to Equation (3), the relative sensitivity only depends on the value of energy difference between thermalized energy levels. The choice of levels with the energy gap larger than 2000 cm⁻¹ may result in the thermalization loss at low temperatures, and even around room temperatures, while the small energy gap gives small relative sensitivities. One should consider that for achieving the Boltzmann’s thermal equilibrium some other conditions must be fulfilled besides the suitable energy difference between the levels, as recently demonstrated by Geitenbeek et al. [11] and Suta et al. [12]. Furthermore, considering the adjacent energy levels of trivalent rare-earth used for thermometry, the largest energy gap is in the Eu³⁺ (between ⁵D₁ and ⁵D₀ levels) and is approximately 1750 cm⁻¹.

Thus, the current research of LIR of a single emission center is aimed at increasing the relative sensitivity without the loss of thermalization (and deviation from the Boltzmann distribution). One recently demonstrated solution is the inclusion of the third, non-adjacent level, with higher energy, which is thermalized with the second level. If the first and second levels are thermalized, and second and third levels are thermalized, then the ratios of emission intensities of the first and third levels will follow the Boltzmann distribution, even if their separation is greater than stated above, see Figure 1 for the case of Er³⁺. The conventional LIR of Er³⁺ is equal to the ratio of emissions from ²H_11/2 (~523 nm) and ⁴S_3/2 (~542 nm) levels, which are separated by ~700 cm⁻¹, thus giving the relative sensitivity of ~1.1% K⁻¹. By observing intensities to the ground level from ⁴F_7/2 (~485 nm) with the ⁴S_3/2, it is evident that their relative change is much larger than with ²H_11/2. This larger energy difference, according to Equation (3), ultimately results in more than a three-fold increase in relative sensitivity.

2.2. Judd–Ofelt Theory and Its Relevance for Luminescence Thermometry

The electronic configuration of trivalent erbium is that of Xenon plus the 11 electrons in the 4f shell, i.e., Er³⁺ has [Xe]4f¹¹ electronic configuration. With only 3 electrons missing from the completely filled 4f shell, Er³⁺ shares the same LS terms and LSJ levels as the Nd³⁺ who has 3 electrons in the 4f shell. The transitions from one to another level are followed by the reception or release of energy. The probability for such phenomena for a given set of initial and final levels is given by the wavefunctions and the appropriate moment operator. The exchange of energy in the intra-configurational 4f transitions with the highest intensity is of induced electric dipole and magnetic dipole types [13]. What was puzzling only half a century ago was the origin of these “electric dipole” interactions, as they were clearly and strictly forbidden by the Parity selection rule, also known as the Laporte rule. The solution to this problem came in 1962 in the papers simultaneously published by Judd [14] and Ofelt [15], to what is latter known as the Judd–Ofelt theory (JO). For the sake of brevity, it will not be explained here, and the reader is instead referred to the excellent references [16,17,18]; however, we will touch on several basics that are the most relevant for the present research.

In RE³⁺ (trivalent rare-earth) ions in general, the electrostatic (H_e) and s–o (H_so) interactions between 4f electrons are dominant and are of the approximately same magnitude, thus the Hamiltonian can be given approximately as H = H_e + H_so [17].

The electrostatic Hamiltonian can be reduced to the electron-electron repulsion form [17], which can be split into its radial (F^k) and angular (f_k) parts:

$$H_e=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \sum }_{i<j}^{11}\frac{e^2}{r_{ij}}={\displaystyle \sum }_k{F}^k{f}_k$$

(5)

The radial parameters are the Slater integrals given by [19]:

$$F^k\left(4f\right)=\frac{e^2}{4\pi {\epsilon }_0}{{\displaystyle \iint }}_0^{\infty }\frac{r_{<}^k}{r_{>}^{k+1}}{R}_{4f}^2\left(r_i\right)R_{4f}^2\left(r_j\right)d{r}_{i}d{r}_j$$

(6)

where r_> is greater and r_< is smaller than r_i and r_j, and R are the radial parts of the wavefunction. The Slater integrals can be evaluated by the Hartree-Fock method; however, it does not provide accurate results, and it is best to obtain them semi-empirically by adjusting them to the experimentally observed energies of 4f levels [20].

H_so mixes all states that have the same J quantum number, and it is proportional to the s–o coupling parameter, ζ, which is further proportional to the number of electrons within the 4f shell. Er³⁺ has a relatively high value of ζ in comparison with other trivalent lanthanide ions, providing a large mixing of states [21]. In this intermediate coupling approximation scheme, the wavefunctions are expressed as a linear combination of all other states in the configuration with the same J quantum number [17,18,22,23]:

$$|4f^{11}SLJ{\rangle }^{\prime }={\displaystyle \sum }_i{c}_i|4f^{11}{S}^{\prime }{L}^{\prime }J\rangle , {\displaystyle \sum }_i{c}_i^2=1$$

(7)

As the 4f electrons are shielded by the outer higher-energy electrons the crystal field (CF) introduces only a perturbation to the Hamiltonian [16]. Nevertheless, that perturbation weakens the already mentioned Laporte (parity) selection rule that forbids the ED transitions within the configuration. The 4f–4f transitions of electric dipole (ED) type become allowed and are known as the induced ED [24]. The radiative transition probability for such spontaneous emission is then equal to [25]:

$$A_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}=\frac{64{\pi }^4{\tilde{\nu }}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}^3}{3h\left(2J+1\right)}\left({\chi }_{ED}{D}_{ED}+{\chi }_{MD}{D}_{MD}\right)$$

(8)

or for the purely induced ED emission (MD is an abbreviation for the magnetic dipole):

$$A_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}=\frac{64{\pi }^4{\tilde{\nu }}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}^3}{3h\left(2J+1\right)}{\chi }_{ED}{D}_{ED}$$

(9)

where h = 6.626 × 10⁻²⁷ erg∙s is the Planck’s constant. Χ is the local field correction, ${\tilde{\nu }}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}$ is the emission barycenter energy, and D is the dipole strength given in esu² cm² units. The emission barycenter is [26]:

$${\tilde{\nu }}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}=\frac{{{\displaystyle \int }}^{ }{\nu }_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}{i}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}\left(\nu \right)d\nu }{{{\displaystyle \int }}^{ }{i}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}\left(\nu \right)d\nu }$$

(10)

where i is the intensity at a given energy. The local field correction for ED emission is given by [27]:

$${\chi }_{ED}=\frac{n{\left(n^2+2\right)}^2}{9}$$

(11)

where n is the refractive index that should be given at the wavelength of the barycenter of the emission. It can be calculated from the Sellmeier’s equation for a given material, which is given in the form [28,29]:

$$n\left(\lambda \right)=\sqrt{1+{{\displaystyle \sum }}_{i=1}^3\frac{B_i{\lambda }^2}{{\lambda }^2-C_i}}$$

(12)

In the JO scheme, the ED strength is given by [26]:

$$D_{ED}^{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}=e^2{\displaystyle \sum }_{\lambda =2,4,6}{\mathsf{\Omega }}_{\lambda }{U}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}^{\lambda }$$

(13)

where e = 4.803 × 10¹⁰ esu, $U_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}^{\lambda }$ is the abbreviation for squared RMEs ${|\langle 4f^{11}SLJ\Vert U^{\lambda }\Vert 4f^{11}{S}^{\prime }{L}^{\prime }{J}^{\prime }\rangle |}^2$, which in turn can be calculated from the Slater integrals and the s–o coupling parameter. Ω_λ are the JO intensity parameters, obtained semi-empirically or by the ab initio calculations (from the crystal-field parameters).

The integrated emission intensity for the transition SLJ→S′L′J′ is given by [30,31]:

$$I_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}={{\displaystyle \int }}^{ }{i}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}\left(\tilde{\nu }\right)d\tilde{\nu }=h{\tilde{\nu }}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}{N}_{SLJ}{A}_{SLJ\to S^{\prime }{L}^{\prime }{J}^{\prime }}$$

(14)

or without the hν if the spectrum is recorded in counts instead of power units [32].

LIR of two emissions from the thermally coupled levels is then given by:

$$LIR\left(T\right)=\frac{I_H}{I_L}=\frac{{\nu }_H{N}_H{A}_H}{{\nu }_L{N}_L{A}_L}$$

(15)

where I_H/L are the integrated intensities from the higher and lower level, respectively (without ν_H/ν_L if recorded in counts).

According to the Boltzmann distribution, the optical center population is given by:

$$\frac{N_H}{N_L}=\frac{g_H}{g_L}\exp \left(-\frac{\mathsf{\Delta }E}{kT}\right)$$

(16)

where g = 2J + 1 are the degeneracies of the selected levels.

Equation (15) can be rewritten as Equation (1) where B is the temperature invariant parameter that is given by:

$$B=\frac{{\nu }_H{g}_H{A}_H}{{\nu }_L{g}_L{A}_L}$$

(17)

or if the intensities are recorded in counts instead of power units, without the ν_H/ν_L. As we have demonstrated in our previous article [8], by inserting Equation (8) into Equation (17), the LIR, the absolute sensitivity (and everything related to it) and temperature resolution can be predicted by JO parameters, as the B parameter can be obtained from:

$$B={\left(\frac{{\tilde{\nu }}_H}{{\tilde{\nu }}_L}\right)}^4\frac{{\chi }_{ED}^H{D}_{ED}^H+{\chi }_{MD}^H{D}_{MD}^H}{{\chi }_{ED}^L{D}_{ED}^L+{\chi }_{MD}^L{D}_{MD}^L}$$

(18)

or in the case of the pure ED transitions:

$$B={\left(\frac{{\tilde{\nu }}_H}{{\tilde{\nu }}_L}\right)}^4\frac{{\chi }_{ED}^H{D}_{ED}^H}{{\chi }_{ED}^L{D}_{ED}^L}$$

(19)

For the case of spectra recorded in counts, ν_H/ν_L should be to the power of 3.

The shielding of 4f electrons by electrons from outer orbitals ensures that the RE³⁺ spectra are featured by sharp peaks whose energies are almost host-independent. This is reflected in the almost host invariant reduced matrix elements. However, as the Slater parameters deviate significantly in Er³⁺, using such approximation may introduce significant errors. For the analysis of this type, it is more accurate to use the reduced matrix elements that are calculated from Slater integrals and s–o coupling parameters, which are calculated semi-empirically from the positions of the energy levels. Analogously, the small variations in energy level positions may provide significant variations in energy level differences, and thus large deviations in absolute and relative sensitivities. Finally, the small differences in refractive index become enormous when they propagate in the local field correction coefficient and, thus, it is of utmost importance to use accurate values. In this study, the observed levels are energetically very close, thus, it is a good approximation to consider the refractive index as wavelength-independent; however, the exact method is always preferred.

3. Results and Discussion

3.1. Calculations of Er³⁺ Radiative Properties in Different Hosts

For the study, we have selected 40 different hosts doped with Er³⁺ (

Table 1. A collection of 40 Er³⁺ doped hosts used in this study. Form: C–Crystal, G–Glass.

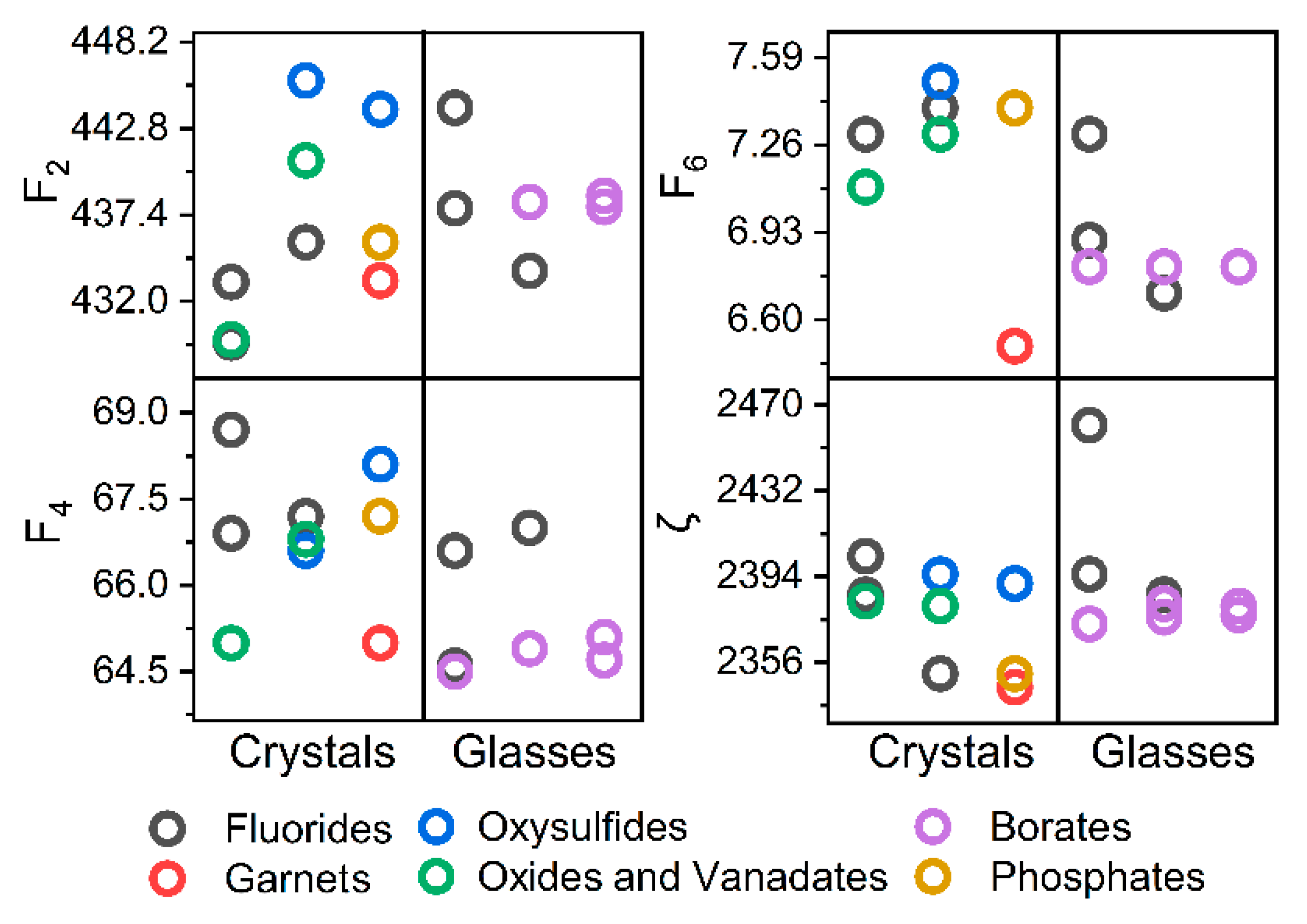
No.	Host	Abbreviation	Name	Er3+ Concentration	Form	Ref.
1 *	β-NaGdF4		Sodium Gadolinium Fluoride	1%	C	[33]
2	LaF3		Lanthanum fluoride	0.05%	C	[34,35]
3	Y3Al5O12	YAG	Yttrium Aluminium Garnet	1.2 at%	C	[36]
4	LaCl3		Lanthanum Chloride	1%	C	[17]
5	La2O2S		Lanthanum oxysulfide	1 mol%	C	[37,38]
6	Y2O2S		Yttrium oxysulfide	1 mol%	C	[37,38]
7	Sb2O3-35P2O5-5MgO-AgCl	SPMEA	Antimony Phosphate	0.17 at%	G	[39]
8	YAlO3		Yttrium Orthoaluminate	1.5 at%	C	[40]
9	KCaF3		Kalium Calcium Fluoride	1.62 at%	C	[41]
10	Y2O3		Yttrium oxide	1%	C	[42,43]
11	YVO4		Yttrium Vanadate	2.5%	C	[44]
12	PbF2-GaF3-(Zn,Mn)F2	PbZnGaLaF	Lead-Based fluoride	0.6%	G	[45]
13 *	CaYAlO4	CYAO	Yttrium Calcium Aluminate	0.5 at%	C	[46]
14	Gd3Ga5O12	GGG	Gadolinium Gallium Garnet	1.2 at%	C	[36]
15	Y3Sc2Ga3O12	YSGG	Yttrium Scandium Gallium Garnet	1.2 at%	C	[36]
16	PbO∙H3BO3∙TiO2∙AlF3	LBTAF	Lead Borate Titanate Aluminium Fluoride	4.8 at%	G	[47]
17	Li2CO3∙H3BO3	LiBO	Lithium Borate	1 mol%	G	[48]
18	Li2CO3∙H3BO3∙MgCO3	MgLiBO	Magnesium Lithium Borate	1 mol%	G	[48]
19	Li2CO3∙H3BO3∙MgCO3	CaLiBO	Calcium Lithium Borate	1 mol%	G	[48]
20	Li2CO3∙H3BO3∙SrCO3	SrLiBO	Strontium Lithium Borate	1 mol%	G	[48]
21	Li2CO3∙H3BO3∙BaCO3	BaLiBO	Barium Lithium Borate	1 mol%	G	[48]
22	ZrO2∙YO1.5	YSZ	Yttria stabilized Zirconia	0.7 at%	C	[49]
23	LiNbO3		Lithium Niobate	1.5 × 1019 cm−3	C	[50]
24	PbO-PbF2		Oxyfluoride	1.35 wt%	G	[51]
25	ZrF4∙BaF2∙LaF3∙AlF3	ZBLA	Fluorozirconate	0.5%	G	[52]
26	ZnO∙Al2O3∙Bi2O3∙B2O3	ZnAlBiB	Zinc Alumino Bismuth Borate	0.5 mol%	G	[53]
27	NaPO3∙TeO2∙AlF3∙LiF	LiTFP	Lithium Fluorophosphate	0.12 at%	G	[54]
28	NaPO3∙TeO2∙AlF3∙NaF	NaTFP	Sodium Fluorophosphate	0.12 at%	G	[54]
29	NaPO3∙TeO2∙AlF3∙KF	KTFP	Kalium Fluorophosphate	0.12 at%	G	[54]
30	Kigre patented		Phosphate	1.51 wt%	G	[55]
31	TeO2∙PbF2∙AlF3		Fluoro-tellurite	0.625 at%	G	[56]
32	SrGdGa3O7		Strontium Gadolinium Gallium Garnet	4.2 × 1021 cm−3	C	[57]
33	YPO4		Yttrium Phosphate	0.6 at%	C	[58]
34	Y2SiO5	YSO	Yttrium Orthosilicate	2 mol%b	C	[59]
35	BaGd2(MoO4)4	BGM	Barium Gadolinium Molybdate	1.4 at%	C	[60]
36	NaY(MoO4)2	NYM	Sodium Yttrium Molybdate	1.25 at%	C	[61]
37	Gd2(MoO4)3		Gadolinium Molybdate	1%	C	[62]
38	LiLa(MoO4)2		Lithium Lanthanum Molybdate	0.55 at%	C	[63]
39 *	LiLa(WO4)2		Lithium Lanthanum Tungstanate	0.65%	C	[64]
40	KY(WO4)2		Kalium Yttrium Tungstanate	0.5%	C	[65]

* Co-doped with Yb³⁺.

), from the literature that contained the most complete set of data needed for the analysis presented in this paper. As the JO parametrization is traditionally performed semi-empirically from the absorption spectrum, powders and non-transparent materials are not included in this analysis.

In the 3rd column,

Table 2. Energies of ⁴S_3/2, ²H_11/2 and ⁴F_7/2 levels in hosts listed in Table 1, their Slater integrals and spin-orbit (s–o) coupling parameters, and JO intensity parameters as reported in the corresponding references.

No.	Host	Energy [cm−1]			Slater Integrals and s–o [cm−1]				JO Parameters × 1020 [cm2]
		4S3/2	2H11/2	4F7/2	F2	F-4	F6	ζ	Ω2	Ω4	Ω6
1	β–NaGdF4	18459	19186	20483	429.4	68.7	7.1	2403	4.97	1.16	2.03
2	LaF3	18353	19118	20412	435.7	67.2	7.4	2351	3.9	1.0	2.3
3	YAG	18166	18967	20344	433.2	65.0	6.5	2345	0.74	0.92	0.70
4	LaCl3	18383	19068	20414	433.2	66.9	7.3	2386	5.45	2.08	0.69
5	La2O2S	18236	18930	20320	445.8	66.6	7.5	2395	4.32	2.32	1.17
6	Y2O2S	18236	18930	20320	444.0	68.1	7.4	2391	2.71	2.10	1.85
7 d	SPMEA	18182	19175	20576	NA	NA	NA	NA	7.89	3.27	1.07
8	YAlO3	18350	19150	20300	NA	NA	NA	NA	0.95	0.58	0.55
9 d	KCaF3	18450	19305	20576	NA	NA	NA	NA	0.74	0.87	0.57
10 b	Y2O3	18071	18931	20266	429.6	65.0	7.1	2383	4.59	1.21	0.48
11 b	YVO4	18209	19059	20371	440.8	66.8	7.3	2381	13.45	2.23	1.67
12	PbZnGaLaF	18552	19193	20618	444.0	64.6	6.9	2395	1.54	1.13	1.19
13	CYAO	18298	19040	20454	NA	NA	NA	NA	3.78	2.52	1.91
14 c	GGG	18450	19168	20387	NA	NA	NA	NA	0.70	0.37	0.86
15 c	YSGG	18433	19127	20345	NA	NA	NA	NA	0.92	0.48	0.87
16 a	LBTAF	18382	19194	20450	433.9	67.0	6.7	2386	5.89	1.10	1.47
17 a	LiBO	18413	19205	20488	437.8	65.1	6.8	2377	3.24	0.92	0.82
18 a	MgLiBO	18389	19168	20462	437.8	64.5	6.8	2373	1.33	0.39	0.62
19 a	CaLiBO	18413	19205	20488	438.2	64.9	6.8	2376	3.68	0.76	1.52
20 a	SrLiBO	18413	19205	20488	438.6	64.7	6.8	2381	2.53	0.39	1.10
21 a	BaLiBO	18403	19205	20488	438.2	64.9	6.8	2382	1.80	0.28	0.90
22 c	YSZ	18416	19342	20534	NA	NA	NA	NA	1.50	0.50	0.22
23 c	LiNbO3	18248	19047	20492	NA	NA	NA	NA	7.29	2.24	1.27
24 a	PbO-PbF2	18501	19297	20601	437.8	66.6	7.3	2461	3.22	1.34	0.61
25	ZBLA	18450	19193	20534	NA	NA	NA	NA	2.54	1.39	0.97
26 c	ZnAlBiB	18484	19193	20491	NA	NA	NA	NA	2.10	1.53	1.43
27	LiTFP	18344	19189	20486	NA	NA	NA	NA	4.70	1.21	1.30
28	NaTFP	18377	19226	20486	NA	NA	NA	NA	5.92	1.07	1.44
29	KTFP	18377	19226	20486	NA	NA	NA	NA	5.09	0.69	1.45
30	Kigre patented	18350	19150	20300	NA	NA	NA	NA	6.28	1.03	1.39
31 c	TeO2∙PbF2∙AlF3	18332	18957	20434	NA	NA	NA	NA	5.52	2.07	1.00
32	SrGdGa3O7	18135	19131	20411	NA	NA	NA	NA	2.46	1.24	0.51
33	YPO4	18348	19083	20449	435.7	67.2	7.4	2351	3.02	3.07	2.58
34 e	YSO	18348	19083	20449	NA	NA	NA	NA	1.29	0.29	2.78
35 c	BGM	18348	19083	20408	NA	NA	NA	NA	12.33	1.96	0.96
36 c	NYM	18148	19157	20449	NA	NA	NA	NA	13.34	1.69	2.29
37	Gd2(MoO4)3	18348	19157	20449	NA	NA	NA	NA	11.74	8.16	3.98
38	LiLa(MoO4)2	18348	19157	20449	NA	NA	NA	NA	8.07	1.06	0.83
39	LiLa(WO4)2	18348	19047	20345	NA	NA	NA	NA	9.03	2.02	0.59
40	KY(WO4)2	18420	19190	20450	NA	NA	NA	NA	7.08	2.30	1.01

^a Slater integrals calculated from F^2,4,6 parameters by Equation (15) in Ref. [17]. ^b Slater integrals calculated from Racah parameters by Equation (17) in Ref. [17]. ^c Slater integrals and spin–orbit coupling parameter not provided, the RME values the authors used are by Carnall in Ref. [66], or by ^d Weber in Ref. [35]. ^e Energy levels are not given in the literature, values in the table are provided approximately.

gives the energies of the ⁴S_3/2, ²H_11/2, and ⁴F_7/2 levels used for the two LIRs that will be theoretically investigated. As stated in the introduction, this is important in the estimation of the thermometric figures of merit, and it is linked to the Slater integrals and s–o parameters. The table also includes the Slater integrals and s–o coupling parameters of the 16 out of the 40 hosts, and the JO intensity parameters for all the hosts, taken from references Table 1.

Figure 2 presents the variation of Slater integrals and s–o coupling parameters in those 16 hosts. Although there are no large differences in parameters between the crystals and glasses, there are certain trends that may be observed by the type of compound. Deviations in parameters’ values from host to host can be large, so the use of Carnall or Weber tables [22,35] for Er³⁺ RMEs can introduce large errors in the later calculations.

Figure 3 presents the JO parameters as given in Table 2. Glass hosts have smaller values of JO parameters than crystals, on average. When crystals are analyzed, the largest values of Ω₂ parameter are found in tungstates and molybdates, while the smallest values are in garnets, phosphates, silicates, and oxysulfides. Ω₆ are expectedly higher in fluorides, phosphates, and silicates. In glasses, borate glasses have lower Ω₂, while phosphate glasses have higher Ω₂. Ω₆ is on average higher in phosphate glasses. No clear correlation could be given for the Ω₄ parameter in crystals or glasses.

The squared RMEs for each transition investigated for LIR are given in

Table 3. Squared RMEs for hosts in Table 1, recalculated by RELIC software [17] from Slater integrals and s–o coupling parameters in Table 2, refractive index values, local corrections for emission, and induced electric dipole strengths. Note: if Slater integrals were not provided in Table 2, the squared RMEs will be given from the tables by Carnall [66], unless indicated that the authors used tables by Weber [35].

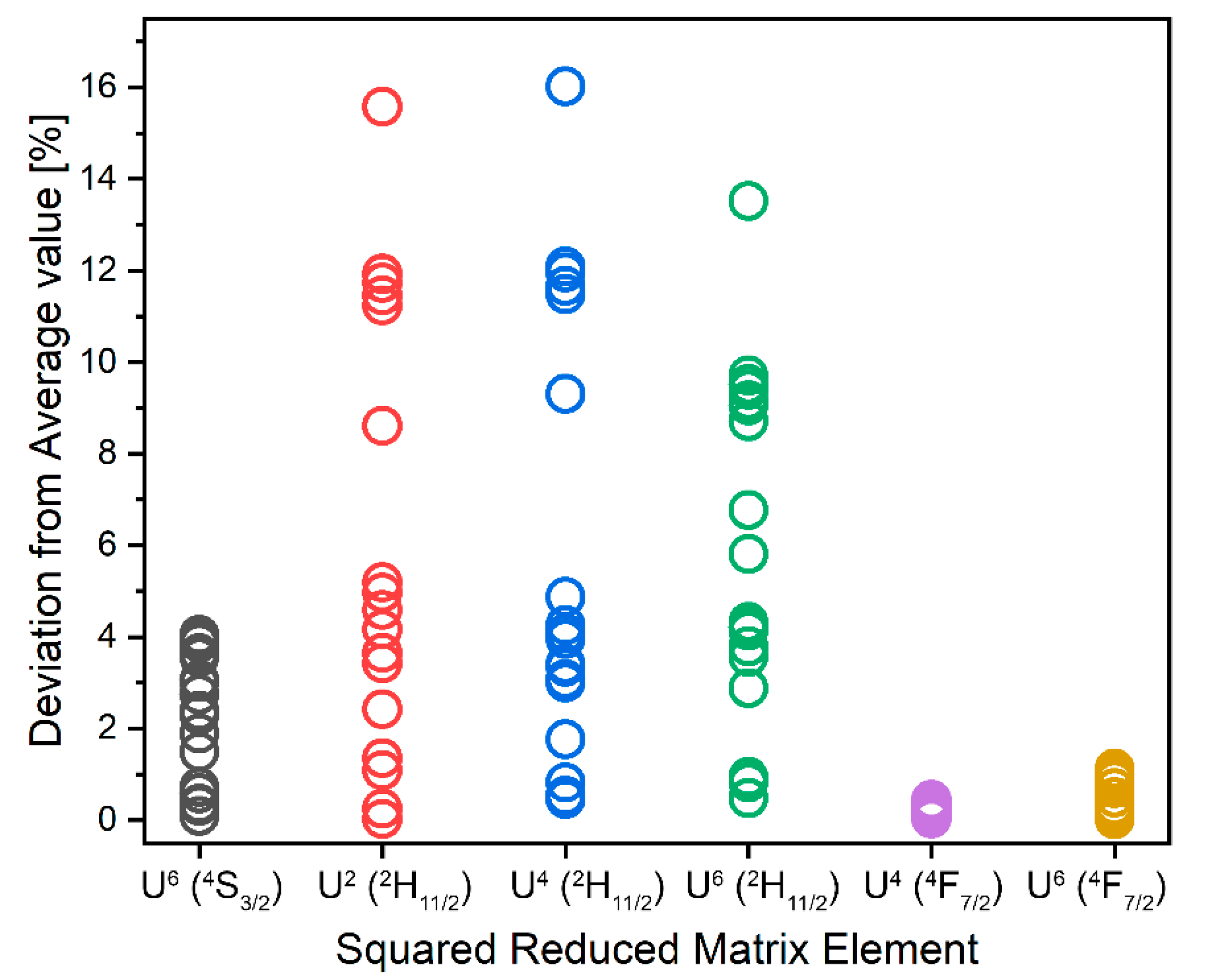
No.	Initial Level	Squared RME			n	χED (Emission)	Ref. for n	D [esu2 cm2] × 1040
		U2	U4	U6
1 b	4S3/2	0	0	0.2216	1.499	3.00	[33]	10.38
	2H11/2	0.7247	0.4159	0.0925	1.499	3.00		98.55
	4F7/2	0	0.1461	0.6298	1.499	3.00		33.40
2	4S3/2	0	0	0.2275	1.516	3.11	[67]	12.07
	2H11/2	0.7141	0.4112	0.0867	1.518	3.12		78.33
	4F7/2	0	0.1473	0.6285	1.522	3.15		36.75
3	4S3/2	0	0	0.2134	1.836	5.88	[36]	3.45
	2H11/2	0.5816	0.3350	0.0756	1.838	5.91		18.26
	4F7/2	0	0.1465	0.6192	1.842	5.95		13.11
4 b	4S3/2	0	0	0.2226	1.7	4.52	[68]	3.54
	2H11/2	0.7205	0.4152	0.0911	1.7	4.52		111.96
	4F7/2	0	0.1467	0.6274	1.7	4.52		17.03
5 b	4S3/2	0	0	0.2240	2.2	11.44	[69]	6.05
	2H11/2	0.6872	0.3971	0.0849	2.2	11.44		92.03
	4F7/2	0	0.1474	0.6247	2.2	11.44		24.75
6 b	4S3/2	0	0	0.2257	2.2	11.44	[69]	9.63
	2H11/2	0.6891	0.3968	0.0841	2.2	11.44		65.89
	4F7/2	0	0.1472	0.6272	2.2	11.44		33.90
7 c	4S3/2	0	0	0.2211	2.35	14.70	[39]	5.64
	2H11/2	0.7125	0.4123	0.0925	2.35	14.70		161.57
	4F7/2	0	0.1468	0.6266	2.35	14.70		26.55
8 a	4S3/2	0	0	0.2211	1.946	7.24	[40,41]	2.81
	2H11/2	0.7125	0.4123	0.0925	1.948	7.27		22.30
	4F7/2	0	0.1468	0.6266	1.953	7.34		9.91
9	4S3/2	0	0	0.2285	1.402	2.45	[35]	3.00
	2H11/2	0.7056	0.4109	0.0870	1.404	2.46		21.44
	4F7/2	0	0.1467	0.6273	1.406	2.47		11.19
10	4S3/2	0	0	0.2171	1.938	7.13	[70]	2.40
	2H11/2	0.6964	0.4022	0.0912	1.942	7.19		85.98
	4F7/2	0	0.1464	0.6238	1.948	7.27		10.99
11	4S3/2	0	0	0.2231	2.017	8.25	[71]	8.59
	2H11/2	0.6796	0.3919	0.0843	2.023	8.34		234.27
	4F7/2	0	0.1471	0.6253	2.036	8.54		31.66
12 b	4S3/2	0	0	0.2182	1.611	3.78	[45]	5.99
	2H11/2	0.6547	0.3795	0.0838	1.611	3.78		35.45
	4F7/2	0	0.1471	0.6200	1.611	3.78		20.85
13 bd	4S3/2	0	0	0.2285	1.85	6.04	[72]	10.07
	2H11/2	0.7056	0.4109	0.0870	1.85	6.04		89.25
	4F7/2	0	0.1467	0.6273	1.85	6.04		36.17
14 ac	4S3/2	0	0	0.2211	1.987	7.81	[36]	4.39
	2H11/2	0.7125	0.4123	0.0925	1.982	7.74		16.86
	4F7/2	0	0.1468	0.6266	1.998	7.97		13.68
15 ac	4S3/2	0	0	0.2211	1.944	7.21	[36]	4.44
	2H11/2	0.7125	0.4123	0.0925	1.948	7.27		21.54
	4F7/2	0	0.1468	0.6266	1.954	7.35		14.20
16 b	4S3/2	0	0	0.2157	1.564	3.44	[47]	7.31
	2H11/2	0.6296	0.3618	0.0815	1.564	3.44		97.49
	4F7/2	0	0.1463	0.6235	1.564	3.44		24.86
17 b	4S3/2	0	0	0.2145	1.478	2.88	[48]	4.06
	2H11/2	0.6115	0.3531	0.0795	1.478	2.88		54.70
	4F7/2	0	0.1466	0.6196	1.478	2.88		14.83
18 b	4S3/2	0	0	0.2138	1.476	2.86	[48]	3.06
	2H11/2	0.6068	0.3507	0.0792	1.476	2.86		22.91
	4F7/2	0	0.1467	0.6185	1.476	2.86		10.17
19 b	4S3/2	0	0	0.2143	1.480	2.89	[48]	7.51
	2H11/2	0.6081	0.3512	0.0791	1.480	2.89		60.55
	4F7/2	0	0.1467	0.6191	1.480	2.89		24.28
20 b	4S3/2	0	0	0.2135	1.479	2.88	[48]	5.42
	2H11/2	0.6067	0.3507	0.0794	1.479	2.88		40.58
	4F7/2	0	0.1466	0.6184	1.479	2.88		17.01
21 b	4S3/2	0	0	0.2137	1.481	2.89	[48]	4.44
	2H11/2	0.6100	0.3524	0.0798	1.481	2.89		29.26
	4F7/2	0	0.1466	0.6190	1.481	2.89		13.80
22 c	4S3/2	0	0	0.2211	2.167	10.80	[73]	1.12
	2H11/2	0.7125	0.4123	0.0925	2.172	10.89		29.88
	4F7/2	0	0.1468	0.6266	2.180	11.04		4.87
23 c	4S3/2	0	0	0.2211	2.316	13.95	[74]	6.48
	2H11/2	0.7125	0.4123	0.0925	2.331	14.31		143.84
	4F7/2	0	0.1468	0.6266	2.349	14.75		25.94
24 b	4S3/2	0	0	0.2156	1.779	5.27	[51]	3.03
	2H11/2	0.7176	0.4147	0.0959	1.779	5.27		67.47
	4F7/2	0	0.1461	0.6243	1.779	5.27		13.30
25 d	4S3/2	0	0	0.2285	1.518	3.12	[52]	5.11
	2H11/2	0.7056	0.4109	0.0870	1.519	3.13		56.47
	4F7/2	0	0.1467	0.6273	1.520	3.14		18.74
26 b	4S3/2	0	0	0.2211	1.819	5.70	[53]	7.29
	2H11/2	0.7125	0.4123	0.0925	1.819	5.70		52.12
	4F7/2	0	0.1468	0.6266	1.819	5.70		25.85
27 bd	4S3/2	0	0	0.2285	1.584	3.58	[75]	6.85
	2H11/2	0.7056	0.4109	0.0870	1.584	3.58		90.58
	4F7/2	0	0.1467	0.6273	1.584	3.58		22.91
28 bd	4S3/2	0	0	0.2285	1.587	3.60	[75]	7.59
	2H11/2	0.7056	0.4109	0.0870	1.587	3.60		109.39
	4F7/2	0	0.1467	0.6273	1.587	3.60		24.46
29 bd	4S3/2	0	0	0.2285	1.588	3.61	[75]	7.64
	2H11/2	0.7056	0.4109	0.0870	1.588	3.61		92.30
	4F7/2	0	0.1467	0.6273	1.588	3.61		23.32
30 a	4S3/2	0	0	0.2211	1.581	3.56	[55]	7.09
	2H11/2	0.7125	0.4125	0.0925	1.587	3.60		115.99
	4F7/2	0	0.1469	0.6266	1.599	3.69		23.58
31 bc	4S3/2	0	0	0.2211	2.116	9.86	[56]	5.10
	2H11/2	0.7125	0.4123	0.0925	2.116	9.86		112.55
	4F7/2	0	0.1468	0.6266	2.116	9.86		21.46
32 bd	4S3/2	0	0	0.2285	1.831	5.83	[57]	2.69
	2H11/2	0.7056	0.4109	0.0870	1.831	5.83		52.82
	4F7/2	0	0.1467	0.6273	1.831	5.83		11.58
33 b	4S3/2	0	0	0.2275	1.77	5.18	[58]	13.54
	2H11/2	0.7141	0.4112	0.0866	1.77	5.18		84.03
	4F7/2	0	0.1473	0.6285	1.77	5.18		47.84
34 bd	4S3/2	0	0	0.2285	1.8	5.49	[76]	14.65
	2H11/2	0.7056	0.4109	0.0870	1.8	5.49		29.33
	4F7/2	0	0.1467	0.6273	1.8	5.49		41.21
35 bc	4S3/2	0	0	0.2211	2.02	8.30	[60]	4.90
	2H11/2	0.7125	0.4123	0.0925	2.02	8.30		223.35
	4F7/2	0	0.1468	0.6266	2.02	8.30		20.51
36 c	4S3/2	0	0	0.2211	2.01	8.15	[61]	11.68
	2H11/2	0.7125	0.4123	0.0925	2.00	8.00		240.22
	4F7/2	0	0.1468	0.6266	2.00	8.00		38.82
37 ad	4S3/2	0	0	0.2211	2.16	10.66	[55,77]	20.30
	2H11/2	0.7125	0.4125	0.0925	2.16	10.66		279.11
	4F7/2	0	0.1469	0.6266	2.16	10.66		85.18
38 d	4S3/2	0	0	0.2285	2.05	8.76	[63]	4.38
	2H11/2	0.7056	0.4109	0.0870	2.05	8.76		143.07
	4F7/2	0	0.1467	0.6273	2.05	8.76		15.60
39 bd	4S3/2	0	0	0.2285	2.0	8.00	[78]	3.11
	2H11/2	0.7056	0.4109	0.0870	2.0	8.00		167.32
	4F7/2	0	0.1467	0.6273	2.0	8.00		15.37
40 bd	4S3/2	0	0	0.2285	2.0	8.00	[79]	5.32
	2H11/2	0.7056	0.4109	0.0870	2.0	8.00		139.07
	4F7/2	0	0.1467	0.6273	2.0	8.00		22.40

^a RME values not calculated by RELIC software, but given in the corresponding reference. ^b Refractive Index values approx. wavelength-independent. ^c RME values from Carnall [66], ^d from Weber [35].

. This list can be used beyond the scope of this paper for accurate calculations of JO parameters. The deviations from the average RME values are given in Figure 4, and they are large for the ²H_11/2→⁴I_15/2 transition. Thus, the use of Carnall’s or Weber’s values [22,35] might introduce significant errors in the JO parameters estimation, as the RMEs were calculated for the LaF₃ and YAlO₃, respectively. The average RMEs values calculated from Table 3 are given in

Table 4. Average RME values estimated from squared RMEs listed in Table 3. Deviations of average values from squared RMEs reported by Carnall (C) and Weber (W), in percentage.

Initial Level	U2	U4	U6	U2(C)	U4(C)	U6(C)	U2(W)	U4(W)	U6(W)
4S3/2	0	0	0.2224	0	0	0.6	0	0	2.7
2H11/2	0.6889	0.3989	0.0874	3.3	3.3	5.5	2.4	2.9	0.5
4F7/2	0	0.1468	0.6254	0	0	0.2	0	0.1	0.3

, together with the deviations from the values by Carnall and Weber. The refractive index values taken from the corresponding references are also listed in Table 3. If Sellmeier’s equation is given, the refractive index is calculated at the wavelength of the emission. From the refractive index value, the local field correction is calculated according to Equation (11). The induced ED strengths (the last column of Table 3) are calculated for each transition and for each using JO parameters from Table 2 and local field corrections and RMEs from Table 3.

3.2. Calculations of LIR Parameters

For this theoretical analysis, two Er³⁺-based LIRs are considered, the traditional LIR that uses the temperature-dependent ratio of emissions from ⁴S_3/2 and ²H₁₁ levels, and the relatively novel concept that uses the temperature-dependent ratio emissions from ⁴S_3/2 and ⁴F_7/2 levels.

Table 5. Calculated luminescence thermometry parameters: energy gaps (ΔE) from Er^{3+ 4}S_3/2 level to ²H_11/2 and ⁴F_7/2, relative temperature sensitivities (S_r) for LIRs between selected levels, B LIR parameters, absolute sensitivities at room temperature (S_a), maximum sensitivity value (S_amax), temperatures at which maximum absolute sensitivity occurs (T(S_amax)), and relative sensitivities at T(S_amax) (S_r(T(S_amax)).

No.	Higher Level	ΔE	Sr (300 K) [% K−1]	B	Sa (300 K) [K−1]	max(Sa) [K−1]	T(max(Sa)) [K] (°C)	Sr (T(max(Sa)) [% K−1]
1	2H11/2	727	1.16	10.66	0.003792	0.0055	523 (250)	0.38
	4F7/2	2024	3.24	4.40	0.000009	0.0008	1456 (1183)	0.14
2	2H11/2	765	1.22	7.37	0.002297	0.0036	550 (277)	0.36
	4F7/2	2059	3.29	4.24	0.000007	0.0008	1481 (1208)	0.14
3	2H11/2	801	1.28	6.05	0.001663	0.0028	576 (303)	0.35
	4F7/2	2178	3.48	5.40	0.000005	0.0009	1567 (1294)	0.13
4	2H11/2	685	1.10	35.26	0.014453	0.0194	493 (220)	0.41
	4F7/2	2031	3.25	6.58	0.000013	0.0012	1461 (1188)	0.14
5	2H11/2	694	1.10	17.03	0.006772	0.0092	499 (226)	0.40
	4F7/2	2084	3.30	5.66	0.000009	0.0010	1499 (1226)	0.13
6	2H11/2	694	1.10	7.65	0.003043	0.0042	499 (226)	0.40
	4F7/2	2084	3.30	4.87	0.000007	0.0009	1499 (1226)	0.13
7	2H11/2	993	1.59	33.60	0.004557	0.0128	714 (441)	0.28
	4F7/2	2394	3.83	6.82	0.000003	0.0011	1722 (1449)	0.12
8	2H11/2	800	1.28	9.07	0.002501	0.0043	576 (303)	0.35
	4F7/2	1950	3.12	4.85	0.000013	0.0009	1403 (1130)	0.14
9	2H11/2	855	1.37	8.21	0.001858	0.0036	615 (342)	0.33
	4F7/2	2126	3.40	5.21	0.000007	0.0009	1529 (1256)	0.13
10	2H11/2	860	1.37	41.42	0.009209	0.0181	619 (346)	0.32
	4F7/2	2195	3.51	6.57	0.000006	0.0011	1579 (1306)	0.13
11	2H11/2	850	1.36	31.60	0.007284	0.0140	612 (339)	0.33
	4F7/2	2162	3.46	5.34	0.000006	0.0009	1555 (1282)	0.13
12	2H11/2	641	1.02	6.55	0.003104	0.0038	461 (188)	0.43
	4F7/2	2066	3.30	4.78	0.000008	0.0009	1486 (1213)	0.13
13	2H11/2	742	1.19	9.99	0.003373	0.0051	534 (261)	0.37
	4F7/2	2156	3.45	5.02	0.000006	0.0009	1551 (1278)	0.13
14	2H11/2	718	1.15	4.27	0.001566	0.0022	517 (244)	0.39
	4F7/2	1937	3.10	4.29	0.000012	0.0008	1394 (1121)	0.14
15	2H11/2	694	1.11	5.46	0.002173	0.0030	499 (226)	0.40
	4F7/2	1912	3.06	4.38	0.000014	0.0009	1376 (1103)	0.15
16	2H11/2	812	1.30	15.17	0.004009	0.0070	584 (311)	0.34
	4F7/2	2068	3.31	4.68	0.000008	0.0009	1488 (1215)	0.13
17	2H11/2	792	1.27	15.30	0.004339	0.0073	570 (297)	0.35
	4F7/2	2075	3.32	5.04	0.000008	0.0009	1493 (1220)	0.13
18	2H11/2	779	1.25	8.48	0.002519	0.0041	560 (287)	0.36
	4F7/2	2073	3.31	4.58	0.000007	0.0008	1491 (1218)	0.13
19	2H11/2	792	1.27	9.14	0.002594	0.0043	570 (297)	0.35
	4F7/2	2075	3.32	4.45	0.000007	0.0008	1493 (1220)	0.13
20	2H11/2	792	1.27	8.50	0.002411	0.0040	570 (297)	0.35
	4F7/2	2075	3.32	4.33	0.000007	0.0008	1493 (1220)	0.13
21	2H11/2	802	1.28	7.50	0.002052	0.0035	577 (304)	0.35
	4F7/2	2085	3.33	4.29	0.000006	0.0008	1500 (1227)	0.13
22	2H11/2	926	1.48	31.12	0.005428	0.0126	666 (393)	0.30
	4F7/2	2118	3.39	6.16	0.000008	0.0011	1524 (1251)	0.13
23	2H11/2	799	1.28	25.90	0.007167	0.0122	575 (302)	0.35
	4F7/2	2244	3.59	6.00	0.000005	0.0010	1614 (1341)	0.12
24	2H11/2	796	1.27	25.24	0.007058	0.0119	573 (300)	0.35
	4F7/2	2100	3.36	6.05	0.000009	0.0011	1511 (1238)	0.13
25	2H11/2	743	1.19	12.46	0.004194	0.0063	535 (262)	0.37
	4F7/2	2084	3.33	5.07	0.000008	0.0009	1499 (1226)	0.13
26	2H11/2	709	1.13	8.00	0.003025	0.0042	510 (237)	0.39
	4F7/2	2007	3.21	4.83	0.000010	0.0009	1444 (1171)	0.14
27	2H11/2	845	1.35	15.13	0.003551	0.0067	608 (335)	0.33
	4F7/2	2142	3.42	4.66	0.000006	0.0008	1541 (1268)	0.13
28	2H11/2	849	1.36	16.50	0.003818	0.0073	611 (338)	0.33
	4F7/2	2109	3.37	4.46	0.000006	0.0008	1517 (1244)	0.13
29	2H11/2	849	1.36	13.83	0.003199	0.0061	611 (338)	0.33
	4F7/2	2109	3.37	4.23	0.000006	0.0008	1517 (1244)	0.13
30	2H11/2	800	1.28	18.82	0.005190	0.0089	576 (303)	0.35
	4F7/2	1950	3.12	4.67	0.000013	0.0009	1403 (1130)	0.14
31	2H11/2	625	1.00	24.40	0.012168	0.0147	450 (177)	0.44
	4F7/2	2102	3.36	5.83	0.000008	0.0010	1512 (1239)	0.13
32	2H11/2	996	1.59	23.07	0.003093	0.0087	717 (444)	0.28
	4F7/2	2276	3.64	6.14	0.000004	0.0010	1637 (1364)	0.12
33	2H11/2	735	1.18	6.98	0.002416	0.0036	529 (256)	0.38
	4F7/2	2101	3.36	4.89	0.000007	0.0009	1512 (1239)	0.13
34	2H11/2	735	1.18	2.25	0.000779	0.0012	529 (256)	0.38
	4F7/2	2101	3.36	3.89	0.000005	0.0007	1512 (1239)	0.13
35	2H11/2	735	1.18	51.32	0.017757	0.0263	529 (256)	0.38
	4F7/2	2060	3.29	5.77	0.000010	0.0011	1482 (1209)	0.13
36	2H11/2	1009	1.61	23.75	0.003032	0.0089	726 (453)	0.28
	4F7/2	2301	3.68	4.67	0.000003	0.0008	1655 (1382)	0.12
37	2H11/2	809	1.29	15.65	0.004179	0.0073	582 (309)	0.34
	4F7/2	2101	3.36	5.81	0.000008	0.0010	1512 (1239)	0.13
38	2H11/2	809	1.29	37.22	0.009940	0.0173	582 (309)	0.34
	4F7/2	2101	3.36	4.94	0.000007	0.0009	1512 (1239)	0.13
39	2H11/2	699	1.12	60.18	0.023537	0.0324	503 (230)	0.40
	4F7/2	1997	3.19	6.74	0.000015	0.0013	1437 (1164)	0.14
40	2H11/2	770	1.23	29.54	0.009052	0.0144	554 (281)	0.36
	4F7/2	2030	3.25	5.76	0.000011	0.0011	1460 (1187)	0.14

provides the energy differences between ⁴S_3/2 and ²H₁₁ and ⁴S_3/2 and ⁴F_7/2 that are used to calculate the room-temperature-relative sensitivities for each host using Equation (2). The temperature invariant B parameters are calculated from the data in Table 3 using Equation (19) (version for spectra recorded in counts). Then, using Equations (2)–(4) and calculated B values, it was possible to derive the LIR’s absolute sensitivity, the maximal absolute sensitivity value, and the temperature at which maximal absolute sensitivity occurs.

The relation between relative and absolute sensitivities of traditional LIR (that uses Er³⁺ emissions from ²H_11/2 and ⁴S_3/2 levels) for different hosts is presented in Figure 5a–c. As a rule of thumb, the higher the sensitivity value the better is the performance of thermometry. From Figure 5a, one can see that glasses tend to perform slightly weaker than crystals, on average. Figure 5b compares the LIR performance of different crystals. Fluorides’, garnets’, phosphates’, and silicates’ performances are worse than for other hosts. The best results are obtained with simple oxides, vanadates, niobates, molybdates, and tungstates. Figure 5c illustrates the performances of only glass hosts. Even the number of hosts in this set is rather small, it is possible to observe that Er³⁺ activated borate glasses perform worse than other glasses. Fluorophosphate glasses show high relative sensitivities, but somewhat small absolute sensitivities. The best combination of sensitivities is achieved in PbO-PbF₂ glass. Similar conclusions can be drawn for the novel LIR type (that uses Er³⁺ emissions from ⁴F_7/2 and ⁴S_3/2 levels), Figure 5d–f. Among different glasses, tellurite-fluoride glasses show the best performance. For crystals, the situation is almost equivalent to that of traditional LIR.

Figure 6a–c gives the relation between relative sensitivity and absolute sensitivity at the temperature at which the absolute sensitivity has its maximum for the traditional LIR, while Figure 6d–f show the same relationship for the novel type LIR. Analogous conclusions can be drawn as in the previous analysis (Figure 5). Among glass hosts, tellurite-fluoride, tungstate, and molybdate glasses show the best performances. Among crystals, the performance trend is almost the same, but the NaY(MoO₄)₂ shows the worst performance at elevated temperatures. The best overall performer is LiLa(WO₄)₂.

As a limit of the study, we must note that the values of the energy levels, Slater integrals and s–o parameters, refractive index values, and JO parameters are taken from literature, so one cannot estimate the level of their accuracy. The extreme outliers are to be taken with caution.

4. Conclusions

The conventional thermometric characterizations are lengthy, complicated, and expensive. Given that there is an infinite number of possible hosts and doping concentrations of luminescent activators, the guidelines in selecting the appropriate material are important, and they can be provided by the Judd–Ofelt thermometric model which predicts thermometric figures of merit from its 3 intensity parameters.

Er³⁺ deserves special attention in luminescence thermometry. It features LIR between ²H_11/2 and ⁴S_3/2 levels with energy separation of ~700 cm⁻¹, and a recently introduced LIR between ⁴F_7/2 and ⁴S_3/2 levels, whose higher energy separation allows for up to 3× larger relative sensitivity. The performances of 40 various crystals and glasses were predicted by the Judd–Ofelt thermometric model, and guidelines were set to aid the search for the best phosphor for LIR thermometry.

It was demonstrated that the Slater integrals and s–o coupling parameters significantly vary from host to host so that their values should not be adopted from other hosts. Consequently, for Er³⁺, the squared reduced matrix elements also significantly vary between hosts (especially for the ²H_11/2→⁴I_15/2 transition). Therefore, RMEs from frequently used Carnall or Weber tables should be replaced by the average RMEs for the three transitions that are used in these LIR read-out schemes, if the exact RMEs cannot be obtained. This will allow for the improved precision in the prediction of thermometric sensor performances, as well as for the improved Judd–Ofelt parametrization of Er³⁺ doped compounds.