Magnetic and Electronic Properties of Heavy Lanthanides (Gd, Tb, Dy, Er, Ho, Tm)
Abstract
:1. Introduction
2. Theoretical Consideration
- axial anisotropy, together with the magnetoelastic forces, favors the maximum momentum at each node for a given configuration of exchange forces, which can only be achieved in a commensurate structure;
- exchange interaction also favors the maximum momentum, providing a change with a periodicity not inconsistent with the maximum . At higher temperatures, increasing entropy in the incommensurable phase likely plays a role in maintaining incommensurability and the development of instability at potential transition points, preventing the occurrence of a phase transition.
3. Results and Discussion
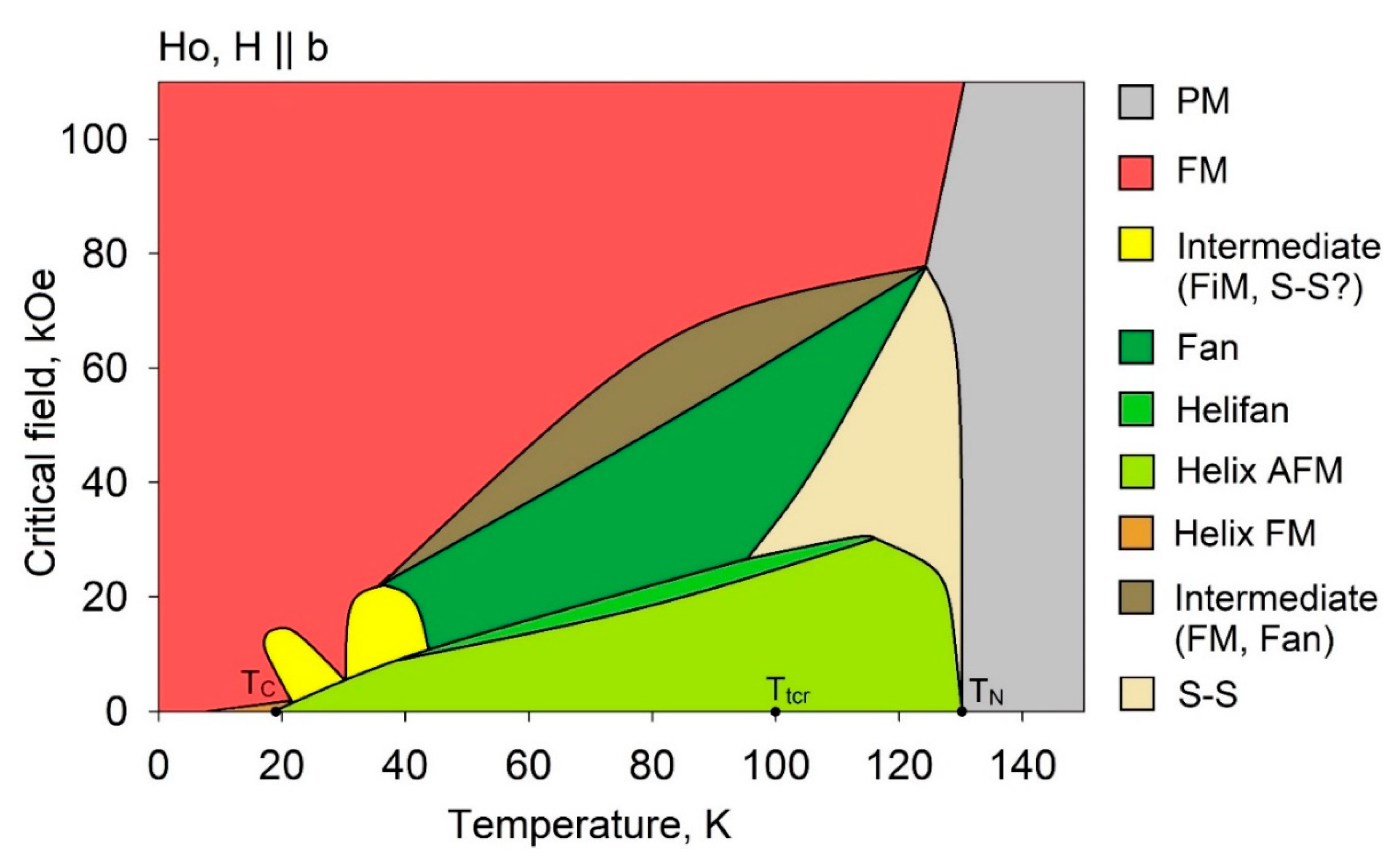
Magnetic Phase Diagrams of Heavy Lanthanides
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miwa, H.; Yosida, K. Magnetic Ordering in the Rare-Earth Metals with More than Half-Filled 4f Shells. Prog. Theor. Phys. 1961, 26, 693–721. [Google Scholar] [CrossRef] [Green Version]
- Kitano, Y.; Nagamiya, T. Magnetization Process of a Screw Spin System. II. Prog. Theor. Phys. 1964, 31, 1–43. [Google Scholar] [CrossRef]
- Nagamiya, T.; Nagata, K.; Kitano, Y. Magnetization Process of a Screw Spin System. Prog. Theor. Phys. 1962, 27, 1253–1271. [Google Scholar] [CrossRef]
- Cooper, B.R.; Elliott, R.J.; Nettel, S.J.; Suhl, H. Theory of Magnetic Resonance in the Heavy Rare-Earth Metals. Phys. Rev. 1962, 127, 57–68. [Google Scholar] [CrossRef]
- Kaplan, T.A. Some Effects of Anisotropy on Spiral Spin-Configurations with Application to Rare-Earth Metals. Phys. Rev. 1961, 124, 329–339. [Google Scholar] [CrossRef]
- Yosida, K.; Watabe, A. Fermi Surfaces and Spin Structures in Heavy Rare-Earth Metals. Prog. Theor. Phys. 1962, 28, 361–370. [Google Scholar] [CrossRef] [Green Version]
- Hughes, I.D.; Däne, M.; Ernst, A.; Hergert, W.; Lüders, M.; Poulter, J.; Staunton, J.B.; Svane, A.; Szotek, Z.; Temmerman, W.M. Lanthanide Contraction and Magnetism in the Heavy Rare Earth Elements. Nature 2007, 446, 650–653. [Google Scholar] [CrossRef]
- Döbrich, K.M.; Bostwick, A.; McChesney, J.L.; Rossnagel, K.; Rotenberg, E.; Kaindl, G. Fermi-Surface Topology and Helical Antiferromagnetism in Heavy Lanthanide Metals. Phys. Rev. Lett. 2010, 104, 246401. [Google Scholar] [CrossRef]
- Locht, I.L.M.; Kvashnin, Y.O.; Rodrigues, D.C.M.; Pereiro, M.; Bergman, A.; Bergqvist, L.; Lichtenstein, A.I.; Katsnelson, M.I.; Delin, A.; Klautau, A.B.; et al. Standard Model of the Rare Earths Analyzed from the Hubbard I Approximation. Phys. Rev. B 2016, 94, 085137. [Google Scholar] [CrossRef] [Green Version]
- Mendive-Tapia, E.; Staunton, J.B. Theory of Magnetic Ordering in the Heavy Rare Earths: Ab Initio Electronic Origin of Pair- and Four-Spin Interactions. Phys. Rev. Lett. 2017, 118, 197202. [Google Scholar] [CrossRef] [Green Version]
- Mendive-Tapia, E.; Staunton, J.B. Caloric Effects around Phase Transitions in Magnetic Materials Described by Ab Initio Theory: The Electronic Glue and Fluctuating Local Moments. J. Appl. Phys. 2020, 127, 113903. [Google Scholar] [CrossRef]
- Tapia, E.M. Ab Initio Theory of Magnetic Ordering: Electronic Origin of Pair- and Multi-Spin Interactions; Springer Theses; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-030-37237-8. [Google Scholar]
- Spedding, F.H.; Hanak, J.J.; Daane, A.H. High Temperature Allotropy and Thermal Expansion of the Rare-Earth Metals. J. Less Common Met. 1961, 3, 110–124. [Google Scholar] [CrossRef]
- Spedding, F.H.; Daane, A.H.; Herrmann, K.W. The Crystal Structures and Lattice Parameters of High-Purity Scandium, Yttrium and the Rare Earth Metals. Acta Crystallogr. 1956, 9, 559–563. [Google Scholar] [CrossRef] [Green Version]
- Banister, J.R.; Legvold, S.; Spedding, F.H. Structure of Gd, Dy, and Er at Low Temperatures. Phys. Rev. 1954, 94, 1140–1142. [Google Scholar] [CrossRef]
- Barson, F.; Legvold, S.; Spedding, F.H. Thermal Expansion of Rare Earth Metals. Phys. Rev. 1957, 105, 418–424. [Google Scholar] [CrossRef]
- Behrendt, D.R.; Legvold, S.; Spedding, F.H. Magnetic Properties of Dysprosium Single Crystals. Phys. Rev. 1958, 109, 1544–1547. [Google Scholar] [CrossRef]
- Elliott, J.F.; Legvold, S.; Spedding, F.H. Some Magnetic Properties of Gadolinium Metal. Phys. Rev. 1953, 91, 28–30. [Google Scholar] [CrossRef]
- Gerstein, B.C.; Griffel, M.; Jennings, L.D.; Miller, R.E.; Skochdopole, R.E.; Spedding, F.H. Heat Capacity of Holmium from 15 to 300° K. J. Chem. Phys. 1957, 27, 394–399. [Google Scholar] [CrossRef]
- Green, R.W.; Legvold, S.; Spedding, F.H. Magnetization and Electrical Resistivity of Erbium Single Crystals. Phys. Rev. 1961, 122, 827–830. [Google Scholar] [CrossRef]
- Rhodes, B.L.; Legvold, S.; Spedding, F.H. Magnetic Properties of Holmium and Thulium Metals. Phys. Rev. 1958, 109, 1547–1550. [Google Scholar] [CrossRef]
- Jennings, L.D.; Stanton, R.M.; Spedding, F.H. Heat Capacity of Terbium from 15 to 350° K. J. Chem. Phys. 1957, 27, 909–913. [Google Scholar] [CrossRef]
- Taylor, K.N.R.; Taylor, K.N.R.; Darby, M.I. Physics of Rare Earth Solids; Chapman and Hall: London, UK, 1972. [Google Scholar]
- Methfessel, S.; Mattis, D.C. Magnetic Semiconductors; Springer: Berlin/Heidelberg, Germany, 1968. [Google Scholar]
- Вoнсoвский, С.В.; Турoв, Е.А. Об Обменнoм Взаимoдействии Валентных и Внутренних Электрoнoв в Кристаллах (s-d-Обменная Мoдель Перехoдных Кристаллoв). ЖЭТФ 1953, 24, 419–428. (In Russian) [Google Scholar]
- Elliott, R.J.; Wedgwood, F.A. The Temperature Dependence of Magnetic Ordering in the Heavy Rare Earth Metals. Proc. Phys. Soc. 1964, 84, 63–75. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E. Character of phase transitions to a helical or sinusoidal state in magnetic materials. Sov. Phys. JETP 1977, 45, 1014–1022. [Google Scholar]
- Dzyaloshinskii, I.E. The Theory of Helicoidal Structures in Antiferromagnets. II. Metals. Sov. Phys. JETP 1965, 20, 223–231. [Google Scholar]
- Evenson, W.E.; Liu, S.H. Theory of Magnetic Ordering in the Heavy Rare Earths. Phys. Rev. 1969, 178, 783–794. [Google Scholar] [CrossRef]
- Evenson, W.E.; Liu, S.H. Generalized Susceptibilities and Magnetic Ordering of Heavy Rare Earths. Phys. Rev. Lett. 1968, 21, 432–434. [Google Scholar] [CrossRef] [Green Version]
- Keeton, S.C.; Loucks, T.L. Electronic Structure of Rare-Earth Metals. I. Relativistic Augmented-Plane-Wave Calculations. Phys. Rev. 1968, 168, 672–678. [Google Scholar] [CrossRef]
- Lu, J.-B.; Cantu, D.C.; Nguyen, M.-T.; Li, J.; Glezakou, V.-A.; Rousseau, R. Norm-Conserving Pseudopotentials and Basis Sets To Explore Lanthanide Chemistry in Complex Environments. J. Chem. Theory Comput. 2019, 15, 5987–5997, Erratum in 2020, 16, 4754. [Google Scholar] [CrossRef]
- Jensen, J.B.; Mackintosh, A.R. Rare Earth Magnetism. Structures and Excitations; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Enkovaara, J.; Rostgaard, C.; Mortensen, J.J.; Chen, J.; Dułak, M.; Ferrighi, L.; Gavnholt, J.; Glinsvad, C.; Haikola, V.; Hansen, H.A.; et al. Electronic Structure Calculations with GPAW: A Real-Space Implementation of the Projector Augmented-Wave Method. J. Phys. Condens. Matter 2010, 22, 253202. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Blaha, P.; Schwarz, K.; Sjöstedt, E.; Nordström, L. Efficient Linearization of the Augmented Plane-Wave Method. Phys. Rev. B 2001, 64, 195134. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Zunger, A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Freeman, A.J. Energy Band Structure, Indirect Exchange Interactions and Magnetic Ordering. In Magnetic Properties of Rare Earth Metals; Elliott, R.J., Ed.; Springer: Boston, MA, USA, 1972; pp. 245–333. ISBN 978-1-4757-5691-3. [Google Scholar]
- Kurz, P.; Bihlmayer, G.; Blügel, S. Magnetism and Electronic Structure of Hcp Gd and the Gd(0001) Surface. J. Phys. Condens. Matter 2002, 14, 6353–6371. [Google Scholar] [CrossRef]
- Tereshina, E.A.; Khmelevskyi, S.; Politova, G.; Kaminskaya, T.; Drulis, H.; Tereshina, I.S. Magnetic Ordering Temperature of Nanocrystalline Gd: Enhancement of Magnetic Interactions via Hydrogenation-Induced “Negative” Pressure. Sci. Rep. 2016, 6, srep22553. [Google Scholar] [CrossRef] [Green Version]
- Sticht, J.; Kübler, J. Electronic Structure of Ferromagnetic Gd. Solid State Commun. 1985, 53, 529–532. [Google Scholar] [CrossRef]
- Gimaev, R.R.; Zverev, V.I.; Mello, V.D. Magnetic Properties of Single-Crystalline Terbium and Holmium—Experiment and Modeling. J. Magn. Magn. Mater. 2020, 505, 166781. [Google Scholar] [CrossRef]
- Elliott, R.J. Phenomenological Discussion of Magnetic Ordering in the Heavy Rare-Earth Metals. Phys. Rev. 1961, 124, 346–353. [Google Scholar] [CrossRef]
- Zverev, V.I.; Gimaev, R.R.; Komlev, A.S.; Kovalev, B.B.; Queiroz, F.G.; Mello, V.D. Magnetic Properties of Dysprosium—Experiment and Modeling. J. Magn. Magn. Mater. 2021, 524, 167593. [Google Scholar] [CrossRef]
- Smart, J.S. Effective Field Theories of Magnetism; Saunders: Philadelphia, PA, USA, 1966. [Google Scholar]
- Jensen, J. Hartree-Fock Renormalization of Magnetic Anisotropy in the Basal-Plane Ferromagnets Terbium and Dysprosium. J. Phys. C Solid State Phys. 1975, 8, 2769. [Google Scholar] [CrossRef]
- Levy, P.M. Antisymmetric Exchange. Phys. Rev. Lett. 1968, 20, 1366–1370. [Google Scholar] [CrossRef]
- Levy, P.M. Indirect Exchange via Spin-Orbit Coupled States. Solid State Commun. 1969, 7, 1813–1818. [Google Scholar] [CrossRef]
- Elliott, R. (Ed.) Magnetic Properties of Rare Earth Metals; Springer: Boston, MA, USA, 1972; ISBN 978-1-4757-5693-7. [Google Scholar]
- Yosida, K. Chapter V Magnetic Structures of Heavy Rare-Earth Metals. In Progress in Low Temperature Physics; Gorter, C.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1964; Volume 4, pp. 265–295. [Google Scholar]
- Sinha, S.K. Chapter 7 Magnetic structures and inelastic neutron scattering: Metals, alloys and compounds. In Handbook on the Physics and Chemistry of Rare Earths; Metals; Elsevier: Amsterdam, The Netherlands, 1978; Volume 1, pp. 489–589. [Google Scholar]
- Sherrington, D. The Tilted Helix: An Intermediate Magnetic Phase. J. Phys. C Solid State Phys. 1973, 6, 1037–1053. [Google Scholar] [CrossRef]
- Izyumov, Y.A. Modulated, or Long-Periodic, Magnetic Structures of Crystals. Sov. Phys. Uspekhi 1984, 27, 845–867. [Google Scholar] [CrossRef]
- Jensen, J. Molecular Field Calculation of the Magnetic Structure in Erbium. J. Phys. F Met. Phys. 1976, 6, 1145. [Google Scholar] [CrossRef] [Green Version]
- Habenschuss, M.; Stassis, C.; Sinha, S.K.; Deckman, H.W.; Spedding, F.H. Neutron Diffraction Study of the Magnetic Structure of Erbium. Phys. Rev. B 1974, 10, 1020–1026. [Google Scholar] [CrossRef]
- Vonsovskii, S.V. Magnetism; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Cooper, B.R. Magnetic Properties of Rare Earth Metals. In Solid State Physics; Seitz, F., Turnbull, D., Ehrenreich, H., Eds.; Academic Press: Cambridge, MA, USA, 1968; Volume 21, pp. 393–490. [Google Scholar]
- Garel, T.; Pfeuty, P. Commensurability Effects on the Critical Behaviour of Systems with Helical Ordering. J. Phys. C Solid State Phys. 1976, 9, L245–L249. [Google Scholar] [CrossRef]
- Plumer, M.L.; Caillé, A. Magnetic Phase Diagrams of the Antiferromagnetic Planar Model on a Stacked Triangular Lattice. Phys. Rev. B 1990, 42, 10388–10396. [Google Scholar] [CrossRef]
- Zverev, V.I.; Tishin, A.M.; Min, Z.; Mudryk, Y.; Gschneidner, K.A.; Pecharsky, V.K. Magnetic and Magnetothermal Properties, and the Magnetic Phase Diagram of Single-Crystal Holmium along the Easy Magnetization Direction. J. Phys. Condens. Matter 2015, 27, 146002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, H.; Collins, M.F.; Holden, T.M.; Wei, W. Magnetic Structure of Erbium. Phys. Rev. B 1992, 45, 12873–12882. [Google Scholar] [CrossRef] [PubMed]
- Watson, B.; Ali, N. On the Phase Diagram of Erbium. J. Alloy. Compd. 1997, 250, 662–665. [Google Scholar] [CrossRef]
- Cooper, B.R. Magnetoelastic Effects and the Magnetic Properties of Rare-Earth Metals. Phys. Rev. Lett. 1967, 19, 900–903. [Google Scholar] [CrossRef]
- Cooper, B.R. Spin Waves and Magnetic Resonance in Rare-Earth Metals: Thermal, Applied-Field, and Magnetoelastic Effects. Phys. Rev. 1968, 169, 281–294. [Google Scholar] [CrossRef]
- Spichkin, Y.I.; Tishin, A.M. Magnetocaloric Effect at the First-Order Magnetic Phase Transitions. J. Alloy. Compd. 2005, 403, 38–44. [Google Scholar] [CrossRef]
- Zverev, V.I.; Gimaev, R.R. Explanation of Relatively High Values of the Magnetic Entropy Change in Single Crystalline Terbium. Phys. B Condens. Matter 2016, 502, 187–189. [Google Scholar] [CrossRef]
- Legvold, S. Chapter 3 Rare earth metals and alloys. In Handbook of Ferromagnetic Materials; Elsevier: Amsterdam, The Netherlands, 1980; Volume 1, pp. 183–295. [Google Scholar]
- Fort, D.; Pecharsky, V.K.; Gschneidner, K.A. Solid State Electrotransport Purification of Dysprosium. J. Alloy. Compd. 1995, 226, 190–196. [Google Scholar] [CrossRef]
- Zverev, V.I.; Tishin, A.M.; Chernyshov, A.S.; Mudryk, Y.; Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetic and Magnetothermal Properties and the Magnetic Phase Diagram of High Purity Single Crystalline Terbium along the Easy Magnetization Direction. J. Phys. Condens. Matter 2014, 26, 066001. [Google Scholar] [CrossRef]
- Dan’kov, S.Y.; Tishin, A.M.; Pecharsky, V.K.; Gschneidner, K.A. Magnetic Phase Transitions and the Magnetothermal Properties of Gadolinium. Phys. Rev. B 1998, 57, 3478–3490. [Google Scholar] [CrossRef]
- Chernyshov, A.S.; Tsokol, A.O.; Tishin, A.M.; Gschneidner, K.A.; Pecharsky, V.K. Magnetic and Magnetocaloric Properties and the Magnetic Phase Diagram of Single-Crystal Dysprosium. Phys. Rev. B 2005, 71, 184410. [Google Scholar] [CrossRef] [Green Version]
- Pechan, M.J.; Stassis, C. Magnetic Structure of Holmium. J. Appl. Phys. 1984, 55, 1900–1902. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A.; Fort, D. Zero-Field and Magnetic-Field Low-Temperature Heat Capacity of Solid-State Electrotransport-Purified Erbium. Phys. Rev. B 1993, 47, 5063–5071. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, S.A.; Tishin, A.M.; Leontiev, P.I. Magnetocaloric Effect and Pressure Influence on Dysprosium Single Crystal Magnetization in the Range of Magnetic Phase Transition. J. Magn. Magn. Mater. 1991, 92, 405–416. [Google Scholar] [CrossRef]
- Nikitin, S.A.; Tishin, A.M.; Red’ko, S.V. Magnetocaloric Effect in Single Crystals of Terbium and Its Alloys with Gadolinium. Phys. Met. Metallogr. 1990, 66, 77–85. [Google Scholar]
- Andreenko, A.S.; Belov, K.P.; Nikitin, S.A.; Tishin, A.M. Magnetocaloric Effects in Rare-Earth Magnetic Materials. Sov. Phys. Uspekhi 1989, 32, 649. [Google Scholar] [CrossRef]
- Belov, K.P.; Levitin, R.Z.; Nikitin, S.A.; Ped’ko, A.V. Magnetic and Magnetoelastic Properties of Dysprosium and Gadolinium. Sov. Phys. JETP 1961, 13, 1096–1101. [Google Scholar]
- Belov, K.P.; Levitin, R.Z.; Ponomarev, B.K. Magnetic and Magnetosriction Properties of an Erbiu Single Crystal in the Paramagnetic Region. JETP 1967, 24, 1101–1104. [Google Scholar]
- Bartholin, H.; Bloch, D. Magnetic Ordering Temperatures of the Single Crystals of Rare Earth Metals at High Pressures: Gadolinium-Terbium-Dysprosium. J. Phys. Chem. Solids 1968, 29, 1063–1075. [Google Scholar] [CrossRef]
- Alberts, L.; du Plessis, P.d.V. Thermal Expansion and Forced Magnetostriction in a Terbium Single Crystal. J. Appl. Phys. 1968, 39, 581–582. [Google Scholar] [CrossRef]
- Darnell, F.J. Lattice Parameters of Terbium and Erbium at Low Temperatures. Phys. Rev. 1963, 132, 1098–1100. [Google Scholar] [CrossRef]
- Ali, N.; Willis, F.; Steinitz, M.O.; Kahrizi, M.; Tindall, D.A. Observation of Transitions to Spin-Slip Structures in Single-Crystal Holmium. Phys. Rev. B 1989, 40, 11414–11416. [Google Scholar] [CrossRef] [PubMed]
- Bates, S.; Patterson, C.; McIntyre, G.J.; Palmer, S.B.; Mayer, A.; Cowley, R.A.; Melville, R. The Magnetic Structure of Holmium. II. J. Phys. C Solid State Phys. 1988, 21, 4125–4141. [Google Scholar] [CrossRef]
- Brits, G.H.F.; du Plessis, P.d.V. Criticalbehaviour of the Planar Helical to or from Paramagnetic Phase Transition in Dysprosium and Holmium. J. Phys. F Met. Phys. 1988, 18, 2659–2668. [Google Scholar] [CrossRef]
- Cowley, R.A.; Bates, S. The Magnetic Structure of Holmium. I. J. Phys. C Solid State Phys. 1988, 21, 4113–4124. [Google Scholar] [CrossRef]
- Alkhafaji, M.T.; Ali, N. Magnetic Phase Diagram of Dysprosium. J. Alloy. Compd. 1997, 250, 659–661. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Gaidukov, Y.P.; Vasil’ev, A.N.; Fawcett, E. The Magnetic Phase Diagrams of Dysprosium. J. Magn. Magn. Mater. 1991, 97, 246–250. [Google Scholar] [CrossRef]
- Astrom, H.U.; Benediktsson, G. Magnetic Transitions in Dysprosium: A Calorimetric Study. J. Phys. F Met. Phys. 1988, 18, 2113–2120. [Google Scholar] [CrossRef]
- Ali, N.; Willis, F. Magnetization of Single-Crystal Erbium. Phys. Rev. B 1990, 42, 6820–6822. [Google Scholar] [CrossRef]
- Buck, S.; Fähnle, M. Ab Initio Calculation of the Giant Magnetostriction in Terbium and Erbium. Phys. Rev. B 1998, 57, R14044–R14047. [Google Scholar] [CrossRef]
- Flippen, R.B. Changes in Magnetization of Single-Crystal Dysprosium, Erbium, and Holmium in High Magnetic Fields. J. Appl. Phys. 1964, 35, 1047–1048. [Google Scholar] [CrossRef]
- Bagguley, D.M.S.; Liesegang, J.; Bleaney, B. Microwave Absorption Phenomena in Rare Earth Metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1967, 300, 497–518. [Google Scholar] [CrossRef]
- Salamon, M.B.; Simons, D.S. Evidence for a Second Magnetic Phase Transition in Godolinium. Phys. Rev. B 1973, 7, 229–232. [Google Scholar] [CrossRef]
- Zverev, V.I.; Gimaev, R.R.; Tishin, A.M.; Mudryk, Y.; Gschneidner, K.A.; Pecharsky, V.K. The Role of Demagnetization Factor in Determining the ‘True’ Value of the Curie Temperature. J. Magn. Magn. Mater. 2011, 323, 2453–2457. [Google Scholar] [CrossRef]
- Belov, K.P.; Ped’ko, A.V. “Helical” Antiferromagnetism of Gadolinium. Sov. Phys. JETP 1962, 15, 62–64. [Google Scholar]
- Graham, C.D., Jr. Magnetocrystalline Anisotropy of Gadolinium. J. Phys. Soc. Jpn. 1962, 17, 1310. [Google Scholar] [CrossRef]
- Cable, J.W.; Wollan, E.O. Neutron Diffraction Study of the Magnetic Behavior of Gadolinium. Phys. Rev. 1968, 165, 733–734. [Google Scholar] [CrossRef]
- Will, G.; Nathans, R.; Alperin, H.A. Neutron Diffraction Investigation of a Gadolinium Single Crystal. J. Appl. Phys. 1964, 35, 1045–1046. [Google Scholar] [CrossRef]
- Kataev, G.I.; Sattarov, M.R.; Tishin, A.M. Influence of Commensurability Effects on the Magnetic Phase Diagram of Terbium Single Crystals. Phys. Status Solidi A 1989, 114, K79–K82. [Google Scholar] [CrossRef]
- Зверев, В.И. Магнитные и Магнитoтеплoвые Свoйства Гадoлиния, Тербия и Гoльмия в Области Магнитных Фазoвых Перехoдoв. Ph.D. Thesis, МГУ им. М.В. Лoмoнoсoва, Moscow, Russia, 2012. (In Russian). [Google Scholar]
- Herz, R.; Kronmüller, H. Field-Induced Magnetic Phase Transitions in Dysprosium. J. Magn. Magn. Mater. 1978, 9, 273–275. [Google Scholar] [CrossRef]
- Willis, F.; Ali, N. Magnetism in Single-crystal Dy below 10 K. J. Appl. Phys. 1991, 70, 6548–6549. [Google Scholar] [CrossRef]
- Yu, J.; LeClair, P.R.; Mankey, G.J.; Robertson, J.L.; Crow, M.L.; Tian, W. Exploring the Magnetic Phase Diagram of Dysprosium with Neutron Diffraction. Phys. Rev. B 2015, 91, 014404. [Google Scholar] [CrossRef] [Green Version]
- Astrom, H.U.; Nogues, J.; Nicolaides, G.K.; Rao, K.V.; Benediktsson, G. Magnetic Transitions in Single-Crystal Thulium. J. Phys. Condens. Matter 1991, 3, 7395–7402. [Google Scholar] [CrossRef]
- Wakabayashi, N.; Cable, J.W.; Robertson, J.L. Magnetic Structures of Dy in Applied Fields. Phys. B Condens. Matter 1997, 241–243, 517–523. [Google Scholar] [CrossRef]
- Jensen, J.; Mackintosh, A.R. Novel Magnetic Phases in Holmium. J. Magn. Magn. Mater. 1992, 104–107, 1481–1484. [Google Scholar] [CrossRef]
- Kosevich, A.M.; Voronov, V.P.; Manzhos, I.V. Nonlinear Collective Excitations in an Easy Plane Magnet. Sov. Phys. JETP 1983, 57, 86–92. [Google Scholar]
- Gor’kov, L.P.; Sokol, A.V. Kinetic Effects in Antiferromagnetic Conductors with Spin Density Waves. Sov. Phys. JETP 1987, 66, 1267–1273. [Google Scholar]
- Koehler, W.C.; Cable, J.W.; Wilkinson, M.K.; Wollan, E.O. Magnetic Structures of Holmium. I. The Virgin State. Phys. Rev. 1966, 151, 414–424. [Google Scholar] [CrossRef]
- Koehler, W.C.; Cable, J.W.; Child, H.R.; Wilkinson, M.K.; Wollan, E.O. Magnetic Structures of Holmium. II. The Magnetization Process. Phys. Rev. 1967, 158, 450–461. [Google Scholar] [CrossRef]
- Akhavan, M.; Blackstead, H.A. Magnetoresistance and Field-Induced Phase Transitions in the Helical and Conical States of Holmium. Phys. Rev. B 1976, 13, 1209–1215. [Google Scholar] [CrossRef]
- Tindall, D.A.; Steinitz, M.O.; Plumer, M.L. Thermal Expansion in the Magnetically Ordered Phases of Holmium. J. Phys. F Met. Phys. 1977, 7, L263–L266. [Google Scholar] [CrossRef]
- Jayasuriya, K.D.; Campbell, S.J.; Stewart, A.M. Specific Heat Study of a Holmium Single Crystal. J. Phys. F Met. Phys. 1985, 15, 225–239. [Google Scholar] [CrossRef]
- Gibbs, D.; Moncton, D.E.; D’Amico, K.L.; Bohr, J.; Grier, B.H. Magnetic X-Ray Scattering Studies of Holmium Using Synchro-Tron Radiation. Phys. Rev. Lett. 1985, 55, 234–237. [Google Scholar] [CrossRef] [PubMed]
- Bohr, J.; Gibbs, D.; Moncton, D.E.; D’Amico, K.L. Spin Slips and Lattice Modulations in Holmium: A Magnetic x-Ray Scattering Study. Phys. A 1986, 140, 349–358. [Google Scholar] [CrossRef]
- Ellerby, M.; McEwen, K.A.; Jensen, J. Magnetoresistance and Magnetization Study of Thulium. Phys. Rev. B 1998, 57, 8416–8423. [Google Scholar] [CrossRef] [Green Version]
- Fynbo, P.B. Magnetic Properties of Thulium. J. Phys. F Met. Phys. 1977, 7, 2179–2191. [Google Scholar] [CrossRef]
- Zochowski, S.W.; McEwen, K.A. Magnetic Phase Diagram of Thulium. J. Magn. Magn. Mater. 1992, 104–107, 1515–1516. [Google Scholar] [CrossRef]
- Gama, S.; Fóglio, M.E. Magnetization of Erbium in the Ordered and Paramagnetic Phases. Phys. Rev. B 1988, 37, 2123–2132. [Google Scholar] [CrossRef] [Green Version]
- Burger, J.P.; Vajda, P.; Daou, J.N.; Chouteau, G. Effect of Hydrogen in Solid Solution upon the Magnetic Properties of Monocrystalline Erbium. J. Phys. F Met. Phys. 1986, 16, 1275–1286. [Google Scholar] [CrossRef]
- Atoji, M. Magnetic Structures of Er Single Crystal in 0–20 KOe Field. Solid State Commun. 1974, 14, 1047–1050. [Google Scholar] [CrossRef]
- Elliott, J.F.; Legvold, S.; Spedding, F.H. Magnetic Properties of Erbium Metal. Phys. Rev. 1955, 100, 1595–1596. [Google Scholar] [CrossRef]
- Willis, F.; Ali, N. Magnetization and Thermal Expansion of Single-crystal Er and Tm. J. Appl. Phys. 1991, 69, 5697–5699. [Google Scholar] [CrossRef]
- Gibbs, D.; Bohr, J.; Axe, J.D.; Moncton, D.E.; D’Amico, K.L. Magnetic Structure of Erbium. Phys. Rev. B 1986, 34, 8182–8185. [Google Scholar] [CrossRef] [PubMed]
- Bohr, J. Magnetic X-Ray Scattering: A New Tool for Magnetic Structure Investigations. J. Magn. Magn. Mater. 1990, 83, 530–534. [Google Scholar] [CrossRef]
- Bohr, J.; Gibbs, D.; Axe, J.D.; Moncton, D.E.; D’amico, K.L.; Majkrzak, C.F.; Kwo, J.; Hong, M.; Chien, C.L.; Jensen, J. Diffraction Studies of Rare Earth Metals and Superlattices. Phys. B Condens. Matter 1989, 159, 93–105. [Google Scholar] [CrossRef]
- Godovikov, S.K.; Kozin, M.G.; Turovtsev, V.V.; Shpinel, V.S. Hyperfine Fields Acting on Diamagnetic Impurities and the Anisotropic Exchange via the S- and d-Electrons in the Rare-Earth Metals. Phys. Status Solidi B 1976, 78, 103–111. [Google Scholar] [CrossRef]
- Bogdanov, P.V.; Godovikov, S.K.; Kozin, M.G.; Moreva, N.I.; Shpinel, V.S. Features of the Hyperfine Interaction of Tin Impurities in Metallic Holmium. Hyperfine Interact. 1977, 5, 333–345. [Google Scholar] [CrossRef]
- Irkhin, V.Y.; Irkhin, Y.P. Charge Screening and Magnetic Anisotropy in Metallic Rare-Earth Systems. Phys. Rev. B 1998, 57, 2697–2700. [Google Scholar] [CrossRef] [Green Version]
- Brun, T.O.; Sinha, S.K.; Wakabayashi, N.; Lander, G.H.; Edwards, L.R.; Spedding, F.H. Temperature Dependence of the Periodicity of the Magnetic Structure of Thulium Metal. Phys. Rev. B 1970, 1, 1251–1253. [Google Scholar] [CrossRef]
- Никитин, C.A. Магнитные Свoйства Редкoземельных Металлoв и Их Сплавoв; Publisher МГУ им. М.В. Лoмoнoсoва: Moscow, Russia, 1989. (In Russian) [Google Scholar]
- Jordan, R.G.; Lee, E.W. Low-Temperature Magnetic Properties of Dysprosium Single Crystals. Proc. Phys. Soc. 1967, 92, 1074–1082. [Google Scholar] [CrossRef]
- Schaub, B.; Mukamel, D. Phase Diagrams of Systems Exhibiting Incommensurate Structures. Phys. Rev. B 1985, 32, 6385–6393. [Google Scholar] [CrossRef] [PubMed]
- Grazhdankina, N.P. Magnetic First Order Phase Transitions. Phys. Uspekhi 1969, 11, 727–745. [Google Scholar] [CrossRef]
- Strukov, B.A. Global Hysteresis in Ferroelectrics with Incommensurate Phases. Phase Transit. 1989, 15, 143–179. [Google Scholar] [CrossRef]
- Levanyuk, A.P.; Osipov, V.V.; Sigov, A.S.; Sobyanin, A.A. Change of Defect Structure and the Resultant Anomalies in the Properties of Substances near Phase-Transition Points. Sov. Phys. JETP 1979, 49, 176–188. [Google Scholar]
- Woods, A.D.B.; Holden, T.M.; Powell, B.M. Observation of Spin Waves in Erbium. Phys. Rev. Lett. 1967, 19, 908–910. [Google Scholar] [CrossRef]
- Stringfellow, M.W.; Holden, T.M.; Powell, B.M.; Woods, A.D.B. Spin-Wave Excitations in the Conical and Spiral Magnetic Phases of Holmium Metal. J. Appl. Phys. 1969, 40, 1443–1445. [Google Scholar] [CrossRef]
- Nicklow, R.M.; Mook, H.A.; Smith, H.G.; Reed, R.E.; Wilkinson, M.K. Spin-Wave Dispersion Relation for Holmium in the Spiral Magnetic Phase. J. Appl. Phys. 1969, 40, 1452–1453. [Google Scholar] [CrossRef]
- Møller, H.B.; Houmann, J.C.G.; Mackintosh, A.R. Magnetic Interactions in Rare-Earth Metals from Inelastic Neutron Scattering. Phys. Rev. Lett. 1967, 19, 312–314. [Google Scholar] [CrossRef] [Green Version]
- Vorob’ev, V.V.; Krupotkin, M.Y.; Finkel’, V.A. Magnetic phase transitions in dysprosium single crystals in weak magnetic fields. Sov. Phys. JETP 1988, 61, 1056–1059. [Google Scholar]
- Bozorth, R.M. Magnetic Properties of Compounds and Solid Solutions of Rare-Earth Metals. J. Appl. Phys. 1967, 38, 1366–1371. [Google Scholar] [CrossRef]
- Weinstein, S.; Craig, R.S.; Wallace, W.E. Structural and Magnetic Characteristics of Dysprosium-Yttrium Solid Solutions. J. Appl. Phys. 1963, 34, 1354–1355. [Google Scholar] [CrossRef]
- Child, H.R.; Cable, J.W. Magnetic Structure Properties of Gd–Y and Gd–Sc Alloys. J. Appl. Phys. 1969, 40, 1003–1005. [Google Scholar] [CrossRef]
- Child, H.R.; Koehler, W.C.; Wollan, E.O.; Cable, J.W. Magnetic Properties of Heavy Rare Earths Diluted by Yttrium and Lutetium. Phys. Rev. 1965, 138, A1655–A1660. [Google Scholar] [CrossRef]
- Bean, C.P.; Rodbell, D.S. Magnetic Disorder as a First-Order Phase Transformation. Phys. Rev. 1962, 126, 104–115. [Google Scholar] [CrossRef]
- Rodbell, D.S.; Bean, C.P. Some Magnetic First-Order Transitions. J. Appl. Phys. 1962, 33, 1037–1041. [Google Scholar] [CrossRef]
- Kittel, C. Model of Exchange-Inversion Magnetization. Phys. Rev. 1960, 120, 335–342. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1, 3rd ed.; Course of Theoretical Physics; Butterworth-Heinemann: Oxford, UK, 1980; Volume 5, ISBN 0-7506-3372-7. [Google Scholar]
- Kuz’min, M.D. Landau-Type Parametrization of the Equation of State of a Ferromagnet. Phys. Rev. B 2008, 77, 184431. [Google Scholar] [CrossRef]
- Zverev, V.I.; Tishin, A.M. Complex Behaviour of Magnetization and Magnetocaloric Effect in Low Magnetic Field in the Vicinity of Magnetic Phase Transitions. Available online: https://iifiir.org/en/fridoc/complex-behaviour-of-magnetization-and-magnetocaloric-effect-in-low-26205 (accessed on 3 December 2020).
- Skochdopole, R.E.; Griffel, M.; Spedding, F.H. Heat Capacity of Erbium from 15 to 320 K. J. Chem. Phys. 1955, 23, 2258–2263. [Google Scholar] [CrossRef]
- Zimm, C.B.; Barclay, J.A.; Harkness, H.H.; Green, G.F.; Patton, W.G. Magnetocaloric Effect in Thulium. Cryogenics 1989, 29, 937–938. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gimaev, R.R.; Komlev, A.S.; Davydov, A.S.; Kovalev, B.B.; Zverev, V.I. Magnetic and Electronic Properties of Heavy Lanthanides (Gd, Tb, Dy, Er, Ho, Tm). Crystals 2021, 11, 82. https://doi.org/10.3390/cryst11020082
Gimaev RR, Komlev AS, Davydov AS, Kovalev BB, Zverev VI. Magnetic and Electronic Properties of Heavy Lanthanides (Gd, Tb, Dy, Er, Ho, Tm). Crystals. 2021; 11(2):82. https://doi.org/10.3390/cryst11020082
Chicago/Turabian StyleGimaev, Radel R., Aleksei S. Komlev, Andrei S. Davydov, Boris B. Kovalev, and Vladimir I. Zverev. 2021. "Magnetic and Electronic Properties of Heavy Lanthanides (Gd, Tb, Dy, Er, Ho, Tm)" Crystals 11, no. 2: 82. https://doi.org/10.3390/cryst11020082






