Thus, eight non-equivalent cationic sites are present in the whitlockite structure:
A(1),
A(2) and
A(3) are located in the general Wyckoff positions 18
b, whereas
X and
M are placed in the 6
a special positions (
Table 3). Two P atoms, occupying the
T(2) and
T(3) sites, and nine O atoms are located at general positions, whereas a third P, occupying the
T(1) site, and one O atom, at the O(10) site, are in 6
a special positions (
Table 3). The
X site is only partially occupied; in the refinement of the
β-TCP structure its occupancy is usually fixed at 50% for charge balance [
12,
36]; this is also the case of natural whitlockite and merrillite crystals, where the
X site occupancy can be variable to compensate for constituents with different formal ionic charge from Ca
2+ such as Na
+ [
32]. In some
β-TCP structures, the
X site may be vacant due to the occurrence of trivalent cations, e.g., for the Ca
9RE(PO
4)
7 compound, trivalent rare earth cations substitute for Ca
2+ [
10,
37]. In the description of bond lengths and angles, we will discuss the NDP data only for clarity, with the XRD results being similar, as can be observed in
Table 5 and
Table 6, where bond distances (Å) and bond valence parameters/sum are reported (BVP/BVS, expressed in valence units = v.u. [
38]), respectively, from XRD (
Table 5) and NDP refinement (
Table 6).
4.2.1. Polyhedral Coordination
The whitlockite structure consists of three independent
T(PO
4)
3− tetrahedra; two of these,
T(2)O
4 and
T(3)O
4, have average <
T(1,3)P-O> bond-distances of, respectively, 1.537(4) Å and 1.538(4) Å, in line with the data from natural and synthetic phosphate samples [
4,
39,
40,
41]. The last tetrahedron, [
T(1)PO
3(OH)], has P
5+ bonded to the
O(10)(OH) group. The [
T(1)PO
3(OH)]
2- unit may flip 180° along the
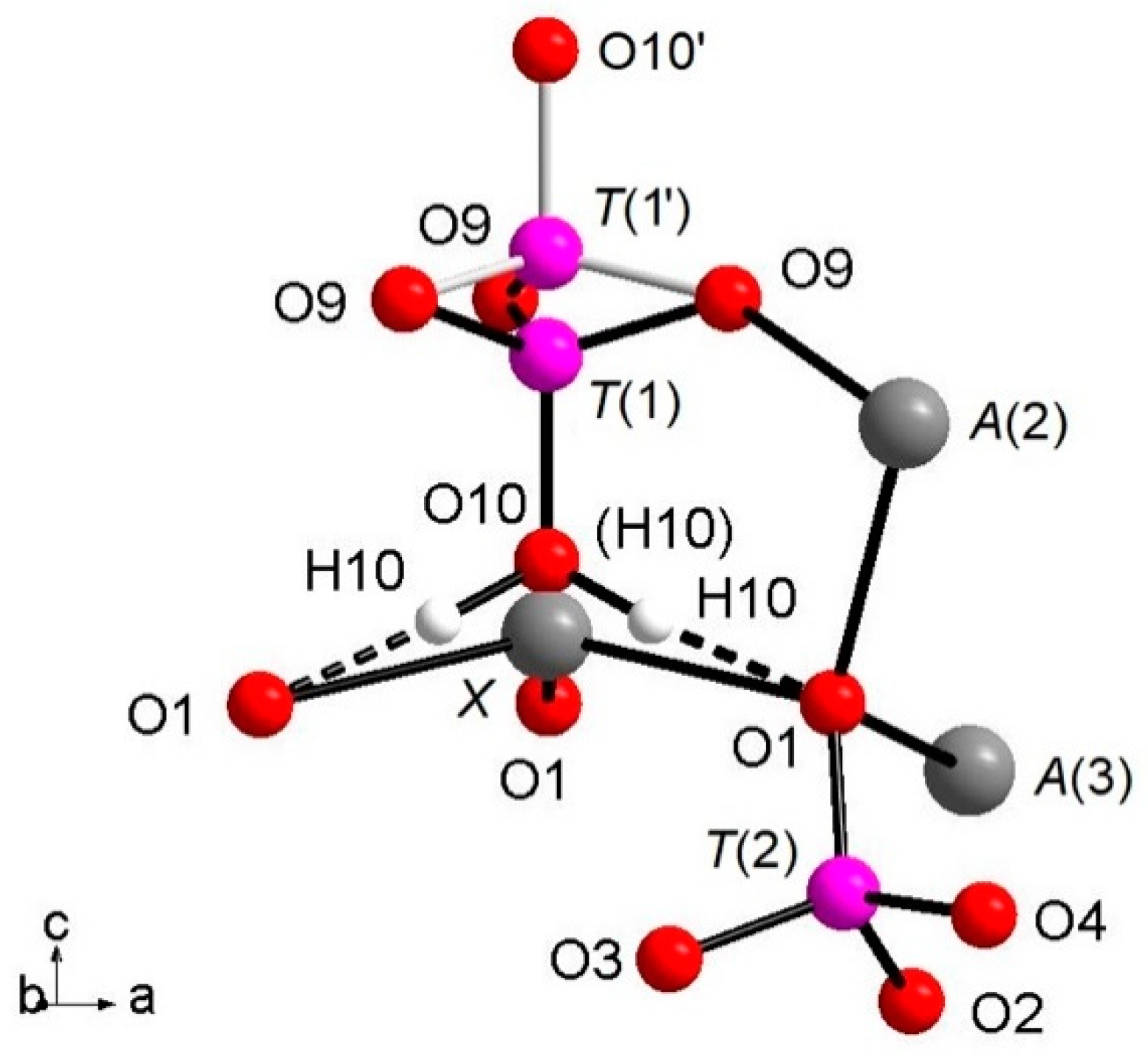
c-axis keeping fixed the position of the O(9) oxygen atoms, but splitting the P-cation position in
T(1) and
T(1′) about 0.76 Å apart with 85% and 15% occupancy, respectively (
Table 3), as displayed in
Figure 1. In detail, when
T(1) is occupied, the tetrahedron points downward (-
c) and the
X site is vacant; it should be noted that the actually geometry of the [
T(1)PO
3(OH)] polyhedron is that of a trigonal pyramid (site symmetry 3) having three
O(9)O atoms as the triangular base and
O(10)(OH) as the apex. Hydrogen ions at the three H(10) sites complete the bond valence to O(1) via hydrogen bridges. When the
T(1′) site is occupied, the tetrahedron points upward (+
c) the apex now being the O(10′) site occupied by O
2-; the Ca
2+ at the
X site coordinates three O
2- ions at O(1) and three O
2- ions at the O(9) site forming a distorted octahedron with very long
XCa-O(9) distances (about 2.96 Å) and a vacant H(10) site. The neutron diffraction data allowed the accurate determination of the
H(10)H bonded to O at the O(10) site. As O(10) is on the three-fold axis, three H(10) sites are generated by symmetry (
Figure 1), with their total occupancy being constrained to that of O(10). It is worth noting that in the final Fourier difference map, no H atom attached to the O at the O(10′) could be found, indicating that the disorder of the phosphate group is not only positional along the symmetry axis, but also compositional, giving rise to the [PO
3(OH)] and (PO
4) stoichiometries, with the latter occurring in a minor amount (about 15%). In summary, the
H(10)H atom is not only bonded to the
O(10)O atom, but it is also involved in a strong hydrogen bond with
O(1)O (
Figure 1) according to the following scheme:
O(10)O–
H(10)H = 1.03(3) Å;
H(10)H···
O(1)O = 1.71(3) Å;
O(10)O–
O(1)O = 2.739(4) Å; (
O(10)O–
O(10)H···
O(1)O) angle = 175(2)°.
The Ca atoms occupy the
A(1,2,3) and
X sites, describing, with the first neighboring oxygen atoms, different polyhedra within a bonding threshold of 2.81 Å. The
A(1) site displays a complex eight-fold coordination environment (
Figure 2), with the shortest and largest bond-distances being
A(1)-O(6) = 2.317(4) Å and
A(1)-O(3) = 2.766(5) Å, respectively, and with an average distance <
A(1)-O> = 2.485(5) Å. In some previous structural studies on whitlockite or synthetic TCP [
36], the
A(1)O
8 polyhedron is described as seven-fold coordinated by excluding the longest
A(1)-O(3) distance (see, e.g., [
12]). However, the
A(1)Ca-
O(3)O bond actually exists from a bond valence perspective.
Table 6 shows that the bond-valence value for
A(1)Ca
2+-
O(3)O
2− = 0.12 valence units (v.u.), is larger than 0.04× the cation valence [
38]. As a result, it is reasonable to consider the
A(1)Ca-
O(3)O bond-distance in the coordination sphere of
A(1).
The
A(2) and
A(3) sites show irregular bonding environments with coordination number = 8 (
Figure 2). Regarding the
A(2)O
8 polyhedron, its shortest and longest bond-distances are, respectively,
A(2)-O(2) = 2.373(4) Å and
A(2)-O(7) = 2.651(5) Å), with <
A(2)-O> = 2.472(5) Å. Considering
A(3)O
8, its shortest distance is
A(3)-O(7) = 2.376(4) Å, whereas its largest distance is
A(3)-O(6) = 2.657(5) Å and
A(3)-O(10)′ = 2.717(9) Å; <
A(3)-O> = 2.512(5) Å (
Table 4). Worth of note is the presence of Na at
A(2), to date refined for the first time within whitlockite sub-group phases (
Table 4). Sodium is a characteristic constituent of merrillite sub-group species, and in the closely related wopmayte Ca
6Na
3□Mn
2+(PO
4)
3(PO
3OH)
4 [
31], it is up to 10 times more abundant than in the studied whitlockite. In wopmayite, Na is strongly ordered at
A(3) [
31], with as a result longer mean <
A(3)-O> bond lengths. Our whitlockite also shows a longer <
A(3)-O> and BVS values slightly lower than 2.00 consistent with the possible presence of a monovalent cation. However, refinement of Na at both
A(3),
A(1) and
X gave negative site occupancy values, thus indicating the occurrence of Na at
A(2) only.
Of particular interest for most of the whitlockite structures is the coordination environment of the cation at the
X site (
Figure 3). This cation is at
6a special position, being involved in a three-fold coordinated regular polyhedron with three equivalent
X-O(1) bond distances at about 2.58(4) Å. Due to the disorder of the [
T(1)PO
3(OH)] unit described above, it is very difficult to characterize the occupancy of the
X site, which is located only ~0.6 Å from O(10). Considering that the occupancy of the
X site is constrained to compensate the charge balance, X-ray/neutron structure refinements were done at first with only the
A(1),
A(2) and
A(3) sites occupied by Ca. The Fourier difference maps in both X-ray and neutron refinements showed a clear peak at the
X-site position. In particular, in the X-rays map, this peak is at 0.65 Å from O(10) with electron density 1.53 e/Å
3, while, in the neutrons map, it is at 0.57 Å from O(10) with a density of 1.64 fm/Å
3. Adding this peak as
X site occupied by Ca to the refinement, a strong correlation between the s.o.f. and the
Uiso of
X occurred. This correlation was resolved by fixing
Uiso of
X to 0.01 Å
2 (i.e., to the average value refined for the other Ca atoms in the structure) in X-ray/neutron refinements. The resulting s.o.f. is virtually the same in both refinements, 0.058(4) from X-rays and 0.06(2) from neutron, whereas the new refined
X position resulted very close to O(10),
X-O(10) = 0.51 Å and 0.57 Å in neutron and X-ray refinement, respectively. Its coordination polyhedron
XO
6 (
Figure 3) comprises the three equivalents O(1) at 2.57–2.58 Å (NDP and XRD, respectively), and three equivalents O(9), belonging to the [
T(1)PO
3(OH)] moiety, at 2.92–2.96 Å. In terms of bond valence, the contribution of
XCa
2+ can be considered as weak: about 0.20 v.u. and 0.08 v.u. for
X-O(1) and
X-O(9), respectively (
Table 6). The six-fold coordination of the
X site is confirmed by the keplerite mineral [
7], though this site is usually described as triangular in isotypic
β-TCP compounds in that the three
X-O(9) interactions tend to disappear being found over 2.96 Å [
12].
The
M site is octahedrally coordinated (
Figure 2), with two groups of three equivalent bond distances,
M-O(4) = 2.075(4) Å and
M-O(5) = 2.096(3) Å, with the average <
M-O> distance = 2.086 Å. This value is fully consistent with the occurrence of Mg and Fe as also observed in other whitlockite refinements [
28,
29,
30]. Note that the
M site is also characterized by low values of isotropic thermal parameters (
Table 3). The
M site population provided by EMP, (Mg
0.533Fe
2+0.342Mn
2+0.062Al
0.046), is fully consistent with X-ray crystal-structure refinement: occupancy 56% of Mg (+ Al, which has X-ray scattering very similar to Mg) and 46% of Fe (+Mn, which has X-ray scattering very similar to Fe). This excellent agreement reflects the fact that same crystal used for XRD was analyzed with EMP. As for the neutron refinement, the
M site occupancy, 80% of Mg and 20% of Fe, shows a slight deviation from what is provided by XRD. This deviation might be ascribed to a possible chemical inhomogeneity in the much bigger volume (about 8 mm
3) of the specimen used for the neutron diffraction.
Bond valence sum (BVS) calculations are in close agreement with the expected values from the empirical formula: 2.07 (v.u.) at A(1), 2.06 at A(2), 1.94 at A(3), 4.98 at T(2) and 4.97 at T(3). Of particular interest are the T(1), T(1′), X and M sites. With regard to T(1), we have to consider the previously mentioned split configuration of the [T(1)PO3(OH)]2- structural unit, which provides a separate contribution to the BVS = 5.07 x 85% + 5.43 × 15% = 5.12 v.u. The BVS incidents at the X site = 0.81 v.u., smaller than what was expected for Ca2+, indicates the occurrence of bond strain and reflects the presence of the split configuration for O(10). Finally, the value of BVS at the M site (2.16 v.u.) is consistent with occurrence of dominant divalent cations (Mg and Fe) and minor trivalent cations (Al3+) at this site, as reported in the empirical chemical formula of the studied whitlockite.
4.2.2. Three-dimensional Framework
The three-dimensional arrangement of whitlockite can be described by the repeat of two columnar arrays, indicated as ‘I’ and ‘II’ in
Figure 4, running along the
c axis. The I array consists of
T(1)O
4–
MO
6 sequence of polyhedra, while the II array is formed by
T(3)O
4–
A(1)O
8–
A(3)O
8–
A(2)O
8–
T(2)O
4–
T(3)O
4 sequence. In the I array, the
MO
6 polyhedron and the P
5+ at
T(1) and
T(1′) do not share any atom; the
MO
6 octahedron is engaged, via corner sharing with
T(2)O
4 and
T(3)O
4 tetrahedra, in the [M(TO
4)
16] pinwheel unit [
32] (see inset (a) in
Figure 4), which can be considered the building block of the whitlockite framework, as later illustrated. All cations in the I array, i.e., those at the
X,
M and
T(1)/
T(1′), are in special position (x = y = 0,
Table 3), and hence, they are constrained along the
c axis. This constraint prevents any positional disorder except that along the
z direction, as previously discussed for
T(1) and O(10).
On the other hand, in the II array, all the cations at
A(1),
A(2),
A(3),
T(2) and
T(3) are located in general positions (
Table 3) and may, thus, cause disorder to give a denser arrangement. Two II arrays are joined together, thus making up a column, via
A(1)-O-
A(2) bonds, with
A(1) and
A(2) belonging to adjacent arrays (see the inset (b) in
Figure 4).
Each I array is surrounded by six II arrays, whereas each II array is surrounded by two I and four II arrays (
Figure 5). The [M(TO
4)
6] pinwheel units assure the link between one I column and the six adjacent II columns, being the pinwheels flat in the
c axis and held together by intralayer
A(1)Ca cations, forming layers perpendicular to
c axis (
Figure 6). These anionic units form a perfectly closest-packed planar arrangement [
32]: these layers are linked by an interlayer of cations at
A(2) and
A(3) from II columns, making up the whitlockite three dimensional framework, further compacted by the interactions formed by the split
T(1)O
4 tetrahedron, which share O(9) with
A(2)O
8 and
A(1)O
8 from different II arrays, and the O(10′) vertex with the
A(3)O
8 polyhedron. This second joining mechanism among I and II arrays, formed by split
T(1)O
4 tetrahedron, is conditioned by the site symmetry of
T(1) (
Table 3). In fact, as previously described, the
T(1)O
4 tetrahedron forms a triangular pyramid, whose three
O(9)O base-vertices are shared at the same time both with one
A(1)O
8 polyhedron from an adjacent II array and with a
A(2)O
8 polyhedron belonging to another II array. Owing to the site symmetry, the joining mechanism is repeated three times, while the split along
c of the tetrahedral unit causes the presence of O(10′) position, joined to three
A(3)O
8 polyhedra from adjacent II arrays. The framework is completed by the X-O bonds, considered as weak interactions owing to the low cation occupancy of the site,
X(Ca
0.034□
0.996)
Σ1.000.
The whitlockite arrangement, as previously stated, is strictly related to that of isotypic
β-TCP [
32]. The occurrence of a trivalent
RE-cation such as Cr
3+ [
42], Fe
3+ [
43] or more frequently
REE3+ [
10] in the
β-TCP structure leads to the formula Ca
9RE3+(PO
4)
7, characterized, compared to whitlockite, by a fully vacant
X-site and by the presence of the [
T(1)PO
3(O)] unit according to the deprotonation-substitution mechanism
RE3+ + O
2− →
R2+ + (OH)
− [
11]. In the case of Cr
3+ and Fe
3+, the mechanism of dopant distribution occurs exclusively at the
M site [
42,
43]. In the case of Ca
9RE(PO
4)
7 β-TCP, the rare earth distribution was discussed in [
11] on the basis of the
RE ionic radii. In detail, for ‘low’ RE (La up to Gd), the dopant element is disordered over the
A(1,2,3) sites, whereas the
M site is fully occupied by Ca. As for the ‘heavy’ RE (from Tb to Lu) the dopant is disordered over
A(1),
A(2) and
M site, with
A(3) being fully occupied by Ca [
11].