Energy Band Gap Modeling of Doped Bismuth Ferrite Multifunctional Material Using Gravitational Search Algorithm Optimized Support Vector Regression
Abstract
1. Introduction
2. Mathematical Description of the Algorithms Employed for the Modeling and Simulation
2.1. Gravitational Search Algorithm
2.2. Support Vector Regression Based Algorithm
3. Empirical Study and Computational Details of the Proposed Hybrid Model
3.1. Data Acquisition Description and Statistical Analysis
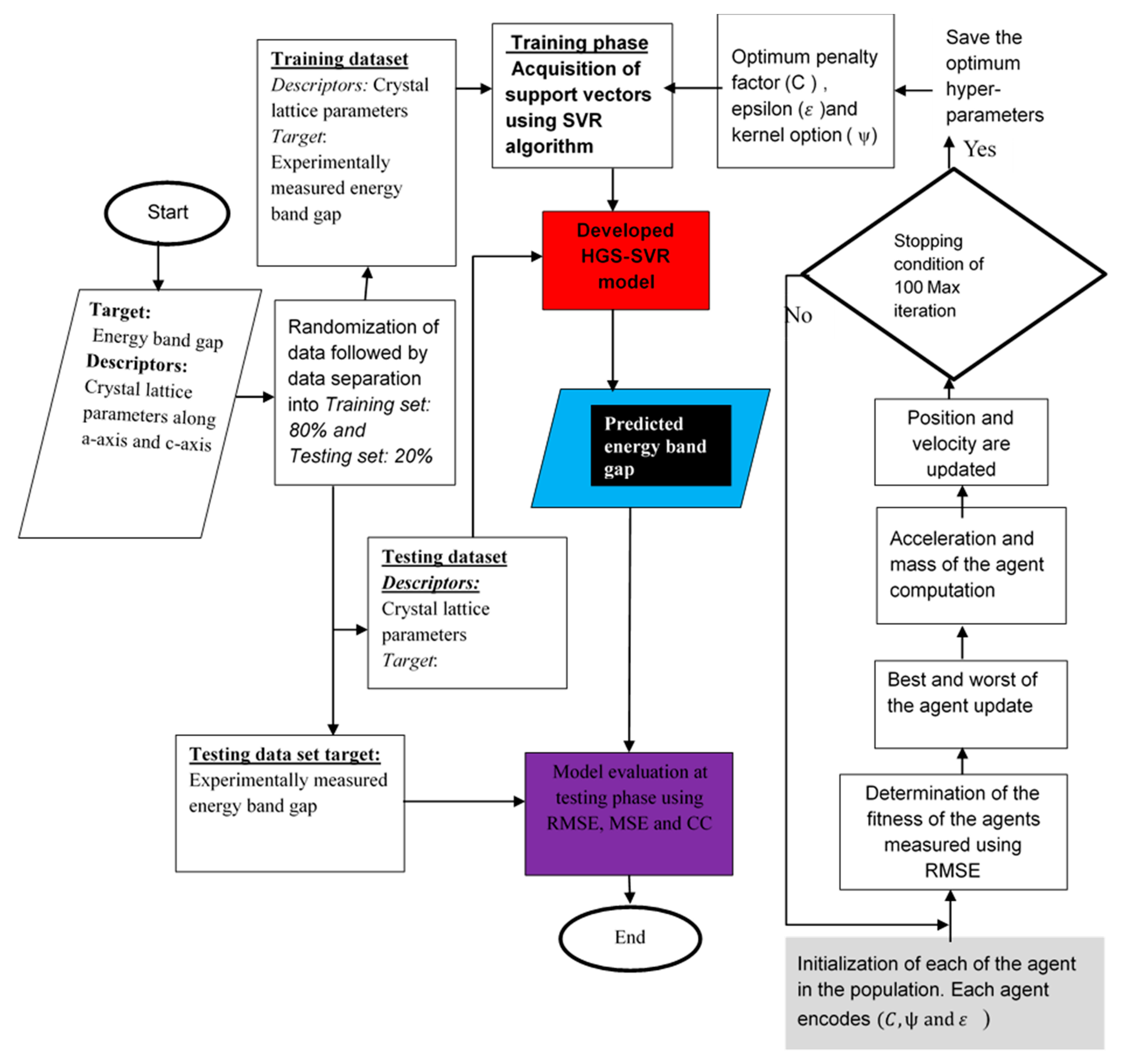
3.2. Computational Methodology Involved in the Developed HGS-SVR Model
4. Results and Discussion
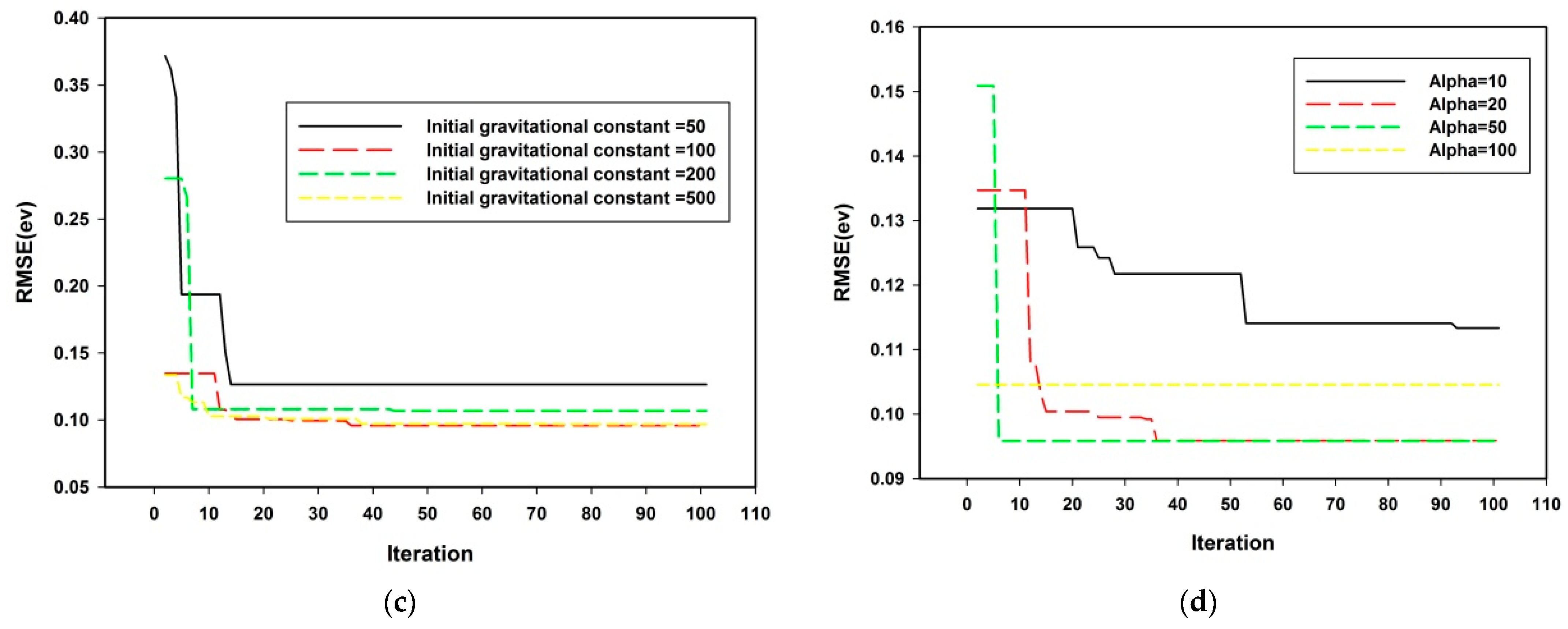
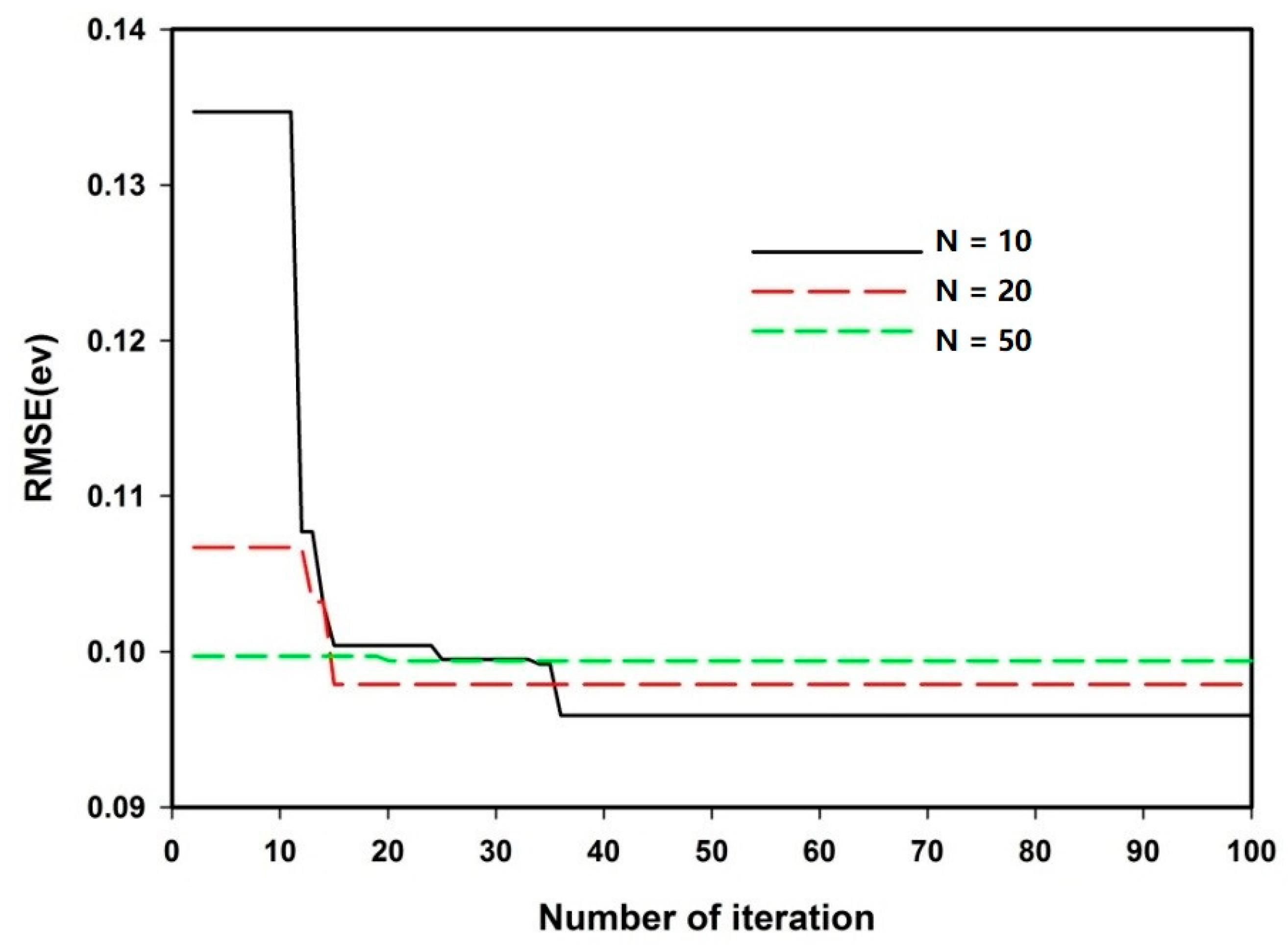
4.1. Convergence of the Developed Hybrid Model
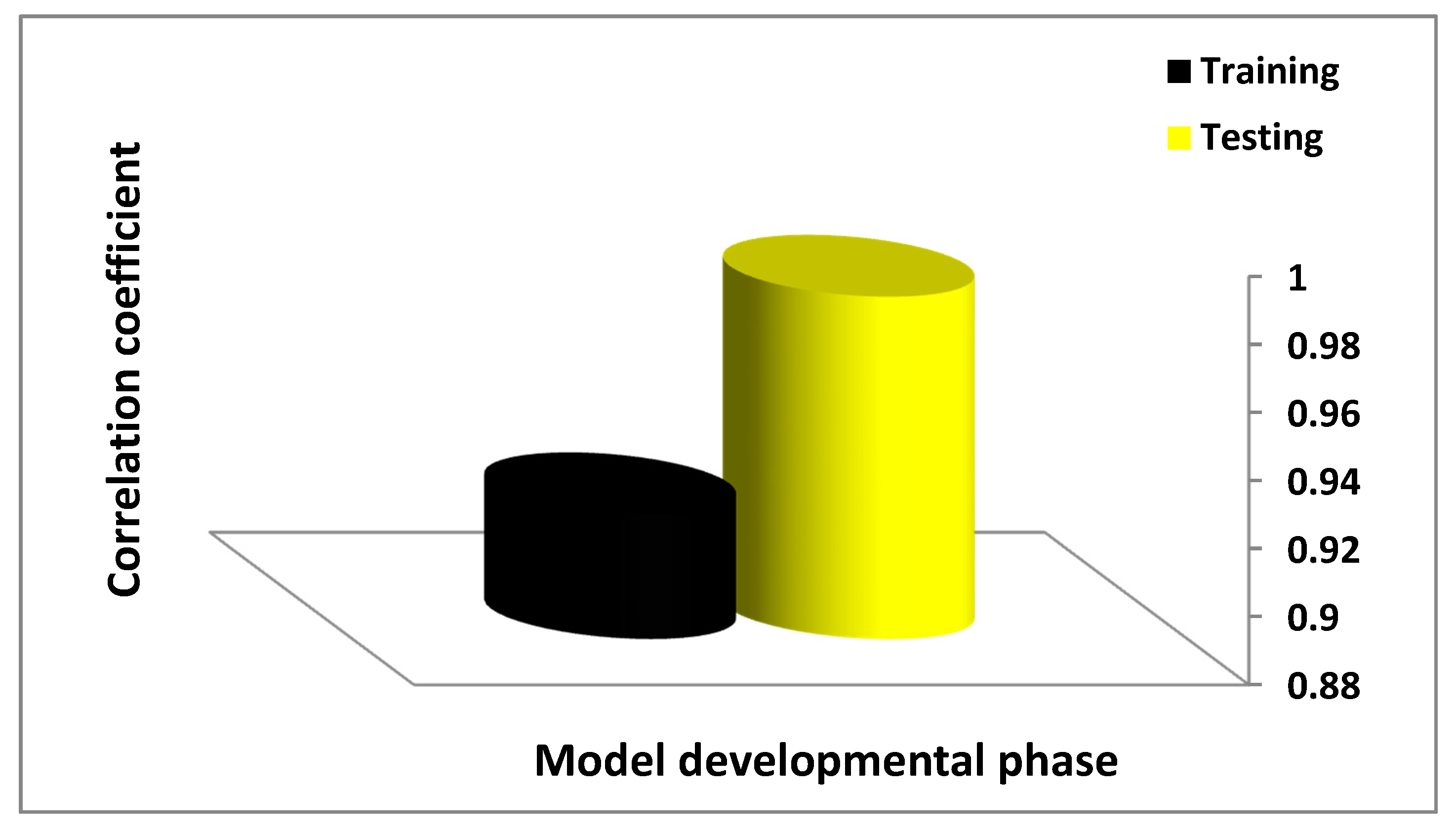
4.2. Evaluation of the Developed Hybrid Model
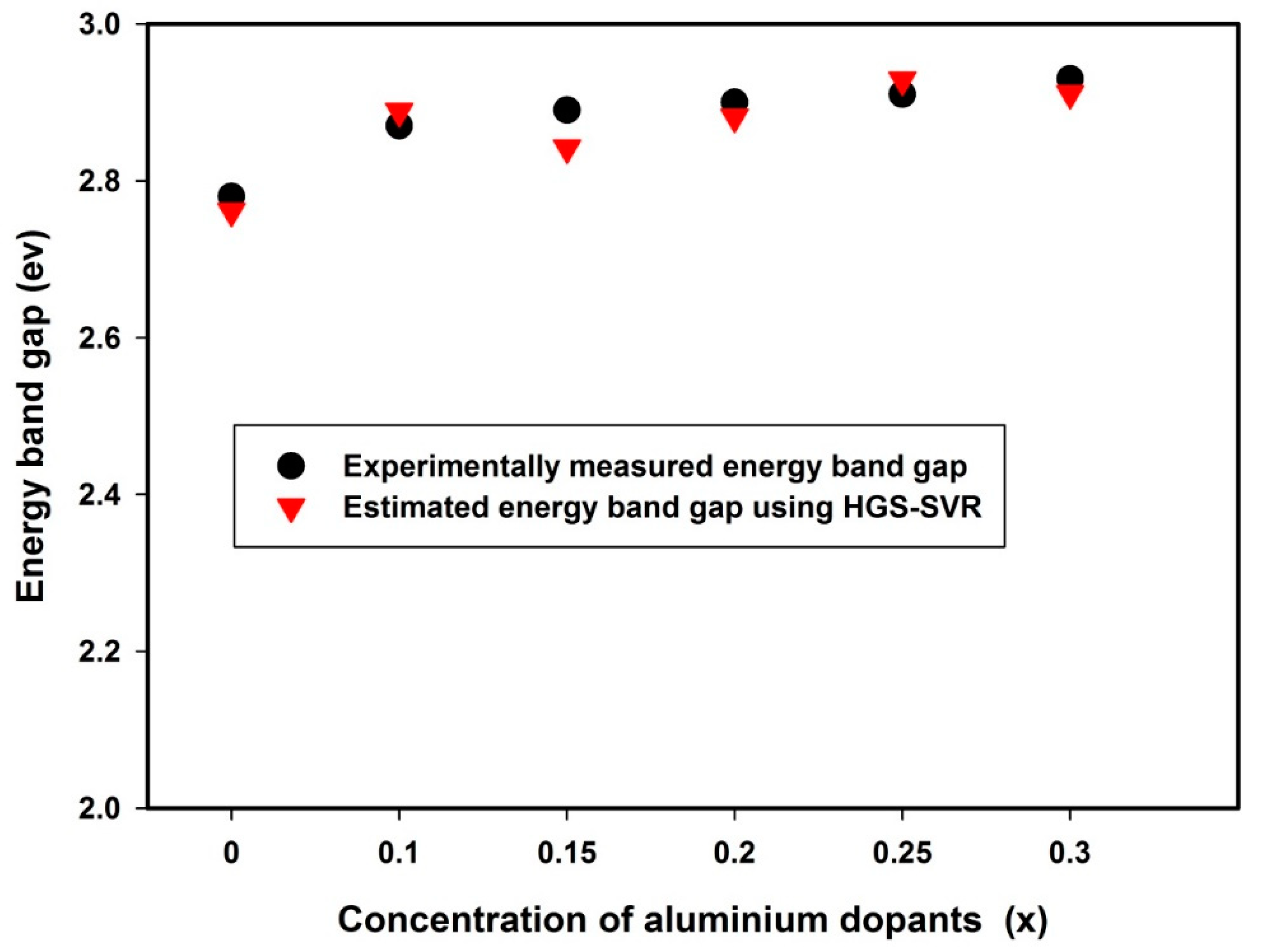
4.3. Influence of Aluminum Particles on Band Gap of Bismuth Ferrite Using HGS-SVR Model
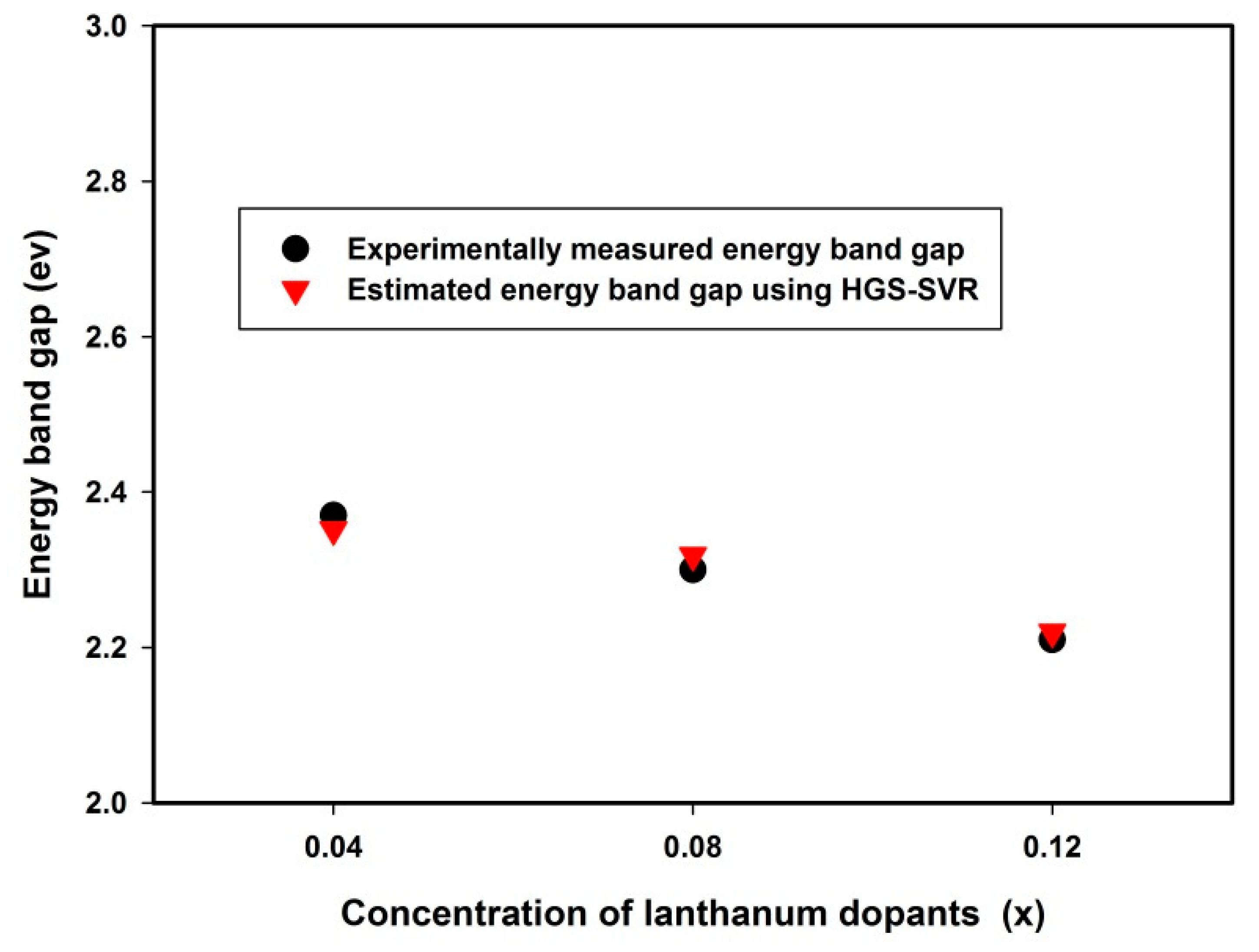
4.4. The Effect of Lanthanum on Band Gap Energy of Bismuth Compound Using HGS-SVR
4.5. Impact of Yttrium Substitution on Energy Band Gap of Bismuth Ferrite Using the Developed Model
4.6. Significance of Samarium Dopants on the Energy Band Gap of Bismuth Ferrite
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Irfan, S.; Zhuanghao, Z.; Li, F.; Chen, Y.-X.; Liang, G.-X.; Luo, J.-T.; Ping, F. Critical review: Bismuth ferrite as an emerging visible light active nanostructured photocatalyst. J. Mater. Res. Technol. 2019, 8, 6375–6389. [Google Scholar] [CrossRef]
- Yao, L.; Wu, X.; Yang, S.; Zhang, Y. Structural and optical properties of Ca doped BiFeO3 thin films prepared by a sol-gel method. Ceram. Int. 2017, 43, S470–S473. [Google Scholar] [CrossRef]
- Haruna, A.; Abdulkadir, I.; Idris, S.O. Heliyon Photocatalytic activity and doping effects of BiFeO3 nanoparticles in model organic dyes. Heliyon 2020, 6, e03237. [Google Scholar] [CrossRef] [PubMed]
- Castelli, E.; Olsen, T. Towards photoferroic materials by design: Recent progress and perspectives towards photoferroic materials by design: Recent progress and perspectives. J. Phys. Energy 2020. [Google Scholar] [CrossRef]
- Peng, L.; Deng, H.; Tian, J.; Ren, Q.; Peng, C.; Huang, Z. Influence of Co doping on structural, optical and magnetic properties of BiFeO3 films deposited on quartz substrates by sol—Gel method. Appl. Surf. Sci. 2013, 268, 146–150. [Google Scholar] [CrossRef]
- Owolabi, T.O. Development of a particle swarm optimization based support vector regression model for titanium dioxide band gap characterization. J. Semicond. 2019, 40. [Google Scholar] [CrossRef]
- Ahmad, S.; Hamad, T.; Sultan, G.; Murtaza, N.U.; Amin, M.W. Effect of Sr 2 + doping on the structural, electrical and optical properties of BiFeO3. Chin. J. Phys. 2018, 56, 2371–2380. [Google Scholar] [CrossRef]
- Puhan, B.; Bhushan, S.; Satpathy, S.; Meena, S.; Nayak, A.K.; Rout, D. Applied surface science facile single phase synthesis of Sr, Co co-doped BiFeO3 nanoparticles for boosting photocatalytic and magnetic properties. Appl. Surf. Sci. 2019, 493, 593–604. [Google Scholar] [CrossRef]
- Vishwakarma, K.; Tripathi, P.; Srivastava, A. Science direct band gap engineering of Gd and Co doped BiFeO3 and their application in hydrogen production through photoelectrochemical route. Int. J. Hydrog. Energy 2017, 42, 22677–22686. [Google Scholar] [CrossRef]
- Satar, N.S.A.; Adnan, R.; Lee, H.L.; Hall, S.R.; Kobayashi, T.; Kassim, M.H.M.; Kaus, N.H.M. Facile green synthesis of ytrium-doped BiFeO3 with highly e ffi cient photocatalytic degradation towards methylene blue. Ceram. Int. 2019, 45, 15964–15973. [Google Scholar] [CrossRef]
- Maleki, H. Characterization and photocatalytic activity of Y-doped BiFeO3 ceramics prepared by solid-state reaction method. Adv. Powder Technol. 2019, 30, 2832–2840. [Google Scholar] [CrossRef]
- Sinha, K.; Bhushan, B.; Gupta, N.; Sen, S.; Prajapat, C.L.; Nuwad, J. Effect of cobalt-doping on dielectric, magnetic and optical properties of BiFeO3 nanocrystals synthesized by sol—Gel technique. Solid State Sci. 2020, 102, 106168. [Google Scholar] [CrossRef]
- Wang, T.; Xu, T.; Gao, S.; Song, S. Effect of Nd and Nb co-doping on the structural, magnetic and optical properties of multiferroic BiFeO3 nanoparticles prepared by sol-gel method. Ceram. Int. 2017, 43, 4489–4495. [Google Scholar] [CrossRef]
- Shamsah, S.M.I.; Owolabi, T.O. Newtonian mechanics based hybrid machine learning method of characterizing energy band gap of doped zno semiconductor. Chin. J. Phys. 2020, 68, 493–506. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O. Application of computational intelligence technique for estimating superconducting transition temperature of YBCO superconductors. Appl. Soft Comput. J. 2016, 43, 143–149. [Google Scholar] [CrossRef]
- Owolabi, T.O. Modeling the magnetocaloric effect of manganite using hybrid genetic and support vector regression algorithms. Phys. Lett. A 2019, 383, 1782–1790. [Google Scholar] [CrossRef]
- Owolabi, T.O. Extreme learning machine and swarm- based support vector regression methods for predicting crystal lattice parameters of pseudo-cubic/cubic perovskites Extreme learning machine and swarm-based support vector regression methods for predicting crystal lat. J. Appl. Phys. 2020, 245107. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Gondal, M.A. Quantitative analysis of LIBS spectra using hybrid chemometric models through fusion of extreme learning machines and support vector regression. J. Intell. Fuzzy Syst. 2018, 35, 6277–6286. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Gondal, M.A. Development of hybrid extreme learning machine based chemo-metrics for precise quantitative analysis of LIBS spectra using internal reference pre-processing method. Anal. Chim. Acta 2018, 1030, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Cisewski, J.; Snyder, E.; Hannig, J.; Oudejans, L. Support vector machine classification of suspect powders using laser-induced breakdown spectroscopy (LIBS) spectral data. J. Chemom. 2012, 26, 143–149. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O. Development and validation of surface energies estimator (SEE) using computational intelligence technique. Comput. Mater. Sci. 2015, 101, 143–151. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O. Estimation of average surface energies of transition metal nitrides using computational intelligence technique. Soft Comput. 2017, 21, 6175–6182. [Google Scholar] [CrossRef]
- Owolabi, T.; Faiz, M.; Olatunji, S.O.; Popoola, I.K. Computational intelligence method of determining the energy band gap of doped ZnO semiconductor. Mater. Des. 2016, 101, 277–284. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Basak, D.; Pal, S.; Patranabis, D.C. Support vector regression. Neural. Inf. Process. Lett. Rev. 2007, 11, 67–80. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Adewumi, A.; Owolabi, T.O.; Alade, I.O.; Olatunji, S.O. Estimation of physical, mechanical and hydrological properties of permeable concrete using computational intelligence approach. Appl. Soft Comput. J. 2016, 42, 342–350. [Google Scholar] [CrossRef]
- Oyehan, T.A.; Alade, I.O.; Bagudu, A.; Sulaiman, K.O.; Olatunji, S.O.; Saleh, T.A. Predicting of the refractive index of haemoglobin using the Hybrid GA-SVR approach. Comput. Biol. Med. 2018, 98, 85–92. [Google Scholar] [CrossRef]
- Ghorbani, M.; Zargar, G.; Jazayeri-Rad, H. Prediction of asphaltene precipitation using support vector regression tuned with genetic algorithms. Petroleum 2016, 2, 301–306. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y. A working likelihood approach to support vector regression with a data-driven insensitivity parameter. arXiv 2020, arXiv:2003.03893. [Google Scholar]
- Awad, M.; Khanna, R. Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers, 1st ed.; Springer Nature Switzerland: Cham, Switzerland, 2015. [Google Scholar]
- Puhan, A.; Bhushan, B.; Kumar, V.; Panda, H.S.; Priyam, A.; Das, D.; Rout, D. Materials Science & Engineering B Tailoring the structural, optical and magnetic properties of BiFeO3 multiferroic nanoparticles by Ba, Cr co-doping. Mater. Sci. Eng. B 2019, 241, 48–54. [Google Scholar]
- Azam, A.; Jawad, A.; Ahmed, S.; Chaman, M.; Naqvi, A.H. Structural, optical and transport properties of Al 3 + doped BiFeO3 nanopowder synthesized by solution combustion method. J. Alloys Compd. 2011, 509, 2909–2913. [Google Scholar] [CrossRef]
- Singh, V.; Sharma, S.; Kumar, M.; Kotnala, R.K.; Dwivedi, R.K. Journal of magnetism and magnetic materials structural transition, magnetic and optical properties of Pr and Ti co-doped BiFeO3 ceramics. J. Magn. Magn. Mater. 2014, 349, 264–267. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, D.; Wang, S.; Zhang, N.; Qin, L.; Huang, Y. Facile synthesis of Sm-doped BiFeO3 nanoparticles for enhanced visible light photocatalytic performance. Mater. Sci. Eng. B 2017, 220, 1–12. [Google Scholar] [CrossRef]
- Thang, D.V.; Do Chung, P.; Hung, N.M.; Van Quang, N.; Van Minh, N. Enhancement of ferroelectric and ferromagnetic properties of Gadolinium. Ceram. Int. 2020, 46, 17423–17429. [Google Scholar]
- Wang, F.L.; Jain, A.; Li, Y.; Wang, N.; Lu, Y.L.; Zhu, L.; Wang, Y.G.; Chen, F.G. Enhanced magnetic, ferroelectric, and photocatalytic properties of (1-x). Ceram. Int. 2020, 46, 16416–16421. [Google Scholar] [CrossRef]
- Fki, H.; Koubaa, M.; Sicard, L.; Cheikhrouhou-koubaa, W.; Cheikhrouhou, A. Influence of Y doping on structural, vibrational, optical and magnetic properties of BiFeO3 ceramics prepared by mechanical activation. Ceram. Int. 2017, 43, 4139–4150. [Google Scholar] [CrossRef]
- Kumar, P.; Chand, P.; Singh, V. La 3 + substituted BiFeO3 -a proficient nanoferrite photo-catalyst under the application of visible light. Chem. Phys. Lett. 2020, 754, 137715. [Google Scholar] [CrossRef]




| Statistical Parameters | a (Ǻ) | c (Ǻ) | Energy Band Gap (ev) |
|---|---|---|---|
| Mean | 5.5766 | 13.8147 | 2.2053 |
| Standard deviation | 0.0299 | 0.1119 | 0.3659 |
| Correlation coefficient | −0.6033 | 0.0926 | |
| Maximum | 5.6430 | 13.9178 | 2.9300 |
| Minimum | 5.5020 | 13.3408 | 1.6100 |
| Model Hyper-Parameter | Optimized Value |
|---|---|
| Kernel mapping function | Gaussian |
| Initial number of agents | 10 |
| Penalty factor (C) | 307.3545 |
| Gaussian kernel option | 0.0299 |
| Epsilon | 0.0186 |
| Hyper-parameter lambda | E-7 |
| Initial value gravitational constant ) | 100 |
| Parameter alpha (α) | 20 |
| Dataset | CC | RMSE (ev) | MSE (ev) |
|---|---|---|---|
| Training phase | 0.917 | 0.1437 | 0.02065 |
| Testing phase | 0.9806 | 0.0958 | 0.009178 |
| Number of Run | CC-Training | CC-Testing | RMSE-Training | RMSE-Testing |
|---|---|---|---|---|
| 1 | 0.9170 | 0.9806 | 0.1437 | 0.0958 |
| 2 | 0.9139 | 0.965 | 0.1495 | 0.1073 |
| 3 | 0.9022 | 0.9747 | 0.1472 | 0.0853 |
| 4 | 0.9026 | 0.9815 | 0.1446 | 0.1405 |
| 5 | 0.9098 | 0.9525 | 0.141 | 0.1440 |
| 6 | 0.9036 | 0.9698 | 0.1404 | 0.1155 |
| Mean | 0.9081 | 0.9707 | 0.1444 | 0.1147 |
| Standard deviation | 0.0063 | 0.0109 | 0.0035 | 0.0237 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owolabi, T.O.; Abd Rahman, M.A. Energy Band Gap Modeling of Doped Bismuth Ferrite Multifunctional Material Using Gravitational Search Algorithm Optimized Support Vector Regression. Crystals 2021, 11, 246. https://doi.org/10.3390/cryst11030246
Owolabi TO, Abd Rahman MA. Energy Band Gap Modeling of Doped Bismuth Ferrite Multifunctional Material Using Gravitational Search Algorithm Optimized Support Vector Regression. Crystals. 2021; 11(3):246. https://doi.org/10.3390/cryst11030246
Chicago/Turabian StyleOwolabi, Taoreed O., and Mohd Amiruddin Abd Rahman. 2021. "Energy Band Gap Modeling of Doped Bismuth Ferrite Multifunctional Material Using Gravitational Search Algorithm Optimized Support Vector Regression" Crystals 11, no. 3: 246. https://doi.org/10.3390/cryst11030246
APA StyleOwolabi, T. O., & Abd Rahman, M. A. (2021). Energy Band Gap Modeling of Doped Bismuth Ferrite Multifunctional Material Using Gravitational Search Algorithm Optimized Support Vector Regression. Crystals, 11(3), 246. https://doi.org/10.3390/cryst11030246








