Topological Properties in a Λ/V-Type Dice Model
Abstract
:1. Introduction
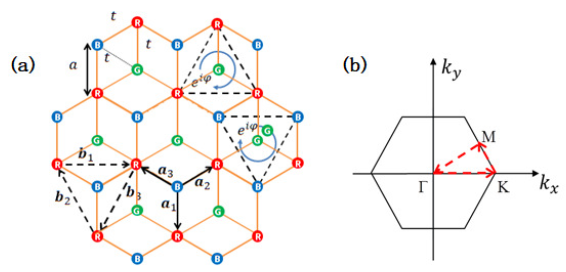
2. Model and Hamiltonian
3. Results and Discussion
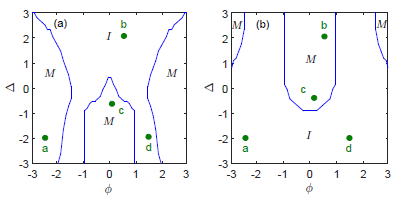
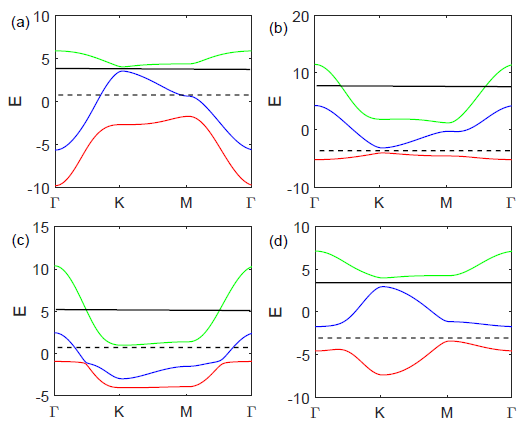
3.1. Band Structures
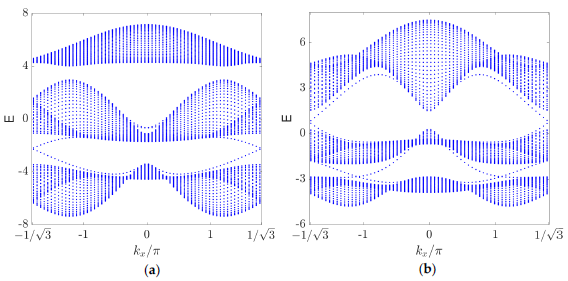
3.2. Chern Numbers and the Edge-State Spectrum
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klitzing, K.V.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. Topological Insulators and Superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.-Q. Topological Insulators; Springer: Berlin, Germany, 2012. [Google Scholar]
- Schnyder, A.P.; Ryu, S.; Furusaki, A.; Ludwig, A.W.W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 2008, 78, 195125. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L.; et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-Z.; Zhao, W.; Kim, D.Y.; Zhang, H.; Assaf, B.A.; Heiman, D.; Zhang, S.-C.; Liu, C.; Chan, M.H.W.; Moodera, J.S. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 2014, 14, 473–477. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Yu, Y.; Shi, M.Z.; Guo, Z.; Xu, Z.; Wang, J.; Chen, X.H.; Zhang, Y. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020, 367, 895–900. [Google Scholar] [CrossRef] [Green Version]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539. [Google Scholar] [CrossRef] [Green Version]
- Thouless, D.J.; Kohmoto, M.; Nightngale, M.P.; den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef] [Green Version]
- Niu, Q.; Thouless, D.J.; Wu, Y.S. Quantized Hall conductance as a topological invariant. Phys. Rev. B 1985, 31, 3372. [Google Scholar] [CrossRef] [Green Version]
- Kohmoto, M. Topological Invariant and the Quantization of the Hall Conductance. Ann. Phys. 1985, 160, 343–354. [Google Scholar] [CrossRef]
- Kohmoto, M. Zero modes and the quantized Hall conductance of the two-dimensional lattice in a magnetic field. Phys. Rev. B 1989, 39, 11943. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. A 1984, 392, 45–57. [Google Scholar]
- Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 1993, 71, 3697. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef]
- Sun, K.; Yao, H.; Fradkin, E.; Kivelson, S.A. Topological insulators and nematic phases from spontaneous symmetry breaking in 2D fermi systems with a quadratic band crossing. Phys. Rev. Lett. 2009, 103, 046811. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.; Pelletier, V.; Chaikin, P.M.; Huse, D.A. Landau levels in the case of two degenerate coupled bands: Kagomé lattice tight-binding spectrum. Phys. Rev. B 2003, 67, 104505. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.M.; Franz, M. Topological insulator on the kagome lattice. Phys. Rev. B 2009, 80, 113102. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.P.; Chen, W.C.; Wang, Y.F.; Gong, C.D. Topological quantum phase transitions on the kagomé and square–octagon lattices. J. Phys. Condens. Matter 2013, 25, 305602. [Google Scholar] [CrossRef]
- Weeks, C.; Franz, M. Topological insulators on the Lieb and perovskite lattices. Phys. Rev. B 2010, 82, 085310. [Google Scholar] [CrossRef] [Green Version]
- Apaja, V.; Hvrkas, M.; Manninen, M. Flat bands, Dirac cones, and atom dynamics in an optical lattice. Phys. Rev. A 2010, 82, 041402(R). [Google Scholar] [CrossRef] [Green Version]
- Goldman, N.; Urban, D.F.; Bercioux, D. Topological phases for fermionic cold atoms on the Lieb lattice. Phys. Rev. A 2011, 83, 063601. [Google Scholar] [CrossRef] [Green Version]
- Tsai, W.-F.; Fang, C.; Yao, H.; Hu, J. Interaction-driven topological and nematic phases on the Lieb lattice. New J. Phys. 2015, 17, 055016. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Gu, Z.-C.; Sun, K.; Das Sarma, S. Topological flat band models with arbitrary Chern numbers. Phys. Rev. B 2012, 86, 241112. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-F.; Yao, H.; Gong, C.-D.; Sheng, D.N. Fractional quantum Hall effect in topological flat bands with Chern number two. Phys. Rev. B 2012, 86, 201101. [Google Scholar] [CrossRef] [Green Version]
- Sticlet, D.; Piėchon, F. Distant-neighbor hopping in graphene and Haldane models. Phys. Rev. B 2013, 87, 115402. [Google Scholar] [CrossRef] [Green Version]
- Hatsugai, Y.; Kohmoto, M. Energy spectrum and the quantum Hall effect on the square lattice with next-nearest-neighbor hopping. Phys. Rev. B 1990, 82, 8282. [Google Scholar] [CrossRef] [Green Version]
- Goldman, N.; Anisimovas, E.; Gerbier, F.; Öhberg, P.; Spielman, I.B.; Juzeliūnas, G. Measuring topology in a laser-coupled honeycomb lattice: From Chern insulators to topological semi-metals. New J. Phys. 2013, 15, 013025. [Google Scholar] [CrossRef] [Green Version]
- Andrijauskas, T.; Anisimovas, E.; Račiūnas, M.; Mekys, A.; Kudriašov, V.; Spielman, I.B.; Juzeliūnas, G. Three-level Haldane-like model on a dice optical lattice. Phys. Rev. A 2015, 92, 033617. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.B.; Zhu, S.-L.; Sheng, L.; Xing, D.Y.; Wang, Z.D. Realizing and Detecting the Quantum Hall Effect without Landau Levels by Using Ultracold Atoms. Phys. Rev. Lett. 2008, 101, 246810. [Google Scholar] [CrossRef]
- Alba, E.; Fernandez-Gonzalvo, X.; Mur-Petit, J.; Pachos, J.K.; Garcia-Ripoll, J.J. Seeing Topological Order in Time-of-Flight Measurements. Phys. Rev. Lett. 2011, 107, 235301. [Google Scholar] [CrossRef] [Green Version]
- Tarruell, L.; Greif, D.; Uehlinger, T.; Jotzu, G.; Essinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 2012, 483, 302–305. [Google Scholar] [CrossRef] [Green Version]
- Jotzu, G.; Messer, M.; Desbuquois, R.; Lebrat, M.; Uehlinger, T.; Greif, D.; Esslinger, T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237–240. [Google Scholar] [CrossRef] [Green Version]
- Sutherland, B. Localization of electronic wave functions due to local topology. Phys. Rev. B 1986, 34, 5208. [Google Scholar] [CrossRef]
- Vidal, J.; Mosseri, R.; Doucot, B. Aharonov-Bohm Cages in Two-Dimensional Structures. Phys. Rev. Lett. 1998, 81, 5888. [Google Scholar] [CrossRef] [Green Version]
- Bercioux, D.; Urban, D.F.; Grabert, H.; Häusler, W. Massless Dirac-Weyl fermions in a T3 optical lattice. Phys. Rev. A 2009, 80, 063603. [Google Scholar] [CrossRef] [Green Version]
- Möller, G.; Cooper, N.R. Correlated Phases of Bosons in the Flat Lowest Band of the Dice Lattice. Phys. Rev. Lett. 2012, 108, 045306. [Google Scholar] [CrossRef] [Green Version]
- Rizzi, M.; Cataudella, V.; Fazio, R. Phase diagram of the Bose-Hubbard model with T3 symmetry. Phys. Rev. B 2006, 73, 144511. [Google Scholar] [CrossRef] [Green Version]
- Burkov, A.A.; Demler, E. Vortex-Peierls States in Optical Lattices. Phys. Rev. Lett. 2006, 96, 180406. [Google Scholar] [CrossRef] [Green Version]
- Bercioux, D.; Goldman, N.; Urban, D.F. Topology-induced phase transitions in quantum spin Hall lattices. Phys. Rev. A 2011, 83, 023609. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Yin, H.; Lu, Z.; He, C.; Wang, P.; Xianlong, G. Predicting large-Chern-number phases in a shaken optical dice lattice. Phys. Rev. A 2020, 101, 043620. [Google Scholar] [CrossRef]
- Dalibard, J.; Gerbier, F.; Juzeliūnas, G.; Ōhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523. [Google Scholar] [CrossRef] [Green Version]
- Goldman, N.; Juzeliūnas, G.; Ōhberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef] [PubMed]
- Khanna, G.; Mukhopadhyay, S.; Simon, R.; Mukunda, N. Geometric phases for SU(3) representations and three level quantum systems. Ann. Phys. 1997, 253, 55–82. [Google Scholar] [CrossRef] [Green Version]
- Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Barnett, R.; Boyd, G.R.; Galitski, V. SU(3) Spin-Orbit Coupling in Systems of Ultracold Atoms. Phys. Rev. Lett. 2012, 109, 235308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Georgi, H. Lie Algebras In Particle Physics: From Isospin To Unified Theories; Benjamin/Cummings: Reading, MA, USA, 1982. [Google Scholar]
- Setyawan, W.; Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, S.; Xiao, D. Transition-Metal Oxide (111) Bilayers. J. Phys. Soc. Jpn. 2018, 87, 041006. [Google Scholar] [CrossRef]
- Rawl, R.; Lee, M.; Choi, E.S.; Li, G.; Chen, K.W.; Baumbach, R.; dela Cruz, C.R.; Ma, J.; Zhou, H.D. Magnetic properties of the triangular lattice magnets A4B′B2O12 (A=Ba, Sr, La; B′=Co, Ni, Mn; B=W, Re). Phys. Rev. B 2017, 95, 174438. [Google Scholar] [CrossRef] [Green Version]
- Schleid, T.; Meyer, G. Crystal structure of digadolinium monocarbide dichloride (1T type), Gd2CCl2. Z. Fur Krist. 1994, 209, 371. [Google Scholar] [CrossRef]
- Ryazanov, M.; Simon, A.; Mattausch, H. New synthesis route to and physical properties of lanthanum monoiodide. Inorg. Chem. 2006, 45, 2068–2074. [Google Scholar] [CrossRef]
- Schleid, T.; Meyer, G. Synthesis and crystal structures of hydrogen and carbon stabilized lutetium monochloride, LuClHx and Lu2Cl2C. Z. Fur Anorg. Undallgemeine Chem. 1987, 552, 90–96. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Gao, X. Topological Properties in a Λ/V-Type Dice Model. Crystals 2021, 11, 467. https://doi.org/10.3390/cryst11050467
Cheng S, Gao X. Topological Properties in a Λ/V-Type Dice Model. Crystals. 2021; 11(5):467. https://doi.org/10.3390/cryst11050467
Chicago/Turabian StyleCheng, Shujie, and Xianlong Gao. 2021. "Topological Properties in a Λ/V-Type Dice Model" Crystals 11, no. 5: 467. https://doi.org/10.3390/cryst11050467





