Anisotropy of X-ray Absorption Cross Section in CeCoGe3 Single Crystal
Abstract
:1. Introduction
2. Materials and Methods
3. Results
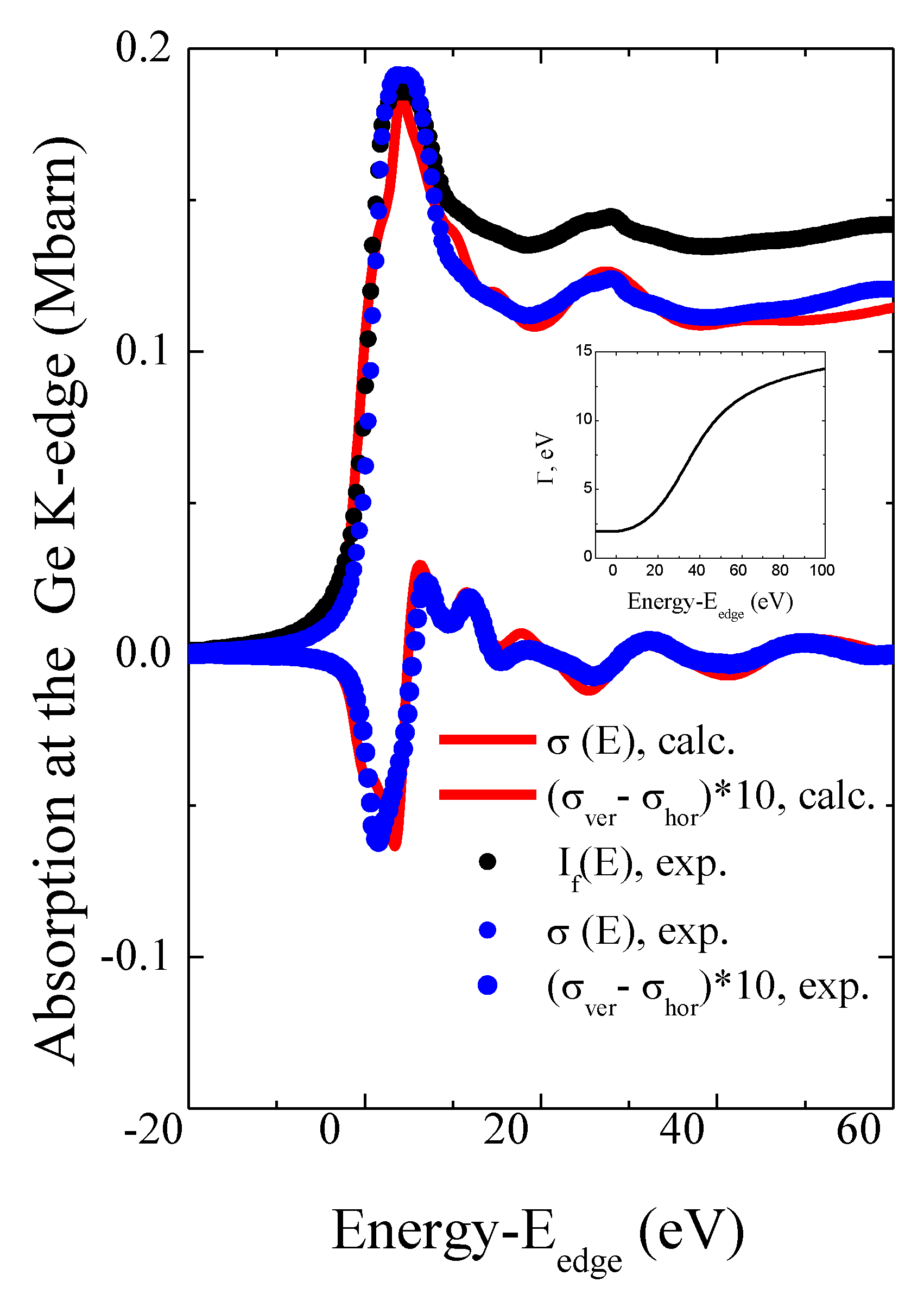
3.1. Anisotropy of the Absorption Cross Section of CeCoGe3 at the Energies Near the K-Edge of Ge
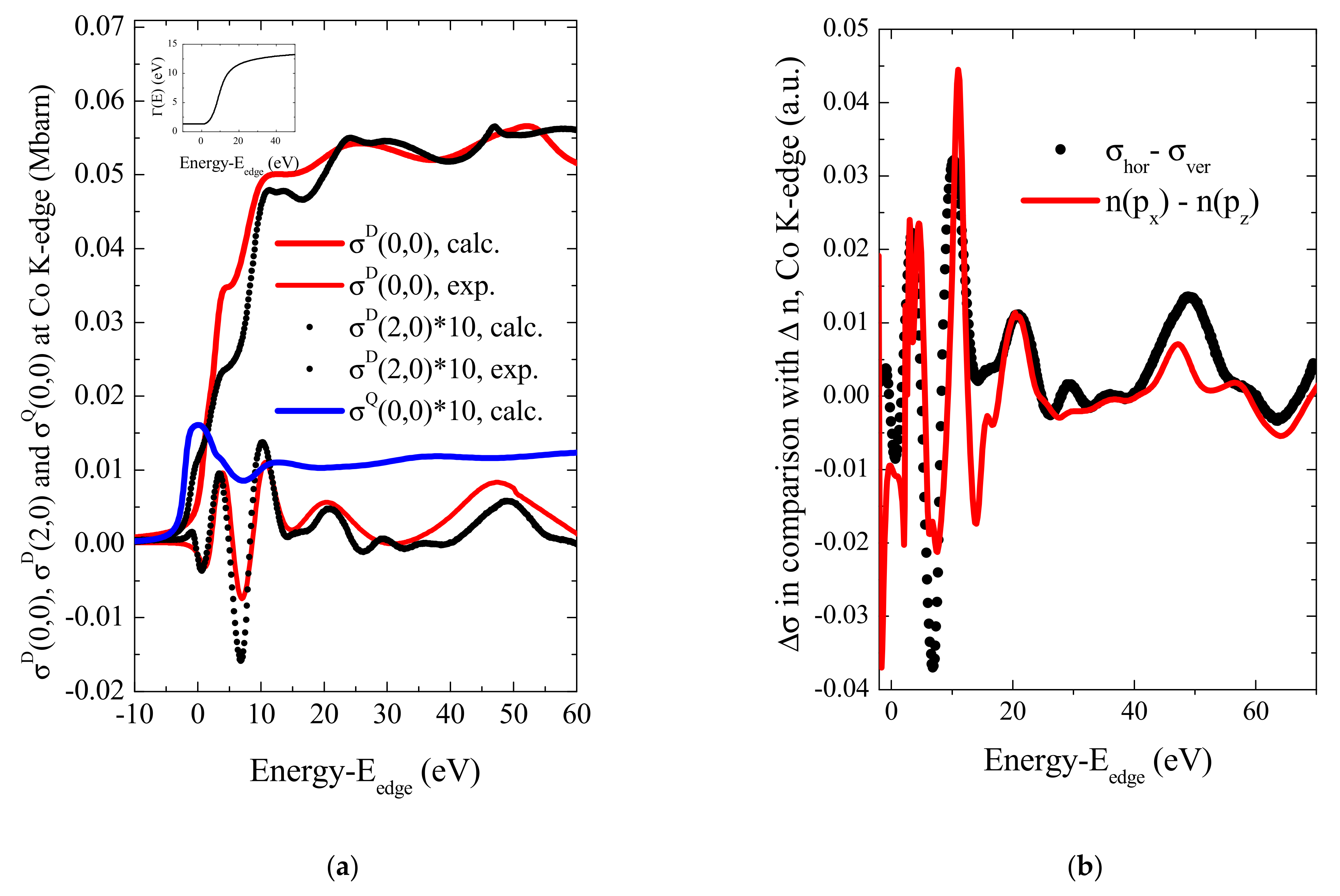
3.2. Anisotropy of the Absorption Cross Section of CeCoGe3 at Energies Near the K-Edge of Co
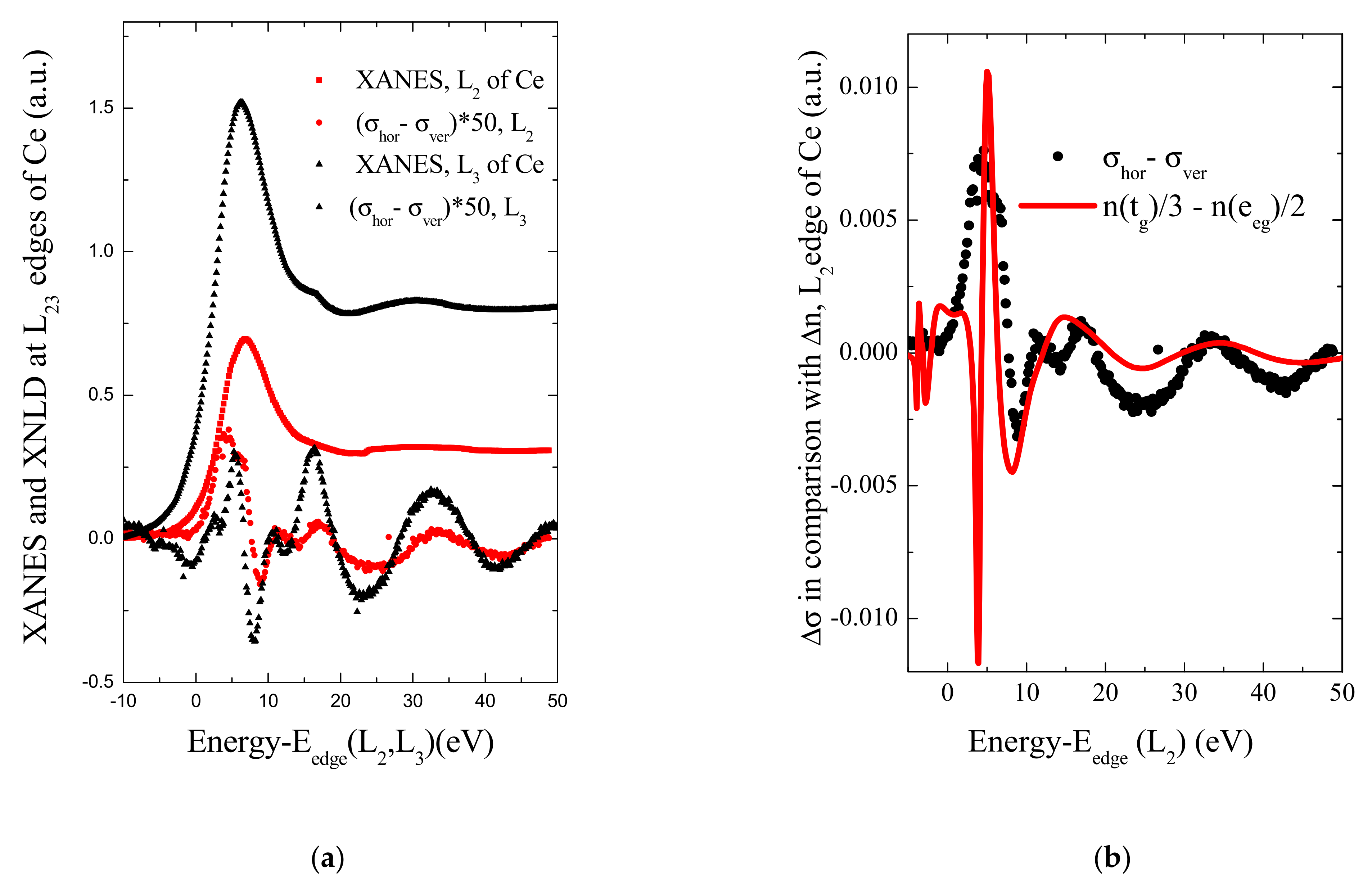
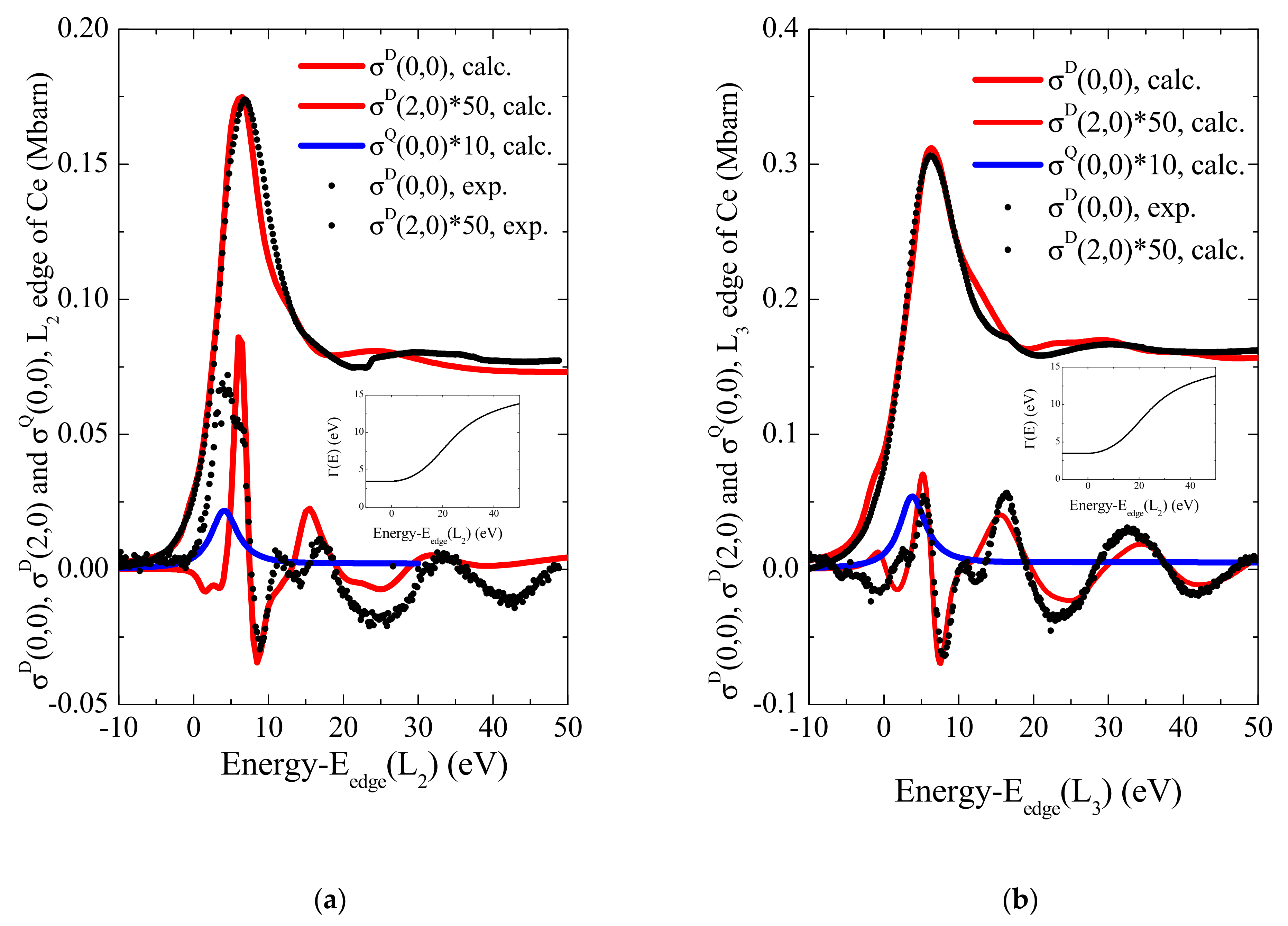
3.3. Anisotropy of the CeCoGe3 Absorption Cross Section at Energies Near L2,3 Edges of Ce
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Bokhoven, J.A.; Lamberti, C. X-ray Absorption and X-ray Emission Spectroscopy: Theory and Applications; John Wiley Sons: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Rehr, J.J.; Albers, R.C. Theoretical approaches to X-ray absorption fine structure. Rev. Mod. Phys. 2000, 72, 621–654. [Google Scholar] [CrossRef]
- Stöhr, J. NEXAFS Spectroscopy; Springer Series in Surface Sciences 25; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Maslen, E.N. X-Ray Absorption. In International Tables for Crystallography; Prince, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; Volume C, pp. 599–608. [Google Scholar]
- Krogstad, R.; Nelson, W.; Stephenson, S.T. X-ray absorption fine structure with polarized X-rays. Phys. Rev. 1953, 92, 1394–1395. [Google Scholar] [CrossRef]
- Hart, M. X-ray polarization phenomena. Philos. Mag. B 1978, 38, 41–56. [Google Scholar] [CrossRef]
- Alexander, E.; Fraenkel, B.S.; Perel, J.; Rabinovitch, K. Orientation dependence of k-absorption extended fine structure of a single crystal of germanium. Phys. Rev. 1963, 132, 1554–1558. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Dmitrienko, V.E. Polarization phenomena in X-ray optics. Sov. Phys. Uspekhi 1989, 32, 697–719. [Google Scholar] [CrossRef]
- Van der Laan, G.; Thole, B.T.; Sawatzky, G.A.; Goedkoop, J.B.; Fuggle, J.C.; Esteva, J.-M.; Karnatak, R.; Remeika, J.P.; Dabkowska, H.A. Experimental proof of magnetic X-ray dichroism. Phys. Rev. B Condens. Matter Mater. Phys. 1986, 34, 6529–6531. [Google Scholar] [CrossRef] [PubMed]
- Schütz, G. Absorption of circularly polarized x rays in iron. Phys. Rev. Lett. 1987, 58, 737–740. [Google Scholar] [CrossRef] [Green Version]
- Templeton, D.H.; Templeton, L.K. X-ray dichroism and polarized anomalous scattering of the uranyl ion. Acta Cryst. Sect. A 1982, 38, 62–67. [Google Scholar] [CrossRef]
- Thole, B.T.; Van-der-laan, G.; Sawatzky, G.A. X-ray absorption spectra of magnetic rare-earth materials. Phys. Rev. Lett. 1985, 55, 2086–2088. [Google Scholar] [CrossRef]
- Thole, B.T.; Carra, P.; Sette, F.; Van-der-laan, G. X-ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 1992, 68, 1943–1946. [Google Scholar] [CrossRef]
- Carra, P.; Thole, B.T.; Altarelli, M.; Wang, X. X-ray circular dichroism and local magnetic fields. Phys. Rev. Lett. 1993, 70, 694–697. [Google Scholar] [CrossRef]
- Rogalev, A.; Wilhelm, F.; Jaouen, N.; Goulon, J.; Kappler, J.-P. X-ray Magnetic Circular Dichroism: Historical Perspective and Recent Highlights. In Magnetism and Synchrotron Radiation; Beaurepaire, E., Scheurer, F., Krill, G., Kappler, J.-P., Eds.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Schütz, G.; Knülle, M.; Ebert, H. X-Ray Magnetic Circular Dichroism and Its Relation to Local Magnetic Structures. In Resonant Anomalous X-ray Scattering. Theory and Application; Materlik, G., Sparks, C.S., Fischer, K., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1994; pp. 535–555. [Google Scholar]
- Stöhr, J. Exploring the microscopic origin of magnetic anisotropies with X-ray magnetic circular dichroism (XMCD) spectroscopy. J. Magn. Magn. Mater. 1999, 200, 470–477. [Google Scholar] [CrossRef]
- Lϋnning, J.; Nolting, F.; Scholl, A.; Seo, J.W.; Fompeyrine, J.; Locquet, J.-P.; Stόhr, J. Determination of the antiferromagnetic spin axis in epitaxial LeFeO3 films by X-ray magnetic linear dichroism. Phys. Rev. B Condens. Matter Mater. Phys. 2003, 67, 214433–214500. [Google Scholar] [CrossRef] [Green Version]
- Van der Laan, G.; Arenholz, E.; Chopdekar, R.V.; Suzuki, Y. Influence of crystal field on anisotropic x-ray magnetic linear dichroism at the Co2+ L2,3 edges. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 064407. [Google Scholar] [CrossRef]
- Stohr, J.; Wu, Y.; Hermsmeier, B.D.; Samant, M.G.; Harp, G.R.; Koranda, S.; Dunham, D.; Tonner, B.P. Element-specific magnetic microscopy with circularly polarized x-rays. Science 1993, 259, 658–661. [Google Scholar] [CrossRef]
- Zhao, T.; Scholl, A.; Zavaliche, F.; Lee, K.; Barry, M.; Doran, A.; Cruz, M.P.; Chu, Y.H.; Ederer, C.; Spaldin, N.A.; et al. Electrical control of antiferromagnetic domains in multiferroic BiFeO3 films at room temperature. Nat. Mater. 2006, 5, 823–829. [Google Scholar] [CrossRef]
- Van der Laan, G.; Telling, N.D.; Potenza, A.; Dhesi, S.S.; Arenholz, E. Anisotropic x-ray magnetic linear dichroism and spectromicroscopy of interfacial Co/NiO(001). Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 064409. [Google Scholar] [CrossRef]
- Stöhr, J.; Scholl, A.; Regan, T.J.; Anders, S.; Lüning, J.; Scheinfein, M.R.; Padmore, H.A.; White, R.L. Images of the antiferromagnetic structure of a NiO (100) surface by means of x-ray magnetic linear dichroism spectromicroscopy. Phys. Rev. Lett. 1999, 83, 1862–1865. [Google Scholar] [CrossRef] [Green Version]
- Nolting, F.; Scholl, A.; Stohr, J.; Seo, J.W.; Fompeyrine, J.; Siegwart, H.; Locquet, J.-P.; Ander, S.; LuÈning, J.; Fullerton, E.E.; et al. Direct observation of the alignment of ferromagnetic spins by antiferromagnetic spins. Nature 2000, 403, 767–768. [Google Scholar] [CrossRef]
- Choe, S.-B.; Acremann, Y.; Scholl, A.; Bauer, A.; Doran, A.; Stöhr, J.; Padmore, H.A. Vortex core-driven magnetization dynamics. Science 2004, 304, 420–422. [Google Scholar] [CrossRef] [Green Version]
- Milne, C.J.; Penfold, T.J.; Chergui, M. Recent experimental and theoretical developments in time-resolved X-ray spectroscopies. Coord. Chem. Rev. 2014, 277–278, 44–68. [Google Scholar] [CrossRef]
- Alagna, L.; Prosperi, N.; Turchini, S.; Rogalev, A.; Coulon-Ginet, C.; Natoli, C.R.; Peacock, R.D.; Stewart, B. X-ray natural circular dichroism. Phys. Rev. Lett. 1998, 80, 4799–4802. [Google Scholar] [CrossRef]
- Goulon, J.; Goulon-Ginet, C.; Rogalev, A.; Gotte, V.; Malgrange, C.; Brouder, C.; Natoli, C.R. X-ray natural dichroism in a uniaxial gyrotropic single crystal of LiIO3. J. Chem. Phys. 1998, 108, 6394–6403. [Google Scholar] [CrossRef]
- Brouder, C.; Natoli, C.R.; Sainctavit, P.; Goulon, J.; Goulon-Ginet, C.; Rogalev, A. Theory of X-ray natural circular dichroism. J. Synchrotron Radiat. 1999, 6, 261–263. [Google Scholar] [CrossRef] [Green Version]
- Goulon, J.; Rogalev, A.; Goulon-Ginet, C.; Benayoun, G.; Paolasini, L.; Brouder, C.; Malgrange, C.; Metcalf, P.A. First observation of nonreciprocal X-ray gyropropy. Phys. Rev. Lett. 2000, 85, 4385–4390. [Google Scholar] [CrossRef]
- Di Matteo, S.; Joly, Y.; Natoli, C.R. Detection of electromagnetic multipoles by X-ray spectroscopies. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 72, 144406. [Google Scholar] [CrossRef] [Green Version]
- Carra, P.; Jerez, A.; Marri, I. X-ray dichroism in noncentrosymmetric crystals. Phys. Rev. B Condens. Matter Mater. Phys. 2003, 67, 045511. [Google Scholar] [CrossRef] [Green Version]
- Kubota, M.; Arima, T.; Kaneko, Y.; He, J.P.; Yu, X.Z.; Tokura, Y. X-ray directional dichroism of a polar ferrimagnet. Phys. Rev. Lett. 2004, 92, 137401. [Google Scholar] [CrossRef]
- Templeton, D.H.; Templeton, L.K. Polarized x-ray absorption and double refraction in vanadil biacetylacetonate. Acta Cryst. 1980, A36, 237–241. [Google Scholar] [CrossRef] [Green Version]
- Templeton, D.H.; Templeton, L.K. X-ray dichroism and polarized anomalous scattering of the uranyl ion. Acta Cryst. 1981, A37, C309. [Google Scholar] [CrossRef]
- Brouder, С. Angular dependence of x-ray absorption spectra. J. Phys. Condens. Matter 1990, 2, 701–738. [Google Scholar] [CrossRef]
- Gaudry, E.; Kiratisin, A.; Sainctavit, P.; Brouder, C.; Mauri, F.; Ramos, A.; Rogalev, A.; Goulon, J. X-ray natural linear dichroism (xnld) applied to the determination of relaxations around transition metal impurities in -Al2O3. Phys. Scr. 2005, T115, 1041–1043. [Google Scholar] [CrossRef]
- Metzler, R.A.; Abrecht, M.; Olabisi, R.M.; Ariosa, D.; Johnson, C.J.; Frazer, B.H.; Coppersmith, S.N.; Gilbert, P.U.P.A. Architecture of columnar nacre, and implications for its formation mechanism. Phys. Rev. Lett. 2007, 98, 268102. [Google Scholar] [CrossRef] [Green Version]
- Polisetty, S.; Zhou, J.; Karthik, J.; Damodaran, A.R.; Chen, D.; Scholl, A.; Martin, L.W.; Holcomb, M. X-ray linear dichroism dependence on ferroelectric polarization. J. Phys. Condens. Matter. 2012, 24, 245902. [Google Scholar] [CrossRef] [Green Version]
- Stifler, A.; Kølln Wittig, N.; Sassi, M.; Sun, C.-Y.; Marcus, M.A.; Birkedal, H.; Beniash, E.; Rosso, K.M.; Gilbert, P.U.P.A. X-ray linear dichroism in apatite crystals. J. Am. Chem. Soc. 2018, 37, 11698–11704. [Google Scholar] [CrossRef] [Green Version]
- Cabaret, D.; Bordage, A.; Juhin, A.; Arfaoui, M.; Gaudry, E. First-principles calculations of X-ray absorption spectra at the K-edge of 3d transition metals: An electronic structure analysis of the pre-edge. Phys. Chem. Chem. Phys. 2010, 12, 5619–5633. [Google Scholar] [CrossRef] [Green Version]
- Cabaret, D.; Joly, Y.; Renevier, H.; Natoli, C.R. Pre-edge structure analysis of Ti K-edge polarized X-ray absorption spectra in TiO2 by full-potential XANES calculations. J. Synchrotron Radiat. 1999, 6, 258–260. [Google Scholar] [CrossRef] [Green Version]
- Rossi, T.C.; Grolimund, D.; Nachtegaal, M.; Cannelli, O.; Mancini, G.F.; Bacellar, C.; Kinsche, D.; Rouxel, J.R.; Ohannessian, N.; Pergolesi, D.; et al. X-ray absorption linear dichroism at the Ti K edge of anatase TiO2 single crystals. Phys. Rev. B Condens. Matter Mater. Phys. 2019, 100, 245207. [Google Scholar] [CrossRef] [Green Version]
- Rossi, T.C.; Grolimund, D.; Cannelli, O.; Mancini, G.F.; Bacellar, C.; Kinschel, D.; Rouxel, J.R.; Chergui, M. X-ray absorption linear dichroism at the Ti K-edge of rutile (001) TiO2 single crystal. J. Synchrotron Radiat. 2020, 27, 425–435. [Google Scholar] [CrossRef]
- Knebel, G.; Aoki, D.; Lapertot, G.; Salce, B.; Flouquet, J.; Kawai, T.; Muranaka, H.; Settai, R.; Ônuki, Y. High Pressure Phase Diagram of the Non-centrosymmetric Antiferromagnet CeCoGe3. J. Phys. Soc. Jpn. 2009, 78, 074714. [Google Scholar] [CrossRef]
- Méasson, M.; Muranaka, H.; Kawai, T.; Ota, Y.; Sugiyama, K.; Hagiwara, M.; Kindo, K.; Takeuchi, T.; Shimizu, K.; Honda, F.; et al. Magnetic properties of RCoGe3 (R: Ce, Pr, and Nd) and strong anisotropy of the upper critical field in non-centrosymmetric compound CeCoGe3. J. Phys. Soc. Jpn. 2009, 78, 124713. [Google Scholar] [CrossRef]
- Knebel, G.; Aoki, D.; Flouquet, J. Antiferromagnetism and superconductivity in cerium based heavy-fermion compounds. C. R. Phys. 2011, 12, 542–566. [Google Scholar] [CrossRef] [Green Version]
- Oreshko, A.P.; Ovchinnikova, E.N.; Rogalev, A.; Wilhelm, F.; Mill, B.V.; Dmitrienko, V.E. X-ray natural circular dichroism in langasite crystal. J. Synchrotron Radiat. 2018, 25, 222–231. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikova, E.N.; Rogalev, A.; Wilhelm, F.; Kozlovskaya, K.A.; Oreshko, A.P.; Dmitrienko, V.E. X-ray natural circular dichroism in copper metaborate. J. Exp. Theor. Phys. 2016, 123, 27–32. [Google Scholar] [CrossRef]
- Beutier, G.; Collins, S.P.; Dmitrienko, V.E.; Lorenzo, J.E.; Hodeau, J.-L.; Kirfel, A.; Joly, Y.; Antonenko, A.A.; Sarkisyan, V.A.; Bombardi, A. Interplay of inequivalent atomic positions in resonant X-ray diffraction of Fe3BO6. J. Phys. Condens. Matter 2009, 21, 265402. [Google Scholar] [CrossRef] [PubMed]
- Goulon, J.; Goulon-Jinet, C.; Cortes, R.; Dubois, J.M. On experimental attenuation factors of the amplitude of the EXAFS oscillations in absorption, reflectivity and luminescence measurements. J. Phys. 1982, 43, 539–548. [Google Scholar] [CrossRef]
- Pfalzer, P.; Urbach, J.-P.; Klemm, M.; denBoer, M.L.; Frenkel, A.I.; Kirkland, J.P. Elimination of self-absorption in fluorescence hard-x-ray absorption. Phys. Rev. B Condens. Matter Mater. 1999, 60, 9335–9339. [Google Scholar] [CrossRef] [Green Version]
- Booth, C.H.; Bridges, F. Absorption correction for fluorescence measurements of extended x-ray absorption fine-structure. Phys. Scr. 2005, T115, 202–204. [Google Scholar] [CrossRef] [Green Version]
- Abe, H.; Aquilanti, G.; Boada, R.; Bunker, B.; Glatzel, P.; Nachtegaal, M.; Pascarelli, S. Improving the quality of XAFS data. J. Synchrotron Radiat. 2018, 25, 972–980. [Google Scholar] [CrossRef]
- Smidman, M.; Adroja, D.T.; Hillier, A.D.; Chapon, L.C.; Taylor, J.W.; Anand, V.K.; Singh, R.P.; Lees, M.R.; Goremychkin, E.A.; Koza, M.M.; et al. Neutron scattering and muon spin relaxation measurements of the noncentrosymmetric antiferromagnet CeCoGe3. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 134416. [Google Scholar] [CrossRef] [Green Version]
- Hahn, T.H. (Ed.) International Tables for Crystallography; Springer: Berlin/Heidelberg, Germany, 2005; Volume 1. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuios Media, 2nd ed.; Eslevier Ltd.: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Carra, P.; Benoist, R. X-ray natural circular dichroism. Phys. Rev. B Condens. Matter Mater. Phys. 2000, 62, R7703(R). [Google Scholar] [CrossRef] [Green Version]
- Schnohr, C.S.; Ridgway, M.C. Introduction to X-Ray Absorption Spectroscopy. In X-ray Absorption Spectroscopy of Semiconductors; Schnohr, C., Ridgway, M., Eds.; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2015; Volume 190. [Google Scholar] [CrossRef]
- Blume, M. Magnetic Effects in Anomalous Dispersion. In Resonant Anomalous Xray Scattering; Materlik, G., Ed.; Elsevier: Amsterdam, The Netherlands, 1994; p. 495. [Google Scholar]
- Joly, Y.; Grenier, S. Theory of X-ray Absorption Near Edge Structure. In X-ray Absorption and X-ray Emission Spectroscopy: Theory and Applications; van Bokhoven, J.A., Lamberti, C., Eds.; Wiley and Sons: Hoboken, NJ, USA, 2016; Chapter 4. [Google Scholar]
- Joly, Y. X-ray absorption near edge structure calculation beyond the muffin-tin approximation. Phys. Rev. B Condens. Matter Mater. Phys. 2001, 63, 125120. [Google Scholar] [CrossRef]
- Joly, Y.; Bunău, O.; Lorenzo, J.E.; Galéra, R.M.; Grenier, S.; Thompson, B. Self-consistency, spin-orbit and other advances in the FDMNES code to simulate XANES and RXD experiments. J. Phys. Conf. Ser. 2009, 190, 012007. [Google Scholar] [CrossRef]
- Joly, Y. The FDMNES Project. Available online: http://fdmnes.neel.cnrs.fr/ (accessed on 12 May 2021).
- Henke, B.L.; Lee, P.; Tanaka, T.J.; Shimabukuro, R.L.; Fujikawa, B.K. Low-energy x-ray interaction coefficients: Photoabsorption, scattering, and reflection, E = 100 − 2000 eV, Z = 1 − 94. At. Data Nucl. Data Tables 1982, 27, 1–144. [Google Scholar] [CrossRef]
- Sadovnichy, V.; Tikhonravov, A.; Voevodin, V.; Opanasenko, V. “Lomonosov”: Supercomputing at Moskow State University. In Contemporary High Performance Computing; Vetter, J., Ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 283–307. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogalev, A.; Wilhelm, F.; Ovchinnikova, E.; Enikeev, A.; Bakonin, R.; Kozlovskaya, K.; Oreshko, A.; Aoki, D.; Dmitrienko, V.E. Anisotropy of X-ray Absorption Cross Section in CeCoGe3 Single Crystal. Crystals 2021, 11, 544. https://doi.org/10.3390/cryst11050544
Rogalev A, Wilhelm F, Ovchinnikova E, Enikeev A, Bakonin R, Kozlovskaya K, Oreshko A, Aoki D, Dmitrienko VE. Anisotropy of X-ray Absorption Cross Section in CeCoGe3 Single Crystal. Crystals. 2021; 11(5):544. https://doi.org/10.3390/cryst11050544
Chicago/Turabian StyleRogalev, Andrei, Fabrice Wilhelm, Elena Ovchinnikova, Aydar Enikeev, Roman Bakonin, Ksenia Kozlovskaya, Alexey Oreshko, Dai Aoki, and Vladimir E. Dmitrienko. 2021. "Anisotropy of X-ray Absorption Cross Section in CeCoGe3 Single Crystal" Crystals 11, no. 5: 544. https://doi.org/10.3390/cryst11050544
APA StyleRogalev, A., Wilhelm, F., Ovchinnikova, E., Enikeev, A., Bakonin, R., Kozlovskaya, K., Oreshko, A., Aoki, D., & Dmitrienko, V. E. (2021). Anisotropy of X-ray Absorption Cross Section in CeCoGe3 Single Crystal. Crystals, 11(5), 544. https://doi.org/10.3390/cryst11050544





