Analysis of Te Inclusion Striations in (Cd,Zn)Te Crystals Grown by Traveling Heater Method
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
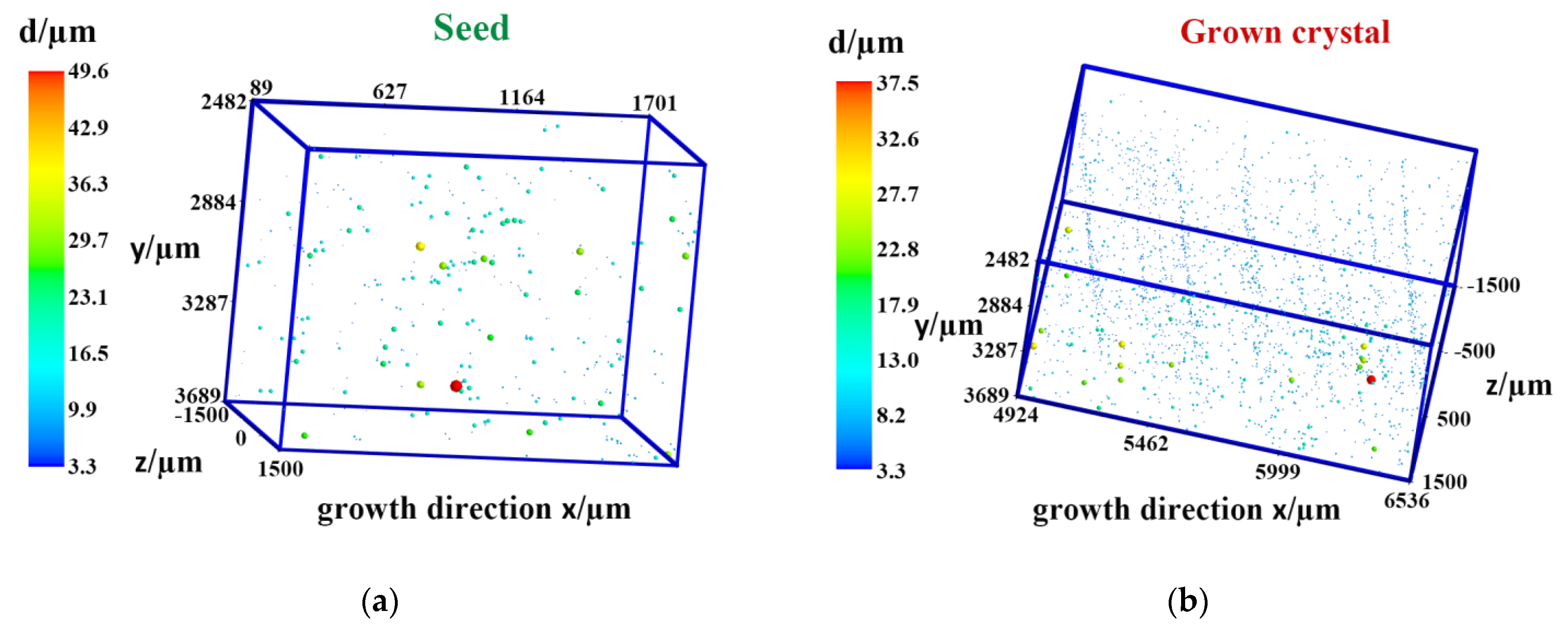
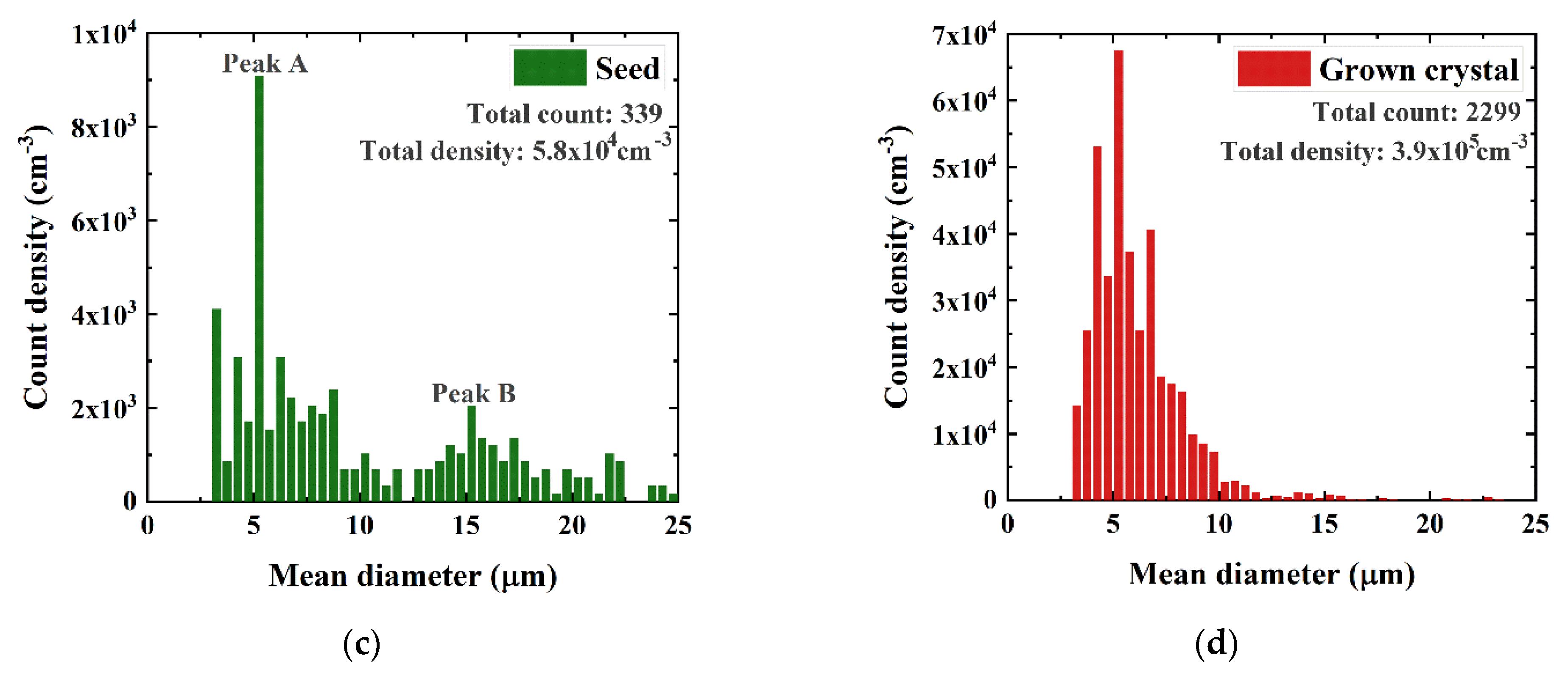
3.1. Comparison of the Inclusions in the Seed and the Grown Crystal
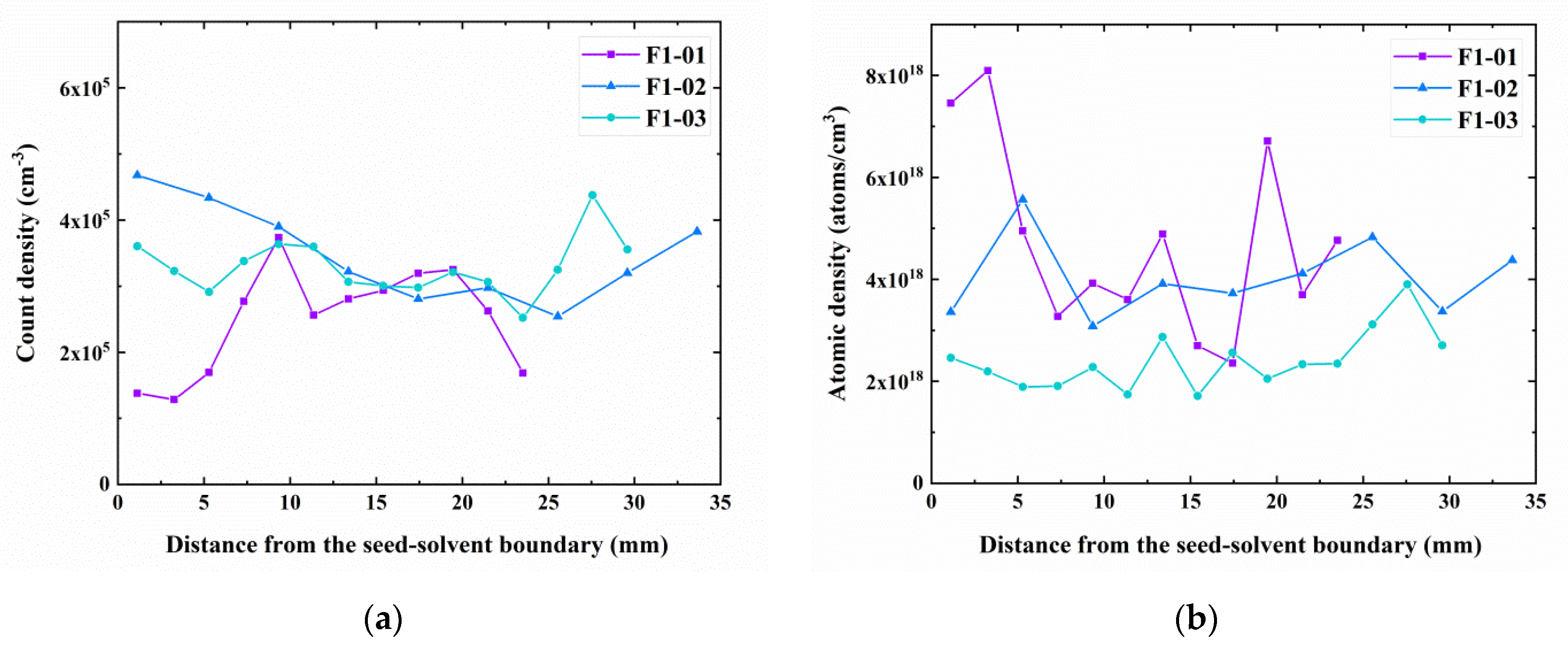
3.2. Axial Inclusion Distribution
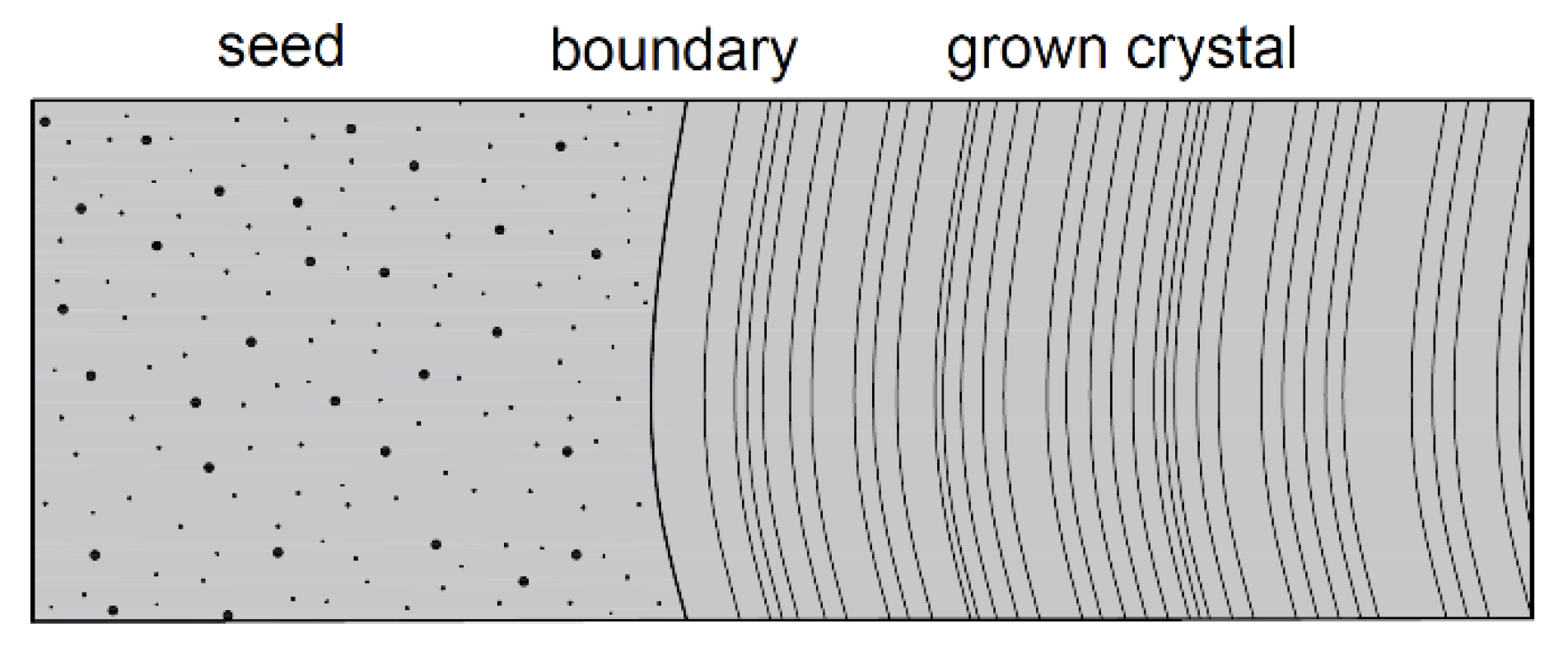
3.3. Striation-Like Patterns
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roy, U.N.; Camarda, G.S.; Cui, Y.; Gul, R.; Hossain, A.; Yang, G.; Zazvorka, J.; Dedic, V.; Franc, J.; James, R.B. Role of Selenium Addition to CdZnTe Matrix for Room-Temperature Radiation Detector Applications. Sci. Rep. 2019, 9, 1620. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Jie, W.; Wang, T.; Yin, L.; Yang, F.; Zhang, B.; Xi, S.; Dong, J. Modification of Growth Interface of CdZnTe Crystals in THM Process by ACRT. J. Cryst. Growth 2018, 483, 281–284. [Google Scholar] [CrossRef]
- Roy, U.N.; Burger, A.; James, R.B. Growth of CdZnTe Crystals by the Traveling Heater Method. J. Cryst. Growth 2013, 379, 57–62. [Google Scholar] [CrossRef]
- Chen, H.; Awadalla, S.A.; Iniewski, K.; Lu, P.H.; Harris, F.; Mackenzie, J.; Hasanen, T.; Chen, W.; Redden, R.; Bindley, G.; et al. Characterization of Large Cadmium Zinc Telluride Crystals Grown by Traveling Heater Method. J. Appl. Phys. 2008, 103, 014903. [Google Scholar] [CrossRef] [Green Version]
- Shiraki, H.; Funaki, M.; Ando, Y.; Tachibana, A.; Kominami, S.; Ohno, R. THM Growth and Characterization of 100 mm Diameter CdTe Single Crystals. IEEE Trans. Nucl. Sci. 2009, 56, 1717–1723. [Google Scholar] [CrossRef]
- Wald, F.V.; Bell, R.O. Natural and Forced Convection during Solution Growth of CdTe by the Traveling Heater Method (THM). J. Cryst. Growth 1975, 30, 29–36. [Google Scholar] [CrossRef]
- Schwenkenbecher, K.; Rudolph, P. Investigation of Convection in the Solution Zone at the Growth of CdTe by THM. Cryst. Res. Technol. 1985, 20, 1609–1613. [Google Scholar] [CrossRef]
- Cherepanova, T.A. Influence of Gravitation on the Processes of Heat and Mass Transfer in Solution Crystal Growth by the Travelling Heater Method (THM) (I). Cryst. Res. Technol. 1982, 17, 735–741. [Google Scholar] [CrossRef]
- Wang, Y.; Kudo, K.; Inatomi, Y.; Ji, R.; Motegi, T. Growth Interface of CdZnTe Grown from Te Solution with THM Technique under Static Magnetic Field. J. Cryst. Growth 2005, 284, 406–411. [Google Scholar] [CrossRef]
- Kumar, V.; Dost, S.; Durst, F. Numerical Modeling of Crystal Growth under Strong Magnetic Fields: An Application to the Travelling Heater Method. Appl. Math. Model. 2007, 31, 589–605. [Google Scholar] [CrossRef]
- Li, Z.; Peterson, J.H.; Yeckel, A.; Derby, J.J. Analysis of the Effects of a Rotating Magnetic Field on the Growth of Cadmium Zinc Telluride by the Traveling Heater Method under Microgravity Conditions. J. Cryst. Growth 2016, 452, 17–21. [Google Scholar] [CrossRef] [Green Version]
- Ghaddar, C.K.; Lee, C.K.; Motakef, S.; Gillies, D.C. Numerical Simulation of THM Growth of CdTe in Presence of Rotating Magnetic Fields (RMF). J. Cryst. Growth 1999, 205, 97–111. [Google Scholar] [CrossRef]
- Salk, M.; Fiederle, M.; Benz, K.W.; Senchenkov, A.S.; Egorov, A.V.; Matioukhin, D.G. CdTe and CdTe0.9Se0.1 Crystals Grown by the Travelling Heater Method Using a Rotating Magnetic Field. J. Cryst. Growth 1994, 138, 161–167. [Google Scholar] [CrossRef]
- Stelian, C.; Duffar, T. Influence of Rotating Magnetic Fields on THM Growth of CdZnTe Crystals under Microgravity and Ground Conditions. J. Cryst. Growth 2015, 429, 19–26. [Google Scholar] [CrossRef]
- Divecha, M.S.; Derby, J.J. Analysis of the Accelerated Crucible Rotation Technique Applied to the Gradient Freeze Growth of Cadmium Zinc Telluride. J. Cryst. Growth 2017, 468, 630–634. [Google Scholar] [CrossRef]
- Swain, S.; McCoy, J.; Lynn, K. Influence of Accelerated Crucible Rotation on Defect Distribution and Detector Characteristics of Melt Grown CdZnTe (Conference Presentation). In Proceedings of the Hard X-Ray, Gamma-Ray, and Neutron Detector Physics XVIII, San Diego, CA, USA, 29–31 August 2016; Volume 9968, p. 996806. [Google Scholar]
- Liu, J. Optimization of Control Parameters of CdZnTe ACRT-Bridgman Single Crystal Growth. Sci. China Ser. E Technol. Sci. 2004, 47, 725–740. [Google Scholar] [CrossRef]
- Capper, P.; Harris, J.E.; O’Keefe, E.; Jones, C.L.; Ard, C.K.; Mackett, P.; Dutton, D. Bridgman Growth and Assessment of CdTe and CdZnTe Using the Accelerated Crucible Rotation Technique. Mater. Sci. Eng. B 1993, 16, 29–39. [Google Scholar] [CrossRef]
- Benz, K.-W.; Fiederle, M. (Eds.) Chapter IC—Crystal growth of CdTe/CdZnTe in microgravity. In CdTe and Related Compounds; Physics, Defects, Hetero- and Nano-Structures, Crystal Growth, Surfaces and Applications; European Materials Research Society Series; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1–144. ISBN 978-0-08-096513-0. [Google Scholar]
- Benz, K.W.; Dold, P. Crystal Growth under Microgravity: Present Results and Future Prospects towards the International Space Station. J. Cryst. Growth 2002, 237–239, 1638–1645. [Google Scholar] [CrossRef]
- Griffin, P.; Motakef, S. Influence of Non Steady Gravity on Natural Convection during Micro-Gravity Solidification of Semiconductors. I—Time Scale Analysis. II—Implications for Crystal Growth Experiments. Appl. Micrograv. Technol. 1989, 2. [Google Scholar]
- Littke, W.; John, C. Materials: Protein Single Crystal Growth Under Microgravity. Science 1984, 225, 203–204. [Google Scholar] [CrossRef]
- McPherson, A.; Greenwood, A.; Day, J. The Effect of Microgravity on Protein Crystal Growth. Adv. Space Res. 1991, 11, 343–356. [Google Scholar] [CrossRef]
- Su, C.-H.; George, M.A.; Palosz, W.; Feth, S.; Lehoczky, S.L. Contactless Growth of ZnSe Single Crystals by Physical Vapor Transport. J. Cryst. Growth 2000, 213, 267–275. [Google Scholar] [CrossRef] [Green Version]
- Kundrot, C.E.; Judge, R.A.; Pusey, M.L.; Snell, E.H. Microgravity and Macromolecular Crystallography. Cryst. Growth Des. 2001, 1, 87–99. [Google Scholar] [CrossRef]
- Duffar, T.; Paret-Harter, I.; Dusserre, P. Crucible De-Wetting during Bridgman Growth of Semiconductors in Microgravity. J. Cryst. Growth 1990, 100, 171–184. [Google Scholar] [CrossRef]
- Peterson, J.H.; Fiederle, M.; Derby, J.J. Analysis of the Traveling Heater Method for the Growth of Cadmium Telluride. J. Cryst. Growth 2016, 454, 45–58. [Google Scholar] [CrossRef] [Green Version]
- Fiederle, M.; Eiche, C.; Joerger, W.; Salk, M.; Senchenkov, A.S.; Egorov, A.V.; Ebling, D.G.; Benz, K.W. Radiation Detector Properties of CdTe0.9Se0.1:Cl Crystals Grown under Microgravity in a Rotating Magnetic Field. J. Cryst. Growth 1996, 166, 256–260. [Google Scholar] [CrossRef]
- Borisenko, E.B.; Kolesnikov, N.N.; Senchenkov, A.S.; Fiederle, M. Crystal Growth of Cd1−xZnxTe by the Traveling Heater Method in Microgravity on Board of Foton-M4 Spacecraft. J. Cryst. Growth 2017, 457, 262–264. [Google Scholar] [CrossRef]
- Eiche, C.; Joerger, W.; Fiederle, M.; Ebling, D.; Salk, M.; Schwarz, R.; Benz, K.W. Characterization of CdTe:Cl Crystals Grown under Microgravity Conditions by Time Dependent Charge Measurements (TDCM). J. Cryst. Growth 1996, 166, 245–250. [Google Scholar] [CrossRef]
- Fiederle, M.; Duffar, T.; Babentsov, V.; Benz, K.W.; Dusserre, P.; Corregidor, V.; Dieguez, E.; Delaye, P.; Roosen, G.; Chevrier, V.; et al. Dewetted Growth of CdTe in Microgravity (STS-95). Cryst. Res. Technol. 2004, 39, 481–490. [Google Scholar] [CrossRef]
- Rudolph, P.; Engel, A.; Schentke, I.; Grochocki, A. Distribution and Genesis of Inclusions in CdTe and (Cd,Zn)Te Single Crystals Grown by the Bridgman Method and by the Travelling Heater Method. J. Cryst. Growth 1995, 147, 297–304. [Google Scholar] [CrossRef]
- Senchenkov, A.S.; Barmin, I.V.; Tomson, A.S.; Krapukhin, V.V. Seedless THM Growth of CdxHg1−xTe (X≈0.2) Single Crystals within Rotating Magnetic Field. J. Cryst. Growth 1999, 197, 552–556. [Google Scholar] [CrossRef]
- Senchenkov, A.S.; Fiederle, M.; Kolesnikov, N.N. CZT Crystal Growth by THM in Microgravity—Preparation of Experiments for FOTON-M4 Mission. In Proceedings of the IAC Proceedings 2014, IAC-14-A2.4.7, Toronto, ON, Canada, 29 September–3 October 2014. [Google Scholar]
- Bolke, J.; O’Brien, K.; Wall, P.; Spicer, M.; Gélinas, G.; Beaudry, J.-N.; Alexander, W.B. Measuring Te Inclusion Uniformity over Large Areas for CdTe/CZT Imaging and Spectrometry Sensors. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXI, Warsaw, Poland, 11–14 September 2017; Volume 10423, p. 104231M. [Google Scholar]
- Roy, U.N.; Weiler, S.; Stein, J. Growth and Interface Study of 2in Diameter CdZnTe by THM Technique. J. Cryst. Growth 2010, 312, 2840–2845. [Google Scholar] [CrossRef]
- Bolotnikov, A.E.; Babalola, S.; Camarda, G.S.; Cui, Y.; Egarievwe, S.U.; Hawrami, R.; Hossain, A.; Yang, G.; James, R.B. Te Inclusions in CZT Detectors: New Method for Correcting Their Adverse Effects. IEEE Trans. Nucl. Sci. 2010, 57, 910–919. [Google Scholar] [CrossRef] [Green Version]
- Carini, G.A.; Bolotnikov, A.E.; Camarda, G.S.; Cui, Y.; Jackson, H.; Burger, A.; Kohman, K.T.; Li, L.; James, R.B. Te Inclusions and Their Relationship to the Performance of CdZnTe Detectors. Hard X-ray and Garnma Ray Detect. Phys. VIII 2006, 6319, 631906. [Google Scholar] [CrossRef] [Green Version]
- Tilli, M. Chapter 4 —Silicon Wafers: Preparation and Properties. In Handbook of Silicon Based MEMS Materials and Technologies, 2nd ed.; Tilli, M., Motooka, T., Airaksinen, V.-M., Franssila, S., Paulasto-Kröckel, M., Lindroos, V., Eds.; Micro and Nano Technologies; William Andrew Publishing: Boston, MA, USA, 2015; pp. 86–103. ISBN 978-0-323-29965-7. [Google Scholar]
- Camp, P.R. Resistivity Striations in Germanium Crystals. J. Appl. Phys. 1954, 25, 459–463. [Google Scholar] [CrossRef]
- Merrell, J.L.; Gray, N.W.; Bolke, J.G.; Merrell, A.N.; Prax, A.G.; Demke, J.M.; Gossett, N.W. Enabling On-Axis InSb Crystal Growth for High-Volume Wafer Production: Characterizing and Eliminating Variation in Electrical Performance for IR Focal Plane Array Applications. In Proceedings of the Infrared Technology and Applications XLII, Baltimore, MD, USA, 18–21 April 2016; Volume 9819, p. 981915. [Google Scholar]
- Le Donne, A.; Binetti, S.; Folegatti, V.; Coletti, G. On the Nature of Striations in N-Type Silicon Solar Cells. Appl. Phys. Lett. 2016, 109, 033907. [Google Scholar] [CrossRef]
- Triboulet, R.; Siffert, P. (Eds.) Chapter I—Crystal Growth and Surfaces. In CdTe and Related Compounds; Physics, Defects, Hetero- and Nano-Structures, Crystal Growth, Surfaces and Applications; European Materials Research Society Series; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1–144. ISBN 978-0-08-096513-0. [Google Scholar]
- Fiederle, M.; Fauler, A.; Zwerger, A. Crystal Growth and Characterization of Detector Grade (Cd,Zn)Te Crystals. IEEE Trans. Nucl. Sci. 2007, 54, 769–772. [Google Scholar] [CrossRef]
- Henager, C.H.; Alvine, K.J.; Bliss, M.; Riley, B.J.; Stave, J.A. The Influence of Constitutional Supercooling on the Distribution of Te-Particles in Melt-Grown CZT. J. Electron. Mater. 2015, 44, 4604–4621. [Google Scholar] [CrossRef]
- McCoy, J.J.; Kakkireni, S.; Gélinas, G.; Garaffa, J.F.; Swain, S.K.; Lynn, K.G. Effects of Excess Te on Flux Inclusion Formation in the Growth of Cadmium Zinc Telluride When Forced Melt Convection Is Applied. J. Cryst. Growth 2020, 535, 125542. [Google Scholar] [CrossRef]
- Rudolph, P. Fundamental Studies on Bridgman Growth of CdTe. Prog. Cryst. Growth Charact. Mater. 1994, 29, 275–381. [Google Scholar] [CrossRef]
- Rudolph, P. Non-Stoichiometry Related Defects at the Melt Growth of Semiconductor Compound Crystals—A Review. Cryst. Res. Technol. 2003, 38, 542–554. [Google Scholar] [CrossRef]
- Chernov, A.A.; Temkin, D.E. Capture of Inclusions in Crystal Growth. In Current Topics of Materials Science: Crystal Growth and Materials; Current Topics of Materials Science: Amsterdam, The Netherlands, 1977; Volume 2, pp. 3–77. [Google Scholar]



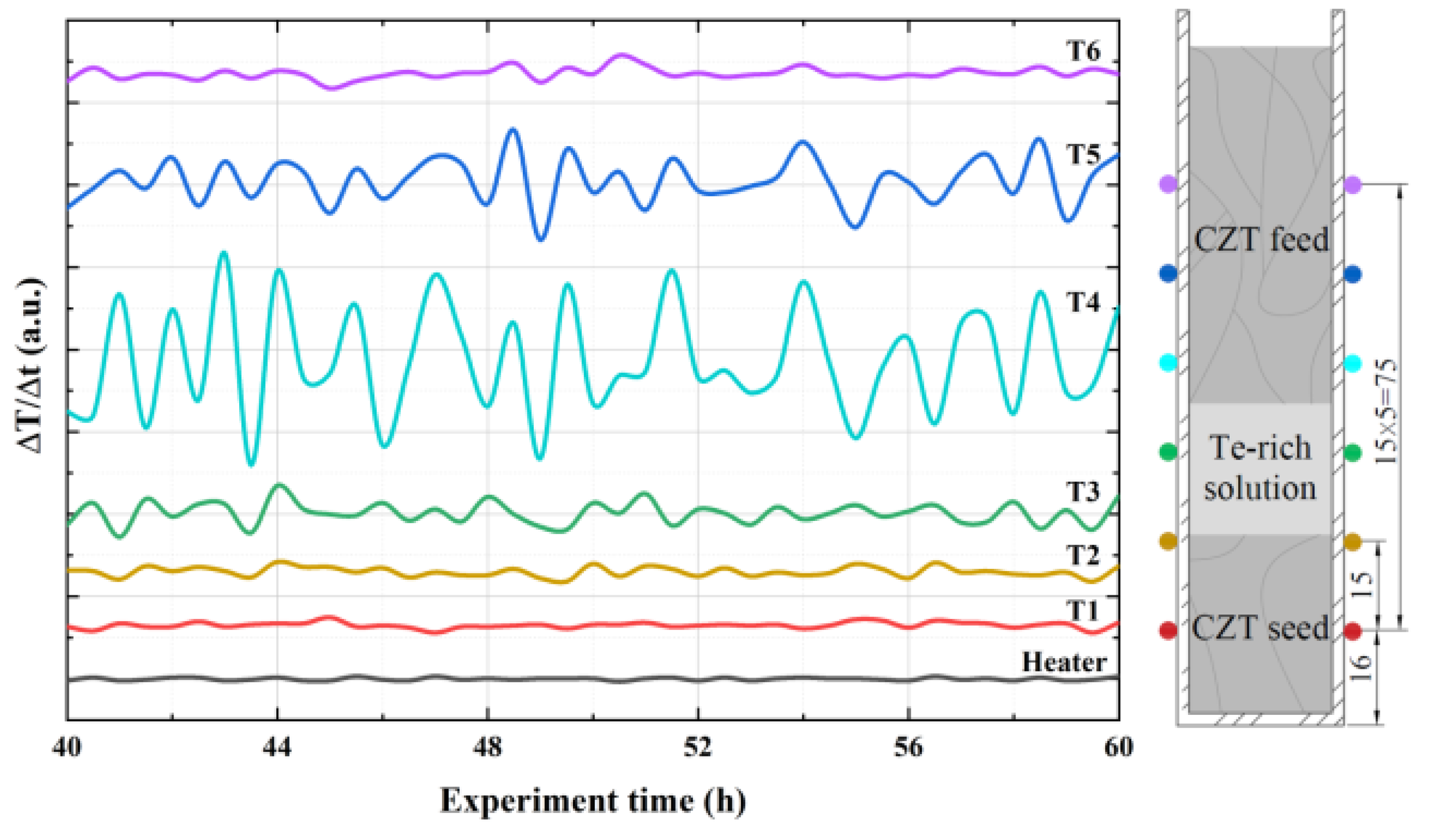
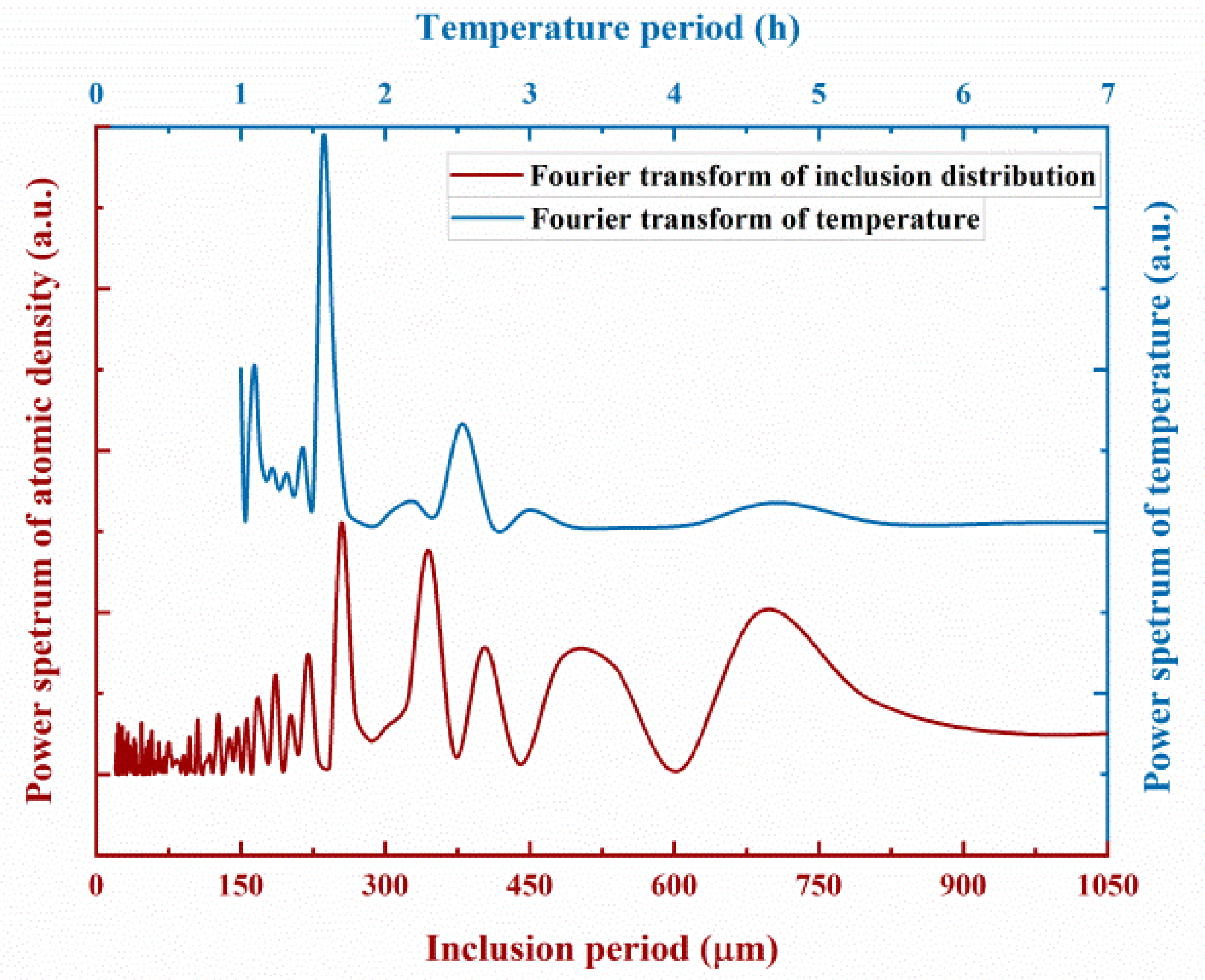
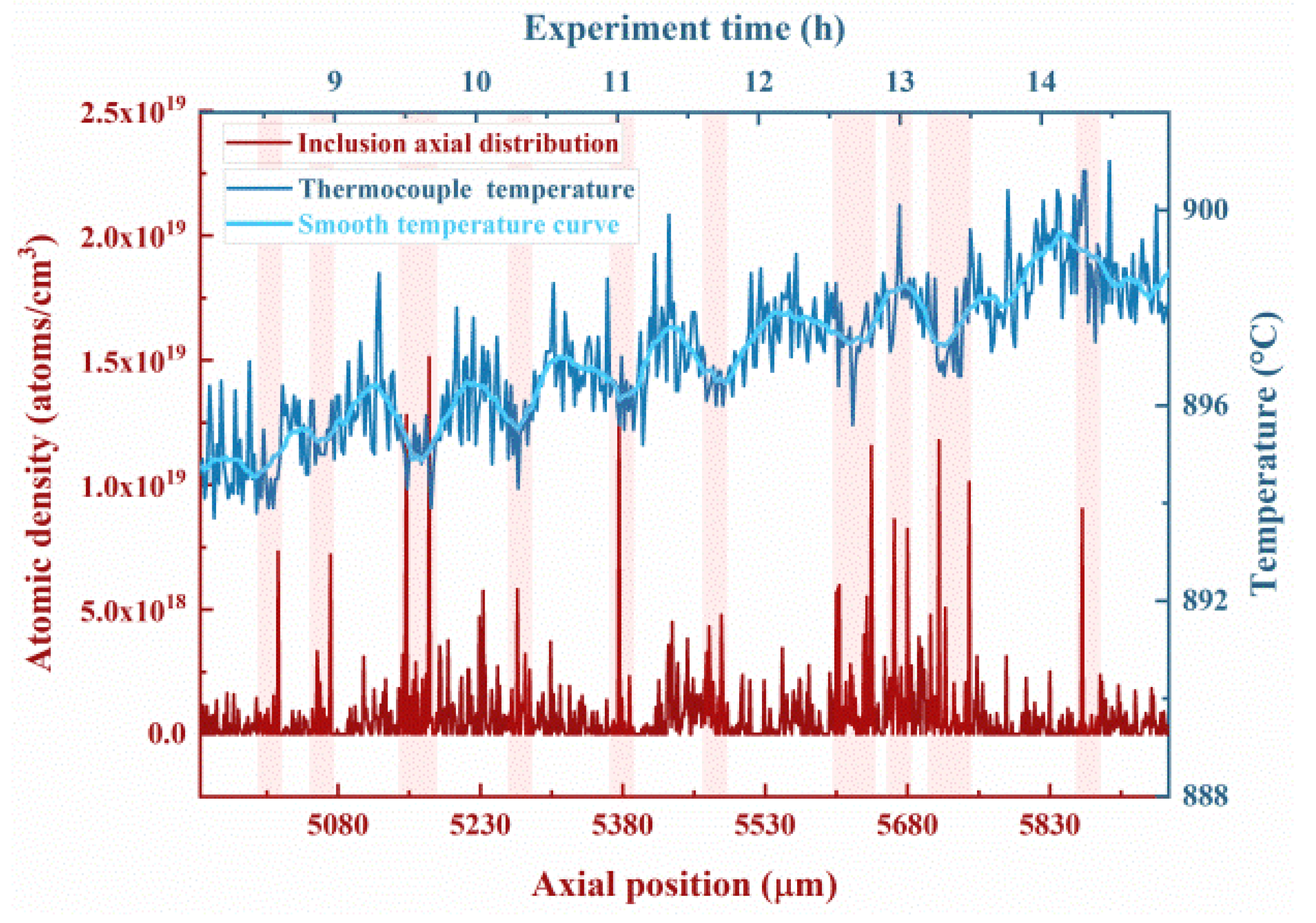
| Sample No. | Dopant | CdTe % in Zone | Heater Temperature | RMF | Heater Starting Position |
|---|---|---|---|---|---|
| F1-01 | In (5 ppm) | 5% | 1080–1100 °C | No | Zone center |
| F1-02 | In (5 ppm) | 5% | 1100–1110 °C | 2 mT, 100 Hz | Zone center −2 mm |
| F1-03 | In (5 ppm) | 10% | 1110–1100–1110 °C | 2 mT, 100 Hz | Zone center −5 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, J.; Fauler, A.; Senchenkov, A.S.; Kolesnikov, N.N.; Fiederle, M. Analysis of Te Inclusion Striations in (Cd,Zn)Te Crystals Grown by Traveling Heater Method. Crystals 2021, 11, 649. https://doi.org/10.3390/cryst11060649
Zou J, Fauler A, Senchenkov AS, Kolesnikov NN, Fiederle M. Analysis of Te Inclusion Striations in (Cd,Zn)Te Crystals Grown by Traveling Heater Method. Crystals. 2021; 11(6):649. https://doi.org/10.3390/cryst11060649
Chicago/Turabian StyleZou, Jiaona, Alex Fauler, Alexander S. Senchenkov, Nikolai N. Kolesnikov, and Michael Fiederle. 2021. "Analysis of Te Inclusion Striations in (Cd,Zn)Te Crystals Grown by Traveling Heater Method" Crystals 11, no. 6: 649. https://doi.org/10.3390/cryst11060649
APA StyleZou, J., Fauler, A., Senchenkov, A. S., Kolesnikov, N. N., & Fiederle, M. (2021). Analysis of Te Inclusion Striations in (Cd,Zn)Te Crystals Grown by Traveling Heater Method. Crystals, 11(6), 649. https://doi.org/10.3390/cryst11060649






