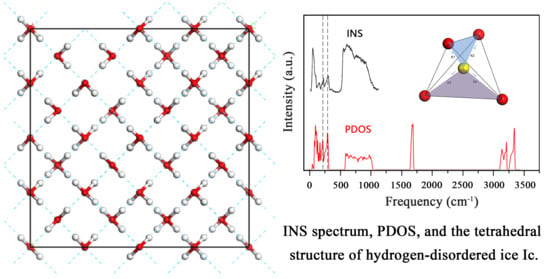
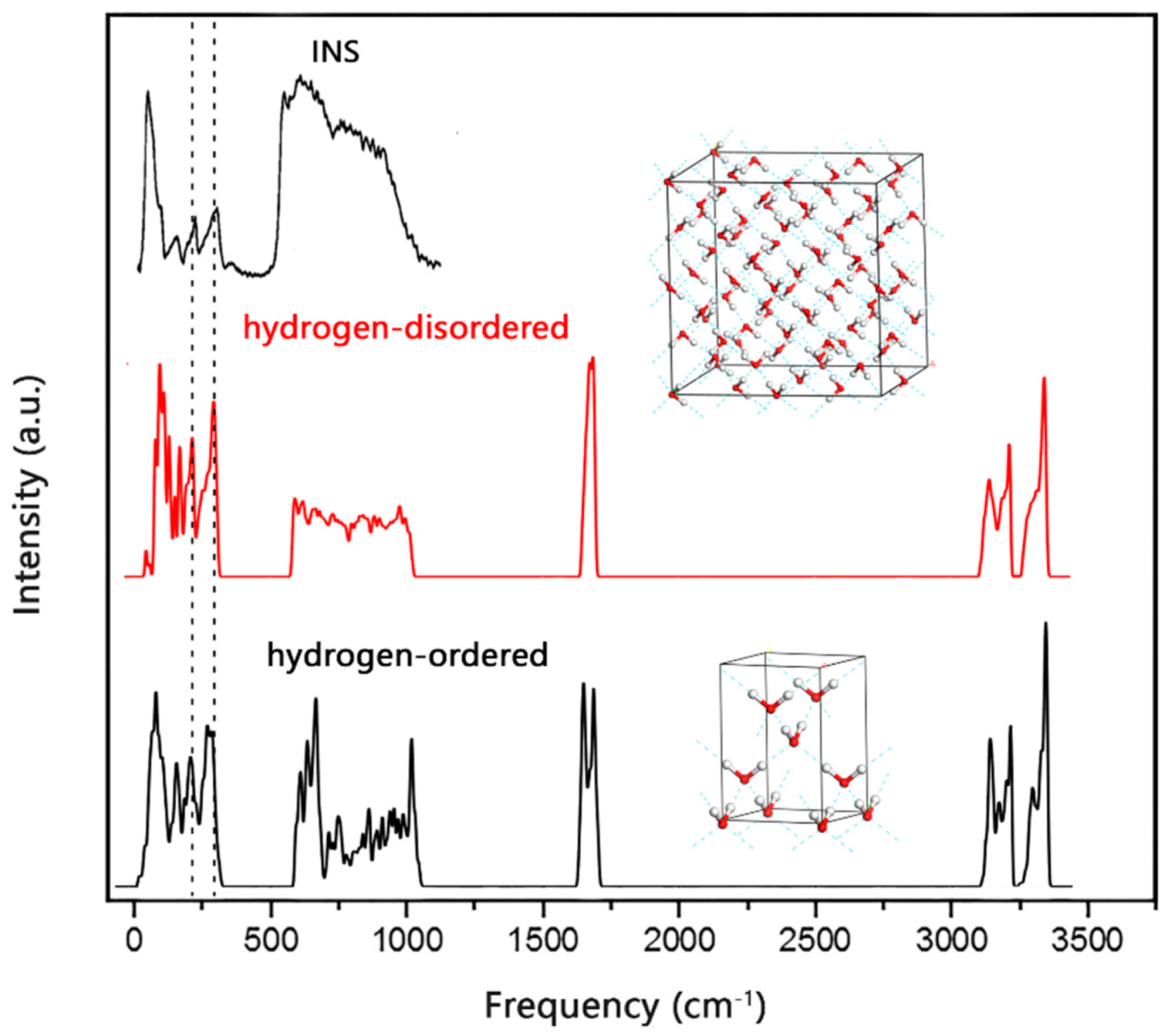
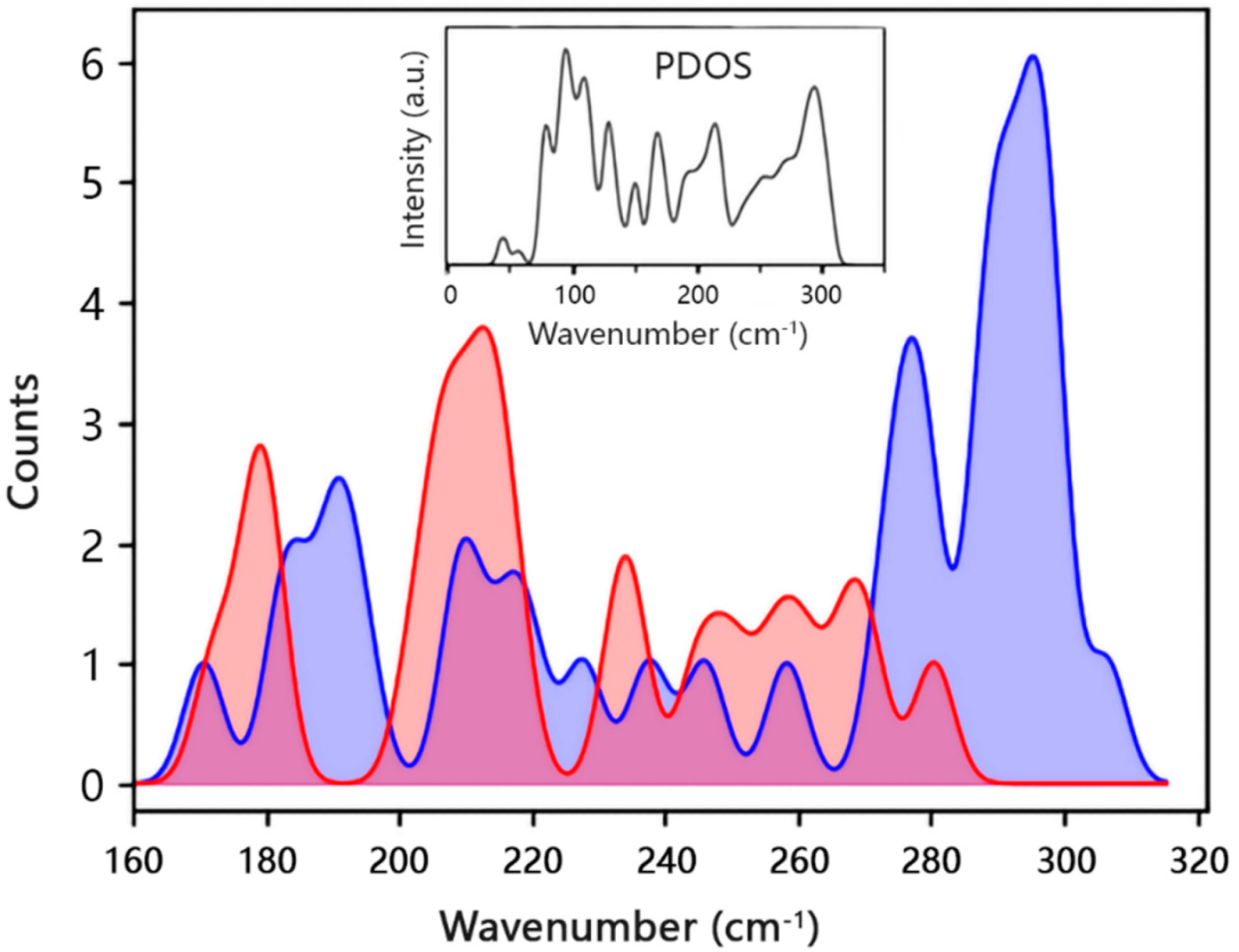
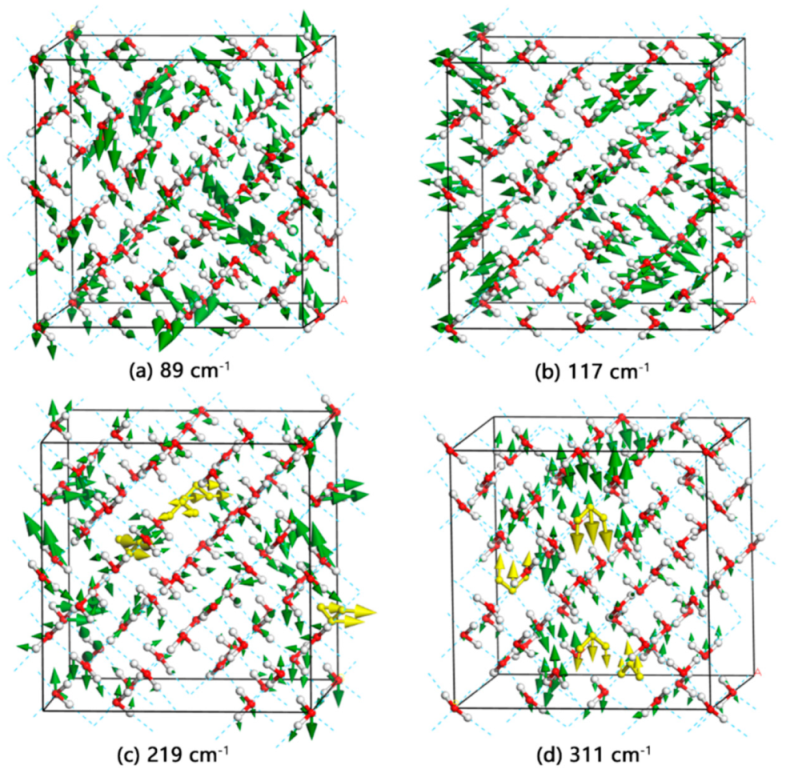
Studies of Hydrogen Bond Vibrations of Hydrogen-Disordered Ice Ic
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bertie, J.E.; Calvert, L.D.; Whalley, E. Transformations of ice II, ice III, and ice V at atmospheric pressure. J. Chem. Phys. 1963, 38, 840–846. [Google Scholar] [CrossRef]
- Bertie, J.E.; Whalley, E. Optical spectra of orientationally disordered crystals. II. Infrared spectrum of ice Ih and ice Ic from 360 to 50 cm−1. J. Chem. Phys. 1967, 46, 1271–1284. [Google Scholar] [CrossRef]
- Whalley, E.; Heath, J.B.R.; Davidson, D.W. Ice IX: An antiferroelectric phase related to ice III. J. Chem. Phys. 1968, 48, 2362–2370. [Google Scholar] [CrossRef]
- Tajima, Y.; Matsuo, T.; Suga, H. Phase transition in KOH-doped hexagonal ice. Nature 1982, 299, 810–812. [Google Scholar] [CrossRef]
- Kuhs, W.F.; Finney, J.L.; Vettier, C.; Bliss, D.V. Structure and hydrogen ordering in ices VI, VII, and VIII by neutron powder diffraction. J. Chem. Phys. 1984, 81, 3612–3623. [Google Scholar] [CrossRef]
- Hirsch, K.R.; Holzapfel, W.B. Effect of high pressure on the Raman spectra of ice VIII and evidence for ice X. J. Chem. Phys. 1986, 84, 2771–2775. [Google Scholar] [CrossRef]
- Lobban, C.; Finney, J.L.; Kuhs, W.F. The structure of a new phase of ice. Nature 1998, 391, 268–270. [Google Scholar] [CrossRef]
- Salzmann, C.G.; Radaelli, P.G.; Hallbrucker, A.; Mayer, E.; Finney, J.L. The preparation and structures of hydrogen-ordered phases of ice. Science 2006, 311, 1758–1761. [Google Scholar] [CrossRef]
- Salzmann, C.G.; Radaelli, P.G.; Mayer, E.; Finney, J.L. Ice XV: A new thermodynamically stable phase of ice. Phys. Rev. Lett. 2009, 103, 105701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falenty, A.; Hansen, T.C.; Kuhs, W.F. Formation and properties of ice XVI obtained by emptying a type sII clathrate hydrate. Nature 2014, 516, 231–233. [Google Scholar] [CrossRef]
- Millot, M.; Coppari, F.; Rygg, J.R.; Barrios, A.C.; Hamel, S.; Swift, D.C.; Eggert, J.H. Nanosecond X-ray diffraction of shock-compressed superionic water ice. Nature 2019, 569, 251–255. [Google Scholar] [CrossRef] [PubMed]
- König, H. Eine kubische Eismodifikation. Z. Für Krist. Cryst. Mater. 1943, 105, 279–286. [Google Scholar] [CrossRef]
- Dowell, L.G.; Rinfret, A.P. Low-temperature forms of ice as studied by X-ray diffraction. Nature 1960, 189, 1144–1148. [Google Scholar] [CrossRef]
- Murray, B.J.; Bertram, A.K. Formation and stability of cubic ice in water droplets. Phys. Chem. Chem. Phys. 2006, 8, 186–192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murray, B.J. Enhanced formation of cubic ice in aqueous organic acid droplets. Environ. Res. Lett. 2008, 3, 025008. [Google Scholar] [CrossRef]
- Malkin, T.L.; Murray, B.J.; Brukhno, A.V.; Anwar, J.; Salzmann, C.G. Structure of ice crystallized from supercooled water. Proc. Natl. Acad. Sci. USA 2012, 109, 1041–1045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mayer, E.; Hallbrucker, A. Cubic ice from liquid water. Nature 1987, 325, 601–602. [Google Scholar] [CrossRef]
- Whalley, E. Scheiner’s halo-Evidence for ice Ic in the atmosphere. Science 1981, 211, 389–390. [Google Scholar] [CrossRef]
- Kuhs, W.F.; Bliss, D.V.; Finney, J.L. High-resolution neutron powder diffraction study of ice-Ic. J. Phys. Colloq. 1987, 48, 631–636. [Google Scholar] [CrossRef]
- Kuhs, W.F.; Sippel, C.; Falenty, A.; Hansen, T.C. Extent and relevance of stacking disorder in “ice I-c”. Proc. Natl. Acad. Sci. USA 2012, 109, 21259–21264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murray, B.; Knopf, D.; Bertram, A. The formation of cubic ice under conditions relevant to Earth’s atmosphere. Nature 2005, 434, 202–205. [Google Scholar] [CrossRef]
- Falenty, A.; Kuhs, W.F. Self-preservation of CO2 gas hydrates-surface microstructure and ice perfection. J. Phys. Chem. B 2009, 113, 15975–15988. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.M.; Dore, J.C.; Behrens, P. Nucleation of ice in confined geometry. J. Phys. Chem. B 1997, 101, 6226–6229. [Google Scholar] [CrossRef]
- Malkin, T.L.; Murray, B.J.; Salzmann, C.G.; Molinero, V.; Pickering, S.J.; Whale, T.F. Stacking disorder in ice I. Phys. Chem. Chem. Phys. 2015, 17, 60–76. [Google Scholar] [CrossRef] [Green Version]
- Del Rosso, L.; Celli, M.; Grazzi, F.; Catti, M.; Ulivi, L. Cubic ice Ic without stacking defects obtained from ice XVII. Nat. Mater. 2020, 19, 663–668. [Google Scholar] [CrossRef]
- Komatsu, K.; Machida, S.; Noritake, F.; Hattori, T.; Kagi, H. Ice I-c without stacking disorder by evacuating hydrogen from hydrogen hydrate. Nat. Commun. 2020, 11, 464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geiger, P.; Dellago, C.; Macher, M.; Franchini, C.; Kresse, G.; Bernard, J.; Stern, J.N.; Loerting, T. Proton ordering of cubic ice Ic: Spectroscopy and computer simulations. J. Phys. Chem. C 2014, 118, 10989–10997. [Google Scholar] [CrossRef]
- Yuan, Z.Y.; Zhang, P.; Yao, S.K.; Lu, Y.B.; Yang, H.Z.; Luo, H.W.; Zhao, Z.J. Computational assignments of lattice vibrations of ice Ic. RSC Adv. 2017, 7, 36801–36806. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.L.; Yuan, Z.Y.; Jiang, L.; Zhang, K.; Wang, Z.R.; Luo, H.W.; Gu, Y.; Cao, J.W.; Qin, X.L.; Zhang, P. Computational analysis of vibrational spectrum and H-bonds of ice XVII. New J. Phys. 2019, 21, 043054. [Google Scholar] [CrossRef]
- Gu, Y.; Zhu, X.L.; Jiang, L.; Cao, J.W.; Qin, X.-L.; Yao, S.K.; Zhang, P. Comparative analysis of H-bond vibrations in ice VIII and VII. J. Phys. Chem. C 2019, 123, 14880–14883. [Google Scholar] [CrossRef]
- Zhu, X.L.; Cao, J.W.; Qin, X.L.; Jiang, L.; Gu, Y.; Wang, H.C.; Liu, Y.; Kolesnikov, A.I.; Zhang, P. Origin of two distinct peaks of ice in the THz region and its application for natural gas hydrate dissociation. J. Phys. Chem. C 2019, 124, 1165–1170. [Google Scholar] [CrossRef]
- Cao, J.W.; Zhu, X.L.; Wang, H.C.; Qin, X.L.; Yuan, X.Q.; Wang, X.C.; Yu, J.L.; Ma, X.T.; Li, M.M.; Zhang, P. A Strategy for the Analysis of the Far-Infrared Vibrational Modes of Hydrogen-Disordered Ice V. J. Phys. Chem. C 2021, 125, 7913–7918. [Google Scholar] [CrossRef]
- Wang, X.C.; Zhu, X.L.; Gu, Y.; Wang, H.C.; Qin, X.L.; Cao, J.W.; Yu, X.H.; Yuan, X.Q.; Zhang, P. Comparative Analysis of Hydrogen-Bonding Vibrations of Ice VI. ACS Omega 2021, 6, 14442–14446. [Google Scholar] [CrossRef]
- Masakazu, M.; Takuma, Y.; Hideki, T. GenIce: Hydrogen-disordered ice generator. J. Comput. Chem. 2018, 39, 61–64. [Google Scholar]
- Bernal, J.D.; Fowler, R.H. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J. Chem. Phys. 1933, 1, 515–548. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef] [Green Version]
- Petrenko, V.; Whitworth, R. Physics of Ice; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Yao, S.K.; Zhang, P.; Zhang, Y.; Lu, Y.B.; Yang, T.L.; Sun, B.G.; Yuan, Z.Y.; Luo, H.W. Computing analysis of lattice vibrations of ice VIII. RSC Adv. 2017, 7, 31789–31794. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zhang, P.; Wang, Z.R.; Zhu, X.L.; Lu, Y.B.; Guan, C.B.; Li, Y.H. DFT analysis of lattice vibrations of ice XIV. Molecules 2018, 23, 1781. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, L.; Yao, S.K.; Zhang, K.; Wang, Z.R.; Luo, H.W.; Zhu, X.L.; Gu, Y.; Zhang, P. Exotic Spectra and Lattice Vibrations of Ice X Using the DFT Method. Molecules 2018, 23, 2780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.R.; Zhu, X.L.; Jiang, L.; Zhang, K.; Luo, H.W.; Gu, Y.; Zhang, P. Investigations of the H-bonds and vibrational spectra of clathrate ice XVI. Materials 2019, 12, 246. [Google Scholar] [CrossRef] [Green Version]
- Qin, X.L.; Zhu, X.L.; Cao, J.W.; Jiang, L.; Gu, Y.; Wang, X.C.; Zhang, P. Computational analysis of exotic molecular and atomic vibrations in ice XV. Molecules 2019, 24, 3115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, J.W.; Chen, J.Y.; Qin, X.L.; Zhu, X.L.; Jiang, L.; Gu, Y.; Yu, X.H.; Zhang, P. DFT investigations of the vibrational spectra and translational modes of ice II. Molecules 2019, 24, 3135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Z.J.; Qin, X.L.; Cao, J.W.; Zhu, X.L.; Yang, Y.C.; Wang, H.C.; Zhang, P. Computing investigations of molecular and atomic vibrations of ice IX. ACS Omega 2019, 4, 18936–18941. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.W.; Zhu, X.L.; Cao, J.W.; Qin, X.L.; Jiang, L.; Gu, Y.; Wang, H.C.; Zhang, P. Two basic vibrational modes of H-bonds in ice XIII. AIP Adv. 2019, 9, 115118. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.-H.; Qin, X.-L.; Dong, X.-T.; Cao, J.-W.; Zhu, X.-L.; Wang, H.-C.; Sun, Y.-J.; Xu, Z.-X.; Zhang, P. Studies of Hydrogen Bond Vibrations of Hydrogen-Disordered Ice Ic. Crystals 2021, 11, 668. https://doi.org/10.3390/cryst11060668
Yu X-H, Qin X-L, Dong X-T, Cao J-W, Zhu X-L, Wang H-C, Sun Y-J, Xu Z-X, Zhang P. Studies of Hydrogen Bond Vibrations of Hydrogen-Disordered Ice Ic. Crystals. 2021; 11(6):668. https://doi.org/10.3390/cryst11060668
Chicago/Turabian StyleYu, Xu-Hao, Xiao-Ling Qin, Xiao-Tong Dong, Jing-Wen Cao, Xu-Liang Zhu, Hao-Cheng Wang, Yan-Ju Sun, Zi-Xun Xu, and Peng Zhang. 2021. "Studies of Hydrogen Bond Vibrations of Hydrogen-Disordered Ice Ic" Crystals 11, no. 6: 668. https://doi.org/10.3390/cryst11060668
APA StyleYu, X.-H., Qin, X.-L., Dong, X.-T., Cao, J.-W., Zhu, X.-L., Wang, H.-C., Sun, Y.-J., Xu, Z.-X., & Zhang, P. (2021). Studies of Hydrogen Bond Vibrations of Hydrogen-Disordered Ice Ic. Crystals, 11(6), 668. https://doi.org/10.3390/cryst11060668