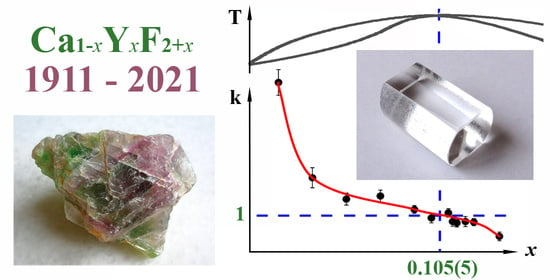
Refinement of the Congruently Melting Composition of Nonstoichiometric Fluorite Crystals Ca1-xYxF2x (x = 0.01–0.14) †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Crystal Growth
2.2. X-ray Diffraction Analysis
3. Results
3.1. The Concentration Dependence of the Lattice Parameter
3.2. Refinement of the Composition of the Maximum on the Melting Curves
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vogt, T. Vorlaufige Mitteilung über Yttrofluorit, eine neue Mineralspezies aus dem nördlichen Norwegen. Cent. F. Min. Etc. 1911, 12, 373–377. [Google Scholar]
- Sobolev, B.P. Part 1, the high temperature chemistry of the rare earth trifluorides. In The Rare Earth Trifluorides; Institutd’ Estudis: Barcelona, Catalans, Spain, 2000; p. 520. [Google Scholar]
- Karimov, D.N.; Krivandina, E.A.; Zhmurova, Z.I.; Sobolev, B.P.; Bezhanov, V.A.; Chernov, S.P.; Shapochkin, G.M. Investigation of Multicomponent Fluoride Optical Materials in the UV Spectral Region. I. Single Crystals of Ca1–xRxF2+x (R = Sc, Y, La, Yb, Lu) Solid Solutions. Crystallogr. Rep. 2006, 51, 1009–1015. [Google Scholar] [CrossRef]
- Vogt, T. Uber Die Flusspat—Yttriumfluoritgruppe. Neues Jahrb. Miner. 1914, 2, 9–15. [Google Scholar]
- Bagdasarov, K.S.; Voronko, Y.K.; Kaminskii, A.A.; Krotova, L.V.; Osiko, V.V. Modification of the Optical Properties of CaF2–TR3+ Crystals by Yttrium Impurities. Phys. Status Solidi. B 1965, 12, 905–912. [Google Scholar] [CrossRef]
- Jiang, D.; Zhan, Y.Y.; Zhang, Q.; Ma, F.; Su, L.; Tang, F.; Qian, X.; Xu, J. Nd,Y:CaF2 laser crystal: Novel spectra properties and laser performances from controlled local structure. CrystEngComm 2015, 17, 7398–7405. [Google Scholar] [CrossRef]
- Basiev, T.T.; Voronko, Y.K.; Karasik, A.Y.; Osiko, V.V.; Shcherbakov, I.A. Spectral migration of electronic excitation along Nd3+ ions in CaF2-YF3 crystal on selective laser excitation. Sov. Phys. JETP 1978, 48, 32–36. [Google Scholar]
- Iparraguirre, I.; Azkargorta, J.; Fernández, J.; Balda, R.; Oleaga, A.; Kaminskii, A.A. Laser Spectral Dynamics of Nd3+ in CaF2–YF3 Crystals. J. Opt. Soc. Am. B 1999, 16, 1439–1446. [Google Scholar] [CrossRef]
- Doroshenko, M.E.; Pierpoint, K.A.; Alimov, O.K.; Papashvili, A.G.; Konyushkin, V.A.; Nakladov, A.N. Formation of Tm-Y Centers in CaF2–YF3: Tm3+ Solid-Solution Crystals. J. Lumin. 2019, 208, 475–478. [Google Scholar] [CrossRef]
- Wu, Y.; Su, L.; Wang, Q.; Li, H.; Zhan, Y.; Jang, D.; Qian, X.; Wang, C.; Zheng, L.; Chen, H.; et al. Spectroscopic Properties of Yb-doped CaF2–YF3 Solid-Solution Laser Crystal. Laser Phys. 2013, 23, 105805. [Google Scholar] [CrossRef]
- Fedorov, P.P.; Sobolev, B.P. Conditions for the formation of maxima on the fusion curves of solid solutions in salt systems. Russ. J. Inorg. Chem. 1979, 24, 574–575. [Google Scholar]
- Recker, K.; Wallrafen, F. Untersuchung von Zweistoffsystemen MeF2–LnF3 Me = Ca, Ba; Ln = Seltene Erden, Y, U. In Züchtung, Kristallchemie und -Physik von Laser- und Halbleiter-Einkristallen, Forschungsberichte des Landes Nordrhein-Westfalen; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 1974; Volume 2469. [Google Scholar] [CrossRef]
- Seiranian, K.B.; Fedorov, P.P.; Garashina, L.S.; Molev, G.V.; Karelin, V.V.; Sobolev, B.P. Phase diagram of the system CaF2−YF3. J. Cryst. Growth. 1974, 26, 61–64. [Google Scholar] [CrossRef]
- Sobolev, B.P.; Fedorov, P.P. Phase diagrams of the CaF2- (Y, Ln) F3 systems I. Experimental. J. Less Common Met. 1978, 60, 33–46. [Google Scholar] [CrossRef]
- Short, J.; Roy, R. Confirmation of Deffect Character in Calcium Fluoride—Yttrium Fluoride Crystalline Solutions. J. Phys. Chem. 1963, 67, 1860–1861. [Google Scholar] [CrossRef]
- Pastor, R.C.; Robinson, M.; Hastings, A.G. Congruently-melting compounds of CaF2–rcRF3. Mat. Res. Bull. 1974, 9, 781–786. [Google Scholar] [CrossRef]
- Greis, O.; Kieser, M. Darstellung und Eigenschaften der festen Losungen (Ca,SE) F2.33 mit SE = Y, La, Ln und der korrespondierenden Ordnungsphasen Ca2SEF7 mit SE = Er–Lu und Y. Z. Anorgan. Allgem. Chem. 1981, 479, 165–170. [Google Scholar] [CrossRef]
- Gettman, W.; Greis, O. Uber fluorit- und tysonitverwandte Ordnungsphasen im System CaF2–YF3. J. Solid State Chem. 1978, 26, 255–263. [Google Scholar] [CrossRef]
- Louër, D.; Boultif, A. Some further considerations in powder diffraction pattern indexing with the dichotomy method. Powder Diffr. 2014, 29, 7–12. [Google Scholar] [CrossRef]
- Allen, R.D. Variations in the chemical and physical properties of fluorite. Am. Mineral. 1952, 37, 910–930. [Google Scholar]





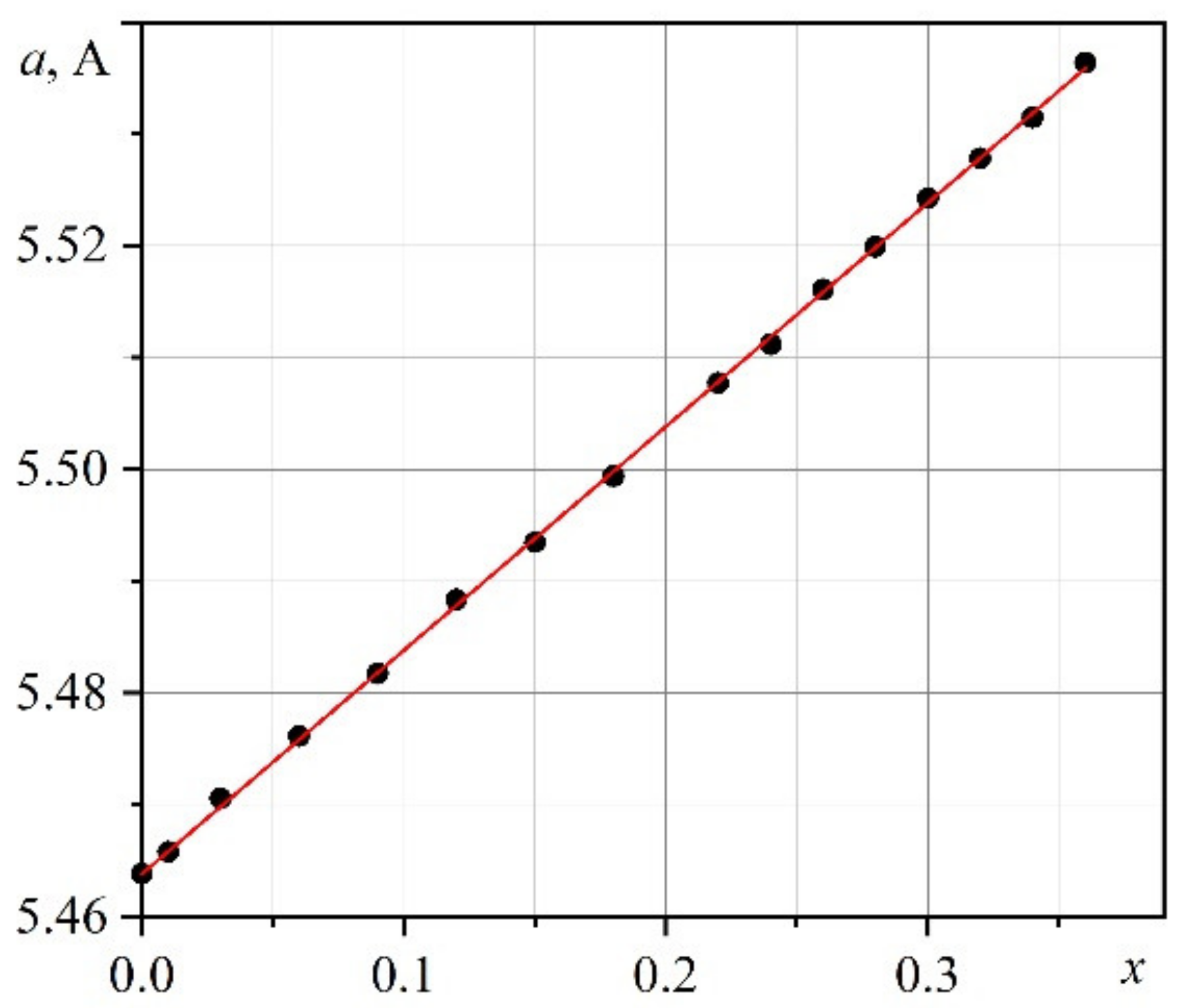

| x, By Charge | a, Å | Losses, Mas. % |
|---|---|---|
| 0 | 5.46385(5) | 0 |
| 0.01 | 5.46581(1) | 0.2 |
| 0.03 | 5.47059(3) | 0 |
| 0.06 | 5.47613(5) | 0.2 |
| 0.09 | 5.48175(4) | 0.2 |
| 0.12 | 5.48833(8) | 0 |
| 0.15 | 5.49348(2) | 0.2 |
| 0.18 | 5.49941(6) | 0 |
| 0.22 | 5.50773(3) | 0.2 |
| 0.24 | 5.51116(9) | 0.2 |
| 0.26 | 5.51609(7) | 0.2 |
| 0.28 | 5.51989(4) | 0.2 |
| 0.30 | 5.52424(9) | 0.2 |
| 0.32 | 5.52780(3) | 0.2 |
| 0.34 | 5.53141(7) | 0 |
| 0.36 | 5.53632(3) | 0 |
| δ, Å | ao | k | Ref. |
|---|---|---|---|
| 9 × 10−5 | 5.46385(5) | 0.1999(4) | present work |
| 3 × 10−4 | 5.4630(2) | 0.20030 | [17,18] |
| 3 × 10−3 | 5.46295(10) [20] | 0.191 | [14] |
| xo | x′ | k | a, Å |
|---|---|---|---|
| 0.010 | 0.011(9) | 1.116(11) | 5.46608(2) |
| 0.030 | 0.031(9) | 1.032(9) | 5.47004(4) |
| 0.050 | 0.051(5) | 1.014(5) | 5.47398(3) |
| 0.070 | 0.071(5) | 1.016(5) | 5.47807(4) |
| 0.090 | 0.091(3) | 1.007(3) | 5.48196(2) |
| 0.100 | 0.100(4) | 0.997(4) | 5.48378(4) |
| 0.110 | 0.110(3) | 1.001(4) | 5.48587(4) |
| 0.113 | 0.112(4) | 0.994(4) | 5.48620(4) |
| 0.115 | 0.114(4) | 0.993(4) | 5.48667(3) |
| 0.120 | 0.119(4) | 0.994(4) | 5.48769(5) |
| 0.125 | 0.124(3) | 0.993(3) | 5.48867(2) |
| 0.140 | 0.137(4) | 0.981(4) | 5.49130(4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimov, D.N.; Sulyanova, E.A.; Sobolev, B.P. Refinement of the Congruently Melting Composition of Nonstoichiometric Fluorite Crystals Ca1-xYxF2x (x = 0.01–0.14). Crystals 2021, 11, 696. https://doi.org/10.3390/cryst11060696
Karimov DN, Sulyanova EA, Sobolev BP. Refinement of the Congruently Melting Composition of Nonstoichiometric Fluorite Crystals Ca1-xYxF2x (x = 0.01–0.14). Crystals. 2021; 11(6):696. https://doi.org/10.3390/cryst11060696
Chicago/Turabian StyleKarimov, Denis N., Elena A. Sulyanova, and Boris P. Sobolev. 2021. "Refinement of the Congruently Melting Composition of Nonstoichiometric Fluorite Crystals Ca1-xYxF2x (x = 0.01–0.14)" Crystals 11, no. 6: 696. https://doi.org/10.3390/cryst11060696
APA StyleKarimov, D. N., Sulyanova, E. A., & Sobolev, B. P. (2021). Refinement of the Congruently Melting Composition of Nonstoichiometric Fluorite Crystals Ca1-xYxF2x (x = 0.01–0.14). Crystals, 11(6), 696. https://doi.org/10.3390/cryst11060696