Effect of Ni, N Co-Doped on Properties of AgSnO₂ Contact Materials

Abstract

The first-principles method based on density functional theory was used to analyze the impurity formation energies, energy bands, density of states, electron overlap population and elastic modulus of SnO₂, SnO₂–Ni, SnO₂–N and SnO₂–Ni–N. SnO₂ powders with different additives were prepared by the sol-gel method, and then X-ray diffraction experiments and wettability experiments were carried out. The powder metallurgy method was used to prepare AgSnO₂ contacts with different additives. The simulation experiments on hardness, electrical conductivity and electrical contact were carried out. The simulation results show that the conductivity of Ni–N co-doped SnO₂ is best, and more impurity levels are introduced into the forbidden band, thereby increasing the carrier concentration, reducing the band gap, and improving the conductivity. The experimental results show that Ni, N doping does not change the structure of SnO₂, so doped SnO₂ still belongs to the tetragonal system. Ni–N co-doping can better improve the wettability between SnO₂ and Ag, reduce the accumulation of SnO₂ on the contact surface and reduce the contact resistance. Ni–N co-doped SnO₂ has the smallest hardness, improving ductility, molding and service life of the AgSnO₂ contact material.

1. Introduction

With the excellent arc erosion resistance, abrasion resistance, switch operation characteristics and good resistance to welding, AgSnO₂ has become a promising material to replace AgCdO electrical contact materials [1]. However, AgSnO₂ contact material has many shortcomings such as large contact resistance, high temperature rise, and processing difficulties, which limit its use. SnO₂ is a wide-bandgap semiconductor material, so it increases the resistance and temperature rise of contacts and has a great impact on the thermal conductivity of contacts [2]. What is more, SnO₂ has a high hardness, leading to the poor plasticity and ductility of AgSnO₂ contact materials and the difficulties of contact modeling [3].

Improving the performance of AgSnO₂ contact materials by doping has always been an important research direction. Reference [4] used powder metallurgy to prepare Bi-doped AgSnO₂ contact materials and analyzed the influence of Bi-doping on electrical properties. Reference [5] used the internal oxidation method to prepare different concentrations of NiO doped AgSnO₂ contact materials, and analyzed the influence of different concentrations of doping on the mechanical properties. The experimental results of references [4,5] show that doping can improve the electrical and mechanical properties of AgSnO₂ contact materials. However, in the use of experimental methods to improve the electrical and mechanical properties of AgSnO₂ contact materials, the types and proportions of doping elements rely on "trial and error" methods, which will cause a lot of waste of financial and material resources. Therefore, the current research on doping to improve the electrical and mechanical properties of AgSnO₂ contact materials urgently needs effective theoretical support. SnO₂, as the reinforcing phase in the AgSnO₂ contact material, directly affects the performance of the AgSnO₂ contact material. Therefore, the performance of the AgSnO₂ contact material can be improved by improving the performance of SnO₂. Doping non-metallic element N can reduce the band gap of SnO₂ and increase the conductivity of SnO₂. Moreover, since the ionic radii of N and O are the closest, it is easier for N atoms to replace O atoms than other non-metallic elements [6]. According to the co-doping theory proposed by Yamamoto and Katayama, the co-doping of two or more elements can further improve the material properties [7]. In this study, the conductivity and toughness of SnO₂ are improved by doping, and the wettability between SnO₂ and Ag is also improved, which can prevent SnO₂ from precipitating out of the Ag liquid to form an enriched area, and reduce the contact resistance of AgSnO₂. 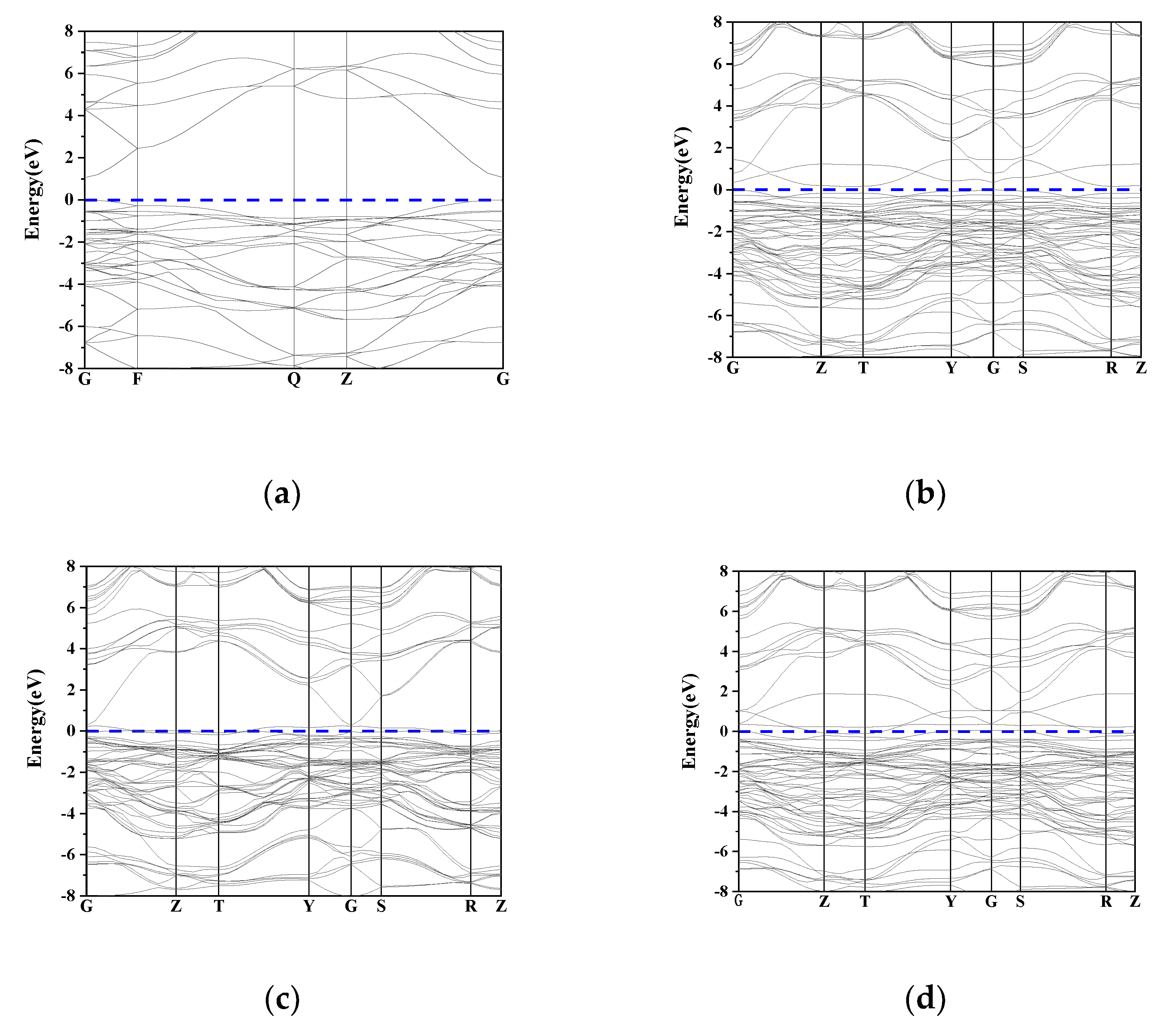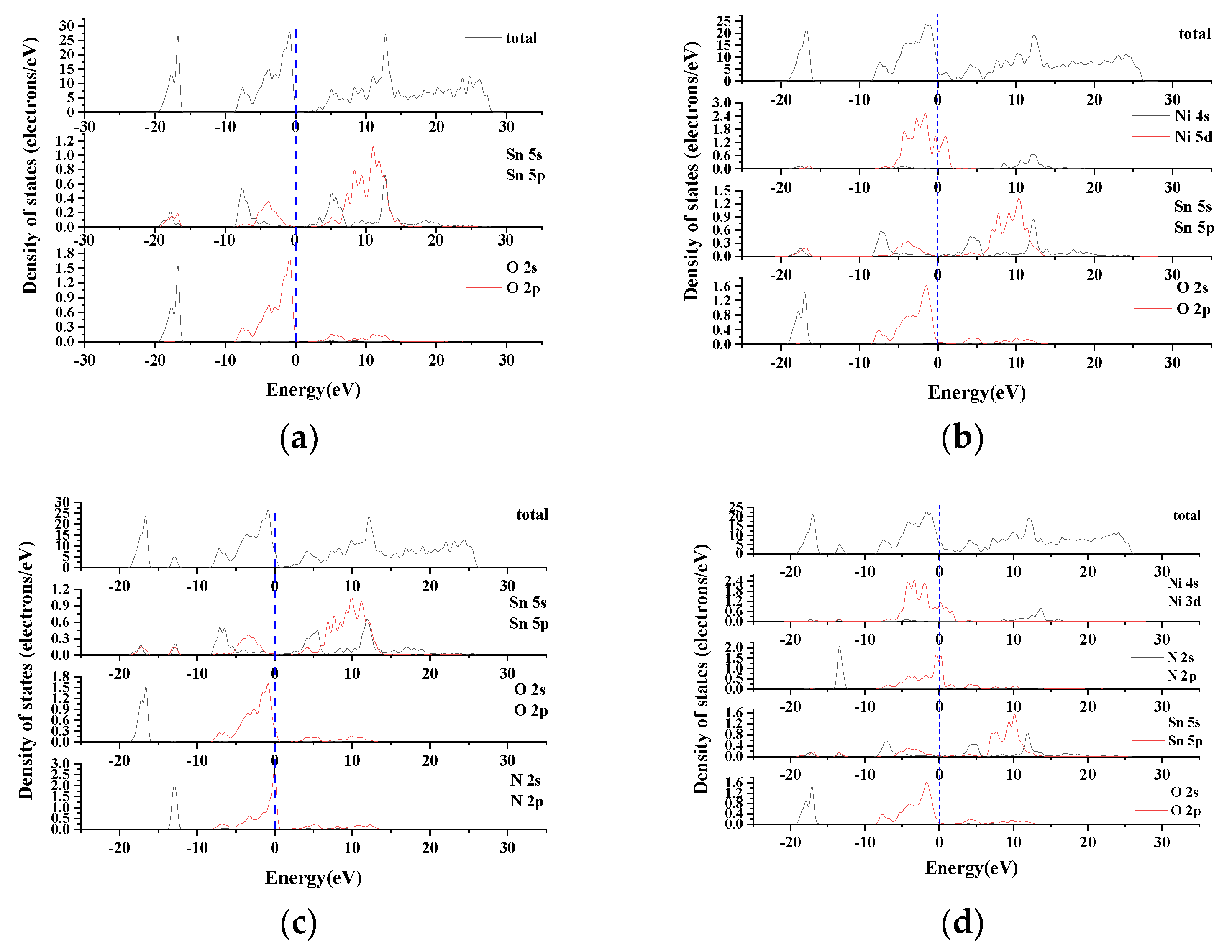Compared with the traditional powder metallurgy process, the SnO₂ particles prepared by the sol-gel method are smaller and can be evenly distributed in the Ag matrix, which can improve the processing performance of the AgSnO₂ contact material. 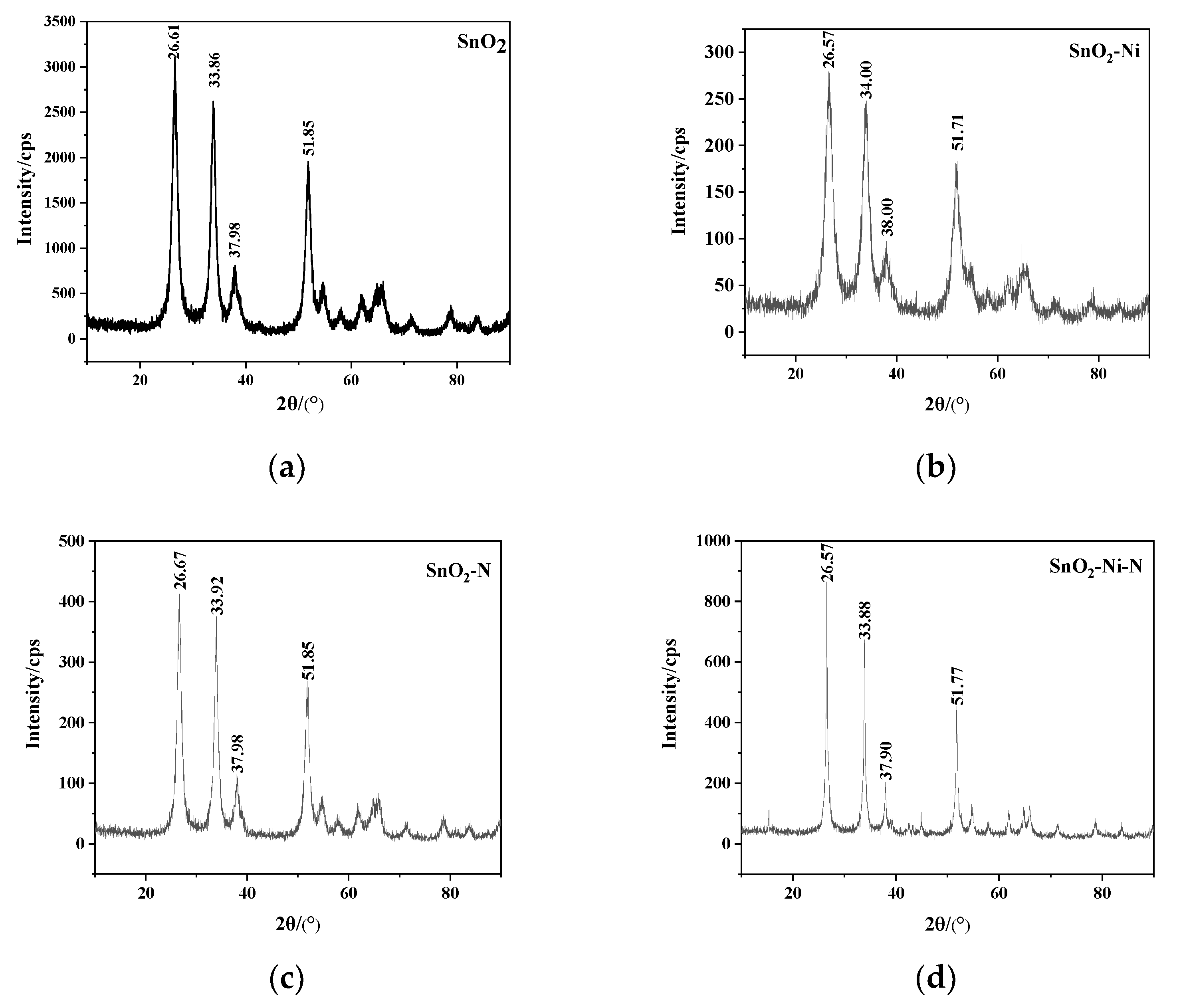In this paper, the first principles based on density functional theory are used to calculate the band structure, density of states, layout elastic modulus and thermodynamic parameters of pure SnO₂, single doped elements Ni, N, and co-doped Ni and N. To analyze the influence of conductivity and mechanical properties before and after doping, the sol-gel method was used to prepare SnO₂ powder with different additives, and the influence of different additives on the wetting angle of Ag and SnO₂ was measured. Then, the powder metallurgy method was used to prepare the AgSnO₂ contact material. Hardness, electrical conductivity and contact resistance are tested to analyze their performance, providing a reference for the further development of AgSnO₂ contact materials.

2. Calculation Method

2.1. Model

SnO₂ is a tetragonal rutile structure, and each SnO₂ unit cell contains 2 Sn atoms and 4 O atoms. In this paper, a 2 × 2 × 1 supercell model is constructed, which contains 8 Sn atoms and 16 O atoms, as shown in Figure 1. The SnO₂ doping model was established by means of atom replacement. Replace 1 Sn atom with Ni atom and 2 O atoms with N atoms to ensure the same doping ratio.

The CASTEP (Cambridge Serial Total Energy Package, MS2017, Dassow, France) module in the Material Studio software is used to calculate the properties of models. This simulation is widely used in the research of ceramics, semiconductors and other materials [8,9]. The generalized gradient Approximation (GGA) solves the problem of the exchange function change when the electron density changes greatly, and the structure optimization and the experimental results are in good agreement. The Local Density Approximation (LDA) is to approximate the exchange correlation energy to the charge density correlation quantity at a certain point. The value of the exchange correlation energy is equal to the exchange correlation energy of a uniform field with the same charge density. It has achieved good results in the calculation of elastic constants [10]. The electrical performance optimization calculation is carried out by using the PBE (Perdew Burke Ernzerhof) method of the Generalized Gradient Approximation (GGA) and the plane wave super soft pseudopotential, and calculation of mechanical properties was obtained by the CA-PZ method of the Local Density Approximation (LDA), used for the correction, and the plane wave super soft pseudopotential. For accuracy and efficiency, the super unit cell model is tested for convergence first, and the plane wave cut-off energy of the reciprocal space is selected to be 400 eV, and the K point of the Buri abyss is 5 × 5 × 5. When optimized, a more stable structure was obtained. Then the band structure, density of states, formation energy and effective mass of electrons of the optimized models were calculated. The unit electron energy change is not more than 1 × 10⁻⁶ eV/atom, the force on each atom is not more than 0.3 eV/nm, the internal stress of the unit cell is less than 0.02 GPa, and the tolerance deviation is stabilized below 5 × 10⁻⁵ nm. On the basis of convergence conditions, the elastic constants are calculated. The valence electron configurations considered for each atom are: Sn–5s²5p², O–2s²2p⁴, N–2s²2p³, Ni–3d⁸4s².

2.2. Lattice Constant and Doping Formation Energy

SnO₂ lattice constant and doping formation energy before and after doping are shown in

Table 1. Lattice constants and doping formation energy.

Model	a/nm	b/nm	c/nm	V/ nm3	Ef/eV
SnO2	0.474	0.474	0.319	0.288	—
SnO2–Ni	0.483	0.4831	0.326	0.303	−1.158
SnO2–N	0.492	0.492	0.330	0.320	1.45
SnO2–Ni–N	0.484	0.484	0.328	0.307	0.3504

. Compared with SnO₂, the lattice constant and volume of SnO₂ doped with different additives are slightly larger. The doping formation energy is used to analyze the difficulty of doping; the smaller the value is, the easier the doping model forms, and the more stable the doping structure is. The calculation formula of single doping and co-doping doping formation energy are as follow [11]:

$$E_f\left(N\right)=E_{tot}-E_{Sn{O}_2}+n{E}_O-m{E}_N$$

(1)

$$E_f\left(Ni\right)=E_{tot}-E_{Sn{O}_2}+a{E}_{Sn}-b{E}_{Ni}$$

(2)

$$E_f\left(N-Ni\right)=E_{tot}-E_{Sn{O}_2}+a{E}_{Sn}+n{E}_O-m{E}_N-b{E}_{Ni}$$

(3)

Among them, $E_{tot}$ is the total energy of the optimized doping system; $E_{Sn{O}_2}$ is the total energy of SnO₂; $E_{Sn}$, $E_O$, $E_N$, $E_{Ni}$ is the ground state energy of each atom; a, b, n, m represent the number of Sn atoms replaced, the number of Ni doped atoms, the number of O atoms replaced and the number of N atoms replaced. Through calculation, the doping formation energies of single doping and co-doping are obtained, as shown in Table 1. The smaller the formation energy of doping, the more stable the structure. The results show that the formation energy of Ni single doping is the smallest and its structure is the most stable. The structure after Ni–N co-doping is more stable than that of N single doping.

2.3. Band Structure

The band structure before and after doping is shown in Figure 2. A 0 eV is chosen as the Fermi level. Considering that the study of deep levels is of little significance, only the band structure near the Fermi level is given. Intrinsic SnO₂ is a wide band gap semiconductor material with a band gap value of 3.6 eV. The band gap value of SnO₂ calculated in this paper is 1.059 eV, which is smaller than the experimental value. It is similar to the band gap value calculated by this method in [12], which is 1.12 eV. This is because the Generalized Gradient Approximation (GGA) used in the calculation underestimates the energy of the excited electrons in the conduction band, which does not affect the trend of the band gap before and after doping. It can be seen from the figure that both before and after doping are direct bandgap semiconductors. Compared with the intrinsic SnO₂, the energy band becomes denser, which enhances locality and electron concentration. Figure 2b shows the band structure of single-doped Ni. It can be seen that the conduction band decreases, the valence band rises and the band gap decreases to 0.3 eV, which increases the carrier concentration and improves the conductivity. Figure 2c shows the energy band structure when single-doped N. The band gap is reduced to 0.047 eV, and the Fermi level passes through the top of the valence band, indicating that N doping is p-type doping. Figure 2d is the energy band structure diagram of N and Ni co-doped SnO₂. The impurity energy level is introduced into the band gap, which is mainly caused by the 2p and 3d orbitals of Ni. The carrier concentration increases and the energy of the band transition to the conduction band reduces. Therefore, the band gap is further reduced to 0.026 eV.

2.4. Density of States

The density of states can reflect the interaction of dopant atoms with other atoms and the formation of chemical bonds. Taking the Fermi level as the reference zero point, the density of states of SnO₂ with different doping forms is shown in Figure 3. Figure 3b is the density of states of SnO₂–Ni. The peak at −5 eV is formed by the hybridization of Ni–5d orbital and O–2p orbital, Sn–5p orbital and O–2p orbital. The contribution of Ni–5d orbital near 0 eV makes the Fermi level cross the valence band top, so that the band gap value is reduced. Figure 3c is the density of states of SnO₂–N. The impurity peaks formed in −10~–15 eV are formed by the s-p hybridization of N–2s orbitals and Sn–5s and Sn–5p orbitals. At −5~0 eV, due to the introduction of N–2p orbital and Sn–5p orbital hybridization, the overlapping area is larger than that of O–2p orbital and Sn–5p orbital hybridization, indicating that hybridization after N atom doping becomes stronger. Figure 3d is the density of states of SnO₂–Ni–N. The impurity peaks formed by O–2p, Sn–5p and Ni–3d, N–2p hybridization at −1~−5eV are wider compared with single doping. The electronic state increases, indicating that the hybridization becomes stronger when co-doped. At 0~−1eV, the impurity peaks formed by the hybridization of Ni–5d and N–2p provide more conductive holes and make the band gap smaller. At 0–2 eV, the impurity peaks are mainly formed by the hybridization of Ni–5d and N–2p, and a very narrow deep main energy level is formed near the Fermi level, which increases the number of holes and enhances locality [13]. On 2–5 eV, N–2p and Sn–5s, Sn–5p have the same peak position, and the impurity peak width formed is larger, indicating that N atoms and Sn atoms have a strong hybridization effect.

2.5. Charge Density Map and Electron Overlap Population

The charge density map shows charge distribution in the unit cell. It can be seen from Figure 4b that compared with the undoped SnO₂, the charge density after doping increases, and the charge density around Ni atoms is much larger than that around Sn and O atoms. The overlap of electron clouds between Ni atoms and O atoms is greater than the overlap between Sn atoms and O atoms, which indicates that the interaction between Ni atoms and O atoms is stronger. In Figure 4c, the electron cloud between N and Sn is more overlapped than that between O and Sn, improving covalentness and conductivity. It can be seen in Figure 4d that the charge density of Ni atoms, O atoms and N atoms is greater than the charge density of Sn atoms, O atoms and N atoms. The degree of electron sharing increases, indicating that doping makes electrons transfer. Compared with single-doped N, the electron cloud gathers in the direction of the impurity atoms, further improving conductivity. The number of electron overlap population is the number of electron overlap between atoms. The larger the value is, the stronger the bonding effect of atoms is.

Table 2. Atom population and electronic overlapping populations.

Model	Atom Population				Bond Population
	Ni	N	Sn	O	Ni–N	Ni–O	Sn–N	Sn–O
SnO2			1.90	−0.95				0.54
SnO2–Ni	0.85		1.85	−0.86		0.45		0.48
SnO2–N		−0.87	1.80	−0.90			0.70	0.50
SnO2–Ni–N	0.82	0–0.67	1.82	−0.83	0.41	0.56	0.85	0.49

shows the electronic overlap population values of SnO₂ and doped SnO₂ under different conditions. The numbers in the table are average values. It can be seen that, compared with the electron overlap population value between Sn and N, the value between Sn and N is larger, electron transfer is intensified and conductivity is increased. With Ni and N co-doped, the electron overlap population value between Sn and N and between Ni and O is larger, indicating that the overlap between atoms increases after co-doping, the electron transfer between atoms is intensified and the conductivity is further enhanced, which is consistent with the analysis result of the charge density map.

2.6. Elastic Modulus

The elastic constants can be used to judge whether the mechanical structure is stable, and to determine the mechanical stability standard of the tetragonal phase crystal system [14]:

$$C_{11}>0,C_{33}>0,C_{44}>0,C_{66}>0$$

$$\left(C_{11}-C_{12}\right)>0,\left(C_{11}+C_{33}-2C_{13}\right)>0$$

(4)

$$\left[2\left(C_{11}{-\mathrm{C}}_{12}\right){+\mathrm{C}}_{33}{+4\mathrm{C}}_{13}\right]>0$$

According to the data in

Table 3. Elastic constants.

Model	C11/GPa	C12/GPa	C13/GPa	C22/GPa	C33/GPa	C44/GPa	C55/GPa	C66/GPa
SnO2	152.0	55.01	64.59	152.0	298.5	90.01	90.01	145.5
SnO2–Ni	248.91	−29.85	63.19	257.40	316.5	86.23	88.48	45.22
SnO2–N	242.44	−30.49	57.50	225.90	287.95	73.06	71.54	40.11
SnO2–Ni–N	269.97	−24.88	70.24	248.38	300.49	73.19	88.31	44.19

, the structure of the three doping forms meets the standard of mechanical stability.

According to the Voigt approximation algorithm [15], the formulas of shear modulus (G_V) and body elastic modulus (B_V) are as follows:

$$G_V=\frac{1}{15}\left(2C_{11}+C_{33}-C_{12}-2C_{13}\right)+\frac{1}{5}\left(2C_{44}+C_{66}\right)$$

(5)

$$B_V=\frac{1}{9}\left(2C_{11}+C_{33}\right)+\frac{2}{9}\left(2C_{13}+C_{12}\right)$$

(6)

According to the Reuss approximation algorithm [16], the formulas of shear modulus (G_R) and body elastic modulus (B_R) are as follows:

$$G_R=15{[\frac{18B_V}{\left(C_{11}+C_{12}\right)C_{33}-2C_{13}^2}+\frac{6}{C_{11}-C_{12}}+\frac{6}{C_{44}}+\frac{3}{C_{66}}]}^{-1}$$

(7)

$$B_R=\frac{\left(C_{11}+C_{12}\right)C_{33}-2C_{13}^2}{C_{11}+C_{12}+2C_{33}-4C_{13}}$$

(8)

Hill believes that the Voigt and Reuss models can calculate the maximum and minimum values of the bulk elastic modulus and the shear modulus, respectively, which proves that the average value of the two is closer to the experimental results [17]; the formula is as follows:

$$G_H=\frac{G_V+G_R}{2}$$

(9)

$$B_H=\frac{B_V+B_R}{2}$$

(10)

The formulas of Young's modulus (E) and Poisson's ratio (δ) are as follows:

$$E=\frac{9B_H{G}_H}{3B_H+G_H}, \delta =\frac{3B_H-2G_H}{2\left(3B_H+G_H\right)}$$

(11)

By fitting the dataset, a correction formula without intercept term is given, which eliminates the negative hardness that is inconsistent with the reality. The formula of Vickers hardness (H_V) [18] is as follows:

$$k=\frac{G_H}{B_H}, H_V=0.92k^{1.137}{G}^{0.708}$$

(12)

According to the results in

Table 4. Bulk modulus (B_H), shear modulus (G_H), Young's modulus(E), Poisson's ratio(δ), Hardness (H_V), Bulk modulus to shear modulus ratio (B_H/G_H) and Universal elastic anisotropy Index (A^U).

Model	BH (GPa)	GH (GPa)	E (GPa)	δ	BH/GH	HV	AU
SnO2	102.92	86.94	203.52	0.17	1.18	17.93	1.37289
SnO2–Ni	108.68	86.01	203.98	0.19	1.26	16.60	0.89761
SnO2–N	99.46	75.32	180.42	0.20	1.32	14.30	0.97578
SnO2–Ni–N	111.61	82.16	197.92	0.20	1.36	14.73	0.89756

, mechanical properties such as hardness, brittleness and toughness of Ni and N single-doped and co-doped SnO₂ were further theoretically calculated. Young's modulus is the ratio of stress and strain to the uniaxial of the material. The larger the ratio, the stronger the ability of the material to resist deformation. It can be seen from Table 4 that Young's modulus of N single-doped and Ni–N co-doped SnO₂ both decreased, and Young's modulus of SnO₂–N decreased the most. Poisson's ratio characterizes the compressibility of a material. The smaller the value, the greater the volume change of the material. It can be seen from Table 4 that the N-doped and Ni–N co-doped SnO₂ Poisson is relatively small, indicating that the volume change of the material is larger when the material is deformed, and the material with a smaller Poisson's ratio has higher stability, so Ni–N stability, when co-doped, is better.

According to the Pugh method criterion [19], the B_H/G_H ratio can be used to judge the brittleness and toughness of the material. Brittleness is defined when the ratio is less than 1.75, and toughness is defined when the ratio is greater than 1.75. The brittle toughness of doped SnO₂ was improved to a certain extent. The universal elastic anisotropy index is a decisive factor for cracks. The smaller the value, the less likely it is to form cracks.

2.7. Debye Temperature

Debye temperature is an important parameter for analyzing the mechanical properties and thermodynamic properties of materials. The higher the Debye temperature is, the stronger the bonding force between atoms, the higher the melting point, and the higher the hardness will be. The formula of Debye temperature is as follows [20]:

$${\Theta }_D=\frac{h}{k_B}{(\frac{3n{N}_A\rho }{4\pi M})}^{\frac{1}{3}}{V}_m$$

(13)

where, ${\Theta }_D$ is the Debye temperature, $k_B$ is the Boltzmann constant, $h$ is the Planck constant, $N_A$ is the Avogadro constant, $n$ is the number of atoms in the unit cell, $M$ is the molecular mass, $\rho$ is the unit cell density and $V_m$ is the average wave velocity.

$$V_m={(\frac{2}{3V_t^3}+\frac{1}{3V_l^3})}^{-\frac{1}{3}},V_t=\sqrt{\frac{G}{\rho }},V_l=\sqrt{\frac{(B+\frac{4G}{3})}{\rho }}$$

(14)

where, $V_t$ is the shear wave velocity, $V_l$ is the longitudinal wave velocity, $B$ is the bulk modulus, and $G$ is the shear modulus.

It can be seen from

Table 5. Density ρ/(g/cm³), transverse wave velocity V_t/(m/s), longitudinal wave velocity V_l/(m/s), average wave velocity V_m/(m/s) and Debye temperature Θ_D/k.

Model	ρ/(g/cm3)	Vt/(m/s)	Vl/(m/s)	Vm/(m/s)	ΘD/k
SnO2	6.998	3524.7	5592.1	3879.2	505.8
SnO2–Ni	6.268	3704.3	5969.5	4083.8	522.1
SnO2–N	6.252	3524.7	5778.8	3892.8	489.4
SnO2–Ni–N	6.176	3647.3	5984.1	2432.9	309.9

that single-doped N and co-doped Ni–N reduce the hardness and melting point of the SnO₂ unit cell. Compared with single-doped SnO₂, Ni and N co-doped SnO₂ have the least hardness, which can effectively improve the ductility of the material. Co-doping of Ni and N reduces the hardness of the material and improves the forming and service life of the AgSnO₂ contact material.

3. Experiment

3.1. X-ray Diffraction

X-ray diffraction (XRD) is a diffraction pattern formed when X-rays pass through the crystal structure, which can analyze the microstructure before and after doping. XRD is used to determine whether doping atoms are doped into the SnO₂ lattice. Using a Bruker D8 DISCOVERX X-ray diffraction instrument, place the powder on the Cu target Kα ray diffractometer for scanning. The power is 1.6 kW, the wavelength is 0.15405 nm, the voltage is 40 kV, the current is 40 mA, the scanning range is 10–90°and the speed is 6°/min. The XRD patterns of single-doped and co-doped SnO₂ powders are shown in Figure 5. It can be seen that, compared with the XRD pattern of the intrinsic SnO₂ powder, the diffraction peak position shift in the XRD pattern of the doped SnO₂ powder is smaller, and there is no other phase peak. It shows that the increase in lattice constant caused by doping atoms causes the shift of the diffraction peak position, and there is no diffraction peak related to Ni and N atoms, so the doped SnO₂ powder still maintains the tetragonal rutile structure. It shows that the doping elements achieve substitutional solid solution in sol-gel preparation process, which corresponds to the model established by simulation.

Calculate the average grain size of the doped powder according to the XRD diffraction pattern, using the Scherrer formula [21]:

$$d=k\lambda /\beta \cos \theta$$

(15)

In the formula, k is a constant, with a value of 0.89, λ is the X-ray diffraction wavelength, β is the half-height width of the strongest diffraction peak, cubic crystal particles need to be converted to the radian system and θ is the half-diffraction angle.

The calculated average grain sizes of SnO₂–Ni, SnO₂–N and SnO₂–Ni–N are: 3.67 nm, 7.85 nm and 32.31 nm, respectively. It can be seen that the size of the powder prepared by the sol-gel method reaches the nanometer level, which is beneficial to powder doping. In addition, the intensity of the diffraction peak of SnO₂ after doping decreases, indicating that doping can reduce the crystallinity of the material, and the decrease in crystallinity can cause the hardness and brittleness of the material to decrease, and the toughness of the material can increase.

3.2. Wettability Experiment

The material wetting angle (θ) is an important parameter for judging the wettability between two phases. When θ = 0°, it indicates that the two phases have been completely wetted. When 0° < θ < 90°, the wettability of the two phases is good; when 90° ≤ θ < 180°, the wettability of the two phases is poor. Therefore, the smaller the wetting angle, the better the wettability between the two phases. During the experiment, the sessile drop method was used to measure the wetting angle between Ag and SnO₂ under different additives.

The masses of SnO₂, SnO₂–Ni, SnO₂–N and SnO₂–Ni–N are all 3 g, and the mass of Ag powder is 0.3 g. The experimental temperature is higher than the melting point of Ag (962 °C) so the temperature is set to rise to 1050 °C and is held for 0.5 h. During the experiment, when the temperature rose to 100 °C, the silver oxide began to decompose into silver and oxygen. When the temperature reaches 300 °C, the silver oxide is completely decomposed. Therefore, the influence of silver oxide on the wetting ability can be ignored in this test. After waiting for the sample to cool, use a contact angle measuring instrument to measure the wetting angle of each doped SnO₂. The wetting angle test chart is shown in Figure 6, and the wetting angle test values are shown in

Table 6. The wetting angle of Ag and SnO₂ under different conditions.

Model	SnO2	SnO2–Ni	SnO2–N	SnO2–Ni–N
Wetting angle(θ/°)	93.20	89.10	83.05	16.05

.

It can be seen from Table 6 that the wetting angle of SnO₂ is 93.20° and wettability is poor, which results in a larger contact resistance of AgSnO₂. The wetting angle of SnO₂–N is 89.10°, which has some improvement in wettability. The wetting angle of SnO₂–Ni is reduced to 83.05°, which improves wettability. The wetting angle of SnO₂–Ni–N is 16.05°, indicating that SnO₂ co-doped with Ni and N further improves the wettability of Ag. Therefore, it is difficult for Ni and N co-doped SnO₂ to precipitate in the Ag liquid to form an enriched area, so that contact resistance can be reduced and conductivity can be enhanced.

3.3. Hardness, Conductivity and Contact Resistance

The hardness, conductivity and contact resistance of the prepared AgSnO₂, AgSnO₂–N, AgSnO₂–Ni and AgSnO₂–Ni–N contact materials were tested. The measurement is used to further verify the improvement effect of Ni and N co-doped AgSnO₂. The HXD1000TMdigital microhardness tester was used to measure the hardness of the sample, and the Sigmascope SMP10 metal conductivity tester was used to measure the conductivity of the sample. Each sample was measured six times, and the average of the final results was obtained. The contact resistance of the contacts is measured by using the JFO4C electrical contact material test system. Each type of sample was processed into a contact with a diameter of 4.5 mm and a thickness of 3 mm. We conducted 25,000 electrical contact simulation experiments on each sample to test the improvement of the contact resistance of AgSnO₂ by Ni and N doping. During the experiment, a pure resistance load was used for testing, the action protection voltage was ±40 V, the voltage was set to DC20V, the current was set to DC10A and the contact pressure was set to 86 cN. The experimental results of hardness, electrical conductivity and contact resistance are shown in

Table 7. Experimental results of hardness, conductivity and contact resistance.

Model	Hardness (Hv)	Conductivity (%IACS)	Contact Resistance (mΩ)
SnO2	127.73	40.66	1.191
SnO2–Ni	117.65	42.08	0.994
SnO2–N	124.31	42.28	0.867
SnO2–Ni–N	101.04	58.15	0.856

.

It can be seen from Table 7 that the hardness and contact resistance of the contacts decrease after doping, and the conductivity increases, which indicates that doping can increase the conductivity and ductility of the AgSnO₂ contact material and improve the molding and service life of AgSnO₂ contact material. The conductivity and hardness of AgSnO₂–Ni–N are the smallest, which improves ductility more effectively. The conductivity of AgSnO₂–Ni, AgSnO₂–N and AgSnO₂–Ni–N contacts is greater than that of AgSnO₂ contact materials, which is consistent with the theoretical analysis results.

In practice, the smaller and more stable the contact resistance of the contact material, the better the contact. According to Figure 7, we can judge the stability and value of the contact resistance of AgSnO₂ contact materials with different additives. According to Figure 7a, the contact resistance of AgSnO₂ contact is relatively large and the stability is poor. In Figure 7c, the contact resistance of the AgSnO₂–Ni electrical contact is relatively stable and small in the first part of the electrical contact simulation experiment, but the stability is poor in the later period, and its variation range and contact resistance are increased. In Figure 7d, the AgSnO₂–Ni–N electrical contact has the smallest contact resistance and better stability. Therefore, the AgSnO₂–Ni–N electrical contact not only has good conductivity and ductility, but also has low and stable contact resistance.

4. Conclusions

The first-principles method based on density functional theory was used to analyze the crystal structure, electrical conductivity and mechanical properties of SnO₂, SnO₂–Ni, SnO₂–N and SnO₂–Ni–N. SnO₂ powders with different additives were prepared by the sol-gel method. The powder metallurgy method was used to prepare AgSnO₂ contacts with different additives, and a series of experiments were carried out. The result shows:

1. The doping of Ni and N increases the lattice constant and volume of SnO₂, but does not change its structure. Therefore, the doped SnO₂ still belongs to the tetragonal rutile structure.

2. Through the measurement of energy band structure, state density, charge population and electrical conductivity, it can be obtained that the conductivity performance of Ni–N co-doped AgSnO₂ is the best.

3. The wetting angle between SnO₂–Ni–N and Ag liquid is the smallest, indicating that Ni–N co-doping can further improve wettability between SnO₂ and Ag liquid, reduce the contact resistance of the contacts and improve the conductivity performance.

4. Through the elastic modulus and hardness test, the Ni–N co-doped AgSnO₂ has the best mechanical properties, improving ductility as well as improving molding and service life of the AgSnO₂ contact material.