Next Article in Journal
Seed-Mediated Preparation of Ag@Au Nanoparticles for Highly Sensitive Surface-Enhanced Raman Detection of Fentanyl
Next Article in Special Issue
The Preparation, Morphological Characterization and Possible Electroanalytical Application of a Hydroxyapatite-Modified Glassy Carbon Electrode
Previous Article in Journal
Vapour Diffusion Sitting Drop Method to Induce Nucleation of Calcium Phosphate on Exfoliated Graphene and Graphene Oxide Flakes
Previous Article in Special Issue
Chalcogen S∙∙∙S Bonding in Supramolecular Assemblies of Cadmium(II) Coordination Polymers with Pyridine-Based Ligands
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 11
Issue 7
10.3390/cryst11070768
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structural Evolution in the RE(OAc)3 · 2AcOH Structure Type. A Non-Linear, One-Dimensional Coordination Polymer with Unequal Interatomic Rare Earth Distances

by
Markus Haase
,
Philipp Rissiek
,
Marianne Gather-Steckhan
,
Felix Henkel
and
Hans Reuter
*
Institute of Chemistry of New Materials, Osnabrück University, Barbarastr. 7, 49069 Osnabrück, Germany
*
Author to whom correspondence should be addressed.
Crystals 2021, 11(7), 768; https://doi.org/10.3390/cryst11070768
Submission received: 31 May 2021 / Revised: 18 June 2021 / Accepted: 23 June 2021 / Published: 30 June 2021
(This article belongs to the Special Issue Coordination Polymers)
Browse Figures
Versions Notes

Abstract

:
The existing range of the centrosymmetric, triclinic RE(OAc)3 · 2AcOH structure type has been extended for RE = Eu and Gd while the structure data of the Nd- and Sm-compounds have been revised and corrected, respectively, using low temperature (T = 100 K), well resolved (2θmax = 56°), highly redundant SCXRD data in order to evaluate the structural evolution within this class of acetic acid solvates by statistical methods. Within the nine-fold mono-capped square-antiprismatic coordination spheres of the RE3+ ions, RE-O distances decrease as a result of lanthanide contraction; some with different rates depending on the coordination modes (2.11/2.21) of the acetate ions. The experimental data show that the internal structural parameters of the acetate ions also correlate with their coordination modes. Both acetic acid molecules act as hydrogen bond donors but only one as monodentate ligand. The geometries of the hydrogen bonds reveal that they are strongly influenced by the size of the rare earth atom. The non-linear, one-dimensional coordination polymer propagates with unequal RE···RE distances along the a-axis. Rods of the coordination polymer are arranged in layers congruently stacked above each other with the hydrogen bonded acetic acid molecules as filler in between. In most cases, data fitting is best described in terms of a quadratic rather than a linear regression analysis.

Graphical Abstract

1. Introduction

Rare earth triacetates are widely used as precursors in the synthesis of NaREF4 and LiYF4 core and core/shell nanocrystals. Usually, rare earth triacetate hydrates, RE(OAc)3 nH2O, are employed since they are commercially available or can easily be prepared by dissolving the appropriate rare earth oxide in acetic acid. When nanocrystals of this kind are doped with lanthanide, ions emitting in the near infrared, anhydrous reaction conditions are advantageous since the luminescence is quenched by hydroxyl groups in the crystal lattice [1,2,3]. An example is NaYF4:Yb,Er/NaYF4 core/shell nanocrystals showing upconversion emission with high quantum yield when anhydrous rare earth triacetates are used in the synthesis of the core particle and the shell [4].
In principle, drying of RE(OAc)3 nH2O can be achieved by removal of their water content by extensive water exhausting in a vacuum at higher temperatures or by use of the reaction of the hydrated molecules with acetic acid anhydride, Ac2O, in glacial acetic acid, AcOH. With regard to a common, reproducible, easily upscaled protocol for the preparation of a large number of various anhydrous rare earth triacetates, RE(OAc)3, we started our attempts with the second method.
We became rapidly aware, however, that extensive drying under vacuum is required after synthesis to obtain a product of constant mass. This indicated that—in addition to the desired anhydrous triacetates—solvates with acetic acid and/or acetic anhydride are formed during the reaction. The formation of such compounds does not seem implausible as several acetic acid solvates, RE(OAc)3 · mAcOH and acetic acid solvates hydrates, RE(OAc)3 · mAcOH · nH2O are already known in addition to various hydrates, RE(OAc)3 · nH2O (Figure 1). All attempts, however, to identify our products by PXRD failed.
We therefore decided to study the reaction products by single crystal X-ray diffraction (SCXRD) in order to identify the different phases formed as a result of the applied preparation and crystallization conditions. Last but not least we hoped to find unknown phases and compounds in the three phase system shown in Figure 1.
While exploring the reaction products with SCXRD we obtained the structural data for many new compounds, some for new composition opening new structure types, some extending or fulfilling the existence range of well-known structure types and others improving or correcting former results. Here we present our results on the crystal structure determinations of compounds belonging to the class of rare earth triacetates acetic acid solvates with composition RE(OAc)3 · 2AcOH belonging to structure type 6, a non-linear one-dimensional coordination polymer with unequal interatomic RE···RE distances, observed in the case of the earlier lanthanides RE = Nd, Sm, Eu and Gd. Preparation and solid state structures of two compounds (RE = Nd, Sm) of this structure type have been formerly described in a doctoral thesis [5] but have never been published. In the Cambridge Structural Database [33] their structural data are deposited under the CSD-numbers 653,311 for RE = Nd (data base identifier: JIPLOK) and 653,320 for RE = Sm (data base identifier: JIPNIG). Although it was measured at the same temperature, the deposited data set of the Sm compound exhibited a significantly larger unit cell volume (793.01 Å3) than the Nd compound (779.15 Å3) and in sharp contrast to the so called lanthanide contraction [34], the decrease of the RE3+ ion radius with increase of the atomic number of the rare earth element.

2. Materials and Methods

Single crystals of the compounds described here have been obtained alongside crystals of other compounds by dissolving the corresponding rare earth oxides in acetic acid and using acetic anhydride to remove all water. In the cases of Eu and Gd, 15 mmol of RE2O3 was dissolved in 100 mL of aqueous acetic acid (50% acetic acid by volume) by heating the suspension to reflux temperature. The solvent of the resulting clear solution was then removed with a rotavap avoiding prolonged drying of the resulting solid. Subsequently, 50 to 60 mL of glacial acetic acid were added and the solid dissolved by heating at 90 °C. After cooling the clear solution to 40 °C, 30 mL of acetic anhydride was added and the flask tightly closed. In the case of Nd and Sm, similar solutions could be prepared in a simpler way by directly dissolving the rare earth oxide in a mixture of glacial acetic acid and acetic anhydride. In this case, 10 mmol of RE2O3 was refluxed in 35 mL of acetic acid and 15 mL of acetic anhydride under nitrogen atmosphere until a clear solution was obtained. After cooling to 40 °C, 30 mL of acetic anhydride was added and the flask tightly closed.
Parts of these solutions were mixed with additional acetic anhydride in a ratio, by volume, of 1:1, 1:2 or 1:3. All solutions were left for crystallization at room temperature. In cases where no crystals were detected after one week, the solution was concentrated on a rotavap by a factor of two. No attempts were made to further optimize the reaction conditions to exclusively obtain the substances described here. In the case of Gd, for instance, crystals of Gd(OAc)3 · 4AcOH also form, in addition to the title compound.
Morphology of the crystals was characterized by a prismatic habit (Figure 2) most often resulting from the combination of the pinacoids {100}, {010} and {001}. Crystals are elongated along the a-axis, the propagation direction of the coordination polymer (see below). Besides the great influence of the reaction and crystallization conditions on the compounds formed, isolation from the mother liquor also turned out to be problematic as in mother liquor most of the compounds are very sensitive towards moisture whereas they are stable at ambient conditions over periods of hours and days when free of remaining solvents. In most cases we could achieve this challenge when taking the crystals out of the mother liquor by use of a spoon spatula and pouring on a filter paper.
Single crystals suitable for X-ray measurements were selected under a microscope and mounted on a 50 μm MicroMesh MiTeGen MicromountTM using FROMBLIN Y perfluoropolyether (LVAC 16/6, Aldrich) before they were centered on a Bruker Kappa APEX II CCD-based 4-circle X-ray diffractometer using graphite monochromated Mo Kα radiation (λ = 0.71073 Å) of a fine focus molybdenum-target X-ray tube operating at 50 kV and 30 mA. The crystal-to-detector distance was 40 mm and exposure time was 5 s per frame for all samples with a scan width of 0.5°. Samples were cooled down to 100 K by use of a Kryoflex low temperature device.
Data were integrated and scaled using the programs SAINT and SADABS [35] within the APEX2 software package of Bruker [36]. Special care was taken regarding the data collection strategy in order to reduce absorption effects. A maximum reduction of absorption effects and remaining electron density was achieved by a high data redundancy and numerical absorption corrections.
Structures were solved by direct methods of SHELXS ([37]) and completed by difference Fourier synthesis with SHELXL [38]. Structure refinements were carried out on F2 using full-matrix least-squares procedures, applying anisotropic thermal displacement parameters for all non-hydrogen atoms.
All H atoms including those of the acetic acid molecules were clearly identified in difference-Fourier syntheses. Hydrogen atoms of the methyl groups were refined with idealized positions and allowed to ride on their parent carbon atoms with d(C-H) = 0.98 Å and common isotropic temperature factors for all hydrogen atoms of each methyl group. Hydrogen atoms of the carboxyl groups were refined with a common O-H distance of 0.96 Å before they were fixed and allowed to ride on the corresponding oxygen atom with one common isotropic temperature factor.
Details on the crystallographic data, data collection parameters and structure refinement results are summarized in Table 1 with Rint = Σ|Fo2 − Fo2(mean)|/Σ[Fo2] and Rσ = Σ[σ(Fo2)]/Σ[Fo2]. Final agreement indices: R1 = Σ||Fo| − |Fc||/Σ|Fo| and wR2 = [Σ[w(Fo2 − Fc2)2]/Σ(Fo2)2]]1/2. Weighting function used: w = 1/[σ2(Fo2) + (pP)2 + qP] with P = (Fo2 + 2Fc2)/3. Goof = [Σ[w(Fo2 − Fc2)2]/(n − p]1/2 where n is the number of reflections and p is the total number of parameters refined.
The listed CCDC numbers (Table 1) contain the supplementary crystallographic data for this paper. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/structures (accessed on 28 June 2021). Molecular graphics were prepared using DIAMOND [39], Mercury [40] and POV-Ray [41], respectively.
In order to compare bond lengths and angles in a simple manner, atoms of all four compounds were labeled according to the common numbering scheme depicted in Figure 3.

3. Results and Discussion

Our measurements of the RE(OAc)3 · 2AcOH structure type confirmed the previous results of a triclinic unit cell with two formula units therein, but in contrast to the deposited data (see above) the unit cell volume of the Gd compound was—in accordance with the lanthanide contraction—smaller than the unit cell volume of the Nd compound.

3.1. Unit Cell

As expected, the unit cell volumes decreased continuously from Nd to Gd (Table 1, Figure 4). The mathematical correlation of unit cell volume with the atomic number of the rare earth element can be calculated by a linear regression analysis (y = ax + b) with a goodness of fit factor R2 of 0.9931. Data, however, are better fitted by use of a quadratic expression (y = ux2 + vx + w) with R2 = 1.000.
With four data points the reliability of these calculations is limited but the trend is in accordance with the observations of Greis and Petzel [42], whose data on the unit cell volumes of isostructural REF3-compounds (orthorhombic YF3-structure type, RE = Sm − Lu, 10 data points; hexagonal LaF3-structure type, RE = Ce − (Pm) − Eu, 5 data points) support the fit of the unit cell volume against the atomic number of the rare earth element by use of a quadratic equation instead of a linear one.

3.2. RE Coordination

Rare earth atoms of the RE(OAc)3 · 2AcOH structure type are ninefold, mono-capped square-antiprismatic coordinated (Figure 5) with a narrow RE-O bond length distribution (Table 2), with the mean value decreasing from RE = Nd to Gd. Statistically, a linear regression analysis of the nine different RE-O distances results in R2-values in the range 0.9996 to 0.9838 but—as in the case of unit cell shrinkage—decrease of bond lengths is best described in all cases by a quadratic regression analysis with R2 values in the range of 1.000 to 0.9984. The coefficients a, b (linear regression) and u, v, w (quadratic regression) of the different approaches are summarized in Table S1.
There are, however, some remarkable exceptions from parallelism in bond length shrinkage: (i) the RE-O(11) distance decreases slower than the RE-O(12)1 distance so that at the end (RE = Gd) both are of equal length although they differ at the beginning (RE = Nd) by 0.005 Å; (ii) a similar trend is observed in the case of the RE-O(22)1 and RE-O(41) distances whenever the difference at the starting point is smaller (0.003 Å) and (iii) the reverse trend is found for RE-O(21)1 and RE-O(32)2, where the difference becomes noticeably larger (0.011 Å) from RE = Nd to Gd.
Besides this global view on the RE-O bond lengths, their detailed inspection in terms of the acetate coordination modes will give a deeper insight into the structural evolution of this structure type as a consequence of lanthanide contraction. In the following we will use the Harris symbol as described by Coxall et al. [43] for the different acetate coordination modes to distinguish the three different crystallographic acetate groups shown in Figure 6. The first one (atoms labelled 1n) exhibits a bridging 2.11 (1κO; 2κO’) coordination mode. In addition, this acetate ligand acts as a hydrogen acceptor in a hydrogen bridge bond.
Both the second and third acetate group (atoms labeled 2n and 3n, respectively) belong to the three-dentate, bridging-chelating coordination mode 2.21 (1:2κ2O; 1κO’), but only the third one behaves as a hydrogen acceptor too.

3.2.1. 2.11-Coordination Mode

RE-O distances in the bridging 2.11-coordination mode are unsymmetrical for RE = Nd [Δ(RE-O) = 0.014 Å] but become more and more symmetrical with shrinkage of the rare earth atom ending with a symmetrical bond distance distribution for RE = Gd [Δ(RE-O) = 0.001 Å]. Moreover, the bond angles associated with the RE coordination of this acetate group are strongly correlated (in Figure 6 marked in red) with this harmonization of bond distances. In summary, both angles become smaller from Nd to Gd.
The average RE-O distances of the 2.11-coordination mode are in good accordance with the data of Janiki et al. [44] who have given a statistical survey on RE-O bond lengths depending on of the coordination number of the RE3+ cation and the coordination modes in a large number of different carboxylate groups. They determined in the subset of the acetate coordination in question (nine-fold coordinated rare earth atom and bridging 2.11 carboxylate groups) somewhat shorter RE-O distances (Janiki et al. [44]/this work: 2.450(50)/2.451(5) Å, Nd; 2.412(50)/2.428(4) Å, Sm; 2.395(43)/2.416(3) Å, Eu; 2.394(50)/2.406(1) Å, Gd).

3.2.2. 2.21-Coordination Mode

The influence of lanthanide contraction on the structural parameters associated with this kind of coordination mode differs for both 2.21-coordinating acetate groups. While all RE-O distances decrease in both cases when the atomic number of the rare earth element increases (see above), the corresponding bonding angles seem to be unaffected for the third acetate group but vary in the case of the second one, indicating a change of their orientation in relation to the coordinated rare earth atoms. Thus the C-O···RE angle of the bridge decreases from 148.7(1)° (RE = Nd) to 148.0(1)° (RE = Gd) equally as the chelating C-O ···RE angle decreases on the opposite side from 96.0(1)° (RE = Nd) to 95.5(1)° (RE = Gd).
In contrast to the foregoing coordination mode, Janiki et al. [44] report on the subset of nine-fold coordinated rare earth atoms and 2.21-coordination mode mean RE-O distances which are to some extent greater than in the present study (Janiki et al. [44]/this work: 2.530(56)/2.502(62) Å, Nd; 2.496(54)/2.475(64) Å, Sm; 2.487(60)/2.464(63) Å, Eu; 2.476(56)/2.454(63) Å, Gd).

3.3. Internal Structural Parameters and Hydrogen Bonding of the Acetate Groups

The present SCXRD data not only give us a deeper insight into acetate coordination modes and the structural evolution of the rare earth coordination sphere as a result of lanthanide contraction but also allow us a detailed look at the internal structural parameters of the acetate groups (Table 3). For C-C bonds of type C(sp2)-C(sp3)RCOO-, Allen et al. [45] reported an overall value of 1.520(11) Å. This value is somewhat longer than the C-C bonds in the present study [1.498(1)–1.506(1) Å], which may be ascribed to the fact that our compounds exclusively have acetate groups. There is an indication that the C-C bond is longer for the bridging 2.11-coordination mode [1.506(1) Å] compared with the corresponding bond length in the 2.21-coordination mode [1.498(1) Å], but the data situation is too poor for a clear statement.
Both C-O bond lengths are unequal in all acetate ligands with the greatest difference [0.047 Å] for the second acetate group (2.21-coordination mode without additional hydrogen bond) followed by the first one (0.033 Å; 2.11-coordination mode with additional hydrogen bond). The most symmetrical bond length distribution [0.024 Å] is observed in the case of the third acetate group of 2.21-coordination mode with additional hydrogen bond.
There are also significant differences in O-C-O bond angles for the three coordination modes. Thus the largest bond angle [mean value: 123.8(1)°] is realized in case of the 2.11-coordination mode of the first acetate group, while in the 2.21-coordination mode the angle is noticeably smaller and depends on whether the acetate group acts as a hydrogen acceptor [mean value: 119.7(2)°] or not [mean value: 118.8(2)°].

3.4. Coordination Modes, Internal Structural Parameters and Hydrogen Bonding of the Acetic Acid Molecules

While both crystallographical different acetic acid molecules (Figure 7) of the RE(OAc)3 · 2AcOH structure type act as hydrogen donors in hydrogen bonds, only the first one (atoms labeled 4n) also acts as an electron donor towards RE in a monodentate fashion (1.10 coordination mode). In the latter case, the RE-O distances [RE-O(41), 2.497(1)–2.445(1) Å; Table 2, Figure 5] are of medium strength.
In comparison with the uncoordinated acetic acid molecule (atom labeled 5n), the C=O bond of the coordinated one is significantly (+0.036 Å) longer, while—on the other hand—the C-OH bond is shorter (−0.009 Å) (Table 4). In their review on bond lengths in organic compounds, Allen et al. [45] recorded a value of 1.308(19) Å for the C-OH single bond [Csp2-O(2); C*-C(=O)-OH)] and a value of 1.214(19) Å for the C=O double bond [Csp2=O(1), C*-C(=O)-OH)] in carboxylic acids. In contrast to the C-O bond lengths, O-C-O bond angles are unaffected [mean values: 122.8(2) to 123.0(2)°] by lanthanide coordination as are the anchoring angles with a mean value of 136.4(1)°.
Both acetic acid molecules act as hydrogen donors. Differences exist as the hydrogen bond of the coordinated acetic acid molecule takes place inside the coordination polymer [O(42)-H···O(12)], while the hydrogen bond of the uncoordinated acetic acid molecule binds this molecule to the coordination polymer [O(52)-H···O32)].
Donor acceptor distances (Table 5) of 2.562(2) to 2.674(2) Å in the hydrogen bonds are in the range of those observed in the orthorhombic polymorph [46] of acetic acid [2.623(1) Å], indicating that they are of the same strength. Gradually those of the coordinated acetic acid molecule forming hydrogen bonds within the coordination polymer are stronger [2.572(2)–2.562(2) Å] than those of the uncoordinated one [2.674(2)–2.665(2) Å].
Although the oxygen atoms of the OH-groups are not involved in rare earth coordination, the structural parameters of both hydrogen bonds show a strong correlation with the size of the rare earth atom. As we could localize the hydrogen atoms of the OH-groups from difference Fourier synthesis (see above), the analysis of the structural evolution of the hydrogen bonds as a function of the size of the rare earth element reveals some remarkable features (Table 5, Figure S1): (i) In the case of the coordinated acetic acid molecule the O···O distance decreases from RE = Nd [2.572(2) Å] to RE = Gd [2.562(2) Å] as does the angle at the bridging hydrogen atom from 173.4° to 167.3°. Both datasets are best fitted by quadratic equations revealing concave curvatures. (ii) In the case of the uncoordinated acetic acid molecule the O···O distance decreases, too, from RE = Nd [2.674(2) Å] to RE = Gd [2.665(2) Å] but in a convex manner while the angle at the bridging hydrogen atoms increases from 162.9° to 164.4° with a concave curvature.

3.5. Packing

The {REO9} building units are connected with each other to a non-linear, one-dimensional coordination polymer along the a-axis with unequal interatomic RE···RE distances (Table 6, Figure 8). Within the series of the investigated compounds, both distances decrease (Table 4) continuously with increasing atomic number as the interatomic RE···RE···RE bond angle decreases from 138.15(1)° (RE = Nd) to 137.80(1)° (RE = Gd).
In spite of the zig-zag-arrangement of the rare earth atoms, the overall one-dimensional coordination polymers exhibit—neglecting the uncoordinated acetic acid molecules—a remarkable circular, rod-like shape with a diameter of about 1.22 nm (Figure 9). In this context, the uncoordinated, only hydrogen bonded acetic acid molecules behave as knobs that fill the space in the square primitive arrangements of the rods (Figure 10) in a zipper-like way.

4. Conclusions

Our low temperature, well resolved single-crystal X-ray data of the rare earth triacetates acetic acids solvates belonging to the RE(OAc)3 · 2AcOH structure type allow a more detailed insight not only into the coordination behavior of the rare earth element but also into the influence of their coordination on the internal structural parameter of the acetate ligands and acetic acid molecules and vice versa.
For the nine-fold mono-capped square-antiprismatic coordination of the rare earth atoms, lanthanide contraction represents the most prominent factor for RE-O bond lengths and RE-O-C bond angles in the different coordination modes of the acetate groups as the specific values most often decrease in accordance with the size of the rare earth atom. The corresponding relationships can be fitted by use of a linear regression analysis but are more often better described by a quadratic equation, an observation that was formerly already observed in the case of some isostructural rare earth trifluorides, REF3 [42], tris-ethylsulfate nonahydrates, RE(C2H5SO4)3 · 9H2O [47], and tris-trifluoromethanesulfonate nonahydrates, RE(CF3SO3)3 · 9H2O [48,49]. Based on these data, the parabolic decay of structural parameters associated with lanthanide contraction has been revisited [50] and theoretically reinforced [51]. Our data also show that not all RE-O bond lengths decrease uniformly. The exceptions show that the corresponding acetate groups occupy a somewhat different orientation in space in order to optimize their interactions with the rare earth atoms.
For the acetate ligands our data indicate that the internal structural parameters strongly depend on their coordination modes (2.11, 2.21) and the hydrogen bonds they are involved in, and in particular the strongly different bond angles between the oxygen atoms of the different acetate groups constitute important indicators for this assumption. Unexpected results came from the hydrogen bridging bonds of the acetic acid molecules as their structural parameters strongly correlated with the size of the lanthanide atom, an observation that has to be confirmed by further experiments. With respect to the extrapolation of these data it seems possible that the hydrogen bridging bonds confine the existence range of the RE(OAc)3 · 2AcOH structure type of the compounds described herein.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/cryst11070768/s1, Figure S1: Bond lengths [Å] and angles [°] of the one dimensional coordination polymer in the RE(OAc)3 · 2AcOH structure type as a function of the rare earth element, trend lines in black with formula of the quadratic regression analysis and R2-values; Figure S2: Characteristic bond lengths [Å] and angles [°] of the hydrogen bonds in the RE(OAc)3 · 2AcOH structure type as a function of the rare earth element, trend lines in black with formula of the quadratic regression analysis and R2-values; Table S1: Parameters and R2 values of the linear and quadratic regression analysis for selected bond lengths [Å] and angles [°] in the compounds of the RE(OAc)3 · 2AOH structure type.

Author Contributions

Conceptualization, M.H. and H.R.; resources, M.G.-S., P.R. and F.H.; original draft preparation, H.R.; visualization, H.R.; funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Deutsche Forschungsgemeinschaft, HA 1649/7-1.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

We thank the Deutsche Forschungsgemeinschaft and the Government of Lower-Saxony for funding the diffractometer and acknowledge support by Deutsche Forschungsgemeinschaft (DFG) and Open Access Publishing Fund of Osnabrück University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rabouw, F.T.; Prins, P.T.; Villanueva-Delgado, P.; Castelijns, M.; Geitenbeek, R.G.; Meijerink, A. Quenching Pathways in NaYF4:Er3+,Yb3+ Upconversion Nanocrystals. ACS Nano 2018, 12, 4812–4823. [Google Scholar] [CrossRef] [Green Version]
  2. Feng, Y.; Li, Z.; Li, Q.; Yuan, J.; Tu, L.; Ning, L.; Zhang, H. Internal OH− induced cascade quenching of upconversion luminescence in NaYF4:Yb/Er nanocrystals. Light. Sci. Appl. 2021, 10, 1–10. [Google Scholar] [CrossRef]
  3. Carl, F.; Birk, L.; Grauel, B.; Pons, M.; Würth, C.; Resch-Genger, U.; Haase, M. LiYF4:Yb/LiYF4 and LiYF4:Yb,Er/LiYF4 core/shell nanocrystals with luminescence decay times similar to YLF laser crystals and the upconversion quantum yield of the Yb,Er doped nanocrystals. Nano Res. 2021, 14, 797–806. [Google Scholar] [CrossRef]
  4. Homann, C.; Krukewitt, L.; Frenzel, F.; Grauel, B.; Würth, C.; Resch-Genger, U.; Haase, M. NaYF4:Yb,Er/NaYF4 Core/Shell Nanocrystals with High Upconversion Luminescence Quantum Yield. Angew. Chem. Int. Ed. 2018, 57, 8765–8769. [Google Scholar] [CrossRef] [PubMed]
  5. Torres, S.G. Synthese neuer Carboxylate von Metallen mit Liebig-Säuren. Ph.D. Thesis, University of Cologne, Cologne, Germany, 2007. [Google Scholar]
  6. Guo, F.-S.; Leng, J.-D.; Liu, J.-L.; Meng, Z.-S.; Tong, M.-L. Polynuclear and Polymeric Gadolinium Acetate Derivatives with Large Magnetocaloric Effect. Inorg. Chem. 2011, 51, 405–413. [Google Scholar] [CrossRef] [PubMed]
  7. Bierke, T. Mono-und bimetallische Carboxylate der Überungangs- und Selten-Erd-Metalle. Ph.D. Thesis, University of Cologne, Cologne, Germany, 2012. [Google Scholar]
  8. Wu, J.-F.; Zhang, H.-X.; Zhang, P.; Zhao, L.; Tang, J.-K. Magnetic relaxation in 1D and 2D dysprosium(III) coordination polymers. Chin. J. Inorg. Chem. 2015, 31, 1847–1854. [Google Scholar]
  9. Janczak, J.; Kubiak, R. Reactivity of the HoPc2I in the acetylacetone–water system. Polyhedron 2014, 81, 695–704. [Google Scholar] [CrossRef]
  10. Junk, P.C.; Kepert, C.J.; Wei-Min, L.; Skelton, B.W.; White, A.H. Structural Systematics of Rare Earth Complexes. X. (‘Maximally’) Hydrated Rare Earth Acetates. Aust. J. Chem. 1999, 52, 437–457. [Google Scholar]
  11. Sadikov, G.G.; Kukina, G.A.; Porai-Koshits, M.A. X-ray structure of cerium triacetate hydrate. J. Struct. Chem. 1968, 8, 551–553. [Google Scholar] [CrossRef]
  12. Ganapathy, S.; Chako, V.P.; Bryant, R.G.; Etter, M.C. Carbon CP-MASS NMR and X-ray Crystal Structure of Paramagentic Lanthanide Acetates. J. Am. Chem. Soc. 1986, 108, 3159–3165. [Google Scholar] [CrossRef]
  13. Lei, H.; Yang, Y.; Liu, Y. Crystal structure of Ln[(CH3COO)3 H2O] (Ln = praseodymium, neodymium). Acta Sci. Nat. Univ. Sunyatseni 1990, 29, 59–64. [Google Scholar]
  14. Lossin, A.; Meyer, G. Dimere und Ketten in Praseodym(III)acetat-sesquihydrat, Pr(CH3COO)3·1,5 H2O/Dimers and Chains in Praseodymium(III)acetate-sesquihydrate, Pr(CH3COO)3 · 1.5 H2O. Z. Naturforsch. B 1992, 47, 1602–1608. [Google Scholar] [CrossRef] [Green Version]
  15. Skelton, B.W.; Ogden, M.I.; Massi, M.; D’Alessio, D. CCDC 1883935: Experimental Crystal Structure Determination; The Cambridge Crystallographic Data Centre (CCDC): Cambridge, UK, 2018. [Google Scholar]
  16. Cañadillas-Delgado, L.; Fabelo, O.; Cano, J.; Pasán, J.; Delgado, F.S.; Lloret, F.; Julve, M.; Ruiz-Pérez, C. Dinuclear and two- and three-dimensional gadolinium(III) complexes with mono- and dicarboxylate ligands: Synthesis, structure and magnetic properties. CrystEngComm 2009, 11, 2131–2142. [Google Scholar] [CrossRef]
  17. Sakagami, N.; Tsunekawa, M.; Konno, T.; Okamoto, K.-I. Synthesis and Structure of Unprecedented Carboxylate-bridged Heteronuclear Cr(III)-Nd(III) Complex. Chem. Lett. 1997, 26, 575–576. [Google Scholar] [CrossRef]
  18. Arias, J.L.; Cabrera, A.; Sharma, P.; Rosas, N.; Garcia, J.L.; Hernandez, S. Catalytic auto-condensation of 2,4-pentanedione promoted by Sm(III) acetylacetonate: The X-ray structure of a novel complex [Sm(CH3COO)3(H2O)2](H2O)2. Inorg. Chim. Acta 2000, 310, 261–264. [Google Scholar] [CrossRef]
  19. Yu, Q.; Zhou, X.; Liu, M.; Chen, J.; Zhou, Z.; Yin, X.; Cai, Y. Syntheses, characterization, and luminescence of two lanthanide complexes [Ln2(acetate)6(H2O)4] · 4H2O (Ln = Tb(1), Sm(2)). J. Rare Earth 2008, 26, 178–184. [Google Scholar] [CrossRef]
  20. Yang, Y.; Luo, L.; Mak, T.C.W. Crystal structure of europium acetato aqua complex [Eu(μ-CH3COO-O)(CH3COO)2(H2O)2]2 4H2O. Jiegou Huaxue 1988, 7, 1–5. [Google Scholar]
  21. De, A.; Pradhan, S.S.; Biswas, B. Coordinated aqua molecules mediated phosphorester cleavage activity of dimeric gadonlinium((()-acetate. J. Ind. Chem. Soc. 2017, 94, 1063–1071. [Google Scholar]
  22. Favas, M.C.; Kepert, D.L.; Skelton, B.W.; White, A.H. Crystal Structure of Gadolinium(III) Acetate Tetrahydrate. Stereochemistry of the Nine-co-ordinate [M(bidentate ligand)3(unidendate ligand)3] System. J. Chem. Soc. 1980. [Google Scholar] [CrossRef]
  23. Evangelisti, M.; Roubeau, O.; Palacios, E.; Camón, A.; Hooper, T.N.; Brechin, E.K.; Alonso, J.J. Cryogenic Magnetocaloric Effect in a Ferromagnetic Molecular Dimer. Angew. Chem. Int. Ed. 2011, 50, 6606–6609. [Google Scholar] [CrossRef] [Green Version]
  24. Hatscher, S.T. CCDC 199395: Experimental Crystal Structure Determination; The Cambridge Crystallographic Data Centre (CCDC): Cambridge, UK, 2005. [Google Scholar]
  25. Baggio, R.; Muñoz, J.C.; Perec, M. Bis(μ-acetato-κ3O,O’:O’)bis[bis(acetato-κ2O,O’)diaquadysprosium(III) tetrahydrate. Acta Crystallogr. 2002, C58, m498–m500. [Google Scholar] [CrossRef] [Green Version]
  26. Lorusso, G.; Roubeau, O.; Evangelisti, M. Rotating Magnetocaloric Effect in an Anisotropic Molecular Dimer. Angew. Chem. 2016, 55, 3360–3363. [Google Scholar] [CrossRef]
  27. Bats, J.W.; Kalus, R.; Fuess, H. Holmium triacetate tetrahydrate. Acta Crystallogr. 1979, 35, 1225–1227. [Google Scholar] [CrossRef]
  28. Sawase, H.; Koizumi, Y.; Suzuki, Y.; Shimoi, M.; Ouchi, A. The Bridging Tridentate-type Carboxylato Ligand in Isomorphous Guanidinium Di(μ-acetato)bis(triacetatoaqualanthanoidates(III), [(NH2)3C]2[M2(CH3CO2)8(H2O)2], (M = La, Ce, Pr, Nd, and Sm). Bull. Chem. Soc. Jpn. 1984, 57, 2730–2737. [Google Scholar] [CrossRef] [Green Version]
  29. Aslanov, L.A.; Abdul’minev, I.K.; Porai-Koshits, M.A.; Ivanov, V.I. Structure of erbium acetate tetrahydrate. Dokl. Akad. Nauk SSSR 1972, 205, 343–345. [Google Scholar]
  30. Fomina, I.G.; Kiskin, M.A.; Martynov, A.G.; Aleksandrov, G.G.; Dobrokhotova, Z.V.; Gorbunova, Y.G.; Shvedenkov, Y.G.; Tsivadze, A.Y.; Novotortsev, V.M.; Eremenko, I.L. Lanthanium(III), europium(III), and thulium(III) binuclear acetates and pivalates: Synthesis, structure, magnetic properties, and solid phase thermolysis. Zh. Neorg. Khim. 2004, 49, 1463–1474. [Google Scholar]
  31. Skelton, B.W. CCDC 1590164: Experimental Crystal Structure Determination; The Cambridge Crystallographic Data Centre (CCDC): Cambridge, UK, 2018. [Google Scholar]
  32. Lossin, A.; Meyer, G. [Sm(CH3COO)3(H2O)2] CH3COOH, ein Essigsäureaddukt des Samarium(III)-acetatdihydrates. Z. Naturforsch. 1992, 47, 179–182. [Google Scholar]
  33. Nefedov, S.E.; Kozitsyna, N.Y.; Akhmadullina, N.S.; Cherkashina, N.V.; Vargaftik, M.N.; Moiseev, I.I. The Role of Water Molecules in Formation of Heterometallic Palladium Acetate Complexes with Cerium and Neodymium. Russ. J. Inorg. Chem. 2011, 56, 357–374. [Google Scholar] [CrossRef]
  34. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef]
  35. Goldschmidt, V.M. Geochemische Verteilungsgesetze der Elemente. 5, Isomorphie und Polymorphie der Sesquioxyde: Die Lanthaniden-Kontraktion und ihre Konsequenzen; Kristiania Dybwad: Oslo, Norway, 1925. [Google Scholar]
  36. Krause, L.; Herbst-Irmer, R.; Sheldrick, G.M.; Stalke, D. Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination. J. Appl. Crystallogr. 2015, 48, 3–10. [Google Scholar] [CrossRef] [Green Version]
  37. Bruker. APEX 2—Suite of Crystallographic Software; Bruker: Madison, WI, USA, 2008. [Google Scholar]
  38. Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. 2008, A64, 112–122. [Google Scholar] [CrossRef] [Green Version]
  39. Brandenburg, K. Diamond—Crystal and Molecular Visualization; Crystal Impact: Bonn, Germany, 2006. [Google Scholar]
  40. Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.J.; van de Streek, J.; Wood, P. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
  41. POV-Ray; The Persistence of Vision Raytracer: Victoria, Australia, 2004.
  42. Greis, O.; Petzel, T. Ein Beitrag zur Strukturchemie der Selten-Erd-Trifluoride. Z. Naturforsch. 1974, 403, 1–22. [Google Scholar] [CrossRef]
  43. Coxall, R.A.; Harris, S.G.; Hernderson, D.K.; Parsons, S.; Takser, P.A.; Winpenny, E.P. Inter-ligand reactions: In situ formation of new polydentate ligands. J. Chem. Soc. 2000, 2349–2356. [Google Scholar] [CrossRef]
  44. Janicki, R.; Mondry, A.; Starynowicz, P. Carboxylates of rare earth elements. Coord. Chem. Rev. 2017, 340, 98–133. [Google Scholar] [CrossRef]
  45. Allen, F.H.; Kennard, O.; Watson, D.G.; Brammer, L.; Orpen, A.G.; Taylor, R. Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J. Chem. Soc. Perkin Trans. 2 1987, S1–S19. [Google Scholar] [CrossRef]
  46. Boese, R.; Blaser, D.; Latz, R.; Bäumen, A. Acetic acid at 40K. Acta Crystallogr. 1999, C55, IUC9900001. [Google Scholar] [CrossRef]
  47. Gerkin, R.E.; Reppart, W.J. The Structures of the Lanthanide Etyl Sulfate Enneahydrates, M(C2H5SO4)3.9H2O [M = La-Lu (except Pm), at 171 K. Acta Crystallogr. 1984, C40, 781–786. [Google Scholar]
  48. Chatterjee, A.; Maslen, E.N.; Watson, K.J. The effect of the lanthanoid contraction on the nonaaqualanthanoid(III) tris(trifluoromethanesulfonates). Acta Crystallogr. 1988, B44, 381–386. [Google Scholar] [CrossRef]
  49. Harrowfield, J.M.; Kepert, D.L.; Patrick, J.M.; White, A.H. Structure and stereochemistry in ‘f-block’ complexes of high coordination number. VIII. The [M(unidentate)9] system. Crystal structures of [M(OH2)9][CF3SO3]3, M = La, Gd, Lu, Y. Aust. J. Chem. 1983, 36, 483–492. [Google Scholar] [CrossRef]
  50. Quadrelli, E.A. Lanthanide Contraction over the 4f Series Follows a Qadratic Decay. Inorg. Chem. 2002, 41, 167–169. [Google Scholar] [CrossRef] [PubMed]
  51. Raymond, K.N.; Wellman, D.L.; Sgarlata, C.; Hill, A.P. Curvature of the lanthanide contraction: An explanation. Comptes Rendus Chim. 2010, 13, 849–852. [Google Scholar] [CrossRef] [Green Version]
Crystals 11 00768 g001 550
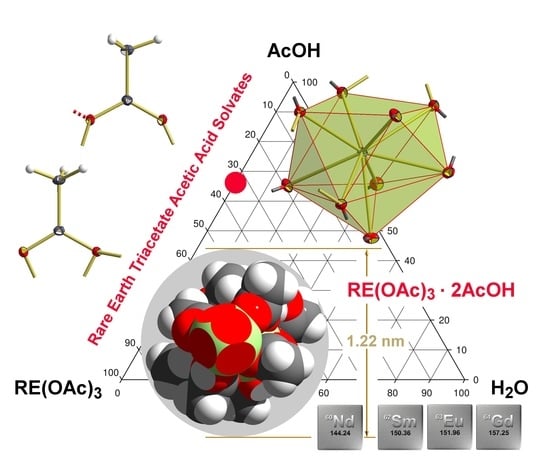
Figure 1. Gibbs triangle on the structurally well documented classes of compounds in the three phase system RE(OAc)3, H2O and AcOH. Hydrates: RE(OAc)3 · nH2O: RE(OAc)3 · ½H2O, 1, (RE = Nd [5], Gd [6], Tb [7], Dy [8], Ho [9], Er [5]); α-RE(OAc)3 · H2O, 2, (RE = Ce [10,11], Pr [12,13]); β-RE(OAc)3 · H2O, 2, (RE = Nd [10,13]); RE(OAc)3 · 1½H2O, 3 (RE = Ce [10], Pr [14]); RE(OAc)3 · 3H2O, 4, (RE = Eu [12,15], Gd [16]); RE(OAc)3 · 4H2O, 5, (RE = Nd [17] without coordinates, Sm [10,18,19], Eu [18], Gd [19,20,21,22], Tb [23], Dy [24,25], Ho [26], Er [27,28], Tm [29], Yb [30], Lu [10]); Acetic acid solvates: RE(OAc)3 · 2AcOH, 6, (RE = Nd, Sm [5]); RE(OAc)3 · 4AcOH, 7, (RE = Pr, Nd [5]); Acetic acid solvate hydrates: RE(OAc)3 ·AcOH · 2H2O, 8, (RE = Sm [31], Eu [10]); α-RE(OAC)3 · 3AcOH · H2O, 9, (RE = Nd [32], Dy [5], Ho [7], Er [5]; β-RE(OAC)3 · 3AcOH · H2O, 9, (RE = Sm [5]).
Figure 1. Gibbs triangle on the structurally well documented classes of compounds in the three phase system RE(OAc)3, H2O and AcOH. Hydrates: RE(OAc)3 · nH2O: RE(OAc)3 · ½H2O, 1, (RE = Nd [5], Gd [6], Tb [7], Dy [8], Ho [9], Er [5]); α-RE(OAc)3 · H2O, 2, (RE = Ce [10,11], Pr [12,13]); β-RE(OAc)3 · H2O, 2, (RE = Nd [10,13]); RE(OAc)3 · 1½H2O, 3 (RE = Ce [10], Pr [14]); RE(OAc)3 · 3H2O, 4, (RE = Eu [12,15], Gd [16]); RE(OAc)3 · 4H2O, 5, (RE = Nd [17] without coordinates, Sm [10,18,19], Eu [18], Gd [19,20,21,22], Tb [23], Dy [24,25], Ho [26], Er [27,28], Tm [29], Yb [30], Lu [10]); Acetic acid solvates: RE(OAc)3 · 2AcOH, 6, (RE = Nd, Sm [5]); RE(OAc)3 · 4AcOH, 7, (RE = Pr, Nd [5]); Acetic acid solvate hydrates: RE(OAc)3 ·AcOH · 2H2O, 8, (RE = Sm [31], Eu [10]); α-RE(OAC)3 · 3AcOH · H2O, 9, (RE = Nd [32], Dy [5], Ho [7], Er [5]; β-RE(OAC)3 · 3AcOH · H2O, 9, (RE = Sm [5]).
Crystals 11 00768 g001
Crystals 11 00768 g002 550
Figure 2. Typical prismatic shape of crystals of the RE(OAc)3 · 2AcOH structure type.
Figure 2. Typical prismatic shape of crystals of the RE(OAc)3 · 2AcOH structure type.
Crystals 11 00768 g002
Crystals 11 00768 g003 550
Figure 3. Unit cell and labelling scheme of the atoms in the asymmetric unit of the RE(OAc)3 · 2AcOH structure type visualized for RE = Nd. All atoms are drawn as thermal displacement ellipsoids of the 40% level. Hydrogen bonds are indicated as broken sticks in red, additional RE-O- bonds to RE atoms outside the asymmetric unit as shortened sticks.
Figure 3. Unit cell and labelling scheme of the atoms in the asymmetric unit of the RE(OAc)3 · 2AcOH structure type visualized for RE = Nd. All atoms are drawn as thermal displacement ellipsoids of the 40% level. Hydrogen bonds are indicated as broken sticks in red, additional RE-O- bonds to RE atoms outside the asymmetric unit as shortened sticks.
Crystals 11 00768 g003
Crystals 11 00768 g004 550
Figure 4. Evolution of the unit cell volumes [Å3] in compounds of the RE(OAc)3 · 2AcOH structure type as a function of the RE atomic number. Trend lines of linear regression analysis and formula are given in green, those of the quadratic regression analysis in red.
Figure 4. Evolution of the unit cell volumes [Å3] in compounds of the RE(OAc)3 · 2AcOH structure type as a function of the RE atomic number. Trend lines of linear regression analysis and formula are given in green, those of the quadratic regression analysis in red.
Crystals 11 00768 g004
Crystals 11 00768 g005 550
Figure 5. (a) Distorted mono-capped square antiprismatic coordination polyhedron of the rare earth atoms in the RE(OAc)3 · 2AcOH structure type; example RE = Nd. All atoms are drawn as thermal displacement ellipsoids of the 40% level. Bonds from oxygen to carbon are drawn in two colors, bonds from oxygen to neighboring rare earth atoms as short sticks. (b) Evaluation of RE-O distances as function of the atomic number of the RE element with trend lines; empty raw of RE = Pm included in order to get an adequate representation; Symmetry codes to generate equivalent atoms: 1 1 − x, 1 − y, 1 − z; 2 −x, 1 − y, 1 − z.
Figure 5. (a) Distorted mono-capped square antiprismatic coordination polyhedron of the rare earth atoms in the RE(OAc)3 · 2AcOH structure type; example RE = Nd. All atoms are drawn as thermal displacement ellipsoids of the 40% level. Bonds from oxygen to carbon are drawn in two colors, bonds from oxygen to neighboring rare earth atoms as short sticks. (b) Evaluation of RE-O distances as function of the atomic number of the RE element with trend lines; empty raw of RE = Pm included in order to get an adequate representation; Symmetry codes to generate equivalent atoms: 1 1 − x, 1 − y, 1 − z; 2 −x, 1 − y, 1 − z.
Crystals 11 00768 g005
Crystals 11 00768 g006 550
Figure 6. Coordination modes of the acetate groups in the RE(OAc)3 · 2AcOH structure type; example RE = Nd. C-C and C-O bond lengths [Å] arithmetically averaged over all 4 compounds, standard deviations of averaging in brackets. Bonds from oxygen to RE are indicated by short sticks, hydrogen bonds by short, dashed sticks in red. Mean values correlating with RE marked in red.
Figure 6. Coordination modes of the acetate groups in the RE(OAc)3 · 2AcOH structure type; example RE = Nd. C-C and C-O bond lengths [Å] arithmetically averaged over all 4 compounds, standard deviations of averaging in brackets. Bonds from oxygen to RE are indicated by short sticks, hydrogen bonds by short, dashed sticks in red. Mean values correlating with RE marked in red.
Crystals 11 00768 g006
Crystals 11 00768 g007 550
Figure 7. Coordination modes and hydrogen bonding of the acetate acid molecules in the RE(OAc)3 · 2AcOH structure type visualized for RE = Nd. C-C and C-O bond lengths [Å] arithmetically averaged over all 4 compounds, standard deviations of averaging in brackets. Bonds from oxygen to RE are indicated by short sticks, hydrogen bonds by short, dashed sticks in red.
Figure 7. Coordination modes and hydrogen bonding of the acetate acid molecules in the RE(OAc)3 · 2AcOH structure type visualized for RE = Nd. C-C and C-O bond lengths [Å] arithmetically averaged over all 4 compounds, standard deviations of averaging in brackets. Bonds from oxygen to RE are indicated by short sticks, hydrogen bonds by short, dashed sticks in red.
Crystals 11 00768 g007
Crystals 11 00768 g008 550
Figure 8. Detail of the non-linear, one-dimensional coordination polymer in the RE(OAc)3 · 2AcOH structure type with RE···RE distances [Å] and angles; example RE = Nd.
Figure 8. Detail of the non-linear, one-dimensional coordination polymer in the RE(OAc)3 · 2AcOH structure type with RE···RE distances [Å] and angles; example RE = Nd.
Crystals 11 00768 g008
Crystals 11 00768 g009 550
Figure 9. Space-filling model showing a section of the one-dimensional coordination polymer in the RE(OAc)3 · 2AcOH structure type illustrating its rod-like shape when omitting the uncoordinated acetic acid molecules; example RE = Nd, positions of subsequent oxygen atoms are visualized by their sectional plane with the RE-spheres in red as are the position of the uncoordinated acetic acids molecules by their sectional planes with the acceptor oxygen atom in red. Color code: oxygen = red, carbon = black, hydrogen = white, neodymium = yellow-green. (a) side-view, (b) front view.
Figure 9. Space-filling model showing a section of the one-dimensional coordination polymer in the RE(OAc)3 · 2AcOH structure type illustrating its rod-like shape when omitting the uncoordinated acetic acid molecules; example RE = Nd, positions of subsequent oxygen atoms are visualized by their sectional plane with the RE-spheres in red as are the position of the uncoordinated acetic acids molecules by their sectional planes with the acceptor oxygen atom in red. Color code: oxygen = red, carbon = black, hydrogen = white, neodymium = yellow-green. (a) side-view, (b) front view.
Crystals 11 00768 g009
Crystals 11 00768 g010 550
Figure 10. Arrangement of the one-dimensional coordination polymers (simplified visualized as rods) in the crystal structure of the RE(OAc)3 · 2AcOH structure type, looking down the a-axis; example RE = Nd. Uncoordinated, but hydrogen bonded acetic acid molecules filling the space between the rods in a zipper-like manner are shown as ball-and-stick model.
Figure 10. Arrangement of the one-dimensional coordination polymers (simplified visualized as rods) in the crystal structure of the RE(OAc)3 · 2AcOH structure type, looking down the a-axis; example RE = Nd. Uncoordinated, but hydrogen bonded acetic acid molecules filling the space between the rods in a zipper-like manner are shown as ball-and-stick model.
Crystals 11 00768 g010
Table
Table 1. Summarized collection on the crystallographic data, data collection and structure refinement of RE(OAc)3 · 2AcOH.
Table 1. Summarized collection on the crystallographic data, data collection and structure refinement of RE(OAc)3 · 2AcOH.
RENdSmEuGd
Empirical formulaC10H17NdO10C10H17O10SmC10H17EuO10C10H17GdO10
Formula weight441.47447.58449.20454.48
Temperature100(2)
Wavelength [Å] 0.71073
Crystal system, space groupTriclinic, P-1
a [Å]7.5841(3)7.5032(2)7.4692(3)7.4333(3)
b [Å]9.0774(4)9.0869(3)9.0908(4)9.0960(4)
c [Å]11.6665(5)11.6631(4)11.6630(6)11.6717(5)
α [°]88.694(2)88.695(2)88.694(2)88.678(2)
ß [°]75.288(2)75.419(2)75.453(2)75.516(2)
γ [°]89.595(2)89.588(2)89.631(2)89.584(2)
Volume [Å3]776.63(6)769.39(4)766.34(6)763.88(6)
Z, dcalc [g/cm3]2, 1.8882, 1.9322, 1.9472, 1.976
µ(MoKα) [mm−1]3.3873.8604.1374.386
F(000)434438440442
2Θmax56°
Reflections collected83,82577,32382,65079,605
Reflections unique, Rint3729, 0.03193699, 0.04533684, 0.03983677, 0.0579
Data/restraints/parameters3729/0/2013699/0/2013684/0/2013677/0/201
Goodness-of-fit on F21.0761.0791.0721.054
R1, wR2 [I > 2σ(I)]0.0140, 0.03670.0139, 0.03320.0121, 0.02890.0155, 0.0340
R1, wR2 [all data]0.0149, 0.03710.0152, 0.03360.0134, 0.02930.0177, 0.0346
Extinction coefficientn/a
±Δ e.Å−30.998/−0.4490.509/−0.4940.518/−0.3160.502/−0.605
CCDC-numbers2,086,1172,086,1182,086,1202,086,121
Table
Table 2. Rare earth oxygen distances [Å] in the ninefold, mono-capped square-antiprismatic coordination spheres of the rare earth atoms in the RE(OAc)3 · 2AcOH structure type.
Table 2. Rare earth oxygen distances [Å] in the ninefold, mono-capped square-antiprismatic coordination spheres of the rare earth atoms in the RE(OAc)3 · 2AcOH structure type.
RENdSmEuGd
RE(1)-O(21)2.420(1)2.395(1)2.386(1)2.377(1)
RE(1)-O(31)2.443(1)2.410(1)2.398(1)2.386(1)
RE(1)-O(11)2.445(1)2.422(1)2.414(1)2.405(2)
RE(1)-O(12) 12.466(1)2.433(1)2.419(1)2.406(2)
RE(1)-O(22) 12.485(1)2.460(1)2.451(1)2.444(2)
RE(1)-O(41)2.497(1)2.468(1)2.458(1)2.445(1)
RE(1)-O(21) 12.540(1)2.513(1)2.498(1)2.485(1)
RE(1)-O(32) 22.545(1)2.518(1)2.507(1)2.496(2)
RE(1)-O(31) 22.577(1)2.556(1)2.543(1)2.533(1)
Mean value2.491(53)2.464(55)2.453(54)2.442(54)
Symmetry codes to generate equivalent atoms: 1 1 − x, 1 − y, 1 − z; 2 −x, 1 − x, 1 − y.
Table
Table 3. Individual bond lengths [Å] within the different acetate groups of the RE(OAc)3 ·2AcOH structure type groups, standard deviations in brackets.
Table 3. Individual bond lengths [Å] within the different acetate groups of the RE(OAc)3 ·2AcOH structure type groups, standard deviations in brackets.
RENdSmEuGdMean Value
O(11)-C(11)1.245(2)1.247(2)1.249(2)1.249(3)1.248(2)
O(12)-C(11)1.281(2)1.282(2)1.279(2)1.280(3)1.281(1)
C(11)-C(12)1.509(3)1.504(3)1.507(2)1.502(3)1.506(3)
O(21)-C(21)1.287(2)1.290(2)1.289(2)1.293(2)1.290(2)
O(22)-C(21)1.245(2)1.242(2)1.245(2)1.241(3)1.243(2)
C(21)-C(22)1.501(2)1.500(3)1.498(3)1.498(3)1.499(1)
O(32)-C(31)1.254(2)1.255(2)1.255(2)1.250(3)1.254(2)
O(31)-C(31)1.279(2)1.278(2)1.275(2)1.278(3)1.278(2)
C(31)-C(32)1.499(3)1.497(3)1.496(2)1.498(3)1.498(1)
Table
Table 4. Bond lengths [Å] within the different acetic acid molecules of the RE(OAc)3 ·2AcOH structure type with mean values and standard deviations in brackets.
Table 4. Bond lengths [Å] within the different acetic acid molecules of the RE(OAc)3 ·2AcOH structure type with mean values and standard deviations in brackets.
RENdSmEuGdMean Value
O(41)-C(41)1.229(2)1.228(2)1.227(2)1.228(3)1.228(1)
O(42)-C(41)1.311(2)1.312(2)1.311(2)1.313(3)1.312(1)
C(41)-C(42)1.493(2)1.492(3)1.494(2)1.494(3)1.493(1)
O(51)-C(51)1.195(3)1.194(3)1.194(3)1.193(3)1.194(1)
O(52)-C(51)1.320(3)1.323(3)1.320(2)1.320(3)1.321(1)
C(51)-C(52)1.500(3)1.499(3)1.497(3)1.501(3)1.499(2)
Table
Table 5. Donor-acceptor distances [Å] and hydrogen bridging angles in the different compounds of the RE(OAc)3 ·2AcOH structure type with standard deviations in brackets.
Table 5. Donor-acceptor distances [Å] and hydrogen bridging angles in the different compounds of the RE(OAc)3 ·2AcOH structure type with standard deviations in brackets.
RENdSmEuGd
O(42)-O(12)12.572(2)2.568(2)2.567(2)2.562(2)
O(52)-C(32)32.674(2)2.667(2)2.665(2)2.665(2)
O(42)-H(42) C(51)173.4°171.9°169.9°167.3°
O(52)-H(52)-C(51)162.9°164.8°164.4°164.4°
Table
Table 6. Interatomic RE···RE distances [Å] and angles in the RE(OAc)3 · 2AcOH structure type.
Table 6. Interatomic RE···RE distances [Å] and angles in the RE(OAc)3 · 2AcOH structure type.
RENdSmEuGd
RE(1)···RE(1) 13.9435(2)3.9008(2)3.8852(2)3.8660(2)
RE(1)···RE(1) 24.1758(2)4.1366(1)4.1183(2)4.1012(2)
RE(1) 1···RE(1)···RE(1) 2138.15(1)°137.97(1)°137.87(1)°137.80(1)°
Symmetry codes to generate equivalent atoms: 1 −x, 1 − y, 1 − z; 2 1 − x, 1 − y, 1 − z.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Haase, M.; Rissiek, P.; Gather-Steckhan, M.; Henkel, F.; Reuter, H. Structural Evolution in the RE(OAc)3 · 2AcOH Structure Type. A Non-Linear, One-Dimensional Coordination Polymer with Unequal Interatomic Rare Earth Distances. Crystals 2021, 11, 768. https://doi.org/10.3390/cryst11070768

AMA Style

Haase M, Rissiek P, Gather-Steckhan M, Henkel F, Reuter H. Structural Evolution in the RE(OAc)3 · 2AcOH Structure Type. A Non-Linear, One-Dimensional Coordination Polymer with Unequal Interatomic Rare Earth Distances. Crystals. 2021; 11(7):768. https://doi.org/10.3390/cryst11070768

Chicago/Turabian Style

Haase, Markus, Philipp Rissiek, Marianne Gather-Steckhan, Felix Henkel, and Hans Reuter. 2021. "Structural Evolution in the RE(OAc)3 · 2AcOH Structure Type. A Non-Linear, One-Dimensional Coordination Polymer with Unequal Interatomic Rare Earth Distances" Crystals 11, no. 7: 768. https://doi.org/10.3390/cryst11070768

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop