Introduction to Colloidal and Microfluidic Nematic Microstructures
Abstract
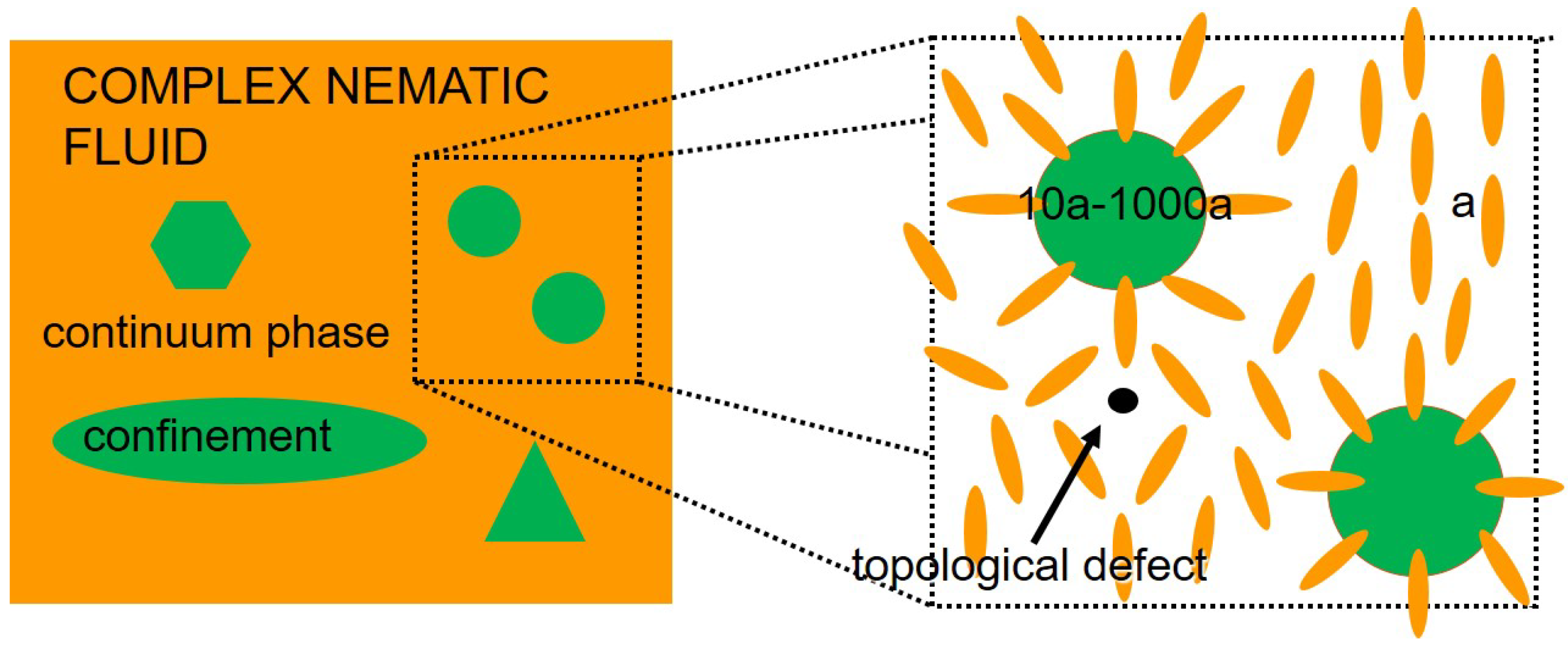
:1. Introduction
2. Mesoscopic Approach to Nematic Complex Fluids
2.1. Landau-de Gennes Free Energy Approach
2.2. Nematodynamics
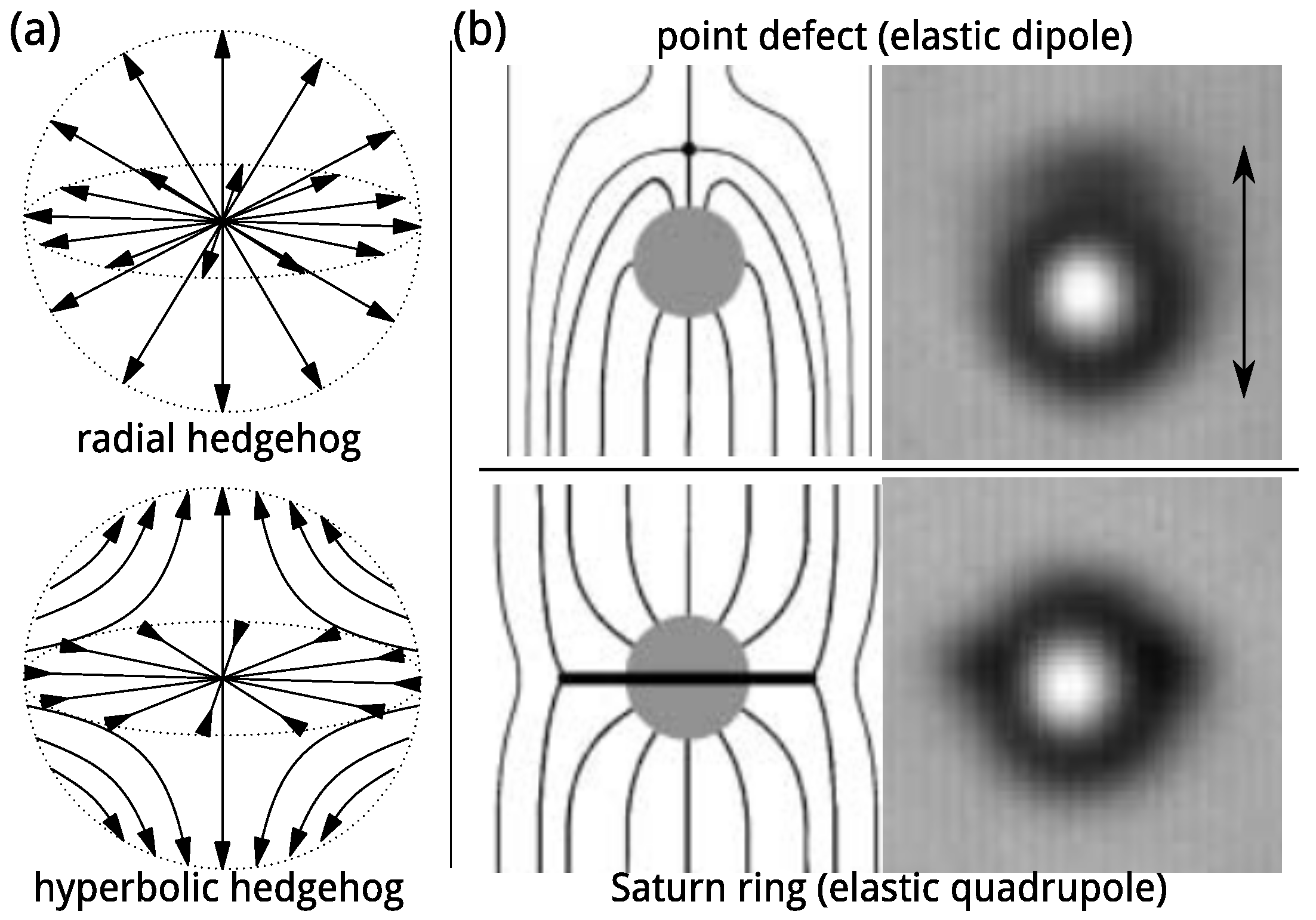
3. Topological Defects and Nematic Colloids
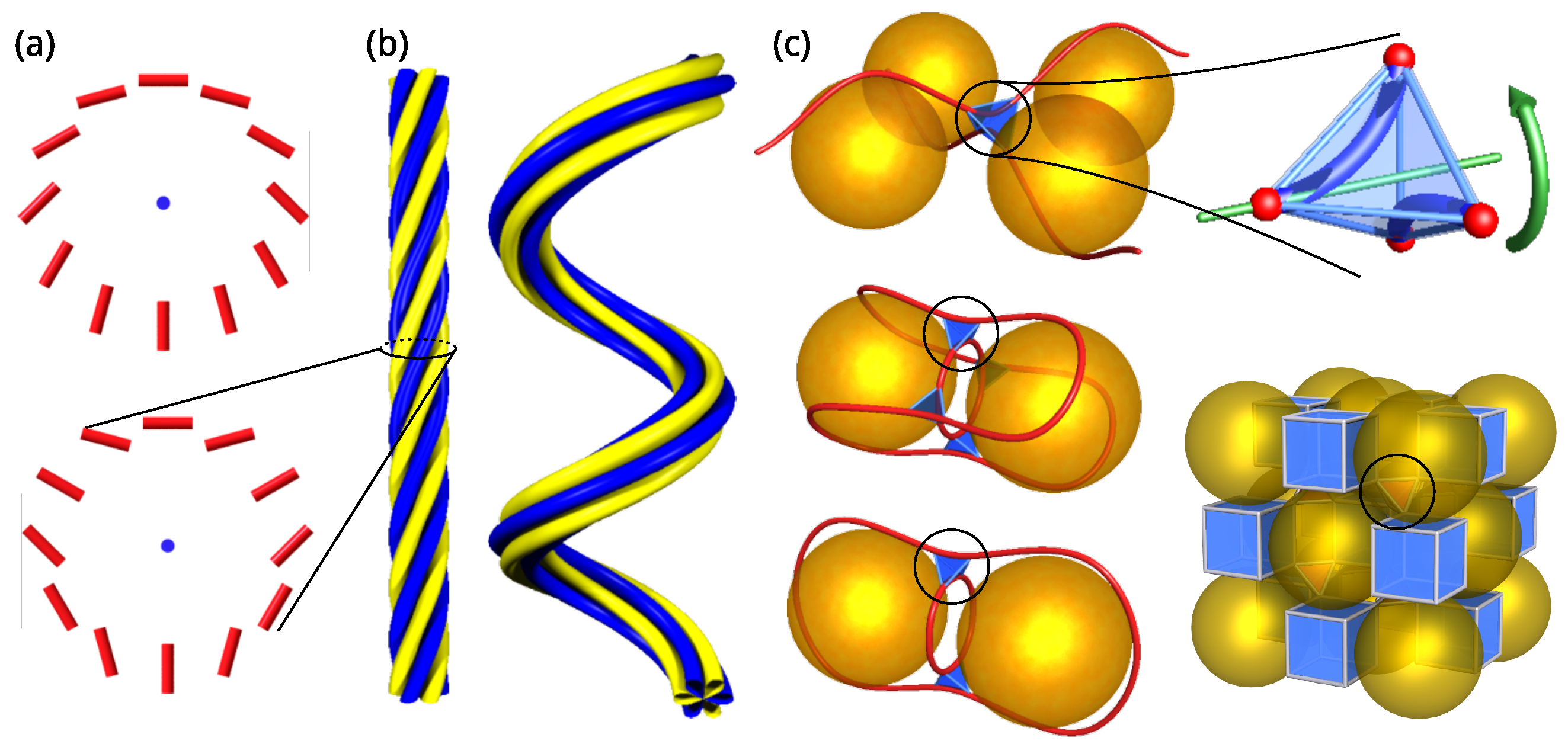
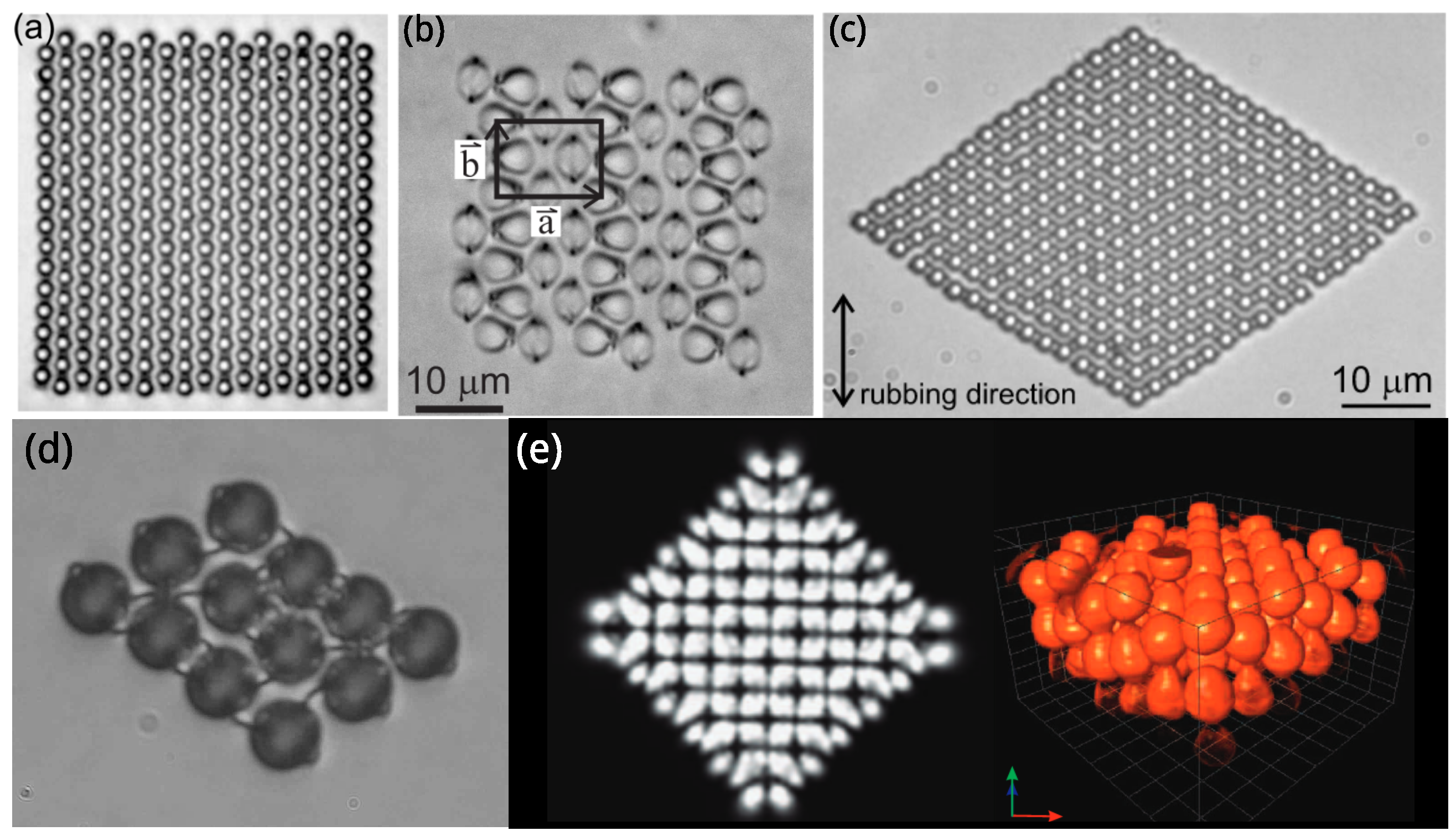
4. Nematic Colloidal Assemblies
5. Stationary Nematic Microfluidic Structures
5.1. Porous Nematic Microfluidics for Generation of Umbilic Defect Structures
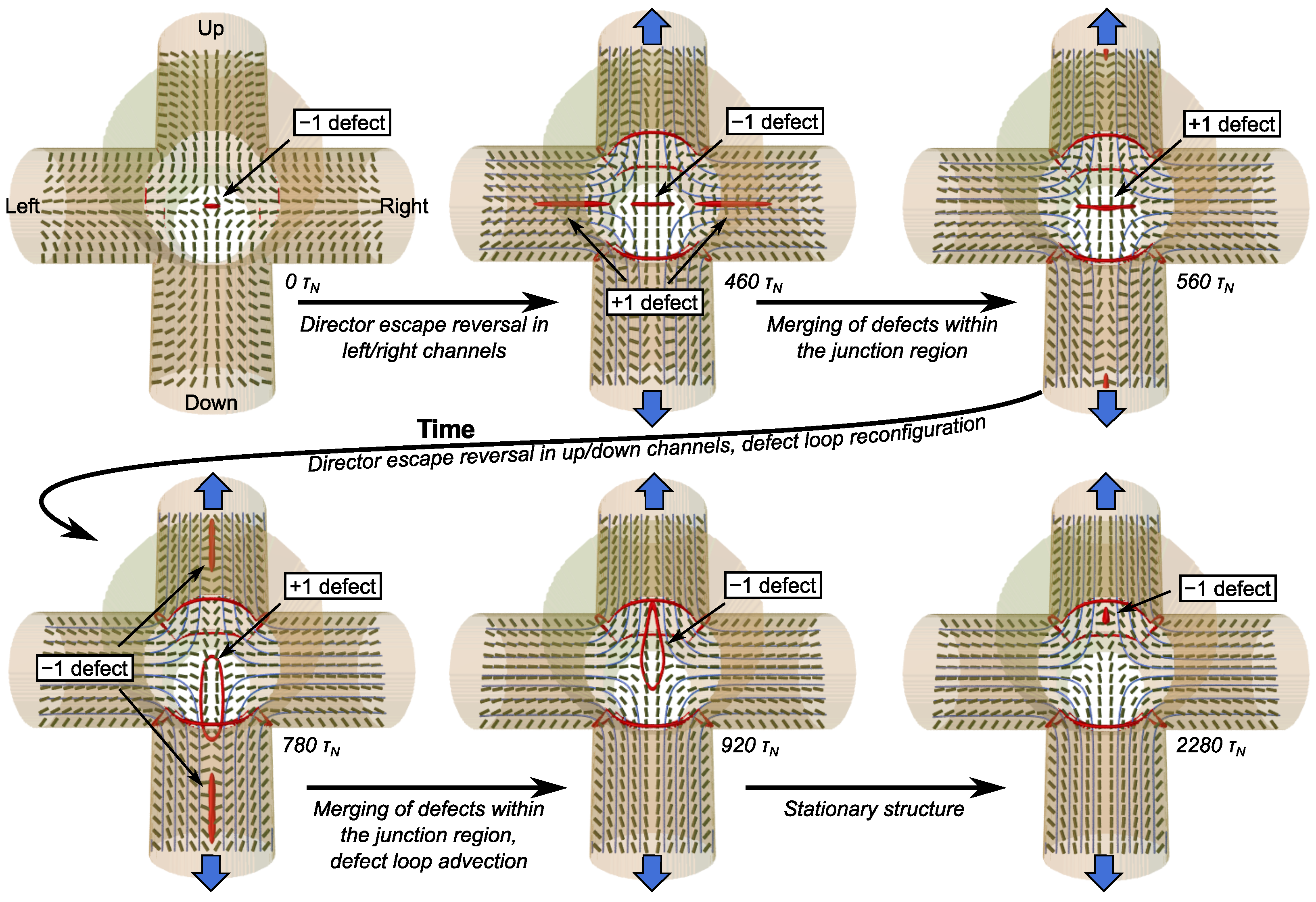
5.2. Stationary Singular Defect Structures in Junctions of Nematic Microfluidic Channels
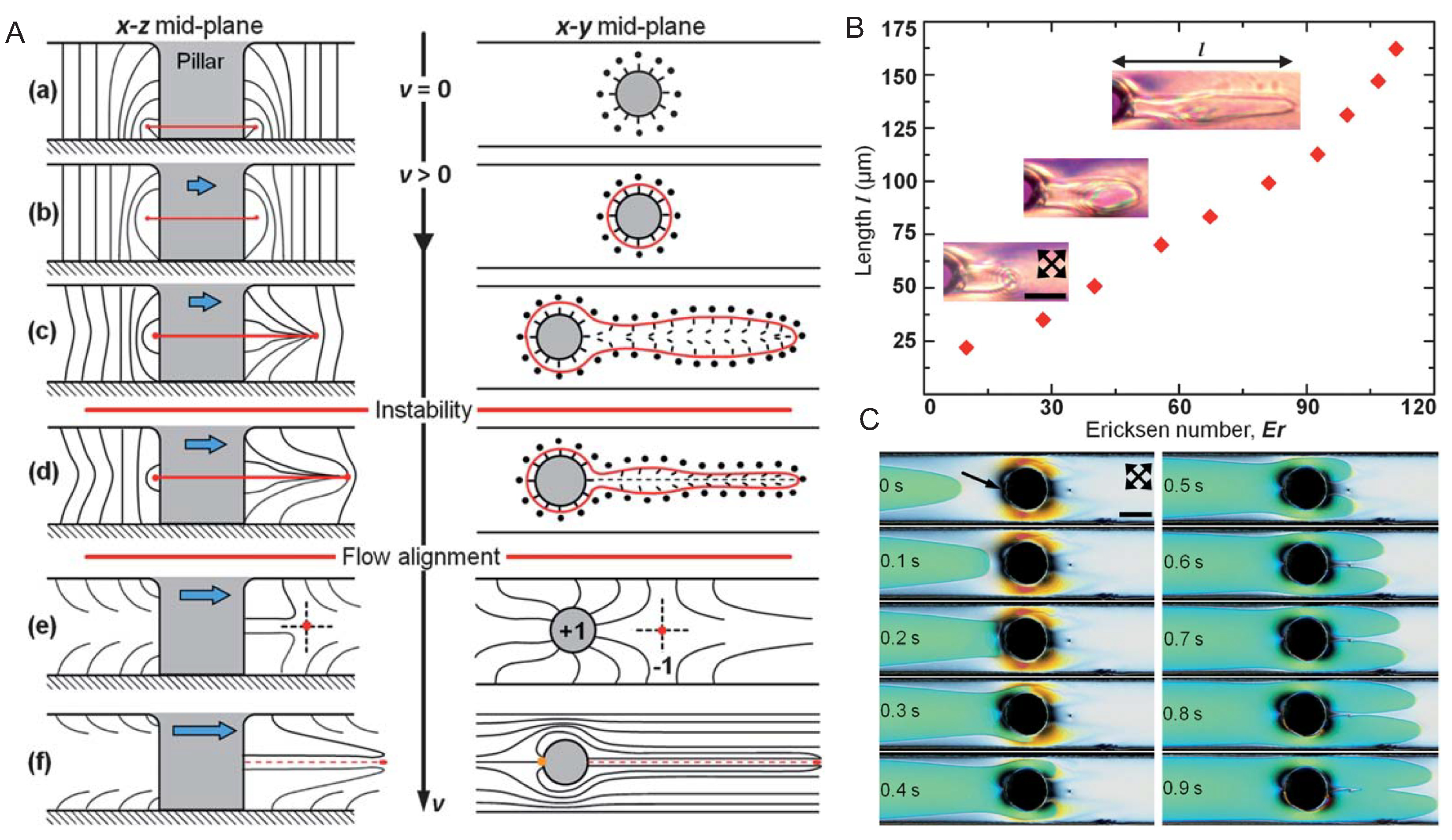
5.3. Nematic Flow Past Microfluidic Obstacles
6. Functionalized Colloids: Ferromagnetic Liquid Crystal Structures
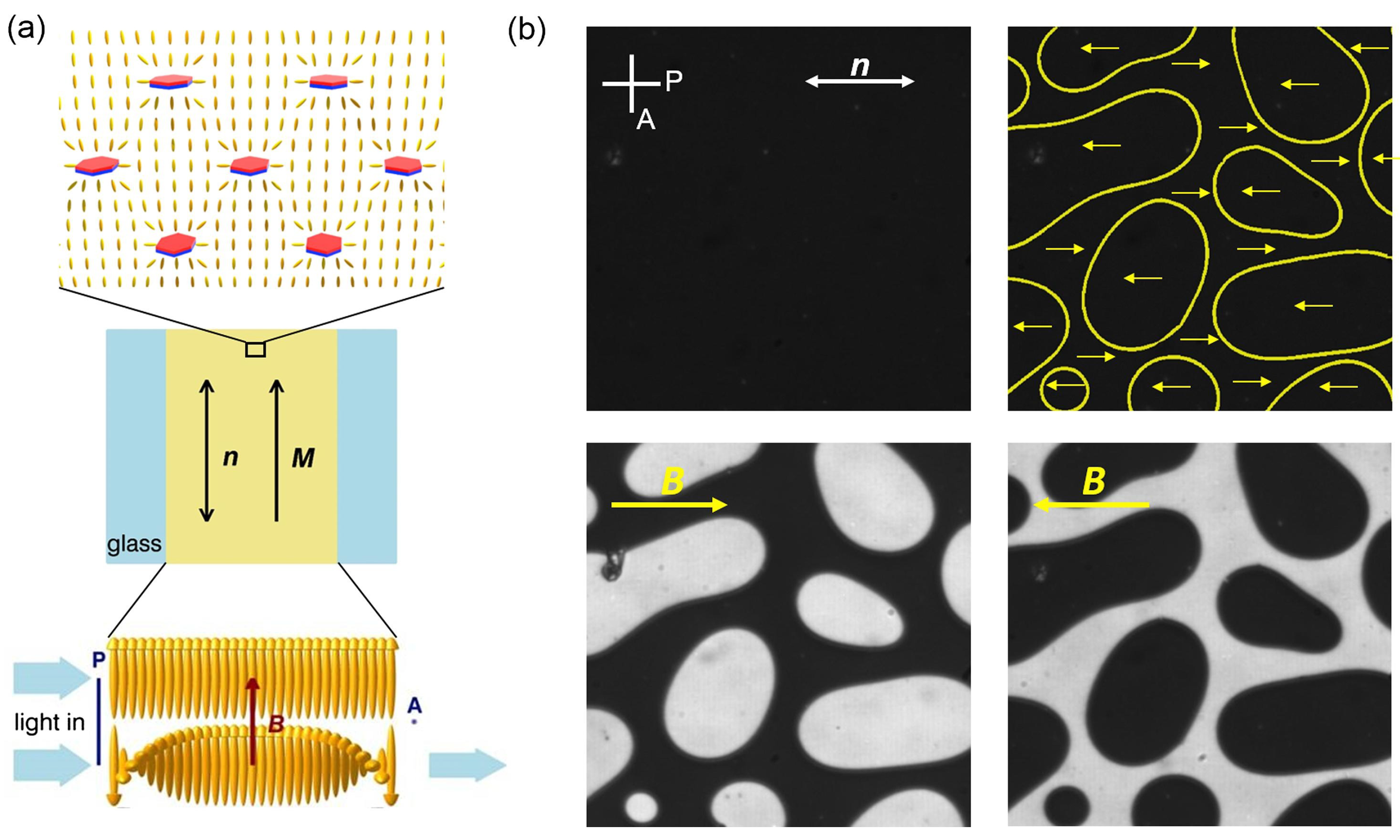
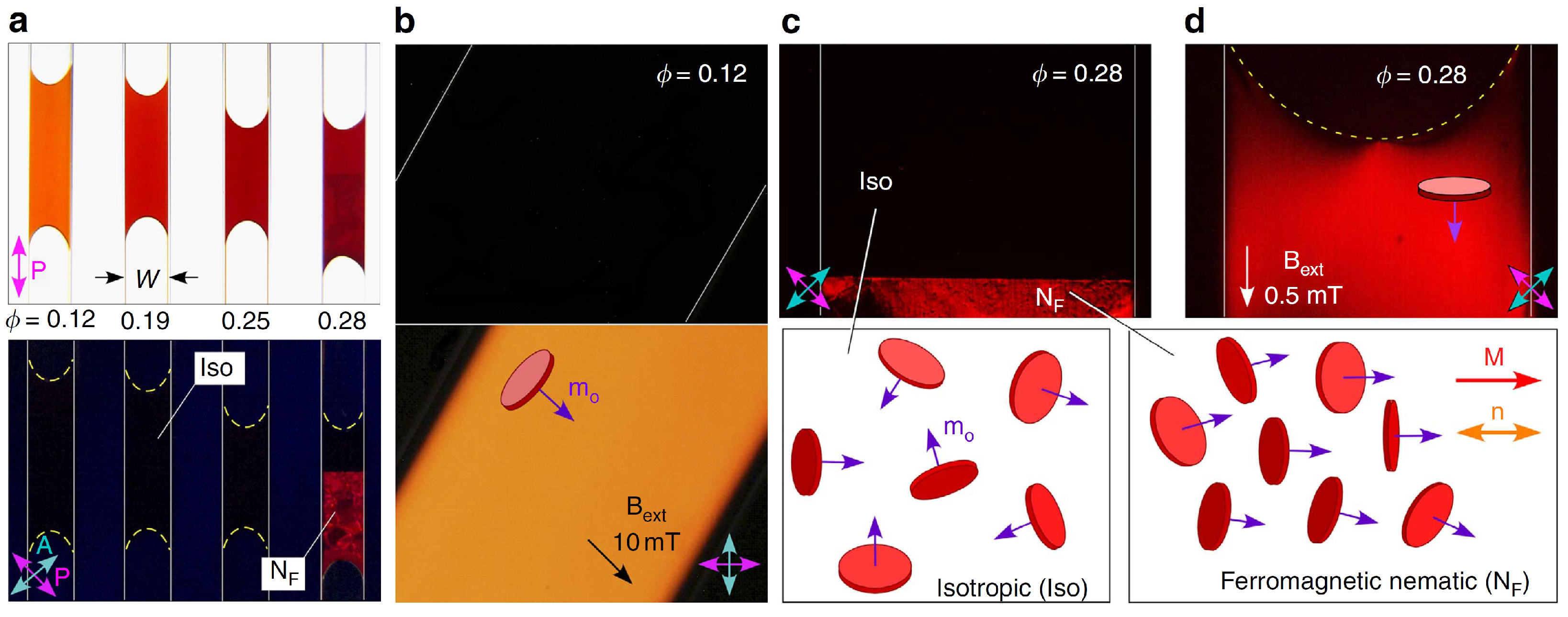
6.1. Suspensions of Magnetic Platelets in Liquid Crystals
6.2. Dense Suspensions of Magnetic Platelets in Isotropic Fluids
7. Conclusions
Funding
Conflicts of Interest
References
- Frank, F.C. I. Liquid crystals. On the theory of liquid crystals. Discuss. Faraday Soc. 1958, 25, 19. [Google Scholar] [CrossRef]
- Maier, W.; Saupe, A. Eine einfache molekulare Theorie des nematischen kristallinflüssigen Zustandes. Z. Naturforsch. 1958, 13, 564–566. [Google Scholar] [CrossRef]
- Maier, W.; Saupe, A. Eine einfache molekular-statistische Theorie der nematischen kristallinflüssigen Phase. Teil I. Z. Naturforsch. 1959, 14, 882–889. [Google Scholar] [CrossRef]
- Maier, W.; Saupe, A. Eine einfache molekular-statistische Theorie der nematischen kristallinflüssigen Phase. Teil II. Z. Naturforsch. 1960, 15, 287–292. [Google Scholar] [CrossRef]
- Gennes, P.G.D. Short Range Order Effects in the Isotropic Phase of Nematics and Cholesterics. Mol. Cryst. Liq. Cryst. 1971, 12, 193. [Google Scholar] [CrossRef]
- Helfrich, W.; Schadt, M. Light Control Cell. Swiss Patent CH532261A, 4 December 1970. [Google Scholar]
- Fergason, J. Display Devices Utilizing Liquid Crystal Light Modulation. U.S. Patent US3731986A, 22 April 1971. [Google Scholar]
- Chen, H.; Wu, S.T. Advanced liquid crystal displays with supreme image qualities. Liq. Cryst. Today 2019, 28, 4. [Google Scholar] [CrossRef] [Green Version]
- Stinson, T.W.; Litster, J.D.; Clark, N.A. Static and Dynamic Behavior near the Order Disorder Transition of Nematic Liquid Crystals. J. Phys. Colloq. 1972, 33, C1–C69. [Google Scholar] [CrossRef]
- Young, C.Y.; Pindak, R.; Clark, N.A.; Meyer, R.B. Light-Scattering Study of Two-Dimensional Molecular-Orientation Fluctuations in a Freely Suspended Ferroelectric Liquid-Crystal Film. Phys. Rev. Lett. 1978, 40, 773. [Google Scholar] [CrossRef]
- Clark, N.A.; Lagerwall, S.T. Submicrosecond bistable electro-optic switching in liquid crystals. Appl. Phys. Lett. 1980, 36, 899. [Google Scholar] [CrossRef]
- Clark, N.A.; Lagerwall, S.T. Chiral Smectic C or H Liquid Crystal Electro-Optical Device. U.S. Patent US4367924A, 11 January 1983. [Google Scholar]
- Safinya, C.R.; Roux, D.; Smith, G.S.; Sinha, S.K.; Dimon, P.; Clark, N.A.; Bellocq, A.M. Steric Interactions in a Model Multimembrane System: A Synchrotron X-ray Study. Phys. Rev. Lett. 1986, 57, 2718. [Google Scholar] [CrossRef]
- Bellini, T.; Clark, N.; Muzny, C.; Wu, L.; Garland, C.; Schaefer, D.; Oliver, B. Phase behavior of the liquid crystal 8CB in a silica aerogel. Phys. Rev. Lett. 1992, 69, 788. [Google Scholar] [CrossRef] [PubMed]
- Link, D.R.; Giorgio Natale, R.S.; Maclennan, J.E.; Clark, N.A.; Körblova, E.; Walba, D.M. Spontaneous Formation of Macroscopic Chiral Domains in a Fluid Smectic Phase of Achiral Molecules. Science 1997, 278, 1924. [Google Scholar] [CrossRef] [PubMed]
- Kang, D.; Maclennan, J.; Clark, N.; Zakhidov, A.; Baughman, R. Electro-optic Behavior of Liquid-Crystal-Filled Silica Opal Photonic Crystals: Effect of Liquid-Crystal Alignment. Phys. Rev. Lett. 2001, 86, 4052. [Google Scholar] [CrossRef] [PubMed]
- Nakata, M.; Zanchetta, G.; Chapman, B.D.; Jones, C.D.; Cross, J.O.; Pindak, R.; Bellini, T.; Clark, N.A. End-to-End Stacking and Liquid Crystal Condensation of 6- to 20-Base Pair DNA Duplexes. Science 2007, 318, 1276. [Google Scholar] [CrossRef] [PubMed]
- Hough, L.E.; Jung, H.T.; Krüerke, D.; Heberling, M.S.; Nakata, M.; Jones, C.D.; Chen, D.; Link, D.R.; Zasadzinski, J.; Heppke, G.; et al. Helical Nanofilament Phases. Science 2009, 325, 456. [Google Scholar] [CrossRef]
- Chen, D.; Porada, J.H.; Hooper, J.B.; Klittnick, A.; Shen, Y.; Tuchband, M.R.; Korblova, E.; Bedrov, D.; Walba, D.M.; Glaser, M.A.; et al. Chiral heliconical ground state of nanoscale pitch in a nematic liquid crystal of achiral molecular dimers. Proc. Natl. Acad. Sci. USA 2013, 110, 15931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shuai, M.; Klittnick, A.; Shen, Y.; Smith, G.P.; Tuchband, M.R.; Zhu, C.; Petschek, R.G.; Mertelj, A.; Lisjak, D.; Čopič, M.; et al. Spontaneous liquid crystal and ferromagnetic ordering of colloidal magnetic nanoplates. Nat. Commun. 2016, 7, 10394. [Google Scholar] [CrossRef] [PubMed]
- Kléman, M. Defect densities in directional media, mainly liquid crystals. Philos. Mag. 1973, 27, 1057. [Google Scholar] [CrossRef]
- Volovik, G.E.; Mineev, V.P. Investigation of singularities in superfluid He3 in liquid crystals by the homotopic topology methods. J. Exp. Theor. Phys. 1977, 45, 1186. [Google Scholar]
- Mermin, N. The topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591. [Google Scholar] [CrossRef]
- Volovik, G.; Lavrentovich, O. Topological dynamics of defects: Boojums in nematic drops. Zh. Eksp. Teor. Fiz. 1983, 85, 1159. [Google Scholar]
- Doane, J.W.; Vaz, N.A.; Wu, B.G.; Žumer, S. Field controlled light scattering from nematic microdroplets. Appl. Phys. Lett. 1986, 48, 269. [Google Scholar] [CrossRef]
- Kurik, M.V.; Lavrentovich, O.D. Defects in liquid crystals: Homotopy theory and experimental studies. Sov. Phys. Usp. 1988, 31, 196. [Google Scholar] [CrossRef]
- Crawford, G.; Allender, D.; Doane, J. Surface elastic and molecular-anchoring properties of nematic liquid crystals confined to cylindrical cavities. Phys. Rev. A 1992, 45, 8693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nelson, D.R. Toward a Tetravalent Chemistry of Colloids. Nano Lett. 2002, 2, 1125. [Google Scholar] [CrossRef] [Green Version]
- Skačej, G.; Zannoni, C. Controlling surface defect valence in colloids. Phys. Rev. Lett. 2008, 100, 197802. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Leon, T.; Koning, V.; Devaiah, K.B.S.; Vitelli, V.; Fernandez-Nieves, A. Frustrated nematic order in spherical geometries. Nat. Phys. 2011, 7, 391. [Google Scholar] [CrossRef] [Green Version]
- Kralj, S.; Rosso, R.; Virga, E.G. Curvature control of valence on nematic shells. Soft Matter 2011, 7, 670. [Google Scholar] [CrossRef]
- Napoli, G.; Vergori, L. Extrinsic Curvature Effects on Nematic Shells. Phys. Rev. Lett. 2012, 108, 207803. [Google Scholar] [CrossRef]
- Terentjev, E. Disclination loops, standing alone and around solid particles, in nematic liquid crystals. Phys. Rev. E 1995, 51, 1330. [Google Scholar] [CrossRef]
- Poulin, P.; Stark, H.; Lubensky, T.C.; Weitz, D.A. Novel Colloidal Interactions in Anisotropic Fluids. Science 1997, 275, 1770. [Google Scholar] [CrossRef] [Green Version]
- Lubensky, T.C.; Pettey, D.; Currier, N.; Stark, H. Topological defects and interactions in nematic emulsions. Phys. Rev. E 1998, 57, 610. [Google Scholar] [CrossRef] [Green Version]
- Stark, H. Physics of colloidal dispersions in nematic liquid crystals. Phys. Rep. 2001, 351, 387. [Google Scholar] [CrossRef]
- Fukuda, J.; Yokoyama, H. Director configuration and dynamics of a nematic liquid crystal around a two-dimensional spherical particle: Numerical analysis using adaptive grids. Eur. Phys. J. E 2001, 4, 389. [Google Scholar] [CrossRef]
- Muševič, I.; Škarabot, M.; Tkalec, U.; Ravnik, M.; Žumer, S. Two-Dimensional Nematic Colloidal Crystals Self-Assembled by Topological Defects. Science 2006, 313, 954. [Google Scholar] [CrossRef] [PubMed]
- Ognysta, U.; Nych, A.; Nazarenko, V.; Škarabot, M.; Muševič, I. Design of 2D Binary Colloidal Crystals in a Nematic Liquid Crystal. Langmuir 2009, 25, 12092. [Google Scholar] [CrossRef] [PubMed]
- Nych, A.; Ognysta, U.; Škarabot, M.; Ravnik, M.; Žumer, S.; Muševič, I. Assembly and control of 3D nematic dipolar colloidal crystals. Nat. Commun. 2013, 4, 1489. [Google Scholar] [CrossRef]
- Luo, Y.; Serra, F.; Beller, D.A.; Gharbi, M.A.; Li, N.; Yang, S.; Kamien, R.D.; Stebe, K.J. Around the corner: Colloidal assembly and wiring in groovy nematic cells. Phys. Rev. E 2016, 93, 032705. [Google Scholar] [CrossRef] [Green Version]
- Ravnik, M.; Škarabot, M.; Žumer, S.; Tkalec, U.; Poberaj, I.; Babič, D.; Osterman, N.; Muševič, I. Entangled Nematic Colloidal Dimers and Wires. Phys. Rev. Lett. 2007, 99, 247801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Čopar, S.; Žumer, S. Nematic Braids: Topological Invariants and Rewiring of Disclinations. Phys. Rev. Lett. 2011, 106, 177801. [Google Scholar] [CrossRef] [Green Version]
- Tkalec, U.; Ravnik, M.; Čopar, S.; Žumer, S.; Muševič, I. Reconfigurable Knots and Links in Chiral Nematic Colloids. Science 2011, 333, 62. [Google Scholar] [CrossRef] [Green Version]
- Araki, T.; Buscaglia, M.; Bellini, T.; Tanaka, H. Memory and topological frustration in nematic liquid crystals confined in porous materials. Nat. Mater. 2011, 10, 303. [Google Scholar] [CrossRef]
- Serra, F.; Vishnubhatla, K.C.; Buscaglia, M.; Cerbino, R.; Osellame, R.; Cerullo, G.; Bellini, T. Topological defects of nematic liquid crystals confined in porous networks. Soft Matter 2011, 7, 10945. [Google Scholar] [CrossRef]
- Čopar, S.; Clark, N.A.; Ravnik, M.; Žumer, S. Elementary building blocks of nematic disclination networks in densely packed 3D colloidal lattices. Soft Matter 2013, 9, 8203. [Google Scholar] [CrossRef]
- Lapointe, C.P.; Mason, T.G.; Smalyukh, I.I. Shape-Controlled Colloidal Interactions in Nematic Liquid Crystals. Science 2009, 326, 1083. [Google Scholar] [CrossRef] [Green Version]
- Dontabhaktuni, J.; Ravnik, M.; Žumer, S. Quasicrystalline tilings with nematic colloidal platelets. Proc. Natl. Acad. Sci. USA 2014, 111, 2464. [Google Scholar] [CrossRef] [Green Version]
- Nikkhou, M.; Škarabot, M.; Čopar, S.; Ravnik, M.; Žumer, S.; Muševič, I. Light-controlled topological charge in a nematic liquid crystal. Nat. Phys. 2015, 11, 183. [Google Scholar] [CrossRef]
- Mundoor, H.; Senyuk, B.; Smalyukh, I.I. Triclinic nematic colloidal crystals from competing elastic and electrostatic interactions. Science 2016, 352, 69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senyuk, B.; Liu, Q.; He, S.; Kamien, R.D.; Kusner, R.B.; Lubensky, T.C.; Smalyukh, I.I. Topological colloids. Nature 2013, 493, 200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martinez, A.; Ravnik, M.; Lucero, B.; Visvanathan, R.; Žumer, S.; Smalyukh, I.I. Mutually tangled colloidal knots and induced defect loops in nematic fields. Nat. Mater. 2014, 13, 258. [Google Scholar] [CrossRef]
- Ravnik, M.; Čopar, S.; Žumer, S. Particles with changeable topology in nematic colloids. J. Phys. Condens. Matter 2015, 27, 354111. [Google Scholar] [CrossRef]
- Yuan, Y.; Tasinkevych, M.; Smalyukh, I.I. Colloidal interactions and unusual crystallization versus de-mixing of elastic multipoles formed by gold mesoflowers. Nat. Commun. 2020, 11, 811. [Google Scholar] [CrossRef] [PubMed]
- Mertelj, A.; Lisjak, D.; Drofenik, M.; Čopič, M. Ferromagnetism in suspensions of magnetic platelets in liquid crystal. Nature 2013, 504, 237. [Google Scholar] [CrossRef]
- Ericksen, J.L. Anisotropic fluids. Arch. Ration. Mech. Anal. 1959, 4, 231. [Google Scholar] [CrossRef]
- Leslie, F. Theory of Flow Phenomena in Liquid Crystals. Adv. Liq. Cryst. 1979, 4, 1–81. [Google Scholar]
- Berreman, D.W. Liquid-crystal twist cell dynamics with backflow. J. Appl. Phys. 1975, 46, 3746. [Google Scholar] [CrossRef]
- Van Doorn, C.Z. Dynamic behavior of twisted nematic liquid-crystal layers in switched fields. J. Appl. Phys. 1975, 46, 3738. [Google Scholar] [CrossRef]
- Kramer, L.; Pesch, W. Convection Instabilities in Nematic Liquid Crystals. Annu. Rev. Fluid Mech. 1995, 27, 515. [Google Scholar] [CrossRef]
- Éber, N.; Salamon, P.; Buka, A. Electrically induced patterns in nematics and how to avoid them. Liq. Cryst. Rev. 2016, 4, 101. [Google Scholar] [CrossRef]
- Doostmohammadi, A.; Shendruk, T.N.; Thijssen, K.; Yeomans, J.M. Onset of meso-scale turbulence in active nematics. Nat. Commun. 2017, 8, 15326. [Google Scholar] [CrossRef]
- Sengupta, A. Topological microfluidics: Present and prospects. Liq. Cryst. Today 2015, 24, 70. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. Physics of Liquid Crystals; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Schiele, K.; Trimper, S. On the Elastic Constants of a Nematic Liquid Crystal. Phys. Stat. Sol. 1983, 118, 267. [Google Scholar] [CrossRef]
- Ravnik, M.; Žumer, S. Landau–de Gennes modelling of nematic liquid crystal colloids. Liq. Cryst. 2009, 36, 1201. [Google Scholar] [CrossRef]
- Sussman, D.M.; Beller, D.A. Fast, Scalable, and Interactive Software for Landau-de Gennes Numerical Modeling of Nematic Topological Defects. Front. Phys. 2019, 7, 273. [Google Scholar] [CrossRef] [Green Version]
- Davis, T.A.; Gartland, E.C. Finite Element Analysis of the Landau–de Gennes Minimization Problem for Liquid Crystals. SIAM J. Numer. Anal. 1998, 35, 336. [Google Scholar] [CrossRef]
- Everts, J.C.; Ravnik, M. Ionically Charged Topological Defects in Nematic Fluids. Phys. Rev. X 2021, 11, 011054. [Google Scholar]
- Nitschke, I.; Reuther, S.; Voigt, A. Liquid crystals on deformable surfaces. Proc. R. Soc. A 2020, 476, 20200313. [Google Scholar] [CrossRef]
- Majumdar, A.; Zarnescu, A. Landau–De Gennes Theory of Nematic Liquid Crystals: The Oseen–Frank Limit and Beyond. Arch. Ration. Mech. Anal. 2010, 196, 227. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A. Equilibrium order parameters of nematic liquid crystals in the Landau-de Gennes theory. Eur. J. Appl. Math. 2010, 21, 181–203. [Google Scholar] [CrossRef] [Green Version]
- Beris, A.N.; Edwards, B.J. Thermodynamics of Flowing Systems with Internal Microstructure; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Qian, T.; Sheng, P. Generalized hydrodynamic equations for nematic liquid crystals. Phys. Rev. E 1998, 58, 7475. [Google Scholar] [CrossRef] [Green Version]
- Sonnet, A.M.; Maffettone, P.L.; Virga, E.G. Continuum theory for nematic liquid crystals with tensorial order. J. Non-Newton. Fluid. 2004, 119, 51. [Google Scholar] [CrossRef]
- Sonnet, A.M. Dissipative Ordered Fluids: Theories for Liquid Crystals; Springer: New York, NY, USA, 2012. [Google Scholar]
- Denniston, C.; Orlandini, E.; Yeomans, J. Lattice {Boltzmann} simulations of liquid crystal hydrodynamics. Phys. Rev. E 2001, 63, 56702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kos, v.; Aplinc, J.; Mur, U.; Ravnik, M. Mesoscopic Approach to Nematic Fluids in Flowing Matter; Toschi, F., Sega, M., Eds.; Springer Open: Berlin, Germany, 2019. [Google Scholar]
- Svenšek, D.; Žumer, S. Hydrodynamics of pair-annihilating disclination lines in nematic liquid crystals. Phys. Rev. E 2002, 66, 21712. [Google Scholar] [CrossRef] [Green Version]
- Tóth, G.; Denniston, C.; Yeomans, J.M. Hydrodynamics of Topological Defects in Nematic Liquid Crystals. Phys. Rev. Lett. 2002, 88, 105504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sengupta, A.; Tkalec, U.; Ravnik, M.; Yeomans, J.; Bahr, C.; Herminghaus, S. Liquid Crystal Microfluidics for Tunable Flow Shaping. Phys. Rev. Lett. 2013, 110, 48303. [Google Scholar] [CrossRef] [PubMed]
- Denniston, C.; Marenduzzo, D.; Orlandini, E.; Yeomans, J. Lattice Boltzmann algorithm for three-dimensional liquid-crystal hydrodynamics. Phil. Trans. R. Soc. A 2004, 362, 1745. [Google Scholar] [CrossRef]
- Cates, M.E.; Stratford, K.; Adhikari, R.; Stansell, P.; Desplat, J.C.; Pagonabarraga, I.; Wagner, A.J. Simulating colloid hydrodynamics with lattice Boltzmann methods. J. Phys. Condens. Matter 2004, 16, S3903. [Google Scholar] [CrossRef]
- James, R.; Willman, E.; FernandezFernandez, F.; Day, S. Finite-element modeling of liquid-crystal hydrodynamics with a variable degree of order. IEEE Trans. Electron. Devices 2006, 53, 1575. [Google Scholar] [CrossRef]
- Mandal, S.; Mazza, M.G. Multiparticle collision dynamics for tensorial nematodynamics. Phys. Rev. E 2019, 99, 89. [Google Scholar] [CrossRef] [Green Version]
- Shendruk, T.N.; Yeomans, J.M. Multi-particle collision dynamics algorithm for nematic fluids. Soft Matter 2015, 11, 5101. [Google Scholar] [CrossRef] [Green Version]
- Kléman, M.; Michel, L.; Toulouse, G. Classification of topologically stable defects in ordered media. J. Phys. Lett. Paris 1977, 38, 195. [Google Scholar] [CrossRef] [Green Version]
- Kleman, M. Defects in liquid crystals. Rep. Prog. Phys. 1989, 52, 555. [Google Scholar] [CrossRef]
- Ramaswamy, S.; Nityananda, R.; Raghunathan, V.A.; Prost, J. Power-Law Forces between Particles in a Nematic. Mol. Cryst. Liq. Crys. A 1996, 288, 175. [Google Scholar] [CrossRef]
- Lavrentovich, O.D. Topological defects in dispersed liquid crystals, or words and worlds around liquid crystal drops. Liq. Cryst. 1998, 24, 117. [Google Scholar] [CrossRef]
- Seč, D.; Čopar, S.; Žumer, S. Topological zoo of free-standing knots in confined chiral nematic fluids. Nat. Commun. 2014, 5, 3057. [Google Scholar] [CrossRef]
- Darmon, A.; Benzaquen, M.; Čopar, S.; Dauchot, O.; Lopez-Leon, T. Topological defects in cholesteric liquid crystal shells. Soft Matter 2016, 12, 9280. [Google Scholar] [CrossRef] [Green Version]
- Posnjak, G.; Čopar, S.; Muševič, I. Hidden topological constellations and polyvalent charges in chiral nematic droplets. Nat. Commun. 2017, 8, 14594. [Google Scholar] [CrossRef]
- Pollard, J.; Posnjak, G.; Čopar, S.; Muševič, I.; Alexander, G.P. Point Defects, Topological Chirality, and Singularity Theory in Cholesteric Liquid-Crystal Droplets. Phys. Rev. X 2019, 9, 1442. [Google Scholar] [CrossRef] [Green Version]
- Vitelli, V.; Nelson, D. Nematic textures in spherical shells. Phys. Rev. E 2006, 74, 021711. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Leon, T.; Fernandez-Nieves, A. Drops and shells of liquid crystal. Colloid Polym. Sci. 2011, 289, 345. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, A.; Zhang, R.; Armas-Perez, J.C.; Martínez-González, J.A.; Rahimi, M.; Sadati, M.; de Pablo, J.J. Mesoscale structure of chiral nematic shells. Soft Matter 2016, 12, 8983. [Google Scholar] [CrossRef] [Green Version]
- Urbanski, M.; Reyes, C.G.; Noh, J.; Sharma, A.; Geng, Y.; Jampani, V.S.R.; Lagerwall, J.P.F. Liquid crystals in micron-scale droplets, shells and fibers. J. Phys. Condens. Matter 2017, 29, 133003. [Google Scholar] [CrossRef] [Green Version]
- Tran, L.; Lavrentovich, M.O.; Durey, G.; Darmon, A.; Haase, M.F.; Li, N.; Lee, D.; Stebe, K.J.; Kamien, R.D.; Lopez-Leon, T. Change in Stripes for Cholesteric Shells via Anchoring in Moderation. Phys. Rev. X 2017, 7, 167. [Google Scholar] [CrossRef] [Green Version]
- Janich, K. Topological properties of ordinary nematics in 3-space. Acta Appl. Math. 1987, 8, 65. [Google Scholar] [CrossRef]
- Alexander, G.P.; ge Chen, B.G.; Matsumoto, E.A.; Kamien, R.D. Colloquium: Disclination loops, point defects, and all that in nematic liquid crystals. Rev. Mod. Phys. 2012, 84, 497. [Google Scholar] [CrossRef] [Green Version]
- Čopar, S. Topology and geometry of nematic braids. Phys. Rep. 2014, 538, 1. [Google Scholar] [CrossRef]
- Machon, T.; Alexander, G.P. Global defect topology in nematic liquid crystals. Proc. R. Soc. A 2016, 472, 20160265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Čopar, S.; Žumer, S. Quaternions and hybrid nematic disclinations. Proc. R. Soc. A 2013, 469, 20130204. [Google Scholar] [CrossRef] [Green Version]
- Binysh, J.; Kos, Ž.; Čopar, S.; Ravnik, M.; Alexander, G.P. Three-Dimensional Active Defect Loops. Phys. Rev. Lett. 2020, 124, 257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beller, D.A.; Machon, T.; Čopar, S.; Sussman, D.M.; Alexander, G.P.; Kamien, R.D.; Mosna, R.A. Geometry of the Cholesteric Phase. Phys. Rev. X 2014, 4, 031050. [Google Scholar] [CrossRef] [Green Version]
- Poenaru, V.; Toulouse, G. The crossing of defects in ordered media and the topology of 3-manifolds. J. Phys. 1977, 38, 887. [Google Scholar] [CrossRef] [Green Version]
- Čopar, S.; Tkalec, U.; Muševič, I.; Žumer, S. Knot theory realizations in nematic colloids. Proc. Natl. Acad. Sci. USA 2015, 112, 1675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Machon, T. The topology of knots and links in nematics. Liq. Cryst. Today 2019, 28, 58. [Google Scholar] [CrossRef] [Green Version]
- Araki, T.; Serra, F.; Tanaka, H. Defect science and engineering of liquid crystals under geometrical frustration. Soft Matter 2013, 9, 8107. [Google Scholar] [CrossRef] [Green Version]
- Sentker, K.; Yildirim, A.; Lippmann, M.; Zantop, A.W.; Bertram, F.; Hofmann, T.; Seeck, O.H.; Kityk, A.V.; Mazza, M.G.; Schönhals, A.; et al. Self-assembly of liquid crystals in nanoporous solids for adaptive photonic metamaterials. Nanoscale 2019, 11, 23304. [Google Scholar] [CrossRef]
- Yi, Y.; Lombardo, G.; Ashby, N.; Barberi, R.; Maclennan, J.E.; Clark, N.A. Topographic-pattern-induced homeotropic alignment of liquid crystals. Phys. Rev. E 2009, 79, 041701. [Google Scholar] [CrossRef]
- Carlton, R.J.; Hunter, J.T.; Miller, D.S.; Abbasi, R.; Mushenheim, P.C.; Tan, L.N.; Abbott, N.L. Chemical and biological sensing using liquid crystals. Liq. Cryst. Rev. 2013, 1, 29. [Google Scholar] [CrossRef] [PubMed]
- Tartan, C.C.; O’Neill, J.J.S.; Salter, P.S.; Aplinc, J.; Booth, M.J.; Ravnik, M.; Morris, S.M.; Elston, S.J. Read on Demand Images in Laser-Written Polymerizable Liquid Crystal Devices. Adv. Opt. Mater. 2018, 6, 1800515. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.S.; Čopar, S.; Tkalec, U.; Yoon, D.K. Mosaics of topological defects in micropatterned liquid crystal textures. Sci. Adv. 2018, 4, eaau8064. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Serra, F. Tunable Dynamic Topological Defect Pattern Formation in Nematic Liquid Crystals. Adv. Opt. Mater. 2020, 8, 1900991. [Google Scholar] [CrossRef]
- Muševič, I. Nematic colloids, topology and photonics. Phil. Trans. R. Soc. A 2013, 371, 20120266. [Google Scholar] [CrossRef] [Green Version]
- Tkalec, U.; Muševič, I. Topology of nematic liquid crystal colloids confined to two dimensions. Soft Matter 2013, 9, 8140. [Google Scholar] [CrossRef]
- Ognysta, U.; Nych, A.; Nazarenko, V.; Muševič, I.; Škarabot, M.; Ravnik, M.; Žumer, S.; Poberaj, I.; Babič, D. 2D Interactions and Binary Crystals of Dipolar and Quadrupolar Nematic Colloids. Phys. Rev. Lett. 2008, 100, 217803. [Google Scholar] [CrossRef]
- Škarabot, M.; Ravnik, M.; Žumer, S.; Tkalec, U.; Poberaj, I.; Babič, D.; Osterman, N.; Muševič, I. Two-dimensional dipolar nematic colloidal crystals. Phys. Rev. E 2007, 76, 51406. [Google Scholar] [CrossRef]
- Škarabot, M.; Ravnik, M.; Žumer, S.; Tkalec, U.; Poberaj, I.; Babič, D.; Osterman, N.; Muševič, I. Interactions of quadrupolar nematic colloids. Phys. Rev. E 2008, 77, 31705. [Google Scholar] [CrossRef] [PubMed]
- Bouligand, Y. Recherches sur les textures des états mésomorphes: Dislocations coins et signification des cloisons de Grandjean-Cano dans les cholestériques. J. Phys. Fr. 1974, 35, 959. [Google Scholar] [CrossRef]
- Tai, J.S.B.; Smalyukh, I.I. Three-dimensional crystals of adaptive knots. Science 2019, 365, 1449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jampani, V.S.R.; Škarabot, M.; Ravnik, M.; Čopar, S.; Žumer, S.; Muševič, I. Colloidal entanglement in highly twisted chiral nematic colloids: Twisted loops, Hopf links, and trefoil knots. Phys. Rev. E 2011, 84, 031703. [Google Scholar] [CrossRef]
- Rasi, M.M.; Pujala, R.K.; Dhara, S. Colloidal analogues of polymer chains, ribbons and 2D crystals employing orientations and interactions of nano-rods dispersed in a nematic liquid crystal. Sci. Rep. 2019, 9, 401001. [Google Scholar]
- Lapointe, C.P.; Hopkins, S.; Mason, T.G.; Smalyukh, I.I. Electrically Driven Multiaxis Rotational Dynamics of Colloidal Platelets in Nematic Liquid Crystals. Phys. Rev. Lett. 2010, 105, 178301. [Google Scholar] [CrossRef] [PubMed]
- Martinez, A.; Hermosillo, L.; Tasinkevych, M.; Smalyukh, I.I. Linked topological colloids in a nematic host. Proc. Natl. Acad. Sci. USA 2015, 112, 4546. [Google Scholar] [CrossRef] [Green Version]
- Lapointe, C.P.; Mayoral, K.; Mason, T.G. Star colloids in nematic liquid crystals. Soft Matter 2013, 9, 7843. [Google Scholar] [CrossRef] [Green Version]
- Senyuk, B.; Liu, Q.; Bililign, E.; Nystrom, P.D.; Smalyukh, I.I. Geometry-guided colloidal interactions and self-tiling of elastic dipoles formed by truncated pyramid particles in liquid crystals. Phys. Rev. E 2015, 91, 040501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senyuk, B.; Pandey, M.B.; Liu, Q.; Tasinkevych, M.; Smalyukh, I.I. Colloidal spirals in nematic liquid crystals. Soft Matter 2015, 11, 8758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sahu, D.K.; Anjali, T.G.; Basavaraj, M.G.; Aplinc, J.; Čopar, S.; Dhara, S. Orientation, elastic interaction and magnetic response of asymmetric colloids in a nematic liquid crystal. Sci. Rep. 2019, 9, 1557. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Martinez, A.; Senyuk, B.; Tasinkevych, M.; Smalyukh, I.I. Chiral liquid crystal colloids. Nat. Mater. 2017, 17, 71. [Google Scholar] [CrossRef] [Green Version]
- Hashemi, S.M.; Jagodič, U.; Mozaffari, M.R.; Ejtehadi, M.R.; Muševič, I.; Ravnik, M. Fractal nematic colloids. Nat. Commun. 2017, 8, 14026. [Google Scholar] [CrossRef]
- Zhao, Q.; Kang, L.; Du, B.; Li, B.; Zhou, J.; Tang, H.; Liang, X.; Zhang, B. Electrically tunable negative permeability metamaterials based on nematic liquid crystals. Appl. Phys. Lett. 2007, 90, 011112. [Google Scholar] [CrossRef]
- Aplinc, J.; Pusovnik, A.; Ravnik, M. Designed self-assembly of metamaterial split-ring colloidal particles in nematic liquid crystals. Soft Matter 2019, 15, 5585. [Google Scholar] [CrossRef]
- Liu, M.; Fan, K.; Padilla, W.; Powell, D.A.; Zhang, X.; Shadrivov, I.V. Tunable Meta-Liquid Crystals. Adv. Mater. 2016, 28, 1553. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Fonseca, I.; Ravnik, M.; Slastikov, V.; Zannoni, C.; Zarnescu, A. Topics in the mathematical design of materials. Phil. Trans. R. Soc. A 2021, 379, 20200108. [Google Scholar] [CrossRef] [PubMed]
- Gharbi, M.A.; Cavallaro, M.; Wu, G.; Beller, D.A.; Kamien, R.D.; Yang, S.; Stebe, K.J. Microbullet assembly: Interactions of oriented dipoles in confined nematic liquid crystal. Liq. Cryst. 2013, 40, 1619. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, K.A.; Sano, M. Universal Fluctuations of Growing Interfaces: Evidence in Turbulent Liquid Crystals. Phys. Rev. Lett. 2010, 104, 230601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiese, O.; Marenduzzo, D.; Henrich, O. Microfluidic flow of cholesteric liquid crystals. Soft Matter 2016, 12, 9223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dogic, Z.; Fraden, S. Ordered phases of filamentous viruses. Curr. Opin. Colloid Interface Sci. 2006, 11, 47. [Google Scholar] [CrossRef]
- Aplinc, J.; Štimulak, M.; Čopar, S.; Ravnik, M. Nematic liquid crystal gyroids as photonic crystals. Liq. Cryst. 2016, 43, 2320. [Google Scholar] [CrossRef]
- Giomi, L.; Kos, Ž.; Ravnik, M.; Sengupta, A. Cross-talk between topological defects in different fields revealed by nematic microfluidics. Proc. Natl. Acad. Sci. USA 2017, 114, E5771. [Google Scholar] [CrossRef] [Green Version]
- Araki, T. Dynamic Coupling between a multistable Defect Pattern and Flow in Nematic Liquid Crystals Confined in a Porous Medium. Phys. Rev. Lett. 2012, 109, 257801. [Google Scholar] [CrossRef] [Green Version]
- Kos, Ž.; Ravnik, M.; Žumer, S. Nematodynamics and structures in junctions of cylindrical micropores. Liq. Cryst. 2017, 44, 2161–2171. [Google Scholar] [CrossRef]
- Sengupta, A.; Pieper, C.; Enderlein, J.; Bahr, C.; Herminghaus, S. Flow of a nematogen past a cylindrical micro-pillar. Soft Matter 2013, 9, 1937. [Google Scholar] [CrossRef]
- Luo, Y.; Beller, D.A.; Boniello, G.; Serra, F.; Stebe, K.J. Tunable colloid trajectories in nematic liquid crystals near wavy walls. Nat. Commun. 2018, 9, 1253751. [Google Scholar] [CrossRef] [Green Version]
- Čopar, S.; Kos, Ž.; Emeršič, T.; Tkalec, U. Microfluidic control over topological states in channel-confined nematic flows. Nat. Commun. 2020, 11, 977. [Google Scholar] [CrossRef]
- Smalyukh, I.I. Liquid Crystal Colloids. Annu. Rev. Condens. Matter Phys. 2018, 9, 207. [Google Scholar] [CrossRef]
- Lisjak, D.; Mertelj, A. Anisotropic magnetic nanoparticles: A review of their properties, syntheses and potential applications. Prog. Mater. Sci. 2018, 95, 286. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čopar, S.; Ravnik, M.; Žumer, S. Introduction to Colloidal and Microfluidic Nematic Microstructures. Crystals 2021, 11, 956. https://doi.org/10.3390/cryst11080956
Čopar S, Ravnik M, Žumer S. Introduction to Colloidal and Microfluidic Nematic Microstructures. Crystals. 2021; 11(8):956. https://doi.org/10.3390/cryst11080956
Chicago/Turabian StyleČopar, Simon, Miha Ravnik, and Slobodan Žumer. 2021. "Introduction to Colloidal and Microfluidic Nematic Microstructures" Crystals 11, no. 8: 956. https://doi.org/10.3390/cryst11080956





