3D Puzzle in Cube Pattern for Anisotropic/Isotropic Mechanical Control of Structure Fabricated by Metal Additive Manufacturing
Abstract
:1. Introduction
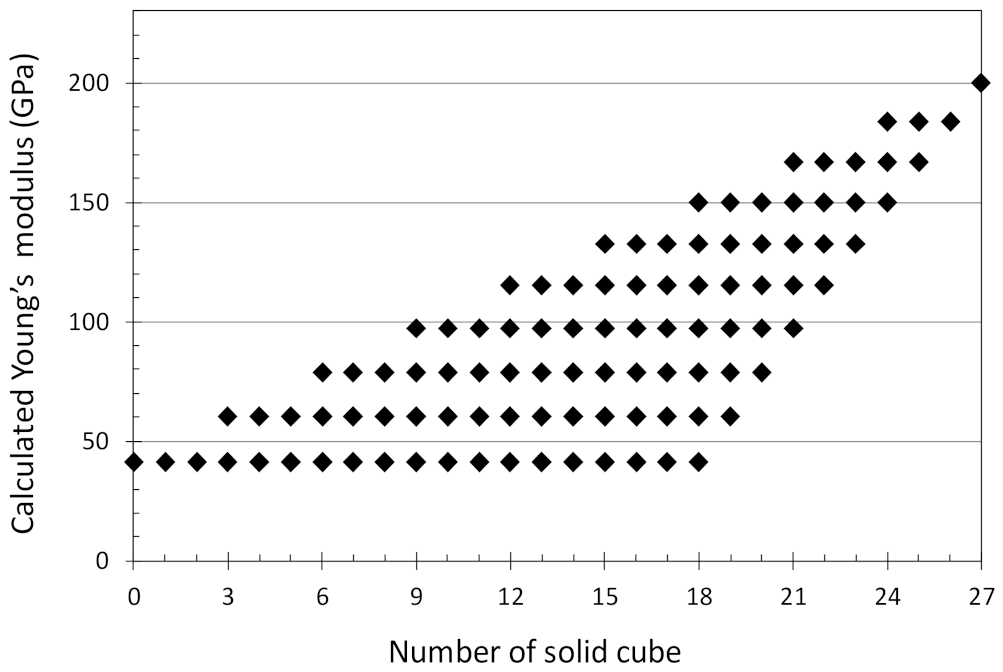
2. Mathematical Model
3. Materials and Methods
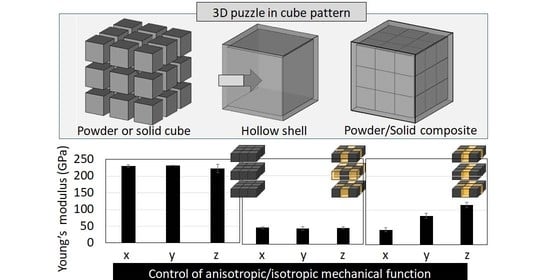
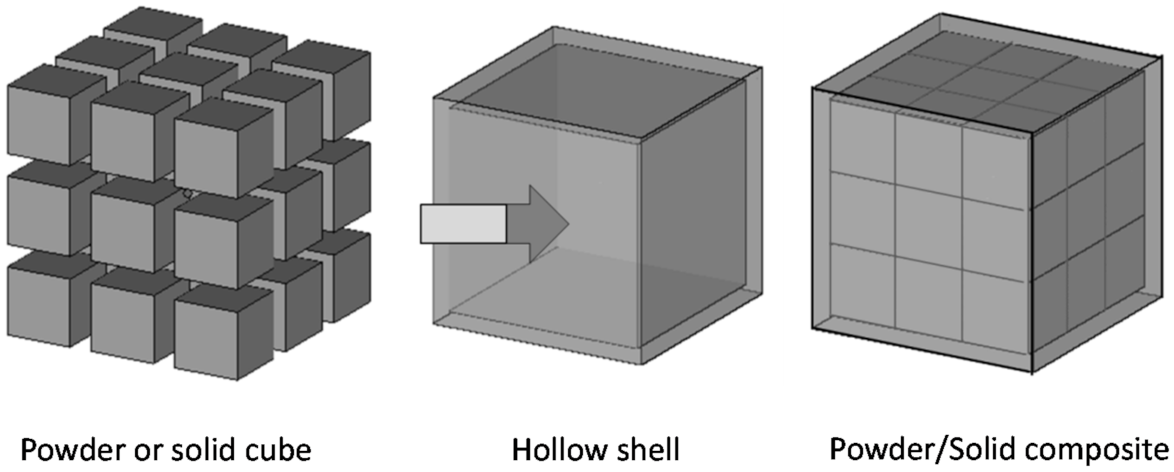
3.1. Designing the Powder/Solid Composite Structure
3.2. Mechanical Test
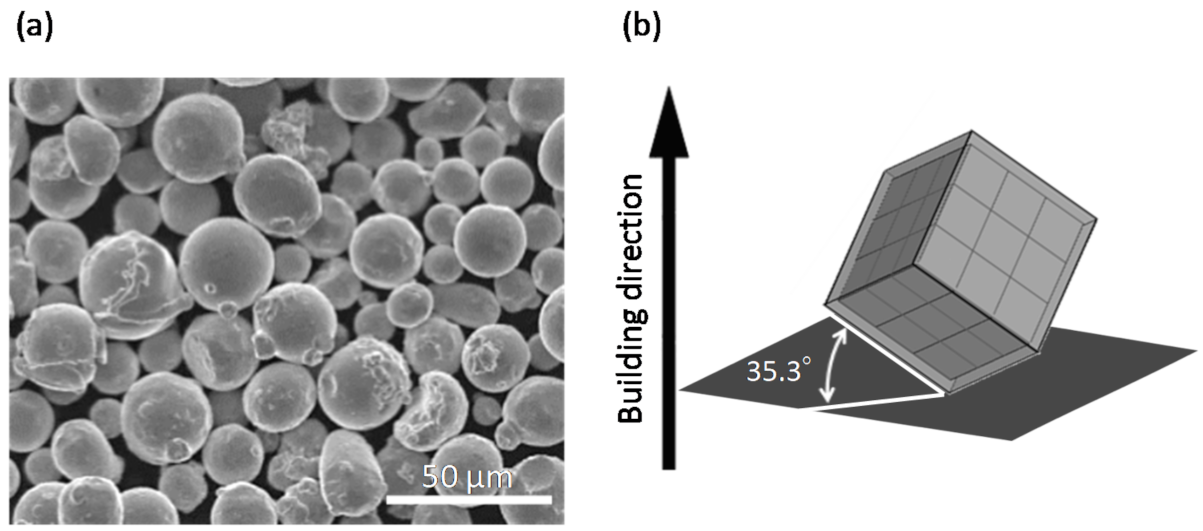
3.3. Crystallographic Texture Analysis
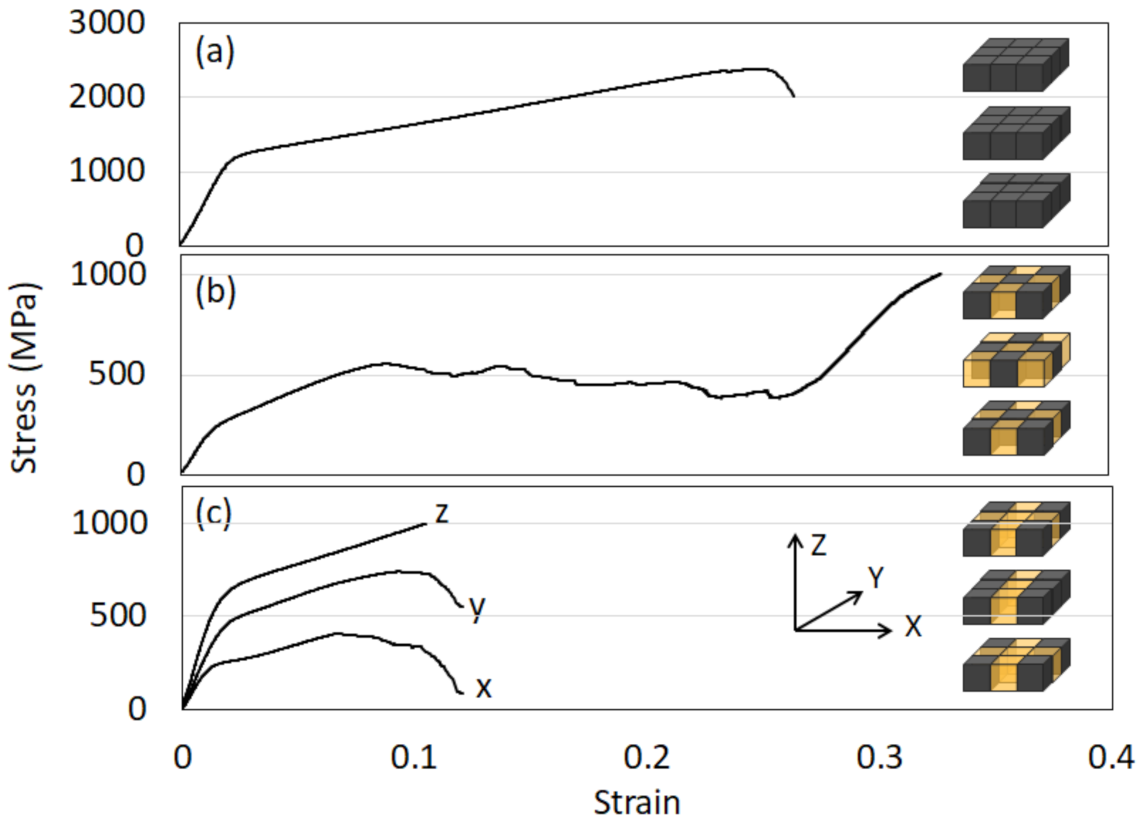
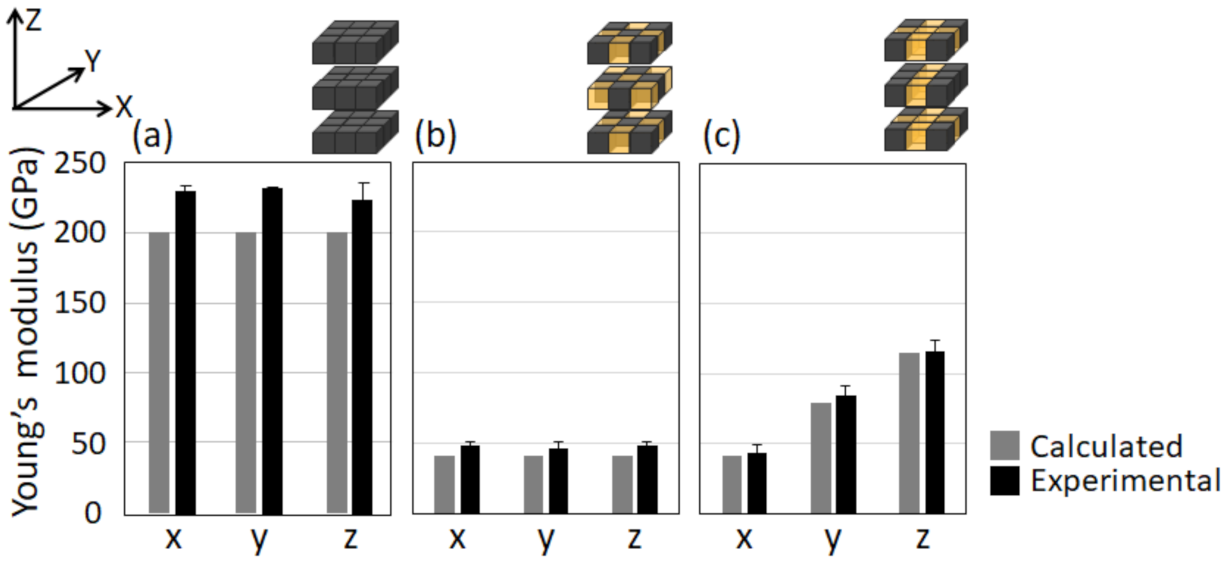
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Zhang, Z.; Ritchie, R.O. Structural orientation and anisotropy in biological materials: Functional designs and mechanics. Adv. Funct. Mater. 2020, 30, 1908121. [Google Scholar] [CrossRef]
- Nakano, T.; Kaibara, K.; Tabata, Y.; Nagata, N.; Enomoto, S.; Marukawa, E.; Umakoshi, Y. Unique alignment and texture of biological apatite crystallites in typical calcified tissues analyzed by micro-beam X-ray diffractometer system. Bone 2002, 31, 479–487. [Google Scholar] [CrossRef]
- Nakano, T.; Kaibara, K.; Ishimoto, T.; Tabata, Y.; Umakoshi, Y. Biological apatite (BAp) crystallographic orientation and texture as a new index for assessing the microstructure and function of bone regenerated by tissue engineering. Bone 2012, 51, 741–747. [Google Scholar] [CrossRef]
- Tanaka, M.; Matsugaki, A.; Ishimoto, T.; Nakano, T. Evaluation of crystallographic orientation of biological apatite at vertebral cortical bone in ovariectomized cynomolgus monkey treated with minodronic acid and alendronate. J. Bone Miner. Metab. 2016, 34, 234–241. [Google Scholar] [CrossRef]
- Ding, H.; Chen, W.; Zhang, L. Solid Mechanics and Its Applications, Elasticity of Transversely Isotropic Material; Springer: Berlin/Heidelberg, Germany, 2006; pp. 29–67. [Google Scholar]
- Maute, K.; Allen, M. Conceptual design of aeroelastic structures by topology optimization. Struct. Multidiscip. Opt. 2004, 27, 27–42. [Google Scholar] [CrossRef]
- Li, C.; Granger, C.; Schutte, H.D., Jr.; Biggers, S.B., Jr.; Kennedy, J.M.; Latour, R.A., Jr. Progressive failure analysis of laminated composite femoral prostheses for total hip arthroplasty. Biomaterials 2002, 23, 4249–4262. [Google Scholar] [CrossRef]
- Cheal, E.; Spector, M.; Hayes, W. Role of loads and prosthesis material properties on the mechanics of the proximal femur after total hip arthroplasty. J. Orthop. Res. 1992, 10, 405–422. [Google Scholar] [CrossRef]
- Noyama, Y.; Miura, T.; Ishimoto, T.; Itaya, T.; Niinomi, M.; Nakano, T. Bone loss and reduced bone quality of the human femur after total hip arthroplasty under stress-shielding effects by titanium-based implant. Mater. Trans. 2012, 53, 565–570. [Google Scholar] [CrossRef] [Green Version]
- Ishimoto, T.; Yamada, K.; Takahashi, H.; Takahata, M.; Ito, M.; Hanawa, T.; Nakano, T. Trabecular health of vertebrae based on anisotropy in trabecular architecture and collagen/apatite micro-arrangement after implantation of intervertebral fusion cages in the sheep spine. Bone 2018, 108, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Noyama, Y.; Nakano, T.; Ishimoto, T.; Sakai, T.; Yoshikawa, H. Design and optimization of the oriented groove on the hip implant surface to promote bone microstructure integrity. Bone 2013, 52, 659–667. [Google Scholar] [CrossRef] [PubMed]
- Loth, F.L.; Liebensteiner, M.C.; Giesinger, J.M.; Giesinger, K.; Bliem, H.R.; Holzner, B. What makes patients aware of their artificial knee joint? BMC Musculoskelet. Disord. 2018, 19, 5. [Google Scholar] [CrossRef] [Green Version]
- Soro, N.; Saintier, N.; Merzeau, J.; Veidt, M.; Dargusch, M.S. Quasi-static and fatigue properties of graded Ti–6Al–4V lattices produced by Laser Powder Bed Fusion (LPBF). Addit. Manuf. 2021, 37, 101653. [Google Scholar]
- Wang, P.; Li, X.; Jiang, Y.; Ling, M.; Nai, S.; Ding, J.; Wei, J. Electron beam melted heterogeneously porous microlattices for metallic bone applications: Design and investigations of boundary and edge effects. Addit. Manuf. 2020, 36, 101566. [Google Scholar] [CrossRef]
- Yuan, L.; Ding, S.; Wen, C. Additive manufacturing technology for porous metal implant applications and triple minimal surface structures: A review. Bioact. Mater. 2019, 4, 56–70. [Google Scholar] [CrossRef]
- Bobbert, F.S.L.; Lietaert, K.; Eftekhari, A.A.; Pouran, B.; Ahmadi, S.M.; Weinans, H.; Zadpoor, A.A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Li, X.; Luo, S.; Ling, M.; Nai, S.; Ding, J.; Wei, J. Additively manufactured heterogeneously porous metallic bone with biostructural functions and bone-like mechanical properties. J. Mater. Sci. Technol. 2021, 62, 173–179. [Google Scholar] [CrossRef]
- Durand-Hill, M.; Henckel, J.; Laura, A.D.; Hart, A.J. Can custom 3D printed implants successfully reconstruct massive acetabular defects? A 3D-CT assessment. J. Orthop. Res. 2020, 38, 2640–2648. [Google Scholar] [CrossRef] [PubMed]
- Sugino, A.; Ohtsuki, C.; Tsuru, K.; Hayakawa, S.; Nakano, T.; Okazaki, Y.; Osaka, A. Effect of spatial design and thermal oxidation on apatite formation on Ti-15Zr-4Ta-4Nb alloy. Acta Biomater. 2008, 5, 298–304. [Google Scholar] [CrossRef] [PubMed]
- Matsugaki, A.; Aramoto, G.; Nakano, T. The alignment of MC3T3-E1 osteoblasts on steps of slip traces introduced by dislocation motion. Biomaterials 2012, 33, 7327–7335. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, Y.; Matsugaki, A.; Kawahara, K.; Ninomiya, T.; Sawada, H.; Nakano, T. Unique arrangement of bone matrix orthogonal to osteoblast alignment controlled by Tspan11-mediated focal adhesion assembly. Biomaterials 2019, 209, 103–110. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Sin, W.J.; Nai, M.L.S.; Wei, J. Effects of processing parameters on surface roughness of additive manufactured Ti-6Al-4V via electron beam melting. Materials 2017, 10, 1121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsugaki, A.; Aramoto, G.; Ninomiya, T.; Sawada, H.; Hata, S.; Nakano, T. Abnormal arrangement of a collagen/apatite extracellular matrix orthogonal to osteoblast alignment is constructed by a nanoscale periodic surface structure. Biomaterials 2015, 37, 134–143. [Google Scholar] [CrossRef] [PubMed]
- Reuss, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. J. Appl. Math. Mechan. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die beziehung zwischen den beiden elasticitätsconstanten isotroper Körper. Annalen. Physik. 1889, 27, 573–587. [Google Scholar] [CrossRef] [Green Version]
- Radlof, W.; Benz, C.; Sander, M. Numerical and experimental investigations of additively manufactured lattice structures under quasi-static compression loading. Mat. Des. Proc. Comm. 2021, 3, e164. [Google Scholar] [CrossRef] [Green Version]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of compressive properties of SLM-fabricated multi-layer lattice structures by experimental test and μ-CT-based finite element analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P. Ti–6Al–4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J. Mech. Behav. Biomed. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soro, N.; Saintier, N.; Attar, H.; Dargusch, M.S. Surface and morphological modification of selectively laser melted titanium lattices using a chemical post treatment. Surf. Coat. Technol. 2020, 393, 125794. [Google Scholar] [CrossRef]
- Li, X.; Tan, Y.H.; Wang, P.; Su, X.; Jean, H.; Herng, T.S.; Ding, J. Metallic microlattice and epoxy interpenetrating phase composites: Experimental and simulation studies on superior mechanical properties and their mechanisms. Compos. Part A Appl. Sci. Manuf. 2020, 135, 105934. [Google Scholar] [CrossRef]
- Ikeo, N.; Ishimoto, T.; Nakano, T. Novel powder/solid composites possessing low Young’s modulus and tunable energy absorption capacity, fabricated by electron beam melting, for biomedical applications. J. Alloys Compd. 2015, 639, 336–340. [Google Scholar] [CrossRef] [Green Version]
- Ikeo, N.; Ishimoto, T.; Hiramoto, N.; Fukuda, H.; Ogisu, H.; Araki, Y.; Nakano, T. Solid/powder clad Ti-6Al-4V alloy with low Young’s modulus and high toughness fabricated by electron beam melting. Mater. Trans. 2015, 56, 755–758. [Google Scholar] [CrossRef] [Green Version]
- Abd-elrhman, Y.; Gepreel, M.A.H.; Abdel-Moniem, A.; Kobayashi, S. Compatibility assessment of new V-free low-cost Ti–4.7 Mo–4.5 Fe alloy for some biomedical applications. Mater. Des. 2016, 97, 445–453. [Google Scholar] [CrossRef]
- Akita, M.; Uematsu, Y.; Kakiuchi, T.; Nakajima, M.; Bai, Y.; Tamada, K. Fatigue behavior of bulk β-type titanium alloy Ti–15Mo–5Zr–3Al annealed in high temperature nitrogen gas. Mater. Sci. Eng. A 2015, 627, 351–359. [Google Scholar] [CrossRef]
- Ishimoto, T.; Hagihara, K.; Hisamoto, K.; Sun, S.-H.; Nakano, T. Crystallographic texture control of beta-type Ti-15Mo-5Zr-3Al alloy by selective laser melting for the development of novel implants with a biocompatible low Young’s modulus. Scr. Mater. 2017, 132, 34–38. [Google Scholar] [CrossRef]
- Todai, M.; Nakano, T.; Liu, T.; Yasuda, H.Y.; Hagihara, K.; Cho, K.; Ueda, M.; Takayama, M. Effect of building direction on the microstructure and tensile properties of Ti-48Al-2Cr-2Nb alloy additively manufactured by electron beam melting. Addit. Manuf. 2017, 13, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Hagihara, K.; Ishimoto, T.; Suzuki, M.; Ozasa, R.; Matsugaki, A.; Wang, P.; Nakano, T. Factor which governs the feature of texture developed during additive manufacturing; clarified from the study on hexagonal C40-NbSi2. Scr. Mater. 2021, 203, 114111. [Google Scholar] [CrossRef]
- Sun, S.-H.; Hagihara, K.; Nakano, T. Effect of scanning strategy on texture formation in Ni-25 at.%Mo alloys fabricated by selective laser melting. Mater. Des. 2017, 140, 307–316. [Google Scholar] [CrossRef]
- Ikeo, N.; Ishimoto, T.; Serizawa, A.; Nakano, T. Control of mechanical properties of three-dimensional Ti-6Al-4V products fabricated by electron beam melting with unidirectional elongated pores. Metal. Mater. Trans. A 2013, 45, 4293–4301. [Google Scholar] [CrossRef]
- Nakano, T.; Kuramoto, K.; Ishimoto, T.; Ikeo, N.; Fukuda, H.; Noyama, Y. Shock absorbing structure and method of manufacturing same. PCT/JP2010/067146 (Japan: 4802277 (2011.8.12), China: ZL 2010 8 0032610.X (2014.5.7), Singapore: 175882 (2013.6.28)).
- Nakano, T.; Ishimoto, T. Powder-based additive manufacturing for development of tailor-made implants for orthopedic applications. Kona 2015, 32, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Yánez, A.; Cuadrado, A.; Martel, O.; Afonso, H.; Monopoli, D. Gyroid porous titanium structures: A versatile solution to be used as scaffolds in bone defect reconstruction. Mater. Des. 2018, 140, 21–29. [Google Scholar] [CrossRef]
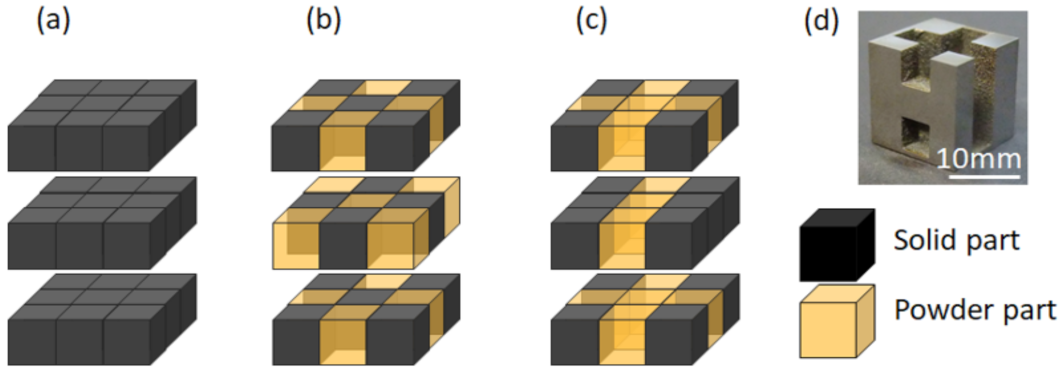

| Element | Co | Cr | Mo | Si | Mn | Fe | C | Ni |
|---|---|---|---|---|---|---|---|---|
| Composition | 60–65 | 26–30 | 5–7 | <1.0 | <1.0 | <0.75 | <0.16 | <0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikeo, N.; Fukuda, H.; Matsugaki, A.; Inoue, T.; Serizawa, A.; Matsuzaka, T.; Ishimoto, T.; Ozasa, R.; Gokcekaya, O.; Nakano, T. 3D Puzzle in Cube Pattern for Anisotropic/Isotropic Mechanical Control of Structure Fabricated by Metal Additive Manufacturing. Crystals 2021, 11, 959. https://doi.org/10.3390/cryst11080959
Ikeo N, Fukuda H, Matsugaki A, Inoue T, Serizawa A, Matsuzaka T, Ishimoto T, Ozasa R, Gokcekaya O, Nakano T. 3D Puzzle in Cube Pattern for Anisotropic/Isotropic Mechanical Control of Structure Fabricated by Metal Additive Manufacturing. Crystals. 2021; 11(8):959. https://doi.org/10.3390/cryst11080959
Chicago/Turabian StyleIkeo, Naoko, Hidetsugu Fukuda, Aira Matsugaki, Toru Inoue, Ai Serizawa, Tadaaki Matsuzaka, Takuya Ishimoto, Ryosuke Ozasa, Ozkan Gokcekaya, and Takayoshi Nakano. 2021. "3D Puzzle in Cube Pattern for Anisotropic/Isotropic Mechanical Control of Structure Fabricated by Metal Additive Manufacturing" Crystals 11, no. 8: 959. https://doi.org/10.3390/cryst11080959
APA StyleIkeo, N., Fukuda, H., Matsugaki, A., Inoue, T., Serizawa, A., Matsuzaka, T., Ishimoto, T., Ozasa, R., Gokcekaya, O., & Nakano, T. (2021). 3D Puzzle in Cube Pattern for Anisotropic/Isotropic Mechanical Control of Structure Fabricated by Metal Additive Manufacturing. Crystals, 11(8), 959. https://doi.org/10.3390/cryst11080959