Computational Study on the Interaction and Moving of ssDNA through Nanosheets

Abstract

The adsorption characteristics and moving through nanopores of a single-stranded deoxyribonucleic acid (ssDNA) molecule on monolayers, such ashexagonal boron nitride and graphene nanosheets, were studied using the continuous approach with the 6–12 Lennard–Jones potential function. The ssDNA molecule is assumed to be at a distance l above the sheet, and the relation between the minimum energy location and the perpendicular distance of the ssDNA molecule from the nanosheet surface is found. In addition, by assuming that there is a hole in the surface of the nanosheet as a pore, the interaction energies for the ssDNA molecule moving through the pore in the surface of the nanosheet (used to calculate the radius p of the hole) are obtained, which provides the minimum energies. Furthermore, a comparative study with graphene was performed in order to compare with hexagonal boron nitride nanosheets. Our results indicate that the binding energies of the ssDNA onto graphene and hexagonal boron nitride nanosheets are approximately 15.488 and 17.582 (kcal/mol), corresponding to perpendicular distances of $l=20.271$ and $l=20.231$ Å, respectively. In addition, we observe that the ssDNA molecule passes through graphene and hexagonal boron nitride nanopores when the gap radius $p>7.5$ Å. Our results provide critical insights to understand and develop the interactions and translocation of DNA molecules with and through nanosheets.

1. Introduction

Due to their geometric and mechanical properties and small size, nanomaterials have been utilised in multiple fields, including commercial, biomedical, clean energy, gas storage, genetics, and drug delivery [1,2,3,4,5]. Graphene (GRA) is a two-dimensional nanosheet consisting of a single layer of carbon atoms, which has been demonstrated to have outstanding electronic and mechanical properties [6,7,8]. Hexagonal Boron nitride (h-BN) sheet is an atomic layer of two-dimensional material similar to graphene, as shown in Figure 1a, constructed from equal numbers of nitrogen (N) and boron (B) atoms [9,10].

BN sheets have several excellent qualities, such as tunable surface affinities, adjustable band gaps, high water solubility, and outstanding thermodynamic, mechanical, and electronic properties [10,11,12,13]. These properties have shown promise for many potential applications in several areas; for example, in the environmental, electronics, and biomedical fields [10]. DNA nanosheets have essential characteristics, making them promising for several research domains and applications, including bioelectronics, photonics, biomedical fields, and bioassays [14,15].

Moreover, nanopores are very tiny gaps on the surface of the sheets, which may be used for transport through the membranes. Nanopores, such as h-BN and GRA nanopores, can provide substantial chances to produce future generations of nanopore devices for different applications, particularly due to their potential for DNA sequencing scanning, microscopy, and applications in the nanomedical field [6,16,17,18]. A number of simulations and experiments have been carried out to examine the behaviour of the interaction and translocation of DNA with h-BN and GRA nanosheets, as well as through nanopores.

Lin et al. examined the adsorption of DNA nucleobases (guanine, G; adenine, A; thymine, T; and cytosine, C) on a hexagonal boron nitride nanosheet using the Vienna ab initio Simulation Package (VASP) [14]. They showed that the adsorption energies is in the region from 0.5–0.69 eV, in the order of G > A > T > C, which might be due to the different of atoms of nucleobases. Lee et al. employed density-functional theory (DFT) calculations to determine the adsorption energy of the DNA nucleobases on the BN sheet [19]. Their results established the ordering of the binding energy as G > A > T > C, depending on the base molecules.

Zhang and Wang used molecular dynamics (MD) simulations to explore the binding energy between the DNA nucleobases (G, C, A, and T) and a BN sheet. They also investigated the movement of a ssDNA through BN nanopores [20]. They found that the G nucleotide had stronger binding than other nucleosides and showed that a pore on h-BN sheet is better suited to DNA sequencing. Tyagi et al. investigated the translocation of ssDNA sequences through h-BN and GRA using MD simulations. They found that the h-BN and GRA nanosheets showed different interactions with ssDNA bases, and their results indicated that the ssDNA passed through h-BN and GRA nanopores with a diameter >15 Å [6].

Mathematical modelling plays a more important role, offering a description of the experimental results, and can be used to forecast novel phenomena and findings. Mathematical modelling may also be used to accurately predict the ideal configurations and the main physical parameters. Mathematical modelling has been widely used to obtain the interaction energies between various nanostructured materials [15,21,22,23,24]. The usual method of modelling in this area is to apply the Lennard–Jones function with the continuous approximation, which assumes that the atoms are uniformly distributed over the volume or surface of the molecules [21].

We note that the use of the Lennard–Jones (L-J) potential is justified in this case, as the dominant forces present within the interaction energies are van der Waals forces, where this method allows for determination of the potential energy between the interacting molecules as integrals over the volume or surface. These integrals can be obtained, in terms of special functions, such as the hypergeometric function $F\left(b^{*},c^{*};d^{*};{\delta }^{*}\right)$, which is useful for quick calculation of the numerical results [21]. In this study, we examine the interactions between ssDNA molecules with h-BN and GRA nanosheets, and then investigate the translocation behaviour for ssDNA molecules through h-BN and GRA nanopores by employing the continuous approach with the 6–12 L-J potential.

2. Modelling Approach

We assume that the ssDNA has an ideal helical geometry, which might be a first step towards modelling more realistic situations, as shown in Figure 1b. This geometry is taken from the predominant B-form double-stranded DNA, which is found in cells [25]. Moreover, the ssDNA is assumed to contain 11 bases, for a total average of 415.25 atoms in one turn of the helix. The total interaction energies might be evaluated as a double integral over the two surfaces of the two molecules, given as:

$$\begin{array}{ccc}\hfill E& =& {\eta }_n{\eta }_m{\int }_{T_1}{\int }_{T_2}P\left({\mu }_{ij}\right)d{T}_{1}d{T}_2,\hfill \end{array}$$

(1)

where ${\eta }_n$ and ${\eta }_m$ are the mean surface densities of the two molecules, $d{T}_1$ and $d{T}_2$ represent the surface elements on the molecules, and $P\left({\mu }_{ij}\right)$ is the L-J potential function for i and j with the distance ${\mu }_{ij}$, obtained by

$$\begin{array}{c}\hfill P\left(\rho \right)=-\frac{A}{{\mu }^6}+\frac{B}{{\mu }^{12}},\end{array}$$

where A and B represent the constants of L-J potential (attractive and repulsive), respectively. We note that the average atoms of a unit cell of an ssDNA is 415.25 atoms, comprising five elements (nitrogen, N; phosphorus, P; oxygen, O; carbon, C; and hydrogen, H). As a result, we calculate the average A and B constants between the DNA molecule interacting with h-BN and GRA nanosheets, which are made up entirely of an equal proportion of nitrogen (N) and boron (B) atoms for the h-BN sheet and carbon atoms for the GRA sheet.

They can be evaluated using the empirical mixing laws ${\sigma }_{12}=({\sigma }_1+{\sigma }_2)/2$ and ${\epsilon }_{12}={\left({\epsilon }_1{\epsilon }_2\right)}^{1/2}$ [26,27], where $\sigma$ is the van der Waals diameter and $\epsilon$ is the well depth, which were taken, for each atom, from Rappi et al. [28]. Due to the large number of atoms in the DNA and nanosheets in this system, we modelled the interactions utilising the continuous approximation, assuming the energy contribution arising from the surfaces; hence, a surface integral was obtained.

Herein, mathematical modelling is utilised to determine the interactions between the nanosheets (h-BN and GRA) and ssDNA molecule, by adopting the continuous approximation with the 6–12 L-J potential function. We use the system $(x,y,z)$, which is the cartesian coordinate, to model the interactions between the two molecules, the ssDNA, and the nanosheets.

Thus, a typical point on the surface of nanosheet might have the coordinates $(x,y,0)$. In addition, the coordinates of a typical point on the surface of the ssDNA molecule can be given as $\left(rtcos\theta ,rtsin\theta ,c\theta /2\pi \right)$, where c and r are the unit cell length and the radius of the ssDNA helix, respectively, and the two parametric variables are in the range $0<t<1$ and $-\pi <\theta <\pi$. As can be seen from Figure 2, the van der Waals interaction force between the ssDNA molecule and the nanosheet is obtained by differentiating the interaction energies E with respect to the axial direction z. The following sub-sections present the binding energies and the translocation of the ssDNA molecule onto and through the h-BN and GRA nanosheets.

3. ssDNA Adsorption on GRA and h-BN Sheets and Translocation through Nanopores

3.1. ssDNA Interacting with Nanosheet

In this section, the interactions regarding the adsorption of the ssDNA molecule onto the nanosheets are determined. Using the coordinate system of the ssDNA molecule and the nanosheet, as presented above, the binding energy can be given by

$$\begin{array}{ccc}\hfill E& =& \frac{rc{\eta }_d{\eta }_{sh}}{2\pi }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\pi }^{\pi }{\int }_0^1\left(\frac{-A}{{\mu }^6}+\frac{B}{{\mu }^{12}}\right){\left(1+\frac{4r^2{\pi }^2}{c^2}{t}^2\right)}^{1/2}dtd\theta dxdy,\hfill \end{array}$$

(2)

where ${\mu }^2=x^2+y^2+{(c\theta /2\pi +l)}^2$, ${\eta }_d$ is the average atomic surface density on the ssDNA, ${\eta }_{sh}$$(sh\in \{G,BN\left\}\right)$ is the atomic surface density of the sheets, and l is the distance from the center of the ssDNA molecule to the surface of the nanosheet, as shown in Figure 2a. After evaluating Equation (2), the total interaction energies can be given by

$$\begin{array}{ccc}\hfill E& =& r\pi {\eta }_d{\eta }_{sh}F\left(\frac{-1}{2},\frac{1}{2};\frac{3}{2};\frac{-4r^2{\pi }^2}{c^2}\right)\left(\frac{-A}{2}{W}_2+\frac{B}{5}{W}_5\right),\hfill \end{array}$$

(3)

where $F\left(a^{*},c^{*};d^{*};{\delta }^{*}\right)$ is the standard hypergeometric function, and $W_n$ is given by

$$\begin{array}{ccc}\hfill W_n& =& {(1-2n)}^{-1}\left[{(c/2+l)}^{-2n+1}-{(l-(c/2))}^{-2n+1}\right].\hfill \end{array}$$

3.2. Translocation of ssDNA through Sheet Pores

The minimum interaction energies are calculated here to determine the optimal pore radius p for the ssDNA moving through the pores. Again, the ssDNA molecule is assumed to be placed above the pore at the perpendicular distance l, as shown in Figure 2b. As before, a typical point on the ssDNA surface might have the coordinates $(\omega ,0,l+c\theta /2\pi )$, where $\omega$ = $rt$. Thus, we might have a distance $\mu$ between the two surfaces of the sheet plane and the ssDNA molecule, as follows:

$$\begin{array}{ccc}\hfill {\mu }^2& =& {(a-\omega )}^2+4a\omega {sin}^2(\theta /2)+{(l+c\theta /2\pi )}^2.\hfill \end{array}$$

Thus, the total interaction energies of the ssDNA with the sheet nanopore are given by

$$\begin{array}{ccc}\hfill E& =& \frac{rc{\eta }_d{\eta }_{sh}}{2\pi }\left(-A{Y}_3+B{Y}_6\right),\hfill \end{array}$$

(4)

where $Y_n$ can be given as

$$\begin{array}{ccc}\hfill Y_n& =& \pi \sum _{k=0}^{n-1}\frac{{(1/2)}_k{(1-n)}_k{\left(4r\right)}^k}{{(k!)}^2}\hfill \\ & \times & {\int }_{-\pi }^{\pi }{\int }_0^1{\int }_p^{\infty }\frac{a^{k+1}{t}^k}{{\left[{(l+c\theta /2\pi )}^2+{(rt-a)}^2\right]}^{n-1/2}{\left[{(a+rt)}^2+{(l+c\theta /2\pi )}^2\right]}^{k+1/2}}\hfill \\ & \times & {\left(1+\frac{4r^2{\pi }^2}{c^2}{t}^2\right)}^{1/2}dadtd\theta .\hfill \end{array}$$

This equation is extremely complex and, thus, a standard integration package can be utilised to evaluate the integrals, such as MAPLE.

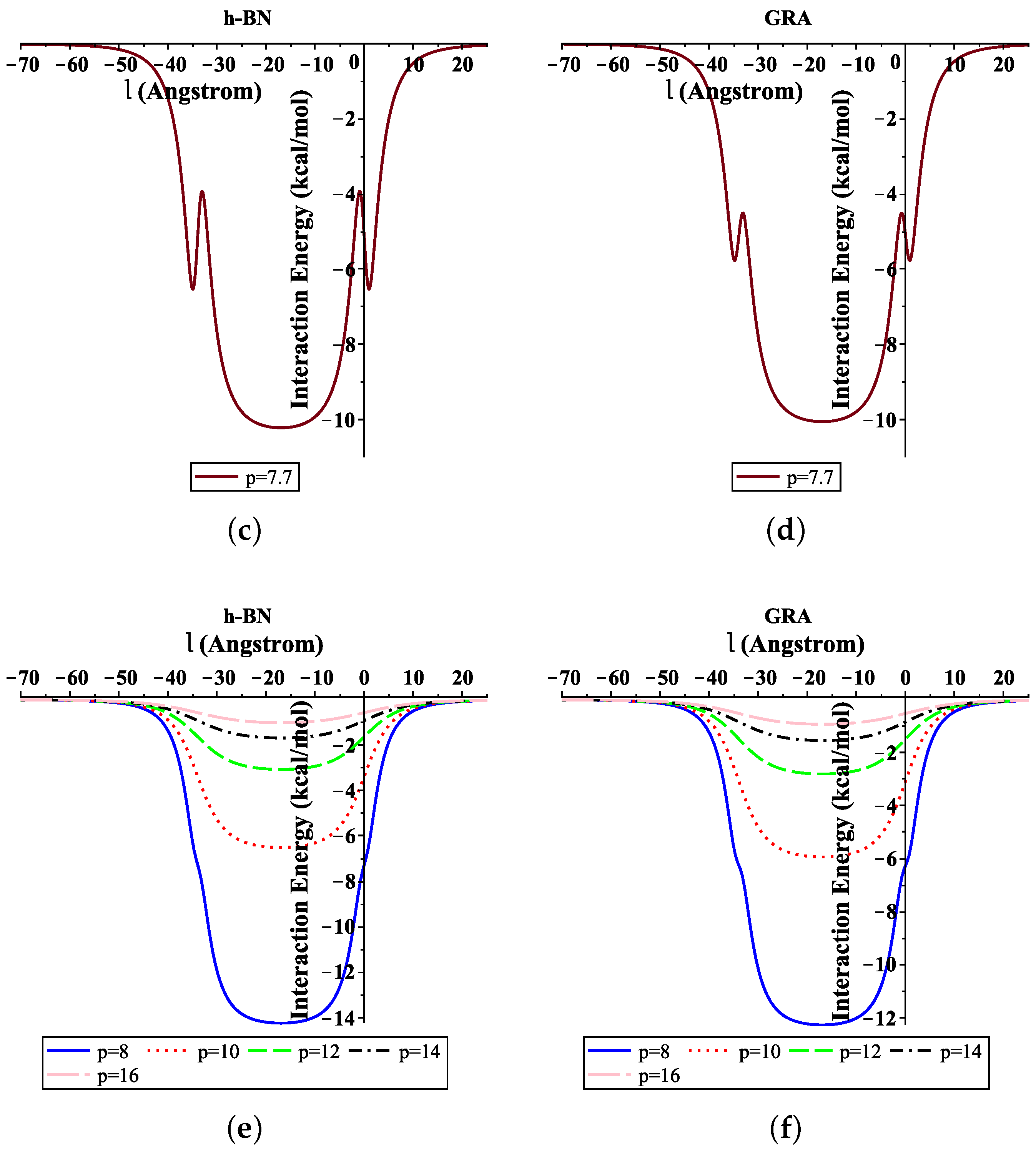
4. Numerical Results and Discussion

To determine the numerical results of the interaction energies between the ssDNA molecule with the nanosheets and the nanopores, we used the algebraic package MAPLE and the constants values given in

Table 1. Values of the constants utilised in this study.

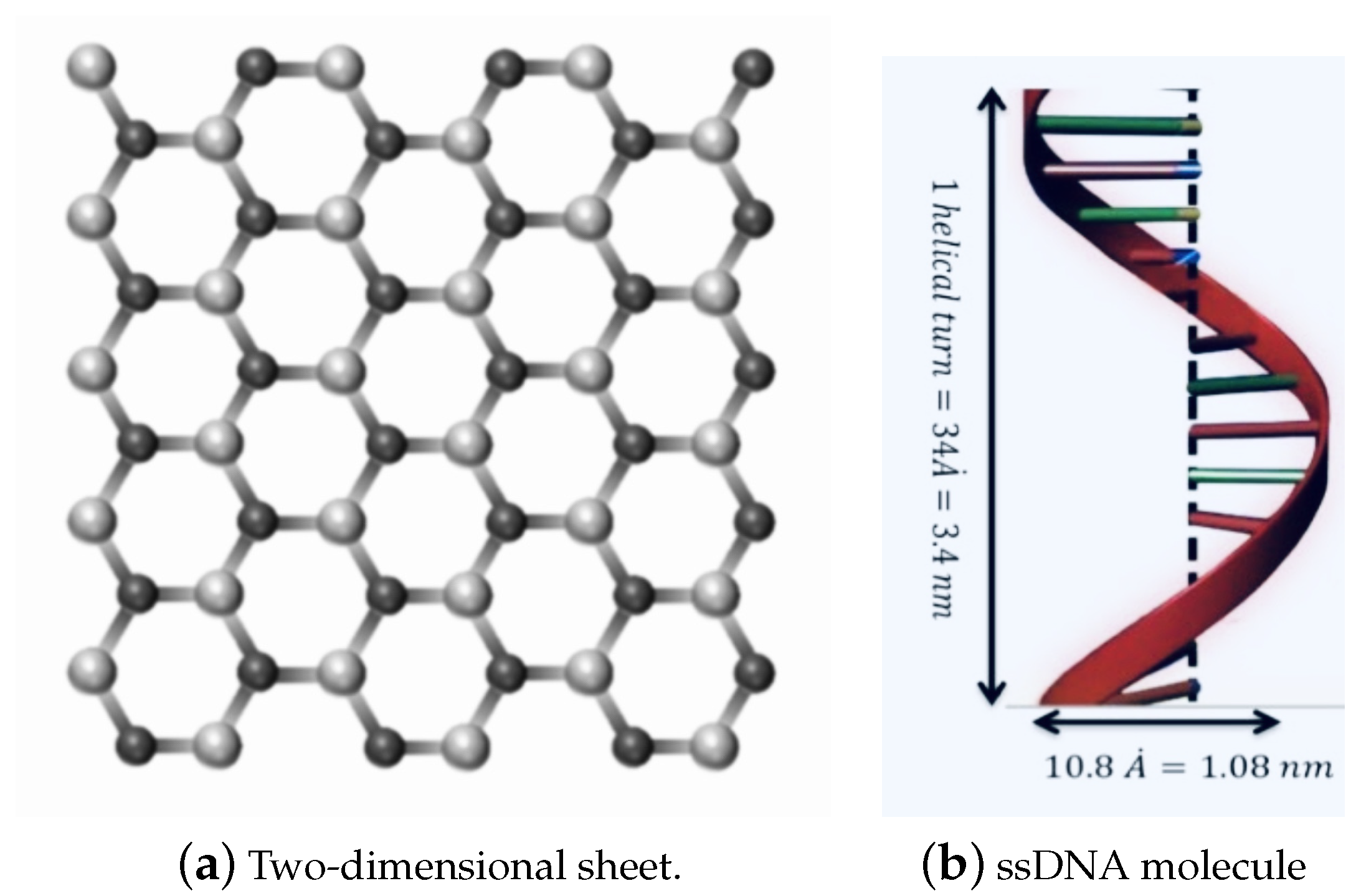
Constant	Value
Atomic density GRA ${\eta }_G$	0.3818 Å${}^{-2}$
Atomic density BN ${\eta }_{BN}$	0.3661 Å${}^{-2}$
Atomic density ssDNA ($\varphi =\pi$) ${\eta }_d$	0.82 Å${}^{-2}$
Radius ssDNA r	5.4 Å
Length of ssDNA c	34 Å

and

Table 2. Lennard–Jones constants (A and B).

	A (Å${}^6$ kcal/mol)	B (Å${}^{12}$ kcal/mol)
DNA–GRA	791.8154556	2,424,599.652
DNA–BN	903.6818110	2,571,946.879

to evaluate Equations (3) and (4), respectively. We show graphically, in Figure 3, the variation of the binding energies with the equilibrium distance for a single-stranded DNA molecule interacting with GRA and h-BN sheets, where the helix axis is perpendicular to the surface of the nanosheet. Our results demonstrate that the locations of the ssDNA molecule where the minimum energy occurs were equal to 15.489 and 17.582 (kcal/mol) corresponding to $l\approx 20.271$ and 20.231 Å, as measured from the centre of the helix for GRA and h-BN, respectively.

In addition, the distances from the edge of the ssDNA molecule to the GRA and h-BN surfaces were approximately 3.271 and 3.231 Å, respectively. By comparing the results of the interaction energies between the ssDNA molecule and the h-BN and GRA nanosheets, we found that the interaction energy with h-BN was stronger than those between ssDNA and GRA, as h-BN showed the lowest minimum energy.

Our results for the binding energies of the ssDNA molecule with the h-BN sheet are in very good agreement with those given in the literature [14]; furthermore, the results that we found here are similar to that of GRA in an earlier study [15]. From our previous work [15], we found that the most stable configuration of the ssDNA molecule from the surface of GRA nanosheet occurred when the helix axis was almost parallel to the surface of GRA. This case can be studied for ssDNA with different types of nanosheets in future research.

Moreover, Figure 4 shows the total interaction energies of the ssDNA interacting with the h-BN and GRA nanopores with respect to the perpendicular distance l for various values of the gap radius p. We indicate that the ssDNA might move through the h-BN and GRA nanopores when the value of the hole radius is bigger than $7.5$ Å, where the difference between the radius of the ssDNA and the hole radius is $7.5-5.4=2.1$ Å. Moreover, we observed that the optimal radius of the gap to allow the single-helix DNA to penetrat into GRA and h-BN nanopores was ≈8 Å when the minimum energy occurred, as shown in Figure 4e,f. Our results are in excellent agreement with those given in [6,20].

In addition, from Figure 4a,b, we show that the ssDNA became closer to the nanosheet surface when the hole radius was equal to 7 (where the difference between the radius of the ssDNA and the hole radius was $7-5.4=1.6$ Å); however, the ssDNA molecule confronts a large energy barrier and, consequently, will not penetrate the sheet. From Figure 4e,f, we can also see that, when the radius of the hole increased, the value of the interaction between the ssDNA molecule with h-BN and GRA tended to zero.

5. Summary

In this study, the interaction energies of a single-stranded DNA molecule with h-BN and GRA nanosheets and nanopores were determined through use of applied mathematical modelling. By minimising the interaction energies, we obtained the equilibrium distance, l, of the ssDNA sheets, where the axis of the helix of the ssDNA is perpendicular to the surface of the nanosheet, and we found that the minimal energies occurred for the distance $l=20.271$ Å of GRA and $l=20.231$ Å of h-BN.

In addition, our results showed that the single-stranded DNA molecule might be passed through nanopores with a radius p larger than 7.5 Å. The fundamental results obtained through the analysis of energetics, geometries, and electronic structures of the above-mentioned systems may provide promising guidance for potential candidates to sense the nucleobases in DNA sequencing and other biomolecules.